ГЕРОТОРНЫЙ МЕХАНИЗМ Российский патент 2005 года по МПК E21B4/02 F04C2/10 F04C18/10 F16H1/34 

Изобретение относится к зубчатым героторным механизмам (ГМ) внутреннего зацепления с разницей в числах зубьев ротора и статора, равной единице. Ось ротора ГМ, совершающего планетарное движение, смещена относительно оси статора на расстояние эксцентриситета зацепления.

ГМ могут быть использованы в различных отраслях горного дела в качестве рабочих органов насосов, гидродвигателей, компрессоров, двигателей внутреннего сгорания и редукторов с прямыми и винтовыми зубьями.

Известен традиционный ГМ с внутренним внецентроидным циклоидальным зацеплением, торцовые профили которого образуются в общем случае как огибающие эквидистанты укороченной циклоидальной рейки при ее обкатке по направляющей окружности [Героторный механизм. А.с.СССР 803572 от 08.10.1979] [1].

Известен классический ГМ предельного типа с однозубым ротором круглого сечения центроидного циклоидального зацепления, торцовый профиль статора которого образуется как эквидистанта траектории точки окружности при качении последней по направляющей окружности удвоенного радиуса [Винтовые насосы, М., Машиностроение, 1983].

Недостатком традиционного ГМ является сложность его исходного профиля, форма которого при заданном контурном диаметре в общем случае определяется сочетанием пяти безразмерных геометрических параметров (кинематического отношения, коэффициентов типа зацепления (эпи или гипо), внецентроидности, формы зуба и смещения рейки), что усложняет технологию изготовления (необходимость выполнения процедур смещения и эквидистантирования контура рейки, приобретения специализированных станков и создания специальных фрез) и выбор оптимальной формы профилей, описываемых сложными математическими выражениями (сочетания значений четырех безразмерных параметров).

Недостатком классического ГМ, форма профилей которого зависит только от одного безразмерного параметра (коэффициента формы зуба), является ограниченность его области применения из-за повышенного перепада давления между рабочими камерами ввиду меньшего числа контактных линий, отделяющих вход и выход гидромашины, что требует при создании высоконапорного насоса значительного увеличения осевого габарита рабочих органов и, как следствие, дополнительных технологических и материальных затрат.

Из известных ГМ наиболее близким к предлагаемому является частный случай традиционного циклоидального ГМ с кинематическим отношением 2:3 (с овальным двузубым ротором), используемый в качестве рабочих органов одновинтовых насосов вместо классических рабочих пар с кинематическим отношением 1:2 с целью повышения давления [2]. Недостатком таких ГМ также являются трудности технологии их изготовления и выбора оптимальной формы профилей.

Задачей изобретения является повышение эффективности проектирования и упрощение технологии изготовления рабочих органов ГМ.

Поставленная задача решается тем, что в качестве исходного контура при образовании ГМ используется эллипс, а профиль рабочего органа ГМ образуется как внешняя огибающая семейства эллипсов при обкатке начальных окружностей (центроид) определенного радиуса в зависимости от требуемого кинематического отношения.

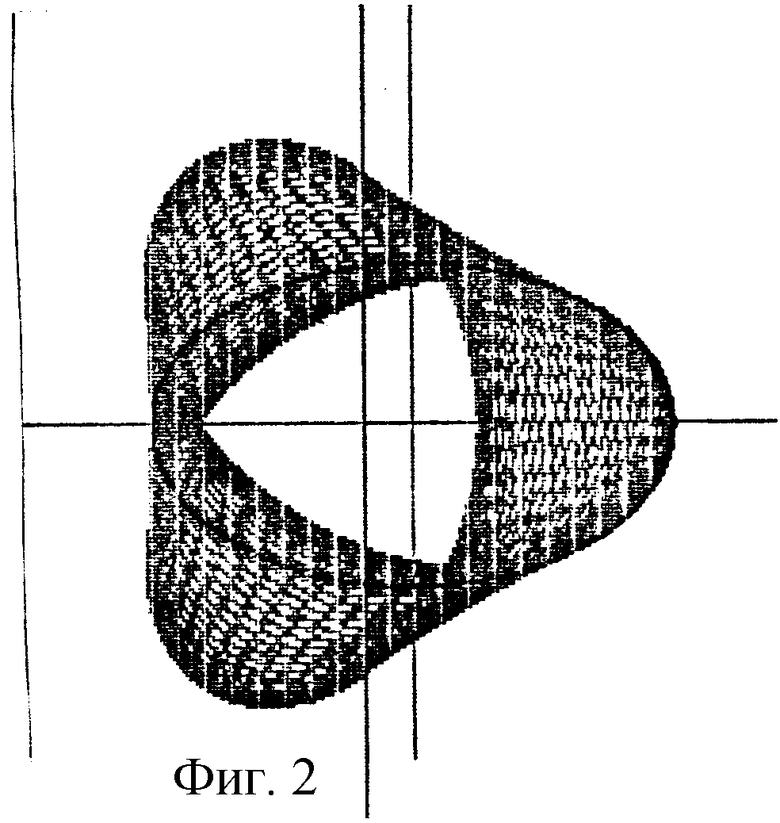
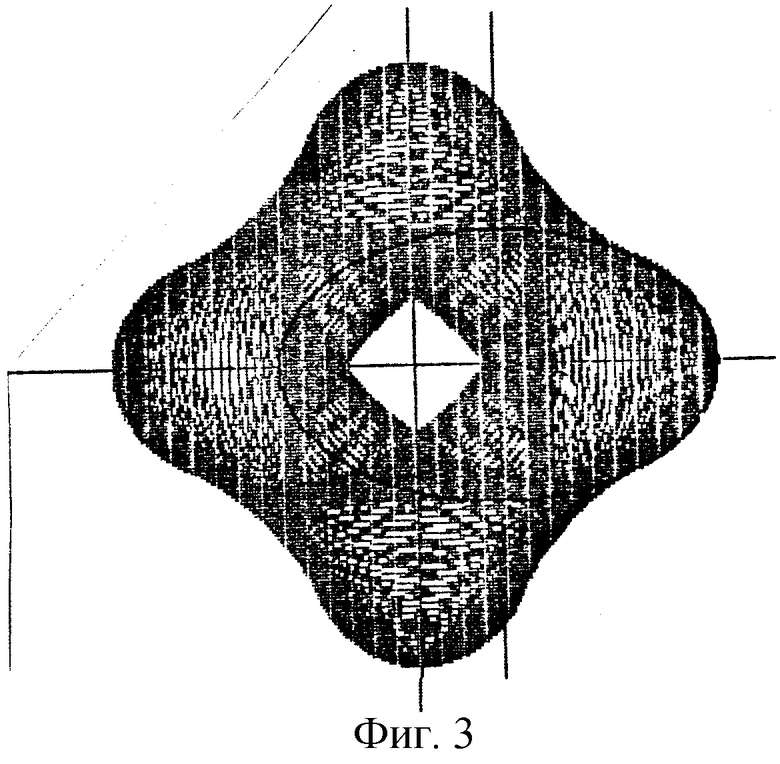
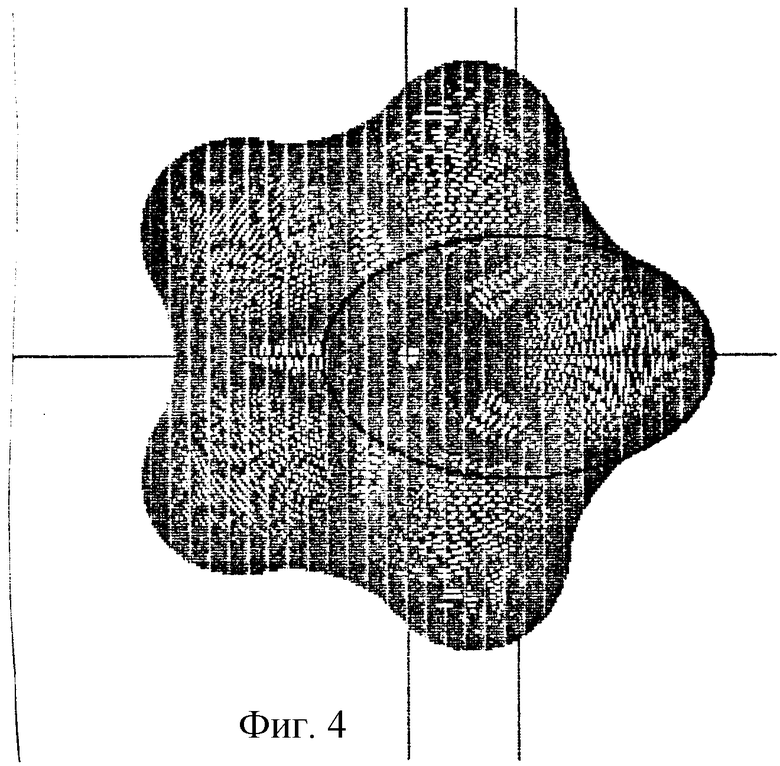
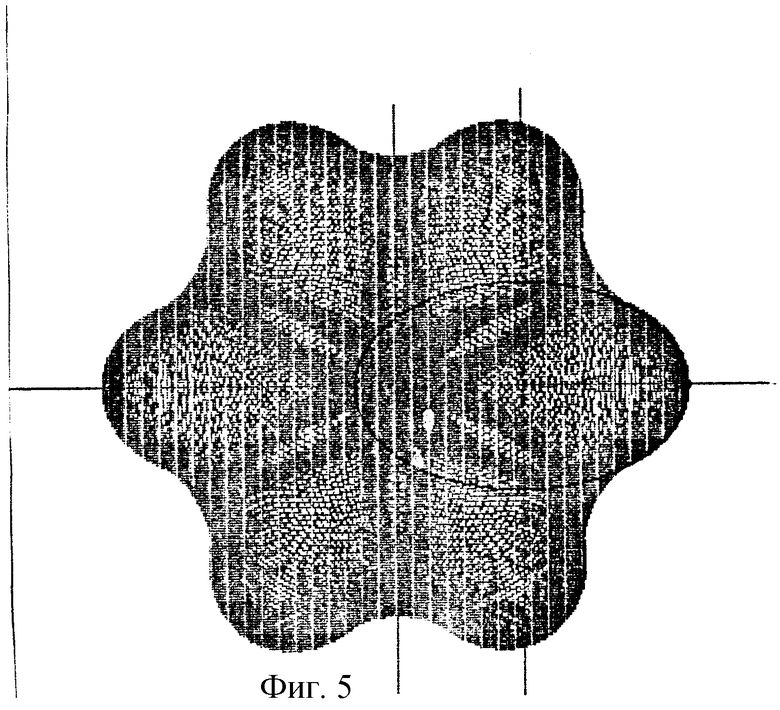
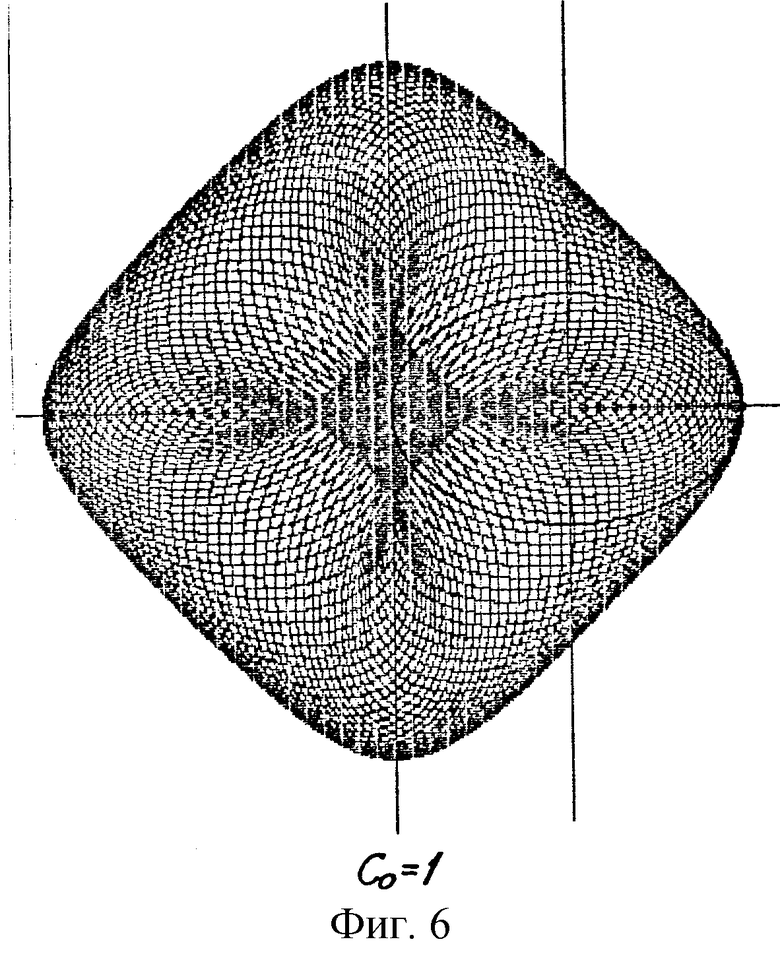
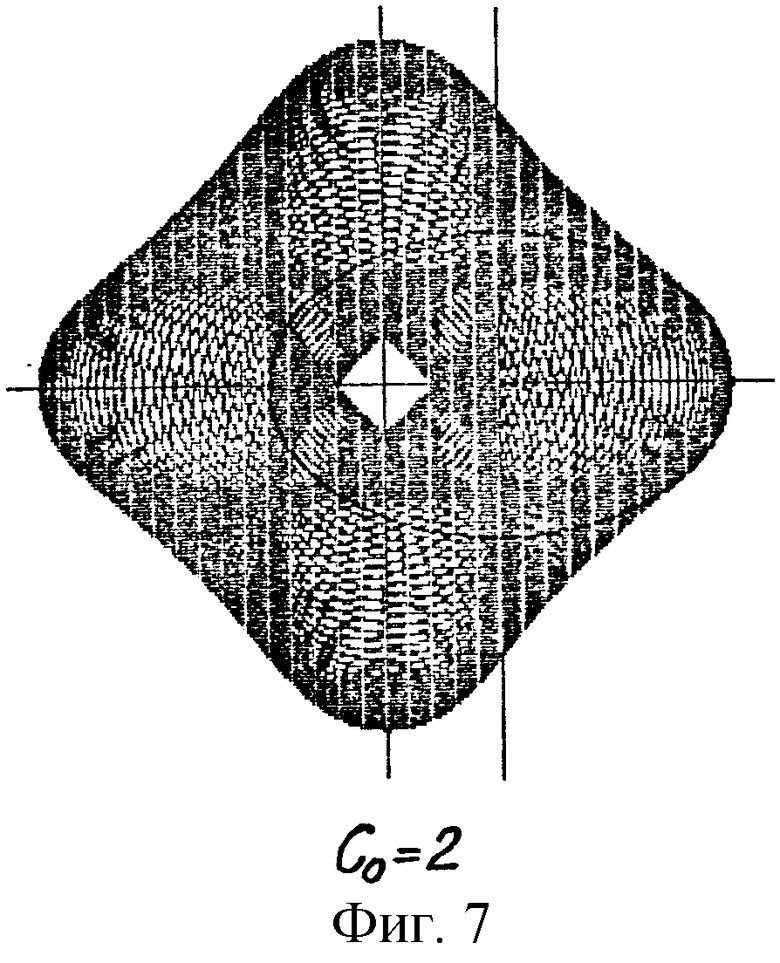
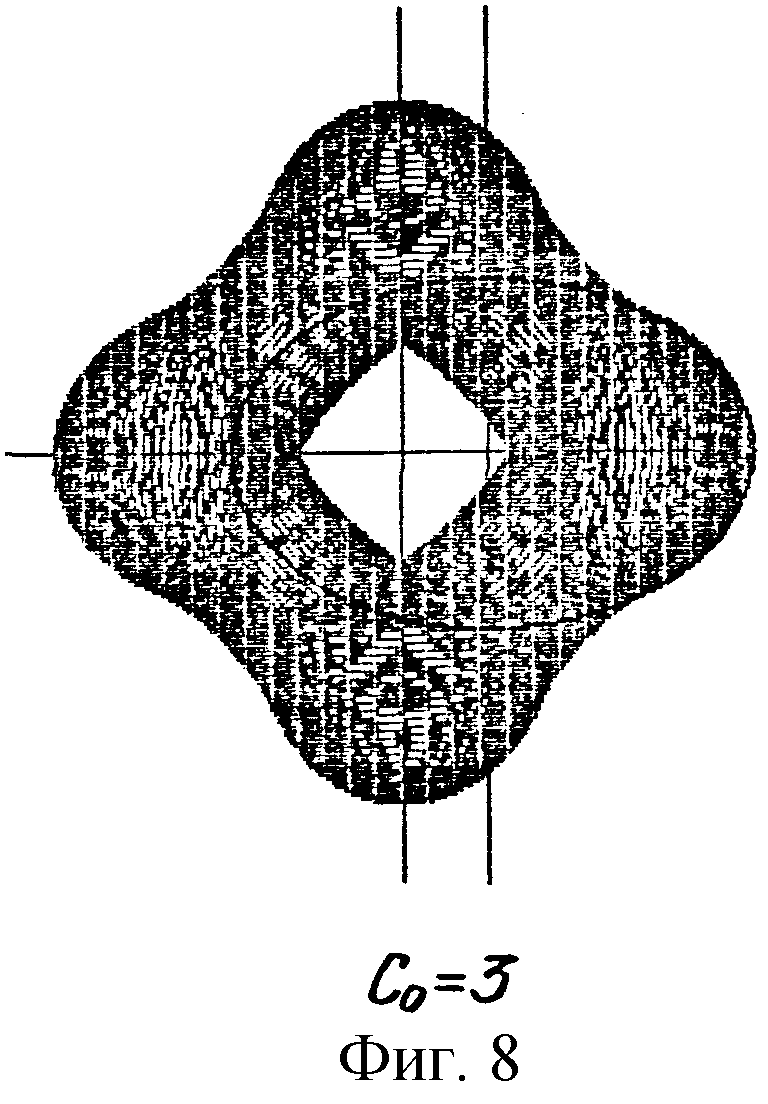
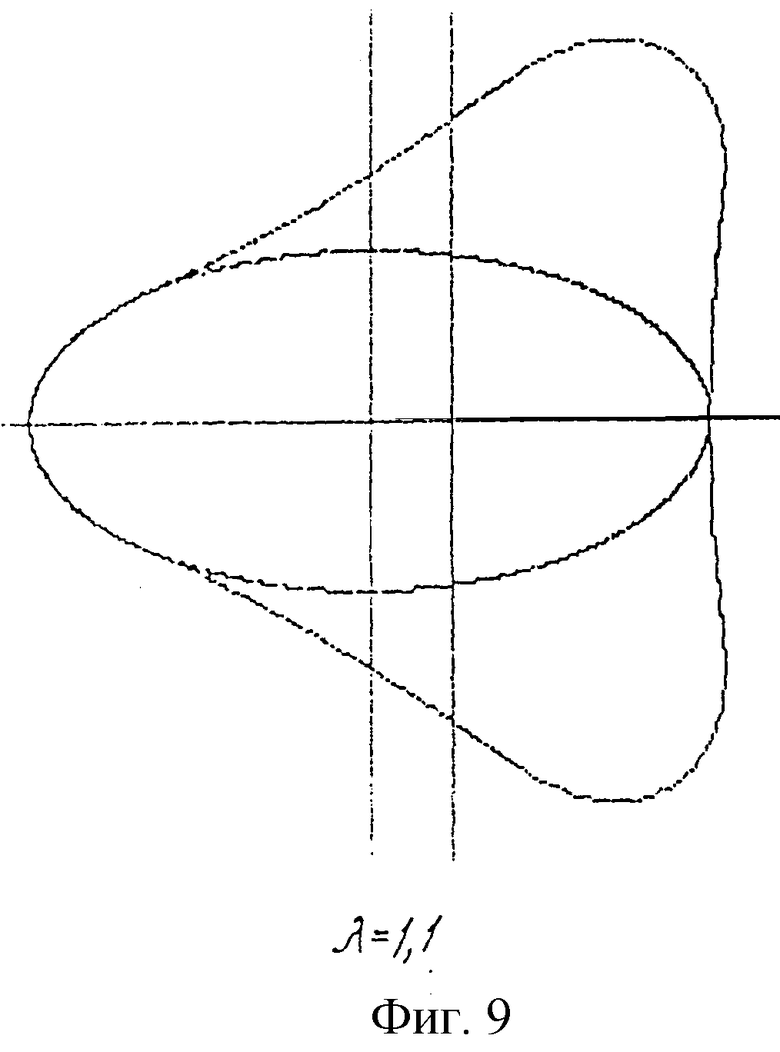
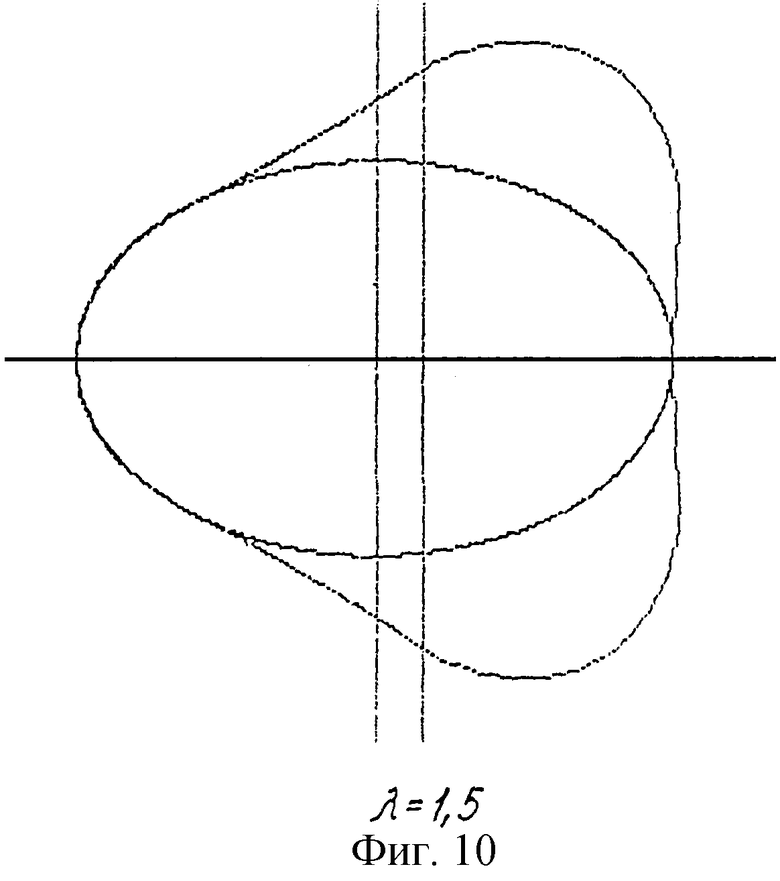
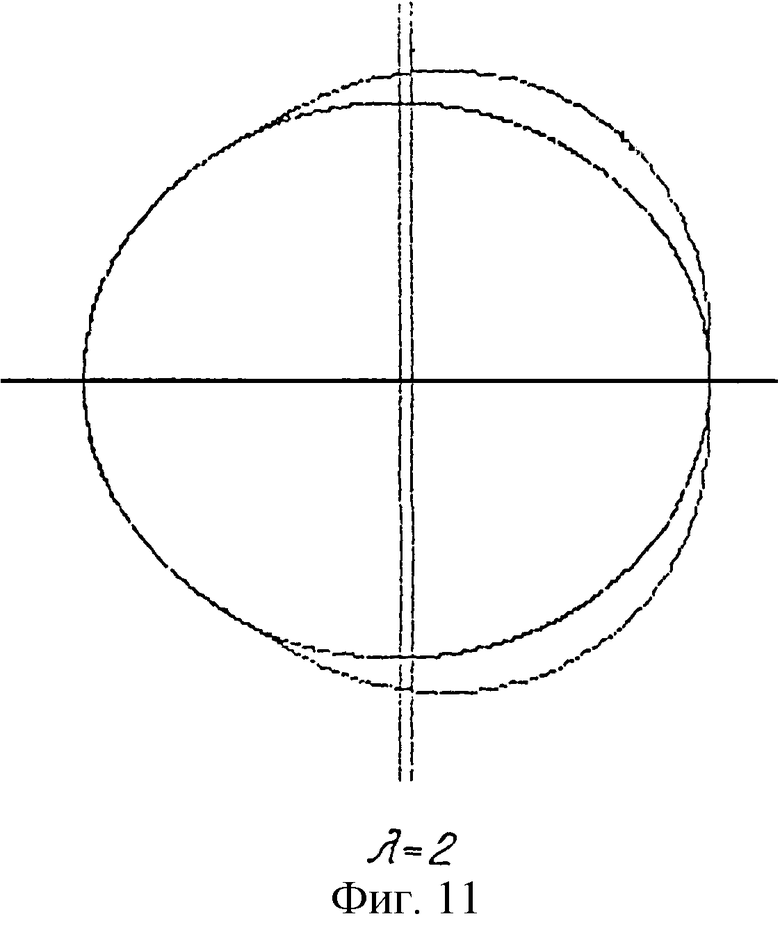
В дальнейшем изобретение поясняется описанием и сопровождается чертежами, где на фиг.1 показано исходное положение начальных окружностей и вспомогательного контура при образовании эллипсоидального профиля; на фиг.2-5 представлены схемы образования профилей эллипсоидального ГМ с различным числом зубьев (соответственно z=3; 4; 5; 6) по методу обкатки эллипса; на фиг.6-8 - профили четырехзубого рабочего органа ГМ при различных значениях коэффициента внецентроидности (соответственно Со=1; 2; 3) и одинаковом коэффициенте формы эллипса (λ=1,5); на фиг.9-11 - сопряженные профили ГМ с эллипсоидальным зацеплением с кинематическим отношением 2:3 при различном коэффициенте формы эллипса (соответственно λ=1,1; 1,5; 2).

Эллипсоидальный ГМ представляет собой зубчатую пару внутреннего зацепления, состоящую из сопряженных z₁-зубого внешнего колеса (статора) и z₂-зубого внутреннего колеса (ротора), разница в числах зубьев которых равна единице (z₁=z₂+1), профили которых образованы от правильного эллипса.

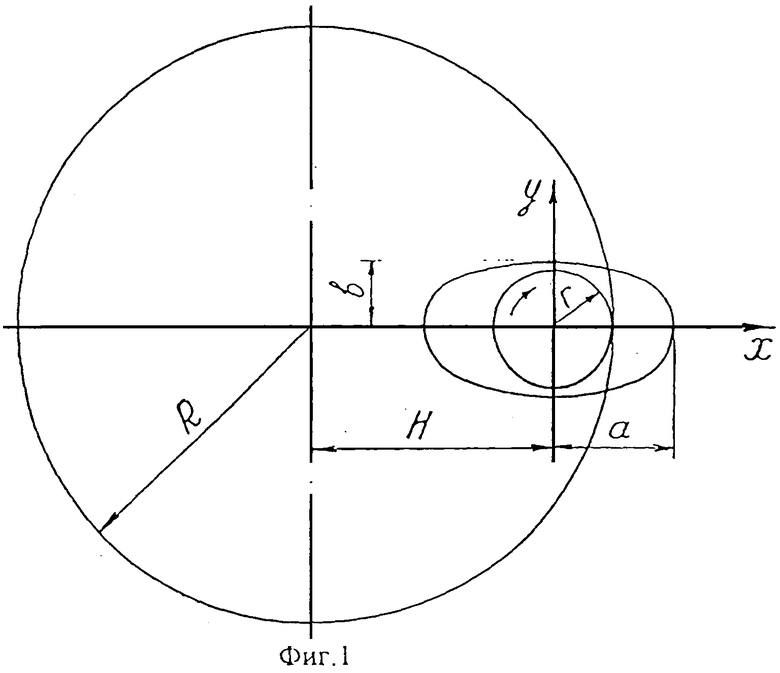
Эллипсоидальный профиль зубчатых колес образуется по методу обкатки начальных окружностей (фиг.1), одна из которых (единичного радиуса r), связанная с исходным вспомогательным контуром, расположена внутри направляющей (большего радиуса R=kr; где k - число, изменяющееся от 1,5 с шагом 0,5: k=1,5; 2; 2,5; 3; 3,5; 4...) и обкатывается без скольжения, совершая планетарное движение.

Профиль зубчатого колеса представляет собой внешнюю огибающую вспомогательного контура.

При профилировании эллипсоидальных колес в качестве исходного вспомогательного контура принимается правильный эллипс, большая и малая полуоси которого соответственно равны а и b, причем оси эллипса совпадают с осями катящейся окружности.

Форма эллипсоидального профиля ГМ при заданном его контурном диаметре (максимальном наружном диаметре) полностью определяется тремя безразмерными геометрическими параметрами:

- числом зубьев колеса, равным удвоенному отношению радиусов начальных окружностей

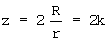
- коэффициентом формы эллипса, равным отношению длин его полуосей:

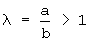
- коэффициентом внецентроидности исходного контура, равным отношению длины большой оси эллипса к радиусу катящейся окружности единичного радиуса:

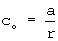
Примеры профилей эллипсоидальных зубчатых колес с различным числом зубьев, полученных методом обкатки, представлены на фиг 2-5. Варьируя значениями коэффициентов λ и c_о, можно в широких пределах изменять форму профиля. Влияние коэффициента внецентроидности на форму четырехзубого профиля показано на фиг.6-8.

Параметрические уравнения исходного вспомогательного контура (правильного эллипса) относительно подвижных осей имеют элементарный вид:

,

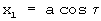где τ - угловой параметр, изменяющийся в интервале от 0 до 2π.

Семейство профилей эллипса при его обкатке описывается следующими координатами относительно центральных осей, связанных с направляющей окружностью:

X=x₁cosϕ-y₁sinϕ+H соsϕ_п,

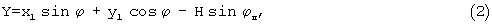
где Н - межцентровое расстояние, H=R-r=(k-1)r;

ϕ_п - угол поворота оси катящейся окружности в переносном движении,

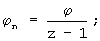
ϕ - угол поворота катящейся окружности в абсолютном движении.

Параметрические уравнения эллипсоидального профиля (огибающей семейства эллипсов) получаются при подстановке в (2) уравнения связи между ϕ и τ, устанавливаемого при помощи основной теоремы зацепления.

Диаметры эллипсоидального колеса по вершинам выступов и впадин его зубьев соответственно составляют

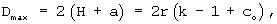
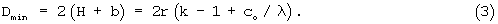
Высота зубьев

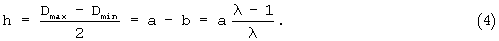
На основе колес с эллипсоидальным зацеплением можно создавать ГМ с различным кинематическим отношением.

В общем случае при выбранном z-зубом эллипсоидальном профиле, принимаемом в качестве исходного, сопряженный ему профиль образуется как внешняя (эпизацепление) или внутренняя (гипозацепление) огибающая исходного профиля при обкатке центроид колес, отношение радиусов которых выбирается в зависимости от кинематического отношения ГМ.

На практике в ГМ, зубья колес наружного элемента которых выполняются эластичными, целесообразно использовать упрощенный метод образования сопряженного профиля, апробированный при изготовлении рабочих органов винтовых машин с циклоидально-реечным зацеплением, когда сопряженный профиль выполняется аналогично исходному по методу обкатки от общего исходного вспомогательного контура.

В общем случае условие сопряженности профилей (условие зацепления вершин выступов и впадин) имеет следующий вид:

где здесь и далее индекс 1 относится к наружному элементу (статору), 2 - к внутреннему (ротору).

В идеальном циклоидальном зацеплении условие (5) соблюдается только для центроидных профилей (c_о=1), то есть может быть реализовано в механизмах 1:2.

В реечном зацеплении для выполнения условия (5) принимают определенное сочетание между смещениями контуров рейки при образовании профилей статора и ротора.

В эллипсоидальном зацеплении с числами зубьев колес, отличающихся на единицу (k₂=k₁-1), условие сопряженности (5) в отличие от циклоидального механизма может быть реализовано для ГМ с любым кинематическим отношением, если обеспечить соотношение между коэффициентами формы эллипса и внецентроидности, выражаемое формулой:

Таким образом, для образования взаимоогибаемых профилей ГМ от общего контура эллипса коэффициенты λ и c_о являются зависимыми параметрами и при выбранной форме эллипса (заданных значениях а и λ) радиус катящейся окружности должен составлять

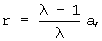
а радиусы направляющих окружностей статора и ротора в зависимости от кинематического отношения механизма выбирают следующим образом:

R₁=kr; R₂=(k-0,5)r.

При этом числа зубьев колес статора и ротора соответственно равны

z₁=2k; z₂=2k-1,

а контурный диаметр (максимальный диаметр статора) согласно (3) и (6) выражается зависимостью

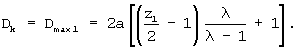
Эксцентриситет зацепления ГМ при заданном контуре эллипса не зависит от кинематического отношения:

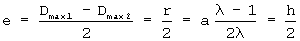
В частном случае трехзубого исходного контура (k=1,5; z₁=3) сопряженным профилем является непосредственно контур эллипса.

Наибольший практический интерес с точки зрения технологичности производства представляет эллипсоидальный ГМ с кинематическим отношением 2:3 (с кратностью действия механизма, равной 2), сечение ротора которого является правильным эллипсом, что позволяет использовать его при создании высоконапорных насосов взамен рабочих органов с кинематическим отношением 1:2.

Используемый в насосостроении подобный ГМ, выполненный на базе традиционного гипоциклоидального зацепления, имеет исходный профиль (в данном случае профиль наружного элемента), описываемый параметрическими уравнениями:

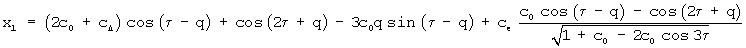
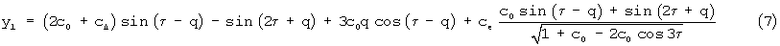
где c_о, cΔ, c_е - безразмерные коэффициенты внецентроидности, смещения и формы зуба;

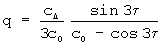
Как видно, параметрические уравнения традиционного исходного профиля (7) значительно сложнее уравнений эллипса (1), что обеспечивает преимущество при проектировании и изготовлении эллиптических рабочих органов, профилирование которых не предусматривает процедур смешения и эквидистантирования вспомогательного контура.

На фиг.9-11 представлены различные варианты исполнения профилей эллипсоидального механизма 2:3, образованных от общего вспомогательного контура и отличающихся коэффициентом формы эллипса.

Изобретение позволит упростить процесс проектирования и изготовления рабочих органов машин и механизмов, использующих в своей конструкции ГМ, что создаст предпосылки дальнейшего повышения эффективности применения роторных машин с плоским и пространственным зацеплением в различных отраслях техники.

Источники информации

1. Авторское свидетельство СССР №803572, 1979.

2. Балденко Д.Ф. и др. Винтовые забойные двигатели, Справочное пособие, Москва, Недра, 1999, с.20-22.

Изобретение относится к зубчатым героторным механизмам (ГМ) внутреннего зацепления с разницей в числах зубьев ротора и статора, равной единице. Ось ротора ГМ, совершающего планетарное движение, смещена относительно оси статора на расстояние эксцентриситета зацепления. ГМ могут быть использованы в различных отраслях горного дела и в общем машиностроении в качестве рабочих органов насосов, гидродвигателей, компрессоров, двигателей внутреннего сгорания и редукторов с прямыми и винтовыми зубьями. Новым является то, что в качестве исходного вспомогательного контура используют эллипс, при этом коэффициент пропорциональности k, определяющий радиус направляющей окружности, принимают равным половине необходимого числа зубьев z колеса (k = z/2), оптимальная форма его зубьев обеспечивается рациональным сочетанием коэффициента формы эллипса λ, равным отношению длин его полуосей и коэффициента внецентроидности вспомогательного контура, представляющим собой отношение длины большой полуоси эллипса к радиусу катящейся окружности, причем внутренний и наружный профили выполняют в виде эллипсоидальных профилей от общего контура эллипса. Обеспечивается упрощение технологии изготовления героторных механизмов при повышении эффективности их проектирования. 2 з.п. ф-лы, 11 ил.

1. Героторный механизм, содержащий внутренний ротор и наружный статор, выполненные в виде колес, зубья которых находятся в непрерывном контакте между собой и имеют разницу в числах зубьев, равную единице, а оси смещены на расстояние эксцентриситета, отличающийся тем, что эллипсоидальный профиль зубчатых колес механизма образован по методу обкатки начальных окружностей, одна из которых единичного радиуса r, концентрично связанная с исходным вспомогательным контуром, расположена внутри другой неподвижной окружности радиуса R=kr с возможностью обкатывания по ней без скольжения, при этом в качестве исходного вспомогательного контура использован эллипс, а коэффициент пропорциональности k, определяющий радиус направляющей окружности, равен половине необходимого числа зубьев z колеса, k = z / 2.2. Героторный механизм по п.1, отличающийся тем, что форма его зубьев обеспечена сочетанием коэффициента формы эллипса λ, равным отношению длин его полуосей и коэффициента внецентроидности вспомогательного контура c_о, представляющего собой отношение длины большой полуоси эллипса к радиусу катящейся окружности.3. Героторный механизм по любому из пп. 1 и 2, отличающийся тем, что внутренний и наружный профили выполнены в виде эллипсоидальных профилей от общего контура эллипса, коэффициент формы эллипса λ и коэффициент внецентроидности c_о для обеспечения условия сопряжения профилей связаны соотношением:

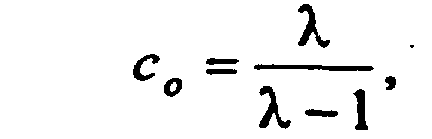
а радиусы направляющих окружностей наружного статора R₁ и внутреннего ротора R₂ равны

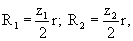
где r - радиус начальной окружности;

z₁; z₂ - соответственно числа зубьев наружного статора и внутреннего ротора.