Предлагаемое изобретение относится к области измерительной техники и может быть использовано в магниторазведке для поиска полезных ископаемых, в области космических исследований для измерения магнитного поля околоземного пространства и магнитного поля планет, в магнитной навигации для определения местоположения судна и т.д.
Известен способ определения коэффициента Пуассона подвижного объекта и устройство для его осуществления (Лысенко А.П. Теория и методы компенсации магнитных помех// Сб. статей "Геофизическое приборостроение". Л. Мингеологии и охраны недр СССР. ОКБ. 1960, вып.7, с. 44 58). Способ заключается в измерении модуля вектора магнитной индукции с помощью модульного датчика, в частности квантового датчика при периодических поперечных кренах подвижного объекта на четырех основных магнитных курсах, соответственно равных 0o, 90o, 180o, 270o, затем измерении модуля вектора магнитной индукции при периодических продольных кренах подвижного объекта на упомянутых четырех основных курсах и по измеренным параметрам магнитного поля на основных четырех курсах объекта при прохождении его над ориентиром, известному наклонению и модулю вектора магнитной индукции геомагнитного поля в районе перемещения объекта определяют из девяти коэффициентов Пуассона, которые можно представить в виде тензора магнитных масс мягкого железа (Гузеев С.Т. Семевский Р.Б. Определение параметров Пуассона по измерениям магнитной индукции T-магнитометром // Геофизическая аппаратура. Л. Недра, 1980, вып. 70, с. 25 - 30).
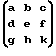
две разности (a k), (e k), три суммы (b + d), (c + q), (f + h), а также составляющие постоянного магнитного поля подвижного объекта, при этом магнитный курс, поперечные и продольные углы кренов определяют соответственно от магнитного компаса и гировертикали, значение модуля вектора магнитной индукции геомагнитного поля определяют, например, по показаниям аэромагнитометра, а наклонение по магнитным картам (Лысенко А.П. Теория и методы компенсации магнитных помех // Сб. статей "Геофизическое приборостроение". Л. Мингеологии и охраны недр СССР. ОКБ, 1960, вып.7, с.54, абз.1, с.56, абз.4). Известное решение обеспечивает только определение двух разностей и трех сумм коэффициентов Пуассона. В известном техническом решении попарное определение коэффициентов Пуассона (a k), (e k), (b + d), (c + q), (f + h) осуществляется при малых кренах объекта, равных примерно 10o, принимая при этом косинусы таких углов равными единице, а синусы этих углов равными соответствующим углам, выраженным в радианах, что снижает точность определения попарных значений коэффициентов Пуассона.
В известном способе и устройстве для определения сумм и разностей коэффициентов Пуассона необходимо иметь значение наклонения, которое определяют по магнитным картам. Но магнитное поле меняется во времени, каждые его изменения определяют по результатам измерений во всех магнитных обсерваториях мира, а также со спутником. Карты же элементов земного магнитного поля составляются ИЗМИР РАН через каждые пять лет и относятся к середине года, кратного пяти (Логачев А.А. Захаров В.П. Магниторазведка. Л. Недра, 1979, с.16, 17). Изменение магнитного поля Земли вызывает изменение наклонения, что приводит к снижению точности определения сумм и разностей коэффициентов Пуассона.
Кроме того, все расчетные формулы для определения коэффициентов Пуассона выведены в предположении, что движение реального объекта, в частности самолета, судна, осуществляется строго по четырем основным курсам, соответственно равным 0o, 90o, 180o, 270o, и выполнение периодических кренов одного вида (поперечных, а затем продольных) с одинаковой амплитудой колебаний. Однако в реальном движении объекта это условие невыполнимо, так как поворот относительно любой из осей объекта вызывает дополнительные (паразитные) повороты относительно двух других осей, причем эти паразитные эволюции при движении могут быть уменьшены только частично (Резник Э.Е. Канторович В.Л. Некоторые вопросы компенсации магнитных полей самолета // Сб. статей "Геофизическое приборостроение". Л. Недра, 1964, вып. 18, с. 26 30).
Известен способ определения коэффициентов Пуассона (Резник Э.Е. Канторович В. Л. Некоторые вопросы компенсации магнитных полей самолета // Сб. статей "Геофизическое приборостроение". Л. Недра, 1984, вып. 18, с. 34 36), который по совокупности существенных признаков наиболее близок к предлагаемому и принят за прототип. Известный способ заключается в изменении углов курса, крена, тангажа подвижного объекта, измерений в процессе изменения упомянутых углов девяти модулей и девяти значений каждой проекции векторов магнитной индукции на оси системы координат объекта, отличных друг от друга, измерении, например, наземными стационарными магнитометрами не искаженного объектом модуля вектора магнитной индукции геомагнитного поля по магнитным картам, а затем по измеренным параметрам магнитного поля определении двух разностей и трех сумм коэффициентов Пуассона, соответственно равных (a k), (e k), (b + d), (c + q), (f + h), а также определении составляющих вектора магнитной индукции постоянного магнитного поля объекта. Из измеренных девяти значений модулей векторов магнитной индукции T1, T2, T9 отнимают значение вектора магнитной индукции геомагнитного поля T и получают девять значений разностей модулей векторов магнитной индукции ΔT1= T1-T, ΔT2= T2-T, ... , ΔT9= T9-T. После этого из каждой предыдущей разности модулей векторов магнитной индукции отнимают последующую, получая восемь значений ΔTi-ΔTi+1 где i 1, 2, 3, и систему восьми уравнений, которую можно представить в следующем общем виде (Резник Э.Е. Канторович В.Л. Некоторые вопросы компенсации магнитных полей самолета // Сб. статей "геофизическое приборостроение". Л. Недра, 1964, вып. 18, с. 35):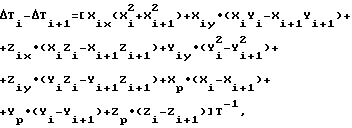
где Xix a k; Xiy b + d; Zix c + q; Yiy e k; Ziy f + h; Xp, Yp, Zp - проекции вектора магнитной индукции постоянного магнитного поля объекта.
Известный способ, как и аналог, обеспечивает определение только двух разностей и трех сумм коэффициентов Пуассона. В известном техническом решении проекции вектора магнитной индукции Xi, Yi, Zi, Xi+1, Yi+1, Zi+1 измеряют на подвижном объекте. Следовательно, значение каждой из этих проекций есть сумма проекций векторов магнитной индукции геомагнитного поля и магнитного поля подвижного объекта. Однако в расчетные формулы упомянутые проекции входят как проекции вектора магнитной индукции только геомагнитного поля (Резник Э. Е. Канторович В.Л. Некоторые вопросы компенсации магнитных полей самолета // Сб. статей "Геофизическое приборостроение". Л. Недра, 1964, вып. 18, с. 34, абз. 1 снизу, с. 35), что приводит к погрешности определения коэффициентов Пуассона, а, следовательно, и к снижению точности определения этих коэффициентов.
В известном способе измеряют девять различных значений проекций векторов магнитной индукции в процессе изменения углов курса, крена, тангажа. Различные же значения отношений проекций векторов магнитной индукции к геомагнитному полю могут не соответствовать значениям направляющих косинусов осей системы координат объекта относительно вектора магнитной индукции геомагнитного поля, так как упомянутые проекции равны сумме проекций геомагнитного поля и магнитного поля объекта, а направляющие косинусы осей системы координат объекта являются функциями наклонения и углов курса, крена, тангажа объекта. Следовательно, решение приведенной ранее системы восьми уравнений может быть неустойчивым, что снижает точность определения коэффициентов Пуассона.
В известном способе, как и в аналоге, для определения коэффициентов Пуассона необходимо знать пространственное распределение модуля вектора магнитной индукции геомагнитного поля в районе движения объекта или значение неискаженного объекта модуля вектора магнитной индукции геомагнитного поля над хорошо опознаваемыми ориентирами, где осуществляется эволюция объекта для определения коэффициентов Пуассона (Логачев А.А. Захаров В.П. Магниторазведка. Л. Недра, 1979, с. 105, 106; Вацуро А.Э. Цирель В.С. Измерение и компенсация магнитных помех самолета АН-2. Принципы и методы) // Геофизическая аппаратура Л. Недра, 1979, вып. 69, с. 100). Следовательно, для определения коэффициентов Пуассона подвижного объекта известными способами должен быть подготовлен участок пространства для подвижного объекта с известными параметрами естественного (неискаженного объектом) магнитного поля. Поэтому известные способы не обеспечивают возможность определения коэффициентов Пуассона в рабочих условиях, в частности, в условиях магнитной съемки.
Известны технические решения для измерения проекций вектора магнитной индукции (Афанасьев Ю.В. Феррозондовые приборы. Л. Энергоатомиздат, 1986, с. 117) и модуля вектора магнитной индукции (Логачев А.А. Захаров В.П. Магниторазведка. Л. Недра, 1979, с. 85 94), которые в совокупности представляют устройство для реализации способа определения коэффициентов Пуассона. Устройство содержит модульный магниточувствительный датчик, измерительно-регистрирующий блок, вход которого подключен к входам упомянутого датчика, трехкомпонентный магниточувствительный датчик, три усилительно-преобразовательных блока, первые входы которых подключены к выходам трехкомпонентного датчика, а первые выходы к входам этого датчика, генератор переменной ЭДС, выходы которого подключены к входу трехкомпонентного датчика и вторым входам усилительно-преобразовательных блоков, и регистрирующий блок, входы которого подключены к выходам усилительно-преобразовательных блоков и к третьему выходу измерительно-регистрирующего блока, состоящего из генератора высокой частоты, фазовращателя и усилителя напряжения переменной частоты. Трехкомпонентный и модульный датчики жестко связаны с подвижным объектом.
Известное устройство работает следующим образом. Напряжение с генератора высокой частоты измерительно-регистрирующего блока, поступающее на вход модульного датчика, осуществляет поляризацию рабочего вещества, например паров цезия упомянутого датчика. В результате этого на выходе датчика появляется напряжение полезного сигнала с частотой прецессии вектора намагниченности рабочего вещества вокруг вектора внешнего магнитного поля, при этом частота прецессии равна произведению гиромагнитного отношения ядра атома рабочего вещества на модуль внешнего магнитного поля. Напряжение это усиливается усилителем переменной частоты измерительно-регистрирующего блока и с одного из выходов этого усилителя подается на регистрирующий блок (частотомер), а с второго выхода на фазовращатель измерительно-регистрирующего блока, выходной сигнал с которого подается на вход модульного датчика, обеспечивая положительную обратную связь. Благодаря положительной обратной связи создается автоколебательная система, генерирующая на резонансной частоте, пропорциональной внешнему магнитному полю. На первый вход трехкомпонентного датчика подается с генератора переменной ЭДС напряжение, возбуждающее этот датчик. В результате этого на выходах трехкомпонентного датчика появляются три ЭДС второй гармоники, каждая из которых пропорциональна проекции вектора магнитной индукции на соответствующую магнитную ось трехкомпонентного датчика (Афанасьев Ю.В. Феррозондовые приборы. Л. Энергоатомиздат, 1986, с. 66). Выходные сигналы с трехкомпонентного датчика усиливаются и детектируются в соответствующих усилительно-преобразовательных блоках. Для детектирования сигналов на вторые входы усилительно-преобразовательных блоков подается переменное напряжение с генератора переменной ЭДС. Выходной сигнал с каждого усилительно-преобразовательного блока подается на регистрирующий блок, обеспечивающий синхронную регистрацию значений проекций векторов магнитной индукции и модулей векторов магнитной индукции при изменении углов курса, крена, тангажа подвижного объекта. По измеренным значениям модулей и проекций векторов магнитной индукции при изменении углового положения подвижного объекта, по значению неискаженным объектом модулю вектора магнитной индукции геомагнитного поля, измеренного, например, стационарным наземным магнитометром в месте расположения опознаваемого ориентира, определяют две разности и три суммы коэффициентов Пуассона, соответственно равных (a k), (e k), (b + d), (f + h), (c + q).
Таким образом, известное устройство обеспечивает определение двух разностей и трех сумм коэффициентов Пуассона. Выходные сигналы с усилительно-преобразовательных блоков известного устройства, расположенного на подвижном объекте, пропорциональны как проекциям вектора магнитной индукции геомагнитного поля, так и проекциям магнитной индукции магнитного поля подвижного объекта. Однако в расчетные формулы упомянутые выходные сигналы входят как проекции вектора магнитной индукции только геомагнитного поля (Резник Э.Е. Канторович В. Л. Некоторые вопросы компенсации магнитных полей самолета // Сб. статей "Геофизическое приборостроение". Л. Недра, 1964, вып. 18, с.34, абз. 1 снизу, с.35), что приводит к снижению точности определения попарных сумм и разностей коэффициентов Пуассона.
Для определения коэффициентов Пуассона известным устройством необходимо знать пространственное распределение не искаженного объектом модуля вектора магнитной индукции геомагнитного поля в районе движения объекта или значение не искаженного объектом модуля вектора магнитной индукции геомагнитного поля над опознаваемым ориентиром, где осуществляется эволюция объекта для определения коэффициентов Пуассона. Следовательно, для определения коэффициентов Пуассона подвижного объекта известным устройством должен быть подготовлен участок пространства (стенд) с известными параметрами геомагнитного поля, поэтому упомянутое устройство не обеспечивает возможность определения коэффициентов Пуассона в рабочих условиях, например, в условиях магнитной съемки.
Кроме того, по совокупности проведенных измерений в известных технических решениях возможно определение попарных значений двух разностей и трех сумм коэффициентов Пуассона только с использованием приближенных формул, полагая, что модуль вектора магнитной индукции геомагнитного поля много больше модуля вектора магнитной индукции подвижного объекта (Вацуро А.Э. Цирель В. С. Измерение и компенсация магнитных помех самолета АН-2 (Принципы и методы) //. Геофизическая аппаратура. Л. Недра, 1979, вып. 69, с.98). Однако для ряда объектов, в частности, для судов водоизмещением от 2 до 7 тыс.т только индуктивное магнитное поле может достигать до 10000 нТл (Гузеев С.Т. Семеновский Р.Б. Определение параметров Пуассона по измерениям магнитной индукции T-магнитометром // Геофизическая аппаратура. Л. Недра, 1980, вып.70, с. 25, абз.2). Диапазон же измерения модуля полного вектора магнитной индукции геомагнитного поля составляет от 33000 нТл до 66000 нТл (Логачев А.А. Захаров В.П. Магниторазведка. Л. Недра, 1979, с.14, абз.1 снизу). Определение попарных значений коэффициентов Пуассона по приближенным расчетным формулам для подвижных объектов, магнитное поле которых отличается от геомагнитного менее, чем на порядок, приводит к снижению точности определения упомянутых коэффициентов.
Задачей предлагаемого изобретения является разработка способа определения всех девяти коэффициентов Пуассона подвижного объекта и устройства для его осуществления, при этом определение коэффициентов Пуассона должно осуществляться не только на специально изготовленных стендах с известным модулем вектора геомагнитного поля, но и в рабочих условиях, в частности в условиях магнитной съемки, когда нет никаких сведений о значении внешнего магнитного поля, например, магнитного поля Земли, не искаженного подвижным объектом. Поставленная задача решается за счет измерения результирующих значений проекций вектора магнитной индукции внешнего поля (магнитного поля Земли) в системе координат подвижного объекта и проекций векторов магнитной индукции индуктивного и постоянного полей объекта в той же системе координат при эволюциях упомянутого объекта (при изменении по крайней мере двух из трех углов курса, крена, тангажа объекта), как и при отсутствии этой информации, но имея сведения о коэффициентах Пуассона образца из мягкого в магнитном отношении железа.
Предлагаемое техническое решение представляет собой два способа и два устройства для осуществления этих способов, связанных между собой настолько, что они образуют единый общий изобретательский замысел.
Предлагаемый способ определения коэффициентов Пуассона подвижного объекта в точке пространства, жестко связанный с системой координат объекта (по первому варианту), заключается в измерении в выбранном месте пространства модуля вектора магнитной индукции при отсутствии подвижного объекта, размещении подвижного объекта в упомянутом месте пространства, изменении курса, крена, тангажа объекта относительно опорной системы координат, измерении в процессе изменения упомянутых углов проекций векторов магнитной индукции на оси системы координат объекта и вычисления коэффициентов Пуассона, используя измеренные значения модуля и проекций девяти векторов магнитной индукции, изменении по крайней мере двух из трех углов курса, крена, тангажа объекта, измерении углов курса, крена, тангажа объекта и по ним определении направляющих косинусов каждой оси системы координат объекта в опорной системе координат, а проекций векторов магнитной индукции измерении синхронно с измерением углов курса, крена, тангажа, выборе проекций десяти векторов магнитной индукции, при которых направляющие косинусы осей системы координат объекта различны при каждом измерении упомянутых проекций, и определении коэффициентов Пуассона по измеренным модулю вектора магнитной индукции при отсутствии объекта и проекциям десяти векторов магнитной индукции, заданных в виде функций направляющих косинусов измеренных углов курса, крена, тангажа и неизвестных параметров, которыми являются проекции магнитной индукции на оси опорной системы координат при отсутствии объекта, постоянного магнитного поля объекта и коэффициентов Пуассона объекта.
Предлагаемый способ определения коэффициентов Пуассона подвижного объекта в точке пространства, жестко связанной с системой координат объекта (по второму варианту), заключается в изменении углов курса, крена, тангажа объекта относительно опорной системы координат, измерении в процессе изменения упомянутых углов проекций векторов магнитной индукции на оси системы координат объекта и вычислении коэффициентов Пуассона, используя измеренные значения проекций девяти векторов магнитной индукции, изменении по крайней мере двух из трех углов курса, крена, тангажа объекта и по ним определении направляющих косинусов каждой оси системы координат объекта в опорной системе координат, а проекций векторов магнитной индукции измерении синхронно с измерением углов курса, крена, тангажа, выборе проекций десяти векторов магнитной индукции, при которых направляющие косинусы осей системы координат объекта различны при каждом измерении упомянутых проекций, затем в дополнительной точке пространства, жестко связанной с системой координат объекта, размещении образца из мягкого в магнитном отношении железа, коэффициенты Пуассона которого известны в основной точке пространства, вновь изменении по крайней мере двух из трех углов курса, крена, тангажа объекта, измерении углов курса, крена, тангажа объекта и по ним определении направляющих косинусов каждой оси системы координат объекта в опорной системе координат, а проекций векторов магнитной индукции измерении синхронно с измерением углов курса, крена, тангажа, выборе проекций десяти векторов магнитной индукции по крайней мере на одну и ту же ось объекта, при которых направляющие косинусы различны при каждом измерении упомянутых проекций, и определении коэффициентов Пуассона объекта по проекциям десяти векторов магнитной индукции при отсутствии образца, заданных в виде функций измеренных углов курса, крена, тангажа и неизвестных параметров, которыми являются проекции магнитной индукции на оси опорной системы координат при отсутствии объекта, постоянного магнитного поля объекта, коэффициентов Пуассона объекта и по проекциям десяти векторов магнитной индукции по крайней мере на одну и ту же ось системы координат объекта при наличии образца, заданных в виде функций направляющих косинусов измеренных углов курса, крена и тангажа, известных коэффициентов Пуассона образца и неизвестных параметров, которыми являются проекции магнитной индукции на оси опорной системы координат при отсутствии объекта и образца, постоянного магнитного поля объекта и образца и коэффициентов Пуассона объекта.
Изменение в предлагаемом изобретении (по способу первого и второго вариантов) по крайней мере двух из трех углов курса, крена, тангажа подвижного объекта приводит к изменению проекций вектора магнитной индукции внешнего поля, например магнитного поля Земли (МПЗ), и изменению вектора магнитной индукции упомянутого объекта на оси координат объекта пропорционально направляющим косинусам каждой оси системы координат объекта относительно опорной системы координат, при этом индуктивное поле объекта является функцией коэффициентов Пуассона объекта и вектора внешнего магнитного поля, в частности, МПЗ. При синхронном измерении проекций десяти векторов магнитной индукции с измерением изменяющихся углов курса, крена, тангажа объекта, при которых направляющие косинусы осей системы координат объекта различны, получают по десять значений каждой проекции вектора магнитной индукции на оси системы координат объекта. Значение каждой из измеренных проекций векторов магнитной индукции можно задать аналитически в виде функций направляющих косинусов измеренных углов курса, крена, тангажа объекта, неизвестных значений проекций векторов магнитной индукции МПЗ, постоянного магнитного поля объекта и коэффициентов Пуассона объекта. Получим тем самым для упомянутых значений проекций на одну и ту же координатную ось объекта систему десяти уравнений.
Для способа по первому варианту общим решением полученных уравнений при измеренном модуле вектора магнитной индукции при отсутствии объекта в выбранном месте пространства являются девять коэффициентов Пуассона объекта, проекции вектора магнитной индукции внешнего магнитного поля, в частности МПЗ, проекций постоянного и индуктивного полей объекта.
Для способа по второму варианту размещение в дополнительной точке пространства, жестко связанной с системой координат объекта, образца из мягкого в магнитном отношении железа, коэффициенты Пуассона которого известны в основной точке пространства, а затем изменение по крайней мере двух из трех углов курса, крена, тангажа подвижного объекта приводит к изменению проекций вектора магнитной индукции внешнего поля, например МПЗ, и к изменению вектора магнитной индукции индуктивного поля объекта и образца пропорционально направляющим косинусам каждой оси системы координат объекта относительно опорной системы координат, при этом индуктивное поле объекта является функцией коэффициентов Пуассона объекта и образца, вектора внешнего магнитного поля, в частности МПЗ. При синхронном измерении проекций десяти векторов магнитной индукции с измерением изменяющихся углов курса, крена, тангажа объекта, при которых направляющие ко- синусы осей системы координат объекта различны, получают по десять значений каждой проекции вектора магнитной индукции на оси системы координат объекта. Значение каждой из измеренных проекций векторов магнитной индукции можно задать аналитически в виде направляющих косинусов измеренных углов курса, крена, тангажа объекта, известных коэффициентов Пуассона образца и неизвестных значений проекции векторов МПЗ постоянного магнитного поля объекта и образца и коэффициентов Пуассона объекта. Получим тем самым для упомянутых значений проекций на одну и ту же координатную ось объекта дополнительную систему десяти уравнений при наличии образца. Общим решением полученных при наличии образца и ранее полученных уравнений при отсутствии образца являются девять коэффициентов Пуассона объекта, проекции вектора магнитной индукции внешнего магнитного поля, в частности МПЗ, постоянного и индуктивного полей объекта и образца.
Таким образом, технический результат предлагаемого способа выражается в определении всех девяти коэффициентов Пуассона подвижного объекта как при наличии сведений о значении магнитного поля, не искаженного объектом (для способа по первому варианту), так и при отсутствии сведений (для способа по второму варианту) о значении внешнего магнитного поля, не искаженного магнитным полем объекта, при этом совокупность результатов измеряемых параметров обеспечивает определение коэффициентов Пуассона объекта не по приближенным, а по точным формулам.
Предлагаемое устройство (по первому варианту) для осуществления способа определения коэффициентов Пуассона подвижного объекта в точке пространства, жестко связанной с системой координат объекта, содержащее трехкомпонентный магниточувствительный датчик, размещенный в упомянутой точке пространства, три усилительно-преобразовательных блока, первые входы которых подключены к выходам упомянутого датчика, генератор переменной ЭДС, первый выход которого подключен к входу трехкомпонентного датчика, а второй выход к вторым входам усилительно-преобразовательных блоков, и регистрирующий блок, входы которого подключены к выходам усилительно-преобразовательных блоков, снабжено углоизмерительным устройством, выходы которого подключены к трем дополнительным входам регистрирующего блока, выполненного с возможностью синхронной регистрации сигналов, пропорциональных значениям проекций векторов магнитной индукции и углов курса, крена, тангажа объекта, и устройством обработки информации, подключенным к выходу регистрирующего блока, с возможностью вычисления коэффициентов Пуассона из следующей системы уравнений:
Bxi=l1i(1+a)•Bxt+m1i(1+a)•Byt+ n1i(1+a)•Bzt+b(l2iBxt+m2iByt+ n2iBzt+c(l3i(Bxt+m3iByt+ n3iBzt)+Bxp;
Byi=l2i(1+e)•Bxt+m2i(1+e)•Byt+ n2i(1+e)•Bzt+d(l1iBxt+m1iByt+ n1iBzt)+f(l3iBxt+m3iByt+ n3iBzt)+Byp;
Bzi=l3i(1+k)•Bxt+m3i(1+k)•Byt+ n3i(1+k)•Bzt+q(l1iBxt+m1iByt+ n1iBzt+h(l2iBxt+m2iByt+ n2iBzt)+Bzp,
где Bxi, Byi, Bzi проекции векторов магнитной индукции на оси системы координат объекта при i-x значениях углов курса, крена, тангажа объекта;
i=1, 2, 10;
Bxt, Byt, Bzt проекции вектора магнитной индукции на оси опорной системы координат при отсутствии объекта;
l1i, m1i, n1i, l2i, m2i, n2i, l3i, m3i, n3i направляющие косинусы осей системы координат объекта при i-x значениях углов курса, крена, тангажа объекта;
Bxp, Byp, Bzp проекции вектора магнитной индукции на оси системы координат объекта, созданные жестким в магнитном отношении железом объекта;
a, b, c, d, e, f, q, h, k коэффициенты Пуассона объекта в точке пространства размещения датчика.
Предлагаемое устройство (по второму варианту) для осуществления способа определения коэффициентов Пуассона подвижного объекта в точке пространства, жестко связанной с системой координат объекта, содержащее трехкомпонентный магниточувствительный датчик, размещенный в упомянутой точке пространства, три усилительно-преобразовательных блока, первые входы которых подключены к выходам упомянутого датчика, генератор переменной ЭДС, первый выход которого подключен к входу трехкомпонентого датчика, а второй выход к вторым входам усилительно-преобразовательных блоков, и регистрирующий блок, входы которого подключены к выходам усилительно-преобразовательных блоков, снабжено углоизмерительным устройством, выходы которого подключены к трем дополнительным входам регистрирующего блока, выполненного с возможностью синхронной регистрации сигналов, пропорциональных значениям проекций векторов магнитной индукции и углов курса, крена, тангажа объекта, образцом из мягкого в магнитном отношении железа с возможностью его размещения в дополнительной точке пространства, жестко связанной с системой координат объекта, и устройством обработки информации, подключенным к выходу регистрирующего блока, с возможностью вычисления коэффициентов Пуассона из следующей системы уравнений:
Bxi=l1i(1+a)•Bxt+m1i(1+a)•Byt+ n1i(1+a)•Bzt+b(l2iBxt+m2iByt+ n2iBzt+c(l3iBxt+m3iByt+ n3iBzt)+Bxp;
Byi=l2i(1+e)•Bxt+m2i(1+e)•Byt+ n2i(1+e)•Bzt+d(l1iBxt+m1iByt+ n1iBzt)+f(l3iBxt+m3iByt+ n3iBzt)+Byp;
Bzi=l3i(1+k)•Bxt+m3i(1+k)•Byt+ n3i(1+k)•Bzt+q(l1iBxt+m1iByt+ n1iBzt+h(l2iBxt+m2iByt+ n2iBzt)+Bzp;
Bxj=l1j(1+a+a0)•Bxt+m1j(1+a+ a0)•Byt+n1j(1+a+a0)•Bzt+ (b+b0)•(l2jBxt+m2jByt+ n2jBzt+(c+c0)•(l3jBxt+ m3jByt+n3jBzt)+Bxp+Bx0; Byj=l2i(1+e+e0)•Bxt+m2j(1+e+ e0)•Byt+n2j(1+e+e0)•Bzt+ (d+d0)•(l1jBxt+m1jByt+ n1jBzt+(f+f0)•(l3jBxt+ m3jByt+n3jBzt)+Byp+By0;
Bzj=l3j(1+k+k0)•Bxt+m3j(1+k+ k0)•Byt+n3j(1+k+k0)•Bzt+ (q+q0)•(l1jBxt+m1jByt+ n1jBzt+(h+h0)•(l2jBxt+m2jByt+n2jBzt)+Bzp+Bzo, где Bxi, Byi, Bzi, Bxj, Byj, Bzj проекции векторов магнитной индукции на оси системы координат объекта при i-x и j-x значениях углов курса, крена, тангажа объекта при наличии и отсутствии образца;
i=1, 2, 10; j=1, 2, 10;
Bxt, Byt, Bzt проекции вектора магнитной индукции на оси опорной системы координат при отсутствии объекта;
l1i, m1i, n1i, l2i, m2i, n2i, l3i, m3i, n3i и l1j, m1j, n1j, l2j, m2j, n2j, l3j, m3j, n3j направляющие косинусы осей системы координат объекта при i-x и j-x значениях углов курса, крена, тангажа объекта;
Bxp, Byp, Bzp, Bx0, By0, Bz0 - проекции вектора магнитной индукции на оси системы координат объекта, созданные жестким в магнитном отношении железом объекта и образца;
a, b, c, d, e, f, q, h, k и a0, b0, c0, d0, e0, f0, q0, h0, k0 коэффициенты Пуассона объекта и образца в точке пространства размещения датчика, при этом коэффициенты Пуассона образца, расположенного в дополнительной точке пространства, известны в точке размещения трехкомпонентного датчика.
Совокупность используемых средств для устройства по первому варианту, одно из которых предназначено для измерения проекций вектора магнитной индукции, состоящее из трехкомпонентного датчика, жестко связанного с подвижным объектом, трех усилительно-преобразовательных блоков и генератора переменной ЭДС, второе для измерения углов курса, крена, тангажа объекта, а не магнитных физических величин и третье для одновременной регистрации проекций векторов магнитной индукции и упомянутых углов объекта и устройства обработки этой информации, образуют единое устройство, обеспечивающее определение девяти коэффициентов Пуассона объекта по синхронно измеренным проекциям векторов магнитной индукции, каждый из которых равен сумме векторов магнитной индукции МПЗ и магнитного поля объекта, с измерением изменяющихся углов курса, крена, тангажа объекта и информации о модуле магнитной индукции МПЗ на стенде, на котором осуществляются измерения.
Совокупность используемых средств для устройства по второму варианту, одно из которых предназначено для измерения проекций вектора магнитной индукции, состоящее из трехкомпонентного датчика, жестко связанного с подвижным объектом, трех усилительно-преобразовательных блоков и генератора переменной ЭДС, второе для измерения углов курса, крена, тангажа объекта, а не магнитных физических величин, третье для одновременной регистрации проекций векторов магнитной индукции и упомянутых углов объекта и устройства обработки информации и четвертое состоящее из образца из мягкого в магнитном отношении железа, с возможностью его размещения в дополнительной точке пространства, коэффициенты Пуассона которого известны в месте размещения датчика, образуют единое устройство, обеспечивающее по синхронно измеренным проекциям векторов магнитной индукции при отсутствии в наличии образца в дополнительной точке пространства, с измерением изменяющихся углов курса, крена, тангажа объекта, определение девяти коэффициентов Пуассона объекта в месте размещения датчика.
Таким образом, технический результат предлагаемого устройства выражается в определении всех девяти коэффициентов Пуассона подвижного объекта как при наличии сведений о модуле вектора магнитной индукции внешнего магнитного поля, в частности МПЗ, не искаженного магнитным полем объекта (для устройства по первому варианту), так и при отсутствии этих сведений (для устройства по второму варианту), что позволяет осуществлять определение коэффициентов Пуассона в рабочих условиях, например в условиях магнитной съемки.
Сущность предлагаемого способа и устройства для его осуществления поясняется следующими графическими материалами.
На фиг. 1 изображена структурная схема устройства для осуществления способа определения коэффициентов Пуассона объекта.
На фиг. 2 изображены направления осей объекта в опорной системе координат при углах курса, крена, тангажа.
Предлагаемое устройство (по первому варианту) для осуществления способа определения коэффициентов Пуассона подвижного объекта по первому варианту состоит (см. фиг. 1) из трехкомпонентного магниточувствительного датчика 1, трех усилительно-преобразовательных блоков 2 4, первые входы которых подключены к выходам датчика 1, генератора переменной ЭДС 5, первый выход которого подключен к входу датчика 1, а второй выход к вторым входам блоков 2 4, регистрирующего блока 6, входы которого подключены к выходам блоков 2 - 4, углоизмерительного устройства 7, выходы которого подключены к трем дополнительным входам блока 6, и устройства обработки информации 8, подключенного к выходу блока 6. При этом датчик 1, блоки 2 4, генератор 5, блок 6, устройство 7 и блок 8 размещены на подвижном объекте 9.
Заявленный способ по первому варианту реализуется посредством предлагаемого устройства (по первому варианту) следующим образом.
На первый вход трехкомпонентного датчика 1 (см. фиг. 1), в частности феррозонда, подается с генератора 5 переменная ЭДС, возбуждающая этот датчик. В результате этого на выходе датчика 1 появляются три ЭДС второй гармоники, каждая из которых пропорциональна проекции вектора магнитной индукции на соответствующую магнитную ось датчика 1 (Афанасьев Ю.В. Феррозондовые приборы. Л. Энергоатомиздат, 1986, с. 66). Выходные сигналы с датчика 1 усиливаются и детектируются в соответствующих блоках 2 -4. Для детектирования сигналов на вторые входы блоков 2 4 подается переменное напряжение с генератора 5. На входы блока 6 поступают сигналы с выходов блоков 2 4, пропорциональные проекциям векторов магнитной индукции, и выходные сигналы с устройства 7, пропорциональные углам курса, крена, тангажа объекта 9. Блок 6 обеспечивает синхронную регистрацию сигналов, пропорциональных значениям проекций векторов магнитной индукции и углов курса, крена, тангажа объекта, и передачу их на устройство обработки информации 8, при введении в которое данных о модуле вектора магнитной индукции внешнего магнитного поля при отсутствии объекта осуществляется определение коэффициентов Пуассона и составляющих магнитного поля объекта. При синхронном измерении проекций десяти векторов магнитной индукции и углов курса, крена и тангажа, например, при циркуляции объекта, при которых направляющие косинусы осей системы координат объекта различны, получают по десять значений проекций векторов магнитной индукции Bxi, Byi, Bzi на одну и ту же ось объекта. Алгебраические выражения Bxi, Byi, Bzi, образующие системы уравнений, представлены ранее в предлагаемом устройстве по первому варианту. В этих уравнениях (l1i, m1i, n1i), (l2i, m2i, n2i), (l3i, m3i, n3i) направляющие косинусы соответствующих осей O'X', O'Y', O'Z' (см. фиг. 2) системы координат объекта O'X'Y'Z', являющиеся функциями углов курса ψ крена qк и тангажа θу относительно опорной системы координат OXYZ. В данных уравнениях неизвестными параметрами являются Bxp, Byp, Bzp и произведения Bxt, Byt, Bzt на коэффициенты Пуассона. Измеренными параметрами являются направляющие косинусы осей системы координат объекта и Bxi, Byi, Bzi при различных друг от друга направляющих косинусах осей системы координат объекта, поэтому каждая из систем упомянутых уравнений имеет устойчивое и единственное решение. Решением этой системы уравнений являются (1+a)•Bxt, (1+a)•Byt, (1+a)•Bzt, b•Bxt, b•Byt, b•Bzt, d•Bxt, d•Byt, d•Bzt, (1+e)•Bxt,
(1+e)•Byt, (1+e)•Bzt, f•Bxt, f•Byt, f•Bzt, q•Bxt, q•Byt, q•Bzt, h•Bxt, h•Byt, h•Bzp, (1+k)•Bxt, (1+k)•Byt, (1+k)•Bzt, Bxp, Byp, Bzp.
По полученным решениям определяют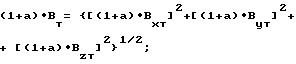
Аналогично определяют (1+e)•Bt, (1+k)•Bt, b•Bt, c•Bt, d•Bt, f•Bt, q•Bt, h•Bt.
Измерив, например, квантовым магнитометром модуль вектора магнитной индукции Bt, как это представлено в работе (Резник Э.Е. Канторович В.Л. Некоторые вопросы компенсации магнитных полей самолета // Сб. статей "Геофизическое приборостроение". Л. Недра, 1964, вып. 18, с. 26 30), при отсутствии влияния магнитного поля объекта и подставляя его значение в полученные решения произведения параметров Пуассона на Bt, определяют все девять параметров Пуассона объекта 9 в месте размещения датчика 1, жестко связанного с объектом 9.
Значение Bt можно определить по географическому местоположению объекта и картам магнитного поля, составленным и периодически корректируемым Институтом земного магнетизма, ионосферы и распространения радиоволн Российской Академии Наук (Логачев А.А. Захаров В.П. Магниторазведка. Л. Недра, 1979).
Предлагаемое устройство (по второму варианту) для осуществления способа определения коэффициентов Пуассона подвижного объекта по второму варианту состоит (см. фиг. 1) из трехкомпонентного магниточувствительного датчика 1, трех усилительно-преобразовательных блоков 2 4, первые входы которых подключены к выходам датчика 1, генератора переменной ЭДС 5, первый выход которого подключен к входу датчика 1, а второй выход к вторым входам блоков 2 4, регистрирующего блока 6, входы которого подключены к выходам блоков 2 - 4, углоизмерительного устройства 7, выходы которого подключены к трем дополнительным входам блока 6, устройства обработки информации 8, подключенного к выходу блока 6, и образца 10 из мягкого в магнитном отношении железа с возможностью его размещения в дополнительной точке пространства, жестко связанной с системой координат объекта 9. При этом коэффициенты Пуассона образца 10, расположенного в дополнительной точке пространства, известны в точке размещения датчика 1.
Заявляемый способ по второму варианту реализуется посредством предлагаемого устройства (по второму варианту) следующим образом.
Устройство по второму варианту при отсутствии в дополнительной точке образца 10 (см. фиг. 1) обеспечивает определение произведений коэффициентов Пуассона объекта на Bt аналогично устройству по первому варианту, значения которых остаются в памяти устройства 8. Затем размещают в дополнительной точке пространства, жестко связанной с системой координат объекта 9, образец 10 из мягкого в магнитном отношении железа, параметры Пуассона которого при выбранной его ориентации известны в месте размещения датчика 1. При синхронном измерении проекций десяти векторов магнитной индукции и углов курса, крена, тангажа, например, при циркуляции объекта, в частности судна, при которых направляющие косинусы осей системы координат объекта различны, получают по десять значений проекций векторов магнитной индукции Bxj, Byj, Bzj на одну и ту же ось объекта. Алгебраические выражения Bxj, Byj, Bzj, образующие системы уравнений, представлены в предлагаемом устройстве по второму варианту. В этих уравнениях (l1j, m1j, n1j), (l2j, m2j, n2j), (l3j, m3j, n3j) направляющие косинусы соответствующих осей O'X', O'Y', O'Z' (см. фиг. 2) системы координат объекта O'X'Y'Z', являющиеся функциями углов курса ψ крена qx и тангажа θy относительно опорной системы координат OXYZ. В данных уравнениях неизвестными параметрами являются Bxp+Bx0, Byp+By0, Bzp+Bz0 и произведения Bxt, Byt, Bzt на соответствующие суммы коэффициентов Пуассона объекта и образца. Измеренными параметрами являются направляющие косинусы осей системы координат объекта, коэффициенты Пуассона образца и Bxj, Byj, Bzj при различных друг от друга направляющих косинусах осей системы координат объекта, поэтому каждая из систем упомянутых уравнений имеет устойчивое и единственное решение. Решением этой системы уравнений являются (1+a+a0)•Bxt, (1+a+a0)•Byt, (1+a+a0)•Bzt, (b+b0)•Bxt, (b+b0)•Byt, (b+b0)•Bzt, (c+c0)•Bxt, (c+c0)•Byt, (c+c0)•Bzt, (d+d0)•Bxt, (d+d0)•Byt, (d+d0)•Bzt, (1+e+e0)•Bxt, (1+e+e0)•Byt, (1+e+e0)•Bzt, (f+f0)•Bxt,
(f+f0)•Byt, (f+f0)•Bzt, (q+q0)•Bxt, (q+q0)•Byt, (q+q0)•Bzt, (h+h0)•bxt,
(h+h0)•Byt, (h+h0)•Bzp, (1+k+k0)•Bxt, (1+k+k0)•Byt, (1+k+k0)•Bzt, Bxp+Bx0, Byp+By0, Bzp+Bz0.
По полученным решениям определяют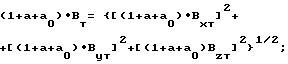
Аналогично определяют (1+e+eo)•Bt, (1+k+ko)•Bt, (b+b0)•Bt, (c+c0)•Bt, (d+d0)•Bt, (f+f0)•Bt, (q+q0)•Bt, (h+h0)•Bt.
Из решения уравнений при отсутствии и наличии образца определяют параметры Пуассона объекта и значения Bxt, Byt, Bzt. Так, например, при отсутствии образца 10 определяют (1+a)•Bt, которое обозначим через N1, а при наличии образца 10 определяют (1+a+a0)Bt, которое обозначим через N2, то есть получают систему двух уравнений:
(1+a)•Bt=N1
(1+a+a0)•Bt=N2
Решением этой системы будет 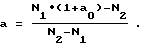
В месте расположения датчика 1 (см. фиг. 1) параметры Пуассона образца правильной геометрической формы, например в виде шара или эллипсоида, можно определить аналитически (Яновский Б.М. Земной магнетизм. Л. ЛГУ, 1978; Кожухов В. П. Воронов В.В. Григорьев В.В. Магнитные компасы. М. Транспорт, 1981) или экспериментально с помощью трехкомпонентной меры магнитной индукции (Афанасьев В.В. Студенов Н.В. Хорев В.Н. и др. Средства измерения параметров магнитного поля. Л. Энергия, 1979) в зависимости от изменения магнитной индукции внешнего намагничивающего поля, например, от изменения магнитной широты, при этом сохраняя неизменным взаимное расположение датчика и образца, которое они должны иметь при работе в полевых условиях.
Техническое решение по второму варианту может быть использовано для контроля коэффициентов Пуассона объекта и определения смещения нуля тесламетра или для корректировки постоянного и индуктивного магнитного поля объекта в рабочих условиях, например, в условиях магнитной съемки.
Таким образом, технический результат предлагаемого технического решения выражается в определении всех девяти коэффициентов Пуассона объекта как при наличии сведений о модуле вектора магнитной индукции внешнего магнитного поля, так и при отсутствии этих сведений.
В предлагаемом техническом решении датчик 1 (см. фиг. 1), блоки 2 4 и генератор 5 выполнены аналогично известному устройству для измерения параметров магнитного поля (Афанасьев Ю.В. Феррозондовые приборы. Л. Энергоатомиздат, 1986, с. 117). При этом каждый блок 2 4 состоит из избирательного усилителя и синхронного детектора (Афанасьев Ю.В. Студенцов Н.В. Щелкин А.П. Магнитометрические преобразователи, приборы, установки. Л. Энергия, 1972, с. 155). Углоизмерительным устройством 7 (см. фиг. 1) может быть гиростабилизированная платформа (ГСП), обеспечивающая измерение трех углов вращения объекта с погрешностью около 0,5 угловых минут за счет трехосной гироскопической стабилизации ГСП относительно трех взаимно перпендикулярных осей опорной системы координат (Теория и конструкция гироскопических приборов и систем // И. В. Одинова, Г.Д. Блюмин, А.В.Карпухин и др. М. Высшая школа, 1971, с. 387 -393, рис. 9.9). Для высокоточного измерения углового положения подвижного объекта в опорной системе координат с погрешностью до десятых долей угловых секунд в предлагаемом техническом решении в качестве углоизмерительного устройства 7 (см. фиг. 1) для измерения углов курса, крена, тангажа могут быть использованы навигационные системы на основе лазерных гироскопов, которыми оснащены самолеты (Тенденция совершенствования гироскопов и гиростабилизированных платформ. Д.П.Лукьянов, Л.А.Северов, Е.Л.Смирнов, А.В.Тиль // Л. Изв. вузов СССР. Приборостроение. Т. 30, N 10, 1987). Регистрирующий блок 6 и устройство обработки информации 8 могут быть реализованы УПК (Универсальным программируемым контроллером), разработанным и выпускаемым АО "ИФ-АТИС" (193131, С. -Петербург, ул. Ивановская, 24, тел. (812)568-37-14, факс (812) 568-37-12).
Образец из мягкого в магнитном отношении железа может быть выполнен из пермаллоя или железа Армко (В.П.Кожухов, В.В.Воробьев, В.В.Григорьев. Магнитные компасы. М. Транспорт, 1981).
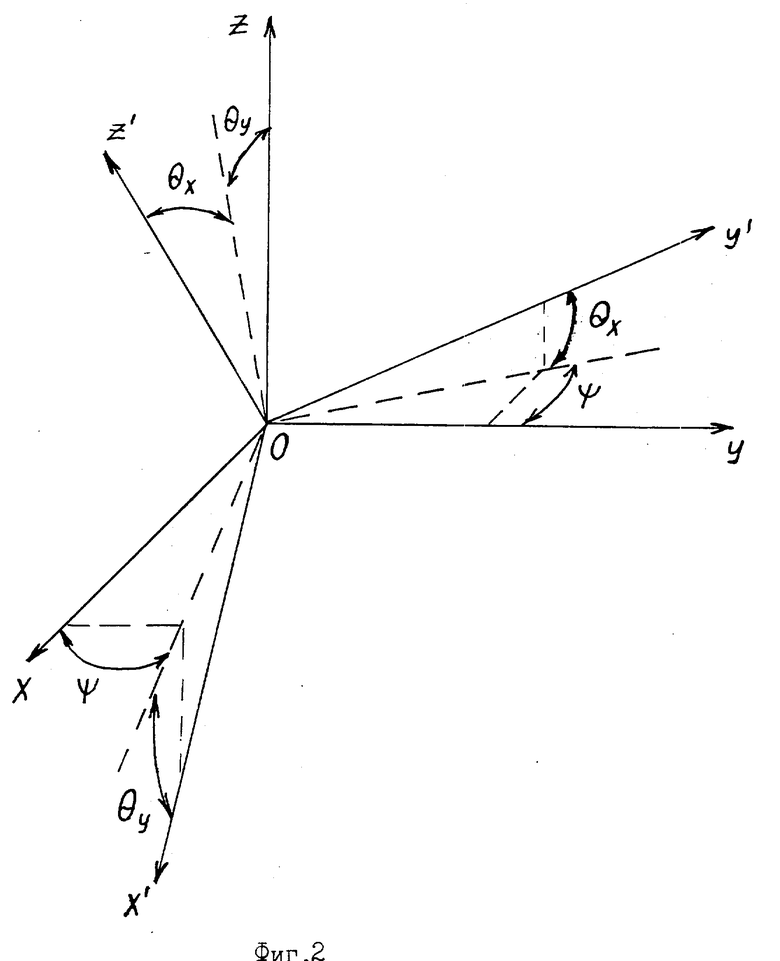
Использование: в магниторазведке для поиска полезных ископаемых, в области космических исследований для измерения магнитного поля околоземного пространства и магнитного поля планет, в магнитной навигации для определения местоположения судна и т.д. Сущность: способ определения коэффициентов Пуассона подвижного объекта заключается в изменении по крайней мере двух из трех углов курса, крена, тангажа объекта относительно опорной системы координат и измерении в процессе изменения упомянутых углов проекций девяти векторов магнитной индукции на оси системы координат объекта, измерении углов курса, крена, тангажа объекта и определении по ним направляющих косинусов каждой оси системы координат объекта в опорной системе координат, измерении проекции векторов магнитной индукции синхронно с измерением углов курса, крена, тангажа, при которых направляющие косинусы осей системы координат объекта различны при каждом измерении упомянутых проекций, затем дополнительном изменении по крайней мере двух из трех углов курса, крена, тангажа объекта и при этих угловых положениях осей системы координат объекта, различных с предыдущими, измерении проекций десятого вектора магнитной индукции и направляющих косинусов каждой оси системы координат объекта и по измеренным проекциям векторов магнитной индукции и соответствующих им направляющим косинусам осей системы координат объекта определении коэффициентов Пуассона. Устройство содержит трехкомпонентный магниточувствительный датчик, жестко связанный с объектом, три усилительно-преобразовательных блока, генератор переменной ЭДС, углоизмерительное устройство, регистрирующий блок и блок обработки информации. 2 с.п. ф-лы, 2 ил.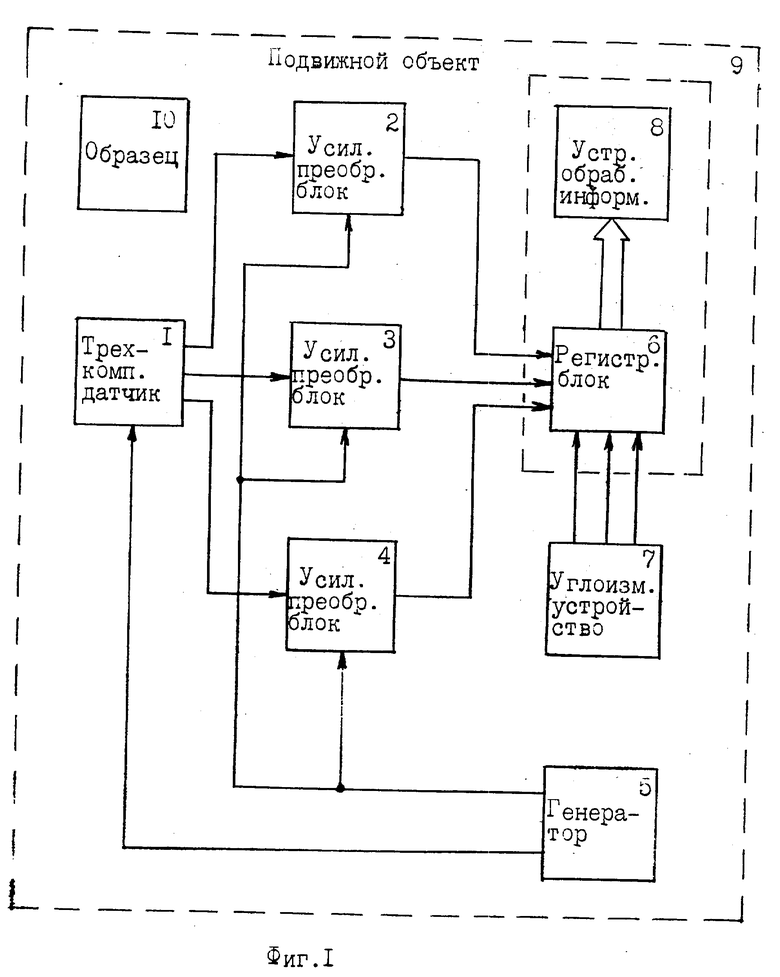
Bx i l1 i(1+a) • Bx t + m1 i(1+a) • By t + n1 i(1+a)Bz т + b(l2 iBx т + m2 iBy т+ n2 iBz т) + c(l3 iBx т + m3 iBy т) + n3 iBzт Bx p; By i l2 i(1 + l)Bx т + m2 i (1 + l)By т + n2 i(1 + е)Bz т + d(l1 iBx т + m1 iBy т + n1 iBz т) + f(l3 iBx т + m3 iBy т + n3 iBz т) + By p;
Bz i l3 i(1 + k)Bx т + m3 i(1 + k)By т + n3 i(1 + k)Bz т + g(l1 iBx т + m1 iBy т + n1 iBz т) + h (l2 iBx т + m2 iBy т + n2 iBz т) + Bz p;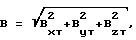
где Bx i, By i, Bz i проекции векторов магнитной индукции на оси системы координат объекта при i-х значениях углов курса, крена, тангажа объекта; i 1,2,10;
Bx т, By т, Bz т проекции вектора магнитной индукции на оси опорной системы координат при отсутствии объекта;
l1 i, m1 i, n1 i, l2 i, m2 i, n2i, l3 i, m3 i, n3 i направляющие косинусы осей системы координат объекта при i-х значениях углов курса, крена, тангажа объекта;
Bx p, By p, Bz p проекции вектора магнитной индукции на оси системы координат объекта, созданные жестким в магнитном отношении железом объекта;
a, b, c, d, e, f, g, h, k коэффициенты Пуаcсона объекта в точке пространства размещения датчика.
| Лысенко А.П | |||
| Теория и методы компенсации магнитных потерь | |||
| Сб | |||
| статьей "Геофизическое приборостроение",- Л.: Мингеология и охрана недр СССР, ОКБ, 1960, вып | |||
| Способ восстановления хромовой кислоты, в частности для получения хромовых квасцов | 1921 |
|
SU7A1 |
| Приспособление для плетения проволочного каркаса для железобетонных пустотелых камней | 1920 |
|
SU44A1 |
| Резник Э.Е | |||
| и др | |||
| Некоторые вопросы компенсации магнитных полей самолета Сб | |||
| статей "Геофизическое приборостроение", Л.: Недра, 1964, вып | |||
| Способ использования делительного аппарата ровничных (чесальных) машин, предназначенных для мериносовой шерсти, с целью переработки на них грубых шерстей | 1921 |
|
SU18A1 |
| Прибор для получения стереоскопических впечатлений от двух изображений различного масштаба | 1917 |
|
SU26A1 |
| Афанасьев Ю.В | |||
| Феррозондовые приборы | |||
| Л.: Энергоатомиздат, 1986, с | |||
| Аппарат для испытания прессованных хлебопекарных дрожжей | 1921 |
|
SU117A1 |
| Логачев А.А | |||
| и др | |||
| Магниторазведка, Л.: Недра, 1979, с | |||
| Устройство для выпрямления опрокинувшихся на бок и затонувших у берега судов | 1922 |
|
SU85A1 |
Авторы
Даты
1997-11-20—Публикация
1995-02-07—Подача