Изобретение относится к области вычислительной томографии, основанной на просвечивании объекта сканирующим конусным пучком излучения, регистрации прошедшего через объект излучения посредством двумерного экрана-преобразователя, последующей трехмерной реконструкции изображения внутренней структуры объекта и может быть примерно в медицинской диагностике и контроле промышленных объектов.
Томографическая система с конусным пучком излучения обычно включает в себя следующие основные компоненты: источник излучения; регистрирующий излучение экран-преобрзователь; механический сканер, перемещающий блок "источник-детектор" относительно объекта; устройство преобразования исходных данных в цифровой код; процессор и программное обеспечение; реализующее какой-либо алгоритм трехмерной реконструкции.
Источник и детектирующий экран обычно жестко связаны между собой, располагаются по разные стороны томографируемого объекта. Сканирование осуществляется путем перемещения блока "источник-детектор" относительно объекта, причем перемещаться может либо объект, либо источник с детектором, либо то и другое совместно. Если предположить, что объект неподвижен, то процесс сканирования определяется траекторией источника излучения. При сканировании данные просвечивания считаются с детектирующего экрана, преобразуются в цифровой код и затем производится трехмерная реконструкция по какому-либо алгоритму. Способ сканирования и алгоритм являются наиболее ответственными аспектами, обеспечивающими точность реконструкции. В реальных условиях невозможно получить точной реконструкции, что связано с погрешностями измерений проекционных данных, конечными шарами дискретизации траектории источника и другими допущениями и погрешностями. Но следует различать две ситуации, когда ошибка реконструкции может становиться сколь угодно малой при уменьшении дискретизации и погрешностей измерений и когда комплекс "траектория источника-алгоритм" не позволяют уменьшать ошибку реконструкции при тех же условиях. В первом случае будем говорить, что способ трехмерной томографии допускает точную реконструкцию, а во втором нет.
Для возможности точной реконструкции траектория источника должна удовлетворять условию полноты. Условие полноты гласит: почти каждая плоскость, пересекающая объект, должна пересекать траекторию источника [1]
Дополнением к условию полноты является требование к угловому раствору конусного пучка. Обычно подразумевается, что для полноты исходных данных пучок должен перекрывать весь объект при просвечивании его из любой точки траектории.
Из литературы известно ограниченное число траекторий, удовлетворяющих условию полноты. Наиболее подробно они представлены в [2]
К ним относятся:
1. Две окружности, имеющие общий центр и расположенные во взаимно перпендикулярных плоскостях.
2. Три спирали, одна из которых выше объекта, другая ниже объекта и третья вокруг объекта.
3. Синус на цилиндре. Эта траектория описывается уравнениями: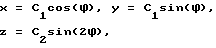
где C1 и C2 выбираются так, чтобы геометрия была полной.
4. Две окружности, связанные прямой линией.
5. Форма шва на бейсбольном мяче.
Среди известных алгоритмов точной трехмерной реконструкции по конусным проекциям можно выделить два наиболее предпочтительных для практического применения. Один из них опубликован Б.Д. Смитом, другой Х.К. Туем. Их описание приводится в работах [1,2] По вычислительным затратам и требованиям к траектории источника эти алгоритмы приблизительно одинаковы. В качестве прототипа [2] рассмотрим способ трехмерной томографии, основанный на применении алгоритма Туя в сочетании с одной из пяти перечисленных выше траекторией источника, например двумя перпендикулярными траекториями.
Формула реконструкции в алгоритме Туя имеет следующий вид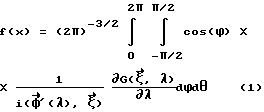
где f(x) функция, зависящая от трехмерного вектора, описывает объект;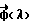 векторная функция от одного параметра, описывает траекторию источника;
векторная функция от одного параметра, описывает траекторию источника;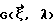 фурье-образ конусной проекции, определяется выражением:
фурье-образ конусной проекции, определяется выражением: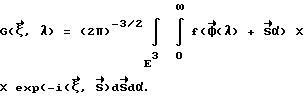
Последовательность работы данного алгоритма можно представить таким образом. Сначала для каждой точки траектории источника вычисляется 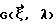 - фурье-образ конусной проекции. Затем выбирается какая либо точка
- фурье-образ конусной проекции. Затем выбирается какая либо точка  принадлежащая объекту, в которой производится реконструкция. Из этой точки проводится единичный вектор
принадлежащая объекту, в которой производится реконструкция. Из этой точки проводится единичный вектор 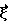 и определяется плоскость, перпендикулярная вектору
и определяется плоскость, перпендикулярная вектору 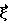 и проходящая через выбранную точку. После этого находится точка пересечения полученной плоскости с траекторией источника и параметр l из условия
и проходящая через выбранную точку. После этого находится точка пересечения полученной плоскости с траекторией источника и параметр l из условия 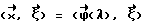 Далее вычисляется подинтегральное выражение в формуле (1). Интегрирование проводится по всем направлениям вектора
Далее вычисляется подинтегральное выражение в формуле (1). Интегрирование проводится по всем направлениям вектора 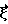 Плоскость, определяемая парой
Плоскость, определяемая парой 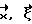 может пересекать траекторию не один, а несколько раз. В этом случае можно выбирать либо одну точку траектории, либо несколько. В последнем случае необходимо результат разделить на число учтенных пересечений.
может пересекать траекторию не один, а несколько раз. В этом случае можно выбирать либо одну точку траектории, либо несколько. В последнем случае необходимо результат разделить на число учтенных пересечений.
Наиболее неудобным в рассматриваемом способе является необходимость сканировать источником по всей траектории, даже в том случае, когда требуется реконструировать часть объекта. Это свойство относится ко всем перечисленным выше траекториям. Иными словами, для реконструкции объекта в одной точке требуются данные просвечивания со всех точек траектории. Для наиболее быстрой реконструкции требуется все эти данные помещать в оперативную память машины.
Задачей данного изобретения является создание такого способа трехмерной томографии, который позволяет с минимальными вычислительными затратами и минимальными требованиями к оперативной памяти осуществить точную реконструкцию объекта при полном сканировании или части объекта при частичном сканировании конусным пучком.
Для решения этой проблемы рассмотрим вопрос о том, какой траектории достаточно для реконструкции объекта в одной точке.
Легко доказать, что условию полноты для выделенной точки удовлетворяет траектория, которая опирается на концы отрезка прямой, проходящей через эту точку. Действительно, любая плоскость, проходящая через выделенную точку, пересекает эту траекторию.
Предположим, что объект вписывается в цилиндр единичного радиуса, а траектория представляет собой винтовую спираль, радиус которой R больше единицы, причем ось спирали и ось цилиндра совпадают. Покажем, что отрезки спирали меньше, чем длина одного витка, можно использовать для реконструкции любой точки внутри цилиндра. Выделим внутри цилиндра круг, плоскость которого перпендикулярна оси цилиндра, и рассмотрим один виток спирали, который расположен симметрично относительно этого круга. Не умаляя общности, предполагаем, что круг расположен в плоскости Z 0, тогда выделенный виток можно описать уравнениями: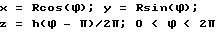
Следует доказать, что для любой точки, принадлежащей кругу x2 + y2≅ 1, z 0, найдется прямая, проходящая через эту точку, и две точки, принадлежащие витку. Поскольку эта задача не решается в аналитическом виде, были проведены численные расчеты, которые показали, что для любой точки рассматриваемого круга найдется непрерывный участок витка, удовлетворяющий поставленным условиям, если радиус спирали превышает радиус цилиндра приблизительно более чем в 1,43 раза. Результат не зависит от шага спирали (предполагается, что h < ∞ ). Если шаг выбрать достаточно большим, то объект придется просвечивать почти вдоль оси, поэтому если он вытянут, то пучок будет сильно ослабляться. Когда шаг мал, то достаточно будет лучей, просвечивающих объект по направлениям, близким к поперечным.
Алгоритмы реконструкции при спиральной траектории подразумевает следующую последовательность действий.
Выбирается плоскость, пересекающая объект, перпендикулярная оси цилиндра, в которой объект вписан.
Определяется виток спирали, расположенный симметрично относительно выбранной плоскости.
Выбирается точка объекта, принадлежащая плоскости, и для нее определяется непрерывный отрезок траектории, концы которого располагаются на прямой, проходящей через выбранную точку.
Выполняется интегрирование по формуле (1).
После реконструкции 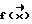 в одной плоскости происходит переход к следующей, отстоящей на небольшом расстоянии и параллельной предыдущей. Следующий виток спирали, необходимый для реконструкции, будет частично совпадать с предыдущим. Часть данных спирали с одной стороны его будет отброшена, а с другой добавлена в оперативную память. Объект может быть просканирован не по всей длине и при этом может быть получена точная реконструкция той части объекта, для которой проекционные данные достаточны.
в одной плоскости происходит переход к следующей, отстоящей на небольшом расстоянии и параллельной предыдущей. Следующий виток спирали, необходимый для реконструкции, будет частично совпадать с предыдущим. Часть данных спирали с одной стороны его будет отброшена, а с другой добавлена в оперативную память. Объект может быть просканирован не по всей длине и при этом может быть получена точная реконструкция той части объекта, для которой проекционные данные достаточны.
Предлагается способ трехмерной вычислительной томографии на основе регистрации конусных проекций, позволяющий получать без искажений внутреннюю структуру объекта по частям, при этом размер объекта по одной из координат может быть произвольным, а для реконструкции объекта в каждой точке используются данные просвечивания минимальной части траектории источника, что минимизирует требуемый размер оперативной памяти. Полученные результаты могут быть применены для медицинской томографии, а также для контроля промышленных объектов.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ДОСМОТРА ГРУЗОВ С ИСПОЛЬЗОВАНИЕМ СПИРАЛЬНОГО СКАНИРОВАНИЯ | 2007 |
|
RU2396551C1 |
| СПОСОБ ДОСМОТРА ГРУЗОВ С ИСПОЛЬЗОВАНИЕМ ПРОСВЕЧИВАНИЯ ИЗЛУЧЕНИЕМ ПОД РАЗНЫМИ УГЛАМИ | 2007 |
|
RU2400735C2 |
| СИСТЕМЫ СПИРАЛЬНОЙ КТ И СПОСОБЫ РЕКОНСТРУКЦИИ | 2015 |
|
RU2595312C1 |
| СПОСОБ КАЛИБРОВКИ НА ОСНОВЕ АЛГОРИТМА НАХОЖДЕНИЯ ЦЕНТРА ВРАЩЕНИЯ ДЛЯ КОРРЕКЦИИ КОЛЬЦЕВЫХ АРТЕФАКТОВ В НЕИДЕАЛЬНЫХ ИЗОЦЕНТРИЧЕСКИХ ТРЕХМЕРНЫХ ВРАЩАТЕЛЬНЫХ РЕНТГЕНОВСКИХ СКАНИРУЮЩИХ СИСТЕМАХ С ИСПОЛЬЗОВАНИЕМ КАЛИБРОВОЧНОГО ФАНТОМА | 2009 |
|
RU2526877C2 |
| СПОСОБ ТОМОГРАФИЧЕСКОГО КОНТРОЛЯ КРУПНОГАБАРИТНЫХ ГРУЗОВ | 1993 |
|
RU2072513C1 |
| УСТАНОВКА ДЛЯ ДОСМОТРА ГРУЗОВ | 2007 |
|
RU2386954C1 |
| СПОСОБ ОПТИЧЕСКОЙ ТОМОГРАФИИ ТРЕХМЕРНЫХ МИКРООБЪЕКТОВ И МИКРОСКОП ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1999 |
|
RU2145109C1 |
| СИСТЕМА СКАНИРОВАНИЯ Х-КТ | 2006 |
|
RU2394494C2 |
| УСТРОЙСТВО ДЛЯ ОБРАБОТКИ ИЗОБРАЖЕНИЯ, СПОСОБ ОБРАБОТКИ ИЗОБРАЖЕНИЯ И СРЕДА ДОЛГОВРЕМЕННОГО ХРАНЕНИЯ ИНФОРМАЦИИ | 2011 |
|
RU2510080C2 |
| СПОСОБ РЕНТГЕНОВСКОГО КОНТРОЛЯ ВНУТРЕННЕЙ СТРУКТУРЫ ИЗДЕЛИЯ | 2019 |
|
RU2718406C1 |
Использование: способ трехмерной компьютерной томографии может быть применен в медицинской диагностике и контроле промышленных объектов. Сущность изобретения: способ предусматривает сканирование объекта конусным пучком излучения путем перемещения источника излучения по некоторой траектории, регистрацию посредством экрана -преобразователя, прошедшего через объект излучения, и восстановления трехмерного изображения по проекционным данным. Для реконструкции объекта в каждой точке используют проекционные данные не всей траектории источника, а ее минимального отрезка, удовлетворяющего условию полноты для данной точки.
Способ трехмерной компьютерной томографии, включающий сканирование объекта конусным пучком путем перемещения источника по некоторой траектории, регистрацию посредством экрана-преобразователя, прошедшего через объект излучения, и восстановление трехмерного изображения по проекционным данным, отличающийся тем, что для реконструкции объекта в каждой точке используют проекционные данные не всей траектории, а ее минимального отрезка, удовлетворяющего условию полноты для данной точки.
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Tuy H.K | |||
| An Inversion formula for cone-beam reconstruction SIAMJ, Appl Math 43, 1983, p | |||
| ВРАЩАТЕЛЬНЫЙ АППАРАТ С ТУРБИННЫМ ДВИГАТЕЛЕМ ДЛЯ ГИДРАВЛИЧЕСКОГО БУРЕНИЯ СКВАЖИН | 1922 |
|
SU546A1 |
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Smith B.D | |||
| Cone-beam tomography: recent and a tutarial Optics Engineering, v | |||
| Солесос | 1922 |
|
SU29A1 |
| МАШИНА ДЛЯ ПРОИЗВОДСТВА ПОДЗЕМНЫХ РАБОТ | 1919 |
|
SU524A1 |
Авторы
Даты
1997-12-20—Публикация
1996-07-26—Подача