СПОСОБ ПОВЫШЕНИЯ ДОЛГОВЕЧНОСТИ ДЕТАЛЕЙ ПОДВИЖНЫХ СОЕДИНЕНИЙ МЕХАНИЗМОВ МАШИН Российский патент 1998 года по МПК G01N3/56 

Изобретение относится к машиностроению и может быть использовано при нанесении износостойких покрытий на трущиеся поверхности деталей, входящих во вращательные кинематические пары механизмов рабочих машин.

Наиболее близким к изобретению является способ, учитывающий распределение износа трущихся поверхностей звеньев механизмов, входящих во вращательную кинематическую пару. Характер изношенных поверхностей в этих случаях определяется нагрузкой (давлением) в зоне контакта и направлением прижимного усилия по отношению к подвижной или неподвижной деталям звеньев.

Однако в рассмотренных примерах не учитывается закон относительного вращения деталей, входящих в кинетическую пару. Как известно закон относительного вращения звеньев зависит от типа механизма и соотношения размеров подвижных звеньев. В рассмотренном способе не учитывается также характер изменения сил в подвижных соединениях. Как известно силовое взаимодействие определяется не только кинематикой (аналогами скоростей и ускорений), но и соотношениями сил движущих и сил полезного сопротивления. Речь идет от том, что реакции в кинематических парах механизмов машин в каждом конкретном значении обобщенной координаты (угла поворота приводного вала) будут различными. Определение их значений в каждом таком положении требует учета индивидуальных особенностей силового взаимодействия отдельных звеньев, их веста, кинематических особенностей относительного движения, а также сил трения в подвижных соединениях. Кроме этого, требуется также учитывать как силы движущие, так и силы технологического (полезного) сопротивления. Другими словами, в отличие от рассмотренного предлагается в оценку конфигурации изношенных поверхностей положить не механизм, а так называемый машинный агрегат, объединяющий в себе привод (двигатель, коробку скоростей), исполнительный механизм, к выходному звену которого приложена сила технологического сопротивления. Иначе говоря, предлагается в основу оценки эпюры износа трущихся поверхностей детали положить силовые, кинематические, массовые и геометрические характеристик конкретной рабочей машины с конкретным двигателем. Такой подход позволит более точно выявить особенности износа трущихся поверхностей подвижных звеньев. Кроме этого, представляется также возможность особенности износа каждой кинетической пары в отдельности. Это в свою очередь, позволяет решить не только проблемы повышения долговечности за счет выявления износа наиболее интенсивно изнашивающихся соединений но и, что немаловажно, решить проблему равноресурсности по износу всех кинематических мер механизмов, входящий в конкретную машину, например, путем формирования износостойких покрытий с различным значением их коэффициентов износа.

Для достижения такого повышения долговечности предлагаются износостойкие покрытия, наносимые на трущиеся поверхности деталей в поперечном направлении, наносить в соответствии с эпюрами их износа так, чтобы на участки поверхности и большим износом наносить покрытия, отличающиеся большей износостойкостью и наоборот. При этом, как отмечалось ранее, при оценке конфигурации изношенных поверхностей подвижных соединений звеньев скорости скольжения и давление в них определяются с учетом кинематических и динамических характеристик машины в целом, т.е. с учетом характеристики приводного двигателя и силы технологического сопротивления.

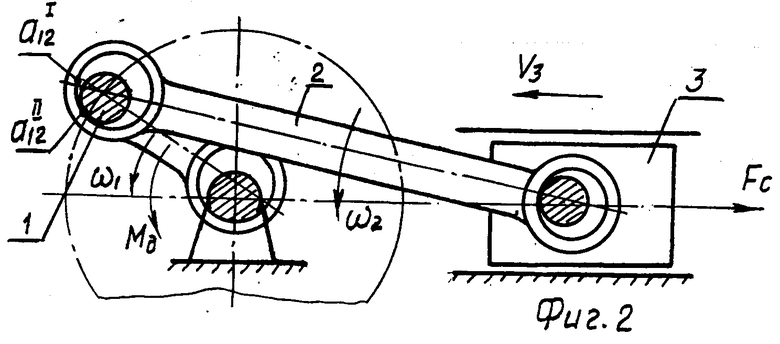
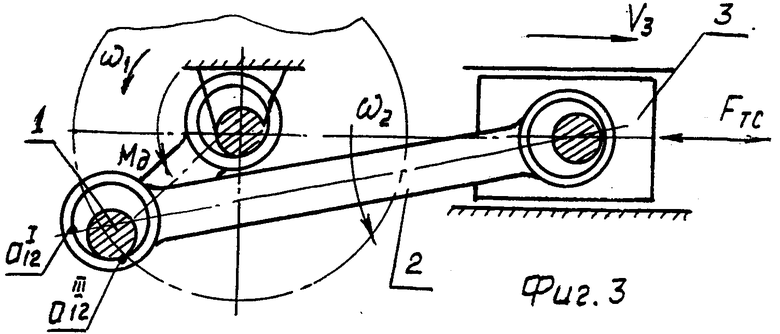
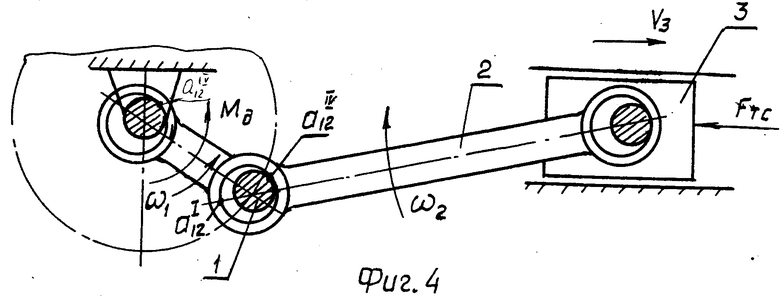
Ко всему сказанному предлагается учитывать также то, что обобщенная скорость машины (скорость вращения ее главного приводного вала) внутри цикла не остается постоянной, а изменяется. Неравномерность вращения приводного вала машины (неравномерность угловой скорости ω₁ , например, кривошипа (см. фиг. 1-4) предлагается учитывать тем, что действительное значение ω₁ определяют, рассматривая динамику всей машины (машинного агрегата).

Решение уравнения движения в дифференциальной или интегральной формах позволяет определить скорость ω₁ и ускорение ε₁ . Действительные же скорости V_si и ускорения a_si точек, совпадающих с центрами масс S_i подвижных звеньев, а также угловые скорости и ускорение ε_i этих звеньев определяются по формулам: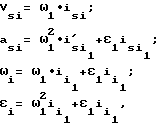

где ω₁, ε₁ - обобщенные скорость и ускорение (скорости и ускорение кривошипа, определенные в результате решения динамических уравнений); 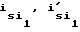- аналоги скорости и ускорения центра масс i-того звена.

Таким образом, определив действительные ускорения звеньев механизма, представляется возможным учесть и действительные значения сил инерции. Этим самым представляется возможность отразить особенности влияния выполняемой технологической операции и характеристики приводного двигателя на характер износа трущихся поверхностей конкретного исполнительного механизма.

На фиг. 1-4 схематично даны особенности контактного взаимодействия трущихся поверхностей подвижных соединений.

На фиг. 1 схематично показано положение точек (зон) контакта подвижных соединений в процессе преобразования движения. Например, общая точка контакта aI12

(см. фиг. 1) перемещается в положение aII12 (см. фиг. 2) и далее в положение aIII12 (см. фиг. 3), и еще далее в положение aIV12 (см. фиг. 4). Рассмотренный пример (фиг. 1 - фиг. 4) отражает схематично закономерности контактного взаимодействия звеньев, входящих во вращательные кинематические пары при наличии F_c сопротивления, приложенной к звену 3 и момента движущих сил M_g, приложенного к звену 1. Поэтому нетрудно представить себе, что ко всему сказанному при оценке износа звеньев, входящих во вращательные кинематические пары, следует учитывать также и соотношение сил как движущих, так и сил сопротивления. В каждом отдельном случае должны учитываться как силы сопротивления и силы (моменты сил) движущие, так и силы веса звеньев и инерционные силы и моменты. Следует отметить также, что в процессе изнашивания (с учетом вышеперечисленных параметров) меняется и конфигурация трущихся деталей, входящих в кинематические пары. При этом для каждого конкретного случая, а именно:
- для конкретной технологической операции;
- для конкретного приводного двигателя;
- типа исполнительного механизма машины;
- размеров его звеньев;
- массовых характеристик подвижных звеньев
конфигурация изношенных поверхностей трудящихся деталей будет вполне определенной. Другими словами, зазоры в подвижных соединениях, образованные износом, должны быть определены моделированием процесса изнашивания с учетом вышеперечисленных параметров. Конечно же время (количество циклов), в течение которого происходит образование одинаковых зазоров во всех кинематических парах, будет разным. Поэтому встает вопрос о распределении износостойкости трущихся деталей, обеспечивающим одинаковое время (количество циклов), в течение которого все кинематические пары изнашивались бы на одинаковую величину. Этим самым достигается равный ресурс выработки по износу всех подвижных соединений машины. Часто требуется увеличить износостойкость отдельной кинематической пары, как наиболее нагруженной и быстро изнашивающейся. В этом случае требуется знать характер износа такого соединения, обусловленный вышеперечисленными параметрами.

Таким образом, вопрос о рациональном распределении износостойкости трущихся поверхностей деталей, входящих в кинематические пары подвижных соединений всей машины, должен решаться с учетом массовых, геометрических кинематических характеристик подвижных звеньев, сил (моментов) движущих и сил (моментов сопротивления).

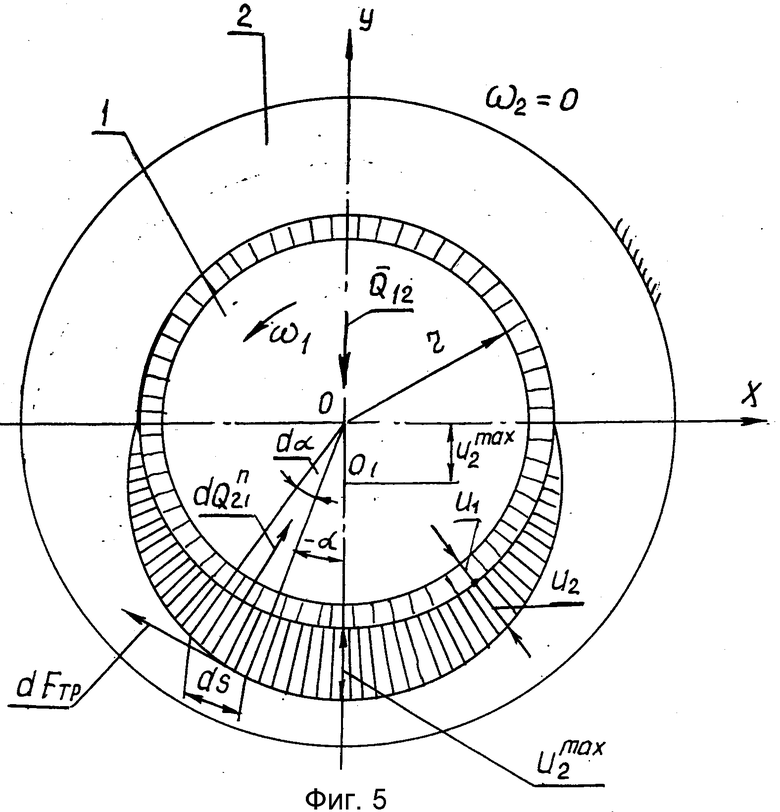
Рассмотрим пример, поясняющий необходимость такого подхода. Пусть вал 1 (см. фиг. 5) вращается равномерно в подшипнике, т.е. ω₁= const, ω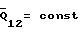·2

= 0 , при этом нормальное усилие . В этом случае U₁=const (вал 1 будет изнашиваться равномерно), а U₂ - переменная величина - подшипник будет изнашиваться неравномерно. Через некоторое число циклов работы центр вала переместиться из положения O в положение O₁, следовательно, износ подшипника 2 в направлении вектора силы 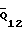будет во всех точках рабочей поверхности одинаковым и равным Umax2= 00₁ , а в направлении нормали и поверхности трения различным, изменяясь, согласно фиг. 5 по закону косинуса:
U₂= Umax2 cosα, (1) ,
где α - угловая координата рассматриваемой точки подшипника 2.

Так как скорость скольжения одинакова для всех точек, (V_ck =const) то и закон распределения давления будет косинусоидальным
P = P_maxcosα. (2) .

Для определения максимального давление P_max в точке, находящейся на линии действия силы 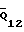, рассмотрим элементарную площадку на втулке подшипника шириной dS = rdα и длиной b (b - размер, перпендикулярный плоскости чертежа).

Элементарная сила в направлении нормали к поверхности трения, приложенная к валу (см. фиг. 5), определяется так:
dQn21

= PbdS = P_maxb•r•cosα•dα
Сила 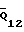уравновешена суммой проекций сил dQn21 на ось y, поэтому
,
откуда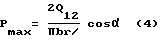

тогда уравнение 2 примет вид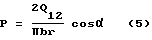

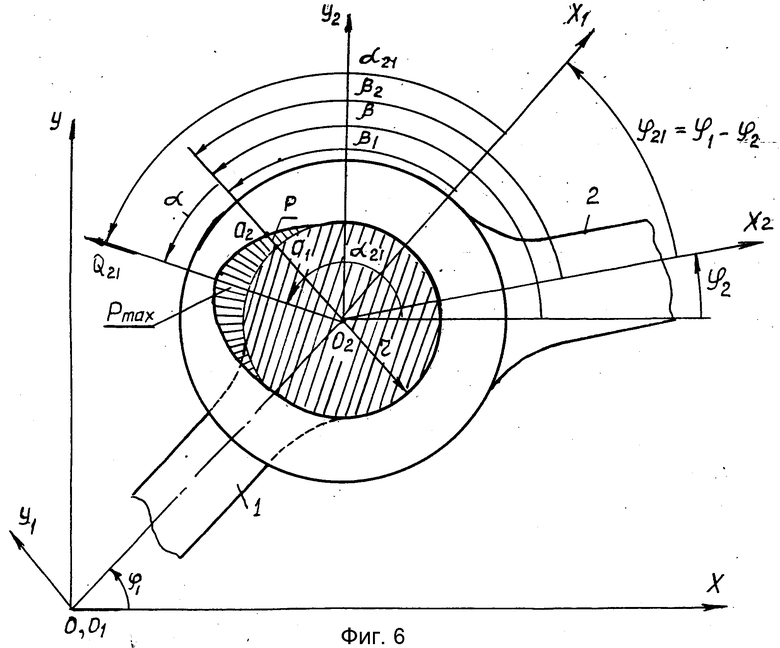
Рассмотренный пример может быть использован только для оценки износа соединения кривошипа 1 со станиной 0 (см. фиг. 1-4) и то с большими погрешностями. Для случая, например, вращательной пары 1-2 рычажного механизма с обобщенной координатной Y₁ (фиг. 6) при переменной по модулю и направлению Q₁₂ формула (5) должна применяться для каждого мгновенного положения. Поэтому при определении одного из элементов пары (например, звена 1 в некоторой точке a) нужно знать угловую координату J₂₁ (см. фиг. 6) и угловую координату α₂₁= α₂₁(ϕ₂₁) вектора силы 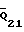, приложенной к этому звену со стороны звена 2, а также в системе координат X₁O₁Y₁, связанной со звеном 1, - угловую координату β используемой точки a₁.

Тогда давление P в точке a₁ определится по формулам (2), (4)
P = P_maxcosα⁽¹⁾, (6) ,
где

а угловая координата α = α⁽²⁾ рассматриваемой точки, например, в системе координат X₂, O₂, Y₂ измеряется от направления вектора силы 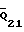, согласно фиг. 6, определяется по формуле
α = α⁽²⁾= α₂₁-β₂+ϕ₂₁ (8)
В системе координат X₁0₁Y₁ координат имеет вид
α = α⁽¹⁾= α₂₁-β₁ (9)
Как видно из фиг.6, связь между углами β в неподвижной системе координат XOY, β₁ и β₂ определится выражением
β-β₂= ϕ₂ (10)
или
β-β₁= ϕ₁ (11)
Таким образом координата α⁽¹⁾ для построения эпюры u₁= f(α) износа первого звена и α⁽²⁾ для построения эпюры износа второго позволяет определить характер износа звеньев в системах, связанных со звеньями. При этом, если 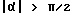, то p=0.

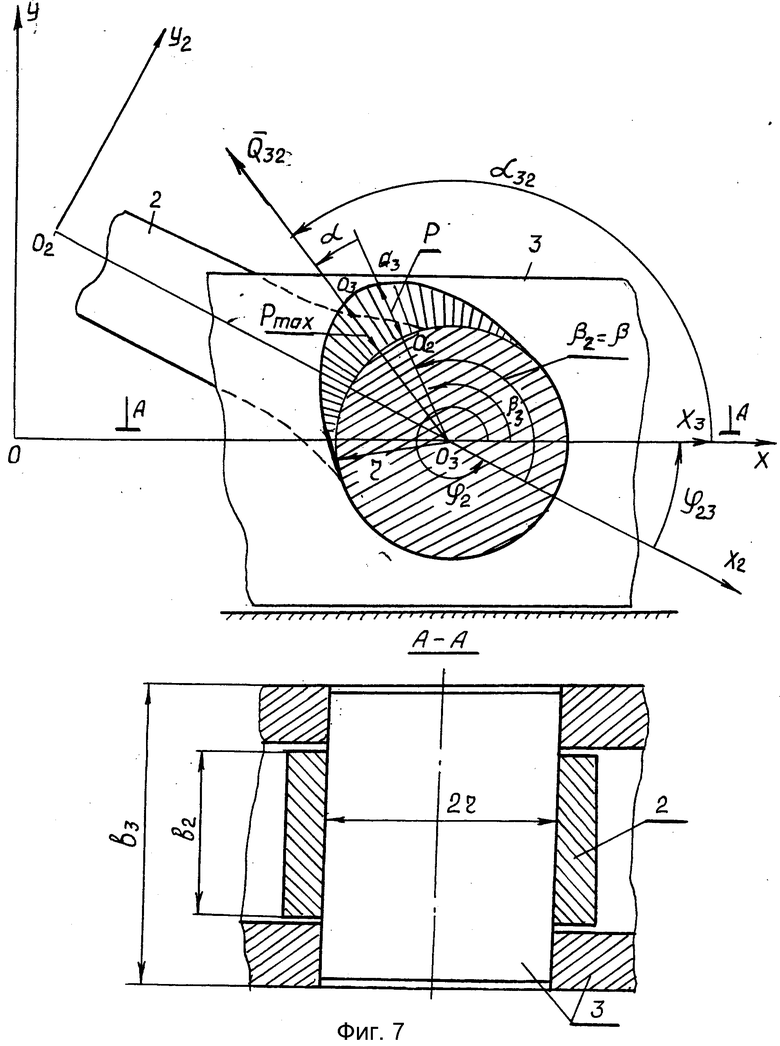
В этом случае имеет место разрыв контакта. Угол α₂₁ вектора силы 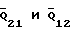в подвижных системах координат или в неподвижной определяется по методике, изложенной выше. Если звено 2 входит во вращательную кинематическую пару со звеном 3, то методика определения соответствующих координат остается в силе, меняются только соответствующие индексы. Если же звено 2 входит во вращательную кинематическую пару со звеном, совершающим поступательное движение, то угловые координаты имеют вид (см. фиг.7).

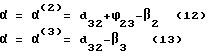
При совпадении осей X неподвижной системы координат с осью X₃ системы, связанной с третьим звеном (ползуном) β = β₃ и скоростью скольжения в точках a₂ и a₂ (см. фиг.6) определяется соотношением
v(12)ск

= ω₁₂r = (ω₁-ω₂)r (14)
Для кинетической пары звено 2 с ползуном 3 (фиг.7) имеем
v(23)ск= ω₂₃r = ω_2r (15),
т.к. ω₃= 0.
Если начальное звено механизма обозначено номером 1, то аналог скорости скольжения для вращательной пары 1-2 определиться выражением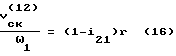

Для схемы соединения звеньев на фиг.7 имеем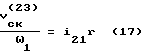

Износ в некоторой точке a₁ с координатой β₂ (см. фиг.6) за 1 цикл (чаще всего на 2π) определится совместным решением уравнений (6), (7), (9), (16) и подстановкой их в уравнение dU=kpV_ckdt, где 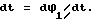. После преобразований получим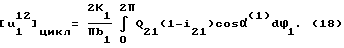

Для точки a₂ звена 2 с координатой β₂ износ за 1 цикл определится аналогично.

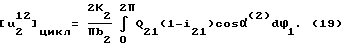
Здесь α⁽²⁾ определяется выражением (8) k₁k₂ - коэффициенты износа материалов звеньев 1 и 2, b₁ - ширина (длина) рабочих участков подшипника скольжения. Для вращательной климатической пары, образованной вращающимся звеном и ползуном (фиг.7) имеем: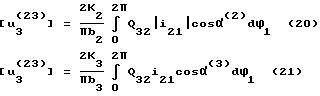

Здесь b₂ - ширина (длина) подшипника скольжения.

В уравнениях (20), (21) углы α⁽²⁾ и α⁽³⁾ определяются выражениями (12), (13). Задаваясь рядом значений углов β₁β₂(β₂β₃) , определяется ряд значений износа и строится эпюра за время, соответствующее N_ц циклом, с использованием формулы
U = U_ц • N_ц
где U_ц - износ за 1 цикл, N_ц - количество циклов нагружения.

В доказательство того, что вышеперечисленные параметры оказывают существенное влияние на износ трущихся поверхностей, приведем результаты численного исследования, проведенного с использованием ЭВМ, конечной целью которого было построение эпюр распределения ожидаемого износа элементов вращательной пары 2-3 (шатун-поршень).

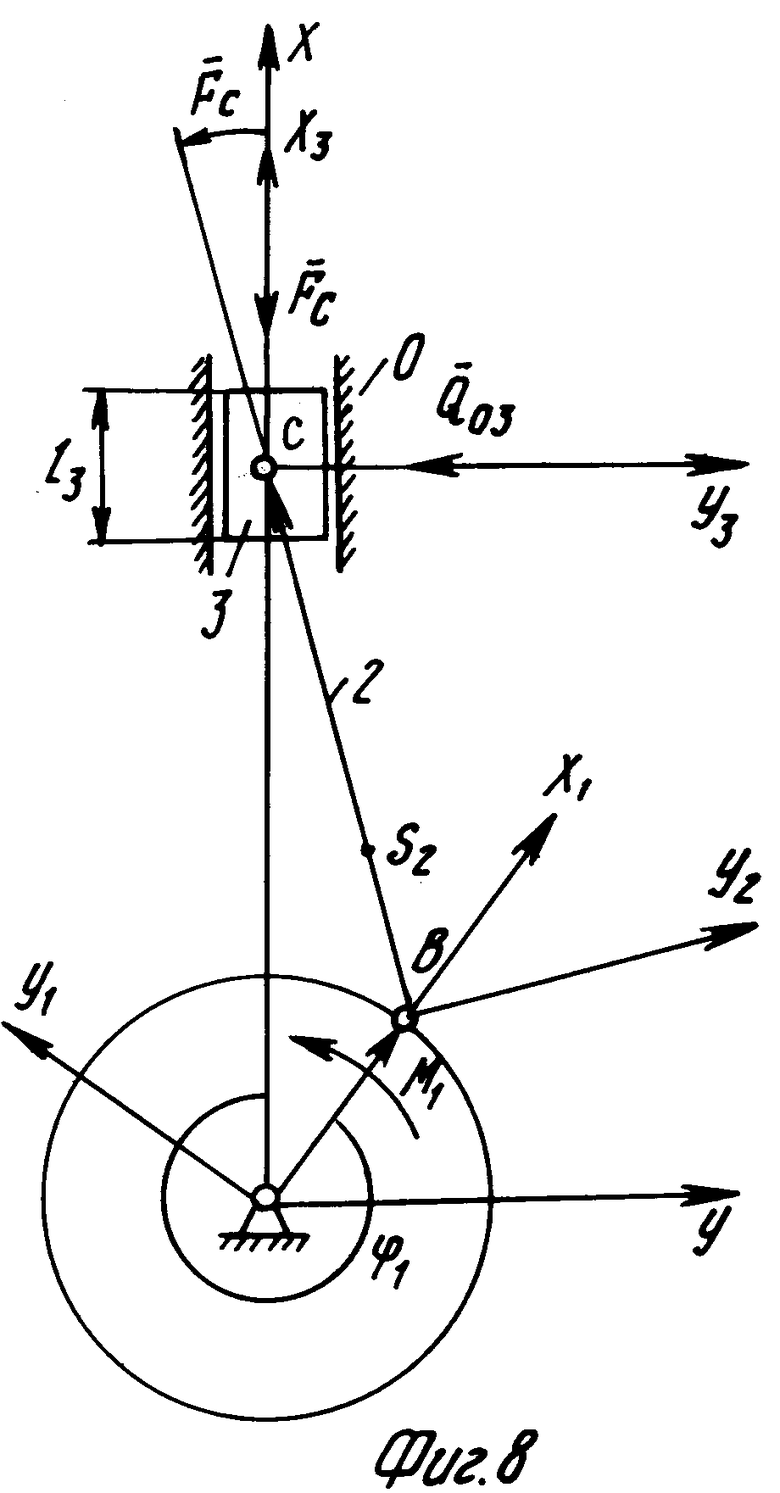
В качестве исполнительного механизма выбран кривошипно-ползунный механизм вертикальной поршневой машины со следующими геометрическими и массовыми характеристиками (см. фиг.8):
1. l₁ = 0,086 м - длина кривошипа;
2. λ_e= l₂/l₁= 4,85 - относительная длина шатуна,
3. λ_S2= l_BS2/l_BS= 0,3 - относительная длина (координата) центра масс шатуна;
4. λ_e= l/l₁= 0 - относительный эксцентриситет, определяемый расстояниями между осями X и X₃;
5. массы звеньев: m₁ = 104 кг, M₂ = 14 кг, m₃ = 12 кг;
6. приведенный момент инерции привода машины к звену приведения (кривошипу) J1/n = 9,43 кгм²;
7. момент инерции шатуна 2 относительно его центра масс J³² = 0,32 кгм²;
8. Частота вращения кривошипа n₁ = 12,16 1/с.

Значения действительной угловой скорости ω₁= ω₁(ϕ₁) и силы F_с технологического сопротивления F_c= f(ϕ₁) приведены в таблице. Результаты кинематического и силового расчета приведены также в таблице.

Для построения эпюры износа элементов кинематических пар 2-3 необходимы следующие дополнительные исходные данные:
d₃ = 0,230 м - диаметр цилиндра 3,
2r = 0,040 м - диаметр поршневого пальца,
b₂ = 0,150 м - длина рабочей части поршневого пальца,
N_ц = 10⁸ - расчетное число циклов.

При частоте вращения кривошипа n₁ = 12,16 1/с = 730 об/м продолжительность работы механизма определится из выражения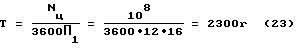

Среднее давление для пары 2-3 в точках рабочей поверхности, расположенных в плоскости, совпадающей с вектором 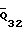, определим по формуле (7) по среднеарифметическому значению P(23)ср

, подсчитанному по позициям из таблицы.

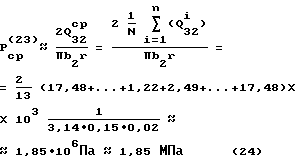
Примем для пары 2-3 сочетание (подшипниковый сплав-сталь). Тогда для втулки подшипника имеем следующую интенсивность изнашивания J_s2 = 4,•10^-10, для поршневого пальца интенсивность изнашивания J_s3 = 1,6•10^-12.

Тогда коэффициенты износа определятся следующим образом

Далее оценка характера износа требует определения его величины в отдельных точках, например, a₂ и a₃ (см. фиг.7), определяемых координатами β₂ и β₃ соответственно. Для этого определяются углы α⁽²⁾ и α⁽³⁾ по формулам (12), (13), используя данные, приведенные в таблице для N позиций по углу ϕ₁ поворота кривошипа (начального звена). Затем cosα⁽²⁾ и cosα⁽³⁾ при этом, если α⁽²⁾ или α⁽³⁾ ≥ π/2/ , контакт отсутствует и давление P=0.

Далее определяются значения произведений .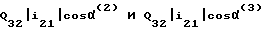

Значение Q₃₂ и i₂₁ в функции ϕ , приведены в таблице. Значения cosα⁽²⁾ и cosα⁽³⁾ , как было сказано выше, определяются формулами (12), (13) для конкретных значений углов β₂ и β₃ . В качестве примера определим для вращательной пары 2-3 износ U₂ в точке Q₂ (см. фиг. 7) элемента звена 2 с координатой β₂= 150^° , измеряемой от оси X₂. Значения угла α⁽²⁾, cosα⁽²⁾ и произведения 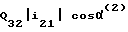приведены в таблице. Износ в точке Q₂ за принятое время T работы определится из соотношений (20), (22) по формуле
.

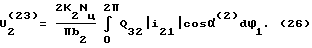Выражение (26), определяющее износ в мкм для рассматриваемого примера примет вид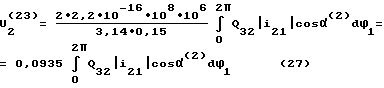
.

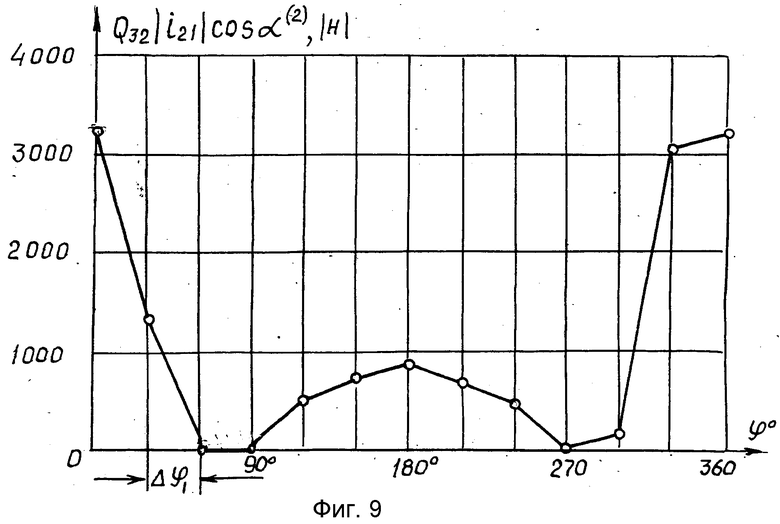
Приближенное значение интеграла в выражении (27) определим суммой площадей прямоугольников, высотой, равной полусумме соседних координат, и шириной Δϕ = 2π/12 радиан из фиг. 9, построенного по результатам, приведенным в таблице.

В этом случае имеем
.

Тогда износ в точке Q₂ за все время работы машины определится как произведение циклового износа на количество циклов, т.е.

U(23)2

= 0,0935•5730 ≈ 0,54 мкм .

Аналогично определяют износ в других точках Q₂, фиксированных в системе координат X₂O₂Y₂ с помощью угла α⁽²⁾ , определяемого по формуле (12) с другими значениями β₂ . На фиг. 10 построена эпюра износа рабочей поверхности звена 2, охватывающая зону 180^o при 60^o≤β≤ 240^o (см. фиг. 7). Суммарный износ рабочей поверхности поршневого пальца определяется суммой износов в отдельный ее зонах. Считая износ в зонах, разбитых на 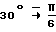, постоянным (см. фиг. 10), получим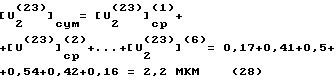

полученный линейный износ характеризует потерю размера рабочей поверхности поршневого пальца. При оценке массового или весового износа общий объем продуктов износа пропорционален 2,2 мкм. Объем же продуктов износа по выделенным участкам рабочей поверхности пропорционален высотам соответствующих прямоугольников на фиг. 10. Поэтому цель изобретения может быть достигнута выравниванием износа отдельных участков рабочей поверхности в соответствии с требуемым (напередзаданным) износом. В рассматриваемом примере требуемым будем считать равномерный износ по всей поверхности [U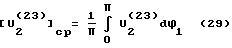(23)2

]₈ (см. фиг. 10). Как известно, форма (конфигурация) изношенной поверхности определяет закон перераспределения давления в зоне контакта трущихся поверхностей. Поэтому повышение долговечности подвижных соединений машины может быть достигнуто и при неравномерном, и другом наперед заданном их износе, обеспечивающем выравнивание давления. Однако в том и другом случае желательно не увеличивать общий (суммарный) объем продуктов износа (суммарный линейный износ). Здесь требуется более благоприятное его распределение по отношению к тому, который был получен при принятом неизменном значении коэффициента износа K (в нашем примере K₂ = 2,2•10^-16). Таким образом, задача сводится к тому, чтобы суммарный полученный неравномерный износ [U(23)2]_сум= 2,2 мкм определялся бы суммой износов такого же количества участков рабочей поверхности с равномерным их износом. Это означает, что площадь, ограниченная кривой фиг. 10, должна быть равна площади прямоугольника шириной π и высотой [U232]_ср , определяемой из соотношения
.

Заменяя площадь под кривой U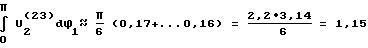(23)2

суммой площадей прямоугольников, получим
.

С учетом последнего соотношения, выражение (29) дает: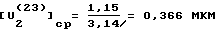
.

Из фиг. 10 видно, что каждый участок поверхности в пределах выбранного значения Δϕ износился в соответствии с высотами прямоугольников [U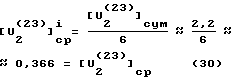(32)2

]iср . Задача же сводится к обеспечению условий равномерного износа, определяемого высотой прямоугольника [U(23)2]_ср . Таким образом, равномерность износа всей рабочей поверхности требует того, чтобы величина [U(23)2]_сум= 2,2 мкм определялась бы суммой равных износов
.

Такое выравнивание можно произвести путем перераспределения коэффициента износа Ki2

по выбранным участкам (см. фиг. 10). В основу такого выравнивания можно положить то, что выровненный средний износ [U(23)2]iср на каждом участке равен среднему износу [U(23)2]_ср на всей рабочей поверхности (см. соотношение 30).

Примем среднее значение силы [Q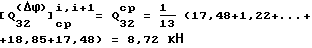(Δϕ)32

]i,i+1ср реакции во вращательной паре 2 равным среднеарифметическому значению силы Qср32 , подсчитанному по N позициям из таблицы, тогда
.

В соответствии формулой (26) может записать следующие выражения, определяющие износ:
.

.

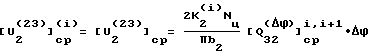Из следующих соотношений получим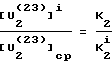

или окончательно имеем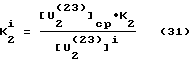
.

Соотношение (31) позволяет получить закон распределения коэффициента износа Ki2

по рабочей поверхности, обеспечивающий ее заданный равномерны износ всей поверхности при условиях, обеспечивающих неравномерное изнашивание отдельных ее участков. Оно позволяет "управлять" конфигурацией изношенной поверхности, выравнивая эпюру распределения износа на отдельных участках и тем самым получать желаемую эпюру распределения путем подбора коэффициентов износа.

Для рассматриваемого примера с учетом принятого допущения о том, что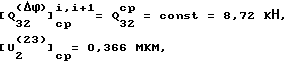
,
а также значений [U(23)2

]iср = в соответствии с фиг. 10 выражение (31) дает:

.

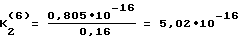На фиг. 11 представлено коэффициентов Ki2

износа, обеспечивающее принятое равномерное распределение износа по рабочей поверхности поршневого пальца в поперечном направлении.

Физический смысл коэффициента K₂ в формуле (20) раскрыт на стр. 7. Как видно из формулы (20), чем большее значение имеет K₂, тем больший износ рабочей поверхности. Поэтому, чем большее значение имеет коэффициент [K(Δϕ)2

]ⁱ , подсчитанный по формуле (31) (см. фиг. 10, 11), на каком-либо участке Δϕ тем более износостойкий материал требуется нанести на данный участок по сравнению с другими участками. Таким образом, распределение износостойкости покрытия, наносимого на рабочую поверхность поршневого пальца в соответствии с полученными значениями коэффициентов [K(Δϕ)2]ⁱ износа по участкам 1...6, приводит к выполнению поставленной цели.

В данном примере это означает, что вся поверхность в среднем износится на 2,2 мкм с износом на каждом участке по 0,366 мкм. Это означает, что общий объем наносимого износостойкого покрытия остается постоянным, но перераспределяется по отдельным участкам в соответствии с фиг. 11.

Пусть в соответствии с рассматриваемым примером при длине поршневого пальца b₂ = 150 мм и диаметре 2r=40 мм и износе его рабочей поверхности на [U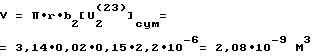(23)2

]_сум= 2,2 мкм объем продуктов износа составит
.

Этот объем износостойкого материала может быть использован для восстановления изношенной поверхности с перераспределением его по зонам в соответствии с фиг. 11 из условий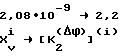

или объем износостойкого материала X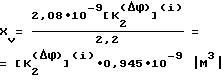iv

по участкам распределится в соответствии с формулой
.

В рассматриваемом примере предполагалось равномерное распределение износа вдоль длины l₂ рабочей поверхности поршневого пальца.

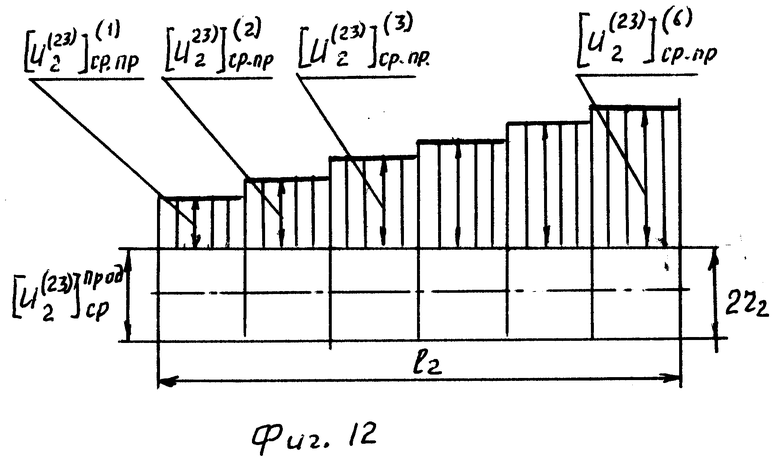
Если же в результате, например, неравномерного распределения давления, обусловленного изменением точки приложения реактивной силы вдоль оси, рабочая поверхность пальца износится неравномерно (см. фиг. 12), то алгоритм достижения равномерного износа остается прежним.

В этом случае формула (31) будет иметь тот же вид, но входящие в нее параметры будут относиться к продольному (осевому) измерению, т.е.

,
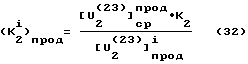где (Ki2

) - коэффициент износа i-того участка рабочей поверхности поршневого пальца в осевом направлении;
[U(23)2]продср - средний постоянный износ рабочей поверхности, соответствующий выбранному коэффициенту K₂ износа;
[U(23)2]iпрод - износ i-того участка рабочей поверхности в продольном направлении.

Если предложенный алгоритм будет использован для выравнивания износа всех подвижных соединений исполнительного механизма машины при выбранном первоначальном одинаковом для всех коэффициентов износостойкости, то после перераспределения коэффициента износостойкости все подвижные соединения износятся равномерно на определенную (известную) величину за одно и то же время T работы машины (за одно и то же количество циклов нагружения). В этом случае при определении среднего суммарного износа по предлагаемой методике будет выявлено слабое звено (подверженное наибольшему износу за время работы машины). Это дает возможность ранжировать по степени изнашивания все подвижные соединения машины. После этого, используя предлагаемый способ перераспределения коэффициентов износа, достигается равноресурсность всех подвижных соединений машины по износу их рабочих поверхностей.

Сущность изобретения: способ повышения долговечности деталей подвижных соединений механизмов машин заключается в том, что перед приведением соединения "вал - втулка" в движение определяют длину b и r одной из деталей соединения и рассчитывают коэффициент износа К детали из зависимости К=Y/P_cр, где P_cр - среднее давление в соединении за цикл, равное 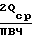, где Q_cp - среднеарифметическое значение силы реакции в соединении за цикл, Y - интенсивность изнашивания, а цикл - время одного оборота вала, перед определением распределения износа трущейся поверхности разбивают трущуюся поверхность детали на i участков и определяют износ в точках на границе каждого участка из зависимости 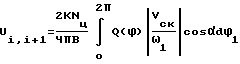, где dϕ₁ - приращение угла поворота вала машины; N_ц - заданное расчетное число циклов нагружения; V_cк = V₁ - V₂ - абсолютные линейные скорости в точке их соприкосновения; α - угловая координата точки, лежащей на трущейся поверхности детали в системе координат, связанной с соединением, определяют суммарный износ U_сум трущейся поверхности, как сумму износа в точках на границе каждого участка, средний износ Uсрi,i+1

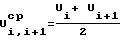из зависимости , средний суммарный износ U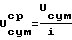срсум из зависимости и коэффициент износа K_i на каждом участке из зависимости 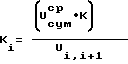, по которому судят о распределении износа, а нанесение покрытия осуществляют в зависимости от величины K_i, причем на участках с большим K_i наносят более износостойкое покрытие, все операции повторяют для другого элемента соединения. 1 з.п.ф-лы, 12 ил., 1 табл.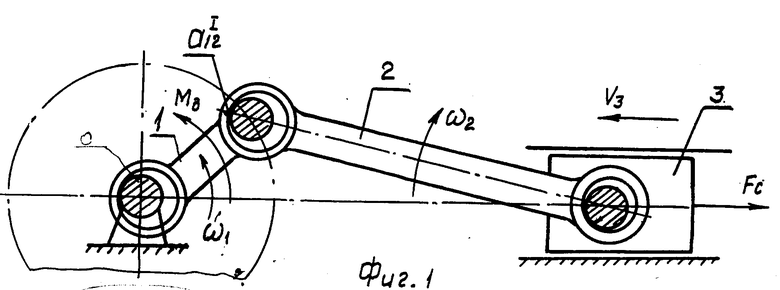

Способ повышения долговечности деталей подвижных соединений механизмом машин, заключающийся в том, что соединение типа "вал-втулка" приводят в движение, определяют давление на трущейся поверхности и направление прижимного усилия и определяют распределение износа трущейся поверхности, с учетом которого наносят на трущиеся поверхности износостойкое покрытие, отличающийся тем, что, перед приведением соединения в движение, определяют длину b и радиус r одной из деталей соединения и рассчитывают коэффициент износа K детали из зависимости K = J/P_с р, где P_с р - среднее давление в соединении за цикл, равное 2Q_ср/πbr , где Q_с р - среднеарифметическое значение силы реакции в соединении за цикл, J - интенсивность изнашивания, а цикл - время одного оборота вала, перед определением износа трущейся поверхности разбивают трущуюся поверхность детали на i участков и определяют износ в точках на границе каждого участка из зависимости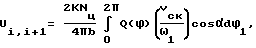

где dϕ₁ - приращение угла поворота вала машины;
N_ц - заданное расчетное число циклов нагружения;
V_с к = V₁ - V₂ - скорость скольжения на трущейся поверхности детали;
V₁ - V₂ - абсолютные линейные скорости в точке их соприкосновения;
α - угловая координата точки, лежащей на трущейся поверхности детали в системе координат, связанной с соединением,
определяют суммарный износ U_с у м трущейся поверхности как сумму износа в точках на границе каждого участка, средний износ U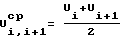срi,i+1

из зависимости
,
средний суммарный износ U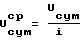2сум из зависимости

и коэффициент износа K_i на каждом участке из зависимости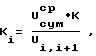

по которому судят о распределении износа, а нанесение покрытия осуществляют в зависимости от величины K_i, причем на участках с большим K_i наносят более износостойкое покрытие, все операции повторяют для другого элемента соединения.