Изобретение относится к автоматике и вычислительной технике и может быть использовано в дискретных автоматах для сложения-вычитания чисел, кодируемые трехуровневыми сигналами по ортогональным составляющим функций Попова.
Известно устройство сложения-вычитания неизбыточного и избыточного аргументов в двоичной системе счисления, которое содержит блоки формирования суммы и переноса, выполненные на логических элементах [1]. Каждый из блоков формирования суммы и переноса содержит две схемы формирования соответственно логического дополнения и действительного значения суммы и переноса, состоящей из трех элементов И, и подключенных к их выходам элементов ИЛИ, связанных с выходом усилителя-инвертора. Первые два входа первых элементов И каждой схемы формирования соединены с шинами логического дополнения положительного и отрицательного значений избыточного аргумента. Третьи входы первых элементов И схем формирования дополнения суммы и переноса блоков формирования суммы и переноса соединены с шиной действительного значения неизбыточного аргумента. Третьи входы элементов И схем формирования действительного значения суммы и переноса - с шиной логического дополнения неизбыточного аргумента. Первые входы вторых и третьих элементов И соединены с шинами действительных положительного и отрицательного значений избыточного аргумента соответственно. Другие входы второго и третьего элементов И схемы формирования дополнения суммы соединены с шинами логического дополнения неизбыточного аргумента. Другие входы второго и третьего элементов И схемы формирования действительного значения суммы - с шинами действительного значения неизбыточного аргумента. Другие входы второго и третьего элементов И схемы формирования дополнения переноса соединены с шиной действительного значения (при сложении) и шиной логического дополнения (при вычитании) управляющего сигнала соответственно. Другие входы второго и третьего элементов И схемы формирования действительного значения переноса соединены с шиной логического дополнения и шиной действительного значения управляющего сигнала соответственно. Выход инвертора схемы формирования дополнения суммы данного разряда и выход инвертора схемы формирования действительного значения переноса блока формирования переноса предшествующего разряда соединены с выходными шинами положительного значения суммы. Выход инвертора схемы формирования действительного значения суммы данного разряда и выход инвертора схемы формирования дополнения переноса предшествующего разряда соединены с выходными шинами отрицательного значения суммы.
Избыточное кодирование осуществляется введением в каждый разряд отрицательной единицы, то есть один из аргументов кодируется в двоичной системе с цифрами -1, 0, 1: сумма в каждом разряде принимает значение, равное 0 или -1, а перенос 0, при этом окончательная сумма в i-ом разряде, получаемая в двоичной системе с цифрами -1, 0, 1, имеет либо положительное, либо отрицательное значение и является простым объединением истинного значения суммы в i-м разряде и логического дополнения переноса из i-го разряда для отрицательного значения окончательной суммы и простым объединением дополнения суммы в i-ом разряде с истинным значением переноса из (i-1)-го разряда для положительного значения окончательной суммы. Под простым объединением понимается то, что каждое значение окончательной суммы в i-ом разряде выдается двумя шинами: соответствующими шинами суммы из i-го разряда и переноса из (i-1)-го разряда.
Устройство сложения-вычитания неизбыточного и избыточного аргументов работает только в двоичной системе счисления.
Известен троичный комбинационный сумматор и способ его работы, принятый за прототип изобретения, который содержит три пороговых элемента, пять входных и четыре выходные шины [2]. Первый пороговый элемент имеет порог +3 и пять входов с весами +2, +1 +1, +2, +1. Второй пороговый элемент имеет порог +5 и шесть входов с весами +2. +1, +1, +2, +1, +3. Третий пороговый элемент имеет порог +6 и семь входов с весами +2, +1, +1, +2 +1, +3, +2. Первые и вторые входы всех пороговых элементов подключены к шине старшего члена разряда первого слагаемого, вторые входы всех пороговых элементов подключены к шине младшего члена разряда первого слагаемого. Третьи входы всех пороговых элементов подключены к шине младшего члена разряда второго слагаемого. Четвертые входы всех пороговых элементов подключены к шине старшего члена разряда второго слагаемого. Пятые входы пороговых элементов подключены к шине переноса из предыдущего разряда сумматора. Шестые входы второго и третьего пороговых элементов подключены к инверсному выходу первого порогового элемента. Седьмой вход третьего порогового элемента подключен к инверсному входу второго порогового элемента.
Цифры троичной системы закодированы согласно табл.16.
Работа троичного сумматора описывается табл.17.
С прямого выхода порогового элемента ПЭ1 снимается перенос С1 в следующий разряд сумматора, с прямого выхода порогового элемента ПЭ2 снимается старший член разряда троичной суммы S
Первые входы всех пороговых элементов соединены вместе и подключены к шине x
Троичный сумматор работает только в трехзначной - троичной системе счисления.
Техническим результатом изобретения является расширение функциональных возможностей способа сложения-вычитания. Расширение функциональных возможностей предусматривает кодирование чисел трехуровневыми сигналами, их сложение и вычитание в системах счисления с основаниями q = 4 и q = 8.
Для кодирования чисел трехуровневыми сигналами, вводятся трехуровневые волновые функции Попова.
1. Дискретные волновые функции.
Для кодирования чисел автор изобретения ввел дискретные волновые трехуровневые, биполярные функции popq(2πk/q), различные для разных оснований q систем счисления и назвал их своим именем - функции Попова. Эти функции представляют парой ортогональных составляющих
popq(2π/q) = copq(2πk/q)+i•sipq(2πk/q), (1)
где q - основание системы счисления, которое может принимать значения от q = 3 до q = 8.
k - число-цифра, которая для одного разряда может принимать значения равные: 0,1,...,(q-1).
При этом каждую цифру k представляют фазой волновой функции Попова ϕkq= 2πk/q, а каждую фазу ϕkq кодируют сочетанием значений ортогональных составляющих copq(ϕkq) и sipq(ϕkq).
Значения ортогональных составляющих copq(2πk/q) и sipq(2πk/q) определяют через значения соответствующих им тригонометрических функций косинус и синус: cos(2πk/q) и sin(2πk/q). Для этого период 2π делят на q равных частей и назначают одинаковые по абсолютному значению положительный и отрицательный пороги ± ξ. Пример такого квантования по фазе для q = 7 приведен на фиг.1. Значения тригонометрических функций в точках аргумента ϕkq= 2πk/q сравнивают с порогами. Если значение тригонометрической функции превышает положительное пороговое значение +ξ, то соответствующей ей трехуровневой ортогональной составляющей приписывают значение + 1, если значение тригонометрической функции меньше отрицательного порогового значения -ξ, то соответствующей функции copϕkq или sipϕkq приписывают значение -1, если значение тригонометрической функции находится между пороговыми значениями +ξ и -ξ, то соответствующей трехуровневой ортогональной составляющей приписывают значение 0. Таким образом, значения ортогональных составляющих трехуровневых волновых функций можно определить, как
Значения порогов ± ξ определяют из условия однозначного кодирования всех q фаз сочетаниями значений функций copq(ϕkq) и sipq(ϕkq), для всех оснований q от q = 3 до q = 8. При этом наихудшим случаем кодирования, с точки зрения допустимого уровня порога, является случай квантования периода для q = 7. Для этого случая (фиг. 1) в точках ϕ2,7= 4π/7 и ϕ5,7= 10π/7 значение cosϕkq= -sinπ/14 ≅ -0,22, а в точках ϕ3,7= 6π/7 и ϕ4,7= 8π/7 значение sinϕ = ± sinπ/7 ≅ ± 0,433, и для однозначного кодирования семи фаз уровнями ортогональных составляющих абсолютное значение порогов ξ должно быть больше sinπ/14 и в то же время меньше sinπ/7, то есть для однозначного кодирования q фаз для всех q от q = 3 до q = 8 значение модуля порога ξ при определении значений дискретных функций copq(2πk/q) и sipq(2πk/q) можно выбирать любым в пределах
sinπ/7 > ξ > sinπ/14 (4)
При таком определении дискретных волновых функций, при использовании сочетания значений ортогональных составляющих copq(2πk/q) и sipq(2πk/q), обеспечивается однозначное кодирование q фаз функций  и, следовательно, q цифр k = 0,1,...,(q-1).
и, следовательно, q цифр k = 0,1,...,(q-1).
Для кодирования чисел в системах счисления, с основаниями q = 4 и q = 8 ограничение на выбор значения порога (4) менее жестко, а именно:
Функции popq(2πk/q), примененные для представления чисел в системе счисления с основанием q, могут быть использованы и для представления чисел в системе счисления с основанием (q + 1). При этом для кодирования (q + 1) цифр множество значений волновых функций дополняют сочетаниями значений ортогональных составляющих "0,0", когда обе ортогональные составляющие принимают нулевое значение. Например, для кодирования чисел в девятеричной системе счисления (q = 9) сочетания значений ортогональных составляющих волновых функций для q = 8 дополняют сочетанием "0,0", соответствующим цифре k = 0, а способ кодирования остальных цифр аналогичен описанному выше с той разницей, что при таком способе кодируют цифры k1 = k+1.
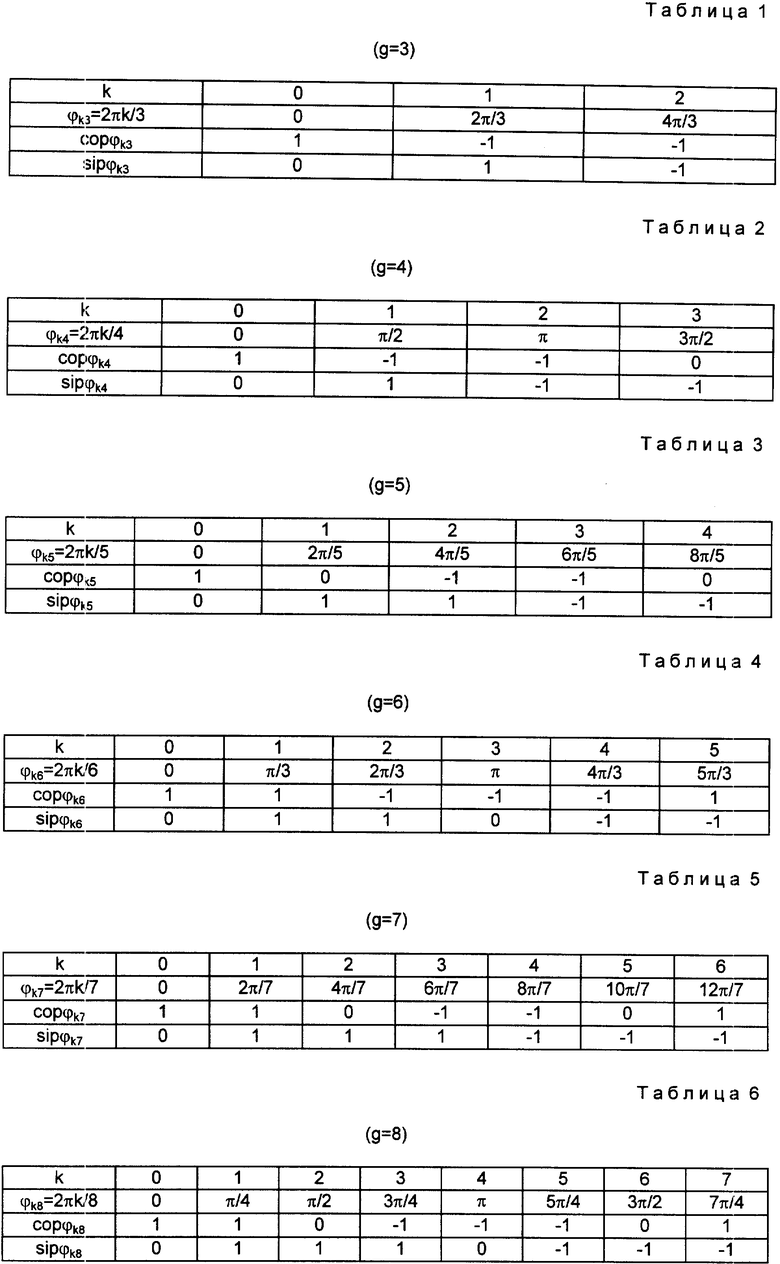
В табл. 1-6 представлены значения фаз ϕkq= 2πk/q и соответствующие им фазо-волновые коды цифр для различных q от q = 3 до q = 8, а в табл.7 представлены фазо-волновые коды цифр девятеричной системы счисления.
Дискретные волновые функции не представляют собой физические сигналы. Для формирования сигналов, представляющих коды цифр, используют непрерывные трехуровневые, биполярные функции, являющиеся обобщением дискретных функций для непрерывного аргумента.
2. Непрерывные трехуровневые биполярные функции Попова.
Трехуровневые биполярные функции непрерывного аргумента ϕ, который изменяется в пределах 0 ≤ ϕ < 2π, представленные ортогональными составляющими
popq(ϕ) = copq(ϕ)+i•sipq(ϕ), (5),
определяют через дискретные трехуровневые функции popq(2πk/q), принимая k = [ϕq/2π], где k[•] - означает целую часть аргумента ϕq/2π.. То есть ортогональные составляющие непрерывных функций copq(ϕ) и sipq(ϕ) сохраняют значения соответствующих им дискретных функций, которые они имели в точках ϕkq= 2πk/q, в секторе аргумента ϕ.:
2πk/q ≤ ϕ < 2π(k+1)/q (6)
Правила сложения чисел по модулю q = 4 определяются табл.8, а правила вычитания чисел по модулю q = 4 - табл.9. Правила сложения чисел по модулю q = 8 определяются табл.10, а правила вычитания чисел по модулю q = 8 определяются - табл.11.
В тех случаях, когда сумма равна или больше основания системы счисления q по модулю, формируют число "1" - переноса в старший разряд. При вычитании число переноса "-1" формируют, когда разность меньше нуля. В табл. 8-11 эти значения сумм и разностей подчеркнуты.
Заменяя в табл. 8-11 цифры их фазо-волновыми кодами, получаем таблицы истинности для операций сложения-вычитания чисел, представленных фазоволновыми кодами табл. 12-15.
Поскольку коды чисел kx и ky слагаемых или уменьшаемого и вычитаемого представляют фазы ϕx= 2πkx/q и ϕy= 2πky/q волновых функций Попова, способ сложения или вычитания сводится к сложению или вычитанию фаз волновых функций слагаемых. Волновые функции Попова обладают свойствами, аналогичными свойствам синусоидальных волн. В частности, для них справедливо правило сложения фаз
и правило вычитания фаз
Способ сложения-вычитания чисел основан на кодировании чисел - цифр kx и ky фазами ϕx= 2πkx/q и ϕy= 2πky/q сигналов Copq(ϕx,y) и Sipq(ϕx,y) по волновым функциям Попова, а также на сложении-вычитании фаз сигналов в соответствии с формулами (7-10). Каждую фазу ϕx,y кодируют значениями уровней сигналов Copq(2πkx,y/q) и Sipq(2πkx,y/q).
Способ сложения-вычитания чисел, состоит в том, что формируют две пары трехуровневых сигналов  по волновым функциям Попова popq(ϕ), которые представляют двумя ортогональными составляющими
по волновым функциям Попова popq(ϕ), которые представляют двумя ортогональными составляющими
popq(ϕ) = copq(ϕ)+i•sipq(ϕ),,
каждое число-цифру kx и ky от kx,y = 0 до kx,y = q-1, в системах счисления с основанием q = 4 и q = 8, представляют фазами ϕx,y= 2πkx,y/q, каждую фазу ϕx,y кодируют значениями уровней сигналов Copq(2πkx,y/q) и Sipq(2πkx,y/q). Значения ортогональных составляющих функций Попова copq(ϕ) и sipq(ϕ) определяют путем сравнения с порогами ± ξ, соответствующих тригонометрических функций cosϕ и sinϕ при значениях аргумента ϕ = 2πk/q, как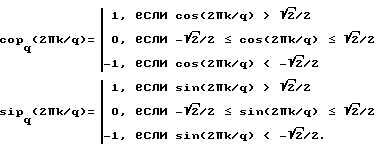
Для сложения фаз формируют два сигнала Сopq(s) и Sipq(s) которые представляют коды суммы чисел слагаемых kx и ky, при этом в соответствии с формулой (7), сигнал Сорq(s) формируют путем перемножения сигналов  , а также перемножения сигналов Sipq(ϕx) и Sipq(ϕy) и вычитания из сигналов первого произведения сигналов второго.
, а также перемножения сигналов Sipq(ϕx) и Sipq(ϕy) и вычитания из сигналов первого произведения сигналов второго.
Сигнал Sipq(s), в соответствии с формулой (8), формируют путем перемножения сигналов Sipq(ϕx) и Copq(ϕy), а также перемножения сигналов Copq(ϕx) и Sipq(ϕy) и суммирования этих произведений сигналов.
Для вычитания фаз изменяют полярность сигналов Sipq(ϕy), формируют сигналы Copq(-s> и Sipq(-s>, которые представляют коды разности чисел уменьшаемого kx и вычитаемого ky. При этом в соответствии с формулой (9), сигнал Copq(-s) формируют путем перемножения сигналов Copq(ϕx) и Copq(ϕy), а также перемножения сигналов Sipq(ϕx) и Sipq(ϕy) и суммирования сигналов этих произведений. Сигнал Sipq (-s) в соответствии с формулой (10) формируют путем перемножения сигналов Sipq(ϕy) и Copq(ϕy), а также перемножения сигналов Copq(ϕx) и Sipq(ϕy) и вычитания из сигналов первого произведения сигналов второго.
Отличительными признаками изобретения являются: кодирование чисел kx и ky фазами ϕx= 2πkx/q и ϕy= 2πky/q сигналов Copq(ϕx,y) и Sipq(ϕx,y) по волновым функциям Попова и сложение-вычитание фаз сигналов по формулам (7-10).
Устройство сложения-вычитания по модулям q=4 и q=8.
Способ сложения-вычитания чисел может быть реализован с помощью устройства сложения-вычитания кодов чисел, которое содержит: пять входных и две выходные шины, четыре четырехквадрантные перемножителя с двумя входами и прямым и инверсным выходами каждый, два элемента вычитания сигналов и переключатель полярности.
Первая входная шина соединена с первым входом первого перемножителя и вторым входом четвертого перемножителя.
Вторая входная шина соединена с первыми входами второго и третьего перемножителей.
Третья входная шина соединена со вторыми входами первого и третьего перемножителей.
Четвертая входная шина через переключатель полярности сигналов соединена с первым входом четвертого перемножителя и вторым входом второго перемножителя.
Пятая входная шина соединена с управляющим входом переключателя полярности.
Прямые (+) выходы первого и второго перемножителей соединены с неинвертирующим и инвертирующим входами первого элемента вычитания сигналов соответственно, а прямой выход третьего и инверсный (-) выход четвертого перемножителя соединены с неинвертирующим и инвертирующим входами второго элемента вычитания сигналов соответственно. Выходы первого и второго элементов вычитания соединены с соответствующими выходными шинами.
Отличительными признаками устройства сложения-вычитания являются: четыре четырехквадрантные перемножителя с двумя входами и двумя выходами каждый, два элемента вычитания сигналов и электрические связи, обусловленные введенными элементами.
Способ суммирования-вычитания чисел, представленных фазо-волновыми кодами, и устройство для его осуществления поясняются чертежами.
На фиг. 1 а,б представлены соответственно графики косинуса и синуса дискретного ϕkq= 2πk/q (сплошные ординаты) и непрерывного ϕ (пунктир) аргументов.
На фиг. 1 в, г представлены соответственно графики дискретных ортогональных составляющих cop7(2πk/q) и sip7(2πk/q) (сплошные ординаты) функции Попова и составляющих сигналов cop7(ϕ) и sip7(ϕ), непрерывной функции Попова при q = 7.
На фиг. 2 представлена структурная электрическая схема преобразователя четырехразрядного унитарного кода в одноразрядный четырехзначный фазо-волновой код pop4(ϕ).
На фиг. 3 представлены эпюры напряжений преобразователя четырехразрядного унитарного кода в одноразрядный четырехзначный фазо-волновой код pop4(ϕ).
На фиг. 4 представлена структурная электрическая схема преобразователя восьмиразрядного унитарного кода в одноразрядный четырехзначный фазо-волновой код pop8(ϕ).
На фиг. 5 представлены эпюры напряжений преобразователя восьмиразрядного унитарного кода в одноразрядный восьмизначный фазо-волновой код pop8(ϕ).
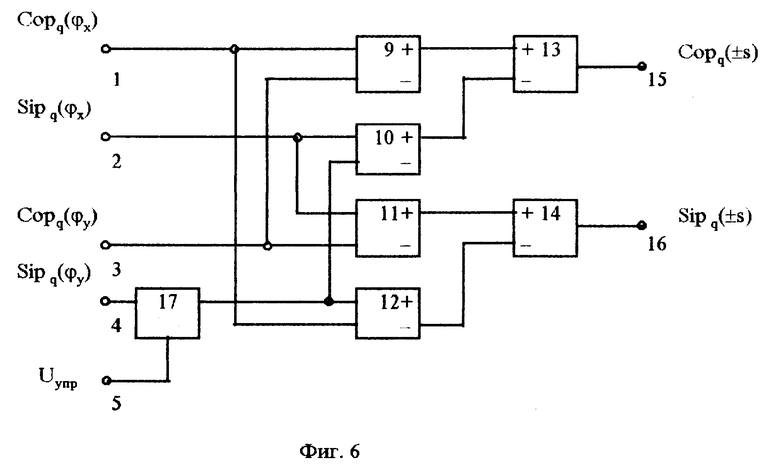
На фиг. 6 представлена структурная электрическая схема устройства суммирования-вычитания по модулям q = 4 и q = 8.
На фиг. 7 представлена принципиальная электрическая схема переключателя полярности.
На чертежах введены обозначения: 1,2,3,4,5,6,7,8 - входные шины (первая, вторая и т.д.); 9,10,11,12 - четырехквадрантные перемножители (первый, второй и т.д.); 13 и 14 - элементы вычитания сигналов (первый и второй); 15 и 16 - выходные шины (первая и вторая); 17 - переключатель полярности сигналов; 18 и 19 - дифференциальные операционные усилители (первый и второй); 20 - резисторы; 21 - ключ; U - управляющее напряжение переключателя полярности сигналов.
Четырехквадрантные перемножители 9-12 могут быть выполнены на дифференциальных делителях тока (Тимофеев В.Н., Величко Л.М., Ткаченко В.А. Аналоговые перемножители сигналов в радиоэлектронной аппаратуре. - М.: Радио и Связь, 1982, с.24-29).
Элементы 13 и 14 вычитания сигналов могут быть выполнены на дифференциальных усилителях.
Переключатель 17 полярности сигналов может быть выполнен на операционном усилителе по схеме фиг.7.
Устройство для кодирования чисел k = 0,1,2,3 четвертичной системы счисления (фиг.2) содержит четыре входные шины 1,2,3,4, две выходные шины 15 и 16 и два дифференциальных усилителя первый 18 и второй 19.
Первая входная шина 1 через резистор R1 соединена с неинвертирующим входом первого дифференциального усилителя 18, вторая входная шина 2 через резистор R2 соединена с инвертирующим входом этого усилителя, третья входная шина 3 через резистор R3 соединена с неинвертирующим входом второго дифференциального усилителя 19, а четвертая входная шина 4 - через резистор R4 с инвертирующим входом этого усилителя. Выходы дифференциальных усилителей 18 и 19 соединены соответственно с выходными шинами 15 и 16.
Устройство работает следующим образом. На первую 1 и вторую 2 входные шины подают сигналы первого U0 и третьего U2 разряда унитарного кода, а на третью 3 и четвертую 4 входные шины - сигналы второго U1 и четвертого U3 разрядов. Сигналы унитарного кода U0, U1, U2 и U3 принимают значение "1" при кодировании соответствующего числа 0,1,2,3, в остальных случаях их значение равно "0". Через дифференциальные усилители 18 и 19 сигналы U0 и U1 проходят без изменения полярности, а сигналы U2 и U3 изменяют полярность. В результате на входе первого дифференциального усилителя 18 формируется сигнал Cop4(ϕ), а на выходе второго усилителя 19 - сигнал Sip4(ϕ), как показано на эпюрах фиг.3.
Устройство для кодирования чисел k = 0,1,2,3,4,5,6,7 восьмеричной системы счисления (фиг.4) содержит восемь входных шин (1,2,...8) и два дифференциальных усилителя - первый 18 и второй 19.
Неинвертирующий вход первого дифференциального усилителя 18 через резисторы R1, R2 и R3 соединены с первой 1, второй 2 и третьей 3 входными шинами, соответственно. Инвертирующий вход этого усилителя через резисторы R4, R5 и R6 - с входными шинами 4,5,6. Неинвентирующий вход второго дифференциального усилителя 19 через резисторы R7, R8 и R9 соединены с входными шинами 2,7,4, соответственно, а инвертирующий вход этого усилителя через резисторы R10, R11 и R12 с входными шинами 6,8 и 3 соответственно. Выход первого дифференциального усилителя 18 соединен с первой выходной шиной 15, а выход второго усилителя 19 со второй выходной шиной 16.
Устройство работает следующим образом. На входные шины 1-8 подают сигналы восьмиразрядного унитарного кода U- - U7. Сигналы принимают значение "1" при кодировании соответствующего числа k = 0,1,...7, в остальных случаях сигналы унитарного кода принимают значения "0", как показано на фиг.5. При этом на первую 1 и вторую 2 входные шины подают сигналы первого U0 и второго U1 разрядов, на третью 3 входную шину - сигнал восьмого разряда U7, на четвертую 4, пятую 5, и шестую 6 входные шины подают сигналы четвертого U3, пятого U4 и шестого U5 разрядов, соответственно. На седьмую 7 шину подают сигнал третьего разряда U2, а на восьмую - сигнал седьмого разряда U6. Сигналы унитарного кода суммируют на дифференциальных усилителях 18 и 19 с полярностью, соответствующей фазо-волновому коду. Таким образом на выходе первого дифференциального усилителя 18 формируют сигнал Cop8(ϕ), а на выходе второго 19 - сигнал Sip8(ϕ) (фиг.4 и 5).
Пример выполнения устройства сложения-вычитания чисел по модулю q = 4 и q = 8.
Устройство сложения-вычитания чисел содержит: пять входных 1,2,3,4,5 и две выходные 15 и 16 шины, четыре четырехквадрантные перемножителя 9,10,11,12 с двумя входами, а также прямым и инверсным выходами каждый, два элемента вычитания сигналов 13 и 14 и переключатель полярности 17 (фиг. 6 и 7).
Первая входная шина 1 соединена с первым входом первого перемножителя 9 и со вторым входом четвертого перемножителя 12. Вторая входная шина 2 соединена с первыми входами второго и третьего перемножителей 10 и 11. Третья входная шина соединена со вторыми входами первого и третьего перемножителей 9 и 11. Четвертая входная шина 4 через переключатель полярности 17 соединена с первым входом четвертого перемножителя 12 и вторым входом второго перемножителя 10. Пятая входная шина соединена с управляющим входом переключателя полярности 17.
Прямые выходы первого и второго перемножителей 9 и 10 соединены с неинвертирующим и инвертирующим входами первого элемента вычитания сигналов 13 соответственно, а прямой выход третьего 11 и инверсный выход четвертого 12 перемножителей соединены с неинвертирующим и инвертирующим входами второго элемента вычитания сигналов 14 соответственно. Выходы элементов 13 и 14 вычитания сигналов соединены с выходными шинами 15 и 16 соответственно.
Перемножители сигналов построенные на дифференциальных делителях тока имеют два выхода - прямой и инверсный. Напряжения на этих выходах имеют вид
Uвых.1 = 1 + UxUy (11)
Uвых.2 = 1 - UxUy (12)
где Ux и Uy - нормированные по амплитуде напряжения.
Обычно для получения напряжения пропорционального произведению входных сигналов сигналы с выходов каждого перемножителя подают на асимметрирующий каскад, выполненный на дифференциальном операционном усилителе, на котором вычитаются выходные сигналы перемножителя.
Для построения устройства сложения-вычитания фаз достаточно двух дифференциальных усилителей, которые выполняют функции асимметрирующего каскада и устройства вычитания сигналов одновременно. Для этого с прямого выхода первого перемножителя 9 снимают сигнал
U1= 1+Copq(ϕx)•Copq(ϕy)
и подают на неинвертирующий вход первого устройства 13 вычитания сигналов. С прямого выхода второго перемножителя 10 снимают сигнал
U2= 1+Sipq(ϕx)•Sipq(ϕy)
и подают на инвертирующий вход устройства вычитания сигналов 13. При этом на выходе первого устройства вычитания сигналов 13 формируется сигнал .
.
С прямого выхода третьего перемножителя 11 снимают сигнал
U3= 1+Sipq(ϕx)•Copq(ϕy),,
а с инверсного выхода четвертого перемножителя 12 снимают сигнал
U4= 1-Copq(ϕx)•Sipq(ϕy)..
Сигналы U3 и U4 вычитаются на устройстве вычитания сигналов 13, на выходе которого формируется сигнал
Амплитуды выходных сигналов U1(s) и U2(s) при преобразовании восьмеричных кодов (q = 8) могут принимать значения 0, ±1, ±2. При необходимости нормировки амплитуды, дифференциальные усилители могут быть дополнены ограничителем амплитуды по уровню Uвых = ±1.
Описанный принцип действия устройства сложения-вычитания относится к режиму сложения фаз сигналов. В этом режиме переключатель полярности 17 не изменяет полярности сигналов Sipq(ϕy).
Для выполнения операции вычитания фаз сигналов на управляющий вход переключателя полярности подают сигнал (Uупр) для инверсии полярности сигналов Sipq(ϕy) (фиг.6). В этом режиме устройство суммирования-вычитания выполняет операцию вычитания фаз сигналов в соответствии с формулами (11) и (12), а следовательно вычитание чисел, кодируемых фазами.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПОЛНОГО СЛОЖЕНИЯ - ВЫЧИТАНИЯ ЧИСЕЛ, КОДИРУЕМЫХ СИГНАЛАМИ, И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1998 |
|
RU2132566C1 |
| ПРЕОБРАЗОВАТЕЛЬ ДВОИЧНОГО КОДА ВО МНОГОЗНАЧНЫЙ КОД (ВАРИАНТЫ) | 1997 |
|
RU2109400C1 |
| УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ ЧАСТОТЫ И РАЗНОСТИ ЧАСТОТ СИГНАЛОВ | 1992 |
|
RU2025738C1 |
| УСТРОЙСТВО ДЛЯ СЛОЖЕНИЯ N ЧИСЕЛ ПО МОДУЛЮ P | 2000 |
|
RU2188448C2 |
| Арифметическое устройство | 1974 |
|
SU544964A1 |
| Устройство для вычисления гиперболических функций | 1980 |
|
SU957208A1 |
| Цифровое логарифмирующее устройство | 1980 |
|
SU918946A1 |
| ПРОТИВОЗАНОСНАЯ ТОРМОЗНАЯ СИСТЕМА С ДОПОЛНИТЕЛЬНЫМИ КОЛЕСАМИ | 1996 |
|
RU2116912C1 |
| Способ определения результатов векторно-матричных преобразований в параллельных акустооптических процессорах | 1989 |
|
SU1735836A1 |
| Устройство для сложения и вычитания | 1980 |
|
SU922730A1 |








Изобретение относится к автоматике и вычислительной технике и может быть использовано в дискретных автоматах для сложения - вычитания чисел, кодируемых трехуровневыми сигналами по ортогональным составляющим функций Попова. Изобретение позволяет кодировать числа трехуровневыми сигналами, осуществлять их сложение, вычитание в системах счисления с основаниями q = 4, q = 8. Способ основан на формировании двух пар трехуровневых сигналов по волновым функциям Попова - popq(ϕ) . Последние представляют двумя ортогональными составляющими popq(ϕ)=copq(ϕ)+i•sipq(ϕ) Каждое число Kx и Ky от Kx , y = 0 до Kx , y = q - 1, в системах счисления с основанием q = 4 и q = 8, представляют фазами  Каждую фазу ϕx,y кодируют значениями уровней сигналов
Каждую фазу ϕx,y кодируют значениями уровней сигналов  Значения ортогональных составляющих функций Попова copq(ϕ) и sipq(ϕ) определяют путем сравнения с порогами ±ζ, соответствующих тригонометрических функций cosϕ,sinϕ при значениях аргумента
Значения ортогональных составляющих функций Попова copq(ϕ) и sipq(ϕ) определяют путем сравнения с порогами ±ζ, соответствующих тригонометрических функций cosϕ,sinϕ при значениях аргумента  . Для сложения фаз формируют сигналы Copq (S) и Sipq (S), для вычитания - Copq (-S) и Sipq (- S). Последние представляют коды суммы и разности чисел слагаемых Kx, Ky. Сложение и вычитание фаз производят в соответствии с известными формулами сложения и вычитания фаз синусоидальных волн. 2 с.п.ф-лы, 17 табл., 7 ил.
. Для сложения фаз формируют сигналы Copq (S) и Sipq (S), для вычитания - Copq (-S) и Sipq (- S). Последние представляют коды суммы и разности чисел слагаемых Kx, Ky. Сложение и вычитание фаз производят в соответствии с известными формулами сложения и вычитания фаз синусоидальных волн. 2 с.п.ф-лы, 17 табл., 7 ил.
 по волновым функциям Попова - popq(ϕ), которые представляют двумя ортогональными составляющими
по волновым функциям Попова - popq(ϕ), которые представляют двумя ортогональными составляющими
popq(ϕ) = copq(ϕ)+i•sipq(ϕ),
каждое число-цифру Kx и Ky от Kx y = 0 до Kx y = q - 1, в системах счисления с основанием q = 4 и q = 8, представляют фазами ϕx,y= 2πkx,y/q, каждую фазу ϕx,y кодируют значениями уровней сигналов copq(2πkx,y/q) и sipq(2πkx,y/q), причем значения ортогональных составляющих функций Попова copq(ϕ) sipq(ϕ) определяют путем сравнения с порогами ±ξ соответствующих тригонометрических функций cosϕ и sinϕ при значениях аргумента ϕ = 2πk/q как
после чего для сложения фаз формируют два сигнала Cорq (S) и Sipq (S), которые представляют коды суммы чисел слагаемых Kx и Ky, при этом сигнал Сорq (S) формируют путем перемножения сигналов copq(ϕx) и copq(ϕy), а также перемножения сигналов sipq(ϕx) и sipq(ϕy) и вычитания из сигналов первого произведения сигналов второго, сигнал Sipq (S) формируют путем перемножения сигналов sipq(ϕx) и copq(ϕy), а также перемножения сигналов copq(ϕx) и sipq(ϕy) и суммирования этих произведений сигналов, причем для вычитания фаз изменяют полярность сигналов sipq(ϕy), при этом формируют сигналы Сорq (-S) и Sipq (-S), которые представляют коды разности чисел уменьшаемого Kx и вычитаемого Ky, при этом сигнал Сорq (-S) формируют путем перемножения сигналов copq(ϕx) и copq(ϕy) , а также сигналов sipq(ϕx) и sipq(ϕy) и суммирования сигналов этих произведений, а сигнал Sipq (-S) формируют путем перемножения сигналов sipq(ϕx) и copq(ϕy) , а также сигналов copq(ϕx) и sipq(ϕy) и вычитания из сигналов первого произведения сигналов второго.
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| SU, авторское свидетельство, 407308, кл | |||
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| SU, авторское свидетельство, 416691, кл | |||
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1998-04-20—Публикация
1997-07-09—Подача