СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА КАЧЕСТВА ДИНАМИЧЕСКИ НАСТРАИВАЕМОГО ГИРОСКОПА Российский патент 1998 года по МПК G01C25/00 

Изобретение относится к точному приборостроению.

Целью способа является повышение точности за счет обеспечения возможности его осуществления в режиме с замкнутой обратной связью.

Указанная цель достигается тем, что в способе определения коэффициента качества динамически настраиваемого гироскопа, заключающемся в отклонении ротора при нерезонансной скорости его вращения по одной из осей чувствительности измерения изменения его параметров вычисления на основании полученных данных коэффициента качества, отклонение ротора производят по гармоническому закону с низкой частотой при замкнутой обратной связи, определяют изменение моментов по обеим осям чувствительности по изменению амплитуды низкочастотных колебаний токов обратной связи, а коэффициент качества F вычисляют по формуле: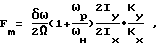

где
ω_р,ω_н - соответственно резонансная и нерезонансная скорости вращения ротора;
Ω - круговая частота отклонения ротора;
k_x, k_y - крутизна по току каналов обратной связи по осям чувствительности x и y соответственно;
2I_x, 2I_y - размах колебаний токов в каналах обратной связи при низкочастотных колебаниях ротора относительно оси x гироскопа;
δω = ω_р-ω_н - величина расстройки.

Устройство, реализующее предложенный способ (ДНГ - с обратной связью по моменту) представлено на чертеже.

В режиме работы ДНГ с обратной связью по моменту сигналы с датчиком угла (ДУ) 1,2 подаются через предварительные усилители (ПУ) 3, 4, фазовые детекторы (ФД) 5, 6, усилители постоянного тока (УПТ) 7, 8, на датчики момента (ДМ) 9, 10 соответствующих каналов обратной связи (КОС).

Пусть с корпусом ДНГ связана правая система координат (СК) OXY. Вектор кинетического момента 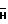направлен по положительному направлению оси O. На чертеже показаны статоры ДУ и ДМ соответствующих КОС. Здесь и ниже под осью ДУ понимается ось чувствительности ДУ, под осью ДМ - ось, по которой направлен вектор момента, развиваемый соответствующим ДМ (рассматривается магнитоэлектрический ДМ).

На чертеже обозначены 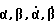- углы и угловые скорости отклонения ротора ДНГ относительно осей x и y соответственно. На чертеже также показано, что на вход соответствующего КОС может быть подано или постоянное напряжение смещения (как в способе-прототипе), или переменное, изменяющееся по гармоническому закону, например, по косинусу, которые обозначены в пересчете на углы отклонения ротора соответственно как 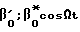для канала коррекции x и 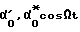для канала коррекции y. В какой канал (x или y) подается напряжение смещения - принципиального значения не имеет, поэтому в дальнейшем для примера взят канал y (смещение α*0

′cosΩt ).

Поскольку рассматривается магнитоэлектрический ДМ, а на чертеже условно показаны его статорные обмотки, то вектор момента, развиваемый ДМ_x при протекании тока в его статорных обмотках будет направлен вдоль оси x, хотя статоры ДМ_x расположены на оси OY. Соответственно, вектор момента, развиваемый ДМ_y, будет направлен вдоль оси y, как это показано на примере момента Eα₀cosΩt для переменного смещения.

Схема работает следующим образом. Поскольку подается гармоническое смещение, примем для определенности без ущерба для общности, что в момент времени t=0 на вход УПТ подано отрицательное напряжение смещения, которое равно в пересчете на угол отклонения ротора 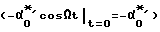. ЭП вынуждена "отработать" возникший (мнимый) угол отклонения (сигнал смещения через УПТ поступает в виде постоянного тока на обмотку ДМ_y). Поэтому ЭП создаст момент E(-α*0

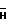cosΩt)_t=0=-Eα*0′, который будет направлен по отрицательной полуоси y, как это показано на фиг., а поскольку этот момент приложен к ротору ДНГ, то ротор начнет процессировать. При этом по известному закону вектор будет стремиться совместиться с вектором внешнего момента по кратчайшему пути. Таким образом возникнет "истинный" угол отклонения ротора 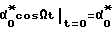(положительный). Отклонения ротора будет продолжаться до тех пор, пока напряжение с ДУ_y не с компенсирует поданное на вход УПТ напряжение смещения, или в пересчете на углы отклонения, пока угол 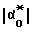не станет равным углу 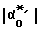. Поскольку напряжение смещения изменяется по гармоническому закону с низкой частотой Ω , то и ротор ДНГ будет вынужден совершать гармонические колебания относительно оси x с той же частотой.

В предположении, что в начальный момент времени (t=0) момент ЭП от поданного сигнала смещения направлен по отрицательной полуоси "y" КОС "y", прецессионные уравнения движения ДНГ будут иметь вид для нерезонансного режима работы (индексом "H" показывается, что скорость вращения ротора равна нерезонансной скорости)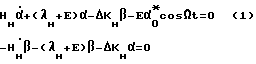

где
H_н - кинетический момент при скорости ;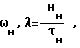
τ - постоянная времени;
ΔK_н - остаточная жесткость;
E - "жесткость" ЭП;
Ω - круговая частота сигнала смещения.

Токи тогда, протекающие в КОС, определяются из выражений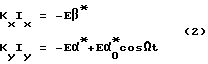
,
где
α^*,β^* - частное решение системы (1) при нулевых начальных условиях (считается, что переходный процесс завершен и производится измерение "установившихся" значений токов).

Решая известными методами систему (1), получим: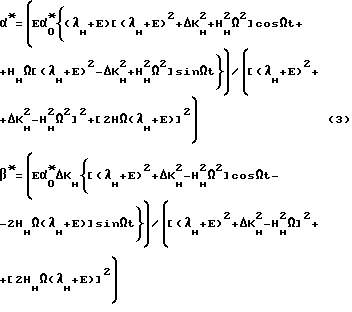

В реальных гироскопах всегда выполняются условия:
E ≫ λ_н, E ≫ ΔK_н,
а для любого H подбором величины Ω можно обеспечить требование: E ≫ HΩ.
Тогда из (3) можно получить: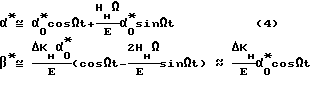

Представляя (4) в (2) получим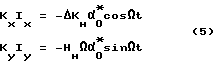

Как видно из (5), токи в КОС будут изменяться с частотой поданного низкочастотного сигнала смещения, причем ток в КОС "y", в который смещение подается, пропорционален величине гироскопического момента H_нΩ, , а в перекрестном канале x - величине момента от остаточной жесткости ΔK_н .

Поскольку удобнее регистрировать размах (удвоенную амплитуду) гармонических колебаний токов в КОС, то из (5) можно получить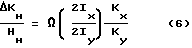
,
где
2I_x, 2I_y - размахи колебаний токов в КОС x и y.

Подставляя полученное значение 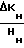в формулу 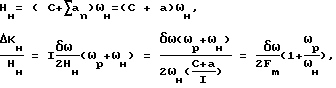7
(7)
где
C - осевой момент инерции ротора гироскопа,
a_n - экваториальный момент инерции карданной рамки,
получим формулу, характеризующую коэффициент качества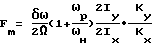

Таким образом, в предложенном способе определение отношения 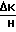производится в режиме с замкнутой обратной связью путем отклонения ротора по гармоническому закону с низкой частотой с измерением амплитуд изменений токов в каналах обратной связи, что позволяет повысить его точность.

Изобретение относится к точному приборостроению. Целью изобретения является повышение точности. Данный способ заключается в определении коэффициента качества гироскопа. Определение данного параметра осуществляется отклонением ротора, которое производят по гармоническому закону с низкой частотой при замкнутой обратной связи, при этом определяют изменение моментов по обеим осям чувствительности по изменению амплитуды низкочастотных колебаний токов обратной связи, а коэффициент качества вычисляют по формуле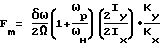

где δω = ω_р-ω_н - величина расстойки, ω_р,ω_н - соответственно резонансная и нерезонансная скорости вращения ротора, K_x, _y - крутизна по току каналов обратной связи DM_x, DM_y; 2I_x, 2I_y - размах колебаний (удвоенные амплитуды) токов в цепях обратной связи x и y при отклонении ротора по гармоническому закону с низкой частотой относительно оси x. 1 ил.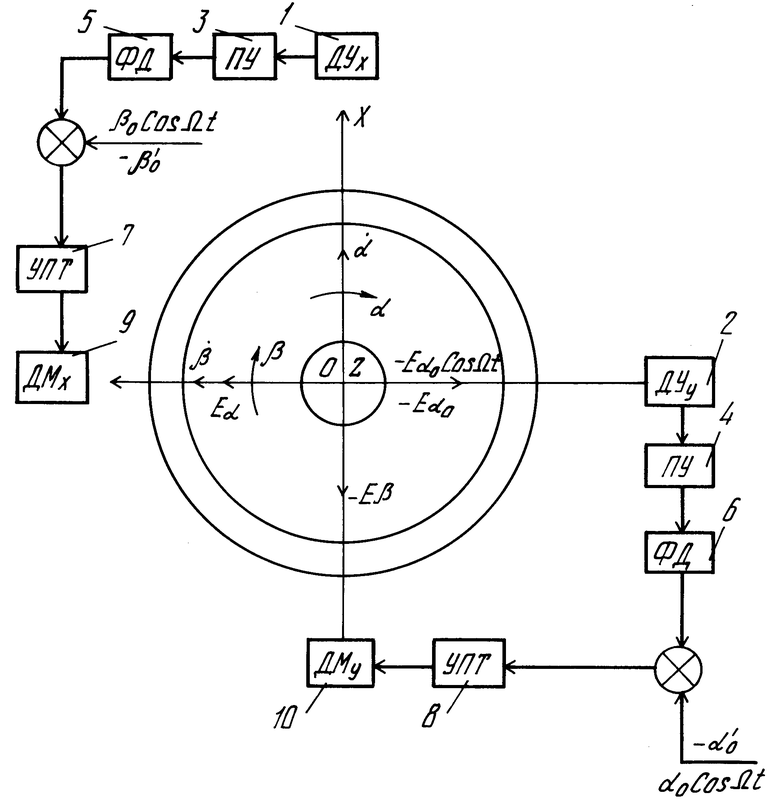

Способ определения коэффициента качества динамически настраиваемого гироскопа, заключающийся в отклонении ротора при нерезонансной скорости его вращения по одной из осей чувствительности, измерении изменения его параметров и вычислении на основании полученных данных коэффициента качества, отличающийся тем, что, с целью повышения точности, отклонение ротора производят по гармоническому закону с низкой частотой при замкнутой обратной связи, определяют изменение моментов по обеим осям чувствительности по изменению амплитуды низкочастотных колебаний токов обратной связи, а коэффициент качества F_m вычисляют по формуле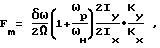

где
ω_р, ω_н - соответственно резонансная и нерезонансная скорости вращения ротора;
Ω - круговая частота отклонения ротора;
К_х, К_у - крутизна по току каналов обратной связи по осям чувствительности х и y соответственно;
2I_x, 2I_y - размах колебаний токов в каналах обратной связи при низкочастотных колебаниях ротора относительно оси х гироскопа;
δω = ω_р-ω_н - величина расстройки.