Предлагаемое изобретение относится к области спутниковой навигации и может быть использовано для определения углового положения объектов в пространстве или на плоскости.
Известен способ угловой ориентации по сигналам космических аппаратов глобальных навигационных спутниковых систем, основанный на приеме сигналов на разнесенные две или более антенны, расположенные параллельно одной или двум осям измеряемого объекта, измерении фазового сдвига между принятыми сигналами на разнесенные антенны от каждого космического аппарата и определении углового положения осей измеряемого объекта путем решения системы уравнений [1].
Недостатком способа является низкая точность измерения углов, обусловленная тем, что антенны требуется располагать на малом расстоянии, меньшем длины волны принимаемых сигналов. При увеличении расстояния между фазовыми центрами разнесенных антенн погрешность измерения углов уменьшается, но появляется неоднозначность фазовых измерений, что приводит к неоднозначному определению углового положения объекта. Для устранения неоднозначности применяется более сложная обработка сигналов, заключающаяся в проведении измерений по различным космическим аппаратам и обработке результатов измерений фазовых сдвигов с помощью фильтра Калмана, позволяющего отбраковать ложные гипотезы. При этом существенное значение имеет время сходимости решения задачи. Время сходимости, т.е. время, требуемое для определения угловой ориентации, может быть достаточно велико. Так при четырех космических аппаратах и геометрическом факторе 5.5 и 3.7 время сходимости системы уравнений составляет соответственно 1600 и 400 с, т.е. является очень большим. Определение угловой ориентации объекта в условиях наличия систематических погрешностей приводит к еще большему увеличению времени, требуемого на решение системы уравнений [1].
Известен способ угловой ориентации объекта по радионавигационным сигналам космических аппаратов [2], в котором по варианту 1, основанному на приеме сигналов от n космических аппаратов двумя или более антенно-приемными устройствами, расположенными параллельно одной или двум осям объекта, выделении сигнала с частотой Доплера, определении набега фаз за интервал времени измерения и определении углового положения объекта, в течение интервала времени измерения производят m измерений фазовых сдвигов между парами антенно-приемных устройств, а угловое положение объекта определяют путем решения следующей системы уравнений:
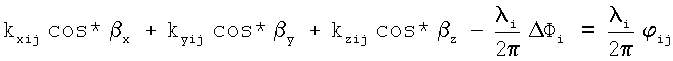 ,
,
где i=1, …, n - текущий номер космического аппарата;
j=1, …, m - текущий номер измерения фазовых сдвигов сигналов n космических аппаратов;
n - общее число принимаемых космических аппаратов;
m - общее число измерений фазовых сдвигов сигналов n космических аппаратов;
cos*βxyz=B·cosβxyz - произведение неизвестной базы В (расстояния между антенно-приемными устройствами) на ее направляющие косинусы cosβxyz, подлежащие определению;
kxij, kyij, kzij - направляющие косинусы направлений потребитель - i-й космический аппарат (КА);
λi- длина волны сигнала i-го КА;
φij - измеренные значения фазовых сдвигов сигналов i-го КА, принятых антеннами потребителя в j-m измерении;
ΔФi - неизвестная систематическая погрешность измеренной разности фаз, обусловленная разным временем прохождения сигналов в каналах приемоиндикатора и неоднозначностью, вызванной тем, что расстояние между антеннами превышает длины волн принимаемых сигналов.
Недостатком способа и его вариантов является необходимость обеспечения неподвижности объекта во время проведения измерений, поскольку значения направляющих косинусов cosβxyz, оцениваемых в системе уравнений, не зависят от времени.
Наиболее близким к заявляемому является способ угловой ориентации объекта по сигналам спутниковых радионавигационных систем [3], основанный на приеме сигналов от космических аппаратов глобальных навигационных спутниковых систем на разнесенные две или более антенны, расположенные параллельно одной или двум осям измеряемого объекта, измерении фазового сдвига между принятыми сигналами от каждого космического аппарата, в котором в течение интервала времени измерения проводят m измерений фазовых сдвигов между парами антенно-приемных устройств, а текущее угловое положение объекта определяют путем решения следующей системы уравнений:
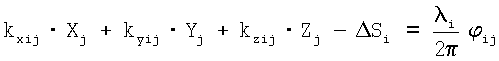 ,
,
где i=1, …, n - текущий номер космического аппарата;
j=1, …, m - текущий номер измерения фазовых сдвигов сигналов n космических аппаратов;
n - общее число принимаемых космических аппаратов;
m - общее число измерений фазовых сдвигов сигналов n космических аппаратов;
kxij, kyij, kzij - направляющие косинусы векторов-направлений от объекта до i-го космического аппарата в j-й момент времени;
φij - значение фазового сдвига сигнала i-го космического аппарата в j-й момент времени;
Xj, Yj, Zj - значения направляющих косинусов в j-й момент времени;
λi - длина волны i-го космического аппарата;
ΔSi - систематическая погрешность измерения фазового сдвига сигнала i-го космического аппарата, складывающаяся из целочисленной неоднозначности и аппаратурной составляющей систематической погрешности.
Недостатком этого способа является необходимость проведения m разновременных измерений фазовых сдвигов между разнесенными антеннами объекта, что увеличивает время, требуемое для нахождения угловой ориентации. Кроме того, точность определения угловой ориентации объекта зависит от величины поворота антенной системы объекта и величины изменения углового положения принимаемых космических аппаратов относительно вектора-базы, образованного разнесенными антеннами объекта. При этом в случае, если антенная система объекта будет малоподвижной в течение времени измерения, время, необходимое для получения заданной точности оценки углового положения, может составлять единицы-десятки минут.
В основу изобретения положена задача уменьшения времени, требуемого для определения угловой ориентации объекта вплоть до выдачи оценки угловой ориентации по результатам одномоментных измерений фазовых сдвигов сигналов n космических аппаратов, принятых антенно-приемными устройствами.
Поставленная задача решается тем, что в способе угловой ориентации объекта по сигналам спутниковых радионавигационных систем, основанном на приеме сигналов от космических аппаратов глобальных навигационных спутниковых систем на разнесенные две или более антенны, расположенные параллельно одной или двум осям измеряемого объекта, измерении фазового сдвига между принятыми сигналами от каждого космического аппарата, проведении в течение интервала времени измерения m измерений фазовых сдвигов между парами антенно-приемных устройств, согласно изобретению осуществляют подбор значений целочисленных неоднозначностей измерений фазовых сдвигов для минимального созвездия космических аппаратов, позволяющий определить возможные значения угловой ориентации, исключение возможных значений угловой ориентации, не соответствующих заранее известным значениям ориентации антенной системы и расстояния между разнесенными антеннами, проверку оставшихся значений угловой ориентации расчетом значений неоднозначности Ni для измеренных фазовых сдвигов дополнительных космических аппаратов, не вошедших в минимальное созвездие, определение угловой ориентации по фазовым сдвигам сигналов космических аппаратов для полного их созвездия, при этом значение, соответствующее искомой угловой ориентации объекта определяется из условия максимума функции правдоподобия, а значения угловой ориентации для минимального и полного созвездий космических аппаратов определяются путем решения системы уравнений, имеющей вид:
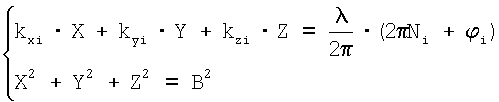 ,
,
где i=1, …, n - текущий номер космического аппарата;
n - число КА, используемых для определения угловой ориентации;
kxi, kyi, kzi - направляющие косинусы векторов-направлений от объекта до i-го космического аппарата в текущий момент времени измерений;
φi - измеренное и скорректированное с учетом систематической погрешности значение фазового сдвига сигнала i-го космического аппарата;
λi - длина волны сигнала i-го космического аппарата;
Ni - значение целочисленной неоднозначности сигнала i-го космического аппарата, удовлетворяющее условию: |Ni|≤int(B/λ+0.5);
В - расстояние между антеннами при n≤2 - известное с высокой точностью, при n>2 - подлежащее уточнению в процессе решения системы уравнений;
X, Y, Z - неизвестные значения относительных координат фазового центра второй антенны относительно первой.
Изобретение поясняется чертежами, где на фиг.1 изображена структурная схема устройства для определения угловой ориентации; на фиг.2 изображена блок-схема алгоритма работы вычислительного блока, реализующего алгоритм определения угловой ориентации в соответствии с предлагаемым способом.
Сущность предлагаемого способа можно пояснить следующим образом. При определении угловой ориентации объектов по сигналам спутниковых радионавигационных систем (СРНС) используют результаты измерений косинусов углов αi между вектором-базой и вектором-направлением на i-й космический аппарат (КА) СРНС.
Фазовый сдвиг (ФС) сигнала i-го КА, принимаемого двумя пространственно разнесенными антеннами, и косинус угла между вектором-базой и вектором-направлением на i-й КА αi связаны между собой выражением:
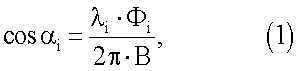
где i=1, …, n;
n - число КА, используемых для определения угловой ориентации объекта;
λi - длина волны сигнала i-го КА;
Фi - фазовый сдвиг сигналов, принятых разнесенными антеннами;
В - расстояние между антеннами.
Вычисление направляющих косинусов вектора-базы осуществляют на основе уравнения, полученного исходя из свойства скалярного произведения векторов в декартовой системе координат:
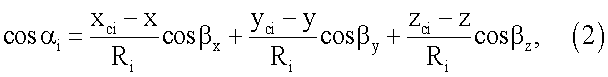
где x, y, z - известные координаты объекта в геоцентрической системе координат (ГЦСК);
xci, yсi, zci - координаты i-го КА в ГЦСК, полученные из решения задачи размножения эфемерид КА;
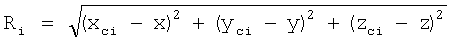 - расстояния между объектом и i-м КА, полученные на основе известных координат КА и объекта, cosβx, cosβy, cosβz - неизвестные направляющие косинусы вектора-базы объекта.
- расстояния между объектом и i-м КА, полученные на основе известных координат КА и объекта, cosβx, cosβy, cosβz - неизвестные направляющие косинусы вектора-базы объекта.
Введем обозначения:
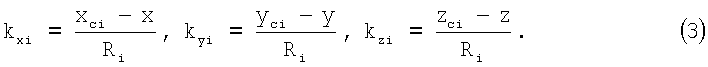
С учетом принятых обозначений система уравнений (2) запишется следующим образом:

Систему уравнений (4) можно дополнить нелинейным уравнением связи между направляющими косинусами вектора-базы:
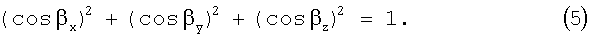
При определении углового положения объекта часто неизвестными являются не только направляющие косинусы вектора-базы, но и сама величина базы В. В связи с этим выражения (4) и (5) запишутся следующим образом:
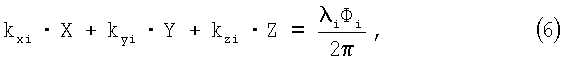
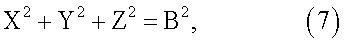
где X=B·cosβx, Y=B·cosβy, Z=B·cosβz.
Величины X, Y, Z являются геоцентрическими координатами фазового центра второй антенны относительно фазового центра первой антенны, взятой в качестве опорной.
Как правило, при определении углового положения вектора-базы в целях повышения точности используется расположение антенн на расстоянии В, существенно превышающем длину волны принимаемых сигналов. Кроме того, при измерениях ФС возникают аппаратурные систематические погрешности, обусловленные разным временем прохождения принятых сигналов в антенно-приемных устройствах. В связи с этим выражение для полного ФС сигнала i-ro KA, принятого разнесенными антеннами объекта Фi, можно записать в виде:
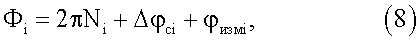
где i=1, …, n -текущий номер измерения ФС i-го KA,
Ni - число целых циклов неоднозначности 360° в ФС сигнала i-го KA;
Δφci - не зависящая от времени аппаратурная систематическая погрешность измерения ФС сигнала i-го KA;
φизмi - измеренное значение ФС сигнала i-го KA, принятого двумя антеннами объекта.
С учетом наличия систематической погрешности и неоднозначности система уравнений (6) примет вид:
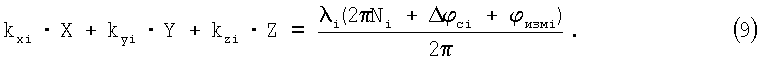
Значения систематических погрешностей измеренных значений ФС Δφci можно определить путем калибровки аппаратуры, например, при помощи имитаторов сигналов СРНС, либо при расположении разнесенных антенн объекта на линии с известной ориентацией.
После определения систематических погрешностей измеренных значений ФС Δφci измеренные значения ФС φизмi принимаемых КА могут быть скорректированы, в результате чего система уравнений для определения угловой ориентации примет вид:
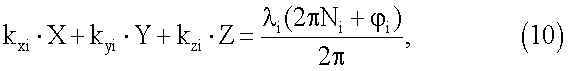
где φi=Δφci+φизмi - измеренное значение ФС с учетом систематической погрешности.
Система уравнений (10) содержит n уравнений (n - число принимаемых сигналов КА) с n+3 неизвестными. Неизвестными в системе (10) являются относительные координаты X, Y, Z второй антенны по отношению к первой, а также целочисленные неоднозначности Ni(i=1, …, n). Поскольку число неизвестных превышает число уравнений, система (10) является вырожденной и на практике не может быть решена.
Для обеспечения решения системы уравнений (10) используют свойство целочисленности неоднозначностей измерения ФС N1, …, Nn. Диапазон изменения целочисленных неоднозначностей определяется максимально возможным числом длин волн принимаемых сигналов, укладывающихся на расстоянии В между антеннами объекта, что соответствует случаю совпадения направления вектора-базы с направлением на данный КА. Таким образом, для нахождения угловой ориентации с использованием уравнения (10) требуется осуществить перебор значений целочисленной неоднозначности Ni для каждого из принимаемых КА в диапазоне:
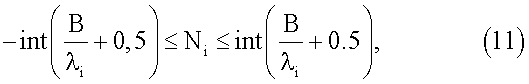
где int() - означает операцию выделения целой части числа, заключенного в скобки;
В - расстояние между антеннами;
λi - длина волны сигнала i-го КА.
Например, при расстоянии между антеннами В=0.7 м диапазон перебираемых неоднозначностей Ni находится в пределах -4≤Ni≤4, т.е. неоднозначность Ni по каждому из космических аппаратов может принять 9 возможных значений, равных -4, -3, -2, -1, 0, 1, 2, 3, 4.
Значения неоднозначностей Ni ФС принимаемых КА могут наблюдаться во всех возможных сочетаниях. Число возможных сочетаний неоднозначностей Nmax для работы по сигналам n КА составляет:
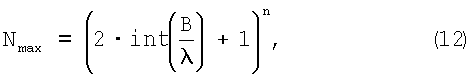
где n - число принимаемых сигналов КА;
λ - среднее значение длины волны КА, принятое для расчетов, равным 0.19 м.
Таким образом, для определения угловой ориентации требуется многократное решение системы уравнений (10) при заданных в каждом случае значениях вектора неоднозначностей NN=(N1, N2, …, Nn)T, в котором каждый из элементов Ni вектора NN определяется в соответствии с условием (11).
Поскольку значения вектора NN подвергаются перебору, они полагаются известными при решении системы уравнений (10). Поэтому, если число принимаемых КА n оказывается больше или равно 3 (n≥3), система уравнений (10) не будет вырожденной и позволит определить неизвестные относительные координаты второй антенны объекта X, Y, Z.
Так как число возможных состояний вектора неоднозначности NN равно Nmax (12), то в результате решения системы (10) будет получено Nmax различных значений X, Y, Z, которые в дальнейшем тексте заявки будем называть возможными значениями угловой ориентации.
При одновременном приеме сигналов СРНС ГЛОНАСС и GPS общее число КА n может достигать 16 и более. Исходя из этого, например, в рассмотренном примере при расстоянии между антеннами интерферометра В=0.7 м общее число возможных значений угловой ориентации Nmax составляет 916≈1.8·1015.
В связи с этим прямое решение системы (10) путем перебора всех возможных значений вектора неоднозначностей NN=(N1, N2, …, Nn)T при большом числе принимаемых сигналов КА n требует очень больших вычислительных и временных затрат, и не может быть реализовано в реальных устройствах измерения угловой ориентации по сигналам СРНС.
Число возможных значений угловой ориентации Nmax может быть уменьшено при переходе к неизбыточной системе уравнений (10), в которой число неизвестных равно числу уравнений и составляет 3.
Для решения неизбыточной системы уравнений (10) достаточно принять на разнесенные антенны и измерить ФС сигналов 3-х КА, а определение неизвестных параметров будет базироваться на решении системы уравнений вида:
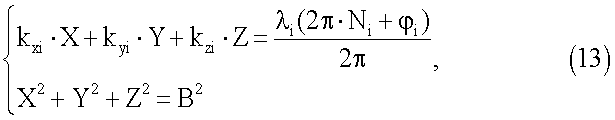
где i=1, …, 3 - текущий номер принимаемого КА.
В данной системе уравнений имеется 4 уравнения, три из которых линейны и составлены для измерений ФС 3-х КА, четвертое уравнение нелинейно и не зависит от ФС сигналов КА. Число неизвестных в данной системе также равно четырем (неизвестны значения X, Y, Z и B), т.е. система может быть решена однозначно.
Решение системы (13) может осуществляться в два этапа: вначале определяют неизвестные значения X, Y, Z из линейных уравнений, а затем, используя нелинейное уравнение, определяют неизвестное расстояние между антеннами В.
Для рассмотренного выше примера определения угловой ориентации при расстоянии между антеннами 5=0.7 м число перебираемых неоднозначностей составляет 93=729.
В случае, когда при определении угловой ориентации расстояние между антеннами В является известной величиной, число КА в минимальном созвездии может быть уменьшено до двух, т.е. система (13) запишется в виде:
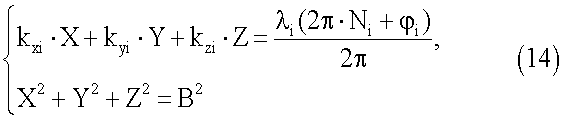
где i=1, 2 - текущий номер КА, входящего в начальное созвездие.
В полученной системе неизвестными являются значения X, Y, Z, и для ее решения достаточно провести измерения всего по двум КА. При этом число перебираемых неоднозначностей составит 92=81 значение при расстоянии между антеннами B=0.7 м.
Число КА в минимальном созвездии может быть равно 1, если помимо того, что расстояние между антеннами В является известной величиной, известно, что антенны находятся, например, в горизонтальной плоскости. В этом случае, систему уравнений (14) удобно записать в топоцентрической системе координат (ТЦСК), причем в данном случае вертикальная топоцентрическая координата YT=0. Система уравнений для определения угловой ориентации по сигналам одного космического аппарата имеет вид:
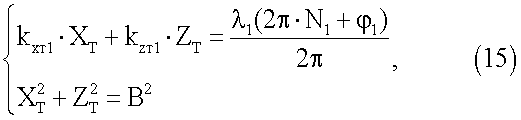
где kxт1, kzт1 - направляющие косинусы направления от потребителя на КА, выраженные в ТЦСК;
ХТ, ZT - координаты второй антенны относительно первой, выраженные в ТЦСК.
Полученные значения направляющих косинусов в ТЦСК позволяют перейти к значению азимута антенной системы объекта ψa, значение угла места при расположении объекта в горизонтальной плоскости является равным нулю.
Таким образом, определение места по сигналам одного КА возможно, когда одна из составляющих угловой ориентации объекта (азимут ψa или угол места ψум) известна, а также известно расстояние между антеннами В. Система уравнений для простейшего случая расположения объекта в горизонтальной плоскости имеет вид (15), в противном случае учитываются соотношения между направляющими косинусами XT, YT, ZT с использованием известных значений азимута ψa или угла места ψум. Число возможных значений угловой ориентации при работе по минимальному созвездию из одного КА, для B=0.7 м составляет 9.
Также минимальное созвездие может быть составлено из четырех и более КА, однако в этом случае число возможных значений угловой ориентации возрастет, например при n=4 для B=0.7 м число возможных значений составит 94=6561, что потребует значительного времени для решения задачи. В рассмотренном случае определение возможных значений угловой ориентации базируется на решении системы уравнений (13) при n=4.
Независимо от используемой для определения угловой ориентации системы уравнений, после нахождения начального набора возможных значений угловой ориентации по минимальному созвездию из n КА образуется набор из 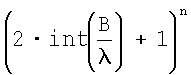 возможных значений угловой ориентации, каждое из которых характеризует возможное угловое положение объекта.
возможных значений угловой ориентации, каждое из которых характеризует возможное угловое положение объекта.
В данных возможных значениях угловой ориентации содержатся:
- неоднозначности, соответствующие каждой угловой ориентации - N1, …, Nn, где n - число КА, находящихся в минимальном созвездии;
- относительные координаты второй антенны - X, Y, Z, найденных в результате решения соответствующей системы уравнений;
- уточненное расстояние между антеннами В (при n>2).
Из полученного набора возможных значений угловой ориентации требуется выбрать одно значение с максимальной вероятностью соответствующее искомому угловому положению объекта.
Для исключения избыточных возможных значений угловой ориентации могут быть использованы следующие методы.
В системе уравнений (13), где происходит определение расстояния между антеннами (n>2) организуется проверка полученных возможных значений угловой ориентации объекта по значению расстояния между антеннами 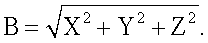
Условием исключения возможных значений угловой ориентации является превышение некоторого заданного порогового значения ΔВдоп между полученным значением В и априорно известным расстоянием Вапр. Следовательно, возможные значения угловой ориентации, удовлетворяющие условию 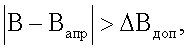 исключаются из числа возможных значений угловой ориентации.
исключаются из числа возможных значений угловой ориентации.
Следующим критерием проверки является соответствие полученной ориентации максимально допустимому для данного объекта углу места вектора-базы. По известным формулам пересчета относительные координаты второй антенны X, Y, Z переводятся в направляющие косинусы вектора - базы объекта cosβx, cosβy, cosβz, заданные в геоцентрической системе координат. Из полученных значений cosβx, cosβy, cosβz используя известные формулы пересчета можно перейти к направляющим косинусам в ТЦСК cosβхт, cosβут, cosβzт, а от них - к угловой ориентации вектора-базы в местной системе координат, заданной азимутом ψа и углом места ψум.
По результатам сравнения полученного угла места ψум с его допустимым значением ψум.доп производится исключение возможных значений, не удовлетворяющих условию:
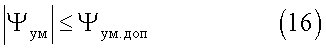
По результатам сравнения полученного азимута ψа и значения азимута, полученного от датчика курса ψад, при его наличии производится исключение возможных значений угловой ориентации, удовлетворяющих условию:
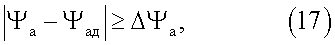
где Δψа - максимально допустимое значение погрешности оценки азимута, определяющееся как сумма максимально допускаемой погрешности определения азимута по сигналам СРНС и предельной погрешности оценки азимута, полученной от датчика курса.
Оставшиеся после исключения возможные значения угловой ориентации подвергаются проверке с использованием не вошедших в начальное созвездие дополнительных КА, в следующей последовательности:
1. Для каждого из оставшихся значений угловой ориентации объекта, в соответствии с используемой системой уравнений для определения углового положения вычисляют значения неоднозначностей дополнительных КА, которые не были использованы в начальном созвездии КА:
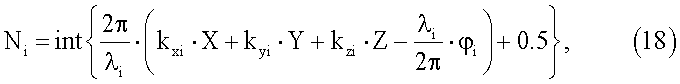
где i - текущий номер дополнительного КА, для которого осуществляется определение неоднозначности.
2. После определения неоднозначностей для всех дополнительных КА осуществляется повторное решение системы уравнений для определения угловой ориентации с привлечением всех доступных измерений ФС по КА. Т.е. в системах уравнений (13) и (14) значение числа КА n, используемых для определения угловой ориентации будет равным общему числу принимаемых КА. Решение систем уравнений для определения угловой ориентации осуществляется, например, по методу наименьших квадратов, позволяющему решать избыточные системы уравнений.
3. После решения системы уравнений для n КА и нахождения уточненных значений неизвестных происходит определение значения функции правдоподобия для полученных значений направляющих косинусов. Функция правдоподобия для нормального распределения погрешностей измерения ФС определяется выражением:
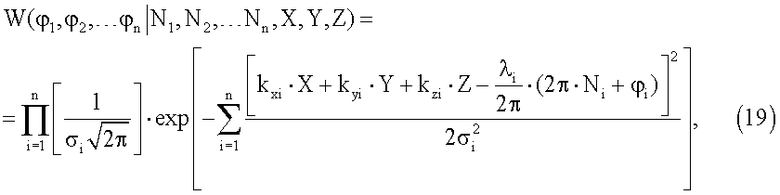
где σi - среднеквадратическая погрешность измерения ФС сигнала i-го КА.
Шаги 1-3 выполняются для всех оставшихся возможных значений угловой ориентации. Из полученных возможных значений угловой ориентации выбирается одно, имеющее максимальное значение функции правдоподобия W. Значение угловой ориентации, соответствующее максимуму W, является значением, с максимальной вероятностью, соответствующей искомой ориентации объекта.
Следует отметить, что согласно [4] для равноточных измерений при нормальном распределении погрешностей, оценка, оптимальная по критерию максимального правдоподобия соответствует оценке, полученной по методу наименьших квадратов.
В связи с этим, для упрощения вычислений для равноточных измерениях ФС и распределении их погрешностей по нормальному закону, критерий выбора оптимального решения может быть сведен к виду:
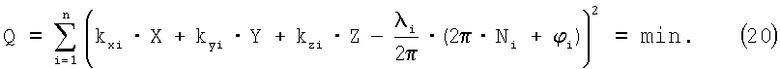
В данном случае максимизация функции правдоподобия (19) сводится к минимизации показателя экспоненты, входящей в ее формулу, представляющего собой квадратичную форму Q.
Действительно, квадратичная форма Q при правильно разрешенной неоднозначности будет иметь значения, определяемые только случайной погрешностью измерения ФС принятых сигналов. В условиях нормального функционирования СРНС значения случайных погрешностей измерения ФС принятых сигналов, переведенные в расстояния, оказываются существенно меньше длины волны принимаемых сигналов, равной 19 см. Экспериментальные исследования показывают, что значения случайных погрешностей измерения ФС, выраженные в единицах длины, не превышают 1-2 см. Следовательно, величина 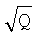 также будет составлять единицы сантиметров. При наличии неправильно разрешенной неоднозначности, когда один или несколько элементов вектора неоднозначности NN найдены неверно, соответствующий элемент суммы, образующей Q станет приблизительно равен длине волны по расстоянию, что приведет к возрастанию Q.
также будет составлять единицы сантиметров. При наличии неправильно разрешенной неоднозначности, когда один или несколько элементов вектора неоднозначности NN найдены неверно, соответствующий элемент суммы, образующей Q станет приблизительно равен длине волны по расстоянию, что приведет к возрастанию Q.
В связи с этим, значение угловой ориентации, соответствующее минимуму Q с высокой вероятностью соответствует искомой угловой ориентации объекта. Вероятность соответствия оказывается тем выше, чем больше КА используется для оценки угловой ориентации. Данный факт объясняется тем, что при накоплении суммы квадратов невязок Q происходит усреднение случайных отклонений суммируемых величин, обусловленных погрешностями измерения ФС сигналов КА.
Критерий поиска решения, соответствующего максимуму функции правдоподобия может быть использован при распределении погрешностей измеренных значений ФС по закону, не соответствующему нормальному. В этом случае изменяется вид функции правдоподобия W (19), однако поиск наиболее вероятного решения по-прежнему основан на поиске максимума функции правдоподобия.
С целью дальнейшего повышения достоверности полученной оценки угловой ориентации может быть организовано накопление значений W или Q по результатам m разновременных измерений для проверяемых возможных значений угловой ориентации, в результате чего обеспечивается уменьшение влияния случайных отклонений, вызванных погрешностями измерения ФС.
На фиг.1 приведена структурная схема устройства, реализующего предложенный способ.
Устройство содержит два идентичных приемных канала, каждый из которых включает последовательно соединенные приемную антенну 11 (12), малошумящий усилитель (МШУ) 21 (22), радиотракт 31 (32) и блок цифровой обработки сигналов 41 (42). При этом блоки цифровой обработки сигналов 41 и 42 и радиотракты 31 и 32 своими вторыми входами подключены к формирователю опорных сигналов 5, входом соединенного с одним из выходов опорного генератора 6, который другим выходом подключен к входу синхронизации вычислительного блока 7, а информационные входы вычислительного блока 7 соединены соответственно с выходами блоков цифровой обработки сигналов 41 и 42.
Сигналы n космических аппаратов принимаются двумя разнесенными антеннами 11 и 12, усиливаются малошумящими усилителями 11 и 22, преобразуются в сигналы промежуточной частоты и усиливаются радиотрактами 31 и 32 и затем поступают в блоки цифровой обработки сигналов 41 и 42, где происходит разделение сигналов каждого из космических аппаратов. Блоки цифровой обработки сигналов 41 и 42 реализованы по схеме оптимального корреляционного приемника, на выходе которого формируются отсчеты корреляционных интегралов I и Q для сигналов каждого из КА, которые соответствуют результатам корреляционного перемножения принимаемых сигналов на синфазную и ортогональную составляющие опорного сигнала, выдаваемого формирователем опорных сигналов 5 для каждого из космических аппаратов. На вычислительный блок 7 возложены функции управления режимами работы приемника, включающими в себя поиск, захват сигналов по частоте и задержке, частотную и фазовую автоподстройку, синхронизацию по метке времени и границе бита служебной информации, прием и декодирование служебной информации, измерение радионавигационных параметров сигнала. К радионавигационным параметрам сигнала относятся его задержка, частота и фаза. Кроме управления режимами работы и измерения радионавигационных параметров вычислительный блок 7 решает задачи вторичной обработки измеренных параметров, заключающиеся в определении координат КА на момент проведения измерений (задача размножения эфемерид) на основе принятой служебной информации, вычисления координат места объекта и определения угловой ориентации антенной платформы. Также на вычислительный блок 7 возложена задача прогноза сеансов навигационных определений и управления режимами работы блоков 41 и 42 для КА, появляющихся или покидающих зону радиовидимости.
Координаты объекта определяются на основе измерений задержек сигналов, принятых от каждого КА. Для проведения таких измерений сигналы каждого КА модулируются псевдослучайными последовательностями (ПСП), называемыми дальномерным кодом. Путем сравнения ПСП сигнала, сформированного блоком 5, с ПСП принятого сигнала происходит определение времени задержки принятого сигнала. Дальность до КА, излучившего сигнал, получают путем умножения времени задержки на скорость распространения радиосигналов. Следует отметить, что вследствие несовпадения бортового времени объекта с опорным временем спутниковой радионавигационной системы, эта дальность не равна геометрической и в связи с этим получила название псевдодальности. Координаты объекта на основе измеренных значений псевдодальностей получают путем решения системы уравнений вида:
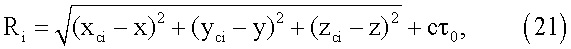
где i=1, …, n - текущий номер сигнала, принимаемого КА;
n - число КА, по которым выполняются измерения псевдодальностей;
xci, усi, zci - координаты i-го КА в геоцентрической системе координат, вычисленные на момент проведения измерений путем решения задачи размножения эфемерид;
x, y, z - неизвестные координаты объекта в геоцентрической системе координат;
Ri - измеренные величины псевдодальностей;
с - скорость распространения радиосигналов в вакууме, принятая равной 299792.5 км/с;
τ0 - неизвестное расхождение шкалы времени объекта с системным временем СРНС.
Система уравнений (21) содержит 4 неизвестных и для ее однозначного решения необходимо принять сигналы не менее 4-х КА. Способы решения таких систем рассмотрены, например, в [5, с.230-231].
Для определения угловой ориентации объекта вычислительный блок 7 производит оптимальную оценку начальных фаз сигналов, принятых антенно-приемными устройствами, на основе значений корреляционных интегралов I и Q, накопленных на измерительном интервале по формуле:
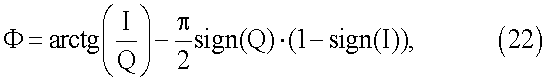
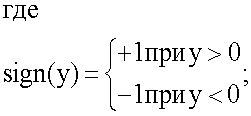
Ф - начальная фаза принятого сигнала в диапазоне однозначных измерений (-π, +π).
После оценки начальных фаз сигналов, принятых каждой из антенн, вычисляют значения фазовых сдвигов сигналов, принятых двумя пространственно разнесенными антеннами φi по каждому из КА, которые в
дальнейшем используются для определения углового положения осей измеряемого объекта путем решения вышеприведенных систем уравнений и поиска оптимального решения из всех перебираемых значений решений.
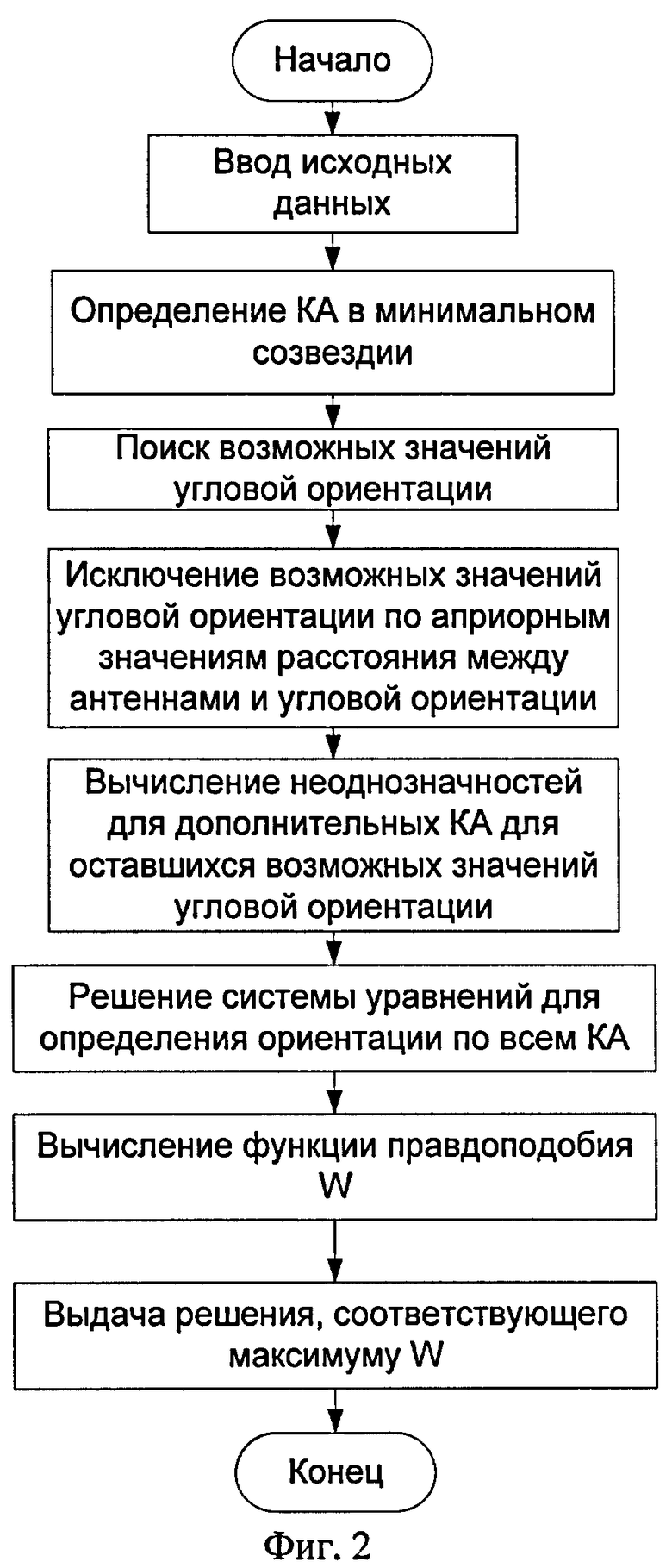
Блок-схема алгоритма работы вычислительного блока при определении угловой ориентации объекта в соответствии с предложенным способом и его вариантами приведена на фиг.2.
Данный алгоритм приведен для одного шага обработки результатов измерений ФС, в аппаратуре предусмотрено циклическое повторение алгоритма по мере поступления измеренных данных.
В соответствии с предложенным алгоритмом обработка начинается с ввода измеренных и исходных данных. Эти данные поступают с блоков цифровой обработки 41 и 42, на основе измерений которых осуществляется вычисление измеренных значений ФС φ1, …, φ2 для сигналов n принимаемых КА в соответствии с (22), а также вводятся значения координат объекта и КА на момент измерений, по которым вычисляются значения направляющих косинусов kxi, kyi, kzi (i=1, …, n) на момент измерений в соответствии с (3).
Кроме того, в памяти вычислительного блока хранятся точные значения систематических погрешностей измерения ФС для несущих частот КА, из которых выбираются значения систематических погрешностей φci для сигналов принимаемых КА с известными значениями несущих частот, а также известные значения расстояния между антеннами Вапр, допустимое значение угла места антенной системы ψум.доп и азимута ψад, а также предельно допустимые погрешности значений базы и азимута ΔВдоп и Δψа.
После ввода измеренных значений и исходных данных в память вычислительного блока 7 осуществляется коррекция измеренных значений ФС с учетом известных систематических погрешностей измерений для каждого из КА, выбор числа КА в минимальном созвездии в зависимости от полноты имеющейся априорной информации. При неизвестном расстоянии между антеннами В начальное созвездие состоит из n=3 КА. При наличии данных о расстоянии между антеннами В число КА в начальном созвездии составляет n=2.
На следующем шаге алгоритма осуществляется поиск возможных значений угловой ориентации путем перебора неоднозначностей и решения систем уравнений (13), (14) или (15) для n≥3, n=2 или n=1 соответственно. После нахождения набора возможных значений угловой ориентации осуществляется их проверка на соответствие значений расстояния между антеннами, азимута и угла места своим априорным значениям с учетом погрешностей измерения и задания априорных значений. Оставшиеся после проверки и исключения значения угловой ориентации используются для вычисления целочисленных неоднозначностей для дополнительных КА в соответствии с (18), после чего осуществляется решение системы уравнений, например, по методу наименьших квадратов для всех принимаемых n КА и вычисление значения функции правдоподобия W для полученных решений.
Решение, соответствующее максимуму функции правдоподобия W, является искомым значением угловой ориентации объекта. Длительность цикла работы вычислительного блока выбирают таким образом, чтобы за время цикла успевали выполняться операции измерения ФС и других параметров, а также вычисления значений угловой ориентации. Вычислительный блок 7 в связи с большим объемом вычислений и сложностью управляющих алгоритмов и программ необходимо реализовать, например, на основе микропроцессора Intel 80386 или его современных быстродействующих аналогов (Intel Pentium и выше) по типовой структуре, описанной, например в [6, стр.13].
Предложенный способ подвергался моделированию с целью оценки погрешностей определения угловой ориентации и вероятности правильного разрешения неоднозначности. В результате моделирования получено, что при работе по начальному созвездию из трех КА (n=3), при расстоянии между антеннами B=0.5 м и среднеквадратической погрешности измерения ФС сигналов КА, равной 3.6° вероятность правильного разрешения фазовой неоднозначности при приеме сигналов n=12 КА превышает 0.99. Обработка экспериментальных данных, измеренных аппаратурой приема сигналов СРНС ГЛОНАСС и GPS, с расстоянием между антеннами β=0.7 м показала, что погрешность определения угловой ориентации объекта составляет 0.2°-0.5°, а погрешность расстояния между антеннами не превышает 2 см. Вероятность правильного разрешения неоднозначности по проведенным экспериментальным исследованиям составила 0.9-0.95 в зависимости от используемого созвездия КА, числа принимаемых сигналов КА n и среднеквадратической погрешности измеренных значений ФС. При этом найденные значения вероятности соответствуют случаю m=1, т.е. оценка ориентации проводилась в момент получения измерения ФС сигналов n КА без использования результатов измерений, полученных в другие моменты времени.
Таким образом, предлагаемый способ в отличие от известного способа определения угловой ориентации является более быстродействующим, поскольку обеспечивает выдачу оценки угловой ориентации объекта по результатам одномоментных измерений ФС сигналов КА, которые могут выполняться с дискретностью 1 раз в секунду и чаще.
Литература
1. Лукин В.Н., Мищенко И.Н., Новиков И.А. Использование системы NAVSTAR для определения угловой ориентации объектов./ Зарубежная радиоэлектроника. 1991, №1.
2. Патент РФ №2122217. Опубл. 1998. Бюл. №32.
3. Патент РФ №2185637. Опубл. 2002. Бюл. №20.
4. Сосулин Ю.Г. Теоретические основы радиолокации и радионавигации: Учеб. пособие для вузов. - М.: Радио и связь, 1992. - 304 с.: ил.
5. B.C.Шебшаевич, П.П.Дмитриев, Н.В.Иванцевич и др. Сетевые спутниковые радионавигационные системы. / Под ред. B.C.Шебшаевича. М.: Радио и связь. 1993.
6. Брамм П., Брамм Д. Микропроцессор 80386 и его программирование: Пер. с англ. - М.: Мир, 1990, - 448 с., ил.
Изобретение может быть использовано для уменьшения времени определения пространственной ориентации объектов интерферометрическим методом. Заявленный способ обеспечивает определение угловой ориентации по результатам одного или нескольких разновременных измерений фазовых сдвигов сигналов n космических аппаратов и реализуется путем подбора целочисленных неоднозначностей измеренных значений фазовых сдвигов, исключения избыточных значений угловой ориентации путем проверки на соответствие априорным данным о расстоянии между антеннами и угловой ориентации, а также проверки с использованием сигналов дополнительных космических аппаратов. Искомое значение угловой ориентации определяется на основе критерия максимального правдоподобия. Достигаемый технический результат - повышение быстродействия определения угловой ориентации объекта вплоть до выдачи результата по результатам одного измерения фазовых сдвигов нескольких космических аппаратов. 2 ил.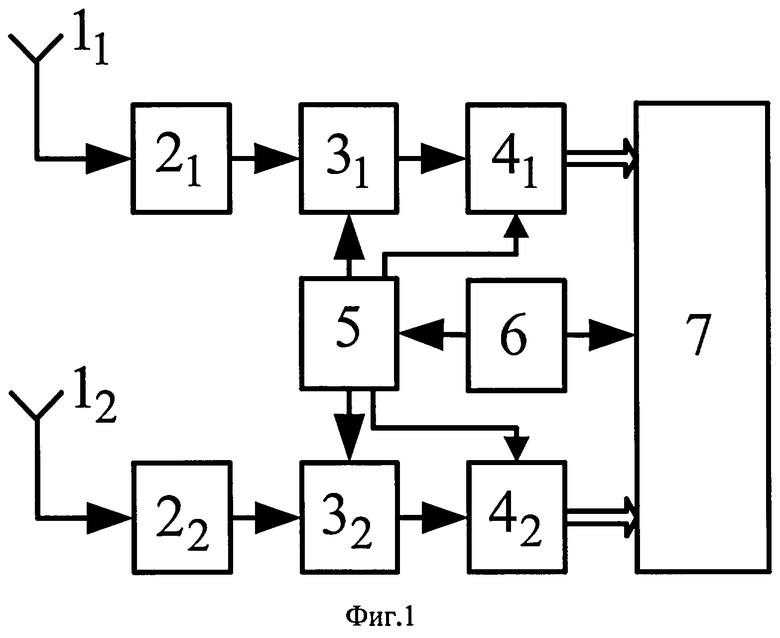
Способ угловой ориентации объекта по сигналам спутниковых радионавигационных систем, основанный на приеме сигналов от космических аппаратов глобальных навигационных спутниковых систем на разнесенные две или более антенн, расположенных параллельно одной или двум осям измеряемого объекта, измерении фазового сдвига между принятыми сигналами от каждого космического аппарата, проведении в течение интервала времени измерения m измерений фазовых сдвигов между парами антенно-приемных устройств, отличающийся тем, что осуществляют подбор значений целочисленных неоднозначностей измерений фазовых сдвигов для минимального созвездия космических аппаратов, позволяющий определить возможные значения угловой ориентации, исключение возможных значений угловой ориентации, не соответствующих заранее известным значениям ориентации антенной системы и расстояния между разнесенными антеннами, проверку оставшихся значений угловой ориентации расчетом значений неоднозначности Ni, для измеренных фазовых сдвигов дополнительных космических аппаратов, не вошедших в минимальное созвездие, определение угловой ориентации по фазовым сдвигам сигналов космических аппаратов для полного их созвездия, при этом значение, соответствующее искомой угловой ориентации объекта, определяется из условия максимума функции правдоподобия, а значения угловой ориентации для минимального и полного созвездий космических аппаратов определяется путем решения системы уравнений, имеющей вид:
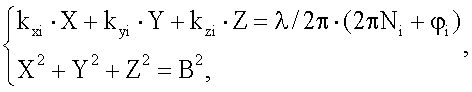
где i=1, …, n - текущий номер космического аппарата,
n - число космических аппаратов, используемых для определения угловой ориентации,
kxi, kyi, kzi - направляющие косинусы векторов-направлений от объекта до i-го космического аппарата в текущий момент времени измерений,
φi - измеренное и скорректированное с учетом систематической погрешности значение фазового сдвига сигнала i-го космического аппарата,
λi - длина волны сигнала i-го космического аппарата,
Ni - значение целочисленной неоднозначности сигнала i-го космического аппарата, удовлетворяющее условию |Ni|≤int(В/λ+0,5),
В - расстояние между антеннами при n≤2 - известное с высокой точностью, при n>2 - подлежащее уточнению в процессе решения системы уравнений,
X, Y, Z - неизвестные значения относительных координат фазового центра второй антенны относительно первой.
| СПОСОБ УГЛОВОЙ ОРИЕНТАЦИИ ОБЪЕКТА ПО СИГНАЛАМ СПУТНИКОВЫХ РАДИОНАВИГАЦИОННЫХ СИСТЕМ (ВАРИАНТЫ) | 2000 |
|
RU2185637C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УГЛОВОЙ ОРИЕНТАЦИИ ОБЪЕКТА | 2003 |
|
RU2248004C2 |
| СПОСОБ УГЛОВОЙ ОРИЕНТАЦИИ ОБЪЕКТОВ ПО РАДИОНАВИГАЦИОННЫМ СИГНАЛАМ КОСМИЧЕСКИХ АППАРАТОВ (ВАРИАНТЫ) | 1997 |
|
RU2122217C1 |
| СПОСОБ УГЛОВОЙ ОРИЕНТАЦИИ ОБЪЕКТОВ ПО СИГНАЛАМ КОСМИЧЕСКИХ АППАРАТОВ ГЛОБАЛЬНЫХ НАВИГАЦИОННЫХ СПУТНИКОВЫХ СИСТЕМ | 1995 |
|
RU2105319C1 |
| US 6292132 B1, 18.09.2001 | |||
| Пусковое приспособление для замедления пуска в ход электродвигателей | 1927 |
|
SU16288A1 |
| US 6154171 A, 28.11.2000 | |||
| FR 2905470 A1, 07.03.2008. | |||
Авторы
Даты
2010-01-20—Публикация
2008-07-28—Подача