Предлагаемое изобретение относится к области космической радионавигации и может быть использовано для определения углового положения объектов в пространстве или на плоскости.
Известен способ угловой ориентации объектов по сигналам космических аппаратов (КА) глобальных навигационных спутниковых систем (ГНСС), основанный на приеме сигналов КА каждым из четырех антенно-приемных устройств, расположенных на осях объектов, выделении сигнала с частотой доплера, определении набега фаз колебаний с частотой доплера путем интегрирования их на мерном интервале и определении углового положения объектов (Патент РФ N 2022294, кл.G 01 S 5/00).
Недостатком способа является длительное время, необходимое для проведения измерения углового положения. Это связано с тем, что для решения задачи угловой ориентации необходимо, чтобы космические аппараты, излучающие сигналы, за время измерения существенно переместились в пространстве. Для КА ГНСС, а в настоящее время существуют две системы: российская система ГЛОНАСС и американская - GPS, период обращения вокруг Земли которых составляет около 12 ч, необходимое время измерения соответствует десяткам минут - часам. Это существенно ограничивает возможность применения этого способа.
Известен способ угловой ориентации объектов по сигналам космических аппаратов глобальных навигационных спутниковых систем, взятый в качестве прототипа, основанный на приеме сигналов от космических аппаратов глобальных навигационных спутниковых систем на разнесенные две или более антенны, расположенные параллельно одной или двум осям измеряемого объекта, измерении фазового сдвига между принятыми сигналами от каждого космического аппарата и определении углового положения осей измеряемого объекта путем решения системы уравнений (Зарубежная радиоэлектроника, 1989, с.46 - 53). Недостатком способа является низкая точность измерения углов, связанная с тем, что антенны необходимо располагать на малом расстоянии - расстоянии, меньшем длины волны. При увеличении расстояния между фазовыми центрами разнесенных антенн погрешность измерения углов уменьшается, но появляется неоднозначность фазовых измерений, что приводит к неоднозначному определению углового положения объекта. Для устранения неоднозначности применяется более сложная обработка, при этом используются измерения фазовых сдвигов в разные моменты времени, но в этом случае увеличивается время определения угловой ориентации объекта. Так при четырех КА и геометрических факторах 5,5 и 3,7 время сходимости системы уравнений составляет соответственно 1600 и 400 с, что в большинстве случаев недопустимо.
Задачей изобретения является создание условий для обеспечения сходимости системы уравнений при больших расстояниях между фазовыми центрами разнесенных антенн за короткое время, что привело бы к повышению точности и уменьшению времени угловой ориентации объектов по сигналам космических аппаратов глобальных навигационных спутниковых систем.
Поставленная задача достигается тем, что в известном способе, основанном на приеме сигналов от космических аппаратов глобальных навигационных спутниковых систем на разнесенные две или более антенны, расположенные параллельно одной или двум осям измеряемого объекта, измерении фазового сдвига между принятыми сигналами от каждого космического аппарата и определении углового положения осей измеряемого объекта путем решения системы уравнений, перед началом измерений или в процессе измерений углового положения осей объекта изменяют угловое положение баз, на концах которых расположены антенны, на произвольный угол, после чего антенны возвращают в исходное состояние. В предложенном способе может быть использовано любое расстояние между антеннами, в том числе и существенно превышающее длину волны, благодаря этому погрешность угловой ориентации может быть достигнута малых значений, например 1 мрад и менее.
Сущность предлагаемого способа заключается в следующем.
При угловых измерениях используются результаты измерения косинусов углов αi между вектором-базой и вектором-направлением на навигационные космические аппараты (НКА) системы "ГЛОНАСС".
Фазовый сдвиг сигнала НКА, принимаемого на две антенны, и косинус угла между вектором-базой и вектором-направлением на НКА связаны выражением:
где λ - длина волны сигнала НКА,
Ф - фазовый сдвиг, B - база антенн, α - угол между вектором-базой и вектором-направлением на НКА.
Вычисление направляющих косинусов вектора-базы осуществляется на основе уравнения
где cosβx,y,z - направляющие косинусы вектора-базы,
Xc, Yc, Xc - координаты НКА,
Xo, Yo, Zo - координаты потребления, - расстояние между потребителем и НКА.
- расстояние между потребителем и НКА.
Кроме уравнения (2) используется также уравнение связи между направляющими косинусами вектора-базы
cos2βx + cos2βy + cos2βz = 1. (3)
При измерении на три и более антенны (две и более базы) можно использовать уравнения связи между векторами-базами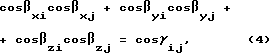
где cosβx,y,zi - направляющие косинусы i-го вектора-базы,
cosβx,y,zj - направляющие косинусы j-го вектора-базы,
γ - угол между i-м и j-м векторами-базами,
являются направляющими косинусами вектора-направления от потребителя до НКА.
Введем обозначения:
X = B•cosβx, Y = B•cosβy, Z = B•cosβz. (6)
Коэффициенты Kx, Ky, Kz являются направляющими косинусами вектора-направления от потребителя до НКА, а коэффициенты X, Y, Z соответствуют координатам фазового центра второй антенны относительно фазового центра первой антенны.
В этом случае система уравнений (2), (3) в случае приема сигналов НКА на две антенны с учетом (1) примет вид:
где i - номер НКА.
Неизвестные X, Y, Z в системе уравнений (7) представляют собой относительные координаты, а величина B - длину вектора-базы.
Для угловых измерений необходимо принять сигналы трех (или более) НКА. При этом можно производить измерения при неизвестной базе. Следует отметить, что для решения навигационной задачи необходимы сигналы четырех НКА, поэтому система уравнений (7) всегда будет избыточной.
При угловых измерениях серьезную проблему составляет систематическая погрешность и погрешность, связанная с неоднозначностью измерения фазового сдвига. Систематическая погрешность измерения фазового сдвига возникает из-за неидентичности антенно-фидерных устройств и измерительных каналов приемоиндикатора.
Неоднозначность измерения фазового сдвига обусловлена ограниченным диапазоном измерения фазоизмерителя. Реальные фазоизмерители имеют диапазон измерения в пределах от 0o до 360o (или от 0o до 180o), фазовый же сдвиг сигналов НКА между двумя антеннами, исходя из выражения (1), может достигать при λ = 19 см, B = 2 м величины 21π или 3790o.
С учетом систематической погрешности полный фазовый сдвиг сигнала i-го НКА равен
Фi = Физмi + 2π•ni- Фci, (8)
где Физмi - измеренный фазовый сдвиг сигнала i-го НКА,
Фсi - систематический фазовый сдвиг, - вектор неоднозначности,
- вектор неоднозначности,
Фм - диапазон измерения фазометра,
[ ] - целая часть числа.
Одним из способов устранения неоднозначности измерения фазового сдвига и систематической погрешности является способ, основанный на измерении приращения фазового сдвига, который обусловлен перемещением по орбите НКА. Запишем систему уравнений (7) в начальный момент времени t0:
К моменту времени t1 направляющие косинусы векторов kx,y,z0i изменяются на величину Δkx,y,zi , а фазовые сдвиги Ф0i - на величину ΔФi . Тогда для момента времени t1 можно записать следующую систему уравнений: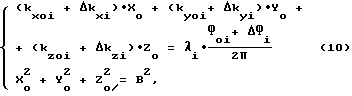
Составим разностную систему уравнений, вычитая из линейных членов системы уравнений (10) линейные члены системы (9):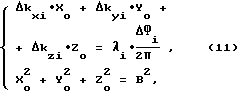
Как видно из системы (11), для получения решения с достаточной точностью необходимо, чтобы выполнялось условие: Δkxi ≫ 0, Δkyi ≫ 0, Δkzi ≫ 0 . Для этого необходимо, чтобы НКА существенно переместились по орбите. В этом основной недостаток этого способа.
В предложенном способе фазовый сдвиг изменяется как за счет движения НКА по орбите, так и за счет изменения углового положения объекта. Для начального положения объекта (будем считать нулевого измерения) система уравнений совпадает с (9). Для j-го измерения систему уравнений можно представить в виде

kxij, kyij, kzij - значения kxi, kyi, kzi в j-ом измерении,
Xj, Yj, Zj - значения X, Y, Z в j-ом измерении,
Фij - значения фазового сдвига в j-ом измерении.
Составим разностную систему уравнений, вычитая из линейных членов уравнений (12) линейные члены системы (9):
Дополнительная система уравнений для всех интервалов
Задаваясь априорными значениями X0, Y0, Z0, можно вычислить приращение координат вектора-базы ΔXj, ΔYj, ΔZj за j-й интервал времени. В первом приближении величинами Δkxij•Xo, Δkyij•Yo, Δkzij•Zo можно пренебречь ввиду малости коэффициентов Δkxij, Δkyij, Δkzij. .
Таким образом, по приращению фазового сдвига можно с высокой точностью определить траекторию вектора-базы ΔX, ΔY, ΔZ за любой интервал времени.
Начальное положение вектора-базы можно определить, решая систему уравнений (14). После определения начального положения объекта определение текущего углового положения производится по соотношениям
Моделирование и экспериментальные исследования показали, что устойчивое решение задачи определения углового положения объекта обеспечивается при изменении начального углового положения в пределах нескольких десятков градусов.
На фиг. 1 приведена структурная схема устройства, реализующего предложенный способ. В качестве примера взято простейшее мультиплексное устройство, измеряющее угловое положение одной осевой линии объекта.
Устройство содержит антенны 1 и 2, расположенные параллельно осевой линии объекта, последовательно соединенные малошумящий усилитель (МШУ) 3, вход которого подключен к антенне 1, первый преобразователь 6, модулятор 8, второй преобразователь 10, ограничитель 12, два параллельно включенных логических элемента 14 и 15 и два параллельно включенных реверсивных счетчика 18 и 19, а также последовательно соединенные МШУ 4, вход которого подключен к антенне 2, коммутатор, второй вход которого подключен к МШУ 3, первый преобразователь 7, модулятор 9, второй преобразователь 11, ограничитель 13, два параллельно включенных логических элемента 16 и 17 и два параллельно включенных реверсивных счетчика 20 и 21, кроме того, устройство содержит синтезатор частот 22, связанный с преобразователями 6, 7, 10, 11, генератор ПСП 23, мультиплексор 24, входы которого подключены к выходам генератора ПСП 23, а выходы - к модуляторам 8 и 9, генератор опорного сигнала 25, вход которого подключен к синтезатору частоты 22, а выходы - к логическим элементам 14 - 17, микропроцессорный вычислительный блок, связанный по информационным и управляющим входам с реверсивными счетчиками 18 - 21, генератором опорного сигнала 25, генератором ПСП 23, синтезатором частоты 22 и коммутатором 5 и мультиплексором, кроме того, синтезатор частоты 22 связан по цепям синхронизации с генератором ПСП 23, генератором опорного сигнала 25, реверсивными счетчиками 18 - 21, микропроцессорным блоком 26 и реверсивными счетчиками 18 - 21.
Предлагаемый способ реализуется следующим образом. Сигналы четырех НКА принимаются на две разнесенные антенны. Принятые сигналы на разнесенные антенны имеют фазовый сдвиг Фi, зависящий от угла между осевой линией объекта и направлением на НКА в соответствии с соотношением (1). Сигнал от антенны 1 поступает на первый канал приема и обработки сигналов непосредственно, сигнал от второй антенны поступает на второй канал приема и обработки сигналов через коммутатор 5, каждый из каналов приема и обработки сигналов состоит из первого преобразователя, модулятора, второго преобразователя, ограничителя, логических элементов и реверсивных счетчиков.
На начальном этапе работы устройство работает аналогично известной навигационной аппаратуре, описанной, например, в книге "Сетевые спутниковые радионавигационные системы" под ред. В.С. Шебшаевича, Радио и связь, 1993. В частности, производится поиск сигнала по частоте доплера и задержке. Для этого происходит перебор частот и задержек с некоторым шагом. Поиск производится до принятия решения о наличии сигнала в соответствии с выбранным алгоритмом и критерием.
В глобальных навигационных спутниковых системах производится фазовая модуляция сигналов псевдослучайной последовательностью (ПСП). Для снятия модуляции используется генератор ПСП 23 и модуляторы 8 и 9. При слежении за несущей генератор формирует базовую ПСП П'(t), которая перемножается в модуляторе 8 с принимаемым сигналом. В режиме слежения за задержкой генератор ПСП формирует разностную ПСП П'(t), которая перемножается с принимаемым сигналом в модуляторе 9. Благодаря использованию разностной ПСП П'(t) формируется дискриминационная характеристика по задержке в режиме слежения за задержкой (особенности использования разностной ПСП рассмотрены в работе А. Grebennikov, M.Chmykh. Noiseimmunity comparison for preudorandom signal delaitracking channels. Second International conference on Development Direction of Radio Communication System and Means. Voronezh, 1995). Поскольку второй канал используется также для измерения фазы сигнала от второй антенны, то на модулятор 9 подается либо базовая П(t), либо разностная П'(t) ПСП. Для ее переключения используется мультиплексор 24, управляемый микропроцессорным вычислительным блоком 26.
Синтезатор частоты формирует n частот в соответствии с частотами НКА, генератор опорного сигнала формирует опорный сигнал в виде меандров, перестраиваемый по частоте для перестройки по частоте доплера, а также слежения по фазе и частоте. Генератор опорного сигнала формирует два квадратурных сигнала, т.е. сдвинутых на 90o. Ограничители 12 и 13 производят безынерционное ограничение сигналов. Логические элементы 14 - 17 производят перемножение опорного и ограниченного принимаемого сигнала, реверсивные счетчики 18 - 21 выполняют функции интеграторов, а вместе логические элементы и реверсивные счетчики выполняют функции корреляционного измерителя фазы и амплитуды сигналов (более подробно см. в кн. М.К.Чмых. "Цифровая фазометрия". Радио и связь, 1993).
Микропроцессорный вычислительный блок производит управление работой устройства, определение радионавигационных параметров (фазы несущей, частоты доплера, задержки сигнала) и вычисление навигационных параметров (координат и углового положения).
Аппаратура построена по мультиплексному принципу. Функционирование аппаратуры зависит от ее режима работы в установившемся состоянии, т.е. после того, как завершится поиск сигнала. После обнаружения сигнала аппаратура переходит в режим слежения по несущей, слежения по задержке и режим измерения фазового сдвига сигналов, принимаемых на разнесенные антенны.
Для обеспечения слежения по несущей предназначен первый канал. Сигнал после перемножения в модуляторе 8 с базовой ПСП П(t), преобразования по частоте и ограничения перемножается с квадратурными составляющими опорного сигнала  , также ограниченными. Ограничение применяется для обеспечения цифрового метода измерения параметров сигнала. Реверсивные счетчики подсчитывают число квантующих импульсов Nc,s, пропорциональных
, также ограниченными. Ограничение применяется для обеспечения цифрового метода измерения параметров сигнала. Реверсивные счетчики подсчитывают число квантующих импульсов Nc,s, пропорциональных
где S*(t) - ограниченный принимаемый сигнал,
k - коэффициент пропорциональности, определяемый частотой квантующих импульсов, поступающих на реверсивные счетчики 18 - 21 от синтезатора частоты, и зависящий от отношения сигнал-шум.
Уровень сигнала определяется в микропроцессорном вычислительном блоке 26 по формуле
а фаза сигнала
Сигнал, пропорциональный фазе сигнала по каждому НКА, фильтруется фильтром Калмана и подается на генератор опорного сигнала для слежения по фазе и частоте.
Второй канал работает в режиме слежения по задержке и измерения фазового сдвига.
В режиме слежения по задержке на модулятор 9 через мультиплексор 24 подается разностная ПСП П'(t). Уровень сигнала, соответствующий положению на дискриминационной характеристике, определяется аналогично (16) и пропорционален сдвигу ПСП во времени относительно принимаемого сигнала. При уровне сигнала, равном нулю, задержка ПСП соответствует измеренной задержке τзi по каждому НКА.
В режиме измерения фазы сигнала коммутатор 5 обеспечивает либо измерение фазы сигнала первой антенны (при этом ко второму каналу подключается первая антенна), либо измерение фазы сигнала второй антенны (при этом ко второму каналу подключается вторая антенна). Фазовый сдвиг сигналов, принятых на разнесенные антенны, рассчитывается путем вычитания результатов измерения фазы сигнала первой и фазы сигнала второй антенны.
По результатам определения фазового сдвига вычисляется угловое положение объекта в соответствии с описанным выше алгоритмом.
В настоящее время остро стоит задача расширения функциональных возможностей глобальных навигационных спутниковых систем, в частности измерения углового положения объектов. При этом возникают проблемы повышения точности и уменьшения времени измерения углового положения. На решение этой проблемы направлен предложенный способ. Предложенный способ угловой ориентации объектов отличается от известного, основанного на приеме сигналов от космических аппаратов глобальных навигационных спутниковых систем на разнесенные две или более антенны, расположенные параллельно одной или двум осям измеряемого объекта, измерении фазового сдвига между принятыми сигналами от каждого космического аппарата и определении углового положения осей измеряемого объекта путем решения системы уравнений, тем, что перед началом измерений или в процессе измерений углового положения осей объекта изменяют угловое положение баз, на концах которых расположены антенны, на произвольный угол, после чего антенны возвращают в исходное состояние. Благодаря этому существенно повышается точность и уменьшается время измерения. 1 ил.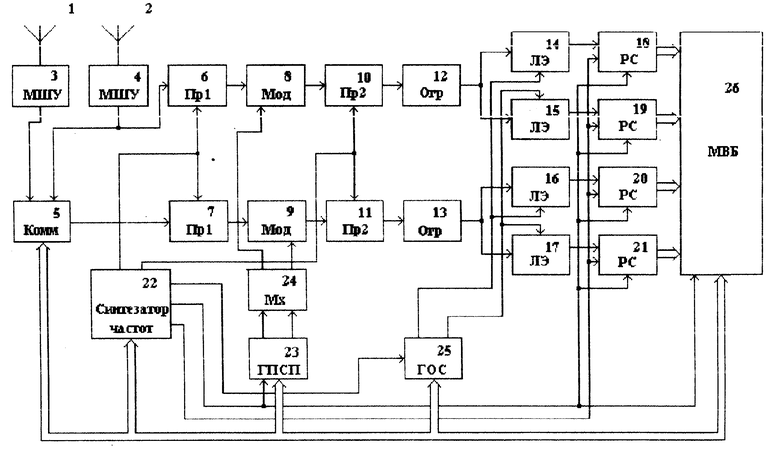
Способ угловой ориентации объектов по сигналам космических аппаратов (КА) глобальных навигационных спутниковых систем, основанный на приеме сигналов от космических аппаратов глобальных навигационных спутниковых систем на разнесенные две или более антенны, расположенные параллельно одной или двум осям измеряемого объекта, измерении фазового сдвига между принятыми сигналами от каждого космического аппарата и определении углового положения осей измеряемого объекта путем решения системы уравнений, отличающийся тем, что перед началом измерений или в процессе измерений углового положения осей объекта изменяют угловое положение баз, на концах которых расположены антенны, на произвольный угол, после чего антенны возвращают в исходное состояние, причем определение углового положения производится последовательным решением первой системы уравнений
и второй дополнительной системы уравнений
X
где Kx i j, Ky i j, Kz i j известные коэффициенты, зависящие от координат космических аппаратов и объекта; приращения коэффициентов;
приращения коэффициентов;
ΔΦij = Φij-Φi1 - разность фазовых сдвигов в i-ом и 1-ом измерениях;
Xo, Yo, Zo измеряемые направляющие косинусы;
ΔXj,ΔYj,ΔZj - приращения направляющих косинусов;
λi - длина волны i-го космического аппарата;
i номер космического аппарата;
j номер измерения фазового сдвига,
при этом на первом шаге в первой системе используется любое значение Xo, Yo, Zo, например Xo Yo Zo 0, а на втором и последующих шагах используется значение Xo, Yo, Zo, соответствующее результату, полученному после решения систем уравнений на предыдущем шаге.
| RU, патент, 2022294, кл | |||
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Зарубежная радиоэлектроника | |||
| Механизм для сообщения поршню рабочего цилиндра возвратно-поступательного движения | 1918 |
|
SU1989A1 |
Авторы
Даты
1998-02-20—Публикация
1995-09-13—Подача