Изобретение относится к навигации и предназначено, в частности, для калибровки гироскопов инерциальных навигационных систем на этапе начальной подготовки.
Наиболее близким к заявляемому способу по технической сущности и достигаемому эффекту является способ калибровки гироскопов инерциальной навигационной системы, в котором измеряется отклонение гиростабилизированной платформы от плоскости горизонта с помощью датчиков акселерометров, измеряется отклонение гиростабилизированной платформы по курсу с помощью датчика угла, на моментные датчики гироскопов подаются сигналы, пропорциональные позиционной и интегральной составляющей горизонтальных компонент кажущегося ускорения и гироскопического курса для построения контура калибровки и определяются дрейфы гироскопов [1].
Недостатком данного способа является невозможность определения мультипликативных составляющих погрешностей гироскопов, что снижает точность калибровки.
Технической задачей изобретения является повышение точности калибровки гироскопов за счет применения расширенной модели погрешностей гироскопов и принудительного вращения курсовертикали относительно трех осей.
Решение технической задачи или сущность изобретения заключается в том, что в способ калибровки гироскопов инерциальной навигационной системы, в котором измеряется отклонение гиростабилизированной платформы от плоскости горизонта с помощью датчиков акселерометров, измеряется отклонение гиростабилизированной платформы по курсу с помощью датчика угла, на моментные датчики гироскопов подаются сигналы, пропорциональные позиционной и интегральной составляющей горизонтальных компонент кажущегося ускорения и гироскопического курса для построения контура калибровки и определяются дрейфы гироскопов, введены новые операции, заключающиеся в том, что инерциальную курсовертикаль с жестко расположенными на ней гироскопами и акселерометрами принудительно вращают относительно трех строительных осей объекта без использования гироскопической стабилизации, измеряют абсолютные угловые скорости вращения курсовертикали с помощью гироскопов и для определения основных составляющих погрешностей гироскопов используют следующую математическую модель калибровки:

Δag= [τ]ag+AΔa1;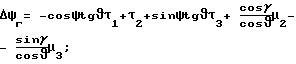

где τ = [τ1τ2τ3]T - ошибки вычисления углов ориентации; - кососимметрическая матрица, составленная из проекций угловой скорости вращения Земли на оси нормальной земной системы координат;
- кососимметрическая матрица, составленная из проекций угловой скорости вращения Земли на оси нормальной земной системы координат; - матрица направляющих косинусов пересчета из нормальной земной системы координат в систему координат, связанную с осями чувствительности гироскопов;
- матрица направляющих косинусов пересчета из нормальной земной системы координат в систему координат, связанную с осями чувствительности гироскопов;
Δω1= [Δωx1Δωy1Δωz1]T - вектор погрешностей гироскопов; - вектор дрейфов гироскопов;
- вектор дрейфов гироскопов;
θ1,θ2,θ3,θ4,θ5,θ6 - перекосы осей чувствительности гироскопов;
kωx1,kωy1,kωz1 - ошибки масштабных коэффициентов гироскопов; - ошибки асимметрии масштабных коэффициентов гироскопов;
- ошибки асимметрии масштабных коэффициентов гироскопов;
ω1= [ωx1ωy1ωz1]T - вектор абсолютной угловой скорости вращения курсовертикали;
Δy = [Δy1Δy2Δy3]T,Δz = [Δz1Δz2Δz3]T, - векторы ошибок корректирующих сигналов Δy1= k1Δazg,Δy2= k3Δψг,Δy3= k5Δaxg;
k1, k3, k5, k' = [k2k4k6] - коэффициенты обратной связи;
Δag= [ΔaxgΔaygΔazg]T - вектор ошибок вычисления ускорения в нормальной земной системе координат;
ag = [axgaygazg]T - вектор ускорений в нормальной земной системе координат;
Δa1= [Δax1Δay1Δaz1]T - вектор погрешностей акселерометров;
Δψг - ошибка вычисления гироскопического курса;
ψ,ϑ,γ - углы курса, тангажа и крена;
μ2,μ3 - погрешности датчиков углов.
Наличие новых действий в способе калибровки гироскопов позволяет повысить точность калибровки с сохранением полной автономности указанного процесса за счет совокупности существенных отличительных признаков:
1) измерения абсолютной угловой скорости с помощью гироскопических датчиков угловой скорости;
2) использования принудительного вращения инерциальной курсовертикали относительно трех строительных осей без использования гироскопической стабилизации;
3) использования математической модели погрешностей гироскопов, учитывающей ошибки масштабных коэффициентов, ошибки асимметрии масштабных коэффициентов и перекосы осей чувствительности гироскопов при объединении их в блок.
Сравнение предложенного технического решения с его прототипом позволило установить соответствие его критерию "новизна". При изучении других технических решений в данной области техники признаки, отличающие заявляемое изобретение от прототипа, не были выявлены и поэтому они обеспечивают заявленному техническому решению соответствие критерию "изобретательский уровень".
Предложенное техническое решение может быть использовано в науке и технике, что обеспечивает соответствие его критерию "промышленная применимость".
Способ заключается в следующем.
Известно [2] , что для вычисления параметров ориентации курсовертикали относительно нормальной земной системы координат используется обобщенное уравнение Пуассона:
 - кососимметричная матрица, составленная из угловых скоростей, измеряемых гироскопами.
- кососимметричная матрица, составленная из угловых скоростей, измеряемых гироскопами.
Для обеспечения устойчивости переходного процесса уравнение (1) может быть изменено следующим образом:
 - кососимметричные матрицы, составленные из корректирующих сигналов обратной связи.
- кососимметричные матрицы, составленные из корректирующих сигналов обратной связи.
В качестве корректирующих сигналов выбраны следующие функции: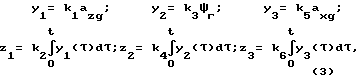
где ψг - гироскопический курс:
axg azg - ускорения по осям нормальной земной системы координат, определяемые по формуле:
ag = Aa1 (4),
где a1=[ax1ay1az1]T - вектор ускорений, измеряемых акселерометрами.
Коэффициенты k1, k2, k3, k4, k5 и k6 выбираются из условия устойчивости контура калибровки и минимизации ошибок оценивания погрешностей гироскопов. Сигнал гироскопического курса может быть получен следующим образом: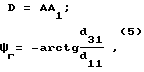
 - матрица направляющих косинусов пересчета из системы координат, связанной с осями чувствительности гироскопов в систему координат, связанную со строительными осями объекта;
- матрица направляющих косинусов пересчета из системы координат, связанной с осями чувствительности гироскопов в систему координат, связанную со строительными осями объекта;
χ1,χ2,χ3 - углы поворота системы координат, связанной с осями чувствительности гироскопов относительно системы координат, связанной со строительными осями объекта; - матрица направляющих косинусов пересчета из системы координат, связанной со строительными осями объекта в нормальную земную систему координат,
- матрица направляющих косинусов пересчета из системы координат, связанной со строительными осями объекта в нормальную земную систему координат,
d11, d31 - элементы матрицы D.
Для получения математической модели калибровки проварьируем выражения (2):
Сделаем замену переменных
ΔA = [τ]A, - кососимметричная матрица, составленная из ошибок вычисления углов ориентации.
- кососимметричная матрица, составленная из ошибок вычисления углов ориентации.
Тогда выражение (6) можно переписать следующим образом:
Умножим левую и правую части выражения (7) на AT справа. Тогда получим:
Так как Aω1= ωg и опорное значение z = ωg/ , то выражение (8) можно переписать в виде:
Можно показать, что [τ][ωg]-[ωg][τ] = -[[ωg]τ] С учетом этого выражение (9) примет вид:
или
Проварьировав уравнения для z1, z2 и z3 из системы (3) и преобразовав их из интегральной формы в дифференциальную, получим:
Далее проварьируем соотношения (4) и (5). После варьирования выражения (4) и несложных преобразований получим:
Δag= [τ]ag+AΔa1. (13)
После варьирования выражения (5) и замены переменных:
ΔA = [τ]A,ΔD = [ν]D,ΔA1= A1[μ], - кососимметричная матрица, составленная из погрешностей датчиков углов;
- кососимметричная матрица, составленная из погрешностей датчиков углов;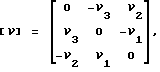
здесь
ν = τ+Dμ. (14)
Значения ошибок углов ориентации объекта Δψ,Δϑ,Δγ связаны со значениями ν1,ν2,ν3 следующими соотношениями [2]:
Подставив в первую формулу (15) значения ν1,ν2,ν3 из (14) и после несложных преобразований, получим:
Систематические погрешности гироскопов можно представить в виде [3]:
Для обеспечения наблюдаемости всех составляющих погрешностей гироскопов в формулах (17) необходимо осуществлять вращение курсовертикали относительно строительных осей объекта с постоянными угловыми скоростями. В этом случае проекции абсолютной угловой скорости вращения курсовертикали на оси чувствительности гироскопов будут иметь вид:
где Ωx,Ωy,Ωz - проекции угловой скорости вращения Земли на строительные оси объекта: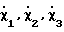 - угловые скорости вращения курсовертикали относительно строительных осей объекта.
- угловые скорости вращения курсовертикали относительно строительных осей объекта.
С помощью математической модели калибровки, описываемой выражениями (11), (12), (13), (16) и (17) можно построить оптимальный фильтр Калмана, который будет оценивать составляющие погрешностей гироскопов  . Для обеспечения наблюдаемости всех составляющих погрешностей гироскопических измерителей угловой скорости оптимальным фильтром в качестве наблюдений необходимо выбрать ошибки корректирующих сигналов Δz1,Δz2Δz3.
. Для обеспечения наблюдаемости всех составляющих погрешностей гироскопических измерителей угловой скорости оптимальным фильтром в качестве наблюдений необходимо выбрать ошибки корректирующих сигналов Δz1,Δz2Δz3.
Источники информации
1. Авиационные приборы и навигационные системы / Под ред. О.А. Бабича.- М.: Издание ВВИА им. проф. Н.Е. Жуковского, 1981.- стр. 525-529. (прототип)
2. Бромберг П. В. Теория инерциальных систем навигации. - М.: Наука, 1979. - 296 с.
3. Иванов М. Н., Лебеденко О.С., Сельвесюк Н.И., Шепеть И.П. Математическая модель возмущений инерциальной навигационной системы с автокомпенсацией погрешностей. М. : ЦВНИИ МО РФ, 1997. - Деп. В ЦСИФ МО РФ. Сер. Б. Вып. N40. инв. В3307. - 11 с.
Изобретение относится к навигации. Техническим результатом является повышение точности калибровки гироскопов на этапе начальной подготовки инерциальной навигационной системы. Инерциальную курсовертикаль с жестко размещенными на ней гироскопическими измерителями угловой скорости и акселерометрами принудительно вращают относительно трех осей без использования гироскопической стабилизации. Из выходных сигналов гироскопов, акселерометров и датчиков углов формируют сигналы, пропорциональные позиционной и интегральной составляющим горизонтальных компонент кажущегося ускорения и гироскопического курса для построения контура калибровки. Определяют дрейф гироскопов, ошибки масштабных коэффициентов, ошибки асимметрии масштабных коэффициентов и перекосы осей чувствительности гироскопов при объединении их в блок.
Способ калибровки гироскопических измерителей угловой скорости, включающий измерение выходных сигналов акселерометров и датчиков углов пространственного положения курсовертикали относительно объекта, формирование сигналов, пропорциональных позиционной и интегральной составляющим горизонтальных компонент кажущегося ускорения и гироскопического курса для построения контура калибровки, отличающийся тем, что инерциальную курсовертикаль с жестко закрепленными на ней гироскопическими измерителями угловой скорости и акселерометрами принудительно вращают относительно трех строительных осей объекта без использования гироскопической стабилизации, измеряют абсолютные угловые скорости вращения курсовертикали с помощью гироскопов и определяют дрейфы гироскопов, ошибки масштабных коэффициентов, ошибки асимметрии масштабных коэффициентов и перекосы осей чувствительности гироскопов, используя следующую математическую модель калибровки

Δag= [τ]ag+AΔa1;

где τ = [ττ2τ3]T - ошибки вычисления углов ориентации; - кососимметрическая матрица, составленная из проекции угловой скорости вращения Земли на оси нормальной земной системы координат;
- кососимметрическая матрица, составленная из проекции угловой скорости вращения Земли на оси нормальной земной системы координат; - матрица направляющих косинусов пересчета из нормальной земной системы координат в систему координат, связанную с осями чувствительности гироскопов;
- матрица направляющих косинусов пересчета из нормальной земной системы координат в систему координат, связанную с осями чувствительности гироскопов;
Δω1= [Δωx1Δωy1Δωz1]T - вектор погрешностей гироскопов; - вектор дрейфов гироскопов;
- вектор дрейфов гироскопов;
θ1,θ2,θ3,θ4,θ5,θ6 - перекосы осей чувствительности гироскопов;
kωx1,kωy1,kωz1 - ошибки масштабных коэффициентов гироскопов; - ошибки асимметрии масштабных коэффициентов гироскопов;
- ошибки асимметрии масштабных коэффициентов гироскопов;
ω1= [ωx1ωy1ωz1]T - вектор абсолютной угловой скорости вращения курсовертикали;
Δy = [Δy1Δy2Δy3]T,Δz = [Δz1Δz2Δz3]T, - векторы ошибок корректирующих сигналов Δy1= k1Δazg,Δy2=k3Δψг,Δy3=k5Δaxg;;
k1, k3, k5, k' = [k2, k4, k6] - коэффициенты обратной связи;
Δag= [ΔaxgΔaygΔazg]T - вектор ошибок вычисления ускорения в нормальной земной системе координат;
ag = [axgaygazg]T - вектор ускорения в нормальной земной системе координат;
Δa1= [Δax1Δay1Δaz1]T - вектор погрешностей акселерометров;
Δψг - ошибка вычисления гироскопического курса;
ψ,ϑ,γ - углы курса, тангажа и крена;
μ2,μ3 - погрешности датчиков углов.
| Авиационные приборы и навигационные системы | |||
| / Под ред.Бабича О.А | |||
| - М.: ВВИА им.Н.Е.Жуковского, 1981, с.525-529 | |||
| СТЕНД ДЛЯ КОНТРОЛЯ ИЗМЕРИТЕЛЕЙ УГЛОВЫХ СКОРОСТЕЙ | 1995 |
|
RU2115128C1 |
| RU 94002637 A1, 27.11.1995. | |||
Авторы
Даты
2000-09-27—Публикация
1999-06-01—Подача