Изобретение относится к электротехнике и может быть испльзовано в электроприводах электропоездов, металлорежущих станков, прокатных станов и других механизмов машиностроения и металлургии с высокими требованиями к качеству регулирования, энергетике и диапазону регулирования, в частности в качестве эталонной модели трехфазного асинхронного двигателя (АД) с короткозамнутым ротором в системах с управлением вектором, а также для исследования динамических режимов работы АД и систем регулирования, для синтеза регуляторов в устройствах для настройки электропроводов во время их опытной эксплуатации, для обучения студентов в вузах.
Известен способ оценки регулируемых переменных трехфазного АД с короткозамкнутым ротором по дифференциальным уравнениям Горева-Парка для обобщенной электрической машины, уравнению электромагнитного момента и уравнению движения [1]. Это способ для уравнений, записанных через потокосцепления, получил наибольшее признание в мире для моделирования динамических режимов работы АД с короткозамкнутым ротором и реализации эталонной модели (модели объекта регулирования) в системах с векторным управлением АД и при оценке регулируемых переменных в более простых системах регулирования. При этом переход от реальной трехфазной машины к обобщенной двухфазной выполняется посредством проецирования регулируемых переменных из реальной системы координат с осями a-b-c, идущими вдоль фаз статора, на ортогональные оси α-β неподвижной относительно статора системы координат или на ортогональные оси d-q системы координат, вращающейся относительно статора с частотой ωr вращения ротора двигателя, или на ортогональные оси x-y системы координат, вращающейся относительно статора с некоторой произвольной частотой вращения ωk.
Общими недостатками всех вариантов известного способа оценки регулируемых переменных двигателя являются:
- низкая точность оценки потокосцеплений по уравнениям Горева-Парка, а следовательно, и низкая точность оценки электромагнитного момента и частоты вращения ротора;
- большая зависимость точности оценки переменных от изменения шага дискретизации в небольшом диапазоне от 5 до 500 мкс [2].
Большей точностью обладают варианты известного способа, использующие проекции сигналов потокосцеплений на ортогональные оси вращающихся систем координат.
Известен [3] способ оценки регулируемых переменных трехфазного АД, по которому для повышения точности оценки проекций потокосцеплений на ортогональные оси d-q вращающейся системы координат измеряют в неподвижной системе координат a-d-c фазные токи статора и фазные напряжения, сначала преобразуют их в проекции на оси α-β также неподвижной системы координат, а затем, используя сигнал угла поворота ротора, сформированный из интеграла сигнала задания частоты вращения поля статора, в проекции на оси d-q вращающейся системы координат.
К недостаткам способа следует отнести:
- большое количество используемых датчиков,
- дополнительный координатный преобразователь (КП) α-β/d-q;
- неточная оценка угла поворота ротора по заданной частоте вращения поля статора, а не по частоте вращения ротора, а следовательно,
- невысокая точность оценки сигнала потокосцеплений по проекциям токов статора и напряжений, при формировании которых использовался приближенно оцененный угол поворота ротора,
- невозможность по приближенно оцененным потокосцеплениям оценивать сигналы электромагнитного момента и частоты вращения ротора.
Известен наиболее точный способ [4] оценки регулируемых координат АД с короткозамнутым ротором по уравнениям Горева-Парка для обобщенной электрической машины, уравнению электромагнитного момента и уравнению движения, записанным в потокосцеплениях в роторной системе координат с осями d-q, по которому электромагнитный момент двигателя формируют по векторному произведению токов ротора и намагничивания, представленных в виде проекций на ортогональный оси d-q.
Это повысило точность оценки электромагнитного момента при шаге дискретизации до 200 мкс по сравнению с другими способами оценки. При этом точность оценки тока намагничивания невысока, так как он формируется по приближенному выражению, связывающему ток намагничивания, токи статора и ротора и потокосцепления статора и ротора.
Этот способ авторами рекомендован для исследования работы асинхронного двигателя в системе регулирования при их симуляции на ПЭВМ в пакете программ Pspice. В случае его использования при регулировании АД к числу недостатков, кроме невысокой точности оценки тока намагничивания, следует отнести использование дополнительного КП α-β/d-q.
Для уменьшения количества используемых координатных преобразователей целесообразно моделировать АД с использованием только неподвижных систем координат a-b-c и α-β, связанных со статором двигателя. Такие модели и являются аналогами предлагаемой модели.
При моделировании АД в осях α-β возникает необходимость повысить точность решения дифференциальных уравнений Горева-Парка.
Среди приемов численного решения дифференциальных уравнений известен метод разности уравнений. Для повышения точности оценки регулируемых переменных АД в дискретные моменты времени на вход модели подают сигнал задания напряжения, равный среднему арифметическому между напряжением в начале и в конце интервала и действительным напряжением, соответствующим моменту времени на полпериода вперед [5]. Такой прием непригоден для моделирования в реальном времени, так как задающий сигнал в замкнутой системе регулирования определяется измеренным сигналом обратной связи.
Известен способ оценки регулируемых переменных АД с КЗ ротором по уравнениям Горева-Парка, записанным через потокосцепления в форме Коши, для моделирования двигателя на средствах аналоговой [6] и цифровой вычислительной техники [7], причем в последнем случае для повышения точности и даже устойчивости решения используется метод А.В.Башарина, заключающийся в том, что на каждом шаге численного решения дифференциального уравнения выполняются две итерации, каждая из которых заканчивается вычислением среднего значения регулируемых переменных на шаге интегрирования.
Несмотря на это, точность оценки регулируемых переменных этим способом невысока и зависит так же, как и устойчивость модели, от шага дискретизации. Точность оценки регулируемых переменных по способам [7] и [5] примерно одинакова.
Известен [8] способ оценки регулируемых переменных трехфазного асинхронного двигателя с короткозамкнутым ротором, основанный на функционировании в дискретные моменты времени математической модели двигателя, настраиваемой по параметрам Т-образной схемы замещения фазы двигателя, для которой измеряют фазные токи статора, фазные напряжения и сигнал позиции, по которым формируют проекции векторов сигналов тока статора и сигналов потокосцеплений статора на ортогональные оси α-β системы координат, неподвижной относительно статора, по векторному произведению которых, умноженному на 1,5, формируют сигнал электромагнитного момента двигателя, по которому, с учетом момента нагрузки и направления вращения двигателя, формируют сигнал динамического момента двигателя. При необходимости частоту вращения ротора двигателя формируют по измеренному сигналу позиции.
Главный недостаток: низкая точность сигналов потокосцеплений, а следовательно, и электромагнитного момента, о чем свидетельствует отсутствие в выражении для вычисления электромагнитного момента произведения индуктивности ветви намагничивания и числа пар полюсов.
Известен [9] способ оценки регулируемых переменных трехфазных асинхронных двигателей с короткозамкнутым ротором, по которому используют функционирующие в дискретные моменты времени и настраиваемые по параметрам Т-образной схемы замещения фазы двигателя и заданной частоте вращения поля статора математическую модель двигателя при имитации объекта регулирования, на вход которой подают сигналы задания питающего напряжения в функции частоты вращения поля статора, и математическую модель с двумя наблюдателями: наблюдателем потока и тока статора и сдвоенным наблюдателем частоты вращения ротора. Математическая модель, имитирующая двигатель как объект регулирования, основана на решении уравнений Горева-Парка для обобщенной двухфазной машины, записанных в форме Коши относительно проекций векторов потокосцеплений статора и ротора на ортогональные оси α-β системы координат, неподвижной относительно статора. Выходом модели являются проекции вектора тока статора на оси α-β, рассматриваемые как предполагаемое задание на ток. Математическая модель с наблюдателями регулируемых переменных основана на решении модифицированных уравнений Горева-Парка. Эта модель в первой своей части повторяют модель-имитатор и предназначена для повышения точности оценки токов, потокосцеплений и частоты вращения ротора.
Недостатки:
- из всех известных в основу обеих моделей двигателя положена модель, имеющая низкую устойчивость к изменению шага дискретизации и самую низкую точность оценки потокосцеплений и токов статора;
- для повышения точности формируемых сигналов потокосцеплений и тока статора, от которых зависит точность оценки частоты вращения ротора, во вторую модель введено несколько наблюдателей: наблюдатель потока и тока статора;
- на вход обеих моделей для настройки их параметров подают сигнал задания частоты вращения поля статора, который отличается на величину абсолютного скольжения от частоты вращения ротора, которая и должна была бы определять параметры модели двигателя. В результате модель может потерять устойчивость при увеличении наклона сигнала задания частоты вращения в случае его линейного изменения и полностью непригодна для использования при подаче сигнала задания скачком.
Недостатками всех вышеперечисленных способов-аналогов являются:
- низкая точность оценки электромагнитного момента и частоты вращения двигателя по проекции потокосцеплений;
- отсутствие аналитического решения, которое можно было бы считать эталоном и с ним сравнивать результаты моделирования численными методами;
- отсутствие аналитического описания, позволяющего аналитическими методами синтезировать регуляторы.
Известен способ [10] (прототип) оценки регулируемых переменных трехфазного асинхронного двигателя с короткозамкнутым ротором, наиболее близким к предлагаемому, основанный на функционирования в дискретные моменты времени математической модели двигателя, настраиваемой по параметрам упрощенной Т-образной схемы замещения фазы двигателя. По этому способу в дискретные моменты времени формируют сигнал ωs задания частоты вращения поля статора, определяют сигналы Us питающего напряжения, формируют сигналы фазных токов isa, isb, isc статора и сигналы фазных токов ima, imb, imc намагничивания по передаточным функциям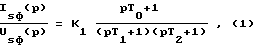
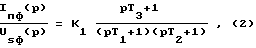
где Usф(p), Isф(p), Imф(p) - преобразования по Лапласу соответственно фазных сигналов питающего напряжения, токов статора и намагничивания,
K1 - коэффициент усиления,
T0, T1, T2, T3 - постоянные времени, зависящие от относительного скольжения s и параметров r1, L1, r'2, L'2, Lm T-образной схемы замещения двигателя,
при относительном скольжении s = 0
K1 = 1/r1,
T1 = (L1 + Lm)/r1, T0 = T2 = T3 = 0
Кроме того, формируют проекции isα,isβ и imα,imβ векторов сигналов тока статора и тока намагничивания на ортогональные оси α-β системы координат, неподвижной относительно статора, по векторному произведению которых формируют сигнал электромагнитного момента двигателя. Параметры передаточных функций зависят от величины относительного скольжения s, которая задается постоянной величиной. При формировании электромагнитного момента используется выражение для векторного произведения токов статора и намагничивания, представляющего собой произведение модулей векторов этих токов на синус угла между ними. При этом угол между векторами тока статора и тока намагничивания принимается постоянным и равным девяноста градусам минус угол между фазными током статора и напряжением в режиме короткого замыкания.
К недостаткам описанного способа следует отнести:
1) возможность использования модели только для качественной оценки переходных процессов из-за:
- очень низкой точности оценки сигналов токов статора и намагничивания, обусловленной, во-первых, применением упрощенной T-образной схемы замещения фазы двигателя и, во-вторых, допущением постоянства относительного скольжения при исследовании динамики двигателя;
- очень низкой точности формирования сигнала электромагнитного момента, обусловленной, во-первых, низкой точностью сигналов токов статора и намагничивания, во-вторых, допущением постоянства угла между векторами тока статора и тока намагничивания и, в-третьих, отсутствием в выражении для электромагнитного момента числа пар полюсов двигателя;
2) невозможность из-за низкой точности оценки токов статора и намагничивания оценивать величину электромагнитного момента по более "быстрому" выражению, основанному на векторном произведении токов статора и намагничивания, выраженных через проекции векторов токов на ортогональные оси α-β системы координат, неподвижной относительно статора.
К достоинствам описанного способа следует отнести представление модели асинхронного двигателя в виде передаточных функций фазных токов по питающему напряжению, что при повышении точности параметров, входящих в эти функции, может позволить получить аналитическую модель - эталон двигателя и осуществить синтез регуляторов тока аналитическими методами.
Поставлена задача: повысить точность оценки регулируемых переменных трехфазного асинхронного двигателя с короткозамкнутым ротором.
На решение этой задачи и направлен предлагаемый способ.
Поставленная задача решается благодаря тому, что:
в дискретные моменты времени
- формируют сигнал относительного скольжения s,
- вычисляют входящие в передаточные функции (1) коэффициент усиления и постоянные времени при относительном скольжении s ≠ 0 по новым выражениям, учитывающим все параметры классической T-образной схемы замещения
K1 = 1/r1,
T0 = s(Lm + L'2)/r'2,
T1 = 2a/(b-c),
T2 =2a/(b+c),
a = L1T0 + LmT3,
b = r1T0 + L1 + Lm,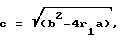
T3 = s (L'2)/r'2,
где r1 и L1 - активное сопротивление и индуктивность фазы статора,
r'2 и L'2 - приведенные к цепи статора активное сопротивление и индуктивность фазы ротора,
Lm - индуктивность ветви намагничивания,
формируют сигналы isa, isb, isc фазных токов статора по передаточным функциям (1) путем цифрового моделирования или по новым выражениям для фазных токов isф(t) статора в функции времени t при сигнале задания питающего напряжения в виде идеальной синусоиды с частотой ω1 одной из гармоник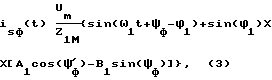
где Um - максимум сигнала питающего напряжения,
ψф - начальный фазовый сдвиг синусоиды питающего напряжения в соответствующей фазе двигателя,
ϕ1 - фазовый сдвиг фазного тока статора по отношению к питающему напряжению фазы, вычисляемый в дискретные моменты времени по параметрам T-образной схемы замещения и новому значению относительного скольжения s,
Z1M - модуль комплексного сопротивления фазному току статора, вычисляемый в дискретные моменты времени,
A1, B1 - коэффициенты, вычисляемые по выражениям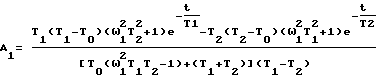
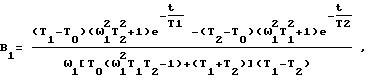
При цифровом моделировании токов статора в зависимости от его цели в качестве сигнала задания напряжения используется сформированный сигнал или измеренный по крайней мере в двух фазах статора двигателя.
С той же точностью можно сформировать сигналы фазных токов намагничивания по выражению (4), аналогичному выражению (3):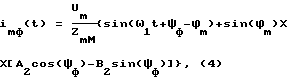
где Um - максимум сигнала питающего напряжения,
ϕm/ - фазовый сдвиг фазного тока намагничивания по отношению к питающему напряжению фазы, вычисляемый в дискретные моменты времени по параметрам T-образной схемы замещения и новому значению относительного скольжения s,
ZmM - модуль комплексного сопротивления фазному току намагничивания, вычисляемый в дискретные моменты времени,
A2, B2 - коэффициенты, вычисляемые по выражениям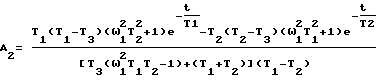
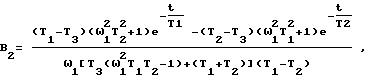
формируют проекции imα и imβ вектора сигналов тока намагничивания на ортогональные оси α-β системы координат, неподвижной относительно статора, путем цифрового моделирования по новой передаточной функции сигналов токов намагничивания по сигналам токов статора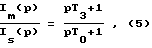
где Im(p), Is(p) - преобразования по Лапласу проекций на ортогональные оси координат α-β соответственно векторов сигналов токов статора и намагничивания.
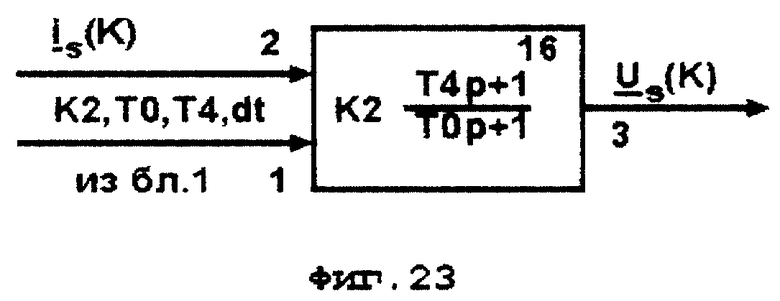
Кроме того, решение поставленной задачи достигается благодаря тому, что сигнал us(t) питающего напряжения статора при относительном скольжении s ≠ 0 формируют путем цифрового моделирования по новой передаточной функции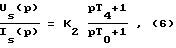
где Us(p), Is(p) - преобразования по Лапласу соответственно сигнала питающего напряжения статора и сигнала тока статора,
K2 - коэффициент усиления, вычисляемой по выражению K2 = r1;
T4 - постоянная времени, вычисляемая по выражению T4 = T1 + T2.
По выражению (6) путем цифрового моделирования можно оценивать:
- сигнал на зажимах статора по измеренным по крайней мере в двух фазах токам статора
и (или)
- сигнал задания напряжения, предназначенный для выдачи в преобразователь частоты и формируемый по измеренному току статора и сигналу с выхода регулятора тока.
Кроме того, решение поставленной задачи может быть достигнуто благодаря тому, что для учета пространственной несимметрии фаз статора двигателя формируют проекции сигналов на мнимую ось β ортогональной системы координат, неподвижной относительно статора, по новым выражениям
isβ= K[isbsin(ψab)-iscsin(ψac)],
где K = isa/[isa+isbcos(ψab)+isccos(ψac)],
ψab,ψac - пространственные углы соответственно между фазами a и b и между фазами a и c.
Высокая точность оценки токов статора is и токов намагничивания im позволяет оценивать:
- фазный ток ротора или его проекции на ортогональные оси координат по выражению
i'r = im - is,
- электромагнитный момент M в отличие от прототипа по выражениям:
самому оптимальному по быстродействию
M = 1,5Lmpτ(isβimα-isαimβ) (7)
или более точному на pτ по сравнению с прототипом
M = 1,5LmpτIsMImMsinα, (8)
или наиболее точным, отличающимся от предыдущих множителем m1/2
M = (m1m2/4)Lmpτ(isβimα-isαimβ) (9)
или
M = (m1m2/4)LmpτIsMImMsinα, (10)
где m1 и m2 - число фаз соответственно в статоре и роторе,
pτ - число пар полюсов в двигателе,
IsM и ImM - модули соответственно векторов тока статора и тока намагничивания,
α - угол между векторами тока статора и тока намагничивания, формируемый в отличие от прототипа по одному из выражений:
α = arctg(isβ/isα)-arctg(imβ/imα)
при вытекающим из выражений (9) и (10) для электромагнитного момента
α = arcsin((isβimα-isαimβ)/(IsMImM))
или
α = arctg((isαimα+isβimβ)/(isβimα-isαimβ)).
Повышение точности оценки сигнала электромагнитного момента M по выражениям (8) и (10) до точности оценки по выражениям (7) и (9), а также введение новой зависимости тока намагничивания от тока статора по выражению (5) открывает новые возможности для поиска новых законов регулирования переменных двигателя в системах с управлением вектором.
Выражение (10) можно получить из известного выражения электромагнитного момента через результирующие комплексные функции потокосцепления и тока:
M = (m2pτ/2)Im[ψ rsi
где ψrs= Lrsmise-jθ - (12) результирующий вектор потокосцепления,
ir * - вектор, сопряженный результирующему вектору тока ротора,
Lrsm = (m1/2)Lm - (13) взаимная индуктивность ротора под влиянием статора,
is - результирующий вектор тока статора, умножением на e-jθ приведен во вращающуюся систему координат ротора,
θ - угол поворота ротора.
Из теории вращающегося поля известно, что результирующие векторы тока статора is, намагничивания im и ротора ir можно следующим образом выразить через мгновенные значения фазных токов двигателя: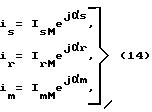
где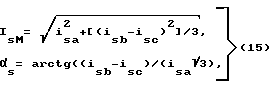
и т.д.
Подставляя в (11) выражения (12)-(14), получим выражение электромагнитного момента через мгновенные значения токов статора и ротора:
M = (m1m2/4)LmpτIsMIrMsin(αs-αr-θ). (16)
Моделирование на ЭВМ момента по выражению (16) показало, что оно непригодно для оценки электромагнитного момента, так как содержащиеся в нем токи статора и ротора очень велики по амплитуде, а угол, заключенный между ними, напротив, очень мал. Небольшая ошибка в оценке угла может привести к неправильным выводам, в частности, о зависимости характера и времени переходного процесса от начального положения ротора, характеризующегося величиной θ0 начального смещения осей ротора по отношению к осям статора. Подставив в (11) ir= imejθ-isejθ и учитывая, что is x is = 0, получим выражению (10) для вращающего момента, из которого видно, что последний зависит от числа фаз в статоре и роторе, индуктивности ветви намагничивания фазы двигателя, числа пар полюсов, амплитуд и разности фаз (α = αs-αr) результирующих токов статора и намагничивания и не зависит от положения ротора.
В процессе поиска аналогов и выбора прототипа среди просмотренных технических решений не были обнаружены признаки, которые сходны с отличительными признаками заявляемого технического решения.
В предлагаемом техническом решении задача по устранению недостатков прототипа решается путем учета всех параметров классической T-образной схемы замещения фазы АД с короткозамкнутым ротором, формирования сигналов токов статора и намагничивания и сигналов питающего напряжения по новым выражениям, формирования в дискретные моменты времени сигналов относительного скольжения и угла между векторами токов статора и намагничивания.
Все это, как будет показано ниже, позволяет повысить точность оценки регулируемых переменных АД.
Данное изобретение поясняется чертежами, представленными на фиг. 1-25.
На фиг. 1 приведена классическая T-образная схема замещения фазы трехфазного АД с короткозамкнутым ротором, положенная в основу предлагаемого способа оценки регулируемых переменных АД.
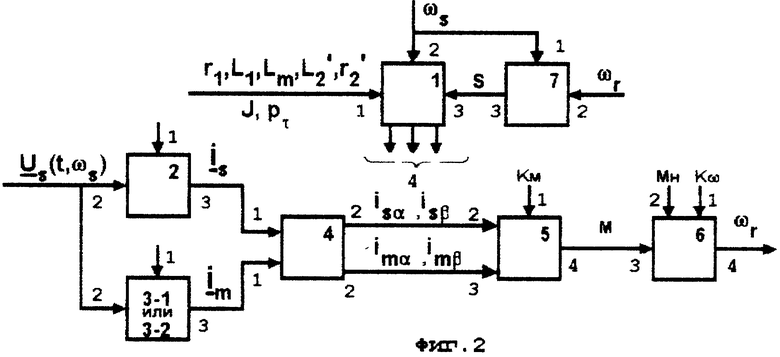
На фиг. 2-4 приведены варианты блок-схем устройств, реализующих оценку наиболее важных регулируемых переменных АД.
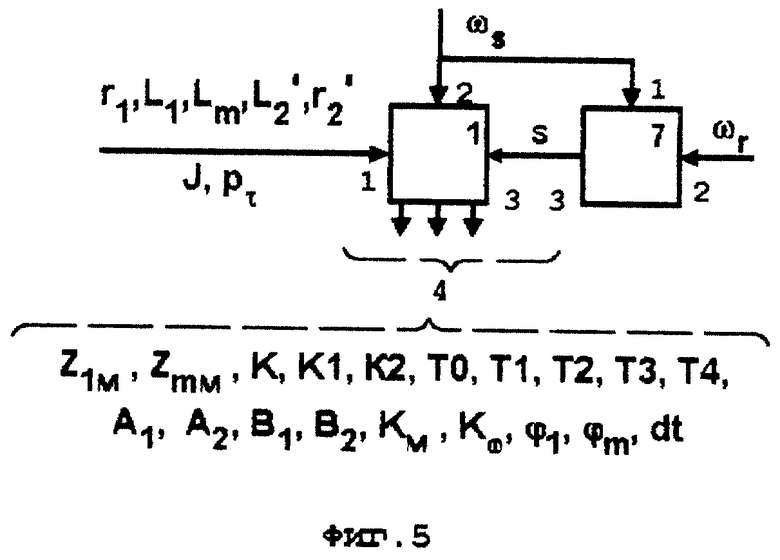
На фиг. 5-11 приведены блок-схемы функциональных блоков 1-7, из которых состоят устройства, схемы которых представлены на фиг. 2-4.
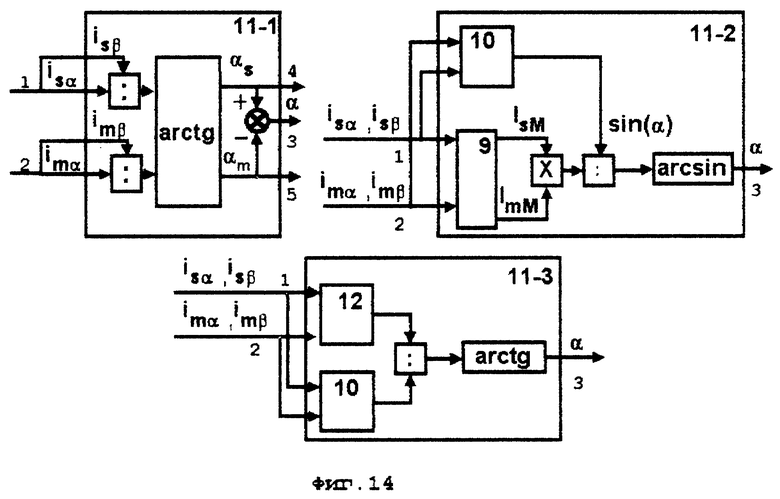
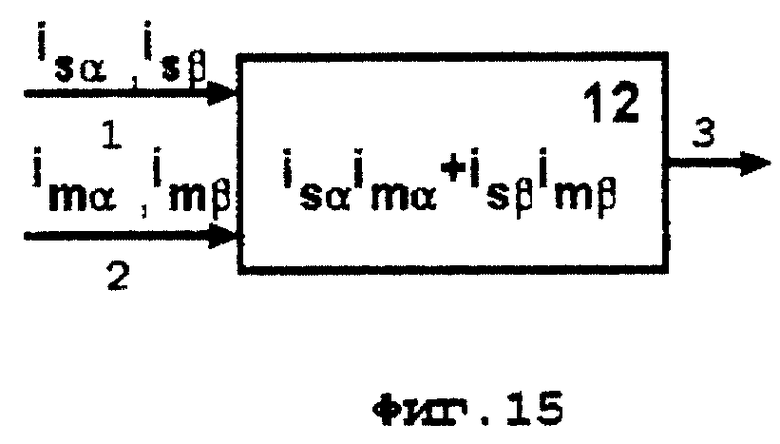
На фиг. 12-15 приведены блок-схемы функциональных блоков 9-12, которые входят в состав блока 5, представленного на фиг.9.
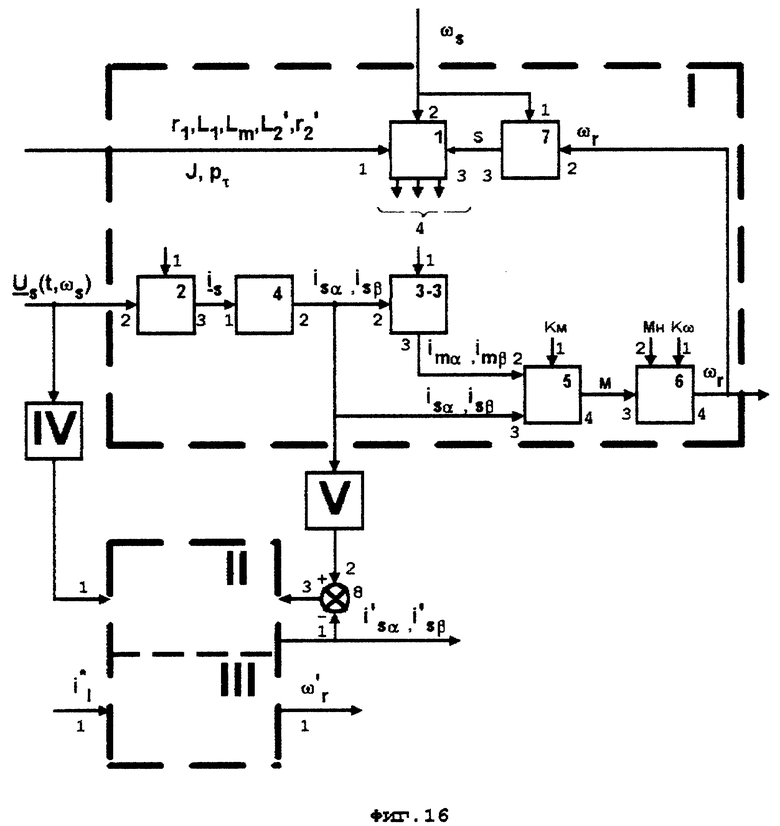
На фиг. 16 приведена блок-схема устройства-аналога [9], использующего модели объекта и модели с наблюдателями переменных, в котором в качестве модели объекта используется устройство, реализованное по предлагаемому способу.
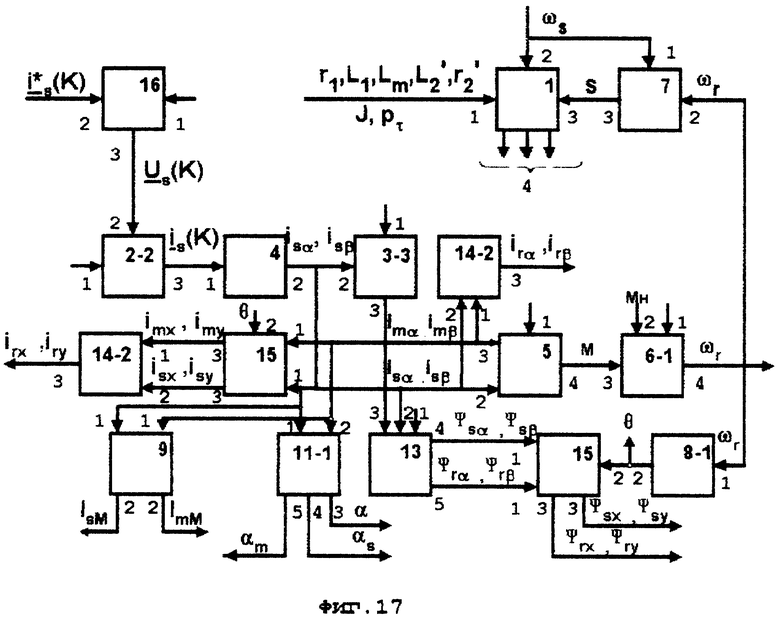
На фиг. 17 приведена блок-схема устройства, осуществляющего оценку известных регулируемых переменных АД, оптимальным по быстродействию способом.
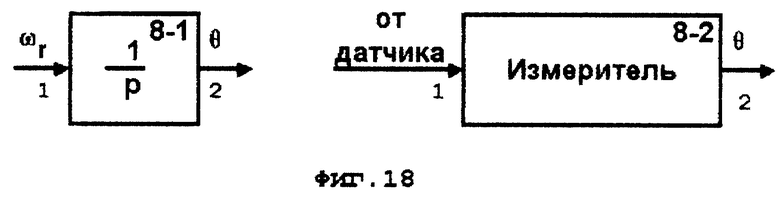
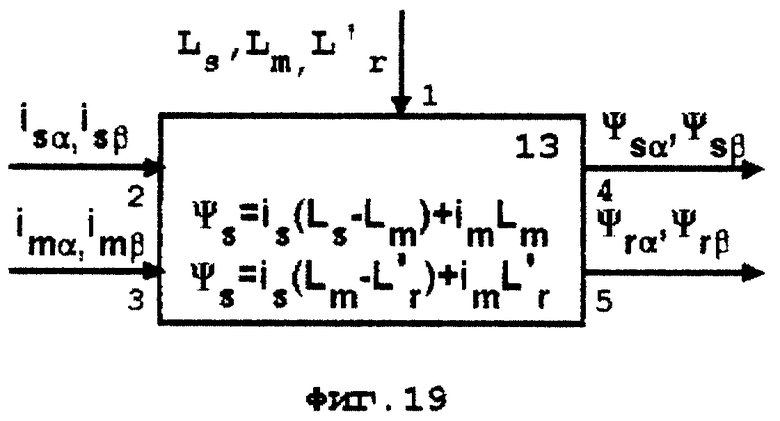
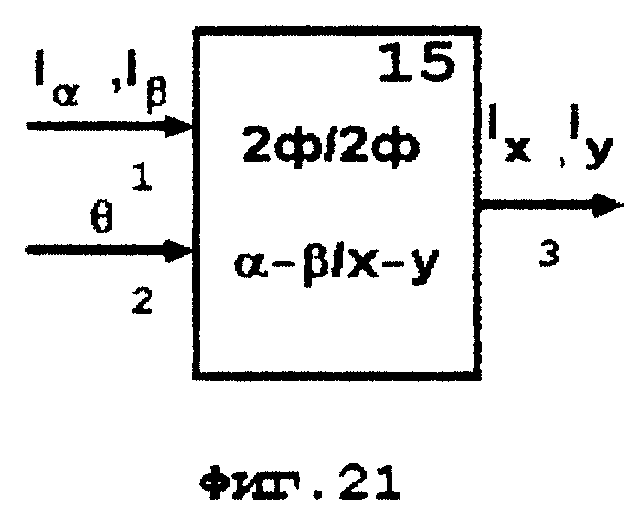
На фиг. 18-21 приведены блок-схемы функциональных блоков 8, 13, 14 и 15. которые входят в состав устройства, схема которого представлена на фиг. 17.
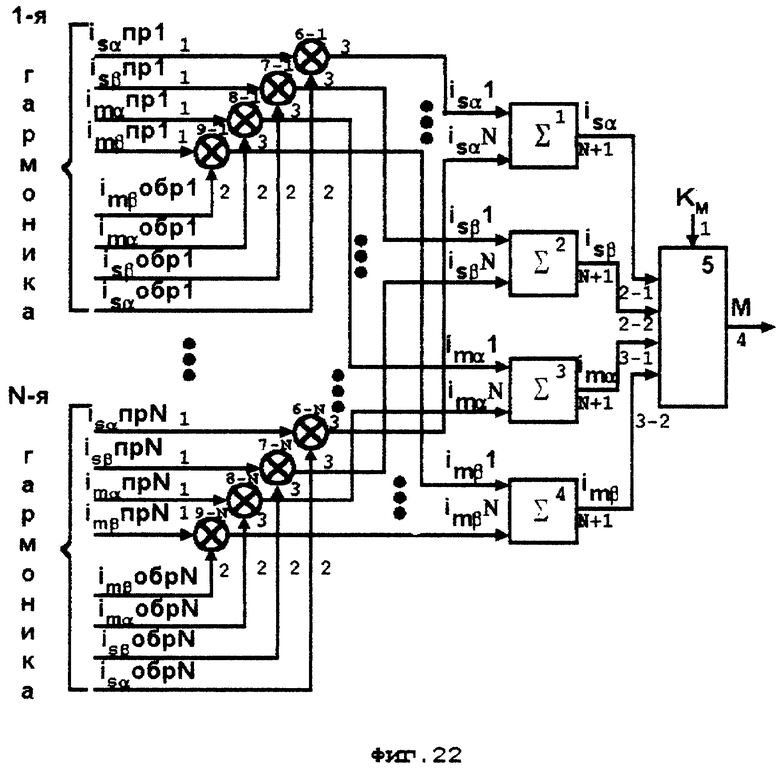
На фиг. 22 приведен фрагмент устройства для оценки токов статора и намагничивания, а также электромагнитного момента АД при несимметричном и несинусоидальном питающем напряжении.
На фиг. 23 приведен блок 16 формирования сигналов питающего напряжения по сигналам токов статора с использованием заявляемой передаточной функции.
На фиг. 24 и 25 приведены графики переходных процессов в электромагнитном моменте М и частоте вращения ротора ωr при прямом пуске АД, подтверждающие высокую точность и устойчивость предлагаемого способа оценки регулируемых переменных двигателя в широком диапазоне изменения шага дискретизации, в том числе и при достаточно малом, равном 5 мкс.
На фиг. 2, 3 и 4 обозначено:
1 - белок вычисления параметров (фиг. 5),
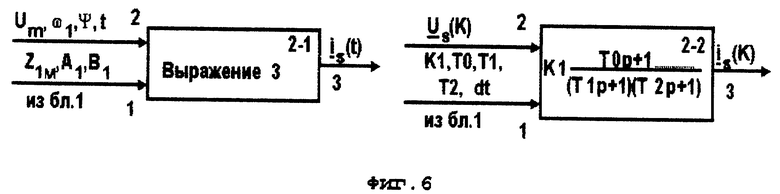
2 - блок формирования тока статора (фиг. 6),
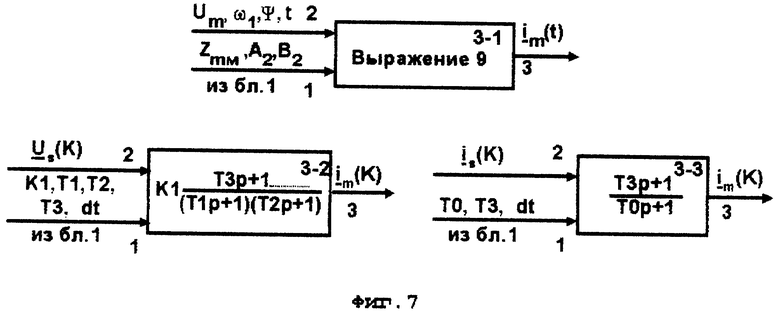
3 - блок формирования тока намагничивания или его проекций на ортогональные оси координат (фиг. 7),
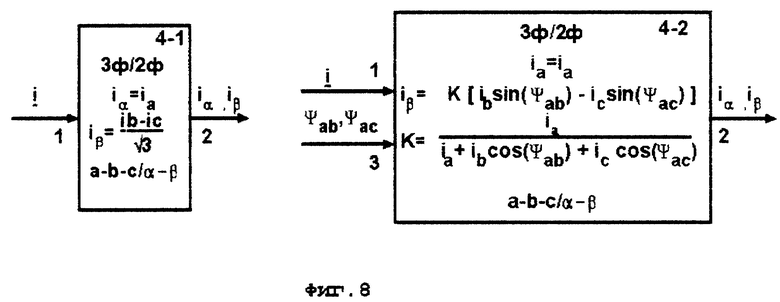
4 - координатный преобразователь (КП) 3ф/2ф (3 фазы/2 фазы) (фиг. 8),
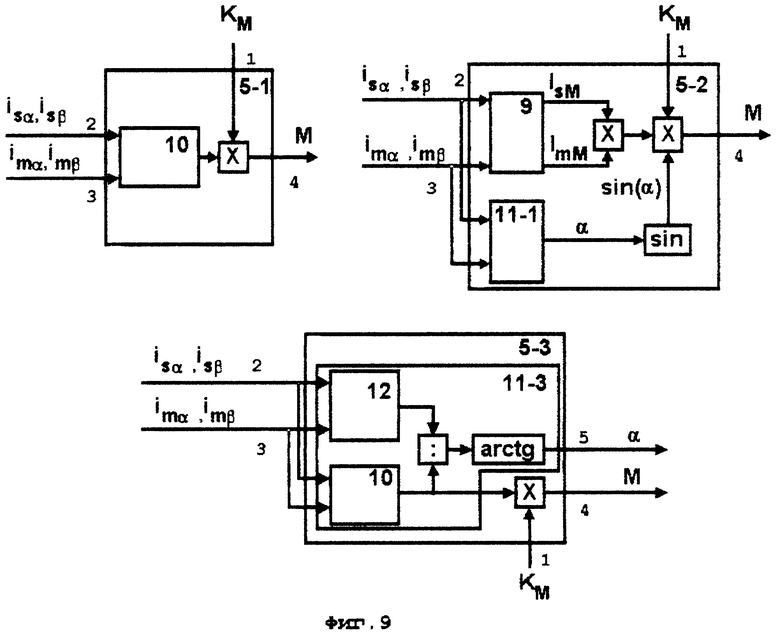
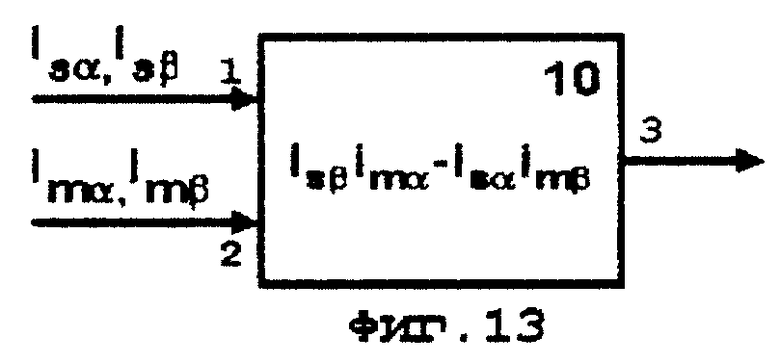
5 - блок формирования электромагнитного момента (фиг. 9),
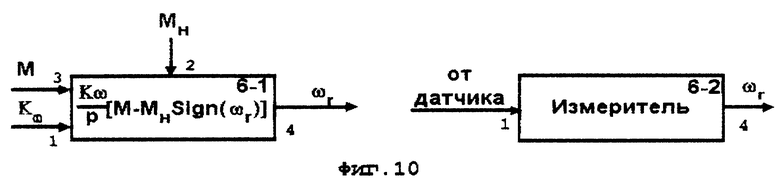
6 - блок формирования частоты вращения ротора (фиг. 10),
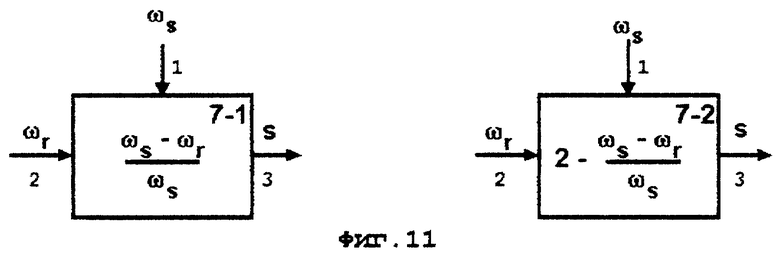
7 - блок формирования относительного скольжения (фиг. 11),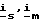 - векторы соответственно сигналов токов статора и намагничивания,
- векторы соответственно сигналов токов статора и намагничивания,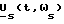 - в общем случае вектор сигнала напряжения статора в функции времени t и частоты вращения поля статора ωs. Для блоков 2-1 и 3-1 это - Um, ω1 , t и ψ для каждой фазы, а для блоков 2-2- и 3-2 это -
- в общем случае вектор сигнала напряжения статора в функции времени t и частоты вращения поля статора ωs. Для блоков 2-1 и 3-1 это - Um, ω1 , t и ψ для каждой фазы, а для блоков 2-2- и 3-2 это -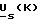 - вектор сигнала напряжения статора, соответствующий моменту времени, определяемому переменной K, равной номеру шага дискретизации.
- вектор сигнала напряжения статора, соответствующий моменту времени, определяемому переменной K, равной номеру шага дискретизации.
Каждый вектор состоит из сигналов фаз a, d и c.
На фиг. 6, 7, 19 обозначено: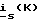 - например, вектор сигнала тока статора, соответствующий моменту времени, определяемому переменной K, равной номеру шага дискретизации.
- например, вектор сигнала тока статора, соответствующий моменту времени, определяемому переменной K, равной номеру шага дискретизации.
В блоке 1 (фиг. 5) обозначено:
1 - вход для ввода параметров АД и его нагрузки,
2 - вход для ввода сигнала ωs задания частоты вращения поля статора,
3 - вход для ввода сигнала s относительного скольжения,
4 - выходы.
Количество вводимых параметров по входу 1 блока 1 и количество выходов 4 определяется количеством оцениваемых сигналов и конкретной реализацией других блоков, на вход которых поступают параметры с выхода 4 блока 1.
В блоках 2, 3, 5, 6, 13 и 16 (фиг. 6, 7, 9, 10, 19 и 23) обозначено:
1 - вход для ввода необходимых переменных из блока 1, причем количество переменных определяется математическим выражением, которое реализует данный блок.
В блок 5 из блока 1 по входу 1 вводится коэффициент Км пропорциональности электромагнитного момента, определяемый выражением (6), или (7), или (8), или (9), реализованным в блоке 5.
В блок 6 из блока 1 по входу 1 вводится коэффициент пропорциональности Kω, определяемый основным уравнением динамики и равный отношению числа пар полюсов двигателя pτ к величине J суммарного момента инерции двигателя и его нагрузки.
В системах регулирования с датчиком частоты вращения и (или) положения ротора блок 6 не используется.
Реализация блоков 1...8 и 11 определяется конкретной решаемой задачей.
В блоках 4-1, 4-2 (фиг. 8) обозначено: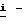 вектор какого-либо сигнала, например тока или напряжения статора в реальных осях a-b-c статора,
вектор какого-либо сигнала, например тока или напряжения статора в реальных осях a-b-c статора,
iα,iβ - проекции вектора какого-либо сигнала на ортогональные оси α-β системы координат, неподвижной относительно статора.
На фиг. 16 обозначено:
1 - блок, реализующий модель объекта регулирования, в частности трехфазного АД с короткозамкнутым ротором по заявляемому способу,
II - блок, реализующий наблюдатели потокосцеплений и тока статора по способу, заявленному в [9],
III - блок, реализующий наблюдатель частоты вращения ротора по способу, заявленному в [9],
IV - блок, реализующий приведение сигнала задания напряжения статора к виду по способу, заявленному в [9],
V - блок, реализующий приведение проекций сигналов тока статора с выхода блока I к виду по способу [9],
8 - блок вычитания проекций isα,isβ векторов сигналов токов с выхода модели объекта регулирования (блок I) и проекций 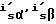 векторов сигналов токов с выхода наблюдателя тока и потокосцеплений (блок II),
векторов сигналов токов с выхода наблюдателя тока и потокосцеплений (блок II),
i1 * - сигнал тока статора по способу, заявленному в [9],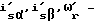 соответственно проекции вектора тока статора на оси α-β ортогональной системы координат,
соответственно проекции вектора тока статора на оси α-β ортогональной системы координат,
неподвижной относительно статора, и частота вращения ротора по способу, заявленному в [9],
На фиг. 17 обозначено:
8 - блок формирования угла поворота ротора (фиг. 18),
13 - блок формирования проекций потокосцеплений статора и ротора на ортогональные оси α-β (фиг. 19),
14 - блок формирования тока ротора (фиг. 20),
15 - известный координатный преобразователь (КП) 2ф/3ф (2 фазы / 2 фазы) (фиг. 21),
isx, isy, irx, iry, imx, imy - соответственно проекции токов статора, ротора и намагничивания на оси системы координат, вращающейся относительно статора с произвольной скоростью ωkk, ψsx,ψsy,ψrx,ψry - соответственно проекции потокосцеплений статора и ротора на оси системы координат, вращающейся относительно статора с произвольной скоростью ωk.
В частном случае ωk= ωr в системе координат с осями d-q вместо x-y.
На фиг. 22 обозначено:
1 - блок суммирования проекций векторов N гармоник токов статора на ось α неподвижной системы координат,
2 - блок суммирования проекций векторов N гармоник токов статора на ось β неподвижной системы координат,
3 - блок суммирования проекций векторов N гармоник токов намагничивания на ось α неподвижной системы координат,
4 - блок суммирования проекций векторов N гармоник токов намагничивания на ось β неподвижной системы координат,
5 - блок формирования электромагнитного момента (фиг. 9), входы 2-1, 2-2 и 3-1, 3-2 блока 1 соответствуют входам 2 и 3 на фиг. 9,
6-1 - блок суммирования проекций векторов первой гармоники токов статора прямой и обратной последовательностей на ось α неподвижной системы координат,
7-1 - блок суммирования проекций векторов первой гармоники токов статора прямой и обратной последовательностей на ось β неподвижной системы координат,
8-1 - блок суммирования проекций векторов первой гармоники токов намагничивания прямой и обратной последовательностей на ось α неподвижной системы координат,
9-1 - блок суммирования проекций векторов первой гармоники токов намагничивания прямой и обратной последовательностей на ось β неподвижной системы координат,
6-N - блок суммирования проекций векторов N-ой гармоники токов статора прямой и обратной последовательностей на ось α неподвижной системы координат,
7-N - блок суммирования проекций векторов N-ой гармоники токов статора прямой и обратной последовательностей на ось β неподвижной системы координат,
8-N - блок суммирования проекций векторов N-ой гармоники токов намагничивания прямой и обратной последовательностей на ось α неподвижной системы координат,
9-N - блок суммирования проекций векторов N-ой гармоники токов намагничивания прямой и обратной последовательностей на ось β неподвижной системы координат,
isαпр1,isβпр1,isαпрN,isβпрN - проекции векторов токов прямой последовательности, например, статора соответственно первой и N-ой гармоник,
isαобр1,isβобр1,isαобрN,isβобрN - проекции векторов токов обратной последовательности, например, статора соответственно первой и N-ой гармоник,
isα1,isαN - например, проекции векторов токов статора соответственно первой и N-ой гармоники.
На фиг. 2 показана блок-схема устройства, аналогичного прототипу. Устройство содержит блок 1 вычисления параметров, вход 2 которого соединен с входом 1 блока 7, а вход 3 - с выходом 3 блока 7, вход 2 которого может быть соединен с выходом 4 блока 6 или с выходом измерителя частоты вращения ротора. Выходы 4 блока 1 соединены с входами 1 блоков 2, 3 (блоки 3-1 или 3-2), 5 и 6. Вход 2 блока 2 соединен с входом 2 блока 3. Выходы 3 блоков 2 и 3 соединены с входом 1 общего или двух разных блоков 4. Выходы 2 блока или двух блоков 4 соединены с входами 2 и 3 блока 5, выход 4 которого соединен с входом 3 блока 6, выход 4 которого может быть соединен с входом 2 блока 7.
Устройство по фиг. 2 реализует оценку по предлагаемому способу фазных токов статора и намагничивания, их проекций на ортогональные оси α-β неподвижной относительно статора системы координат, электромагнитного момента двигателя, относительного скольжения и, при необходимости, частоты вращения ротора.
Устройство по фиг. 2 функционирует следующим образом. В дискретные моменты времени на входы 1 и 2 блока 7-1 одновременно подают соответственно сигнал ωs задания частоты вращения поля статора и измеренный или сформированный в блоке 6 (выход 4) сигнал частоты вращения ротора для формирования сигнала относительного скольжения s, который с выхода 3 блока 7-1 подают на вход 3 блока 1. Одновременно с этим подают на вход 2 сигнал ωs задания частоты вращения поля статора и на вход 1 параметры, характеризующие двигатель и его нагрузку. С выходов 4 блока 1 сформированные коэффициенты и постоянные времени подают на входы 1 блоков 2, 3, 5 и, при необходимости, блока 6. Кроме того, на входы 2 блоков 2 и 3 (3-1 или 3-2) подают измеренный по крайней мере в двух фазах и(или) сформированный в блоке 16 (фиг. 23) вектор 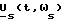 сигнала задания напряжения статора АД. Сформированные в блоках 2 и 3 векторы
сигнала задания напряжения статора АД. Сформированные в блоках 2 и 3 векторы 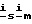 сигналов токов соответственно статора и намагничивания с выходов 3 вышеназванных блоков подают на вход 1 одного или двух блоков 4, формирующих проекции векторов сигналов токов на ортогональные оси α-β системы координат, неподвижной относительно статора, которые с выходов 2 блоков 4 подают на входы 2 и 3 блока 5. Сформированный сигнал M электромагнитного момента с выхода 4 блока 5 подают на вход 3 блока 6, на вход 2 которого подают сигнал Mн момента нагрузки. Сформированный сигнал ωs с выхода блока 6 подают, при необходимости, на вход 2 блока 1 в качестве сигнала обратной связи.
сигналов токов соответственно статора и намагничивания с выходов 3 вышеназванных блоков подают на вход 1 одного или двух блоков 4, формирующих проекции векторов сигналов токов на ортогональные оси α-β системы координат, неподвижной относительно статора, которые с выходов 2 блоков 4 подают на входы 2 и 3 блока 5. Сформированный сигнал M электромагнитного момента с выхода 4 блока 5 подают на вход 3 блока 6, на вход 2 которого подают сигнал Mн момента нагрузки. Сформированный сигнал ωs с выхода блока 6 подают, при необходимости, на вход 2 блока 1 в качестве сигнала обратной связи.
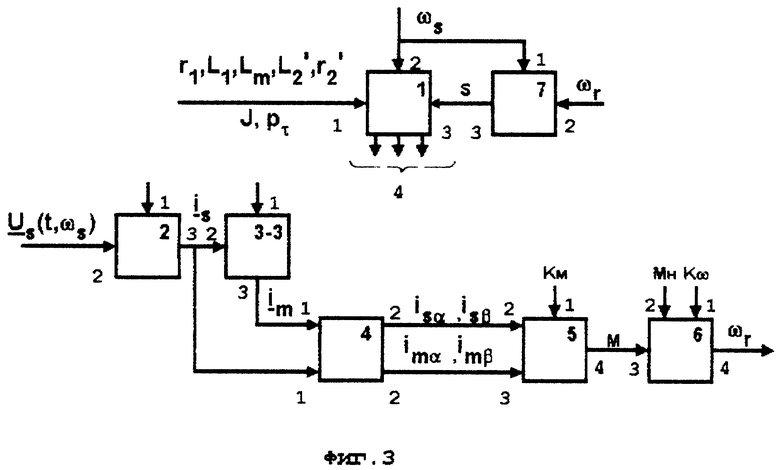
На фиг. 3 показана блок-схема варианта устройства, отличающегося от устройства, представленного на фиг. 2 тем, что блок 3-1 или 3-2 формирования тока намагничивания заменен на блок 3-3, вход 2 которого соединен с выходом 3 блока 1. Преимущественном данного устройства по сравнению с устройством-аналогом прототипа, представленным на фиг. 2, является более простая реализация блока 3-3 по сравнению с блоками 3-1 и 3-2 при сохранении той же точности оценки сигналов фазных токов намагничивания.
Общим недостатком устройств по фиг. 2 и 3 является наличие двух координатных преобразователей, реализованных в блоке 4 или более сложном блоке на базе блока 4, который последовательно по одному входу получает сигналы от блоков 2 и 3 и, обработав их, выдает выходные сигналы на разные выходы. По быстродействию и простоте реализации на основе аналоговой техники преимущество остается за использованием двух координатных преобразователей на основе блока 4 по числу сигналов токов, а именно: тока статора и тока намагничивания. Кроме того, при регулировании переменных АД мгновенные значения сигналов фазных токов намагничивания (выходы блоков 3-1, или 3-2 по фиг. 2, или 3-3 по фиг. 3) требуются только для формирования проекций сигналов токов намагничивания на ортогональные оси координат. Поэтому в этих случаях целесообразно применять устройства, позволяющие "быстрее" оценить регулируемые переменные АД, зависящие от сигналов тока намагничивания.
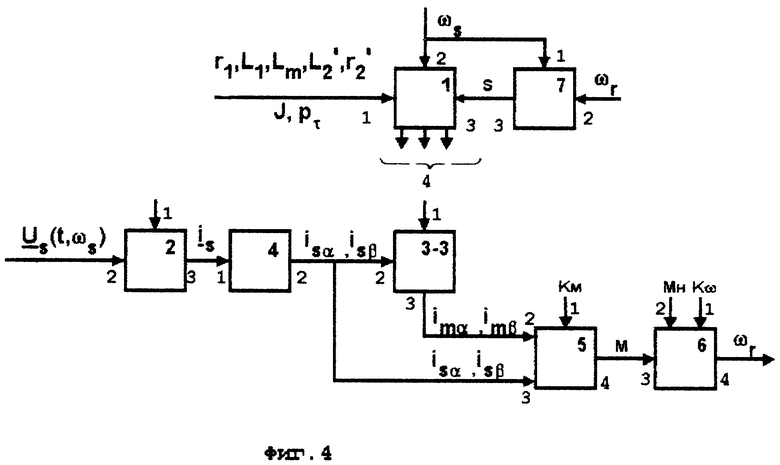
Так, например, на фиг. 4 показана блок-схема варианта устройства, реализующего предлагаемый способ оценки сигналов токов статора и намагничивания, повышающий быстродействие устройства, оценивающего, например, сигналы электромагнитного момента и, при необходимости, частоты вращения ротора.
Устройство содержит блок 1 вычисления параметров, вход 2 которого соединен с входом 1 блока 7, а вход 3 - с выходом 3 блока 7, вход 2 которого может быть соединен с выходом 4 блока 6 или выходом измерителя частоты вращения ротора. Выходы 4 блока 1 соединены с выходами 1 блоков 2, 3-3, 5 и 6. Выход 3 блока 2 соединены с входом 1 единственного координатного преобразователя на основе блока 4, выходы 2 которого соединены с входами 3 блока 5 и входами 2 блока 3-3, выход 3 которого соединен с выходами 2 блока 5, выход 4 которого соединен с входом 3 блока 6, выход 4 которого может быть соединен с входом 2 блока 7 в системе регулирования без датчика частоты вращения и(или) положения ротора или с выходом измерителя частоты вращения ротора при наличии такового.
Устройство, показанное на фиг. 4, реализует оценку по предлагаемому способу фазных токов статора, их проекций на ортогональные оси α-β неподвижной относительно статора системы координат проекций на те же оси вектора тока намагничивания, электромагнитного момента двигателя, относительного скольжения и, при необходимости, частоты вращения ротора. В этом устройстве, по сравнению с приведенными на фиг. 2 и 3, используется только один координатный преобразователь на основе блока 4 вместо двух, на вход 2 блока 3-3 подают два сигнала вместо трех и на выходе 3 блока 3-3 получают также два сигнала вместо трех.
При оценке регулируемых переменных, включая частоту вращения ротора трехфазного асинхронного двигателя с кроткозамкнутым ротором, выделяют два состояния устройства: пуск и циклическое функционирование в дискретные моменты времени.
При пуске устройства подают на вход 1 блока 1 начальные значения r1, L1, Lm, L'2, r'2 параметров T-образной схемы замещения, число Pr пар полюсов двигателя и момент J инерции двигателя с нагрузкой, на вход 2 блока 1 и вход 1 блока 7 подают начальное значение сигнала ωs задания частоты вращения поля статора, на вход 2 блока 7 - начальное нулевое значение сигнала ωr частоты вращения ротора двигателя.
Далее в дискретные моменты времени на вход 2 блока 1 и вход 1 блока 2 подают очередное значение сигнала ωs задания частоты вращения поля статора, на вход 2 блока 7 подают сигнал ωr обратной связи по частоте вращения ротора, например, с выхода 4 блока 6, с выхода 3 блока 7 на вход 3 блока 1 подают сформированный в блоке 7 сигнал обратной связи по относительному скольжению s, на вход 1 блока 1 подают параметры r1, L1, Lm, L'2, r'2 T-образной схемы замещения двигателя (они могут быть постоянными или изменяться от нагрева и (или) насыщения металла), число pτ пар полюсов двигателя и момент J инерции двигателя с нагрузкой, с выходов 4 блока 1 подают необходимые коэффициенты и постоянные времени на входы 1 блоков 2, 3-3, 5 и 6, измеряют по крайней мере в двух фазах и(или) формируют, например, в блоке 16, вектор 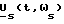 сигналов напряжения статора (измерение и формирование сигналов задания напряжения могут выполняться до начала очередного цикла функционирования устройства по фиг. 4, но с тем же периодом дискретизации dt), который подают на вход 2 блока 2, с выхода 3 которого сформированный вектор
сигналов напряжения статора (измерение и формирование сигналов задания напряжения могут выполняться до начала очередного цикла функционирования устройства по фиг. 4, но с тем же периодом дискретизации dt), который подают на вход 2 блока 2, с выхода 3 которого сформированный вектор 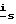 тока статора подают на вход 1 блока 4, с выхода 2 которого сформированные проекции isα,isβ на ортогональные оси α-β сигналов токов статора подают на вход 2 блока 3-3 и вход 3 блока 5, на вход 2 которого также подают проекции imα,imβ на ортогональные оси α-β сигналов токов намагничивания, сформированный сигнал M электромагнитного момента с выхода 4 блока 5 подают на вход блока 6, на вход 2 которого также подают сигнал Mн момента нагрузки, на выходе 4 блока 6 получают сигнал ωr частоты вращения ротора.
тока статора подают на вход 1 блока 4, с выхода 2 которого сформированные проекции isα,isβ на ортогональные оси α-β сигналов токов статора подают на вход 2 блока 3-3 и вход 3 блока 5, на вход 2 которого также подают проекции imα,imβ на ортогональные оси α-β сигналов токов намагничивания, сформированный сигнал M электромагнитного момента с выхода 4 блока 5 подают на вход блока 6, на вход 2 которого также подают сигнал Mн момента нагрузки, на выходе 4 блока 6 получают сигнал ωr частоты вращения ротора.
Далее устройство работает в цикле с периодом dt по описанному алгоритму.
На фиг. 16 приведена блок-схема устройства-аналога [9], функционирующего в замкнутой системе регулирования с повышенными требованиями к качеству регулирования. В этом устройстве используются модель объекта регулирования (блок I), реализованная по предлагаемому способу, и модели с наблюдателями переменных (блоки II и III), реализованные по способу, изложенному в [9].
Устройство по фиг. 16 отличается от описанного в [9] лишь блоком I, имитирующим объект регулирования по заявляемому способу. В данном случае блок I реализуется по структуре, представленной на фиг. 4. Так же как и в известном устройстве блок I имеет один выход, соединенный с входом блока V известного устройства, и один общий входной сигнал с блоком IV известного устройства.
Достоинством данного устройства по сравнению с известным является большая точность оценки тока статора по заявляемому способу, что обеспечит повышение точности оценки других переменных по известному способу.
На фиг. 17 приведена блок-схема устройства, осуществляющего оценку с высокой точностью оптимальным по быстродействию способом следующих регулируемых переменных АД: питающего напряжения 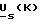 по заданному, например, с выхода регулятора тока или измеренному току статора
по заданному, например, с выхода регулятора тока или измеренному току статора 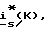 фазных токов статора
фазных токов статора 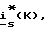 их проекций isα,isβ на ортогональные оси α-β неподвижной относительно статора системы координат, проекций imα,imβ на те же оси векторов токов намагничивания и irα,irβ ротора и ψsα,ψsβ векторов потокосцеплений статора и ψrα,ψrβ ротора, электромагнитного момента двигателя M относительного скольжения S, частоты вращения ротора ωr угла поворота ротора θ, проекций isx, isy на ортогональные оси x-y вращающейся системы координат векторов токов статора, imx, imy намагничивания и irx, iru ротора, проекций ψsx,ψsy на те же оси векторов потокосцеплений статора и ψrx,ψsy ротора, модулей векторов токов статора IsM и намагничивания ImM, фазовых сдвигов αs между вектором ток статора и вещественной осью координат, αm между вектором тока намагничивания и вещественной осью координат и α между векторами токов статора и намагничивания. Повышение точности оценки перечисленных регулируемых переменных AD открывает новые возможности при реализации систем управления вектором.
их проекций isα,isβ на ортогональные оси α-β неподвижной относительно статора системы координат, проекций imα,imβ на те же оси векторов токов намагничивания и irα,irβ ротора и ψsα,ψsβ векторов потокосцеплений статора и ψrα,ψrβ ротора, электромагнитного момента двигателя M относительного скольжения S, частоты вращения ротора ωr угла поворота ротора θ, проекций isx, isy на ортогональные оси x-y вращающейся системы координат векторов токов статора, imx, imy намагничивания и irx, iru ротора, проекций ψsx,ψsy на те же оси векторов потокосцеплений статора и ψrx,ψsy ротора, модулей векторов токов статора IsM и намагничивания ImM, фазовых сдвигов αs между вектором ток статора и вещественной осью координат, αm между вектором тока намагничивания и вещественной осью координат и α между векторами токов статора и намагничивания. Повышение точности оценки перечисленных регулируемых переменных AD открывает новые возможности при реализации систем управления вектором.
В основу устройства по фиг. 17 положено устройство по фиг. 4. Оно дополнено:
- блоком 16, выход 3 которого соединен с входом 2 блока 2,
- блоком 14 - 2, вход 1 которого соединен с выходом 3 блока 3 - 3, а выход 2 - с выходом 2 блока 4 - 1, с выхода 3 блока 14 получают сигналы проекций вектора тока ротора на оси α-β;
- одним или двумя блоками 15, входы 1 которых соединены с выходом 2 блока 4 - 1, входы 2 - с выходом 2 дополнительного блока 8 - 1, а выходы 3 - с входами 1 и 2 дополнительного блока 14 - 2, с выхода 3 которого получают сигналы проекций вектора тока ротора на оси x - y;
- одним или двумя блоками 13, входы 1 которых соединены с выходом 4 блока 1, входы 2 - с выходом 2 блока 4 - 1, входы 3 - с выходом 3 блока 3 - 3, а выходы 4 и 5 с входом 1 одного или двух дополнительных блоков 15, входы 2 которых соединены с выходом 2 блока 8 - 1, а с выходов 3 которых получают сигналы проекций векторов потокосцеплений статора и ротора на оси x - y;
- блоком 11 - 1, вход 1 которого соединен с выходом 2 блока 4 - 1, вход 2 - с выходом блока 3 - 3, с выхода 3 получают сигнал фазового сдвига между векторами токов статора и намагничивания, с выхода 4 - сигнал фазового сдвига между вектором тока статора и осью α, с выхода 5 - сигнал фазового сдвига между вектором тока намагничивания и осью α;
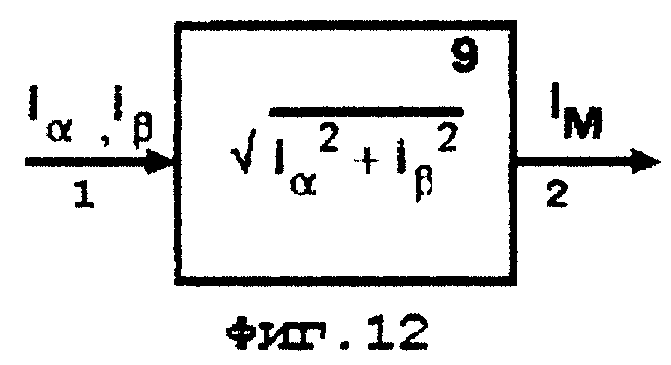
- одним или двумя блоками 9, входы 1 которых соединены с выходом 2 блока 4 - 1 и выходом 3 блока 3 - 3, а с выходом 2 получают сигналы соответственно модулей токов статора и намагничивания.
На фиг. 22 представлен фрагмент устройства, предназначенный для повышения точности оценки токов статора и зависящих от них переменных двигателя при несимметричном и несинусоидальном питающем напряжении. Этот фрагмент может быть подключен перед блоком 5 к устройству, представленному на фиг. 4, которое, в свою очередь, становится фрагментом более сложного устройства.
Во фрагменте устройства по фиг. 22 на входы 1 блоков 6 - 1, 7 - 1, 8 - 1, 9 - 1... 6 - N, 7 - N, 9 - N подают сигналы проекций на оси α-β векторов токов статора и намагничивания прямой последовательности для N гармоник, на входы 2 - аналогичные сигналы для токов обратной последовательности, выходы 2 блоков 6 - 1, 6 - 2... 6 - N соединены с входами 1,2..N блока 1, выход N + 1 которого соединен с входом 2 - 1 блока 5, выходы 2 блоков 7 - 1, 7 - 2... 7 - N соединены с входами 1, 2..N блока 2, выход N + 1 которого соединен с входом 2 - 2 блока 5, выходы 2 блоков 8 - 1, 8 - 2...8 - N соединены с входами 1,2. ..N блока 3, выход N + 1 которого соединен с входом 3 - 1 блока 5, выходы 2 блоков 9 - 1, 9 - 2... 9 - N соединены с входами 1,2..N блока 4, выход N + 1 которого соединен с входом 3 - 4 блока 5, с выхода 4 которого получают сигнал M электромагнитного момента.
При несимметрии питающего напряжения формируют для трех фаз сигналы напряжений прямой и обратной последовательностей, формируют (блок 7 - 2, фиг. 11) для сигналов обратной последовательности сигнал относительного скольжения, равный "двум" минус относительное скольжение s, сформированное (блок 7 - 1, фиг. 11) для токов прямой последовательности, вычисляют для сигналов прямой и обратной последовательностей постоянные времени и коэффициенты усиления, входящие в передаточные функции, и другие параметры, зависящие от величины относительного скольжения (блок 1, фиг. 5), формируют для токов прямой и обратной последовательностей проекции на ортогональные оси α-β векторов сигналов токов статора isαпр1,isβпр1...isαпрN,isβпрN,isαобр1,isβобр1... и намагничивания 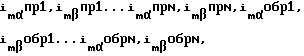 формируют (блоки 6 - 1, 7 - 1, 8 - 1, 9 - 1...6 - N, 7 - N, 8 - N, 9 - N, фиг. 22) проекции на те же оси векторов сигналов токов статора isα1,isβ1...isαN,isβN и намагничивания imα1,imβ1...imαN,imβN, формируют (блоки 1, 2, 3, 4, фиг. 22) проекции на те же оси векторов сигналов токов статора isα,isβ и намагничивания imα,imβ, по векторному произведению которых формируют (блок 5, фиг. 22) сигнал M электромагнитного момента двигателя.
формируют (блоки 6 - 1, 7 - 1, 8 - 1, 9 - 1...6 - N, 7 - N, 8 - N, 9 - N, фиг. 22) проекции на те же оси векторов сигналов токов статора isα1,isβ1...isαN,isβN и намагничивания imα1,imβ1...imαN,imβN, формируют (блоки 1, 2, 3, 4, фиг. 22) проекции на те же оси векторов сигналов токов статора isα,isβ и намагничивания imα,imβ, по векторному произведению которых формируют (блок 5, фиг. 22) сигнал M электромагнитного момента двигателя.
При несинусоидальности питающего напряжения из его сигналов выделяют сигналы, соответствующие с 1-ой по N-ую гармоникам, формируют проекции векторов сигналов токов статора и намагничивания на ортогональные оси α-β для каждой гармоники, по векторному произведению одноименных сумм которых формируют сигнал электромагнитного момента двигателя.
При пространственной несимметрии фаз статора АД во всех устройствах заменяют координатный преобразователь 3ф/2ф, реализованный по структуре блока 4 - 1 (фиг. 8), на преобразователь по структуре блока 4 - 2 (фиг. 8).
В общем случае последовательность формирования сигналов определяется их функциональными связями. Независимые друг от друга сигналы могут формироваться в любой последовательности. Если устройство предназначено для оценки регулируемых переменных двигателя, имеющего какие-либо параметры, не меняющиеся во времени в процессе эксплуатации двигателя, например число пар полюсов, в ряде случаев момент инерции двигателя с нагрузкой и др., то ввод таких параметров или их расчет может быть выполнен один раз до начала циклического функционирования устройства в дискретные моменты времени.
Заявляемый способ реализован в виде пакета программ для ПЭВМ, работающего в среде Windows и позволяющего исследовать трехфазный асинхронный двигатель с корокозамкнутым ротором как объект регулирования.
Заявляемый способ оценки регулируемых переменных трехфазного асинхронного двигателя с короткозамкнутым ротором базируется на аналитических и цифровых моделях.
Аналитическая модель реализуется с помощью блоков 2 - 1, 4 - 1 (для АД с пространственной симметрией статора) или 4 - 2 (для АД с пространственной несимметрией статора), 3 - 1, 5 - 1 или 5 - 2, 6 - 1, 7 - 1. Блоки 3 - 1 и 5 - 1 реализуются путем цифрового моделирования. Аналитическая модель имеет хорошую устойчивость при шаге дискретизации в диапазоне 5 - 200 мкс.
Эталонной можно считать аналитическую модель двигателя, реализованную при шаге дискретизации 50 мкс, так как результаты аналитического моделирования при шаге дискретизации из диапазона 5 - 50 мкс практически не отличаются.
Можно отметить следующие достоинства и области применения аналитической модели трехфазного асинхронного двигателя с короткозамкнутым ротором:
1) высокая точность оценки регулируемых переменных, делающая модель эталоном для цифровых моделей, созданных на основе T-образной схемы замещения и уравнений Горева-Парка, описывающих электромагнитные процессы, происходящие в двигателе, и позволяющая ее использовать для имитации объекта регулирования в системах прямого микропроцессорного управления с повышенными требованиями к качеству и диапазону регулирования;
2) возможность синтеза регуляторов аналитическими методами по передаточным функциям;
3) возможность анализа двигателя как объекта регулирования для выбора вида регуляторов и законов управления.
Цифровая модель реализуется с помощью блоков 2 - 2, 4 - 1 (для АД с пространственной симметрией статора) или 4 - 2 (для АД с пространственной несимметрией статора), 3 - 1, 5 - 1 или 5 - 2, 6 - 1, 7 - 1. Блоки 2 - 2, 3 - 1 и 5 - 1 реализуются путем цифрового моделирования. Цифровая модель имеет хорошую устойчивость при шаге дискретизации в диапазоне 0,005 - 1,8 мс.
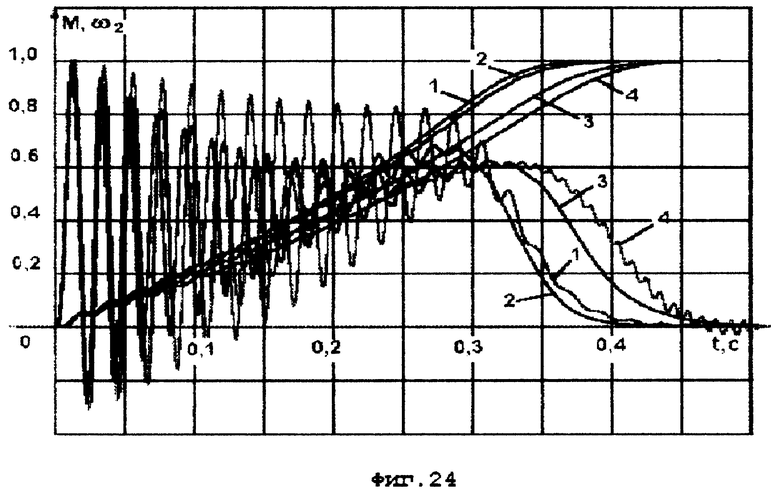
На фиг. 24 и 25 приведены графики переходных процессов в электромагнитном моменте M и частоте вращения ротора ωr при прямом пуске двигателя 4A100/L4Y3 на напряжение Uмакс = 380 В частотой f1 = 50 Гц при скачкообразном изменении частоты и моменте нагрузки Мн = 0, полученные с помощью вышеописанного пакета программ.
Графики, представленные на фиг. 24, позволяют сравнить точность заявляемой модели двигателя с моделью-аналогом [7], описывающей двигатель системой дифференциальных уравнений Горева-Парка, записанных в форме Коши и решенных в приращениях при использовании метода А.Б. Баширина для повышения точности и устойчивости модели; электромагнитный момент двигателя выражен через проекции потокосцеплений статора и ротора на ортогональные оси α-β системы координат, неподвижной относительно статора.
На фиг. 24 : 1 - эталонная аналитическая модель (dt = 50 мкс), 2 - цифровая модель с дискретизацией по методу, 3 - цифровая модель с дискретизацией по методу уравнений в конечных разностях, 4 - модель-аналог [7]. Шаг дискретизации dt = 50 мкс для эталона и dt = 1 мс для остальных моделей.
Наиболее близкой к аналитической модели 1 оказалась модель 2 с дискретизацией по методу трапеций. Из графиков 1 и 2 фиг. 24 видно, что оценка частоты вращения ротора ωr по методу трапеций дает высокую точность, несмотря на существенное отличие от эталонного графика мгновенных значений момента двигателя, определенных по методу трапеций. Это можно объяснить высокой точностью совпадения с эталонным среднего момента, полученного при моделировании методом трапеций. Результаты моделирования мгновенных значений электромагнитного момента по выражениям (6) и (7) отличаются от результатов моделирования по выражениям (8) и (9) в m1/2 раз, что существенно при регулировании момента по его мгновенным значениям и безразлично при регулировании среднего момента или оценки по моменту частоты вращения ротора.
Таким образом, точность оценки электромагнитного момента, а по нему частоты вращения ротора двигателя по токам статора и намагничивания значительно выше, чем по потокосцеплениям статора и ротора.
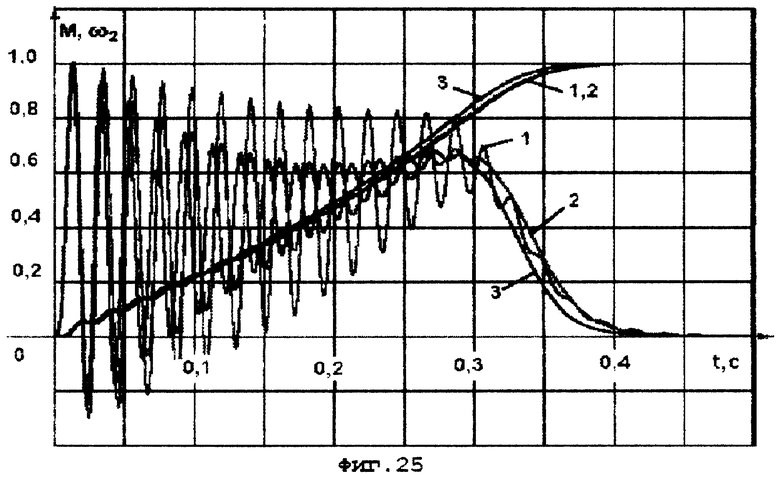
На фиг. 25 приведены графики, подтверждающие высокую точность и устойчивость заявляемого способа оценки регулируемых переменных двигателя в широком диапазоне изменения шага дискретизации, в том числе и при достаточно малом, равном 5 мкс.
На фиг. 25: 1 - эталонная аналитическая модель при шаге дискретизации dt = 50 мкс, 2 - цифровая модель с дискретизацией по методу трапеций и шагом dt = 50 мкс, 3 - цифровая модель с дискретизацией по методу трапеций и шагом dt = 1 мс.
Предлагаемая цифровая модель с дискретизацией по методу трапеций, в отличие от аналогов и прототипа, имеет хорошую устойчивость и точность без дополнительных мероприятий, повышающих их, при изменении шага дискретизации от 5 мкс до 1,8 мс.
Системы управления электроприводами с повышенными динамическими и регулировочными характеристиками традиционно реализуются на цифроаналоговой технике. В каждом конкретном случае функциональные блоки системы управления строятся на той элементной базе, которая оптимально удовлетворяет требованиям по быстродействию, точности, помехозащищенности и стоимости.
При реализации заявляемого способа в составе системы прямого микропроцессорного управления электроприводами можно использовать различные элементы современной цифроаналоговой техники. К таким средствам следует отнести:
- цифровые сигнальные процессоры (ЦСП) серии TMS320 фирмы TEXAS INSTRUMENTS [11] и ЦСП-контроллеры на их основе, на которых реализуется дополнительное моделирование системы;
- аналоговые, цифроаналоговые и цифровые микросистемы фирмы ANALOG DEVICES [12];
- программируемые логические устройства фирмы ALTERA [13, 14],
- на базе RISC+CISC процесса C167 фирмы Siemens [15].
Устройство фирмы TEXAS INSTRUMENTS обладают широкими возможностями, но являются самыми дорогими из перечисленных.
Устройства фирмы ALTERA являются наиболее дешевыми и быстродействующими, но сигнальный процессор находится в стадии создания. Поэтому эти устройства пока целесообразно использовать только для реализации отдельных функций, таких как координатные преобразования, быстрое преобразование Фурье, фильтры.
Из устройства фирмы ANALOG DEVICES для управления машинами переменного тока нашли применение [12]:
- цифровые быстродействующие сигнальные процессоры серии ADSP-21XX,
- специализированные векторные сопроцессоры ADMC200 и ADMC201, позволяющие создавать различные типы координатных преобразователей.
Разработана и опробована на IBM486 (тактовая частота процессора 66 МГц + сопроцессор для операций с плавающей запятой) цифровая модель, имитирующая оценку регулируемых переменных трехфазного асинхронного двигателя при прямом микропроцессорном управлении по основной гармонике питающего напряжения статора. Время выполнения одного цикла оценки регулируемых переменных - около 700 мкс, что обеспечивает приемлемую точность для приводов с невысокими требованиями по точности и частотой вращения ротора двигателя до 60 Гц.
На базе процессора C167 фирмы Siemens устройство по заявляемому способу может быть реализовано при шаге дискретизации dt ≈ 500 мкс при частоте процессора 16 мГц. При реализации способа на базе сигнальных процессоров шаг дискретизации будет в десятки раз меньше, что позволяет реализовать системы с управлением вектором. При таком малом шаге дискретизации способы оценки регулируемых переменных, использующие проекции потокосцеплений на ортогональные оси вращающихся систем координат, не обеспечивают необходимой точности оценки [2].
При реализации заявляемого способа будет получен следующий положительный технический эффект:
1) создание устойчивых в широком диапазоне изменения шага дискретизации аналитической и цифровой моделей-эталонов трехфазного асинхронного двигателя с короткозамкнутым ротором, позволяющим решить в комплексе задачу создания системы регулирования электроприводов на базе АД с короткозамкнутым ротором, а именно выполнить:
- анализ двигателя как объекта регулирования,
- аналитический синтез регуляторов,
- цифровое моделирование системы регулирования с целью оптимальной настройки регуляторов и выбора законов регулирования,
- прямое микропроцессорное управление,
- настройку электроприводов при пуске их в опытную эксплуатацию;
2) сокращение числа используемых датчиков и координатных преобразователей при прямом микропроцессорном управлении.
Источники информации
1. Копылов И.П. Математическое моделирование электрических машин: Учеб. для вузов по спец. "Электрич. машины". - М.: Высш. шк., 1987, с. 30-39, с. 51-52.
2. Analysis of dynamic induction motor dehavoir / Andonov Zdravko, Mirceviski Slobodan A.// Comput. Syst. and Res. Autom.: Proc. 9th Int. Conf. "Syst. Autom. Cong. and Res." (SAER' 95) and DECUS Wat. Users Group Semin. 95, Varna, Sept. 24-26, 1995. - Sofia, 1995. - С. 188-192. - англ.
3. Патент США N 5481172, кл. H 02 M 7/00 (318-800), 1996.
4. Salo J. , Pyrhonen J., Niemela M. A. Space Vector Induction Motor Model for the Pspice Circuit Simulator // EPE Journal. - 1996. - Vol.5. - N 3/4. -С. 56-62.
5. Копылов И. П. Электромеханические преобразователи энергии. - М.: Энергия, 1973, с. 134-138.
6. Копылов И. П. Электромеханические преобразователи энергии. - М.: Энергия, 1973, с. 164, с. 189.
7. Башарин А. В. , Постников Ю.В. Примеры расчета автоматизированного электропривода на ЭВМ: Учебное пособие для вузов. - 3-е изд. - Л.: Энергоатомиздат. Ленингр. Отд-ние, 1990, с. 225-228, с. 177-180, с. 483.
8. Патент США N 4904920, кл. H 02 P 5/40 (318-800), 1990.
9. Патент Германии N 4433551, кл. H 02 P 7/44, 1996.
10. Ковач К.П. и Рац И. Переходные процессы в машинах переменного тока. - М. -Л.: Госэнергоиздат, 1963, с. 493-548 (прототип)
11. Новые средства ускоряют разработку современного цифрового управления электродвигателями: По материалам ежемесячника DETAILS ON SIGNAL PROCESSING (июль 1997 г.) // CHIP NEWS. - 1997. N 7-8 (16-17). С. 27.
12. Денисов К. , Ермилов А., Карпенко Д. Способы управления машинами переменного тока и их практическая реализация на базе компонентов фирмы ANALOG DEVICES //CHIP NEWS. - 1997. - N 7-8 (16-17). - С. 18-26.
13. Братенев В. и Братенов Г. ALTERA предлагает создать свой сигнальный процессор //CHIP NEWS. - 1997. - N 7-8 (16-17). - С. 39-41.
14. Губанов Д. , Стешенко В. и др. Перспективы реализации алгоритмов цифровой фильтрации на основе ПЛИС фирмы ALTERA //CHIP NEWS. - 1997. -N 9-10 (18-19). - С. 26-33.
15. С167 Derivatives. 16-Bit CMOS Single-Chip Microcontrollers. User' s Manual 03.96, Version 2.0. Siemens, 1996.
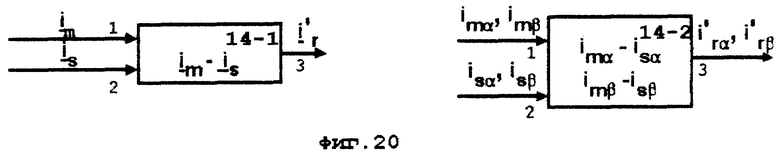
Изобретение может быть использовано в электроприводах электропоездов и механизмов машиностроения и металлургии, в частности в системах с управлением вектором, а также для исследования динамических режимов работы асинхронного двигателя (АД) и систем регулирования, для аналитического синтеза регуляторов и в устройствах для настройки электроприводов. В изобретении используется классическая Т-образная схема замещения фазы АД. Формируют сигналы токов статора, намагничивания и питающего напряжения по новым выражениям. Создана аналитическая модель-эталон АД. Техническим результатом является повышение точности оценки регулируемых переменных АД, включая ток намагничивания, электромагнитный момент и частоту вращения ротора, в широком диапазоне изменения шага дискретизации, благодаря чему расширяется область применения способа. 2 з.п. ф-лы, 25 ил.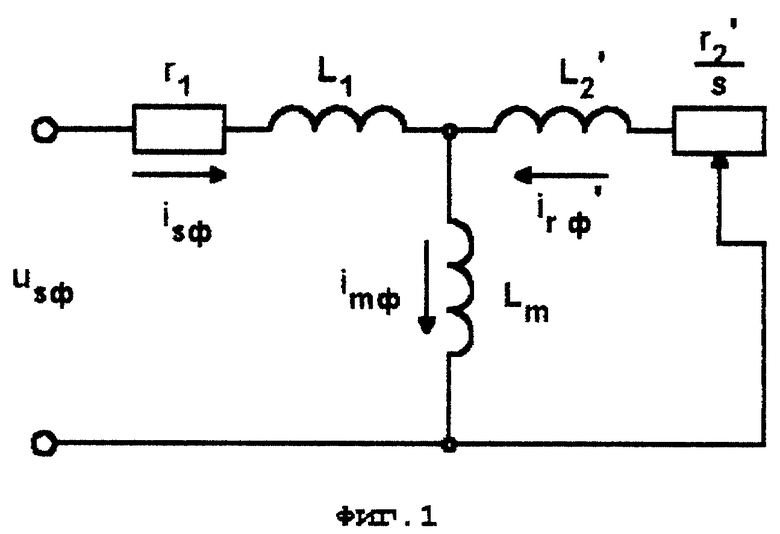
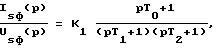
где Usф(p), Isф(p) - преобразования по Лапласу соответственно сигналов питающего напряжения и тока статора в фазе двигателя, формируют по передаточным функциям сигналы фазных токов isa, isb, isc статора, формируют проекции isα, isβ и imα, imβ векторов сигналов тока статора и намагничивания на ортогональные оси α-β системы координат, неподвижной относительно статора, отличающийся тем, что в дискретные моменты времени формируют сигнал относительного скольжения S, вычисляют входящие в передаточные функции указанные коэффициент усиления и постоянные времени при относительном скольжении S ≠ 0 по выражениям:
K1 = 1/r1,
T0 = S (Lm + L2 1)/r2 1,
T1 = 2a/(b - c),
T2 = 2a/(b + c),
a = L1 T0 + Lm T3,
b = r1 T0 + L1 + Lm,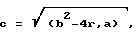
T3 = S (L2 1)/r2 1,
r1 и L1 - активное сопротивление и индуктивность фазы статора,
r2 1 и L2 1 - приведенные к цепи статора активное сопротивление и индуктивность фазы ротора,
Lm - индуктивность ветви намагничивания, формируют указанные сигналы isa, isb, isc фазных токов статора по передаточным функциям путем цифрового моделирования или по выражениям для фазных токов isф(t) статора в функции времени t при сигнале задания питающего напряжения в виде идеальной синусоиды с частотой w1 одной из гармоник: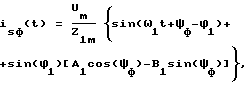
где Um - максимум сигнала питающего напряжения,
ψф - начальный фазовый сдвиг синусоиды питающего напряжения в соответствующей фазе двигателя,
ϕ1 - фазовый сдвиг фазного тока статора по отношению к питающему напряжению фазы, вычисляемый в дискретные моменты времени,
Z1м - модуль комплексного сопротивления фазному току статора, вычисляемый в дискретные моменты времени,
A1, B1 - коэффициенты, вычисляемые по выражениям: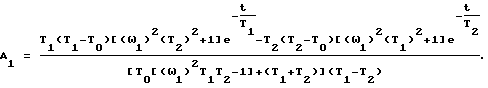
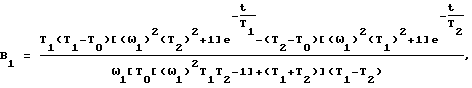
формируют указанные проекции imα и imβ вектора сигналов тока намагничивания на ортогональные оси α-β системы координат, неподвижной относительно статора, путем цифрового моделирования по передаточной функции сигналов токов намагничивания по сигналам токов статора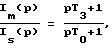
где Im(p), Is(p) - преобразования по Лапласу проекций на ортогональные оси координат α-β соответственно векторов сигналов токов намагничивания и статора.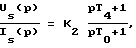
где Us(p), Is(p) - преобразования по Лапласу соответственно сигнала питающего напряжения статора и сигнала тока статора,
K2 - коэффициент усиления, вычисляемый по выражению
K2 = r1,
T4 - постоянная времени, вычисляемая по выражению:
T4 = T1 + T2.
isβ = K[isbsin(ψab)-iscsin(Ψac)],
где
K = isa/[isa+isbcos(ψab)+isccos(ψac)],
ψab, ψac - пространственные углы соответственно между фазами a и b и между фазами a и c.
| КОВАЧ К.П | |||
| и др | |||
| Переходные процессы в машинах переменного тока | |||
| Москва - Ленинград, Госэнергоиздат, 1963, с.493-548 | |||
| Асинхронный электропривод | 1990 |
|
SU1767690A1 |
| Частотно-регулируемый электропривод | 1988 |
|
SU1605307A1 |
| Частотно-управляемый электропривод | 1990 |
|
SU1778906A1 |
| Частотно-регулируемый электропривод | 1989 |
|
SU1798884A1 |
| Устройство для изучения дифракции медленных электронов | 1934 |
|
SU43973A1 |
| Передвижное транспортерное устройство | 1927 |
|
SU19138A1 |
Авторы
Даты
2000-10-27—Публикация
1998-11-12—Подача