Изобретение относится к зубчатым героторным механизмам (ГМ) и может быть использовано в области бурения нефтяных и газовых скважин в качестве рабочих органов (РО) гидродвигателей, насосов, компрессоров и редукторов.
Известен внецентроидный многозаходный героторный механизм, используемый в рабочих органах винтовых забойных двигателей, с традиционным профилем при (Z2≥2), постоянными коэффициентами внецентроидности (Co = 1,175) и формой зуба (Ce = 2,175), в котором коэффициент смещения CΔ исходного контура рейки, исходя из обеспечения плавности профилей, может изменяться в диапазоне CΔ = 2...2 (Отраслевой стандарт ОСТ 39-164-84. Передача зубчатая ротор-статор винтового забойного двигателя).
Известен героторный механизм с классическим профилем с однозаходным ротором (Z2 = 1) гипоциклоидального центроидного зацепления (Co = 1), образованным без смещения исходного контура рейки (CΔ = 0). Героторный механизм используется в РО одновинтового насоса (Винтовые насосы. М., Недра, 1983, с. 17-30).
Недостатком героторных механизмов с традиционным и классическим профилем является независимость принимаемых безразмерных коэффициентов (C0,Ce,CΔ) от качественных показателей зацепления, что не всегда позволяет получить оптимальную форму ГМ.
Наиболее близким техническим решением к предлагаемому является многозаходная одновинтовая гидромашина, обеспечивающая плавность профилей и минимум контактных напряжений в паре ротор-статор (Забойные винтовые двигатели для бурения скважин. М., Недра, 1981, с. 86-94). Однако при проектировании этих профилей не учитывается влияние смещения исходного контура рейки на кривизну и уровень контактных напряжений, что не позволяет получить оптимальный профиль ГМ для обеспечения минимального износа.
Задачей изобретения является повышение износостойкости и долговечности героторных механизмов за счет уменьшения контактных напряжений в паре ротор-статор.
Поставленная задача решается за счет того, что в героторном механизме, содержащем пару ротор-статор внутреннего гипоциклоидального зацепления, знаки кривизны замкнутых сопряженных профилей ротора и статора одинаковы и не изменяются по всему контуру, при этом при числе зубьев ротора, равным двум, и коэффициенте внецентроидности Co = r/e, близком к единице (Co≅ 1,5), смещение исходного контура рейки выполняют положительным (CΔ = Δx/e = 0,8-1,4), а коэффициент формы зуба Ce = rц/e выбирают в диапазоне Ce = 3-6, где e - эксцентриситет зацепления, м; r - радиус катящейся окружности, м; rц - радиус эквидистанты, м; Δx - смещение исходного контура рейки, м.
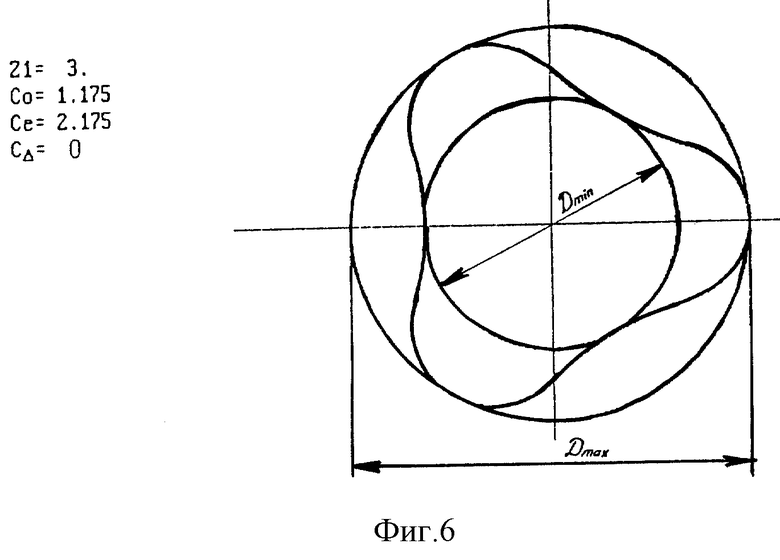
Изобретение поясняется чертежами, где на фиг. 1 представлены героторные механизмы с кинематическим отношением 2:3 и 5:6 с традиционным профилем; на фиг. 2 - схема образования гипоциклоидального профиля методом обкатки рейки; на фиг. 3, 4 - графики изменения радиуса кривизны профиля трехзубого статора соответственно с традиционными и оптимальными геометрическими параметрами; на фиг 5 - профили ГМ кинематического отношения 1:2 и 2:3 с однозначной (положительной) кривизной РО; на фиг. 6 - соотношение максимального и минимального диаметров традиционного гипоциклоидального профиля статора.
ГМ представляет собой зубчатую пару внутреннего циклоидального зацепления, состоящую из Z1 - зубового статора 1 и Z2 - зубового (Z1 = Z2 + 1) ротора 2, между профилями которых образуются рабочие камеры.
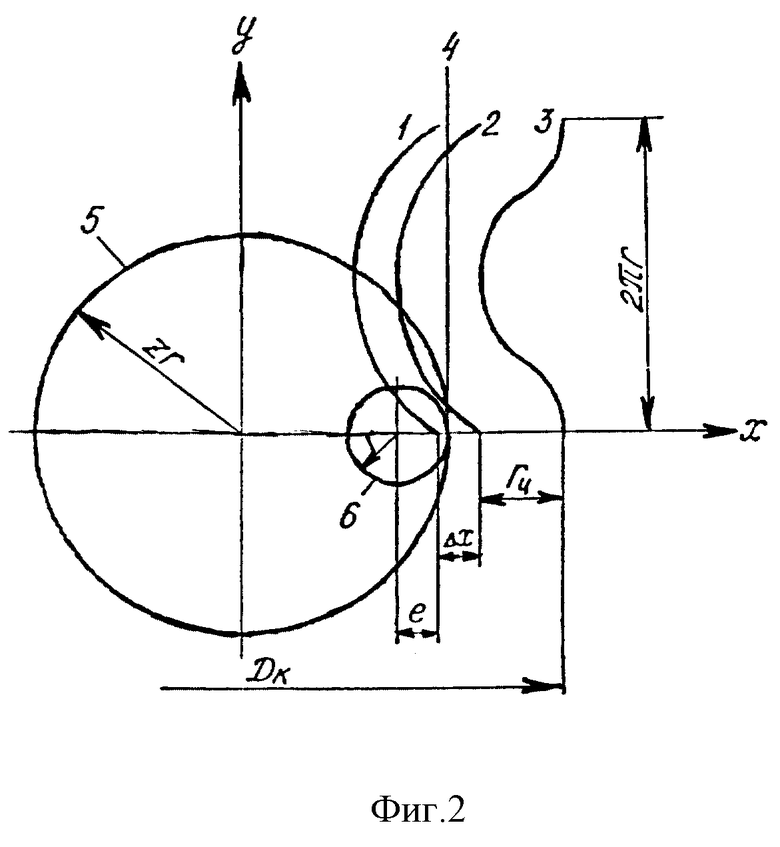
ГМ профилируются (фиг. 2) от исходного контура циклоидальной рейки 3 (эквидистанты смещенной укороченной циклоиды 1), связанного и инструментальной прямой 3, по которой для образования циклоиды перекатывается окружность 6. Циклоидально-реечный профиль образуется как огибающая семейства контуров рейки при обкатке инструментальной прямой неподвижной направляющей окружности 5. В общем случае для обеспечения заданного контурного диаметра РО Dк рейка смещается относительно инструментальной прямой на величину Δx (фиг. 2). Если смещение отсутствует (Δx=0), реечный профиль переходит в идеальный циклоидальный профиль. Графически он может быть получен и классическим способом при качении окружности 6 по направляющей окружности 5.
Форму РО при заданном контурном диаметре полностью характеризуют пять безразмерных коэффициентов:
- коэффициент типа зацепления 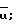
- кинематическое отношение i = Z2:Z1;
- коэффициент внецентроидности Co = re;
- коэффициент формы зуба Ce = rц/e;
- коэффициент смещения исходного контура рейки CΔ = Δx/e;
где r - радиус катящейся окружности, м; rц - радиус эквидистанты, м; e - эксцентриситет, м.
Знак коэффициента типа зацепления определяет тип циклоидального зацепления. В гидромашинах получило распространение гипоциклоидальное зацепление 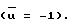
Традиционные (Co = 1,175, Ce = 2,175) профили гипоциклоидальных ГМ с различным кинематическим отношением представлены на фиг. 2.
Поскольку наработка до отказа ГМ определяется главным образом фрикционным износом пары ротор-статор, в качестве критерия оптимальности формы ГМ принимается минимум скорости изнашивания РО.
В сопряжениях с переменными условиями касания подобных ГМ скорость изнашивания в общем случае зависит от контактного напряжения и скорости скольжения. Теоретические и экспериментальные исследования показывают, что в ГМ доминирующее влияние на скорость изнашивания оказывают контактные напряжения в паре ротор-статор, на минимизации которых основано большинство методов оптимизации РО.
Контактные напряжения зависят от действующих гидравлических и инерционных сил, геометрических параметров и упругих свойств материалов РО. С достаточной точностью контактные напряжения К определяются по формуле Герца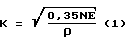
где N - удельная нормальная нагрузка, Н/м; E - приведенный модуль упругости материалов рабочих органов, Па; ρ - приведенный радиус кривизны сопряженных профилей РО, м.
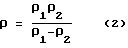
где: ρ1,ρ2 - радиусы кривизны профилей статора и ротора с учетом их знаков, м.
В теории зубчатых зацеплений минимизация контактных напряжений осуществляется выбором формы РО, обеспечивающей максимум. При этом считается, что в общем случае многозаходного ГМ кривизна профиля статора имеет знакопеременный характер (фиг. 3) и профиль статора разбивается на участки с положительной и отрицательной кривизной. В этом случае согласно (2) приведенный радиус кривизны профилей достигает минимального значения на контакте выступа зуба ротора (ρ2 = rц > 0) с участком профиля статора, обладающим отрицательной кривизной (ρ1 < 0):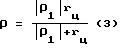
Оптимизация формы ГМ, исходя из наличия выпукло-вогнутого контакта профилей, лежит в основе выбора коэффициента формы зуба РО одновинтовых гидромашин.
Вместе с тем исследования кривизны профилей ГМ показывают, что представленный на фиг. 3 знакопеременный график изменения кривизны профиля статора не является общим. При профилировании ГМ от циклоидальной рейки путем соответствующего сочетания безразмерных параметров C0,Ce,CΔ можно реализовать профиль с положительной кривизной (ρ1 > 0) на всех участках замкнутого контура (фиг. 4). Тогда во всех фазах зацепления будет иметь место выпукло-вогнутый контакт профилей с максимальным приведенным радиусом кривизны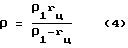
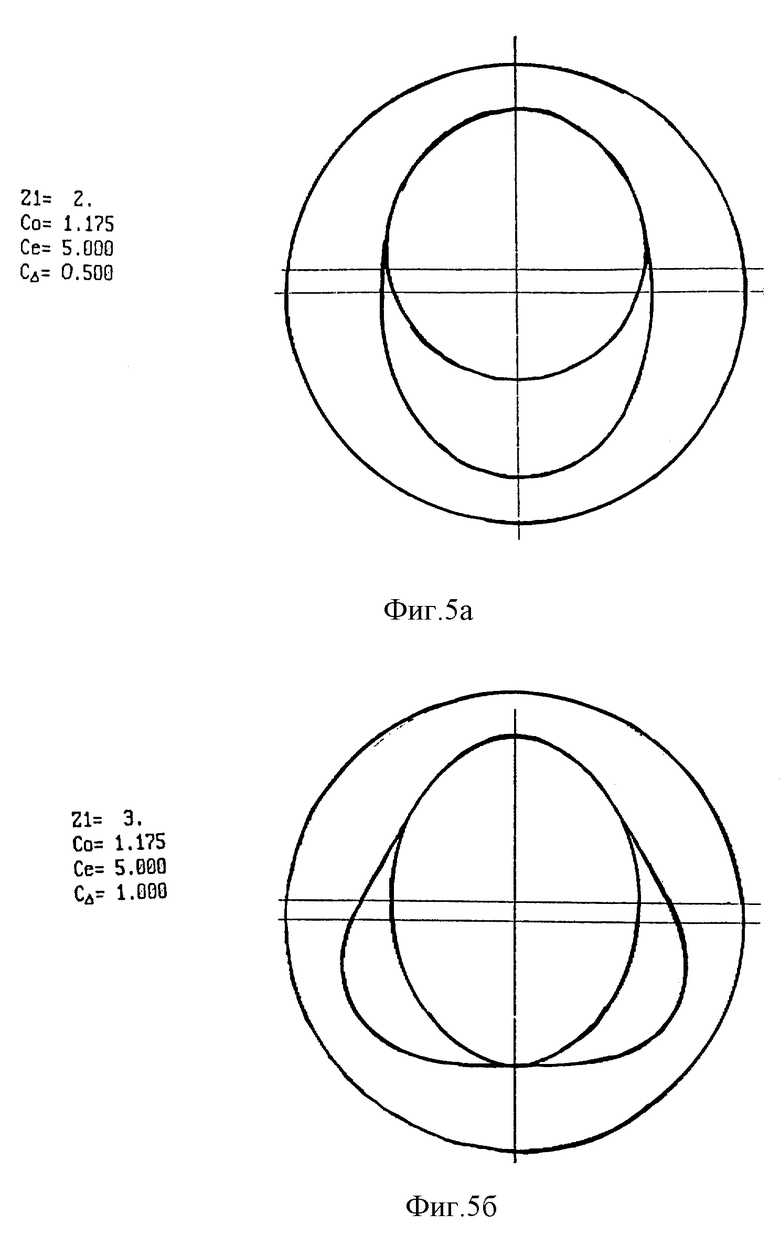
Практически профиль статора с положительной кривизной (ГМ с одинаковыми знаками кривизны РО) можно реализовать в механизмах с кинематическим отношением 1:2 и 2:3. В качестве примера на фиг. 5 приведены поперечные сечения таких механизмов с коэффициентом внецентроидности Co = 1,175. В этом случае для обеспечения однозначной кривизны профилей необходимо соблюдать оптимальную взаимосвязь между коэффициентами Ce и CΔ.
Наибольший интерес представляет профилирование многозаходных ГМ с кинематическим отношением 2:3, обладающих повышенной (по сравнению с ГМ с однозаходным ротором) нагрузочной способностью (давлением насоса или крутящим моментом гидродвигателя).
В механизме с i = 2:3 при коэффициенте внецентроидности, близким к единице (Co ≅ 1,5), оптимальный профиль с однозначной кривизной РО и отсутствием подрезов и самопересечений обеспечивается при положительном смещении исходного контура рейки (CΔ = 0,8-1,4) и повышенных значениях коэффициента формы зуба (Ce=3-6).
Геометрическое толкование оптимальной (в отношении кривизны) взаимосвязи между коэффициентами зацепления состоит в том, что для обеспечения постоянства знака кривизны трехзубого профиля необходимо соблюдать определенное соотношение между его максимальным и минимальным диаметрами (фиг. 6).

Для получения профиля с однозначной кривизной необходимо стремиться к уменьшению величины μ, в пределе (Ce →∞) профиль переходит в окружность (Dmin= Dmax).
Для гипоциклоидального зацепления
Таким образом
Для традиционного идеального профиля (см.фиг. 2a) μ = 1,567, для оптимального профиля, представленного на фиг. 5b, μ = 1,272.
Преимуществом заявляемого героторного механизма является повышение износостойкости РО за счет снижения контактных напряжений при сохранении высоких показателей характеристик машины, что позволит значительно увеличить срок службы героторных механизмов.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПТИМИЗАЦИИ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ПРОФИЛЯ РАБОЧИХ ОРГАНОВ ОДНОВИНТОВОЙ ГИДРОМАШИНЫ | 1998 |
|
RU2150566C1 |
| ГЕРОТОРНЫЙ МЕХАНИЗМ | 2002 |
|
RU2250340C2 |
| ГЕРОТОРНЫЙ МЕХАНИЗМ ВИНТОВОЙ ГИДРОМАШИНЫ | 2002 |
|
RU2205998C1 |
| ГЕРОТОРНЫЙ МЕХАНИЗМ ВИНТОВОГО ЗАБОЙНОГО ДВИГАТЕЛЯ | 2007 |
|
RU2360129C2 |
| ГЕРОТОРНЫЙ МЕХАНИЗМ ВИНТОВОЙ ГИДРОМАШИНЫ | 2003 |
|
RU2232317C1 |
| ГЕРОТОРНЫЙ МЕХАНИЗМ ВИНТОВОЙ ЗАБОЙНОЙ ГИДРОМАШИНЫ (ВАРИАНТЫ) | 2000 |
|
RU2166603C1 |
| МНОГОЗАХОДНЫЙ ГЕРОТОРНЫЙ МЕХАНИЗМ ВИНТОВОЙ ГИДРАВЛИЧЕСКОЙ МАШИНЫ | 2001 |
|
RU2194880C2 |
| ГЕРОТОРНЫЙ МЕХАНИЗМ ВИНТОВОГО ЗАБОЙНОГО ДВИГАТЕЛЯ | 2000 |
|
RU2165531C1 |
| ГЕРОТОРНАЯ МАШИНА | 2007 |
|
RU2345208C1 |
| ШАРНИРНОЕ УСТРОЙСТВО | 2002 |
|
RU2235228C2 |


Изобретение относится к зубчатым героторным механизмам и может быть использовано в бурении нефтяных и газовых скважин в качестве рабочих органов гидродвигателей, насосов, компрессоров и редукторов. Задача изобретения - повышение износостойкости и долговечности героторных механизмов за счет уменьшения контактных напряжений в паре ротор - статор. Героторный механизм содержит пару ротор - статор внутреннего гипоциклоидального зацепления. Новым в устройстве является то, что знаки кривизны замкнутых сопряженных профилей ротора и статора одинаковы и не изменяются по всему контуру, при этом при числе зубьев ротора, равным двум, и коэффициенте внецентроидности Сo = r/е, близком к единице ( Сo ≅ 1,5), смещение исходного контура рейки выполняют положительным (CΔ= Δx/e = 0,8-1,4), а коэффициент формы зуба Сe = rц/е выбирают в диапазоне Сe = 3-6, где е - эксцентриситет зацепления, м, r - радиус катящейся окружности, м; rц - радиус эквидистанты, м; Δx - смещение исходного контура рейки, м. 8 ил.
Героторный механизм, содержащий пару ротор-статор внутреннего гипоциклоидального зацепления, отличающийся тем, что знаки кривизны замкнутых сопряженных профилей ротора и статора одинаковы и не изменяются по всему контуру, при этом при числе зубьев ротора, равным двум, и коэффициенте внецентроидности Cо = r/e, близком к единице (Cо ≅ 1,5), смещение исходного контура рейки выполняют положительным CΔ = Δx/e = 0,8-1,4, а коэффициент формы зуба Cе = rц/е выбирают в диапазоне Cе = 3 - 6, где е - эксцентриситет зацепления, м; r - радиус катящейся окружности, м; rц - радиус эквидистанты, м.; Δx смещение исходного контура рейки, м.
| ГУСМАН М.Т., и др., Забойные винтовые двигатели для бурения скважин | |||
| - М.: Недра, 1981, с.86 - 94 | |||
| Забойный винтовой двигатель | 1979 |
|
SU926209A1 |
| Забойный двигатель | 1976 |
|
SU943387A1 |
| Гидравлический забойный двигатель | 1980 |
|
SU1616523A3 |
| Гидравлический забойный двигатель | 1990 |
|
SU1756525A1 |
| БАЛДЕНКО Д.Ф | |||
| и др | |||
| Винтовые забойные двигатели | |||
| - М.: Недра, 1999, с.84 - 103. | |||
Авторы
Даты
2001-02-10—Публикация
2000-01-26—Подача