Изобретение относится к измерительной технике и может быть, например, использовано для построения математической модели сложной механической или электромеханической системы с распределенными параметрами, что необходимо для анализа нестационарных процессов в механических, электромеханических и электрических системах.
Заявляемое изобретение направлено на решение задачи, заключающейся в устранении погрешности, повышении точности измерений и унификации аппаратных средств, необходимых для экспериментального снятия амплитудно-фазочастотных характеристик (АФЧХ) с целью построения по ним математической модели эквивалентной электромеханической системы.
Известен способ определения коэффициентов демпфирования, основанный на обработке АФЧХ (см. Патент РФ N 2093808, МПК6 G 01 M 7/02, 20.10.1997), в соответствии с которым возбуждают колебания системы гармоническим воздействием в диапазоне ее собственных частот, измеряют кинематический параметр колебаний, регистрируют амплитудно-фазовую частотную характеристику измеряемого кинематического параметра, для каждой степени свободы фиксируют характерные частоты, соответствующие экстремумам действительной и мнимой составляющих кинематического параметра, и по ее частотам рассчитывают относительные коэффициенты демпфирования. В качестве кинематического параметра колебаний измеряют скорость перемещения, фиксируют характерные частоты 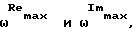 соответствующие максимальным значениям действительной и мнимой составляющих скорости перемещения, а относительный коэффициент γ демпфирования рассчитывают по формуле:
соответствующие максимальным значениям действительной и мнимой составляющих скорости перемещения, а относительный коэффициент γ демпфирования рассчитывают по формуле: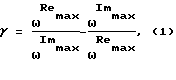
К причинам, препятствующим достижению указанного ниже технического результата при использовании известного способа, относится то, что известный способ оказывается слабозащищенным от помех.
Наиболее близким способом того же назначения к заявленному изобретению по совокупности признаков является способ определения относительных коэффициентов демпфирования механических колебательных систем, в котором определяются коэффициенты демпфирования по перемещению по формуле: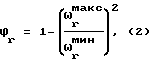
где ω
γr - относительный коэффициент демпфирования для данного тона амплитудно-фазовой частотной характеристики,
принятый за прототип (см. авт. свид. СССР N 1206713, кл. G 01 R 3/00, 1985 г.)
К причинам, препятствующим достижению указанного ниже технического результата при использовании известного способа, принятого за прототип, относится то, что известный способ оказывается так же слабозащищенным от помех.
Сущность изобретения заключается в следующем. Изобретение решает задачу определения коэффициентов усиления и постоянных времени динамических систем, представляющих собой произведение двух интегрирующих колебательных звеньев, по их АФЧХ, например таких, как сложная электрическая цепь, когда ее внутреннее строение не известно.
Технический результат позволяет практически полностью исключить случайную помеху с нулевым средним значением и этим самым повысить точность определения постоянных времени динамической системы.
Указанный технический результат при осуществлении изобретения достигается тем, что возбуждают колебания системы гармоническим воздействием в диапазоне ее собственных частот, измеряют кинематический параметр колебаний, регистрируют амплитудно-фазовую частотную характеристику измеряемого кинематического параметра, для каждой степени свободы фиксируют характерные частоты, соответствующие экстремумам действительной и мнимой составляющих кинематического параметра, и рассчитывают по ее частотам постоянные времени и коэффициенты усиления.
Особенность способа заключается в том, что в качестве кинематического параметра используют двойной интеграл от выходного сигнала колебательной системы, то есть берут передаточную функцию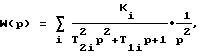
для которой постоянные времени и коэффициенты усиления определяют по формулам: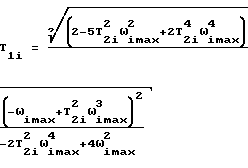
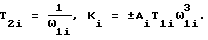
где ωimax и ω1i - частоты, соответствующие экстремальным значениям вещественной и мнимой частей АФЧХ, построенной по выше приведенной формуле для W(p).
Сущность заключается в том, что получена новая формула для определения коэффициента демпфирования по экстремальным точкам АФЧХ для динамических систем, представляющих собой произведение двух интегрирующих и колебательных звеньев.
Рассмотрим передаточную функцию: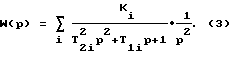
Положив p = j ω, получим: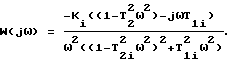
Выделим действительную и мнимую части этой передаточной функции: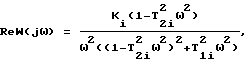
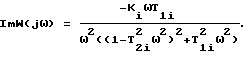
Исследуем вещественную часть на экстремум. Для этого найдем производную: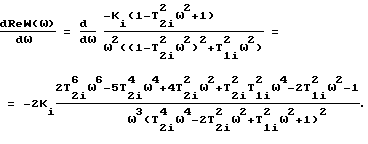
Приравниваем производную к нулю при 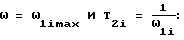
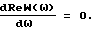
Рассмотрим числитель этого выражения: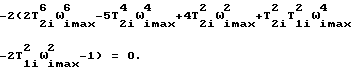
В результате решения этого уравнения получим формулу для определения постоянной времени демпфирования по экстремальным точкам АФЧХ для динамических систем, представляющих собой произведение двух интегрирующих и колебательных звеньев: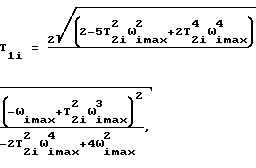
где ωimax и ω1i - частоты, соответствующие экстремальным значениям мнимой и вещественной части АФЧХ, построенной по формуле (3).
Коэффициенты усиления находим по формулам:
Ki = ±AiT1iω
где Ai - размер петли АФЧХ по мнимой оси; Ki > 0, если петля АФЧХ находится выше своей начальной точки, Ki < 0, если петля АФЧХ лежит ниже начальной точки.
Относительный коэффициент демпфирования находим по формуле: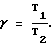
Кроме того, особенность способа заключается в том, что измерения можно производить на той же самой аппаратуре, что и в случае использования АФЧХ по перемещению, всего лишь включая в цепь измерения два интегрирующих звена, используя формулу (3).
На фиг. 1 показана АФЧХ по перемещению для вертикально-фрезерного станка модели 654, которая описывается формулой: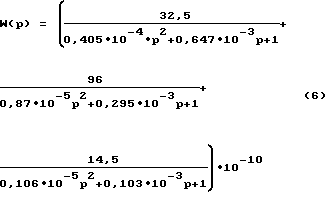
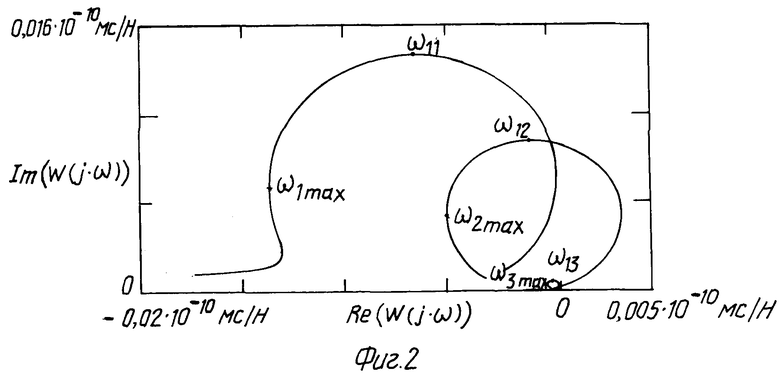
(см. Ю. Н. Санкин. "Динамические характеристики вязко-упругих систем с распределенными параметрами" - Изд-во Саратовского университета, 1977, с. 250). На фиг. 2 - АФЧХ для той же системы, при наличии двух интегрирующих звеньев в цепи измерения, то есть АФЧХ, построенная по формуле:
Для определения постоянных времени T2i в формуле (4) используют соотношение: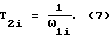
Формулы для построения АФЧХ на фиг. 1 и на фиг. 2 различны, хотя их применение в обоих случаях по затратам труда и точности практически эквивалентны, однако применение АФЧХ для систем, представляющих собой произведение интегрирующих и колебательных звеньев, предпочтительнее, так как практически полностью исключена случайная помеха с нулевым средним значением, и тем самым повышается точность определения постоянной времени динамической системы.
Проверка способа проводилась при снятии АФЧХ вертикально-фрезерного станка модели 654 (см. фиг. 2). Например, для одного из образцов станка значения характерных частот равны:
ω11 = 156,5 с-1; ω11max = 146,7 с-1;
ω12 = 337,7 с-1; ω12max= 319,4 с-1;
ω13 = 967,7 с-1; ω13max = 918,1 с-1.
Постоянные времени T2i и T1i, полученные по формулам (7) и (4) соответственно:
T21 = 6.39·10-3 c; T11 = 6.796·10-4 с;
T22 = 2.96·10-3 с; T12 = 2.798·10-4 с;
T23 = 0.103·10-2 с; T13 = 9.28·10-5 с.
В результате получаем ранее приведенную функцию упругой системы станка согласно формуле (6).
Определение передаточной функции может производиться автоматически на аппаратуре, описанной в авторском свидетельстве СССР N 1206713, кл. G 01 R 3/00, 1986, включая в измерительную цепь два интегрирующих звена.
Изобретение предназначено для построения математической модели сложной динамической системы с распределенными параметрами и может быть использовано для анализа нестационарных процессов в механических, электромеханических и электрических системах. Способ основан на возбуждении колебаний системы гармоническим воздействием в диапазоне ее собственных частот и регистрации амплитудно-фазовой частотной характеристики измеряемого кинематического параметра. Для каждой степени свободы системы фиксируют характерные частоты, соответствующие экстремумам действительной и мнимой составляющих кинематического параметра. По этим частотам рассчитывают постоянные времени и коэффициенты усиления. Особенностью способа является то, что в качестве кинематического параметра используют двойной интеграл от выходного сигнала колебательной системы, а передаточную функцию системы представляют в виде двойного интеграла суммы передаточных функций колебательных звеньев. Способ позволяет практически полностью исключить случайную помеху с нулевым средним значением и тем самым повысить точность определения постоянной времени динамической системы. 2 ил.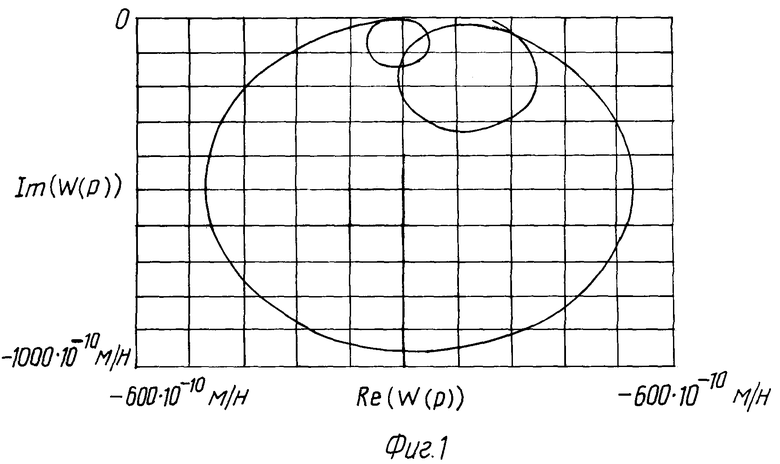
Способ определения постоянных времени механических и электромеханических колебательных систем при наличии двух интегрирующих усилителей в цепи измерения, по которому возбуждают колебания системы гармоническим воздействием в диапазоне ее собственных частот, измеряют кинематический параметр колебаний, регистрируют амплитудно-фазовую частотную характеристику измеряемого кинематического параметра, для каждой степени свободы фиксируют характерные частоты, соответствующие экстремумам действительной и мнимой составляющих кинематического параметра, и рассчитывают по этим частотам постоянные времени и коэффициенты усиления, отличающийся тем, что в качестве кинематического параметра используют двойной интеграл от выходного сигнала колебательной системы, берут передаточную функцию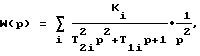
для которой постоянные времени Т1i, Т2i и коэффициенты усиления Кi определяют по формулам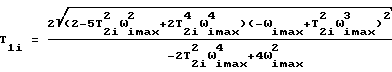
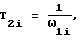
Ki = ±AiT1iω
где ωimax и ω1i - частоты, соответствующие экстремальным значениям вещественной и мнимой части амплитудно-фазовой частотной характеристики, построенной по вышеприведенной формуле для W(p);
Ai - размер петли амплитудно-фазовой частотной характеристики по мнимой оси,
при этом Кi > 0, если петля амплитудно-фазовой частотной характеристики находится выше своей начальной точки, и Кi < 0, если петля амплитудно-фазовой частотной характеристики лежит ниже начальной точки.
| СПОСОБ ПОСТРОЕНИЯ ДИНАМИЧЕСКОЙ МОДЕЛИ ЭКВИВАЛЕНТНОЙ УПРУГОЙ СИСТЕМЫ МЕТАЛЛОРЕЖУЩЕГО СТАНКА В ЗОНЕ РЕЗАНИЯ | 1996 |
|
RU2130598C1 |
| SU 1206713 A, 23.01.1986 | |||
| СПОСОБ ОПРЕДЕЛЕНИЯ ОТНОСИТЕЛЬНЫХ КОЭФФИЦИЕНТОВ ДЕМПФИРОВАНИЯ МЕХАНИЧЕСКИХ И ЭЛЕКТРОМЕХАНИЧЕСКИХ КОЛЕБАТЕЛЬНЫХ СИСТЕМ | 1994 |
|
RU2093808C1 |
| US 4061017 A, 06.12.1977 | |||
| Устройство для охлаждения водою паров жидкостей, кипящих выше воды, в применении к разделению смесей жидкостей при перегонке с дефлегматором | 1915 |
|
SU59A1 |
| Способ формирования спектра случайных широкополосных вибраций | 1979 |
|
SU862018A1 |
| Способ вибродиагностики валопровода турбоагрегата | 1987 |
|
SU1578546A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ОПОР РОТОРОВ ТУРБОАГРЕГАТОВ | 1991 |
|
RU2019801C1 |
Авторы
Даты
2001-02-20—Публикация
1999-09-17—Подача