Изобретение относится к измерительной технике и может быть, например, использовано для построения математической модели сложной механической или электромеханической системы с распределенными параметрами, что необходимо для анализа нестационарных процессов в механических, электромеханических и электрических системах.
Заявляемое изобретение направлено на решение задачи, заключающейся в повышении точности измерений и унификации аппаратных средств, необходимых для экспериментального снятия амплитудно-фазо-частотных характеристик (АФЧХ) с целью построения по ней математической модели эквивалентной электромеханической системы.
Известен способ определения коэффициентов демпфирования, основанный на обработке АФЧХ (см. Патент РФ N2093808, МПК6 G 01 M 7/02, 20.10.1997), в соответствии с которым возбуждают колебания системы гармоническим воздействием в диапазоне ее собственных частот, измеряют кинематический параметр колебаний, регистрируют амплитудно-фазовую частотную характеристику измеряемого кинематического параметра, для каждой степени свободы фиксируют характерные частоты, соответствующие экстремумам действительной и мнимой составляющих кинематического параметра, и по ее частотам рассчитывают относительные коэффициенты демпфирования. В качестве кинематического параметра колебаний измеряют скорость перемещения, фиксируют характерные частоты 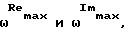 соответствующие максимальным значениям действительной и мнимой составляющих скорости перемещения, а относительный коэффициент γ демпфирования рассчитывают по формуле:
соответствующие максимальным значениям действительной и мнимой составляющих скорости перемещения, а относительный коэффициент γ демпфирования рассчитывают по формуле: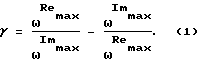
К причинам, препятствующим достижению указанного ниже технического результата при использовании известного способа, относится то, что известный способ оказывается слабозащищенным от помех.
Наиболее близким способом того же назначения к заявленному изобретению по совокупности признаков является способ определения относительных коэффициентов демпфирования механических колебательных систем, в котором определяются коэффициенты демпфирования по перемещению по формуле: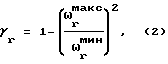
где ω
γr - относительный коэффициент демпфирования для данного тона амплитудно-фазовой частотной характеристики,
принятой за прототип (см. авт. свид. СССР N1206713, кл. G 01 R 3/00, 1985 г.).
К причинам, препятствующим достижению указанного ниже технического результата при использовании известного способа, принятого за прототип, относится то, что известный способ оказывается так же слабозащищенным от помех.
Сущность изобретения заключается в следующем. Изобретение решает задачу определения коэффициентов усиления и постоянных времени динамических систем, представляющих собой произведение интегрирующего и колебательных звеньев, по их АФЧХ, например таких, как сложная электрическая цепь, когда ее внутреннее строение неизвестно.
Технический результат позволяет практически полностью исключать случайную помеху с нулевым средним значением и этим самым повысить точность определения постоянных времени динамической системы.
Указанный технический результат при осуществлении изобретения достигается тем, что способ определяет коэффициенты усиления и постоянные времени динамических систем, включающие возбуждение колебаний системы гармоническим воздействием в диапазоне ее собственных частот, измеряют кинематический параметр колебаний, регистрируют амплитудно-фазовую частотную характеристику измеряемого кинематического параметра, для каждой степени свободы фиксируют характерные частоты, соответствующие экстремумам действительной и мнимой составляющих кинематического параметра, и по ее частотам рассчитывают постоянные времени и коэффициенты усиления.
Особенность способа заключается в том, что в качестве кинематического параметра используют интеграл от выходного сигнала колебательной системы.
Сущность заключается в том, что получена новая формула для определения коэффициента демпфирования по экстремальным точкам АФЧХ для динамических систем, представляющих собой произведение интегрирующего и колебательных звеньев.
Рассмотрим передаточную функцию: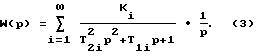
Положив p=jω, получим: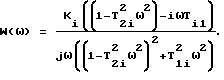
Выделим действительную и мнимую части этой передаточной функции: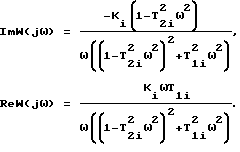
Исследуем мнимую часть на экстремум. Для этого найдем производную: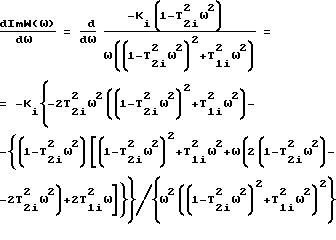
Приравниваем производную к нулю при 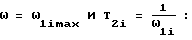
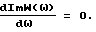
Рассмотрим числитель этого выражения: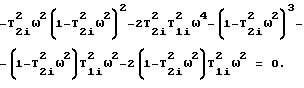
После некоторых математических преобразований получим следующее выражение: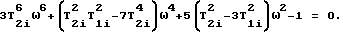
Обозначим ω2 = Ω. Тогда получим: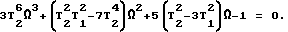
Преобразуем это выражение: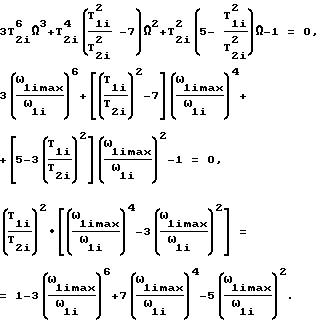
В результате получим новую формулу для определения коэффициента демпфирования по экстремальным точкам АФЧХ для динамических систем, представляющих собой произведение интегрирующего и колебательных звеньев: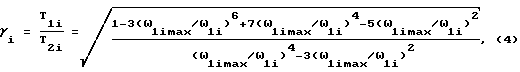
где ω1imax и ω1i - частоты, соответствующие экстремальным значениям мнимой и вещественной части АФЧХ, построенной по формуле (3).
Коэффициенты усиления находим по формулам:
Ki = -AiT1iω
где Ai, - размер петли АФЧХ по вещественной оси.
Кроме того, особенность способа заключается в том, что измерения можно производить на той же самой аппаратуре, что и в случае использования АФЧХ по перемещению, всего лишь включая в цепь измерения интегрирующее звено, используя формулу (3).
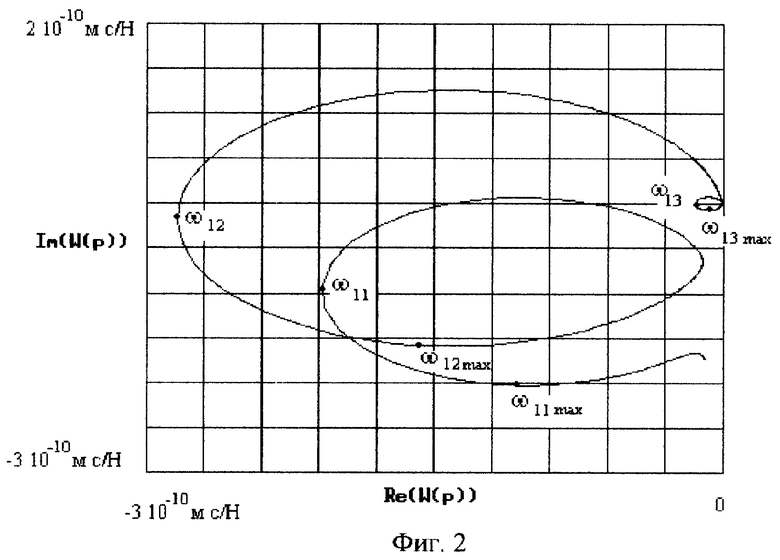
На фиг. 1 показана АФЧХ по перемещению для вертикально-фрезерного станка модели 654, которая описывается формулой:
(см. Ю. Н. Санкин. "Динамические характеристики вязко-упругих систем с распределенными параметрами" - Изд-во саратовского университета, 1977, с. 250. На фиг. 2 - АФЧХ для той же системы, при наличии интегрирующего звена в цепи измерителя, то есть АФЧХ, построенная по формуле:
Для определения постоянных времени T2i в формуле (4), используют соотношение: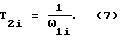
Формулы для построения АФЧХ на фиг. 1 и на фиг. 2 различны, хотя их применение в обоих случаях по затратам труда и точности практически эквивалентны, однако применение АФЧХ для систем, представляющих собой произведение интегрирующих и колебательных звеньев предпочтительнее, так как практически полностью исключена случайная помеха с нулевым средним значением, и тем самым повышается точность определения постоянной времени динамической системы.
Проверка способа проводилась при снятии АФЧХ вертикально-фрезерного станка модели 654 (см. фиг. 2). Например, для одного из образцов станка значения характерных частот равны: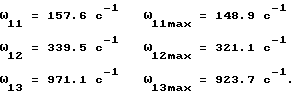
Размеры витков АФЧХ по горизонтали: A1 = 2.01, A2 = 2.83, A3 = 0.154. Постоянные времени T2i и T1i, полученные по формулам (7) и (4) соответственно:
T21 = 6.35•10-3 с, T11 = 0.65•10-3 с
T22 = 0.29•10-2 с, T12 = 0.294•10-3 с
T23 = 0.103•10-2 с, T13 = 0.1•10-3 с
В результате получаем ранее приведенную функцию упругой системы станка согласно формуле (6).
Определение передаточной функции может производиться автоматически на аппаратуре, описанной в авторском свидетельстве СССР N1206713, кл. G 01 R 3/00, 1986, включая в измерительную цепь интегрирующее звено.
Способ предназначен для построения математической модели сложной механической или электромеханической системы с распределенными параметрами и может быть использован для анализа нестационарных процессов в механических, электромеханических и электрических системах. Способ основан на возбуждении колебаний системы гармоническим воздействием в диапазоне ее собственных частот и регистрации амплитудно-фазовой частотной характеристики измеряемого кинематического параметра. Для каждой степени свободы системы фиксируют характерные частоты, соответствующие экстремумам действительной и мнимой составляющих кинематического параметра. По этим частотам рассчитывают постоянные времени и коэффициенты усиления. Особенностью способа является то, что в качестве кинематического параметра используют интеграл от выходного сигнала колебательной системы, а передаточную функцию системы представляют в виде интеграла суммы передаточных функций колебательных звеньев. Способ позволяет исключить случайную помеху с нулевым средним значением и тем самым повысить точность определения постоянной времени динамической системы. 2 ил.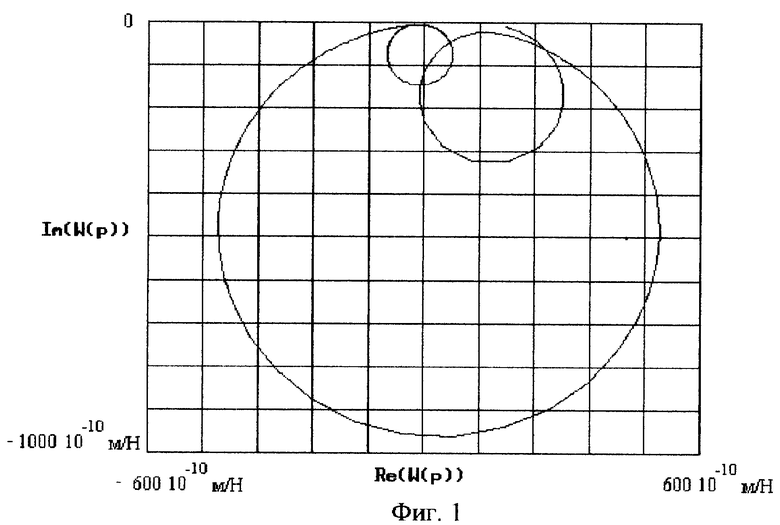
Способ определения постоянных времени механических и электромеханических колебательных систем при наличии интегрирующего усилителя в цепи измерения, по которому возбуждают колебания системы гармоническим воздействием в диапазоне ее собственных частот, измеряют кинематический параметр колебаний, регистрируют амплитудно-фазовую частотную характеристику измеряемого кинематического параметра, для каждой степени свободы фиксируют характерные частоты, соответствующие экстремумам действительной и мнимой составляющих кинематического параметра, и рассчитывают по этим частотам постоянные времени и коэффициенты усиления, отличающийся тем, что в качестве кинематического параметра используют интеграл от выходного сигнала колебательной системы, берут передаточную функцию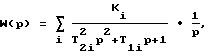
для которой постоянные времени T1i, T2i и коэффициенты усиления Ki определяют по формулам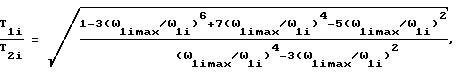
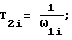
Ki= -AiT1iω
где ω1imax и ω1i - частоты, соответствующие экстремальным значениям мнимой и вещественной части амплитудно-фазовой частотной характеристики, построенной по вышеприведенной формуле для W(p);
Ai - размер петли амплитудно-фазовой частотной характеристики по вещественной оси.
| SU 1206713 A, 23.01.1986 | |||
| СПОСОБ ОПРЕДЕЛЕНИЯ ОТНОСИТЕЛЬНЫХ КОЭФФИЦИЕНТОВ ДЕМПФИРОВАНИЯ МЕХАНИЧЕСКИХ И ЭЛЕКТРОМЕХАНИЧЕСКИХ КОЛЕБАТЕЛЬНЫХ СИСТЕМ | 1994 |
|
RU2093808C1 |
| US 4061017 A, 06.12.1977 | |||
| Устройство для охлаждения водою паров жидкостей, кипящих выше воды, в применении к разделению смесей жидкостей при перегонке с дефлегматором | 1915 |
|
SU59A1 |
| Способ формирования спектра случайных широкополосных вибраций | 1979 |
|
SU862018A1 |
| Способ вибродиагностики валопровода турбоагрегата | 1987 |
|
SU1578546A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ОПОР РОТОРОВ ТУРБОАГРЕГАТОВ | 1991 |
|
RU2019801C1 |
Авторы
Даты
2000-07-10—Публикация
1998-08-07—Подача