Изобретение относится к измерительной технике и может быть использовано для построения математической модели эквивалентной упругой системы металлорежущего станка в зоне резания, что необходимо для разработки систем автоматического управления резанием, а так же для анализа динамических явлений при резании.
Заявляемое изобретение направлено на решение задачи, заключающейся в упрощении аппаратных средств, необходимых для экспериментального снятия АФЧХ с целью построения по ней математической модели эквивалентной упругой системы в зоне резания.
Известен способ построения математической модели эквивалентной упругой системы математической модели эквивалентной упругой системы металлорежущего станка в зоне резания (см. Санкин Ю.Н. Динамика несущих систем металлорежущих станков, - М.: Машиностроение, 1986. - 96 с.), основанный на использовании амплитудно-фазовой частной характеристики относительного перемещения в зоне резания между вершиной резца и заготовкой при единичной постоянной амплитуде возмущающей силы.
Недостатком прототипа является регистрация АФЧХ по перемещению при единичной гармонической силе, что связано с затруднениями, возникающими в связи с контролем амплитуды этой силы, так как на практике амплитуда силы является переменной и зависит от частоты возмущающего воздействия и, следовательно, с необходимостью применения тензометрических датчиков для измерения усилия, что ведет к аппаратурному усложнению измерительной схемы.
У прототипа и заявляемого изобретения имеются следующие сходные существенные признаки: необходимо приложение к системе гармонического возмущающего воздействия, измерение относительного перемещения в зоне резания между заготовкой и вершиной резца в зависимости от частоты, определение сдвига фаз между возмущающей силой и перемещением, построение АФЧХ, определение постоянных времени и коэффициентов усиления.
Технический результат - управление контроля за возмущающей силой вибратора, что ведет к аппаратурному упрощению измерительной схемы.
Указанный технический результат реализуется тем, что согласно способу построения динамической модели эквивалентной упругой системы (ЭУС) металлорежущего станка в зоне резания возбуждают колебания ЭУС гармоническим воздействием x = a sinωt с ограничением на амплитуду перемещения подвижной части вибратора в диапазоне ее собственных частот. При этом сила, воздействующая на ЭУС, будет пропорциональна квадрату частоты
F = -mω2a sinωt, (1)
где F - сила воздействия;
m - масса подвижной части вибратора;
ω - частота колебаний вибратора;
a - амплитуда колебаний подвижной части вибратора;
при фиксированной амплитуде колебаний подвижной части вибратора a измеряют кинематический параметр колебаний, в качестве которого берут относительное перемещение в зоне резания между двумя точками упругого объекта (резцом и шпинделем), которое пропорционально ускорению благодаря зависимости амплитуды возмущающей силы от частоты. Зарегистрированная таким образом АФЧХ не пересчитывается на единичное силовое воздействие, а используется в дальнейшем в том виде, в котором она зарегистрирована.
Особенностью способа является то, что при приложении силы с переменной амплитудой, пропорциональной квадрату частоты, регистрируют АФЧХ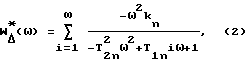
по экстремальным точкам АФЧХ, соответствующим максимальным значениям мнимой составляющей ω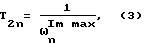
по экстремальным точкам АФЧХ, соответствующим минимальным значениям вещественной составляющей ω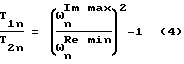
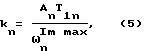
где An - размер n-го витка АФЧХ по мнимой оси, определяется по графику АФЧХ.
Таким образом, по этим характеристикам рассчитывают постоянные времени и коэффициенты усиления для передаточной функции, являющейся математической моделью эквивалентной упругой системы в зоне резания: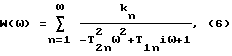
где kn - коэффициент усиления n-го колебательного звена;
T2n, T1n - постоянные инерционная и демпфирования n-го колебательного звена.
На практике в формулах (2) и (6) ограничиваются числом членов ряда, равным числу существенно проявляющих себя витков АФЧХ.
На фиг. 1 показана АФЧХ по перемещению для вертикально-фрезерного станка модели 654, которая описывается формулой
(см. Санкин Ю. Н. Динамические характеристики вязкоупругих систем с распределенными параметрами. - Саратов: Изд-во СГУ, 1977. - 309 с.), f - текущая частота, Гц. На фиг. 2 - АФЧХ.
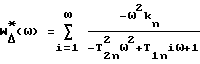
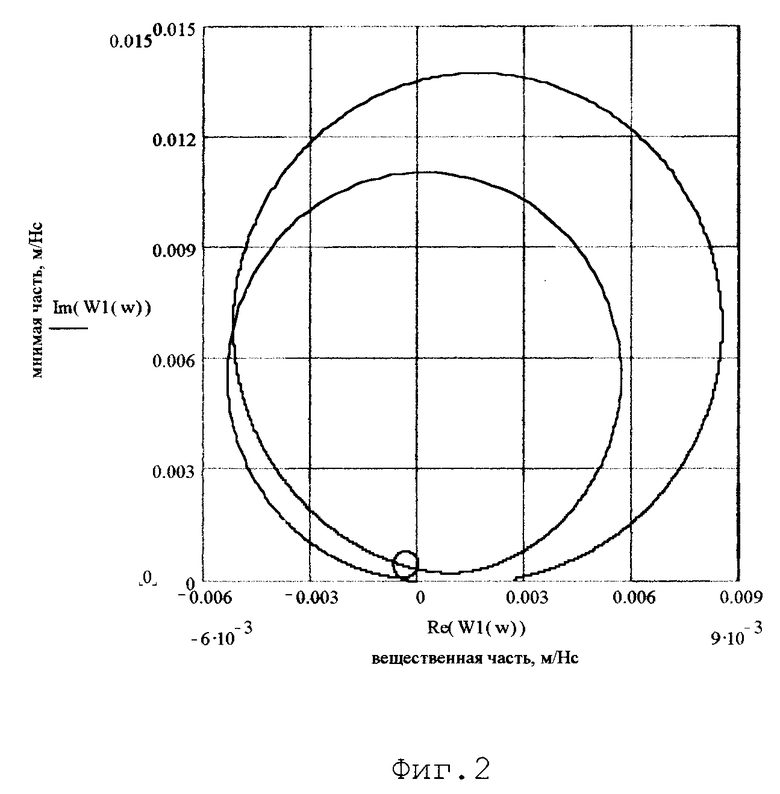
для того же станка,
где ω
ω
An - размер n-го витка АФЧХ по мнимой оси, определяется по графику АФЧХ.
Способ основан на использовании общего решения задачи динамики вязкоупругого тела в виде ряда по колебательным звеньям, в том числе и от действия на систему сосредоточенной силы. Математическая модель относительных перемещений между резцом и заготовкой также может быть представлена в виде суммы колебательных звеньев, и, следовательно, ее идентификация осуществляется теми же средствами, как и для действия одной сосредоточенной силы при определении абсолютного перемещения. Толщина срезаемой стружки определяется относительным перемещением между вершиной резца и заготовкой под действием равных по величине и противоположно направленных сил, имеющих общую линию действия. Поэтому не очевидно, что математическая модель системы дается формулой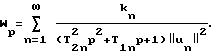
Для того чтобы описать динамические характеристики эквивалентной упругой системы в зоне резания, воспользуемся известным решением уравнения динамики упругого тела, преобразованного по Лапласу при нулевых начальных условиях, а также при условии подобия оператора рассеяния энергии оператору упругости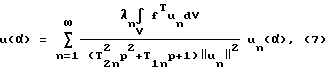
где un(α) - формы колебаний;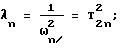
f = f(β) - внешние силы, действующие на тело;
V - область, занимаемая упругим телом;
α, β - пространственные координаты;
∥un∥ - норма n-й формы колебаний;
При действии сосредоточенной силы из (7) получаем
u(α) = W(p)f(β), (8)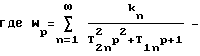 передаточная матрица упругой системы;
передаточная матрица упругой системы;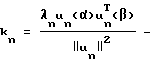 матрица коэффициентов усиления.
матрица коэффициентов усиления.
При действии двух равных по величине, противоположно направленных сил, учитывая, что f(α) = f(β) имеет согласно (7)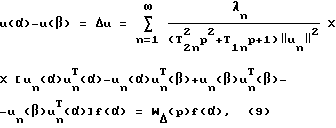
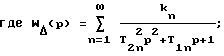
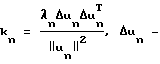 вектор относительного перемещения между точками приложения сил.
вектор относительного перемещения между точками приложения сил.
Следовательно, формула (9) подобна формуле (8) при действии возмущающей силы, которая создается вибратором, имеющим фиксированную амплитуду подвижной части x = a•sinωt порождается сила, амплитуда которой пропорциональна его частоте F = -mω2a sinωt,
Тогда при действии возмущающей силы вместо АФЧХ (6) будет сниматься АФЧХ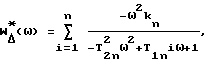
т.е. есть АФЧХ по ускорению.
Если выделить в (2) вещественную часть ReW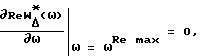
получаем формулу для определения постоянных времени (4).
Формулы для определения постоянных времени T2n и коэффициентов усиления kn по определению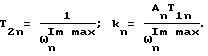
Формулы для построения передаточных функций (6) и (2) различны, хоты их применение в обоих случаях по затратам труда и точности практически эквивалентны, однако снятие АФЧХ по ускорению, то есть согласно формуле (2), предпочтительнее, так как соответствующая измерительная схема получается значительно проще.
Отличие заключается в том, что в известном способе снимается АФЧХ по перемещению при фиксированной амплитуде возмущающей силы, в предпочтительном же способе прикладывается возмущающая сила, пропорциональная квадрату частоты, что достигается использованием вибратора с ограниченным перемещением подвижной части вибратора, благодаря чему АФЧХ, зарегистрированное таким образом, выглядит как АФЧХ по ускорению. Необходимость в контроле подвижной части вибратора отсутствует.
Способ предназначен для использования при разработке систем автоматического управления резанием, а также для анализа динамических явлений при резании. Возбуждают колебания системы гармоническим воздействием в диапазоне ее собственных частот. Измеряют кинематический параметр колебаний. Регистрируют амплитудно-фазовую частотную характеристику (АФЧХ) параметра. В качестве параметра берут относительное перемещение в зоне резания между двумя точками упругого объекта. Воздействия осуществляют силой с амплитудой, пропорциональной квадрату частоты при фиксированной амплитуде колебаний подвижной части вибратора. Фиксируют характерные частоты, соответствующие минимальной действительной и максимальной мнимой составляющим зарегистрированной АФЧХ. Определяют постоянные времени и коэффициенты усиления для передаточной функции по приведенным в описании формулам. Упраздняется контроль за возмущающей силой вибратора, что ведет к аппаратурному упрощению измерительной схемы. 2 ил.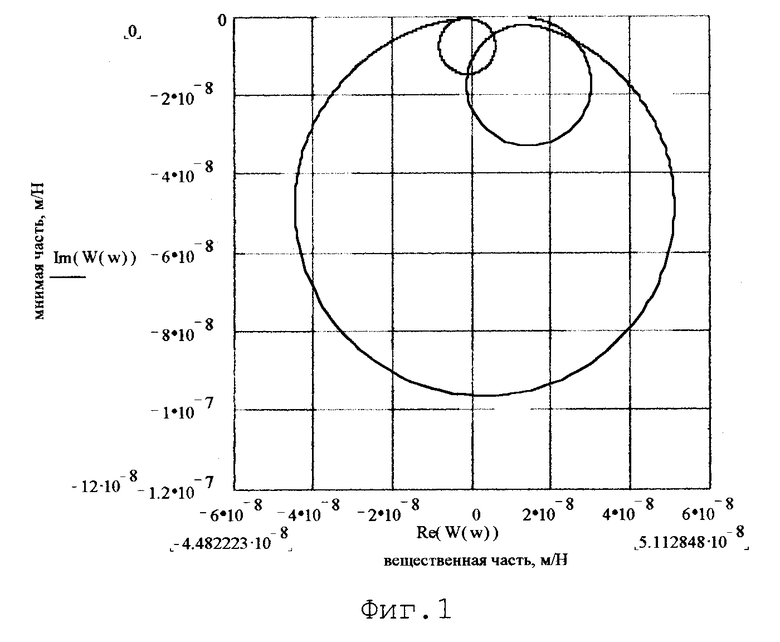
Способ построения динамической модели эквивалентной упругой системы металлорежущего станка в зоне резания, заключающийся в том, что возбуждают колебания системы гармоническим воздействием в диапазоне ее собственных частот, измеряют кинематический параметр колебаний, регистрируют амплитудно-фазовую частотную характеристику измеряемого кинематического параметра, для каждого витка амплитудно-фазовой частотной характеристики фиксируют характерные частоты, соответствующие экстремумам действительной и мнимой составляющих параметра, в качестве которого берут относительное перемещение в зоне резания между двумя точками упругого объекта, и по этим частотам рассчитывают постоянные времени и коэффициенты усиления для передаточной функции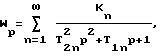
отличающийся тем, что гармоническое воздействие осуществляют силой с амплитудой, пропорциональной квадрату частоты F = -mω2asinωt при фиксированной амплитуде a колебаний подвижной части массой m вибратора, фиксируют характерные частоты
ω
соответствующие минимальной действительной и максимальной мнимой составляющим зарегистрированной амплитудно-фазовой частотной характеристики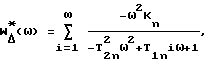
а постоянные времени и коэффициенты усиления для W(p) определяют по формулам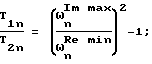
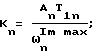
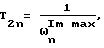
где T1n - постоянная рассеяния энергии;
T2n - инерционная постоянная;
An - амплитуда мнимой составляющей n-го витка.
| Санкин Ю.Н | |||
| Динамика несущих систем металлорежущих станков | |||
| - М.: Машиностроение, 1986, с.96 | |||
| СПОСОБ ОПРЕДЕЛЕНИЯ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ОПОР РОТОРОВ ТУРБОАГРЕГАТОВ | 1991 |
|
RU2019801C1 |
| Способ вибродиагностики валопровода турбоагрегата | 1987 |
|
SU1578546A1 |
| Способ получения на волокне оливково-зеленой окраски путем образования никелевого лака азокрасителя | 1920 |
|
SU57A1 |
| DE 3332979 A, 04.04.85. | |||
Авторы
Даты
1999-05-20—Публикация
1996-06-11—Подача