Предлагаемое изобретение относится к области физики рентгеновских лучей, преимущественно к способам определения параметров тонкой кристаллической структуры различных поликристаллических материалов, методом рентгеновской дифрактометрии, в частности определения параметров тонкой кристаллической структуры металлических и твердых сплавов.
Известен способ определения размеров областей когерентного рассеяния (блоков мозаики) поликристаллического материала по эффекту экстинкции [1, С.125-128], заключающийся в измерении изменений интенсивности линий с малыми индексами HKL, для чего определяют интенсивность первых линий у исследуемого образца и идеально мозаичного эталона, далее находят отношение интенсивностей линий исследуемого и эталонного образцов, находят значение nq по данным отношениям интенсивностей, где n - число отражающих плоскостей в блоке, q - отражательная способность плоскости, далее определяют значение q, а затем определяют значение n и по найденному значению n определяют размер D блоков по формуле D=n·dНКL, где dHKL - межплоскостное расстояние для плоскостей (HKL).
Недостатками известного способа являются: невозможность определения размеров блоков, меньших 0,2 мкм, а также невозможность одновременного определения размеров блоков и величины микродеформаций кристаллической решетки.
Наиболее близким к заявляемому способу является способ одновременного определения двух параметров тонкой кристаллической структуры поликристаллического материала размеров (D) областей когерентного рассеяния (блоков мозаики) и величины микронапряжений (ε ) - методом аппрокимации [1, С.131-138], позволяющей определять размеры блоков, меньшие 0,2 мкм, и микронапряжения, большие 2· 10-4, и включающий подготовку образцов без пластической деформации, воздействие на образец рентгеновского излучения для регистрации его дифракционного спектра, определение физических уширений (β ) двух порядков отражения от одной совокупности кристаллографических плоскостей, т.е. β 1 и β 2, и угловых положений центров тяжести (θ ) выбранных линий, т.е. θ 1 и θ 2, выбор конкретного вида функций (М(х) и N(х)), аппроксимирующих, соответственно, профиль линии, обусловленной дисперсностью блоков с размерами D≤ 0,2 мкм и с интегральной шириной β м=(0,94λ /D)·secθ , и профиль линии, обусловленной микродеформациями (ε ) кристаллической решетки с величиной ε ≥ 2·10-4 и интегральной шириной β N=4ε tgθ , и построение номограммы, позволяющей по величине отношения β 2/β 1, найти β M и β N и, тем самым, D и ε .
Недостатком прототипа является его сложность и малая точность определения значений параметров тонкой кристаллической структуры D и ε , связанные с необходимостью построения номограммы и отсчета по ней значений β M и β N.
Заявляемое изобретение направлено на увеличение эффективности способа за счет его упрощения и повышения точности. Указанный результат достигается тем, что осуществляется подготовка образцов без пластической деформации, воздействие на образец рентгеновского излучения для регистрации его дифракционного спектра, определение физических уширений (β ) двух порядков отражения от одной совокупности кристаллографических плоскостей, т.е. β 1 и β 2, и угловых положений центров тяжести (θ ) выбранных линий, т.е. θ 1 и θ 2, и определение размеров блоков D и величины микродеформаций кристаллической решетки ε по следующим формулам:
D=C1·M,
ε =C2·N,
где C1=(0,94λ ·secθ 1)/β 1, C2=β 1/4tgθ 1,
M=(a2-bc)/(a2-b2), N=[(b2-bc)/(a2-bc)]1/2;
а=tgθ 2/tgθ 1, b=β 2/β 1, c=secθ 2/secθ 1, λ - длина волны рентгеновского излучения, и последующее определение ошибок измерений по формулам:
Δ D/D=Δ M/M+Δ β 1/β 1,
Δ ε /ε =Δ N/N+Δ β 1/β 1,
где Δ M/M=F· M, Δ N/N=F/2N2;
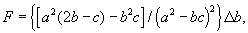
Δ b=b(Δ β 1/β 1+Δ β 2/β 2), Δ β 1 и Δ β 2 - ошибки определения β 1 и β 2, соответственно.
Заявляемое изобретение поясняется нижеследующим описанием.
Согласно [1, С.131-138] наилучшей аппрокимацией функции М(х) является функция Коши, a N(x) - функция Гаусса. Тогда связь между β , β M и β N дается выражением
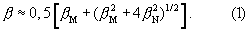
Используя уравнение (1) для интегральной ширины физического профиля, например: первого (HKL) и второго (2H2K2L) порядка отражения, получим систему уравнений
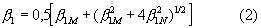
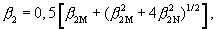
где β 1M=(0,94λ /D)secθ 1, β 2M=(0,94λ /D)secθ 2,
β 1N=4ε tgθ 1, β 2N=4ε tgθ 2
Для решения системы уравнений (2) введем следующие обозначения:
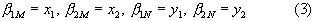
Тогда система уравнений (2) примет вид:
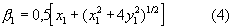
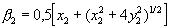
Умножением обеих частей уравнений (4) на 2 и переносом в левые части уравнений неизвестных x1 и х2 приведем систему (4) к виду
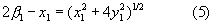
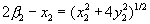
Возведя левые и правые части уравнений (5) в квадрат и произведя приведение подобных членов, получим:
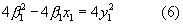
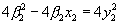
После сокращения на 4 система уравнений (6) принимает вид:
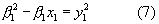
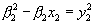
Система уравнений (7) может быть использована для нахождения искомых неизвестных: х1, х2, у1, у2. Действительно, разделив левую и правую части второго уравнения (7) соответственно на левую и правую части первого уравнения, получаем:
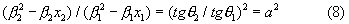
Преобразуем левую часть уравнения (8)
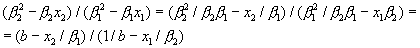
где b=β 2/β 1.
Таким образом,
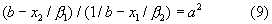
Дальнейшие алгебраические преобразования уравнения (9) позволяют получить уравнение первой степени относительно одного неизвестного - x1.
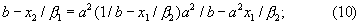
a2/b-b=a2x1/β 2-x2/β 1=x1(a2/β 2-c/β 1),
где c=secθ 2/secθ 1=x2/x1
Из уравнения (10) получаем
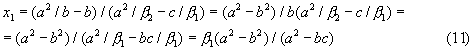
Итак,
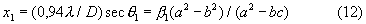
Разрешая (12) относительно D, окончательно получаем:
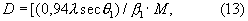
где 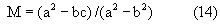
Та же формула (13) может быть получена, если разрешить среднюю часть уравнения (10) относительно другого неизвестного - х2
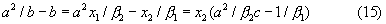
Разрешая правую часть уравнения (15) относительно х2, получаем
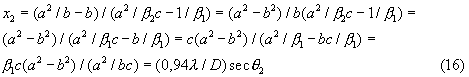
Разрешая (16) относительно D, получаем
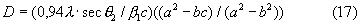
Но из определения c=secθ 2/secθ 1 вытекает, что формула (17) тождественна формуле (13).
Найдем теперь вторую пару неизвестных: y1 и y2.
Из первого уравнения (7) и уравнения (11) следует
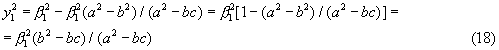
Итак,
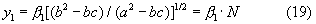
где N=[(b2-bc)/(a2-bc)]1/2;
Учитывая (3), находим
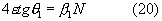
Откуда
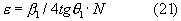
Ту же формулу (21) получаем, если воспользоваться вторым уравнением (7), определяющим другое неизвестное - y2 и уравнением (15).
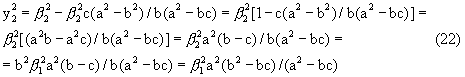
Т.е.
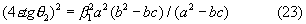
Подставляя в (23) значение а2, получаем
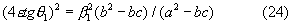
Откуда вытекают формулы (20) и (21)
Для определения относительных ошибок измерений, которые, в соответствии с [2], равны:
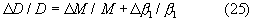
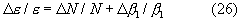
воспользуемся правилом дифференцирования натурального логарифма функции:
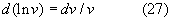
Поэтому
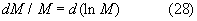
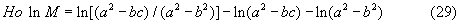
Следовательно,
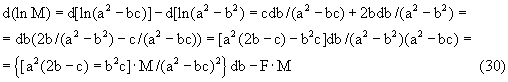
где
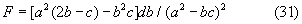
В свою очередь, согласно [2],
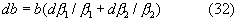
Аналогично предыдущему находим dN/N
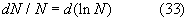
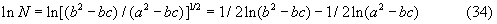
Следовательно,
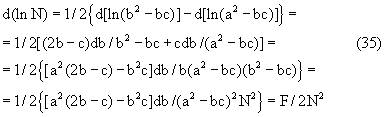
Итак,
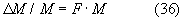
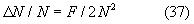
Абсолютные ошибки определения D и ε (Δ D и Δ ε ) получаются умножением найденных значений Δ D/D и Δ ε /ε на D и ε соответственно.
Заметим, что в интервале с<b<а корректирующие множители М и N действительны и положительны, В точке b=с М=1, N=0; в точке b=а М=∞ , N=1.
Если b>а, то полагают, что
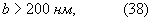
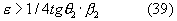
Справедливость последней формулы может быть пояснена следующим рассуждением. В интервале a<b<a2/c M<0 (что не имеет физического смысла), а 1<N<∞ . Но вывод формулы (21) для расчета N основывался на таком выборе функций, аппроксимирующих М(х) и N(x) (функции Коши и Гаусса), который несправедлив при b>а [3]. Поэтому естественно взять в качестве предельного значения N его значение, равное единице. Но при N=1
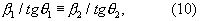
что легко доказывается из определения функций а и b. На практике при экспериментальных значениях b>а равенство (40) не выполняется. Следовательно, значения ε в этом случае будут больше, чем рассчитываемые при N=1 по формуле (21). Ниже в примерах 1 и 2 будет экспериментально обоснован вид формулы (39).
Заявленный способ использован на практике для исследования изменений тонкой кристаллической структуры компонентов твердых сплавов, вызываемых различными видами их обработок. Ниже следуют примеры использования способа.
Пример 1. Изменение параметров тонкой кристаллической структуры монокарбида вольфрама WC в режущих пластинах из твердого сплава ВК6ОМ после течения и облучения γ -квантами.
Точение осуществлялось на ОАО ММП им. В.В.Чернышева при механической обработке заготовок пластинами из твердого сплава ВК6ОМ (состав в маc.%: WC-94, Со-6). Облучение γ -квантами от радиоизотопного источника Cs137 с энергией 661 кэВ проводилось в ФГУП НИИ "Пульсар". Рентгеновские измерения выполнялись в МИСиС. Использовалось излучение СuКa. Исследовались рентгеновские линии WC 20,1 (θ 1=42,2 угл. град.) и θ 2=21,1 58,6 угл. град.).
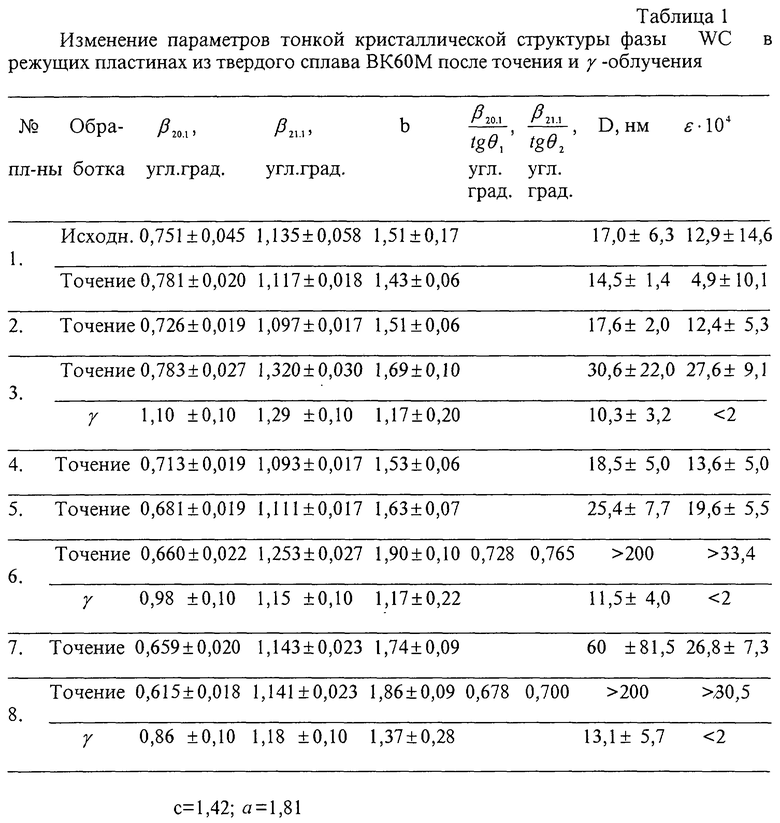
Результаты определения параметров тонкой кристаллической структуры (ТКС) монокарбида вольфрама WC по формулам (15), (21) и ошибок измерений по формулам (25), (26), (36), (37) заявляемого способа представлены в табл. 1. Там же указаны значения а и с.
Следует отметить, что, как правило, точение слабо изменяет параметры ТКС фазы WC. Исключение составляют лишь три пластины: 3, 6 и 8. В них после точения размера блоков либо были велики (пластина 3), либо не могли быть измерены методом рентгеновской дифрактометрии (пластины 6 и 8) (b>a, D>200 нм). Интересно отметить, что после облучения этих образцов γ -квантами с экспозиционной дозой 6· 104 рентген произошла перестройка дефектной структуры: упругая энергия перераспределилась от микродеформаций кристаллической решетки WC к границам блоков.
В пластинах 6 и 8 до облученния электронами (когда b больше а) значения ε не могут быть рассчитаны по формуле (21), а должны определяться по формуле (39). Ее справедливость подтверждается приведенными в табл. 1 значениями отношений β 20,1/tgθ 1 и β 21,1/tgθ 2.
Как видно из табл. 1, в обеих пластинах 6 и 8 второе отношение больше первого отношения. Как будет показано ниже в примере 3 (табл. 3), указанное положение выполняется всегда. Оно объясняется весьма большими трудностями определения истинных значений β 1: как правило расчет дает заниженные их значения.
В пластинах 3, 6 и 8 после облучения электронами (когда b делается меньше с) значения D должны рассчитываться по формуле (13), в которой следует положить М≡ 1, что и проделано в табл. 1.
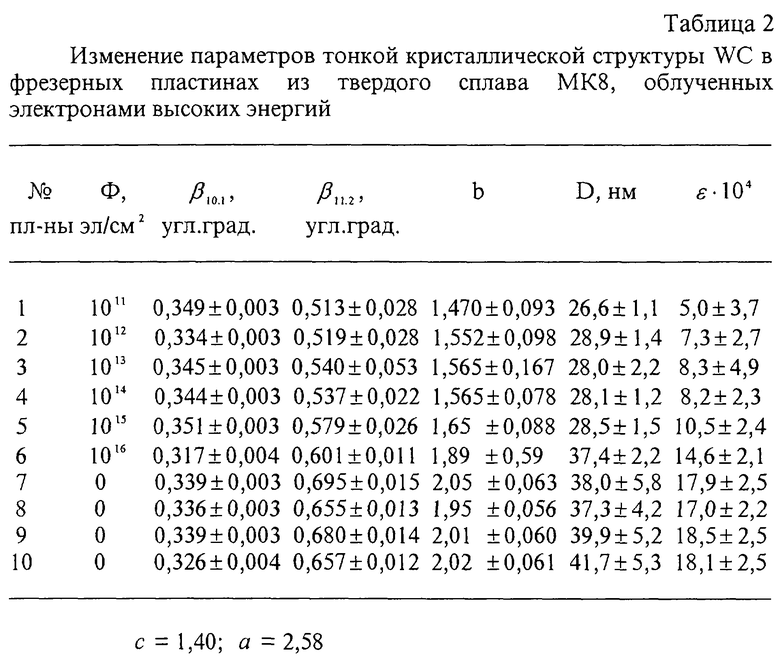
Пример 2. Изменение параметров тонкой кристаллической структуры в фазах WC и (Ti, W)C в фрезерных пластинах из твердого сплава МК8, облученных электронами высоких энергий.
Облучение электронами фрезерных пластин из твердого сплава МК8 (состав в маc.%: WC-85,0; TiC-7,7; Co-7,3) осуществлялось от радиоизотопного источника Sr90+Y90 (Ee max≈2,3 МэВ) на ФГУП НИИ "Пульсар". Рентгеновские измерения проводились в МИСиС при тех же условиях, что и в примере 1. Исследовались линии фазы WC 10,1 (θ 1=24,4 угл. град.) и 11,2 (θ 2=49,4 угл. град.) и линии фазы (Ti, W)C 220 (θ 1=30,5 угл. град.) и 422 (θ 2=61,1 угл. град.).
В табл. 2 приведены данные об изменении ТКС фазы WC в пластинах из твердого сплава МК8, подвергнутых облучению электронами в интервале флюенсов Ф от 1011 до 1016 эл/см2. Из табл. 2 следует, что всюду параметр b заключен в интервале (с, а): с<b<а. Облучение всюду (за исключением Ф=1· 1016 эл/см2) уменьшает значения как ε , так и D по сравнению с исходными пластинами.
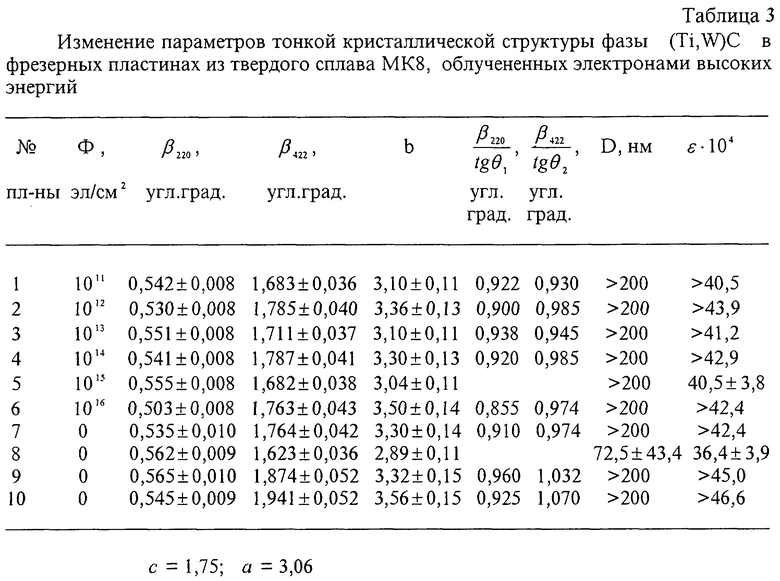
В табл. 3 представлены изменения параметров ТКС двойного карбида-фазы (Ti, W)C вследствие облучения электронами высоких энергий. Как видно из табл. 3, облучение фазы (Ti, W)C электронами практически не изменяет ее тонкую кристаллическую структуру. В табл. 3 параметр b, как правило, превосходит значения a (h>a), при этом β 2/tgθ 2/>β 1/tgθ 1 всегда. Поэтому расчет ε осуществлен по формуле (39).
Данные, представленные в примерах 1 и 2, подтверждают, что заявленный способ позволяет рассчитать значения размеров блоков D и микродеформаций кристаллической решетки ε без построения номограммы (чего требует способ-прототип), а также оценить ошибки расчета D и ε .
Источники информации
1. Горелик С.С., Скаков Ю.А., Расторгуев Л.И. Рентгенографический и электронно-оптический анализ. Учебное пособие для вузов. Изд. 4-е, перераб. и доп. - М: МИСиС, 2002, - 360 с.
2. Физический практикум. Изд. - 3-е/Под ред.проф. В.И.Ивероновой - М: Гостехиздат. 1955, - 636 с.
3. Селиванов В.И., Смыслов Е.Ф. Рентгеноструктурный анализ дислокационной структуры поликристаллов по распределению микродеформаций. / Заводская лаборатория. - 1994. - Т.60, №2, - с.31-36.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ КОНТРОЛЯ КАЧЕСТВА ИЗДЕЛИЙ ИЗ ТВЕРДЫХ СПЛАВОВ ПОСЛЕ РАДИАЦИОННО-ТЕРМИЧЕСКОЙ ОБРАБОТКИ | 2006 |
|
RU2303257C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК НАЛОЖИВШИХСЯ ДРУГ НА ДРУГА РАДИОСИГНАЛОВ ОДНОЙ ЧАСТОТЫ | 2013 |
|
RU2551115C1 |
| СПОСОБ РЕНТГЕНОСТРУКТУРНОГО АНАЛИЗА | 1998 |
|
RU2142623C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СТРУКТУРЫ МОЛЕКУЛЯРНЫХ КРИСТАЛЛОВ | 2014 |
|
RU2566399C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ С ПОВЫШЕННЫМ БЫСТРОДЕЙСТВИЕМ АЗИМУТАЛЬНОГО И УГЛОМЕСТНОГО ПЕЛЕНГОВ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЯ И НАЧАЛЬНОЙ ФАЗЫ ЕГО СИГНАЛА | 2013 |
|
RU2539649C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЗЕНИТНОГО И ВИЗИРНОГО УГЛОВ СКВАЖИНЫ | 1991 |
|
RU2017950C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЯ | 2013 |
|
RU2551355C1 |
| СПОСОБ ОГРАНИЧЕНИЯ СКОРОСТИ АВТОМОБИЛЯ В ЗАВИСИМОСТИ ОТ КОЛИЧЕСТВА ЕГО ПАССАЖИРОВ | 2010 |
|
RU2468937C2 |
| ИНСТРУМЕНТ ИЗ СТАЛИ Х12МФ | 2005 |
|
RU2306207C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПЕЛЕНГАЦИОННОЙ ПАНОРАМЫ ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЯ НА ОДНОЙ ЧАСТОТЕ | 2012 |
|
RU2528177C2 |
Изобретение относится к области определения параметров тонкой кристаллической структуры различных поликристаллических материалов методом рентгеновской дифрактометрии. Способ определения параметров тонкой кристаллической структуры поликристаллического материала включает в себя подготовку образцов без пластической деформации, воздействие на образец рентгеновского излучения для регистрации его дифракционного спектра, определение физических уширений (β) двух порядков отражения от одной совокупности кристаллографических плоскостей, т.е. β1 и β2, и угловых положений центров тяжести (θ) выбранных линий, т.е. θ1 и θ2, и определение расчетным путем размеров блоков D и величины микродеформаций кристаллической решетки ε, а также соответствующих ошибок измерений. Данное изобретение направлено на увеличение эффективности способа за счет его упрощения и повышения точности. 3 табл.
Способ определения параметров тонкой кристаллической структуры поликристаллического материала, включающий подготовку образцов без пластической деформации, воздействие на образец рентгеновского излучения для регистрации его дифракционного спектра, определение физических уширений (β) двух порядков отражения от одной совокупности кристаллографических плоскостей, т.е. β1 и β2, угловых положений центров тяжести (θ) выбранных линий, т.е. θ1 и θ2, определение размеров блоков D и величины микродеформаций кристаллической решетки ε по следующим формулам:
D=C1·М,
ε=С2·N,
где C1=(0,94λ·secθ1)/β1, C2=β1/4tgθ1,
M=(a2-bc)/(a2-b2), N=[(b2-bc)/(a2-bc)]1/2;
a=tgθ2/tgθ1, b=β2/β1, c=secθ2/secθ1,
λ - длина волны рентгеновского излучения,
и последующее определение ошибок измерений по формулам:
ΔD/D=ΔМ/М+Δβ1/β1,
Δε/ε=ΔN/N+Δβ1/β1,
где ΔМ/М=F·М, ΔN/N=F/2N2, F={[a2(2b-c)-b2c]/(a2-bc)2}Δb,
Δb=b(Δβ1/β1+Δβ2/β2), Δβ1 и Δβ2 - ошибки определения β1 и β2 соответственно.
| Способ рентгенографического исследования структуры полимеров | 1981 |
|
SU1000868A1 |
| СПОСОБ КОНТРОЛЯ ПАРАМЕТРОВ ПЛЕНОЧНЫХ ПОКРЫТИЙ И ПОВЕРХНОСТЕЙ В РЕАЛЬНОМ ВРЕМЕНИ И УСТРОЙСТВО ЕГО ОСУЩЕСТВЛЕНИЯ | 1998 |
|
RU2194272C2 |
| СПОСОБ АНАЛИЗА КОЛИЧЕСТВЕННОГО СОСТАВА ПОВЕРХНОСТИ ТВЕРДОГО ТЕЛА | 1993 |
|
RU2064707C1 |
| Способ неразрушающего послойного рентгеноструктурного анализа поликристаллических массивных объектов | 1984 |
|
SU1221558A1 |
| DE 4407278 А1, 07.09.1995 | |||
| US 4128762 А, 05.12.1978 | |||
| DE 3139128 А1, 17.03.1983. | |||
Авторы
Даты
2004-08-10—Публикация
2002-12-27—Подача