СПОСОБ ОПРЕДЕЛЕНИЯ С ПОВЫШЕННЫМ БЫСТРОДЕЙСТВИЕМ АЗИМУТАЛЬНОГО И УГЛОМЕСТНОГО ПЕЛЕНГОВ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЯ И НАЧАЛЬНОЙ ФАЗЫ ЕГО СИГНАЛА Российский патент 2015 года по МПК G01S5/04 

Область техники

Изобретение относится к радиотехнике, в частности к односигнальной радиопеленгации источника радиоизлучения (ИРИ).

Уровень техники

Пеленгация ИРИ имеет место в процессе мониторинга радиоэлектронной обстановки. При этом необходимо определять азимутальные, угломестные пеленги ИРИ и амплитуду сигнала. Пеленгатор регистрирует излучение путем записи сигналов на элементах антенной системы (AC) - вибраторах. Выполняя различные действия над сигналами с вибраторов, определяют параметры излучения. Проблема в том, какие действия над сигналами окажутся более эффективными (точными и быстрыми).

Известен способ [1], согласно которому азимутальные и угломестные пеленги определяют посредством поиска максимумов квадрата модуля углового спектра, полученного при помощи двухмерного преобразования Фурье от свертки комплексных сигналов, полученных с m-го элемента AC, m=1; 2; …; М, М - количество элементов АС, и комплексного сигнала, полученного с опорного элемента АС. При этом вводится двумерная сетка по азимуту θ и по углу места β.

Недостатком способа [1] является высокая вычислительная сложность, обусловленная необходимостью вычисления двухмерного преобразования Фурье, и необходимость наличия в АС достаточно большого количества элементов для получения приемлемых результатов. Но по начальной фазе сигнала φ₀ сетка не вводилась, так как и так громоздкое решение задачи становилось еще более громоздким, а при этом считалось, что начальная фаза мало влияет на получение истинного результата.

Авторский способ определения пеленгов ИРИ [2] принят за прототип. В прототипе предложено использовать одну сетку, получить произведения функций косинусов углов пеленгов менее громоздкими методами, а затем определить из системы двух уравнений углы пеленгов, по-прежнему не учитывая начальную фазу. Для этого нелинейную АС логически разделяют на две части таким образом, чтобы линии отсчета азимутальных пеленгов каждой из частей не были параллельны друг другу (системы координат, связанные с каждой из частей были развернуты относительно друг друга). В каждой из частей выбирают опорный элемент (элемент, относительно которого производят измерение набегов фаз на остальных элементах части АС). Одни и те же элементы АС могут входить в обе выделенные части одновременно. Любым способом, например, при помощи поиска максимумов квадрата модуля одномерного углового спектра, полученного посредством одномерного преобразования Фурье, вычисляют произведение косинусов азимутального и угломестного пеленгов для каждого ИРИ в системах координат, связанных с первой и со второй логическими частями АС (в аналитическое выражение комплексной амплитуды сигнала на m-м элементе АС азимутальные и угломестные пеленги входят в качестве произведения их косинусов), причем вычисления производят на основе набегов фаз на элементах АС относительно соответствующих опорных вибраторов. Азимутальные пеленги всех ИРИ, измеренные в системах координат, связанных с различными логическими частями АС, отличаются на величину угла γ между соответствующими линиями отсчета пеленгов. Вычисления азимутального и угломестного пеленгов k-го ИРИ осуществляют по формулам

$${\theta }_k=arctg\left\{\frac{P_2-P{}_{1}cos\gamma }{P_1\sin \gamma }\right\}$$ ,

$${\beta }_k=\arccos \left\{\frac{P_1}{\cos {\theta }_k}\right\}$$

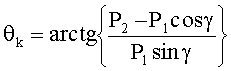
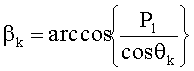
где P₁ - величина произведения косинусов азимутального и угломестного пеленгов k-го ИРИ, k=1; 2; …; К, где К - количество ИРИ, полученного в системе координат, связанной с первой логической частью АС; P₂ - величина аналогичного произведения, полученного в системе координат, связанной со второй логической частью АС.

Прототип имеет следующие недостатки.

1. В расчетах не учитывается начальная фаза сигнала φ₀, которая влияет на набег фаз, из которых и определяются пеленги. Поэтому искажаются значения пеленгов. В большинстве практических случаев фаза сигнала φ₀ не равна нулю.

2. Высокая вычислительная сложность, обусловленная необходимостью вычисления одномерного преобразования Фурье, а, как следствие, большие временные затраты.

3. Нелинейную АС логически разделяют только на две части и таким образом, чтобы линии отсчета азимутальных пеленгов каждой из частей не были параллельны друг другу (системы координат, связанные с каждой из частей, были бы развернуты относительно друг друга). Однако этого недостаточно для исключения влияния начальной фазы φ₀ на нахождение наиболее приближенным к истинным величин пеленгов.

Раскрытие изобретения

Достигаемый технический результат - существенное повышение скорости и точности определения азимутальных и угломестных составляющих пеленгов и начальной фазы сигнала при приеме радиосигнала одного ИРИ с использованием нелинейных (в т.ч. кольцевых) АС, состоящих из слабонаправленных элементов (вибраторов). Повышение точности и скорости определения пеленгов достигается за счет использования особенностей нелинейных АС, позволяющих устранить влияние на значения пеленгов неучтенной начальной фазы сигнала φ₀ и сведения алгоритма определения параметров сигнала к прямому расчету по элементарным формулам (в предлагаемом изобретении устранены все громоздкие вычислительные операции).

В предлагаемом способе сигналы рассматриваются как детерминированные, подверженные аддитивной помехе, оценки параметров которых подлежат определению.

Для достижения технического результата предлагается способ определения азимутального и угломестного пеленгов источника радиоизлучения и начальной фазы φ₀ его сигнала, включающий в себя разделение произвольной нелинейной антенной системы (АС) на логические части по элементам (вибраторам) АС, восстановление вектора комплексных амплитуд сигналов, полученных с выхода каждого элемента АС, с последующим его разделением, соответствующим логическому разделению АС, тригонометрические формулы пеленгов, по которым определяют углы пеленгов. При этом разделение производят на n частей, но не менее чем на три части - три элемента АС под разными углами к направлению нулевого отсчета углов γ элементов АС. Измеренные комплексные амплитуды сигналов, полученные с выхода каждого элемента АС, поступают в блок вычисления натуральных логарифмов, затем - в вычислитель, куда заранее введены аналитические выражения натурального логарифма от функции, описывающей комплексную огибающую выходных сигналов элементов АС, действительные и мнимые части которой приравнивают действительным и мнимым частям натурального логарифма измеренных комплексных амплитуд сигналов, полученных с выхода каждого элемента АС. Получают систему алгебраических уравнений, из которой определяют аналитические выражения для вычисления азимутального пеленга θ, угломестного пеленга β, начальной фазы сигнала φ₀ согласно матричным тригонометрическим формулам

$$\left(\begin{array}{c}tg\theta (P_1-{\stackrel{⌢}{\varphi }}_0)\\ {\stackrel{⌢}{\varphi }}_0\end{array}\right)={(A^{T}A)}^{-1}{A}^{T}Y$$ ; $$\cos \beta =\frac{p_1-{\stackrel{⌢}{\varphi }}_0}{\cos \theta }$$ ,

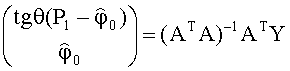
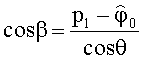
где γ_m - угол между m-м элементом АС и направлением отсчета при m=1…n;

γ₁=0 (угол 1-го элемента АС) - начало отсчета углов γ_m;

$$P_m=2\pi \frac{R}{\lambda }\cos (\theta -{\gamma }_m)\cos \beta +{\varphi }_0$$ ; $$p_m=\frac{P_m\lambda }{2\pi R}$$ при m=1, …, n; $$P_1=2\pi \frac{R}{\lambda }\cos \theta \cos \beta +{\varphi }_0$$ ;

$${\stackrel{⌢}{\varphi }}_0=\frac{{\varphi }_0\lambda }{2\pi R}$$ , где λ - длина волны сигналов ИРИ, R - радиус круговой АС;

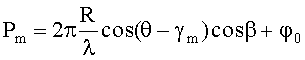
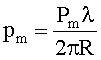
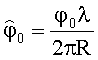
матрица 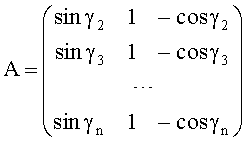$$A=\left(\begin{array}{c}\sin {\gamma }_{2}1-\cos {\gamma }_2\\ \sin {\gamma }_{3}1-\cos {\gamma }_3\\ \cdots \\ \sin {\gamma }_{n}1-\cos {\gamma }_n\end{array}\right)$$ ;

вектор-столбец 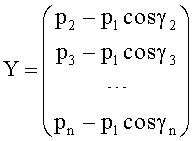$$Y=\left(\begin{array}{c}{p}_2-p_1\cos {\gamma }_2\\ p_3-p_1\cos {\gamma }_3\\ \cdots \\ p_n-p_1\cos {\gamma }_n\end{array}\right)$$ ;

после нахождения значений пеленга θ и начальной фазы φ₀ определяют пеленг β.

Чтобы исключить влияние начальной фазы φ₀ на результаты определения углов пеленгов, надо разделить АС на число частей не меньше трех (в принципе, чем больше будет частей разделения АС, тем точнее будут результаты).

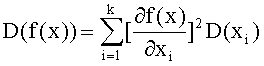
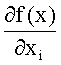
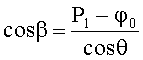
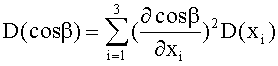
Для нахождения доверительных интервалов определяемых параметров дополнительно вычисляют дисперсии D значений азимутального и угломестного пеленгов и начальной фазы сигнала источника радиоизлучения по общей формуле $$D(f(x))={\displaystyle \sum _{i=1}^k{[\frac{\partial f(x)}{\partial x_i}]}^{2}D(x_i)}$$ , где f(x) - функция, определяющая значение искомого параметра; x_i - i-я переменная, входящая в f(x_i), i=1, 2, …, k, k - число переменных; с использованием аналитических выражений частных производных $$\frac{\partial f(x)}{\partial x_i}$$ и заранее известных величин дисперсий D(x_i) переменных x_i. В данном случае в качестве f(x) выступают формулы для cosβ, tgθ, φ₀, а в качестве x_i выступают все другие переменные, входящие в формулу, а именно: $$\cos \beta =\frac{P_1-{\varphi }_0}{\cos \theta }$$ ; тогда f(x)=cosβ, P₁≡x₁; φ₀≡x₂; cosθ≡x₃. и $$D(\cos \beta )={\displaystyle \sum _{i=1}^3{(\frac{\partial \cos \beta }{\partial x_i})}^{2}D(x_i)}$$ .

Дисперсии вычисляют, чтобы определить доверительный интервал (возможный разброс значений) при заданной доверительной вероятности. Но для практики нужна не сама дисперсия, а корень квадратный из нее - среднее квадратическое отклонение (СКО σ). То что получают из решения базовой системы уравнений - это наиболее вероятное значение при заданных исходных данных. При других данных получат другое решение, которое попадет в доверительный интервал. Если к решению добавить ±σ, то с вероятностью 0,68 при изменении данных (за счет помехи) решения будут находиться в этом интервале. Первичные операции над сигналами - моменты первого порядка, разброс значений - единицы процентов. Коэффициенты корреляции - моменты второго порядка - имеют разбросы значений сотни процентов.

Осуществление изобретения

Предлагаемый способ показан на примере круговой АС.

1. В круговой АС каждый элемент-вибратор смещен на некоторый угол от другого, т.е. круговая АС может быть автоматически разделена на число областей, равное числу вибраторов. Восстанавливают вектор комплексных амплитуд сигналов y=[y₁ y₂ … y_M]^T, полученных с выхода каждого элемента АС. Вектор y восстанавливают единожды для всей АС (то есть производят одно физическое измерение).

2. Запишем нелинейную систему уравнений, правая часть которой является аналитическим выражением комплексной амплитуды сигнала на m-м элементе АС, комплексной огибающей выходов элементов круговой АС

$$y_m(\theta ,\beta ,t)=u\exp \left\{j\left[2\pi f_{0}t+{\varphi }_0+(2\pi /\lambda )R\cos (\theta -{\gamma }_m)\cos \beta \right]\right\};(1)$$

где m=1, …, n;

j - мнимая единица, 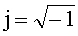$$j=\sqrt{-1}$$ ,

θ - азимутальный пеленг,

β - угломестный пеленг,

γ_m - угол между m-м элементом АС и направлением отсчета,

f₀ - частота сигналов, излучаемых пеленгуемыми ИРИ,

u - амплитуда сигнала,

φ₀ - начальная фаза сигнала,

t - время, в данном случае его можно положить равным нулю,

λ - длина волны сигналов ИРИ,

R - радиус антенной системы.

3. Логарифмируем выражение (1), получим

$$\ln \left|y_m\right|+j\arg y_m=\ln u+j(2\pi \frac{R}{\lambda }\cos (\theta -{\gamma }_m)\cos \beta +{\varphi }_0).(2)$$

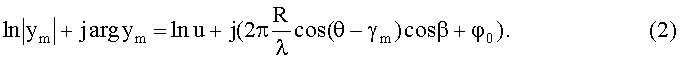
Обозначим argy_m=P_m и приравняем соответственно действительные и мнимые части: u=|y_m|; таким образом определим амплитуду u. Далее обозначим:

$$P_m=2\pi \frac{R}{\lambda }\cos (\theta -{\gamma }_m)\cos \beta +{\varphi }_0$$ или:

$$p_m=\cos (\theta -{\gamma }_m)\cos \beta +{\stackrel{⌢}{\varphi }}_0$$ , m=1, …, n;

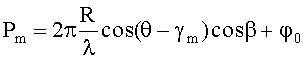
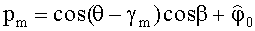
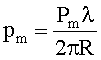
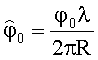
где $$p_m=\frac{P_m\lambda }{2\pi R}$$ ; $${\stackrel{⌢}{\varphi }}_0=\frac{{\varphi }_0\lambda }{2\pi R}$$ ; γ₁=0 - начало отсчета углов γ_m.

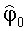
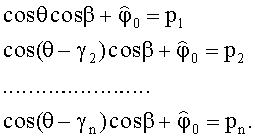
4. Составим систему уравнений для пеленгов θ, β и начальной фазы сигнала $${\stackrel{⌢}{\varphi }}_0$$ :

$$\begin{array}{l}\cos \theta \cos \beta +{\stackrel{⌢}{\varphi }}_0=p_1\\ \cos (\theta -{\gamma }_2)\cos \beta +{\stackrel{⌢}{\varphi }}_0=p_2\\ \mathrm{.........................}\\ \cos (\theta -{\gamma }_n)\cos \beta +{\stackrel{⌢}{\varphi }}_0=p_n.\end{array}$$

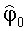
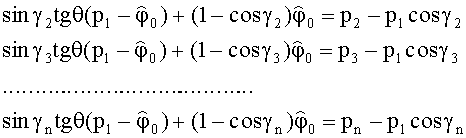
Решить эту систему можно разными методами. Приведем следующий. Переносим $${\stackrel{⌢}{\varphi }}_0$$ вправо, делим все уравнения на первое. Получим

$$\begin{array}{l}\sin {\gamma }_{2}tg\theta (p_1-{\stackrel{⌢}{\varphi }}_0)+(1-\cos {\gamma }_2){\stackrel{⌢}{\varphi }}_0=p_2-p_1\cos {\gamma }_2\\ \sin {\gamma }_{3}tg\theta (p_1-{\stackrel{⌢}{\varphi }}_0)+(1-\cos {\gamma }_3){\stackrel{⌢}{\varphi }}_0=p_3-p_1\cos {\gamma }_3\\ \mathrm{...........................................}\\ \sin {\gamma }_{n}tg\theta (p_1-{\stackrel{⌢}{\varphi }}_0)+(1-\cos {\gamma }_n){\stackrel{⌢}{\varphi }}_0=p_n-p_1\cos {\gamma }_n\end{array}$$

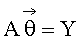
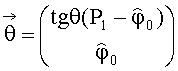
или в матричном виде: $$A\overrightarrow{\theta }=Y$$ , где

$$A=\left(\begin{array}{c}\sin {\gamma }_{2}1-\cos {\gamma }_2\\ \sin {\gamma }_{3}1-\cos {\gamma }_3\\ \cdots \\ \sin {\gamma }_{n}1-\cos {\gamma }_n\end{array}\right)$$ ; $$\overrightarrow{\theta }=\left(\begin{array}{c}tg\theta (P_1-{\stackrel{⌢}{\varphi }}_0)\\ {\stackrel{⌢}{\varphi }}_0\end{array}\right)$$ ; $$Y=\left(\begin{array}{c}{p}_2-p_1\cos {\gamma }_2\\ p_3-p_1\cos {\gamma }_3\\ \cdots \\ p_n-p_1\cos {\gamma }_n\end{array}\right)$$ .

Отсюда решение

$$\left(\begin{array}{c}tg\theta (P_1-{\stackrel{⌢}{\varphi }}_0)\\ {\stackrel{⌢}{\varphi }}_0\end{array}\right)={(A^{T}A)}^{-1}{A}^{T}Y;\cos \beta =\frac{p_1-{\stackrel{⌢}{\varphi }}_0}{\cos \theta }.(3)$$ .

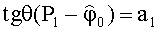
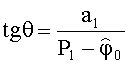
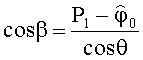
Формула (3) - это матричная формула для tgθ и φ₀. Компьютеру задают матрицы и формулу (3), а компьютер выдает 2 числа: значения $$tg\theta (P_1-{\stackrel{⌢}{\varphi }}_0)=a_1$$ и φ₀=a₂. Тогда $$tg\theta =\frac{a_1}{P_1-{\stackrel{⌢}{\varphi }}_0}$$ и φ₀=a₂; $$\cos \beta =\frac{P_1-{\stackrel{⌢}{\varphi }}_0}{\cos \theta }$$ .

Но можно поступить и по другому, а именно: записать функционал метода наименьших квадратов и минимизировать его:

$$F={\displaystyle \sum _{i=2}^n{(\sin {\gamma }_{i}tg\theta (P_1-{\varphi }_0)+(1-\cos {\gamma }_i){\varphi }_0-P_i+P_1\cos {\gamma }_i)}^2}$$

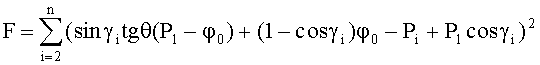
Тогда значение tgθ находится из условия 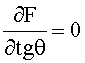$$\frac{\partial F}{\partial tg\theta }=0$$ ;

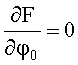
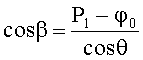
φ₀ - из условия $$\frac{\partial F}{\partial {\varphi }_0}=0$$ ; $$\cos \beta =\frac{P_1-{\varphi }_0}{\cos \theta }$$ .

Можно выбирать любой из двух указанных подходов. В конце после нахождения пеленга θ и начальной фазы φ₀ определяют пеленг β.

Из-за простоты вычислений значительно увеличивается точность определения пеленгов. Кроме того, точность определения пеленгов повышается, т.к. учтена величина φ₀, которая входит в набег фаз, что и определяет значения пеленгов.

Следует отметить, что операции, имеющие место в формулах (2) и (3), не представляют большой вычислительной сложности и, соответственно, требуют малых временных затрат. Если сравнивать предлагаемый способ со способом-прототипом, то в данном случае вместо одномерного преобразования Фурье вычисляют логарифм функции, описывающей комплексную амплитуду сигнала на m-м элементе и аналитически получают формулы для непосредственного вычисления искомых величин, что также серьезно снижает вычислительную сложность, уменьшает время обработки сигнала и уменьшает ошибку в определении пеленгов.

Предлагаемый способ может применяться в совокупности с любым способом пеленгации для уменьшения вычислительных (а соответственно и временных) затрат на определение значений азимутальных и угломестных пеленгов ИРИ, т.к. вычисление произведения косинусов азимутального и угломестного пеленгов гораздо менее сложная операция, чем вычисление упомянутых пеленгов по отдельности.

Реализация изобретения:

1. Для функционирующей АС (до проведения измерений) один раз аналитически вычисляют натуральный логарифм (2) от функции, описывающей комплексную огибающую выходов элементов АС (1).

2. Измеренные комплексные амплитуды сигналов с каждого элемента АС поступают в блок вычисления натуральных логарифмов, где определяется их натуральный логарифм, затем поступают в вычислитель,

3. Аналитические выражения натурального логарифма комплексной огибающей выходов элементов АС (2) вводят в вычислитель пеленгатора, где действительные и мнимые части полученных выражений приравниваются соответственно действительным и мнимым частям натурального логарифма y_m.

4. Приходим к системе алгебраических уравнений, из которой определяются аналитические выражения для вычисления азимутального пеленга θ, угломестного пеленга β, начальной фазы сигнала φ₀.

5. Согласно формулам (3) вычисляют азимутальный пеленг θ, начальную фазу сигнала β, а затем угломестный пеленг φ₀.

6. При необходимости вычисляют дисперсии полученных значений азимутального пеленга θ, начальной фазы сигнала φ₀ и угломестного пеленга β.

Сравним результаты получаемых значений азимутального пеленга θ и угломестного пеленга β, по прототипу и предлагаемым способом, используя три элемента АС (первые три уравнения). По предлагаемому способу пеленг θ равен

$$tg\theta =\frac{p_2-p_3+p_1(\cos {\gamma }_3-\cos {\gamma }_2)}{p_1(\sin {\gamma }_2-\sin {\gamma }_3)}$$ (по прототипу: $$tg\theta =\frac{p_2-p_1\cos {\gamma }_2}{p_1\sin {\gamma }_2}$$ ).

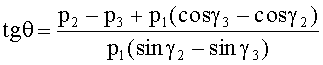
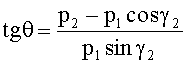
Отличие очевидно. Из формулы (3) следует, что и угломестный пеленг β будет иметь также другое значение.

Рассмотрим числовой пример.

На круговой АС радиусом 50 м на частоте 1 МГц при соотношении сигнал/шум, равном 10, зарегистрирован сигнал. На первых трех элементах-вибраторах зарегистрированы следующие фазы: P₁=35 град, P₂=P₃=45,98 град. Угол между элементами АС γ_m, равен 30 град. Подставим исходные данные в формулу

$$P_m=2\pi \frac{R}{\lambda }\cos (\theta -{\gamma }_m)\cos \beta +{\varphi }_0$$ .

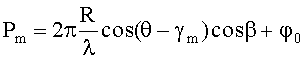
Для первого вибратора получим:

$$35=\frac{2\times 180\times 50\times {1.10}^6}{{3.10}^8}\cos \theta \cos \beta +\varphi =60\cos \theta \cos \beta +{\varphi }_0$$ .

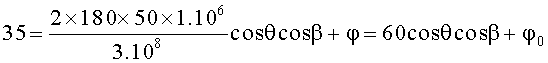
Аналогично, для второго - 45,98=60cos(θ-30)cosβ+φ₀;

для третьего - 45,98=60cos(θ-60)cosβ+φ₀.

По формулам (3) получено: θ=45 град, β=45 град, φ₀=5 град. Среднее квадратическое отклонение (СКО σ) θ равно 0,006 град, СКО σ по β равно 0,009 град.

По формулам прототипа $${\theta }_k=arctg\left\{\frac{P_2-P_1\cos \gamma }{P_1\sin \gamma }\right\}$$ и $${\beta }_k=\arccos \left\{\frac{P_1}{\cos {\theta }_k}\right\}$$ получено: θ=41,8 град, β=38,5 град. С увеличением значения φ₀ ошибка резко возрастает.

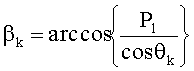
Модельный расчет пеленга проводился на компьютере с процессором с тактовой частотой 2 ГГц. Время счета порядка 0,001 с. А при ручном счете потребуется порядка 1 мин, так как в каждом измерении изменяются только P_m.

Источники информации

1. Патент RU 2151406, опубликовано 20.06.2000, МПК G01S 5/04, G01S 5/14, Н04В 17/00.

2. Патент RU 2380720, опубликовано 27.01.2010, МПК G01S 5/04.

3. Грешилов А.А. Математические методы принятия решений: Учебное пособие для вузов. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. - 584 с.

Изобретение относится к радиотехнике, в частности к односигнальной радиопеленгации источника радиоизлучения (ИРИ). Достигаемый технический результат - повышение скорости и точности определения азимутальных и угломестных составляющих пеленгов и начальной фазы сигнала ИРИ. Указанный результат достигается тем, что способ включает в себя разделение произвольной нелинейной антенной системы (АС) на логические части по элементам (вибраторам) АС. Разделение производят на n-частей, но не менее чем на три части (три элемента АС). Измеренные комплексные амплитуды сигналов, полученные с выхода каждого элемента, поступают в блок вычисления натуральных логарифмов, затем в вычислитель, куда заранее введены аналитические выражения натурального логарифма от функции, описывающей комплексную огибающую выходных сигналов элементов АС, действительные и мнимые части которой приравнивают действительным и мнимым частям натурального логарифма измеренных комплексных амплитуд сигналов, полученных с выхода каждого элемента АС. Получают систему алгебраических уравнений, из которой определяют аналитические выражения для вычисления азимутального пеленга θ, угломестного пеленга β, начальной фазы сигнала φ₀ согласно определенным матричным тригонометрическим формулам. После нахождения значений пеленга θ и начальной фазы φ₀ определяют пеленг β. Для нахождения доверительных интервалов определяемых параметров дополнительно вычисляют дисперсии D найденных значений параметров.

Способ определения азимутального и угломестного пеленгов источника радиоизлучения (ИРИ) и начальной фазы φ₀ его сигнала, включающий в себя разделение произвольной нелинейной антенной системы (АС) на логические части по элементам (вибраторам) АС, восстановление вектора комплексных амплитуд сигналов, полученных с выхода каждого элемента АС, с последующим его разделением, соответствующим логическому разделению АС, тригонометрические формулы пеленгов, по которым определяют углы пеленгов, отличающийся тем, что разделение производят на n частей, но не менее чем на три части - три элемента АС под разными углами к направлению нулевого отсчета углов γ, измеренные комплексные амплитуды сигналов, полученные с выхода каждого элемента АС, поступают в блок вычисления натуральных логарифмов, затем - в вычислитель, куда заранее введены аналитические выражения натурального логарифма от функции, описывающей комплексную огибающую выходных сигналов элементов АС, действительные и мнимые части которой приравнивают действительным и мнимым частям натурального логарифма измеренных комплексных амплитуд сигналов, полученных с выхода каждого элемента АС, получают систему алгебраических уравнений, из которой определяют аналитические выражения для вычисления азимутального пеленга θ, угломестного пеленга β, начальной фазы сигнала φ₀ согласно матричным тригонометрическим формулам

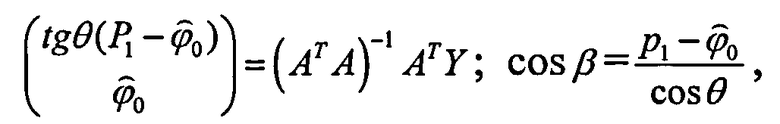
где γ_m - угол между m-ым элементом АС и направлением отсчета при m=1…n;
γ₁=0 (угол 1-го элемента AC) - начало отсчета углов γ_m;

$${\stackrel{⌢}{\phi }}_0=\frac{{\phi }_0\lambda }{2\pi R}$$ , где λ - длина волны сигналов ИРИ, R - радиус круговой АС;
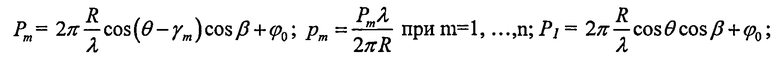
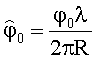
матрица 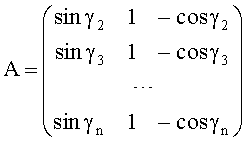$$A=\left(\begin{array}{c}\sin {\gamma }_{2}1-\cos {\gamma }_2\\ \sin {\gamma }_{3}1-\cos {\gamma }_3\\ \cdots \\ \sin {\gamma }_{n}1-\cos {\gamma }_n\end{array}\right)$$ ;
вектор-столбец 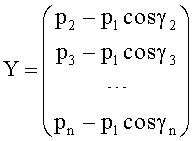$$Y=\left(\begin{array}{c}{p}_2-p_1\cos {\gamma }_2\\ p_3-p_1\cos {\gamma }_3\\ \cdots \\ p_n-p_1\cos {\gamma }_n\end{array}\right)$$ ;
после нахождения значений пеленга θ и начальной фазы φ₀ определяют пеленг β.