Область техники, к которой относится изобретение
Настоящее изобретение относится к программным вычислительным системам, основанным на коробах. В частности, изобретение относится к архитектуре вычислительной системы, использующей коробы для представления и обработки данных.
Уровень техники
Давно было обнаружено, что возможности обработки информации традиционных вычислительных систем значительно отличаются от возможностей обработки информации животного интеллекта, в том числе человеческого интеллекта. Живые системы животного интеллекта лидерствуют при решении задач за счет обращения к аналогиям с прошлым опытом. Традиционные цифровые вычислительные системы лидерствуют при следовании некоторой последовательности шагов для достижения результата. Традиционные аналоговые вычислительные системы лидерствуют в очень специфических вычислительных задачах, а именно тех, которые содержат решение дифференциальных уравнений. Традиционные связывающие вычислительные системы лидерствуют в выполнении интерполяций из одного многомерного пространства в другое на основании примеров, связывающих два пространства по точкам. Традиционные вычислительные системы, в целом сгруппированные под термином "системы искусственного интеллекта", в действительности пытаются эмулировать возможности обработки, имеющиеся у животного интеллекта, но успешность таких попыток ограничена.
Возможности живых систем животного интеллекта обрабатывать информацию являются аналоговыми и очень надежными по своей природе. Такие системы лидерствуют в видении и выполнении того, что аналогично виденному и выполненному ранее, и весьма снисходительны к ошибкам в данных. Термин "коррелитм" часто используется для родового описания процессов, в которых лидерствуют живые системы обработки информации, чтобы отличать их от алгоритмов, т.е. процессов, для которых лидерствуют традиционные системы обработки информации. Построение вычислительных систем, способных приблизиться или повторить эти и прочие уникальные возможности живых систем по обработке информации, было одной из наиболее сложных и наиболее интенсивно преследуемых целей исследований и разработок в течение всей истории искусственных вычислительных систем, и все же результаты на сегодняшний день скудны.
Возможности традиционных вычислительных систем несравненно ниже при решении тех типов задач, с которыми особенно успешно справляются живые вычислительные системы.
Традиционные цифровые вычислительные системы исключительно точны, но неустойчивы. Вычисления в этих системах выполняются посредством изящно оркестрованной последовательности дискретных шагов, включая точные данные. Ошибки всего лишь в единственном бите - минимальной единице различения данных в этих системах - в последовательности ли шагов или в данных, часто делает результат вычисления бесполезным. Мощные усилия в течение многих лет были направлены как на системы аппаратного обеспечения, так и на программное обеспечение, которое исполняется этим аппаратным обеспечением, чтобы избежать или минимизировать такие ошибки. Точность таких традиционных цифровых вычислительных систем и успешность предотвращения неустойчивости исполнения, обусловленной такой точностью, являются ключевыми величинами в развитии цифровой вычислительной индустрии. Точность и неустойчивость, однако, очень далеки от надежной аналоговой обработки информации в живых системах.
Обычно традиционные аналоговые вычислительные системы используются для решения математических уравнений, в частности, дифференциальных уравнений, путем исследования. Выполненные в виде электронных схем эквиваленты таких математических операторов, как сложение, умножение, взятие интеграла и так далее, взаимосвязаны для выработки общего электронного эквивалента конкретного уравнения. Путем варьирования параметров отдельных схем общий электронный эквивалент эмпирически исследует характеристики уравнения, которое он реализует. Хотя аналоговые вычислительные системы обеспечивают в высшей степени полезные функциональные возможности, ясно, что типы вычислений, которые можно приспособить к этой форме вычислений, чрезвычайно специфичны и ограничены. Кроме того, живые системы не очень функциональны при решении уравнений. Поэтому не представляется вероятным, чтобы аналоговые компьютеры могли бы внести значительный вклад в попытку воспроизведения живых систем обработки информации, и в действительности на сегодняшний день аналоговые компьютеры не сделали такого вклада.
Как класс, традиционные связывающие вычислительные системы функционируют в качестве систем интерполяции. Интерполяционные функции, обеспечиваемые многими связывающими системами, берутся из конкретных примеров, называемых "обучающим множеством", которое перечисляет точки в области определения функции интерполяции и для каждой из этих точек указывает единственную точку изображения в области значений функции интерполяции. Другие связывающие системы используют обучающее множество, состоящее только из точек области определения, вырабатывая свои собственные единственные и пригодные точки области значений для каждой из точек области определения. Подробности архитектур, конструкций и операций связывающих систем широко варьируются, как и средства, используемые каждой из таких систем для выработки приемлемых функций интерполяции из обучающих множеств. Для каждого обучающего множества обычно существует много альтернативных связывающих систем, которые обеспечат практически эквивалентные результаты, но в конце концов, все связывающие вычислительные системы обеспечивают приемлемое математическое отображение из одного многомерного пространства в другое.
Связывающие системы показали обеспечение очень полезных функциональных возможностей, которые на самом деле могут быть аналогичны определенным низкоуровневым элементам систем животного интеллекта, но сложно прогнозировать, что появится что-либо подобное полному диапазону возможностей обработки информации животного интеллекта только из функциональных возможностей связывающих систем.
Традиционно компьютерные системы, сгруппированные под термином "искусственный интеллект", сфокусированы непосредственно на попытках дублирования или приближения к различным характеристикам обработки информации систем животного интеллекта. Аспекты области искусственного интеллекта содержат экспертные системы, распознавание образов, робототехнику, эвристику и различные технологии структурирования, сортировки и поиска данных. Было сделано так много впечатляющих ошибок в зафиксированной истории этого вопроса, что сегодня большинство ученых смотрят на искусственный интеллект с некоторым скептицизмом. Несмотря на то, что были достигнуты ограниченные успехи, остается верным часто произносимая сентенция о том, что "эти системы работают в тех случаях, для которых они разработаны, в противном случае они ошибаются". В основе ошибок лежит тот факт, что традиционно практикуемая технология искусственного интеллекта весьма неустойчива. Не хватает именно некоторых надежных аналоговых способностей, всегда имеющихся в изобилии в живых системах обработки информации. Это кажется странным, учитывая предпринимаемые в течение долгих лет расширяющиеся попытки приблизиться к системам искусственного интеллекта, но это подчеркивает тот непреклонный факт, что вся компьютерная промышленность не достигает поставленных перед ней целей.
Сегодня точно неизвестно, как представляются, хранятся и обрабатываются данные в живых системах обработки информации. Работа по раскрытию этих секретов активно велась в течение многих лет и была в основном сфокусирована на биохимических, нейрофизиологических и структурных аспектах живых нейросистем. В ходе этой работы были идентифицированы некоторые ограниченные вычислительные механизмы, но не было описано никаких математических структур данных для родового представления информации в живых нейросистемах, не было выстроено общей теории манипуляций данными и вычислений в живых нейросистемах, и, что наиболее важно, не создано приемлимой общей теории, которая описывала бы вычислительные возможности систем животного интеллекта способами, которые достаточны для поддержания разработки новых неживых систем, способных проявлять подобные характеристики обработки информации.
Объекты изобретения
Соответственно, общей целью данного настоящего изобретения является обеспечение архитектуры (структуры) вычислительной системы, которая преодолевает недостатки известного уровня техники.
Подобным же образом, целью настоящего изобретения является обеспечение архитектуры (структуры) для вычислительной системы, вычислительные достоинства которой лежат в областях, подобных областям вычислительных достоинств живых систем обработки информации.
Еще одной целью настоящего изобретения является обеспечение архитектуры вычислительной системы, которая в большой мере увеличивает аналоговые функциональные возможности, способность системы "видеть и делать" подобно "виденному и деланному" в прошлом.
Дополнительной целью настоящего изобретения является обеспечение архитектуры вычислительной системы, которая в значительной мере увеличивает надежность, устойчивость к ошибкам в очень широком диапазоне задач по обработке информации.
Дополнительной целью настоящего изобретения является обеспечение компонентов, несущих преимущества коробов, уникальных математических и вычислительных объектов данных, которые автор настоящего изобретения открыл и которые могут являться надежной основой функциональных возможностей живых систем обработки информации.
Дополнительной целью настоящего изобретения является обеспечение архитектуры (структуры) вычислительной системы, использующей коробы.
Дополнительной целью настоящего изобретения является обеспечение архитектуры (структуры) основанной на коробах вычислительной системы, являющейся "совершенной машиной Тьюринга", т.е. способной воплощать любую вычислимую функцию, ограничиваясь только объемом физической памяти и временем.
Дополнительной целью настоящего изобретения является обеспечение средства для использования коробов в качестве структур данных.
Дополнительной целью настоящего изобретения является обеспечение средства для выполнения обработки информации с помощью коробов.
Дополнительной целью настоящего изобретения является обеспечение средства для выполнения параллельной обработки с помощью коробов.
Прочие цели и преимущества изобретения очевидны для специалистов данной области техники после прочтения последующего описания и прилагаемой формулы изобретения, и при обращении к сопровождающим чертежам.
Сущность изобретения
Автор настоящего изобретения обнаружил, что очень простой конструкт, "короб", имеет важные вычислительные свойства, не являющиеся очевидными, и поддерживающие новую парадигму для вычислений, которая обладает новыми вычислительными преимуществами в коррелитмах, а именно в тех областях вычислений, которые ранее считались областью живых систем обработки информации. Настоящее изобретение раскрывает архитектуру (структуру) вычислительной системы, реализующую эту новую вычислительную парадигму и осуществляющую доступ к этим новым вычислительным преимуществам.
Цели изобретения достигаются с помощью структуры вычислительной системы, реализующей новую вычислительную парадигму путем использования коробов в качестве первичных структур данных для представления и манипулирования информацией и, тем самым, использования преимущества математических и вычислительных свойств коробов, которые открыл автор настоящего изобретения, описывается конструкт, пригодный для содержания короба для дальнейшего использования. Определяется низкоуровневый компонент архитектуры, называемый "ячейка", функция которого заключается в отображении входных коробов в значения выходного состояния способом, согласующимся с коробами и со связанными значениями состояния, ранее хранившимися этой ячейкой. Ячейки объединяются в вычислительную структуру, которая поддерживает определение взаимосвязей между ячейками так, что текущее состояние любой ячейки может обеспечивать компонент входного короба любой ячейки в вычислительной системе. Вход вычислительной системы достигается посредством влияющих значений состояния конкретизированных "входных" ячеек. Выход системы подобным же образом достигается извлечением значений состояния конкретизированных "выходных" ячеек.
В соответствии с настоящим изобретением структура основанной на коробах вычислительной системы является очень гибкой. Заданная основанная на коробах вычислительная система состоит из определенного количества доступных ячеек. Все основанные на коробах вычислительные системы могут поддерживать три различных фазы программирования и использования: фазу архитектуры, фазу обучения и фазу работы.
Практические следствия использования коробов в вычислениях означают, что многие долгое время недостижимые свойства живых систем обработки информации теперь становятся доступными в уже готовом виде. Эти свойства включают в себя способность, подобно животным, видеть и делать подобное виденному и деланному в прошлом, новую надежность, доступную всем вычислимым по Тьюрингу процессам, новую форму параллельного вычисления и новый класс аналоговых компьютеров общего назначения. Путем реализации новой вычислительной парадигмы настоящее изобретение не только обеспечивает вычислительные преимущества в областях, ранее являвшихся сферой живых систем обработки информации, но и обещает обобщить всю традиционную науку о компьютерах путем решения давно стоящей проблемы буквального мышления и неустойчивости всех компьютерных систем.
Выводы являются как широкими и далеко идущими, так и прямыми и непосредственными. Данная технология обещает непосредственный прорыв не только в компьютерной науке, но и в понимании живых систем обработки информации. Ожидается вклад в такие области, как нейрофизиология, нейроанатомия и биохимия. Данная технология также обещает значимые новые результаты во многих других областях, в том числе в математике, психологии и даже социологии.
Краткое описание чертежей
Фиг.1 является схематическим представлением живого нейрона.
Фиг.2 является схематическим представлением приспособления, посредством которого нейроны передают переменные своего состояния одному нейрону.
Фиг.3 является схематическим чертежом, иллюстрирующим главные компоненты ячейки короба по настоящему изобретению.
Фиг.4 является схематическим чертежом, иллюстрирующим главные компоненты короб-вычислительной системы по настоящему изобретению.
Ссылочные позиции на чертежах
12 тело ячейки
14 аксон
16 входные дендриты
18 выходные дендриты
20 первый входной нейрон
21 множество входных нейронов
22 второй входной нейрон
24 последний входной нейрон
26 нейрон
28 линия выходных данных
40 входной регистр короба
42 управляющий элемент
44 память короба
46 регистр выходного состояния
50 массив ячеек короба
52 средство отображения
54 сенсорные ячейки
56 ячейки актора
Подробное описание изобретения
Последующее подробное описание обеспечит более полное понимание данного изобретения. Однако описанное ниже выполнение является лишь примером реализации изобретения, и изобретение не ограничивается этим выполнением. Будет понятно, что структура по настоящему изобретению может быть реализована с помощью различных конфигураций процессоров при помощи подходящей модификации. Соответственно, конкретная конфигурация описанного ниже процессора обеспечивает неограничительный пример реализации настоящего изобретения. Будет далее понятно, что в некоторых условиях могут быть опущены подробности, необязательные для понимания сущности настоящего изобретения.
Словарь терминов
Для простоты ссылок ниже определяются термины, использованные в описании настоящего изобретения. Как очевидно для специалистов, определения содержат как принятые стандартные значения, так и расширенные значения в случае необходимости. Даются следующие определения:
потенциал действия: импульс в аксоне живого нейрона,
актор: сокращенный термин для понятия "действующая ячейка" (клетка) (actor cell). Действующие ячейки обеспечивают средство, которым внешнее средство может считывать данные из короб-вычислительной системы,
животный интеллект: функциональные возможности живой системы обработки информации,
архитектура, фаза архитектуры: в основанной на коробах вычислительной системе - процесс определения того, какая из ячеек короба, если такие существуют, установлена для выполнения функции сенсорных ячеек, и какая установлена для выполнения функции действующих ячеек, и какие из ячеек короба обеспечивают входные данные для ячеек короба;
ассоциация: составление пары из короба в пространстве с произвольным, но конкретным объектом данных, обычно внутри системы памяти короба;
ограниченное пространство: многомерный куб или гиперпрямоугольник,
емкость (системы короба): количество равноудаленных коробов, для которых система может выступать в роли ведущей без ухудшения общей равноудаленности системы более, чем на заданный коэффициент ухудшения,
декартова метрика расстояний: квадратный корень из суммы квадратов разностей в каждом измерении между двумя коробами, подходящим образом распространенное на дробную природу размеров обобщенных подпространств короба,
ячейка, ячейка короба: основанная на коробах модель живого нейрона, архитектурный конструкт настоящего изобретения,
короб (corob): первичная структура представления данных и манипуляций ими в короб-системах. Выражение "Короб" представляет собой сокращение из слов "КОРрелитмический ОБъект". Точка в обобщенном подпространстве частного пространства. А также архитектурный конструкт - т.е. область данных короба - по настоящему изобретению, пригодный для содержания данных короба, когда использование ясно из контекста,
область данных короб-вычислительной системы: архитектурный конструкт по настоящему изобретению, пригодный для содержания данных короб-вычислительной системы,
область данных ячейки короба: архитектурный конструкт по настоящему изобретению, пригодный для содержания данных ячейки короба,
область данных короба: архитектурный конструкт по настоящему изобретению, пригодный для содержания данных короба,
система памяти короба: система памяти, в которой коробы в пространстве спарены с произвольными, но конкретными объектами данных в ассоциации, так что коробы могут представлять ассоциированные произвольные объекты данных, архитектурный конструкт по настоящему изобретению,
область данных системы памяти короба: архитектурный конструкт по настоящему изобретению, пригодный для содержания данных системы памяти короба,
метрика короба: метрика, которая, будучи примененной для измерения расстояния от короба до другого короба того же пространства, дает расстояние, монотонно связанное с расстоянием, даваемым декартовым измерением в том же направлении между теми же двумя коробами. Метрика короба может быть реализована посредством нейронной сети,
короб-система, короб-вычислительная система: вычислительная система, основанная на ячейках короба, которая может являться, а может и не являться совершенной машиной Тьюринга, архитектурный конструкт по настоящему изобретению,
архитектура короб-системы: структуры, функциональные возможности и прочие релевантные детали систем, использующих коробы в качестве средства представления данных или манипулирования ими,
коррелитм [комбинация КОРРЕЛяция + алгорИТМ]: любой систематический способ решения задач с помощью подобий известным примерам. Традиционные системы обработки информации функциональны в алгоритмических, или процедурно-ориентированных вычислениях, живые системы обработки информации функциональны в коррелитмических, или ориентированных на аналогию вычислениях,
текущий короб: короб, присутствующий в текущий момент во входном регистре ячейки короба, короб, который ячейка короба сопрягает со своей памятью короба,
определенный короб: короб, элементы которого установлены процессом, отличным от случайного. Определенные коробы обычно возникают из представлений внешних сенсоров и акторов,
коэффициент ухудшения: заданное число, отклонение от свойства равноудаленности в короб-системе, которое достигается, когда количество равноудаленных коробов, равное емкости системы, добавлено к системе,
домен: множество ячеек, обеспечивающих входные данные,
обучение, фаза обучения: в основанной на коробах вычислительной системе - процесс инсталляции соответствующих данных, состоящих из пар короб-состояние, в различные памяти короба. Термин "статическое обучение" подразумевает одноразовую инициализацию памятей короба, обычно во время фазы обучения, в то время как термин "динамическое обучение" подразумевает процесс разрешения основанной на коробах вычислительной системе решать для себя автоматически, какие данные, состоящие из пар короб-состояние, пригодны для хранения в различных памятях короба, обычно во время фазы действия,
элемент (короба): короб является вектором элементов. Элементы могут быть отдельными числами любого типа, в том числе одноразрядными двоичными числами, натуральными числами, целыми числами, действительными числами, комплексными числами и так далее, либо элементы могут быть более сложными, содержащими пары чисел, группы чисел или другие объекты данных,
функция среды: любая функциональная возможность, принимающая данные от ячеек актора короб-системы, обрабатывающая их и представляющая данные сенсорным ячейкам короб-системы,
равноудаленность: свойство не связанных другим образом коробов частного (отдельно взятого) пространства. Если верно, что порядки обобщенных подпространств этих коробов приблизительно одинаковы, то декартово измерение расстояний стремится к рефлексивности, а расстояние от любого одного из этих коробов до любого другого, измеренное этой метрикой, в сильной степени стремится к стандартному расстоянию. В этом случае рассматриваемые коробы называются "равноудаленными",
исполнение: по отношению к ячейке короба - процесс генерирования нового значения в выходном состоянии ячейки, в свете текущего содержания выходного короба ячейки и памяти короба ячейки. Может выполняться интерполяцией, как в предпочтительной форме реализации изобретения, или с помощью любой традиционной искусственной нейронной сети. Важными являются использование коробов и необходимые функциональные возможности, а не конкретное средство, которое может иметь много эквивалентов,
полное множество ячеек, полное множество: в основанной на коробах вычислительной системе - полный набор ячеек короба, которые доступны для системы, а именно, все внутренние ячейки,
обобщенное подпространство: подпространство S1 пространства S2, состоящее из всех измерений S2, каждое взвешено посредством дроби из диапазона от 0,0 до 1,0 включительно,
главное пространство: частное пространство, в котором определяются обобщенные подпространства, которые содержат точки, представляющие коробы, иначе говоря, частное пространство, в котором определено (имеется) заданное множество коробов,
входная ячейка: любая из ячеек короба основанной на коробах вычислительной системы, которые установлены в качестве сенсорных ячеек,
внутренняя ячейка: в основанной на коробах вычислительной системе - любая из полного набора ячеек короба, доступная системе,
обучение: по отношению к ячейке короба - процесс обновления памяти короба в ячейке путем ассоциации входного короба ячейки с выходным состоянием ячейки. Отметим, что обучение в этом контексте может выполняться путем использования режима обучения любой традиционной искусственной нейронной сети. Для короб-систем важны использование коробов и функциональные возможности памяти короба,
живая вычислительная система: другое название живой системы обработки информации,
живая система обработки информации: та часть живой системы, которая направлена на обработку информации,
живой интеллект: возможности обработки информации живых нейросистем,
живой нейрон: строительный блок живой системы обработки информации,
механизм (например, в сочетании "механизм короба"):
процесс или процедура, единственным образом пригодная для воплощения в короб-вычислительных системах; механизмы в короб-вычислительных системах являются аналогами программ в традиционных вычислительных системах,
метрика: сообразное средство, формула или критерий измерения; метрика является сообразной математической основой для измерения некоторого количества,
действие, фаза действия: та часть программирования и использования основанной на коробах вычислительной системы, которая состоит из непрерывной итерации компонентов системы. Фаза действия в короб-вычислительных системах сравнима с непрерывным процессом исполнения в традиционных вычислительных системах,
порядок (обобщенного подпространства): сумма взвешивающих дробей подпространства,
выходная ячейка: любая из ячеек короба основанной на коробах вычислительной системы, установленных в качестве ячеек актора,
случайный короб: короб, для которого точка, которую он представляет, и, возможно, его подпространство, если таковое есть, выбирается случайным образом. Более обобщенно: короб, элементы которого в большой степени нескоррелированы друг с другом, особенно во времени,
случайное состояние: состояние, внутреннее значение или значения которого выбираются случайным образом,
случайное блуждание: любой статистический процесс, вырабатывающий последовательность чисел, в которой близость к последовательности приводит к увеличенной корреляции,
рефлексивность (свойство): математическая концепция, связанная с оператором, таким, как знак "=", по которой А=В предполагает В=А, и наоборот. Декартово измерение расстояний не является по сути рефлексивным, хотя см. равноудаленность,
скалярная тяжесть: способ интерполяции, способ взвешивания элементов интерполированного значения путем взятия обратных квадратов метрических расстояний до примерных точек. Назван так по аналогии со способом убывания силы тяготения пропорционально квадрату расстояния и отсутствием информации о направлении или векторе этой силы. Скалярная тяжесть дает результаты интерполяции, очень похожие на результаты, получаемые широким диапазоном так называемых "нейронно-сетевых" способов интерполяции,
сенсор: сокращенный термин для "сенсорной ячейки". Сенсорная ячейка может иметь свое значение состояния, которое устанавливается или на которое оказывается воздействие с помощью средства, внешнего по отношению к короб-вычислительной системе. Сенсорные ячейки обеспечивают средство, с помощью которого внешние данные могут быть внесены в короб-вычислительную систему,
значимость: название, в целом даваемое взвешивающей дроби в каждом направлении обобщенного подпространства пространства,
пространство: геометрический объект, состоящий из нуля или более измерений,
стандартное расстояние: ожидаемое расстояние, обычно выраженное в числах среднеквадратичных отклонений, от короба, выбранного случайным образом, до другого короба, выбранного случайным образом, в пространстве,
состояние: единственный элемент короба,
область данных состояния: архитектурный конструкт по настоящему изобретению, пригодный для содержания данных одного измерения короба,
строковый короб: если список случайных при прочих условиях коробов генерируется способом, который удовлетворяет условию, что коробы, более близкие друг к другу в пронумерованном порядке списка коробов, также являются более близкими друг к другу в применяемой метрике расстояния, и, наоборот, коробы, более далекие в пронумерованном порядке списка коробов, также являются более далекими друг от друга в применяемой метрике расстояния, то такой список в целом называется "строковым коробом",
подпространство: пространство S1, которое состоит из некоторых или всех измерений другого пространства S2, как в выражении "S1 является подпространством S2",
пороговая модель: традиционная модель живого нейрона,
совершенная машина Тьюринга: термин, применяющийся к любой вычислительной системе, которая может вычислять любую вычислимую функцию, ограничиваясь только временем и объемом памяти,
взвешивающая дробь: в обобщенном подпространстве - число между 0,0 и 1,0 включительно, которое показывает степень участия отдельного измерения подпространства в соответствующем измерении содержащего пространства.
Введение
Для понимания сущности настоящего изобретения необходимо понимать архитектуру короб-системы. Для понимания архитектуры короб-системы необходимо понимать ячейку, т.е. фундаментальный стандартный блок архитектуры короб-системы. Для понимания ячейки необходимо понимание короба, т.е. первичной единицы представления данных и манипуляций ими в короб-системах. Для понимания короба необходимо понимать модель живых нейронных систем, из которых был выведен короб и архитектура короб-системы. Поэтому автор изобретения обращается к этим понятиям в обратном порядке, начиная с живых нейронных систем.
Живые нейронные системы
Упрощенное схематическое представление живого нейрона, известное специалистам, представлено на фиг.1. Живой нейрон по фиг.1 содержит, по меньшей мере, тело 12 ячейки, аксон 14, входные дендриты 16 и выходные дендриты 18. Живой нейрон по фиг.1 очевидно является прибором, который некоторым образом принимает входное воздействие от других живых нейронов через входные дендриты 16, преобразует это входное воздействие в переменную состояния посредством плохо понимаемого процесса, выражает эту переменную состояния в виде сигнала на аксоне 14, который проводит ее к выходным дендритам 18, а затем на входные дендриты других живых нейронов.
Традиционная модель живого нейрона называется "пороговой моделью". В пороговой модели формируется взвешенная сумма входных сигналов во входных дендритах 16, а затем сравнивается с пороговым значением. Если взвешенная сумма превышает пороговое значение, то на аксоне 14 появляется импульс, называемый "потенциалом действия"; в противном случае потенциал действия не вырабатывается. Если потенциал действия вырабатывается, он проводится аксоном 14 к выходным дендритам 18, где он представляется в качестве входа для других живых нейронов.
Наличие или отсутствие потенциала действия в аксоне 14 живого нейрона по фиг.1 традиционно предполагается при описании состояния живого нейрона по фиг.1.
Огромные усилия были предприняты для биохимического и нейрофизиологического понимания функционирования живых нейронов. Традиционная пороговая модель продолжает существовать сегодня в качестве одной из первичных моделей для описания функционирования живого нейрона.
В 1968 году в диссертации в Массачусеттском Технологическом Институте автор изобретения описал альтернативную модель живого нейрона. Подробности этой альтернативной модели несущественны для понимания настоящего изобретения, за исключением одного момента. В этой альтернативной модели интенсивность потенциалов действия в аксоне 14 содержит переменную состояния для живого нейрона. Интенсивность потенциалов действия, определяемая разнесением между потенциалами действия, бралась стандартным образом, знакомым специалистам по теории модуляции, в качестве некоего вида фазово-импульсной модуляции, т.е. непрерывной переменной состояния, сильно отличающейся от дискретной переменной состояния, предполагаемой при рассмотрении каждого потенциала действия отдельно, как это делалось в традиционной модели.
Далее в этой диссертации автор изобретения показал, что его альтернативная модель живого нейрона может дублировать все функции, обеспечиваемые традиционной моделью живого нейрона. Хотя его альтернативная модель не вводила фундаментально новых возможностей, она все же обеспечила новый взгляд на функциональные возможности нейрона, который упростил понимание и описание таких непрерывных функций в живых нейронных системах, как пропорциональное управление мышцами.
В настоящем изобретении ячейка, которая будет вкратце описана, функционирует как аналог живого нейрона. В соответствии с альтернативной моделью живого нейрона, состояние ячейки следует принимать в качестве непрерывной переменной. Живые нейроны обладают минимальной и максимальной интенсивностью потенциала действия. Соответственно, автор изобретения ограничивает диапазон этой непрерывной переменной, которая является состоянием ячейки. Это удобно и не дает в результате потери целостности, если представить этот диапазон как диапазон от 0,0 до 1,0 включая как 0,0, так и 1,0, а также все значения между ними. Значение 0,0 представляет минимальную переменную состояния ячейки, в то время как значение 1,0 представляет максимальную переменную состояния ячейки.
Следует отметить, что, хотя предпочтительный вариант выполнения настоящего изобретения и позволяет переменной состояния ячейки принимать любое значение из только что описанного диапазона, иногда полезно ограничивать допустимые значения заданным количеством дискретных значений. Если переменная состояния представлена непрерывным по своей природе физическим свойством, таким как напряжение, то переменная состояния также будет непрерывной. Если переменная состояния представлена, например, элементом данных в программе, то она может быть более дискретной. Например, число с плавающей запятой имеет конечное количество различных представлений в заданном цифровом компьютере. Целое число обычно имеет еще меньше различных представлений в заданном цифровом компьютере, чем число с плавающей запятой. Оба этих типа данных полезны при представлении переменной состояния. В некоторых случаях полезна также двоичная форма, при которой переменная состояния может принимать одно из только двух значений - 0 и 1. Обычно более дискретные представления переменной состояния обеспечивают более быстрое исполнение в цифровых компьютерах. Разумеется, прямое представление переменной состояния посредством непрерывного по своей природе физического свойства, такого как напряжение, может на самом деле обеспечить более быстрое исполнение, чем любая цифровая реализация, в зависимости от специфики реализации.
Коробы
Короб является первичной структурой представления данных и манипуляций ими в короб-системе. Коробы выведены как результат из обучения живых систем обработки информации. Простая математическая модель раскрыла некоторые неожиданные свойства. Настоящее изобретение основано на этих самых свойствах.
По фиг.1 живой нейрон получает входное воздействие от других живых нейронов через свои входные дендриты 16. Предположительно, входное значение, подаваемое любым из входных нейронов, является значением состояния этого нейрона. Как указано ранее, автор изобретения будет считать такие значения состояния непрерывными переменными в диапазоне от 0,0 до 1,0 включительно.
Взаимодействие этих нейронов может быть схематически представлено по фиг.2. Множество 21 входных нейронов состоит из множества отдельных нейронов, схематически показанных как нейроны 20, 22 и 24, с дополнительными нейронами, не показанными, но обозначенными тремя вертикальными точками во множестве 21 входных нейронов. Каждый нейрон во множестве 21 входных нейронов поставляет переменную своего состояния нейрону 26, который обрабатывает эти переменные состояния нижеописанным способом для получения своей собственной переменной состояния в качестве выходных данных на линии 28 выходных данных.
При отсутствии дополнительной информации переменные состояния нейронов множества 21 входных нейронов могут рассматриваться как независимые в статистическом смысле. В живых нейронных системах, вероятно, на самом деле существуют связи между нейронами во множестве 21 входных нейронов, которые не показаны на фиг.2, однако в качестве первого приближения разумно предположить статистическую независимость. Даже если статистическая независимость не является полной, все же до тех пор, пока статистическая независимость переменных состояния во множестве 21 входных нейронов большей частью истинна, могут быть установлены полезные свойства коробов. На самом деле многие полезные свойства коробов могут быть установлены, даже если переменным состояния множества 21 входных нейронов человек умышленно присвоит конкретные значения. Эти свойства коробов, используемые настоящим изобретением, являются очень устойчивыми.
Для понимания того, что представляют собой эти свойства коробов, как они возникают и, разумеется, что именно описывает термин "короб", представим переменные состояния множества 21 входных нейронов в виде вектора чисел, которые все находятся в диапазоне от 0,0 до 1,0 включительно. Эти переменные состояния множества 21 входных нейронов могут эквивалентно описываться в виде многомерного единичного куба. Частный (отдельно взятый) вектор, т.е. вектор, содержащий частные значения в каждом из своих элементов, может затем приравниваться к единственной математической точке в многомерном единичном кубе. Термин "ограниченное пространство" может альтернативно использоваться для описания ограниченной многомерной области, в которой каждое измерение имеет верхнее и нижнее предельное значение, как у только что описанного многомерного единичного куба. Поскольку подразумевается граничное значение в каждом измерении (по каждой оси) пространства, вместо термина "ограниченное пространство" может использоваться термин "пространство".
Дополнительным термином, который автору изобретения потребуется, является термин "подпространство", который представляет собой пространство, состоящее из некоторых или всех измерений (размерностей) другого пространства. Отметим, что подпространство S1 пространства S2 может состоять точно из всех измерений S2 или только некоторых из них. Если оно состоит из всех измерений, то корректно говорить, что "S1 является подпространством S2" или "S2 является подпространством S1": пространства S1 и S2 идентичны. Если S1 состоит из меньшего количества измерений, чем S2, то S1 является подпространством S2, но S2 не является подпространством S1.
Здесь требуется обобщение термина "подпространство", которое обычно нечасто используется в традиционной работе с пространствами, хотя известен специалистам. Обычно каждое измерение пространства S2 либо является измерением подпространства S1, либо нет. Другими словами, наличие измерения S2 в S1 является альтернативным решением: оно либо присутствует, либо нет. Обобщение этого обеспечивает частичное наличие измерений (размерностей) S2 в S1. В качестве конкретного примера предположим, что S2 состоит из десяти измерений, пронумерованных от 1 до 10 (10-мерное пространство). В двоичном случае подпространство S1 может быть задано, как содержащее точно измерения S2, пронумерованные от 1 до 5. В более общем дробном случае эта ситуация могла быть описана так, что S1 состоит из измерений от 1 до 5, каждое из которых взвешено дробью 1,0, а измерения от 6 до 10 взвешены дробью 0,0. Другими словами, в более общем смысле подпространство S1 состоит из всех измерений пространства S2, взвешенных дробями от 0,0 до 1,0 включительно. В качестве дополнительного примера, при этом обобщении можно было бы описать подпространство S3 пространства S2, в котором измерения от 1 до 3 взвешены дробью 1,0, измерения от 4 до 7 взвешены дробью 0,5, а измерения от 8 до 10 взвешены дробью 0,0. Это обобщение концепции подпространства необходимо для описания предпочтительного выполнения настоящего изобретения.
Теперь "короб" может быть задан в качестве точки в обобщенном подпространстве частного пространства.
"Порядок" обобщенного подпространства задается как сумма взвешивающих дробей. Если все такие дроби равны либо 1,0, либо 0,0, то это определение согласуется с более знакомым значением порядка подпространства, а именно с количеством измерений (размерностей).
Коробы любых размерностей полезны, хотя существует компромисс. Коробы меньших размерностей имеют меньшие требования к хранению и обработке, но также дают в результате более слабые свойства короба, чем это может быть необходимо для конкретного применения, в то время как коробы больших размерностей обеспечивают достаточно сильные для большинства требований свойства за счет повышенных требований к хранению и обработке. Размерности коробов менее пяти имеют ограниченную применимость. Размерности коробов от 50 до 100 успешно применялись для широкого спектра приложений. Размерности выше 100 полезны в сложных ситуациях.
Следующим необходимым автору изобретения для продолжения описания природы коробов концептом является концепт метрики расстояний между коробами. Термин "метрика" описывает очень широкий научный концепт, подходящее средство, формулу или критерий измерения. Полное формальное описание термина "метрика" здесь не нужно. Неформально метрика представляет собой подходящую математическую основу для измерения некоторого количества.
Количеством, которое требуется измерять, является расстояние между двумя коробами. Одной из простейших форм метрики, удовлетворяющей данной цели, называется метрика "декартовых расстояний", которая задается как квадратный корень из суммы квадратов разностей в каждом направлении между коробами, с подходящими расширениями для работы с дробной природой измерений обобщенных подпространств короба. Метрика декартовых расстояний является метрикой, выбранной для предпочтительного вида реализации настоящего изобретения. В этих целях может также использоваться большое количество других метрик. Требуется только, чтобы применение выбранной метрики к парам коробов обязательно приводило к свойствам короба, которые следует кратко обсудить. Обычно это будет делать любая функциональная форма метрики при применении для измерения расстояния от одного короба до другого короба того же пространства, давая в результате расстояние, которое монотонно связано с расстоянием, полученным посредством метрики декартовых расстояний в том же направлении между теми же двумя коробами. Это описание класса метрик, пригодных для использования с коробами и короб-системами, будет понятно для любого специалиста в математических метриках.
Предпочтительная форма метрики декартовых расстояний для измерения расстояния от короба С1 до короба С2, расширенная для текущих целей, задается следующим образом. Предположим, что S1 и S2 являются обобщенными подпространствами пространства S. Предположим, что два короба С1 и С2 заданы в S1 и S2 соответственно. Возьмем С1. В соответствии с определениями в каждом измерении i из N измерений пространства S, где i принимает все целые значения от 1 до N, C1 будет иметь точечное значение vli между 0,0 и 1,0 включительно, и связанную с ним взвешивающую дробь, или "значимость", sli, которая также находится между 0,0 и 1,0 включительно. Подобным же образом С2 будет иметь значение v2i в каждом измерении i. Для каждого измерения i зададим разность xi как (v2i-v1i). Затем просуммируем произведение (sli·xi·xi) no i и возьмем квадратный корень от всей суммы. Результат является предпочтительным видом метрики декартовых расстояний для настоящего изобретения, хотя, как отмечалось ранее, вместо нее могут использоваться многочисленные другие метрики.
Отметим, что это определение содержит значимости или взвешивания измерения подпространства короба C1, но не содержит этих характеристик короба С2. Это невозвратное задание метрики вытекает из обращения к подпространствам S1 и S2, которые не являются идентичными. При ближайшем рассмотрении оно вполне интуитивно.
Во-первых, возьмем случай, в котором все значения "s" короба С1 в S1 равны либо 1,0, либо 0,0. Для измерений (координатных осей), в которых данное значение "s" равно 1,0, выражение (sli·xi·xi) превращается просто в (xi·xi), или в квадрат разности в этом измерении. Когда значение "s" равно 0,0, это выражение равно нулю. Квадратный корень суммы этих выражений в этом случае является просто известной многомерной декартовой диагональю.
Если S2 идентично S1, то С1 сравнивается с хорошо определенной точкой в С2, поскольку все полностью действительные (у которых sli=1,0) измерения С1 тождественны всем полностью действительным (у которых sli=1,0) измерениям С2. Если С2 на самом деле является тем же идентичным С1 коробом, что означает, что оба подпространства S1 и S2 тождественны, и обе точки С1 и С2 тождественны внутри этих подпространств, то применение этой метрики приводит к расстоянию, равному 0,0, т.е. минимально возможному расстоянию между двумя коробами.
Если для каждого полностью действительного (у которого s1i=1,0) измерения С1 соответствующее измерение С2 полностью недействительно (s1i=0,0), то точка, представленная коробом С1, лежит в подпространстве S1, которое отделено от подпространства S2 и, следовательно, от короба С2. Короб С1, таким образом, будет сравниваться со всеми значениями, которые могут появиться среди значений С2 в соответствующих, но недействительных измерений S2. На первый взгляд это может показаться бессмысленным, но как скоро будет показано, это на самом деле весьма ценно. Результатом этого является метрика расстояний, значение которой является приблизительно "стандартным расстоянием" - важным свойством коробов.
Все прочие применения этой метрики для получения измерений расстояния от С1 до С2 содержат случаи, в которых некоторые или все значения "s" либо S1, либо S2 не равны в точности 1,0 или 0,0.
Для понимания того, почему метрика определяется именно так, следует рассмотреть статистику метрики.
Предположим, что в пространстве S задано большое количество коробов. Допустим, что подпространства и точки, представленные этими коробами, выбраны случайным образом. Выберем любой один из этих коробов, например, короб С1. Допустим, что предпочтительная метрика декартовых расстояний применяется для расчета расстояний от С1 до каждого из оставшихся коробов, и допустим, что вычисляется среднее значение и среднеквадратичное отклонение получившихся расстояний. Можно показать как с помощью прямого вычисления, так и посредством математического анализа, что отношение данного среднего значения к данному среднеквадратичному отклонению монотонно растет при увеличении количества измерений S. Это соотношение выражает среднее или ожидаемое расстояние между двумя выбранными случайно коробами в терминах некоторого числа среднеквадратичных отклонений. Даже для относительно малых пространств, состоящих из возможно нескольких десятков измерений, ожидаемое расстояние равно нескольким среднеквадратичным отклонениям. Для пространств из 50 измерений ожидаемое расстояние приблизительно равно девяти среднеквадратичным расстояниям, в то время как для пространств из 100 измерений ожидаемое расстояние приблизительно равно 13 или 14 среднеквадратичным отклонениям. Число среднеквадратичных отклонений приблизительно пропорционально квадратному корню из числа измерений пространства S.
При таких больших статистических различиях между случайно выбранными коробами представляется естественным задаться вопросом, подтверждаются ли экспериментально выражаемые ими распределения. Подтверждаются. Автор изобретения провел описанный эксперимент для пространств, состоящих из 1000 и более измерений, для буквально миллионов коробов в большой группе. Статистическое распределение расстояний между тестовым коробом и остальными коробами большой группы коробов строго следовало кривой, полностью удовлетворявшей ожиданиям от концепции среднего значения и среднеквадратичного отклонения. Даже для относительно малых пространств чрезвычайно маловероятно, чтобы два выбранных случайным образом короба располагались очень близко друг к другу при данной метрике.
Автор изобретения обнаружил эту статистику в ходе выполнения компьютерных моделирований правдоподобных простых моделей живых нейронов. Последствия этого открытия огромны и ведут прямо к настоящему изобретению.
Первым следствием открытия автора настоящего изобретения является тот факт, что оно ведет непосредственно к правдоподобной структуре данных для представления информации и манипулирования ею в живых нейронных системах, а именно к случайно выбранным коробам, состоящим из состояний множества живых нейронов. Коробы в соответствии с открытием автора настоящего изобретения далеко отстоят друг от друга, поэтому всякий раз, когда живой нейрон видит в своих входных дендритах короб, который по сравнению с ожидаемым количеством среднеквадратичных отклонений между такими коробами близок к коробу, виденному ранее, маловероятно, что это случайность. Чем меньше расстояние, тем меньше вероятность случайного появления. Если живые нейроны могут каким-либо образом хранить предыдущие короба, связанные с переменной состояния живого нейрона в момент видения каждого предыдущего короба, то текущее состояние живого нейрона можно сделать отражающим это предыдущее состояние. Более того, если обычным состоянием живого нейрона является некоторый тип непрерывной случайной переменной, такой как простое случайное блуждание, то измерение расстояния может выполняться для управления распределением непрерывной переменной по ранее сохраненному значению состояния, так что чем меньше расстояние, тем меньшее случайное отклонение от ранее сохраненной переменной состояния наблюдается в текущей переменной состояния.
Для воспроизведения этого поведения в живых нейронных системах существует и может быть продемонстрирован простой механизм. Автор изобретения полагает, что это есть фундаментальный принцип обработки данных в живых нейронных системах, т.е. принцип, который долгое время скрывался от исследователей.
Концепции коробов могут быть расширены для моделирования многих других ситуаций. Например, представим себе человеческое общество. Смоделируем это общество так, чтобы каждый индивид был аналогичен живому нейрону. Тогда можно описать групповую динамику в терминах коробов, содержащих индивидов, где каждый индивид имеет состояние, и группу других индивидов, от которых зависит состояние этого индивида. Тогда общее мнение становится просто доминантным коробом внутри группы.
Ожидаемое расстояние, выраженное обычно в терминах числа среднеквадратичных отклонений, от случайно выбранного короба до другого случайно выбранного короба внутри пространства, обычно обозначается как "стандартное расстояние". Стандартное расстояние является неожиданно большим числом среднеквадратичных отклонений для короб-систем всех размерностей, и стандартное расстояние стремится расти пропорционально квадратному корню из размерности пространства, в котором оно задано.
Свойство стандартного расстояния ведет непосредственно к двум важным свойствам короб-систем: равноудаленности и емкости.
Если справедливо, что все порядки подпространств, в которых определены не связанные другим образом коробы частного пространства, приблизительно одинаковы, то метрика стремится к рефлексивности, и расстояние, измеренное с помощью данной метрики от одного из этих коробов до любого другого, в сильной степени приближается к стандартному расстоянию. В этом случае рассматриваемые короба будут называться "равноудаленными", а рассматриваемые короба, взятые как группа, имеют свойство "равноудаленности".
"Емкостью" короб-системы является количество равноудаленных коробов, которое она может вмещать без ухудшения общей равноудаленности системы более чем на заданную величину, называемую "коэффициентом ухудшения". Очевидно, коэффициент ухудшения и емкость короб-системы имеют функциональную зависимость.
Истинная, устойчивая и большая равноудаленность не связанных другим образом коробов в подпространствах одинаковых порядков, которые все заданы в одном пространстве, приводит к огромным емкостям коробов в таких пространствах. При росте размерности главного пространства емкость короб-системы, которую оно содержит, приближается к числу различимых состояний системы. Чем больше коэффициент ухудшения, тем более это верно, но большой размер стандартного расстояния поддерживает значительные коэффициенты ухудшения.
Превышение емкостей малых короб-систем в живой системе может быть механизмом, обусловливающим "вспышки озарения" или "неожиданные вдохновения", когда коробы, которые обычно не добавляются, если емкость системы не была превышена, находятся необычно близко к другим сохраненным коробам в результате статистического опережения.
Особым случаем общей концепции короба является "строковый короб". Если список случайных в прочих отношениях коробов вырабатывается таким способом, что удовлетворяет условию, чтобы коробы, более близкие друг к другу в порядке перечисления списка коробов, являлись также более близкими друг к другу в применяемой метрике расстояний и, обратно, коробы, дальше отстоящие в порядке перечисления списка коробов, также дальше отстояли в применяемой метрике расстояний, то список в целом называется "строковым коробом". Удовлетворить это условие и получить в результате строковый короб весьма просто с помощью различных способов. Во-первых, первый короб в списке строкового короба генерируется путем выбора случайных значений в качестве его элементов. Второй короб в строковом коробе затем генерируется путем применения некоторой формы классического статистического процесса, называемого "случайным блужданием", к некоторым или ко всем элементам первого короба. Этот процесс продолжается рекурсивно, генерируя в каждом случае следующий короб в списке строкового короба из текущего короба путем случайного блуждания.
Случайным блужданием является любой статистический процесс, вырабатывающий последовательность чисел, в которой близость к последовательности приводит к увеличению корреляции. Например, фрагмент кода на языке С в Таблице 1 проиллюстрирует одно из средств для получения случайного блуждания.

В Таблице 1 номера строк добавлены для упрощения обсуждения. Оно приводится ниже.
Строка 1 в Таблице 1 задает накопитель для целочисленной переменной управления циклом, которая будет использована в дальнейшем. Строка 2 в Таблице 1 определяет накопитель для списка чисел двойной точности, которые будут генерироваться и составят случайное блуждание. Строка 3 в Таблице 1 задает накопитель для дроби с двойной точностью, которая будет использоваться для управления расчетом случайного блуждания, и устанавливает ее в значение 0,1. Строка 4 в Таблице 1 содержит многоточие, показывающее, что здесь в условиях работы был бы необходим другой фрагмент кода на языке С, чтобы сделать этот фрагмент кода на языке С реально выполнимым. Специалистам в написании программ на языке С будет очевидно, что еще потребуется в любой заданной ситуации от компилятора и компьютерной системы. Строка 5 в Таблице 1 устанавливает первый элемент списка случайного блуждания равным значению псевдослучайного числа с двойной точностью между 0,0 и 1,0. Функция "random()" в строке 5 в Таблице 1 является стандартной библиотечной функцией языка С, выводящей псевдослучайное целое число в диапазоне между 0 и заданной константой LONG_MAX. Деление на LONG_MAX здесь, при вычислениях с двойной точностью, дает желательное псевдослучайное число с двойной точностью. Строки 6-9 в Таблице 1 вычисляют оставшуюся часть списка случайного блуждания. Строка 6 в Таблице 1 задает выполнение цикла с еще 99 итерациями. Строки 7 и 8 в Таблице 1 составляют один оператор присваивания языка С, который присваивает i-му элементу списка значение, полученное из (i-1)-гo, или предыдущего, элемента списка, i-й элемент списка будет равен значению (i-1)-гo элемента списка плюс число между + дробью и -дробью, рассчитанное в строке 8 в Таблице 1.
Результатом фрагмента, написанного на языке С кода в Таблице 1, будет последовательность случайных чисел, обладающих тем свойством, что смежные элементы в списке отличаются не более чем на значение дроби в сторону уменьшения или увеличения. Элементы, отстоящие в списке на большее расстояние, могут отличаться на большее значение. Это удовлетворяет требованиям случайного блуждания.
Для генерирования строкового короба применим процесс случайного блуждания к последовательным элементам в списке коробов так, чтобы в заданном коробе элементы этого короба являлись случайными друг по отношению к другу, но соответствующие элементы в последовательности коробов получались посредством случайного блуждания.
Строковые коробы чрезвычайно полезны в распознавании образцов последовательностей. Когда последовательность случайных коробов должна храниться способом, поддерживающим распознавание последовательности в целом или компонентов последовательности, последовательность может покоробно образовывать пары с коробами выработанного строкового короба. Получающийся список парных коробов сохраняет случайные значения коробов распознаваемой последовательности, а также свойства строкового короба. Это упорядочивает список, несколько сходно с нумерацией исходной последовательности случайных коробов. Этот конструкт поддерживает механизм короба, который может использоваться для идентификации, а также для реконструкции исходной последовательности.
Теперь должно быть ясно, что хотя автор изобретения описал предпочтительный вид коробов, коробы на самом деле являются очень общей сущностью. Короб является вектором элементов. Элементы могут быть отдельными числами любого типа, в том числе одноразрядными двоичными числами, натуральными числами, целыми числами, действительными числами, комплексными числами и так далее, либо элементы могут быть более сложными, содержащими пары чисел, группы чисел или другие объекты данных. То, что делает их коробами - это наличие метрики расстояний, которая может быть монотонно связана с метрикой декартовых расстояний, в соответствии с которой, как определил автор изобретения, если применить эту метрику последовательно для измерения расстояния между парами большого количества кандидатов в коробы, а затем вычислить среднее значение и среднеквадратичное отклонение полученных значений, получится среднее значение, величина которого значительно больше величины полученного таким образом среднеквадратичного отклонения. Главное сделанное автором изобретения открытие, делающее короб-вычислительные системы столь общими, заключается в том, что эта определяющая характеристика может быть получена большим количеством способов. В частности, она возникает почти из любого процесса, который обрабатывает элементы каждого короба-кандидата независимо от большинства прочих элементов того же короба, даже если независимость всего лишь приблизительна.
Статистика коробов, даже коробов скромного размера, гарантирует, что коробы будут равноудаленными в своем пространстве и статистически будут далеко разнесены. Это делает их идеальными структурами данных для представления информации и манипулирования ею.
Коробы и системы памяти короба
Первым приложением, которое покажет автор изобретения для коробов, является система памяти короба, в которой коробы связаны в пространстве с объектами данных так, чтобы представлять их.
Таблица 2 показывает законченный модуль кода на языке С, который реализует элементы системы памяти короба по настоящему изобретению. Строки кода на языке С пронумерованы для упрощения обсуждения, но код на языке С во всем остальном должен быть полностью функционирующим при предъявлении одному из современных компиляторов языка С. Код в Таблице 2 (и все образцы кода в данном рассмотрении) были протестированы при помощи компилятора GNU GCC.


Код на языке С в Таблице 2 показывает четыре функции и описание типа для нового типа данных - COROB, в предпочтительном виде.
Строки 1-4 в Таблице 2 содержат стандартные заголовочные файлы языка С, которые встречаются в любом завершенном современном компиляторе языка С. Файл stdio.h в строке 1 в Таблице 2 обеспечивает поддержку стандартного ввода и вывода языка С. Файл stdlib.h в строке 2 в Таблице 2 обеспечивает поддержку стандартных утилит языка С, таких как функция генерирования случайного числа, использующаяся в строках 33 и 34 в Таблице 2. Файл math.h в строке 3 в Таблице 2 обеспечивает поддержку математических функций, таких как функция вычисления квадратного корня в строке 44 в Таблице 2. Файл limits.h в строке 4 в Таблице 2 обеспечивает описания констант, таких как константа LONG_MAX, присутствующая в строках 33 и 34 в Таблице 2.
Строки 6 и 7 в Таблице 2 задают некоторые операционные характеристики коробов, которые задаются и подвергаются манипуляциям в данном написанном на языке С коде. Локальная константа NBR_OF_DIMS устанавливается в строке 6 в Таблице 2 равной 100 и представляет число элементов, которые будут представлены в каждом коробе, поддерживаемом данным написанным на языке С кодом. Локальная константа NBR_OF_COROBS устанавливается в строке 7 в Таблице 2 равной 1000 и представляет максимальное число коробов, которое поддерживает данный написанный на языке С код. При полной своей функциональности данный написанный на языке С код прежде всего приводится для примера. В более общей реализации эти константы вероятнее всего будут заменены переменными, обеспечивая пользователю данного кода более гибкий подход. То, как это делается, будет очевидно для специалистов в программировании на языке С.
Строки 9-12 в Таблице 2 задают природу коробов, которые будут поддерживаться данным написанным на языке С кодом. Использование ключевого слова typedef языка С в строке 9 в Таблице 2 приводит к тому, что строки 9-12 кода в Таблице 2 будут описывать новый тип данных, который будет называться "COROB", как указано в строке 12 в Таблице 2. Каждый такой COROB будет состоять из двух массивов чисел с двойной точностью, состоящих оба из NBR_OF_DIMS элементов, массив val[] описывается в строке 10 в Таблице 2, а массив sig[] описывается в строке 11 в Таблице 2. Каждый конкретный элемент val[], такой как val[1], имеет соответствующий элемент sig[], в данном случае sig[l]. Элемент val вместе с элементом sig с одним и тем же индексом составляют накопитель для элемента короба. Массив val[] содержит значения, задающие координаты короба, в то время как массив sig[] содержит величины значимости, задающие обобщенное подпространство короба в данной предпочтительной реализации. Из этого кода должно быть очевидным для специалистов, как сюда подставить прочие описания COROB, согласующиеся с уже представленной теорией о коробах.
Строка 13 в Таблице 2 создает массив из элементов COROB длиной NBR_OF_COROBS для использования данной системой памяти короба. Этот массив будет содержать все коробы для целей памяти, которые поддерживает данный написанный на языке С код. Индекс этого массива функционирует в качестве данных, ассоциируемых с каждым коробом, сохраненным в памяти. Этот подход является на самом деле весьма общим, поскольку эти индексы могут использоваться в другом коде, таком как стандартная система управления базами данных, выступая в качестве индекса просмотра для объекта данных любого типа, который может быть определен. Поэтому приведенной здесь информации достаточно для иллюстрирования того, как могут быть построены памяти короб-систем и как они используются для связывания индексов с коробами.
В строке 15 в Таблице 2 присваивается имя, assign_corob_to_index, первой функции в написанном на языке С коде. Эта функция принимает один целочисленный параметр, new-index, который является индексом массива corob[], для которого определяется короб. Функция вырабатывает новый короб в corob[new index] и возвращает значение new_index или -1, если произошла ошибка. Строка 16 в Таблице 2 проверяет тот факт, что значение, подаваемое вызывающей программой в переменную new_index, находится в пределах массива corob[], и возвращает -1, если это не так. Строка 17 в Таблице 2 вызывает процедуру generate_corob() для получения требуемого короба и задает адрес элемента corob[new_index] в качестве места для получения следующего короба. Функция generate_corob() задается позже в Таблице 2.
Строки 21-29 в Таблице 2 задают следующую функцию, find_nearest_corob(), которая принимает два параметра - указатель на переменную с двойной точностью, distance, и указатель на переменную с типа COROB. Эта функция принимает с в качестве входа и ищет в массиве corob[] короб, наиболее близкий к с, в соответствии с функцией metric() измерения расстояния, которая будет кратко определена. Индекс ближайшего короба в массиве corob[] выводится этой функцией, и это расстояние сохраняется в ячейке памяти, на которую указывает переменная distance. В строке 23 в Таблице 2 накопитель distance устанавливается в значение NBR_OF_DIMS, которое в данном написанном на языке С коде гарантированно больше любого расстояния между двумя коробами, рассчитанного посредством функции metric (). Затем в строках 24-27 в Таблице 2 запускается цикл, систематически рассчитывающий расстояние между с и каждым элементом массива corob[] для нахождения минимального расстояния.
Строки 31-36 в Таблице 2 задают функцию generate_corob(), создающую новый короб. Эта функция принимает адрес с области памяти COROB, в котором следует строить новый короб. Цикл в строках 32-35 в Таблице 2 выполняет конструкционную работу, сохраняя псевдослучайные числа из диапазона от 0,0 до 1,0 в элементах val[] и sig[] с. Функция random(), используемая в строках 33 и 34 в Таблице 2, является стандартной функцией языка С, выдающей целое число в диапазоне между 0 и LONG_MAX. Деление этого целого числа на LONG_MAX при вычислении с двойной точностью дает желательное псевдослучайное число с двойной точностью.
Написанный на языке С код в Таблице 2 содержит конкретное описание области данных короба, т.е. архитектурного конструкта по настоящему изобретению, пригодного для содержания данных математического короба для дальнейшего использования. Этот конструкт иногда сам обозначается словом короб, и из контекста будет ясно, когда этот конструкт подразумевается под словом "короб", а когда под этим словом подразумевается математический или вычислительный объект данных. Конкретный код на языке С, описывающий этот архитектурный конструкт, уже обсуждался и состоит из строк 6 и 7 в Таблице 2, задающих константы NBR_OF_DIMS и NBR_OF_COROBS, строк 9-12 в Таблице 2, дающих конкретное описание архитектурного конструкта, называемого термином "область данных короба", или просто "коробом", строки 13 в Таблице 2, которая описывает, как составляются коробы, и строк 31-36 в Таблице 2, которые описывают, как загружается архитектурный конструкт короб в соответствии с настоящим изобретением.
Последней функцией является metric(), задаваемая в строках 38-45 в Таблице 2. Она реализует предпочтительную метрику декартовых расстояний, расширенную для использования в обобщенных подпространствах. Она берет в качестве входа адреса трех накопителей -накопителя с двойной точностью, называемого "distance", и двух накопителей типа COROB, называемых "от" (to) и "от" (from). Метрика вычисляется по принципу "от (from)-короба "до (to)-короба, как можно ожидать, и результат выдается в накопитель, называемый "distance". Цикл, показанный в строках 40-43 в Таблице 2, генерирует сумму, состоящую из элементов. Элементы состоят из квадратов разностей между соответствующими элементами val[] в "from"-и "tо"-коробах, причем каждый умножен на соответствующий элемент sig[] из "frоm"-короба. В строке 44 в Таблице 2 берется квадратный корень из этой суммы, и результат сохраняется в накопителе под названием "distance". Отметим, что если все элементы sig[] "from"-короба имеют значение 1,0, то данный написанный на языке С код просто реализует известную декартову диагональ между двумя многомерными точками. Отклонения массива sig[] "from"-короба от значений, равных единице, приводят к тому, что данная функция имеет дало с обобщенными подпространствами.
В этом простом написанном на языке С коде в Таблице 2 скрыта ловушка: что, если массив corob [] не полностью заполнен действительными коробами? Этот случай не обрабатывается, чтобы сохранить простоту и иллюстративность данного написанного на языке С кода. Когда вызывается функция find_nearest_corob(), эта функция производит сравнения с любыми данными, которые могут быть представлены в зарезервированных для коробов местах, независимо от того, содержат ли они действительные коробы или нет. В последующих примерах автор изобретения всегда будет полностью заполнять массив corob[], поэтому ситуация сравнения с недействительными коробами не возникает. Однако более общий код может быть легко написан специалистами в программировании на языке С, например, с помощью установки в структуре короба в строках 9 -12 в Таблице 2 флага, указывающего действительность данных в коробе, а также проверки этого флага в функции find_nearest_corob() для обхождения тех случаев, когда коробы в массиве corob[] не заданы.
Чтобы проиллюстрировать использование системы памяти короба в Таблице 2, а также некоторые свойства, заявляемые для коробов, автор изобретения теперь приведет пару примеров.
Первый пример показывает, что написанный на языке С код в Таблице 2 может на самом деле использоваться для выполнения заявленных действий, а именно для сохранения и для поиска коробов и связанных с ними индексов. Написанный на языке С код в Таблице 3 должен быть связан с написанным на языке С кодом в Таблице 2.

Показанный в Таблице 3 написанный на языке С код обеспечивает функцию main(), которая создает завершенную программу на языке С. Строка 1 в Таблице 3 начинает задание функции main(). Строки 3-5 в Таблице 3 генерируют действительный короб в каждом элементе массива corob[] в Таблице 2. В строке 6 в Таблице 3 из этой группы выбирается отдельный короб, в данном случае corob[100], и предъявляется функции find_nearest_corob(), которая выводит расстояние и индекс для ближайшего соответствия. Строка 7 в Таблице 3 печатает результаты, которые выглядят так: ближайший короб:
idx=100, distance=0.000000.
Разумеется, это в точности то, что и следовало ожидать, поскольку автор изобретения явным образом использует один из элементов массива corob[] - corob[100] - в качестве "from"-короба, находящегося в массиве corob[]. Выдаваемый индекс равен 100, что верно, а выдаваемое расстояние равно нулю, что также верно.
Этот пример показывает, что система памяти короба, по меньшей мере, способна правильно находить одно из своих ранее сохраненных значений.
Далее, представим, что произойдет, если предъявляется случайный короб вместо одного из сохраненного множества. Теперь с написанным на языке С кодом Таблицы 2 нужно связать написанный на языке С код в Таблице 4.

Написанный на языке С код в Таблице 4 содержит новую функцию main(). Снова массив corob[] полностью заполнен. На этот раз в строке 6 в Таблице 4 генерируется дополнительный короб с, который предположительно не скоррелирован со всеми коробами в массиве corob[]. Затем в строках 7-10 в Таблице 4 вычисляется расстояние от с до каждого короба в массиве corob[] и записывается в виде стандартного выхода. При вычислении некоторой простой статистики этого стандартного выхода были получены следующие результаты:
Количество измерений: 100
Количество коробов в массиве corob[]: 1000
Среднее расстояние: 2,747503
Среднеквадратичное отклонение расстояний: 0,172003
Наименьшее расстояние: 2,121537
При использовании коробов со 100 измерениями или элементами и при расчете (применении) метрики от короба до массива из 1000 коробов, среднее расстояние приблизительно равно 2,75, среднеквадратичное отклонение расстояний приблизительно равно 0,17, а из 1000 коробов массива corob[] ближайший к тестовому коробу короб находится на расстоянии приблизительно 2,12. Отметив, что точное соответствие тестовому коробу дало бы нулевое расстояние, можно прийти к выводу, что среднее расстояние в этом случае равно приблизительно шестнадцати среднеквадратичным отклонениям от точного соответствия и что короб, ближайший к тестовому коробу с в списке 1000 коробов массива corob[], находится на расстоянии более двенадцати среднеквадратичных отклонений.
Путем варьирования констант NBR_OF_DIMS и NBR_OF_COROBS в строках 6 и 7 в Таблице 2 и перекомпиляции можно составить Таблицу 5, содержащую только что рассмотренный случай:
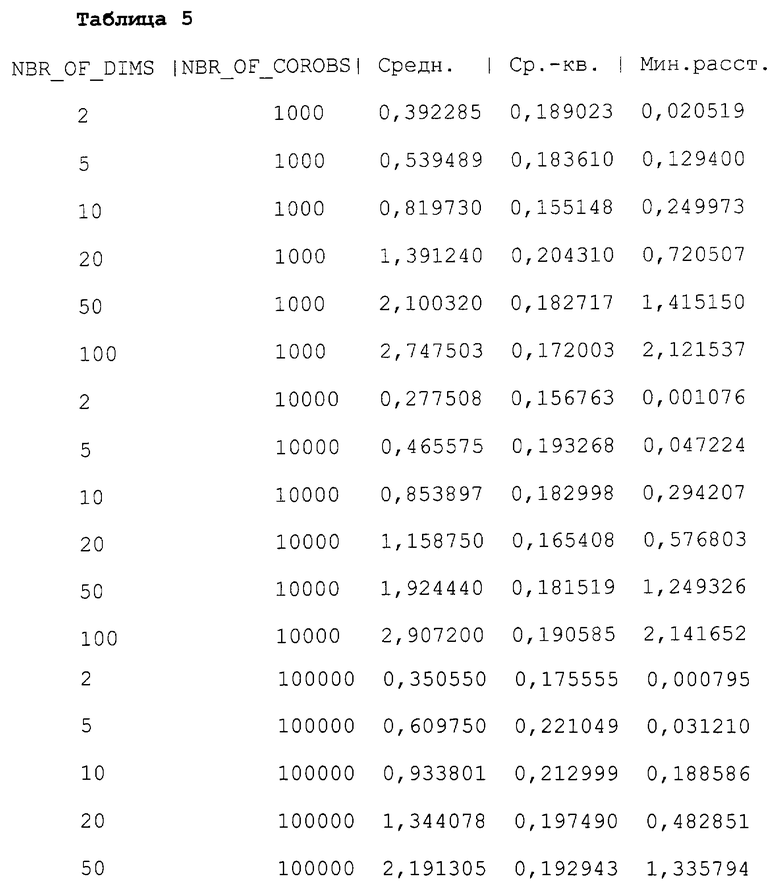
Таблица 5 показывает полученные средние расстояния, среднеквадратичные отклонения и минимальные расстояния или ближайшие коробы для массивов corob[], состоящих из 1000 коробов, 10000 коробов и 100000 коробов. В каждом из этих случаев размеры коробов являются 2, 5, 10, 20, 50 и 100 - мерными, за исключением последней группы, где для 100000 100-размерных коробов не хватило мощности компьютера автора изобретения. Эти данные считаются репрезентативными для коробов вообще, хотя различные алгоритмы выработки псевдослучайных чисел в функции random() в Таблице 2, а также различные начальные значения для генератора случайных чисел создают вариации в точных значениях. Варьирование метрики или варьирование задания коробов в терминах составляющих их элементов также вызовет вариации подробностей.
Таблица 5 наводит на несколько поясняющих и практических моментов касательно коробов. Отметим, во-первых, что среднее значение больше, зачастую больше в несколько раз, чем среднеквадратичное отклонение. Даже для коробов размерностью 2 и 5 среднее значение в два или более раз больше величины среднеквадратичного отклонения. Для больших коробов оно может быть больше в десять и более раз. Таблица 5 свидетельствует, что большие короб-системы, являющиеся системами коробов, в которых коробы имеют много элементов, стремятся к большему отношению среднего значения к среднеквадратичному отклонению. Это справедливо в общем случае. Столбец в Таблице 5, озаглавленный "Мин. расст.", показывает расстояние до ближайшего к тестовому коробу короба в массиве corob[]. Это расстояние колеблется практически от нуля до значения в несколько раз большего, чем среднеквадратичное отклонение, а также растет с ростом количества элементов в коробах. Таким образом, инженер сможет найти полезную оптимальную точку для минимизации размера короба (и, следовательно, требований к хранению короба и скорости исполнения) при максимизации раздельности короба (так, чтобы в системе памяти короба было задано требуемое количество отдельных коробов), с помощью несложных компьютерных экспериментов показанного в Таблице 5 типа.
Таблица 5 обеспечивает прямое обоснование утверждения автора изобретения о том, что правильно сконструированные коробы являются приблизительно равноудаленными, а также его утверждения о том, что их раздельность резко возрастает с ростом размера коробов. Это прямо подтверждает способность хранить полезное количество коробов однозначно в одном накопителе короба.
До сих пор автор изобретения обсудил, как система памяти короба может точно сохранять и затребовать коробы и как можно продемонстрировать концепцию равноудаленности. Теперь он проиллюстрирует способность системы памяти короба отыскивать правильный короб даже при наличии значительного шума. Обнаружение и исправление ошибок, разумеется, широко известно из уровня техники, но технология обнаружения и исправления ошибок до сих пор требовала очень точных алгоритмов для идентификации образцов или областей пространства обнаружения или исправления ошибок. Системы памяти короба обеспечивают возможности исправления ошибок, основанные на свойстве равноудаленности коробов, что означает, что очень простые, неточные, случайные процессы, лежащие в основе коробов, могут теперь заменить очень точные алгоритмы обнаружения и исправления ошибок. Кажется удивительным, что эти короб-ориентированные случайные процессы ведут непосредственно к таким возможностям обнаружения и исправления ошибок, однако, возможно, это неудивительно при условии, что системы памяти короба представляются первичным механизмом функционирования живых нейронных систем.
Чтобы проиллюстрировать функционирование системы памяти короба при наличии шума, мы должны связать написанный на языке С код в Таблице 6 с кодом в Таблице 2:

Функция main() снова полностью заполняет массив corob[] в строках 3-5 в Таблице 6. Цикл в строках 6-16 в Таблице 6 заставляет переменную fraction изменяться от значения 0,0, при котором шум отсутствует, до значения 1,0, представляющего сплошной шум, с шагом 0,1. Тестовый короб с генерируется в цикле из строк 7-12 в Таблице 6. Если переменная fraction равна 0,0, то числа, помещенные в с в строках 8-11 в Таблице 6, будут точно соответствовать числам конкретного элемента массива corob[] - в данном случае, corob[100]. Если переменная fraction равна 1,0, то числа, помещенные в с в строках 8-11 в Таблице 6, будут чисто случайными числами. Промежуточные значения переменной fraction дадут в результате промежуточные смеси из элемента corob[100] и случайных чисел. Таким образом, переменная fraction управляет количеством шума, представленного в с по сравнению с коробом в элементе corob[100]. В строках 13-15 в Таблице 6 находится ближайший короб и распечатываются результаты.
Константа NBR_OF_DIMS была установлена на значение 100, а константа NBR_OF_COROBS была установлена на значение 1000, после чего код был скомпилирован и исполнен. Вот выход написанного на языке С кода, содержащего функцию main() из Таблицы 6:

В каждой строке данного выхода показана переменная fraction тестового короба с, являющаяся шумом, затем индекс и расстояние до ближайшего короба. Первая строка, в которой fraction=0,0, показывает, что ближайший короб имеет индекс 100 и расстояние, равное 0,0, которые он и должен иметь, поскольку тестовый короб с является точной копией элемента corob[100]. Последняя строка, в которой fraction=1,0, показывает, что ближайшим коробом должен быть 651 на расстоянии приблизительно 2,24. Ранее для 1000 коробов по 100 элементов каждый мы видели, что ближайший к случайному тестовому коробу короб в массиве corob[] находился на расстоянии приблизительно 2,12. Этот предыдущий случай дал также среднее значение, равное приблизительно 2,75, и среднеквадратичное отклонение приблизительно 0,17. Таким образом, числа в данном случае для полностью случайного короба, когда fraction=1,0, не кажутся бессмысленными в свете ранее показанной статистики для случая этого типа.
Отметим, что до тех пор, пока переменная fraction не достигнет значения 0,80, что соответствует 80 процентам случайного шума, выдается правильный индекс. Это невероятно надежное выполнение обнаружения в соответствии с любым стандартом. То, что такое надежное поведение проявляет система памяти короба, основанная на таких простых статистических процессах и метриках, является совершенно неожиданным, и на самом деле чем-то изумительным. Аспект системы памяти короба короб-вычислительных систем по настоящему изобретению, таким образом, является действительно новым, неочевидным и очень полезным.
Ячейки короба
Далее автор изобретения переходит к реализации ячеек короба. Автор изобретения слегка доработает систему памяти короба для создания фундаментального компонента короб-вычислительных систем, ячейки короба. Исходя из ячеек короба, кратко будет описана вся короб-вычислительная система.
Фиг.3 является схематическим чертежом, иллюстрирующим главные компоненты ячейки короба по настоящему изобретению. Регистр 40 входных данных короба обеспечивает накопитель для входных данных короба, который представлен в качестве входного для ячейки по фиг.3. Управляющий элемент 42 принимает входные данные короба из регистра 40 входных данных короба и направляет обработку этих входных данных короба. Регистр 46 выходного состояния обеспечивает накопитель для выходных данных. Существует два режима действия ячейки короба по фиг.3 - обучение и исполнение. Во время обучения данные регистра 40 входных данных короба совместно с данными регистра 46 выходного состояния передаются управляющим элементом 42 памяти 44 короба для сохранения подходящим образом. В ходе исполнения управляющий элемент 42 принимает значение из регистра 40 входных данных короба и вырабатывает новые значения регистра 46 выходного состояния, учитывая текущее состояние в памяти 44 короба и действуя в соответствии с настоящим изобретением.
Отметим, что при некоторых условиях, а именно в ходе процесса инициализации или обновления памяти 44 короба, внешние процессы могут предопределять текущее выходное значение в регистре 46 выходного состояния.
Теперь автор изобретения предоставляет подробный пример структуры и действия ячейки короба по фиг.3. Этот пример воплощает предпочтительную форму ячейки короба. Тем не менее, настоящее изобретение подразумевает, что конструкция и дизайн короб-систем могут содержать множество переменных и решений и что доступны широкие диапазоны при назначении этих переменных и принятии этих решений, так что определенный выбор, даже в предпочтительном виде, не может иметь больше преимуществ, чем остальные выборы, и даже может уступать другим вариантам при определенных обстоятельствах. Данный пример представлен на языке программирования С для удобства выражения концепции. Специалистам, как в области программирования, так и в области системотехники хорошо известно, что любая функциональная возможность написанной на языке С программы всегда может быть реализована в электронном аппаратном эквиваленте и, наоборот, с ограничением только по соображениям времени и стоимости. Подобным же образом функциональная возможность написанной на языке С программы может быть реализована на других языках программирования, либо заново воссоздана на языке С в виде другой, но эквивалентной С-программы без существенных отклонений от функциональных возможностей исходной С-программы.
В данном примере используется имеющийся в языке С тип данных "float" (число с плавающей запятой). Тип данных "float" обычно требует меньше места для хранения, чем более общий тип данных "double" (с двойной точностью). Используя плавающую запятую, автор изобретения показывает, что тип данных "double" не требуется для успешной реализации ячейки короба. На самом деле сравнимая ячейка короба может быть построена на языке С и успешно работать при использовании типов данных "int" (целое число) и даже "char" (символ) вместо типа данных "float". Ячейка короба может даже быть построена и успешно работать, если переменные типа "float" заменить одноразрядными переменными. Достигнув понимания концепций короб-вычислительной системы, специалисты в программировании будут способны реализовать эти альтернативные ситуации со ссылкой на данный текущий приведенный для примера код, написанный на языке С, а также посредством использования хорошо известных методов и способов, имеющих дело с программными источниками замены типов переменных в программе.
В Таблице 7 приводятся структура и функциональные прототипы ячейки короба по фиг.3 в виде заголовочного файла С. Номера строк добавлены к стандартному С-коду с целью облегчения обсуждения.
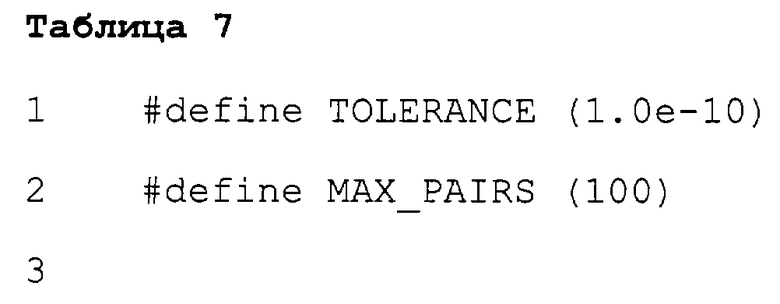


Константа TOLERANCE в строке 1 в Таблице 7 управляет одним аспектом исполнения ячейки и будет описана ниже при описании исполнения ячейки.
Константа MAX_PAIRS в строке 2 в Таблице 7 будет описана кратко.
Строки 4-7 в Таблице 7 задает (typedef) структуру типа STATE, являющуюся единственным элементом короба. В этом примере предпочтительного выполнения STATE состоит из двух переменных, val и sig, причем обе имеют тип "float". STATE может также принимать многие другие формы. Могут быть построены очень эффективные короб-системы, не имеющие значения sig. В таких системах все коробы будут задаваться в обычных подпространствах, имеющих то же количество измерений, что и пространство, в котором заданы эти подпространства. Также во многих случаях полезно приравнять значение sig[] либо к 1,0, либо к 0,0, к примеру, путем сравнивания рассчитанного значения sig с предельным значением и выбора значения 1,0, если значение выше предельного, и значения 0,0, если ниже. Коробы, сконструированные из структур STATE таким способом, будут заданы в обычных подпространствах с размерностью, которая (обычно) меньше размерности пространства, в котором заданы эти подпространства. Возможно задавать STATE по-другому в той степени, пока коробы, появляющиеся в результате выбора одной из опций, согласуются с определением короба как "точки в обобщенном подпространстве частного пространства".
Строки 9-13 в Таблице 7 задают (typedef) структуру типа данных COROB для целей данного текущего примера. Строка 10 в Таблице 7 задает накопитель для переменной nbr_of_dims, показывающей количество измерений в пространстве (размерность пространства), которое содержит короб и его подпространство. Строки 11 и 12 в Таблице 7 практически идентичны типу STATE, хотя автор изобретения выбрал реализацию элементов типа COROB в виде массивов вместо прямого использования типа данных STATE.
Строки 15-24 в Таблице 7 задают (typedef) структуру CELL (ячейки) и показывают пример структуры области данных ячейки короба. Упомянутая структура CELL была показана в условном виде в ячейке короба по фиг.3. Сначала в виде переменной nbr_of_dims задается накопитель для количества измерений главного пространства для подпространств коробов. Эквивалент регистра 40 входного короба ячейки короба по фиг.3 задается в виде переменной input_corob типа COROB, в строке 17 в Таблице 7. Эквивалент регистра 46 выходного состояния ячейки короба по фиг.3 задается в виде переменной current_state типа STATE, в строке 18 в Таблице 7. Эквивалент памяти 40 короба ячейки короба по фиг.3 задается в виде переменной corob_memory в строке 19-23 в Таблице 7, и corob_memory, являющаяся примером области данных памяти короба, является структурным типом данных, состоящим из переменной nbr_of_entries типа "int", в строке 20 Таблицы 7, переменной corob типа "массив COROB", в строке 21 в таблице 7, и переменной state типа "массив STATE", в строке 22 в Таблице 7. Переменная nbr_of_entries в строке 20 в Таблице 7 обеспечивает накопитель для текущего количества вхождений в системе памяти короба данной ячейки. Для удобства написания кода максимальное количество вхождений задается в виде константы MAX_PAIRS в строке 2 в Таблице 7. MAX_PAIRS используется в строках 21 и 22 в Таблице 7 для указания того, сколько пространства хранения следует предусмотреть в соответствующем находящемся там массиве переменных. Значение MAX_PAIRS произвольным образом устанавливается здесь равным 100, хотя в ячейке короба могут эффективно использоваться гораздо большие значения, при ограничении только реализацией компьютерной системы или электронного оборудования.
Функциональные прототипы, показанные в строках 26-33 в Таблице 7, полезны в написанных на языке С программах для упрощения отладки. Каждая из этих функций будет кратко обсуждена более подробно.
Далее автор изобретения рассматривает фундаментальные функции, требуемые для ячейки короба по фиг.3. По фиг.3 эти функциональные возможности включают в себя способность создавать и инициализировать состояния, коробы и ячейки, способность загружать значения в регистр 40 входного короба и регистр 46 выходного состояния, способность сохранять входные данные короба, содержащиеся в регистре 40 входных данных короба, вместе со значением выходного состояния, содержащимся в регистре 46 выходного состояния, в памяти 44 короба, способность к обработке ячейки короба для расчета нового значения для регистра 46 выходного состояния, исходя из короба в регистре 40 входных данных короба и текущего содержимого в памяти 44 короба в соответствии с изложением настоящего изобретения, и, наконец, рассчитывать метрику расстояния от одного короба до другого, обычно от короба, находящегося в регистре 40 входных данных короба, до одного из коробов, находящихся в памяти 44 короба. Каждая из этих функций представлена примером в виде отдельного написанного на языке С программного модуля.
Таблица 8 является примером процедуры, в виде функции на языке С, для создания и инициализации состояния в соответствии с предпочтительным видом настоящего изобретения.

В строках 2 и 3 в Таблице 8 создается состояние. В строках 4 и 5 в Таблице 8 созданное состояние устанавливается равным случайному значению в пределах от 0,0 до 1,0 включительно. Эта стандартная инициализация может, конечно, при необходимости быть переписана в последующем коде, но достаточно часто нужны рандомизированные значения переменных val и sig, делая такое поведение по умолчанию полезным. Содержимое завершенного накопителя выдается вызвавшей процедуре в строке 6 в Таблице 8.
Таблица 9 является примером процедуры, в виде функции на языке С, для создания и инициализации короба в соответствии с предпочтительным видом настоящего изобретения.

В строках 3-6 в Таблице 9 создается короб. В дополнение к созданию структуры короба в строке 3 в Таблице 9 строки 4-6 в Таблице 9 создают накопитель для массивов val и sig накопителя структуры короба, длины которых по числу элементов равны значению переменной nbr_of_dims, передаваемой в качестве параметра от вызывающей процедуры в строке 1 в Таблице 9. Эта переменная nbr of dims устанавливает количество измерений главного пространства короба, как описано в настоящем изобретении. Строки 7-10 в Таблице 9 задают случайный короб в только что созданном накопителе для короба, причем каждый из элементов короба является числом от 0,0 до 1,0 включительно. Эта инициализация по умолчанию может, конечно, при необходимости быть переписана в последующем коде, но случайный короб достаточно часто нужен, делая такое поведение по умолчанию полезным. Содержимое завершенного накопителя выдается вызвавшей процедуре в строке 11 в Таблице 9.
Таблица 10 является примером процедуры, в виде функции на языке С, для создания и инициализации ячейки в соответствии с предпочтительным видом настоящего изобретения.

В строках 4-7 в Таблице 10 создается ячейка. В дополнение к созданию структуры ячейки в строке 4 в Таблице 10 строки 5 -7 в Таблице 10 создают накопитель для массивов val и sig регистра 40 входного короба по фиг.3. Строки 8-13 в Таблице 10 завершают создание памяти 44 короба по фиг.3 путем создания накопителя для элементов отдельных коробов массива коробов, показанного в строке 22 в Таблице 7. Создание накопителя для ячейки в строках 4-7 в Таблице 10 создает оба фиксированных массива - массив коробов и массив состояний, строки 21 и 22 в Таблице 7 соответственно. Массив состояний не требует дополнительного назначения, поскольку его элементы являются отдельными фиксированными переменными структуры STATE, val и sig. Содержимое завершенного накопителя выдается вызвавшей процедуре в строке 14 в Таблице 10.
Таблица 11 является примером процедуры, в виде функции на языке С, для загрузки регистра 40 входного короба ячейки по фиг.3 коробом в соответствии с предпочтительным видом настоящего изобретения.

В строке 1 в Таблице 11 вызывающая процедура передает указатель ячейки и накопителя, содержащего короб. Строки 4-7 в Таблице 11 копируют данные короба, т.е. содержимое переменной corob, в подходящее место в ячейке, т.е. в часть структуры ячейки, обозначенную переменной input_corob. В строке 8 в Таблице 11 количество измерений (размерность) скопированного короба, corob.nbr_of_dims, копируется в структуру данных ячейки. Это завершает загрузку короба в регистр 40 входных данных короба ячейки по фиг.3. Функция, пример которой содержит Таблица 11, полезна в последующей работе ячейки, как будет кратко описано.
Таблица 12 является примером процедуры, в виде функции на языке С, для загрузки регистра 46 выходного состояния ячейки по фиг.3 состоянием в соответствии с предпочтительным видом настоящего изобретения.

В строке 1 в Таблице 12 вызывающая процедура передает указатель ячейки и накопителя, содержащего состояние. Строки 3 и 4 в Таблице 12 копируют данные состояния, т.е. содержимое переменной state, в подходящее место в ячейке, т.е. в часть структуры ячейки, обозначенную переменной current_state. Это завершает загрузку состояния в регистр 46 выходного состояния ячейки по фиг.3. Функция, пример которой содержит Таблица 12, полезна в последующей работе ячейки, как будет кратко описано.
Таблица 13 является примером процедуры, в виде функции на языке С, для загрузки нового вхождения в память 44 короба ячейки по фиг.3. Вхождение состоит из короба, содержимого регистра 40 входного короба ячейки по фиг.3, вместе с состоянием, содержимым регистра 46 выходного состояния ячейки по фиг.3.

В строке 1 в Таблице 13 в функцию learn() передается указатель на обрабатываемую ячейку. Строки 4-12 в Таблице 13 выполняют собственно перемещение вхождения в память 44 короба по фиг.3. Короб-часть вхождения перемещается в правильную позицию в строках 5-8 в Таблице 13, а часть состояния вхождения перемещается в правильную позицию в строках 9 и 10 в Таблице 12. Для удобства в строке 4 в Таблице 13 временная переменная idx задается равной текущему числу вхождений в память 44 короба ячейки по фиг.3. Это значение увеличивается на единицу в строке 11 в Таблице 13 для отражения того факта, что вхождение добавлено в память 44 короба по фиг.3. Это завершает загрузку нового вхождения в память 44 короба по фиг.3 - функцию, необходимую для обеспечения инсталляции программной информации в ячейку, чтобы она могла действовать.
Таблица 14 является примером предпочтительной процедуры, в виде функции на языке С, для исполнения ячейки короба для расчета нового значения для регистра 46 выходного состояния по фиг.3, исходя из короба в регистре 46 входного короба по фиг.3 и текущего содержимого памяти 44 короба по фиг.3 в соответствии с настоящим изобретением.



Комментарии, появляющиеся в написанном на языке С коде в Таблице 14, обеспечивают высокоуровневое описание его функционирования. В строке 1 в Таблице 14 функции execute() передается указатель на обрабатываемую ячейку. Код в строках 5-9 в Таблице 14 определяет и загружает вектор метрики *mt, каждый элемент которого состоит из расстояния, полученного применением функции метрики metric(), от короба в регистре 40 входных данных короба по фиг.3 до одного из коробов в памяти 44 короба ячейки по фиг.3. Код в строках 11-21 в Таблице 14 определяет и загружает вектор веса *wt, который показывает релевантность, в соответствии с вектором метрики *mt, каждого из коробов в памяти 44 короба по фиг.3 по отношению к коробу в регистре 40 входных данных короба по фиг.3. Строка 12 в Таблице 14 создает накопитель для вектора веса *wt. Строки 13 -18 в Таблице 14 вычисляют каждый элемент вектора веса *wt в виде величины, обратной квадрату соответствующего элемента вектора метрики *mt. В случае если это расстояние равно 0,0, что соответствует точному соответствию входного короба в регистре 40 входных данных короба по фиг.3 коробу, рассматриваемому в текущий момент в памяти 44 короба по фиг.3, то в строке 16 в Таблице 14 появилось бы "деление на ноль", если бы не было строки 15 в коде Таблице 14. Константа TOLERANCE, определяемая в строке 1 в Таблице 7, обеспечивает минимальное значение, которое может принимать элемент вектора метрики *mt. Константа TOLERANCE назначается равной подходящему малому значению, которое является практически нулевым при сравнении с наиболее вероятной метрикой для коробов в памяти 44 короба по фиг.3, для которых не предполагается нахождение рядом с коробом в регистре 40 входных данных короба по фиг.3. Таким образом, точное соответствие или очень близкое соответствие не даст ошибки "деления на ноль". В целях нормировки, если говорить коротко, вычисляется сумма totwt вектора веса *wt в строках 13 и 17 в Таблице 14. Строки 19-21 в Таблице 14 выполняют нормировку вектора веса *wt так, что после нормировки сумма элементов вектора веса будет равна 1,0.
Строки 23-27 в Таблице 14 иллюстрируют пример функционирования, необходимого для создания val-части состояния, которое следует записать в регистр 46 выходного состояния по фиг.3. Это просто сумма val-элементов состояний, сохраненных в памяти 44 короба по фиг.3, соответствующих коробам, сохраненным в памяти 44 короба по фиг.3, причем каждое val взвешено нормирующим вектором веса *wt. Таким образом, чем ближе короб в памяти 44 короба по фиг.3 к коробу в регистре 40 входного короба по фиг.3, тем более сильно соответствующий val-элемент будет влиять на конечное значение val-части состояния, записанного в регистр 46 выходного состояния по фиг.3.
В часть значимости sig состояния, записываемого в регистр 46 выходного состояния по фиг.3, должно быть записано число, которое представляет значимость val-части, рассчитанную в строках 23-27 в Таблице 14. Существует множество проверок значимости, и большинство из них могут эффективно использоваться для выполнения этой задачи. Требуется, чтобы полученное в результате значение sig, отражало то, насколько близкое совпадение с входным коробом в регистре 40 входных данных короба по фиг.3 обнаруживается в памяти 44 короба по фиг.3. Значение sig, кроме того, должно быть числом между 0,0 и 1,0 в предпочтительной реализации, где значение 0,0 представляет тот факт, что в памяти короба не было короба более близкого к коробу во входном регистре, чем приблизительное стандартное расстояние, значение 1,0 представляет тот факт, что в памяти короба найдено точное соответствие, а промежуточные между 0,0 и 1,0 значения представляют промежуточные случаи. Код в строках 29-34 в Таблице 14 достигает этой цели за счет простого нахождения наибольшего элемента нормированного вектора веса *wt и присвоения этого значения величине sig выходного состояния, записанного в регистр 46 выходного состояния по фиг.3. Это весьма произвольный выбор средства, и специалисты в области статистики поймут, что, конечно, существует много альтернативных выборов, которые можно сделать, оставаясь в рамках настоящего изобретения.
Последняя функция реализована в строках 36-38 в Таблице 14. val-часть значения состояния, вычисленная выше, смешивается со случайным числом в пределах от 0,0 до 1,0 включительно, в свете sig-части значения состояния, вычисленной выше. Смешивание выполняется так, что, если sig-часть значения состояния равна 1,0, val-часть значения состояния не меняется; если sig-часть значения состояния равна 0,0, val-часть значения состояния игнорируется и полностью заменяется случайным числом от 0,0 до 1,0; а промежуточные значения sig-части значения состояния дают промежуточные смешивания val-части вычисленного значения состояния и случайного числа от 0,0 до 1,0. Это смешивание не является обязательным. Оно представлено в предпочтительном варианте реализации настоящего изобретения из-за того, что оно придает приблизительную природу вычисленному значению состояния, которая полезна, когда комбинируются значения состояния многих ячеек короба, формируя коробы в короб-вычислительной системе, содержащей много ячеек короба. Приблизительная природа значения состояния, введенная в настоящий предпочтительный вид ячейки короба, обеспечивает приблизительную природу тех результирующих коробов, которые отражают значимость коробов вообще, когда они используются в качестве структур данных. Как и в других частях настоящего изобретения, точная форма описанного здесь смешивания не слишком важна при условии, что сохраняется общая функциональная характеристика, согласно которой более высокие значимости, т.е.  рассчитанные значения sig-части состояния дают в результате то, что val-часть рассчитанного состояния сильнее отражает действительное рассчитанное значение val-части, и наоборот.
рассчитанные значения sig-части состояния дают в результате то, что val-часть рассчитанного состояния сильнее отражает действительное рассчитанное значение val-части, и наоборот.
Описанная выше и проиллюстрированная в Таблице 14 функциональная возможность является на самом деле специфическим методом интерполяции, для которого существует множество альтернативных вычислительных способов, которые приведут практически к тем же результатам. Автор изобретения называет этот способ взвешивания с помощью значений, обратных квадратам метрических расстояний избранных точек, способом "скалярной тяжести" из-за его схожести с падением силы притяжения пропорционально квадрату расстояния и из-за отсутствия здесь информации о направлении или векторе этой силы. Скалярная тяжесть дает интерполяционные результаты, очень похожие на результаты, которые можно получить при интерполяции с помощью широкого круга так называемых "способов нейронных сетей". Скалярная тяжесть обладает чрезвычайной простотой и скоростью в дополнение к обеспечению такого типа интерполяционных возможностей, который требуется в настоящем изобретении, и все это делает ее предпочтительней большинства других способов. Однако понимание настоящего изобретения и играемой в нем роли скалярной тяжести убедят читателя, что важна именно функциональная возможность этого типа интерполяции, и применение альтернативных способов интерполяции, в том числе любого из способов нейронных сетей, вместо скалярной тяжести в настоящем изобретении не создаст конструкта, значительно отличающегося от настоящего изобретения.
Автор изобретения также отмечает, что другие значения показателя способа скалярной тяжести, т.е. значения, отличные от минус двух, что соответствует обратному значению квадрата, могут использоваться для увеличения эффекта при определенных обстоятельствах. Отрицательные значения намного больше двух, вплоть до бесконечности, дадут разделение интерполяционного пространства на все более хорошо описанные (заданные) участки со все более резкими границами, таким образом все более выделяя ранее виденную ближайшую интерполяционную точку данных, до тех пор, пока при приближении к интерполируемому значению не будет использоваться только ближайшая интерполяционная точка. Отрицательные значения меньше двух, вплоть до нуля, дадут эффективную гомогенизацию интерполяционного пространства, содержащего, таким образом, все более близкие интерполяционные точки данных, до тех пор, пока, в нуле, результатом интерполяции не станет просто среднее значение всех доступных интерполяционных точек данных. Этот показатель может регулироваться, моделируя поведение узкого или широкого поля практически любого интерполяционного способа нейронной сети.
Строки 41 и 42 в Таблице 14 просто очищают накопитель, который нужен только для данной функции execute(). Этим завершается описание функций, представленных в Таблице 14.
Таблица 15 является примером процедуры, в виде функции на языке С, для расчета метрики от одного короба до другого в предпочтительном виде по изобретению.

Рассматриваемые данные короба обеспечиваются в строке 1 в Таблице 15 в виде двух переменных, причем обе имеют тип данных COROB. Эти переменные обозначены именами "to" и "from", чтобы было прямо видно, в каком направлении выполняют расчет посредством метрики: от короба "from" до короба "to". Конкретные вычисления производятся в строках 3-7 в Таблице 15. Строка 3 в Таблице 15 реализует функциональную возможность управляющего цикла, обеспечивающую рассмотрение по порядку каждого соответствующего состояния короба для двух данных коробов. Для каждого состояния в строке 4 в Таблице 15 формируется разность между val-частью соответствующих состояний двух коробов в виде значения переменной xi. В строке 5 в Таблице 15 значение xi возводится в квадрат, взвешивается с помощью sig-части соответствующего состояния только короба "from", и результат накапливается в переменной sum. В строке 7 в Таблице 15 вызвавшей процедуре выдается квадратный корень из значения переменной sum.
Причина того, что в данной метрике содержится sig-часть только короба "from", обсуждалась ранее. Это средство точного обеспечения простого декартова расстояния, квадратного корня из суммы квадратов, между двумя точками, известными еще как коробы, в пространстве в случае, если каждое из значений sig sig-части короба "from" точно равно 1,0 - в этом случае подпространство короба "from" точно совпадает с пространством, в котором это подпространство задано. Если некоторые или все из этих значений sig отклоняются от значения 1,0, то получается обобщенное подпространство. В обобщенном подпространстве два короба, к которым применяется метрика, могут не задаваться и, вероятно, на самом деле не задаются в идентичных обобщенных подпространствах пространства. В таком случае большая часть метрики расстояний становится нерефлексивной, т.е. может не давать одинаковых результатов измерений при измерении от одного короба к другому и при измерении в обратном направлении. Метрика, выбранная здесь в качестве предпочтительной формы для настоящего изобретения, является метрикой, дающей знакомые результаты вычислений декартовых расстояний в знакомых условиях необобщенного подпространства, и дает пригодные результаты при наличии обобщенных подпространств. Возможно, множество других вариантов, удовлетворяющих ранее обсуждавшимся условиям по отношению к метрике.
Конкретный пример использования функциональных возможностей архитектуры ячейки короба, описанных выше, представлен в Таблице 16.



Данный пример создает ячейку короба по фиг.3, полностью загружает ее данными, затем извлекает одну из ассоциаций, т.е. одну из пар короб-состояние, из памяти 44 короба ячейки по фиг.3 и использует часть короба этой пары для загрузки регистра 40 входных данных короба по фиг.3. Затем ячейка исполняется, давая новое значение состояния в регистре 46 выходного состояния по фиг.3, которое затем может сравниваться с частью состояния пары, извлеченной из памяти 44 короба по фиг.3.
В таблице 16 строки 1-4 задают в стандартом заголовке языка С файлы, необходимые для остальной части программы. Строка 5 в Таблице 16 вводит файл "cell.h" ячейки по фиг.3. Файл "cell.h" показан в таблице 7. Строка 6 в Таблице 16 устанавливает размер коробов, которые будут использоваться в этом примере, - конкретно, коробов, главное пространство которых имеет 100 измерений. Строка 7 в Таблице 16 является точкой входа, в которой начинается исполнение. Строка 7 в Таблице 16 обеспечивает стандартное средство списка параметров для получения данных из командной строки. Строка 8 в Таблице 16 задает различные имена накопителей и переменных, которые необходимы для данной программы. Строка 9 в Таблице 16 получает объект данных из командной строки и сохраняет его в переменной fract. Этой программе запускаться из командной строки с различными данными без необходимости в перекомпилировании. Строка 10 в Таблице 16 создает структуру данных для клетки и сохраняет ее в переменной cell. Строки 11-19 в Таблице 16 загружают в память 44 короба по фиг.3 клетки по фиг.3 случайные коробы, каждый из которых связан со случайным состоянием. Строка 11 в Таблице 16 является управляющей командой цикла, систематически проходящего все доступные места расположения накопителей в памяти 44 короба по фиг.3, общее количество которых задано константой MAX_PAIRS, определенной в строке 2 в Таблице 7. Строка 12 в Таблице 16 создает новый случайный короб, а строка 13 в Таблице 16 загружает этот короб в регистр 40 входного короба по фиг.3. Строка 14 в Таблице 16 создает новое случайное состояние, а строка 15 в Таблице 16 загружает это состояние в регистр 46 выходного состояния по фиг.3. Этим завершаются требования к инициализации для хранения данных в памяти короба клетки, так что в строке 16 в Таблице 16 вызывается функция learn() для выполнения переноса пары короб/состояние в память короба клетки. Строка 17 в Таблице 16 освобождает место для короба и для состояния, созданных ранее в цикле, чтобы избежать утечек памяти.
В таблице 16 строки 20-30 устанавливают проверку клетки и ее данных, которые были определены. Строка 20 в Таблице 16 создает новый случайный короб. В этом случае данные в коробе нерелевантны целям данного кода, и в строке 20 в Таблице 16 важно только выделение накопителя. Строки 21-30 в Таблице 16 систематически заменяют данные в коробе, созданном в строке 20 в Таблице 16, выбранным коробом из памяти короба, возможно, нарушенным каким-либо шумом, так что затребованный таким образом короб может быть представлен клетке, чтобы проверить, может ли клетка выработать значение состояния, которое было связано с этим коробом в ходе цикла в строках 11 -19 в Таблице 16. Строка 22 в Таблице 16 загружает в переменную fuzz случайное число в диапазоне от (-0,5*fract) до (+0,5*fract), где fract вводится пользователем программы из командной строки в строке 9 в Таблице 16. В строке 23 в Таблице 16 из памяти короба затребуется corob[0], являющийся первым коробом памяти короба данной клетки, и переменная fuzz добавляется к val-части каждого элемента короба, а результат этого вычисления сохраняется, затем в соответствующей val-части переменной corob. Строка 23 в Таблице 16 обеспечивает пользователя данной программы средством введения управляемых значений случайного шума в переменную corob, которая содержит короб, выбранный из памяти короба. В строках 24 и 25 в Таблице 16 выполняются регулировки вычисленного таким образом числа, так что результирующая val-часть переменной corob не будет выходить за пределы диапазона от 0,0 до 1,0 включительно. В строках 27 -29 в Таблице 16 подобная процедура применяется к sig-части выбранного короба. При выходе из цикла в строках 21-30 в Таблице 16 переменная corob будет содержать точную копию выбранного короба из памяти короба, если переменная fract имеет значение 0,0, и будет содержать приблизительную копию выбранного короба, если переменная fract имеет значение, отличное от 0,0. Чем больше значение переменной fract, тем больше отклонение результирующего короба в переменной corob от короба, выбранного в памяти короба. Этот механизм обеспечивает пользователя данной программы средством для проверки эффектов таких приближений.
В Таблице 16 строка 31 загружает регистр 40 входного короба по фиг.3 клетки по фиг.3 только что созданными данными в переменной corob. Строка 32 в Таблице 16 сообщает пользователю значение переменной fract, определенное пользователем. Строка 33 в Таблице 16 сообщает пользователю val-часть состояния, связанного в памяти короба с выбранным коробом, и эта val-часть должна рассматриваться как "правильный" ответ, который должен вырабатываться посредством исполнения клетки. При инициализированной памяти короба и загруженном входном регистре клетка может быть исполнена, и это делается в строке 34 в Таблице 16. Строки 35 и 36 в Таблице 16 сообщают пользователю содержание регистра 46 выходного состояния по фиг.3, после того, как клетка была исполнена. Это содержание может затем сравниваться с так называемым "правильным" ответом, чтобы увидеть, насколько хорошо клетка выполняет свои различные функции.
Теперь автор изобретения покажет результаты, предъявленные пользователю при двух исполнениях программы по Таблице 16. Вот первый результат:
коэффициент шума: fract=0,000000
исходное значение val=0,293723
клетка вырабатывает val=0,293723 и sig=1,000000
Вышеприведенный первый результат показывает, что значение переменной fract, определяемое пользователем в командной строке, равно 0,0 и что "правильное" значение, хранящееся в памяти короба, для val-части состояния равно 0,293723. На выходе установлено, что клетка вырабатывает val, равное 0,293723 со значением sig, или значимости, равным 1,000000. Таким образом, если в короб не введено шума, клетка вырабатывает в точности "правильный" ответ со стопроцентной доверительностью.
Вот второй результат:
коэффициент шума: fract=0,010000
исходное значение val=0,293723
клетка вырабатывает val=0,295516 и sig=0,995363
В вышеприведенном втором результате вводится однопроцентный коэффициент шума, значение переменной fract, равное 0,01. В этом случае выход показывает, что клетка выработала значение val, равное 0,295516 при значении sig, равном 0,995363. Таким образом, небольшой шум дает слабую вариацию в выработанной переменной val при слегка уменьшенной доверительности, что и ожидалось.
Отметим, что доступна генерализация клетки короба. Регистр 46 выходного состояния по фиг.3 клетки может быть сделан так, чтобы удерживать короб, множество состояний вместо одного состояния. Память 44 короба по фиг.3 затем могла бы расширяться для восприятия обучающих ассоциаций входных коробов клетки выходными коробами, а не только выходными состояниями. Исполнение клетки просто применяло бы взвешивающую функцию к заданному соответствующему элементу всех выходных коробов, формируя соответствующий элемент нового выходного короба. Это фактически эквивалентно конструкции из такого количества клеток, сколько элементов содержится в данном выходном коробе, где каждая клетка содержит только один элемент короба или состояние в качестве размера выходного регистра. Клетка короб-короб изначально более эффективна, чем клетка короб-состояние, если она может быть использована в данном приложении. Для сохранения общности короб-систем автор изобретения, тем не менее, не будет использовать такую клетку короб-короб, поскольку, как можно будет вскоре увидеть, короб-системы могут требовать модели короб-состояние. Использование клеток короб-короб в такой ситуации было бы неэффективным, поскольку большая часть выходного короба была бы проигнорирована и растрачена впустую.
Архитектура короб-вычислительной системы
Далее автор изобретения описывает реализацию короб-вычислительных систем, которые являются системами клеток короба. Короб-компьютерные системы являются полнофункциональными, с неограниченным использованием, полными по Тьюрингу вычислительными системами, которые могут исполнять любую вычислимую функцию, и вычислительные возможности которых лежат в областях, подобных областям вычислительных возможностей живых систем обработки информации.
Фиг.4 является схематическим чертежом, иллюстрирующим основные компоненты короб-вычислительной системы по настоящему изобретению. Массив клеток 50 короба состоит из определенного числа клеток короба. Для удобства обсуждения автор изобретения обозначает самую левую клетку короба массива клеток 50 короба как клетку 1 короба массива; клетка короба, находящаяся непосредственно справа от нее в массиве 50 клеток короба, будет обозначена как клетка 2 короба, и так далее, вплоть до самой правой клетки короба в массиве клеток 50 короба, которая будет обозначена как N, где "N" представляет собой определенное количество клеток короба, которые составляют массив клеток 50 короба.
На фиг.4 все клетки массива клеток 50 короба называются "внутренними" клетками короба, указывая на то, что они являются элементами клеток, составляющих данную короб-вычислительную систему, а также эквивалентно показывает, что они являются элементами массива клеток 50 короба.
На фиг.4 некоторые или все клетки массива клеток 50 короба могут также иметь одно из дополнительных обозначений "сенсор" или "актор", либо оба этих обозначения. Клетка-сенсор массива клеток 50 может иметь значение состояния, приписанное ей целиком или частично; т.е. значение в регистре 46 выходного состояния по фиг.3 клетки-сенсора массива клеток 50 короба по фиг.4 может содержать данные, которые устанавливаются или на которые оказывает влияние средство, внешнее по отношению к короб-вычислительной системе. Клетка-актор массива клеток 50 короба может иметь свое значение состояния, скопированное целиком или частично в положение, находящееся вне самой короб-вычислительной системы; т.е. значение регистра 46 выходного состояния по фиг.3 клетки-актора массива клеток 50 короба по фиг.4 может иметь данные, считываемые или частично считываемые с помощью средства, которое является внешним по отношению к короб-вычислительной системе.
Клетки-сенсоры обеспечивают средство, с помощью которого внешние средства могут подавать данные в короб-вычислительную систему, в то время как клетки-акторы обеспечивают средство, с помощью которого внешние средства могут считывать данные из короб-вычислительной системы.
На фиг.4 группа клеток, помеченная позицией "54", содержит обозначенное множество клеток-сенсоров 54 массива клеток 50 короба, а группа клеток, помеченная позицией "56", содержит обозначенное множество клеток-акторов 56 массива клеток 50 короба. Как отмечалось, любая клетка короба массива клеток 50 короба может функционировать как клетка-сенсор, как клетка-актор, как и клетка-сенсор и клетка-актор, либо ни как клетка-сенсор, ни как клетка-актор, в зависимости от точных указаний для частной короб-вычислительной системы в контексте настоящего изобретения, что может определяться разработчиком.
На фиг.4 отображение 52 определяет связи между клетками короба массива клеток 50 короба. Отображение 52 является двумерным регистровым массивом элементов хранения данных, которые могут содержать значения либо "истинно", либо "ложно" в соответствующих представлениях, либо могут содержать более сложные значения. Двумерный массив элементов, а следовательно, и отображение 52 состоит из N столбцов по N элементов хранения данных в каждом, где "N" - определенное количество клеток короба в массиве клеток 50 короба. Каждый столбец отображения 52 соответствует в точности одной клетке короба массива клеток 50 короба. Каждый элемент хранения данных данного столбца отображения 52 также соответствует в точности одной клетке короба в массиве клеток 50 короба. Значения в элементах хранения данных отображения 52 определяют, какие клетки короба в массиве клеток 50 короба принимают вход от клеток короба в массиве клеток 50 короба.
Например, выберем отдельный элемент отображения 52. Предположим, что этот выбранный элемент находится в столбце "с" в строке "r" отображения 52 определенного количества клеток короба в массиве клеток 50 короба, где "с" и "r" представляют собой числа от 1 до N. Тогда значение "истинно" в выбранном элементе показывает, что клетка короба массива клеток 50 короба под номером "с" будет принимать вход от клетки короба массива клеток 50 короба под номером "r", в то время как значение "ложно" в том же самом выбранном элементе показывает, что вход не будет приниматься. Если каждый элемент хранения данных отображения 52 способен принимать больше, чем просто значение "истинно" или "ложно", например, если эти элементы хранения данных могут хранить число типа данных "integer" (целое) или число типа данных "float" (число с плавающей запятой), то может быть определена более распространенная зависимость между клетками короба массива клеток 50 короба, такая как математическая пропорция. Однако в предпочтительном виде настоящего изобретения каждый элемент должен принимать только значения "истинно" или "ложно", соответствующим образом представленные в конкретной реализации.
Более точно, когда автор изобретения утверждает, что клетка с короба массива клеток 50 короба "принимает вход" от другой такой клетки r короба, он имеет в виду то, что один из элементов хранения данных регистра 40 входного короба по фиг.3 клетки с короба зарезервирован исключительно для состояний, время от времени затребуемых из содержимого регистра 46 выходного состояния по фиг.3 клетки r короба. Вскоре будет описано, когда в точности и при каких обстоятельствах такое затребование имеет место.
Отметим, в частности, что отображение 52 обеспечивает средство, которое позволяет каждой клетке короба массива клеток 50 короба принимать вход от любых или от всех клеток короба массива клеток 50 короба, в том числе от самой себя. Отображение 52 составляет то, что обычно называется специалистами многократным координатным соединителем. Таким образом, как определено, многократный координатный соединитель является компонентом короб-вычислительной системы.
Короб-вычислительная система является компьютером общего назначения. Как таковая, она должна программироваться для каждой отдельной задачи, которую она должна выполнять. Одной частью этого необходимого программирования для выполнения отдельной задачи является определение содержания каждого элемента хранения данных отображения 52. То, как именно выполнить такое определение, как запрограммировать короб-вычислительную систему в целом, не входит в рассматриваемый здесь объем изобретения, так же, как искусство программирования традиционной вычислительной системы находится вне объема описания природы традиционного программируемого компьютера. Важным здесь является тот факт, что настоящее изобретение обеспечивает средство для выполнения такого программирования.
Ранее было отмечено, что все основанные на коробах вычислительные системы могут поддерживать три различных фазы программирования и использования: фазу архитектуры, фазу обучения и фазу действия. Эти три фазы теперь могут быть более полно поняты с учетом фиг.4.
Фаза архитектуры программирования и использования основанной на коробах вычислительной системы состоит из определения: количества клеток короба, которые будут составлять массив клеток 50 короба; содержания отображения 52, которое определяет взаимосвязи между клетками короба массива клеток 50 короба; отдельных клеток короба массива клеток 50 короба, которые следует обозначить в качестве клеток- "сенсоров"; и отдельных клеток короба массива клеток 50 короба, которые следует обозначить в качестве клеток- "акторов". Обычно необходимо также при разработке конкретной прикладной программы для основанной на коробах вычислительной системы, но не в качестве части программирования и использования самой основанной на коробах вычислительной системы, определить природу любой сенсорной или акторной функциональной возможности, внешней по отношению к клеткам-сенсорам и к клеткам-акторам, требуемой для подготовки данных для ввода в клетки-сенсоры или для обработки данных, принятых от клеток-акторов, и природу взаимодействий, которые могут иметь место между этими внешними функциональными возможностями и клетками-сенсорами и клетками-акторами основанной на коробах вычислительной системы. Проще говоря, программист должен решить, как и с какой целью клеткам-сенсорам основанной на коробах вычислительной системы будут присвоены значения состояния, а также как и с какой целью будут затребоваться состояния клеток-акторов. В живых системах внешние сенсорные функциональные возможности часто включают в себя такие сущности, как глаза и уши, в то время как внешние акторные функциональные возможности выражаются в движении мышц.
Фаза обучения программирования и использования основанной на коробах вычислительной системы может иметь статический или динамический компонент, либо оба этих компонента. Статическое обучение основанной на коробах вычислительной системы состоит из инсталляции подходящих данных, т.е. пар коробов и состояний, в различные экземпляры памяти 44 короба по фиг.3. То, как именно следует разработать эти подходящие данные, находится далеко за пределами объема патентной защиты настоящего изобретения. Тем не менее, вскоре будет представлен простой пример. Динамическое обучение основанной на коробах вычислительной системы состоит из разрешения основанной на коробах компьютерной системе решать для себя автоматически, какие данные, т.е. пары короб-состояние, пригодны для хранения в различных экземплярах памяти 44 короба по фиг.3. Исследуются способы достижения этой цели, и это снова далеко выходит за пределы текущего объема патентной защиты настоящего изобретения. Однако можно описать один простой способ динамического обучения.
Каждый раз, когда данной клетке короба не удается найти в своей памяти 44 короба по фиг.3 "хорошее" соответствие коробу, присутствующему в данный момент в регистре 40 входного короба по фиг.3 клетки короба, обычно обозначаемого как "текущий короб", клетка короба может реагировать посредством сохранения текущего короба в паре с текущим состоянием в памяти короба. Это является эффективной обучающей стратегией для многих ситуаций и на самом деле опирается на живые нейронные системы.
Фаза действия программирования и использования основанной на коробах вычислительной системы состоит из продолжающейся итерации, каждый шаг которой состоит из следующей последовательности: принять любой доступный для клеток-сенсоров по фиг.4 вход; загрузить регистр 40 входного короба по фиг.3 всех клеток короба массива клеток 50 короба по фиг.4 путем доступа к содержанию регистра 46 выходного состояния клеток короба, обозначенных для каждой клетки короба в отображении 52 по фиг.4; исполнить по очереди каждую клетку короба в соответствии с ее функциональной возможностью для получения нового значения состояния в ее регистре 46 выходного состояния по фиг.3 из ее регистра 40 входных данных короба по фиг.3 и ее памяти 44 короба по фиг.3; и, наконец, для каждой ячейки-актора, сделать доступными для внешней функциональной возможности данные в регистре 46 выходного состояния по фиг.3 этой ячейки. Будучи инициированным, этот процесс продолжается бесконечно, подобно тому, как машинный цикл традиционного компьютера продолжается бесконечно, независимо от того, какую программу может выполнять эта машина. Автор изобретения представляет подробный пример структуры и действия короб-вычислительной системы по фиг.4. Этот пример реализует предпочтительный вид короб-вычислительной системы. Тем не менее, как указывалось ранее, данный патент предусматривает, что дизайн и конструкция короб-вычислительных систем содержит множество переменных и решений и что существуют широкие колебания в задании этих переменных и принятии этих решений, так что точный выбор, даже в предпочтительном виде, не может давать большого преимущества над другими выборами при данном наборе условий. Как и предыдущие примеры, этот пример приводится на языке программирования С для удобства в выражении концепций. Как хорошо известно специалистам и в программировании, и в проектировании электронных схем, любая написанная на языке С программа всегда может быть реализована в виде эквивалентного электронного аппаратного обеспечения и наоборот, с ограничением только по времени и стоимости. Подобным же образом, написанная на языке С программа может быть реализована на других языках программирования, либо реализована в виде другой, но эквивалентной С-программы без значительного отклонения от функциональных возможностей исходной написанной на языке С программы.
Пример предпочтительного вида короб-вычислительной системы по фиг.4 начинается в Таблице 17. Структура и функциональные прототипы короб-вычислительной системы по фиг.4 объясняются в виде файла заголовка на языке С. Номера строк добавлены к стандартному коду, написанному на языке С, для упрощения обсуждения.

Ранее автор изобретения отметил, что средство 52 отображения по фиг.4 является двумерным массивом, каждый столбец которого задает, какие ячейки короба массива ячеек 50 короба по фиг.4 обеспечивают входные данные для ячейки короба массива ячеек 50 короба по фиг.4, соответствующей отдельному столбцу. В строках 1-4 в Таблице 17 столбец средства 52 отображения по фиг.4 представляется в виде структуры данных typedef, которая устанавливает имя MAP типа данных. Тип данных MAP будет использоваться для построения столбцов средства 52 отображения по фиг.4 и для других целей, как вскоре будет видно. Строка 2 в Таблице 17 задает количество ячеек, т.е. длину столбца. Напомним, что элементы хранения данных столбца заданы для всех ячеек короба в массиве ячеек 50 короба по фиг.4, переменная nbr_of_cells в строке 2 будет установлена на то же значение, что и переменная nbr_of_cells в строке 7, которая задает общее количество ячеек короба в массиве ячеек 50 короба по фиг.4. Затем в строке 3 в Таблице 17 задается указатель на накопитель для столбца, а пространство хранения будет выделено позже в функции make_map(), что вскоре будет обсуждено. В больших короб-вычислительных системах это общее количество ячеек короба может быть весьма большим, в то время как количество ячеек, от которых любая заданная ячейка получает входные данные, может быть гораздо меньше, из-за чего большинство элементов данных в столбце помечаются значением "ложно", а несколько оставшихся помечаются значением "истинно". Это весьма расточительный подход, которого можно избежать посредством несколько более сложной схемы хранения, которая сохраняет только индексы ячеек, помеченных значением "истинно", вместо индикаторов для каждой ячейки, но описанный здесь подход, конечно же, более ясен для читателя. Производственная короб-система, вероятнее всего, воспользуется более эффективным подходом, таким как только что описанный.
Строки 6-13 в Таблице 17 задают (typedef) структуру короб-системы, соответствующей структуре, показанной в качестве предмета фиг.4, и приводят пример области данных короб-вычислительной системы. Как указано выше, строка 7 в Таблице 17 задает общее количество ячеек короба в массиве ячеек 50 короба по фиг.4. Строка 11 в Таблице 17 обеспечивает указатель массива ячеек 50 короба по фиг.4, который будет вскоре размещен в функции make_corob_system(). Строка 10 подобным же образом обеспечивает указатель накопителя, который будет содержать средство 52 отображения по фиг.4. Строки 7 и 8 в Таблице 17 используют тип данных MAP для задания накопителя для данных, описывающих, какие ячейки являются обозначенными ячейками-сенсорами, а какие ячейки являются обозначенными ячейками-акторами, соответственно. Переменная prev_stat в строке 12 в Таблице 17 используется для того, чтобы содержать предыдущие состояния всех ячеек массива ячеек 50 короба по фиг.4 в ходе текущей итерации короб-системы для предотвращения исполнения отдельной ячейки от использования заново вычисленных значений ячеек вместо значений, являющихся результатом предыдущей итерации, что может случиться, когда ячейка принимает входные данные от ячеек, которые уже были исполнены в ходе итерации. Этот накопитель может быть легко удален - и должен быть удален - в текущем предпочтительном виде настоящего изобретения путем простого сохранения всех состояний ячеек во входных регистрах ячеек, которым они нужны, как это описывалось ранее, однако опять-таки показанная форма представляется более понятной читателю.
Функциональные прототипы, показанные в строках 15-18 в Таблице 17, полезны в написанных на языке С программах при отладке. Каждая из этих функциональных возможностей прототипов будет теперь подробно рассмотрена в виде отдельного написанного на языке С программного модуля.
Таблица 18 приводит в качестве примера в виде написанной на языке С функции, make_map(), процедуру для создания и инициализации накопителя, называемого здесь по имени переменной mар, используемого для принятия столбца средства 52 отображения по фиг.4, и для содержания подобных данных средства отображения в соответствии с предпочтительным видом настоящего изобретения.

В строке 3 в Таблице 18 создается переменная mар. Строка 4 в Таблице 18 задает длину выделяемого накопителя, в то время как строка 5 в Таблице 18 выполняет само выделение накопителя. Строки 6 и 7 в Таблице 18 выполняют цикл над элементами массива mар, устанавливая каждый элемент равным значению, обеспечиваемому массивом map_data, вводимым через список параметров функции в строке 1 в Таблице 18. Строка 7 в Таблице 18 выдает накопитель вызвавшей процедуре для дальнейшего использования.
Таблица 19 приводит в качестве примера в виде написанной на языке С функции, make_corob_system(), процедуру для создания и инициализации накопителя, называемого здесь именем переменной сs, используемого для содержания вычислительной системы, являющейся предметом фиг.4.

Строки 1-3 в Таблице 19 показывают несколько важных параметров. В строке 2 в Таблице 19 переменная nbr_of_cellsзaдaeт, сколько ячеек будет содержать массив ячеек 50 короба по фиг.4. Строка 2 в таблице 19 обеспечивает также переменный массив nbr_of_dims[], который является размером пространства короба для каждой ячейки. Строка 3 в Таблице 19 обеспечивает переменные sensor, actor и internal, которые будут использоваться для содержания элементов завершенной структуры данных короб-системы. Строка 5 в Таблице 19 создает накопитель для самой короб-системы. Строка 6 в Таблице 19 устанавливает количество ячеек в короб-системе. Строка 7 в Таблице 19 создает накопитель для переменной sensor, который будет содержать указания на то, какие ячейки являются ячейками-сенсорами 54 по фиг.4, и инициализирует его с помощью данных, обеспечиваемых в строке 3 в Таблице 19. Строка 8 в Таблице 19 создает накопитель для переменной actor, который будет содержать указания на то, какие ячейки являются ячейками-акторами 56 по фиг.4, и инициализирует его с помощью данных, обеспечиваемых в строке 3 в Таблице 19. Строка 9 в Таблице 19 создает накопитель для переменной internal, который будет содержать отображение 52 по фиг.4. В строке 10 в Таблице 19 задается указатель, который будет указывать на накопитель массива для ячеек массива ячеек 50 короба по фиг.4. Строки 11-14 в Таблице 19 создают накопитель и инициализируют ячейки массива ячеек 50 короба по фиг.4 и средства 52 отображения по фиг.4. Строка 12 в Таблице 19 создает накопитель, затем перемещает данные столбца для ячейки "i" в их правильное место в структуре данных короб-системы. Строка 13 в Таблице 19 создает накопитель и инициализирует отдельную ячейку, как ранее было описано в разделе о функции make_cell(). Наконец, строка 16 в Таблице 19 выдает вызывающей процедуре завершенную структуру короб-вычислительной системы по фиг.4 для дальнейшего использования.
Таблица 20 приводит в качестве примера в виде написанной на языке С функции, execute_cells(), процедуру для исполнения одной внутренней итерации ячеек короб-вычислительной системы по фиг.4

В строке 1 в Таблице 20 указатель на короб-вычислительную систему, с которой должны производиться итерации, передается в функцию. Строки 3-6 в Таблице 20 перемещают содержимое регистра 46 выходного состояния по фиг.3 каждой из ячеек в массиве ячеек 50 короба по фиг.4 в область хранения, как было описано ранее, чтобы гарантировать, что каждая ячейка использует правильную информацию в ходе своего исполнения. Может оказаться более эффективным перемещать данные непосредственно в регистр 40 входных данных короба по фиг.3 каждой ячейки в массиве ячеек 50 короба по фиг.4, но показанный здесь способ кажется более ясным представлением функциональной возможности для читателя. Цикл, показанный в строках 7-20 в Таблице 20, задает значения регистра 40 входных данных короба по фиг.3 для каждой ячейки, а затем исполняет ячейку. Строки 9-17 в Таблице 20 выполняют первое, в то время, как строка 19 в Таблице 20 выполняет последнее. Когда цикл в строках 7-20 в Таблице 20 завершается, выполнена одна внутренняя итерация короб-вычислительной системы. Все, что остается - запустить любую внешнюю акторную функциональную возможность для обеспечения выхода короб-вычислительной системы для данного цикла итерации, затем запустить любую внешнюю сенсорную функциональную возможность для обеспечения подобным же образом входа. Как это сделать, будет вскоре показано.
Полный программный пример использования функциональных возможностей короб-вычислительной системы, описанной выше, представлен в Таблице 21, Таблице 22 и Таблице 23. Этот пример показывает каждую из фаз короб-вычислений - фазы архитектуры, обучения и действия. В целом, пример сохраняет сто пар короб/короб (как вскоре будет определено) в массиве из десяти ячеек, затем восстанавливает их. Коробы задаются так, что выходные данные короба первой сохраненной пары коробов становятся входными данными короба для второй пары коробов, выходные данные короба второй сохраненной пары коробов становится входными данными короба третьей пары коробов, и так далее для всех сохраненных пар. Во время действия входные данные короба первой пары предъявляются системе посредством сенсорного ввода, а выходные данные короба затребуются посредством акторного вывода. Затем затребованный короб становится “входным” коробом и затребуется новый “выходной” короб, и так далее, пока не произойдет столько итераций, сколько коробов сохранено. Если система работает по указанной схеме, этот "цепной" подход должен привести к тому, что последний короб будет таким же, как и изначально сохраненный “выходной” короб последней сохраненной пары. В этом примере используется метрика для определения того, что это действительно так.
В описании функциональных возможностей ячейки короба автор изобретения показал пример, связывающий “входной” короб с состоянием. Короба состоят из элементов, называемых состояниями, поэтому естественным является собрать выходные состояния некоторого количества ячеек короба в один короб. Это на самом деле является фундаментальной концепцией в короб-вычислительных системах, и в данном примере это будет проиллюстрировано.


В Таблице 21 строки 1-4 вводят стандартные заголовочные файлы на языке С, необходимые для остальной программы. Строка 5 в Таблице 21 вводит задание ячейки короба по фиг.3, которой является файл "cell.h", показанный в Таблице 7. Строка 6 в Таблице 21 вводит задание короб-вычислительной системы по фиг.4, которой является файл "corob_system.h", показанный в Таблице 17. Строка 8 в Таблице 21 является заданием константы, которая будет использоваться для установления общего количества ячеек массива ячеек 50 короба по фиг.4 в данном примере.
Строка 9 в Таблице 21 задает константу, которая будет использоваться для ограничения количества итераций в данном примере. Строки 11 и 12 в Таблице 21 обеспечивают информацию прототипа, используемую компиляторами языка С при отладке. Строка 14 в Таблице 21 создает переменную cs типа данных COROB_SYSTEM, которая будет хранить короб-систему для данного примера.
Строки 16-33 в Таблице 21 функционируют в качестве программного кода для фазы архитектуры данного примера короб-вычислительной системы. Строка 16 в Таблице 21 задает ячейки-сенсоры 54 по фиг.4 как первые пять (самых левых) ячеек из десяти ячеек массива ячеек 50 короба по фиг.4, идентифицируемые с помощью значений "1" в первых пяти позициях массива sensor_map в Таблице 21. В этом и в других отображениях данного примера значение "1" будет означать "истинно", а значение "0" будет означать "ложно". Подобно ячейкам-сенсорам в строке 16 в Таблице 21, строка 18 в Таблице 21 задает ячейки-акторы 56 по фиг.4 как последние пять ячеек десяти ячеек короб-системы. Строки 20-31 в Таблице 21 задают средство 52 отображения по фиг.4. Строка 21 в Таблице 21, состоящая только из значений "0" или "ложно", указывает на то, что первая (самая левая) ячейка массива ячеек 50 короба по фиг.4 не принимает входных данных от какой-либо другой ячейки в массиве ячеек 50 короба по фиг.4. Так и должно быть, поскольку эта ячейка уже была задана как ячейка-сенсор, которая принимает входные данные извне короб-системы, способом, который вскоре будет описан. Подобным же образом строки 22-25 в Таблице 21 указывают, что оставшиеся четыре ячейки-сенсора не принимают входных данных от какой-либо другой ячейки массива ячеек 50 короба по фиг.4. Строка 26 в Таблице 21 указывает, что шестая ячейка массива ячеек 50 короба по фиг.4 принимает входные данные только от ячеек 1-5, что показано пятью значениями "1" или "истинно" в первых пяти позициях строки 26, и значениями "0" или "ложно" в остальных позициях. Остальные ячейки массива ячеек 50 короба по фиг.4, а именно ячейки 7-10, подобным же образом задаются в строках 27 -30 в Таблице 21, принимая входные данные от ячеек 1-5. Наконец, строка 33 в Таблице 21 задает размерность, которая должна использоваться для каждой из десяти ячеек массива ячеек 50 короба по фиг.4. Информация в строке 33 в Таблице 21 может, разумеется, вырабатываться автоматически из информации в строках 20-31 в Таблице 21, поскольку эти строки задают зависимости каждой ячейки, но строка 33 в Таблице 21 делает это здесь исключительно для ясности.
Таблица 22 задает С-функцию set_sensor(), которая используется для загрузки короба в ячейки-сенсоры 54 по фиг.4.

Строка 1 в Таблице 22 обозначает имя функции set_sensor() и задает и короб-систему по фиг.4, в которую эта функция должна войти для задания ячеек-сенсоров, являющуюся параметром cs, и параметр corob, который следует использовать в качестве значений, которые задаются для этих ячеек-сенсоров. Цикл в строках 5-7 в Таблице 22 выполняет это задание ячеек-сенсоров.
Таблица 23 представляет собой управляющую программу для данного примера короб-системы. Она содержит разделы для фазы архитектуры, фазы обучения и фазы действия системы и имеет дело с сенсорами и акторами.



Раздел архитектуры данного примера показан в строках 4-6 в Таблице 23. Строка 4 в Таблице 23 является строкой комментария, а строки 5 и 6 в Таблице 23 составляют один оператор языка С, который вызывает функцию make_corob_system() для построения короб-системы с заданными параметрами, затем присваивает переменной cs получившиеся данные для дальнейшего использования. Каждый из параметров вызова функции описан в Таблице 21, которая обсуждалась ранее.
Строки 8-19 в Таблице 23 содержат раздел обучения данного примера. В данном примере используется статическое обучение, что означает, что сначала автор изобретения проинсталлирует все содержание экземпляров памяти 44 короба по фиг.3 ячеек массива ячеек 50 короба по фиг.4 до перехода к разделу действия, и это содержание не будет изменяться в процессе действия. Цикл в строке 10 в Таблице 23 создает массив cin[i] входных коробов и инициализирует короба в виде случайных коробов для дальнейшего обращения. Отметим, что создается на один короб больше, чем число CASES, которое в соответствии со строкой 9 в Таблице 21 равно 100. Цикл в строках 11-19 в Таблице 23 управляет тем фактом, что будет сохранено количество пар коробов, равное значению константы CASES. Цикл в строках 12-18 в Таблице 23 загружает пары значений коробов и состояний в ячейки массива ячеек 50 короба по фиг.4. Строка 13 в Таблице 23 пропускает те строки, в которых нет зависимости в соответствии с массивом nbr_of_dims[], что обсуждалось ранее. Строка 14 в Таблице 23 загружает короб пары, а строки 15 и 16 в Таблице 23 загружают состояние пары. Отметим, что в строке 15 в Таблице 23 в val-элемент ячейки загружается val-элемент, взятый из подходящего места следующего, не текущего индекса массива cin[] “входных” коробов. Это устанавливает "цепную" природу последовательных коробов, являющуюся характеристикой данного примера. Отметим также, что в строке 16 в Таблице 23 sig-элемент каждой ячейки устанавливается равным "1,0", задавая то, что, когда применяется метрическое расстояние, автор изобретения предпочитает точные соответствия, либо настолько близкие к точным, насколько возможно. Строка 17 в Таблице 23 увеличивает переменную, индексирующую состояние в “выходном” коробе, cout[i], для загрузки в текущую загруженную ячейку. Строка 18 в Таблице 23 инсталлирует эту пару в память 44 короба ячейки по фиг.3. Цикл в строках 10-19 в Таблице 23 заканчивается, когда все данные загружены, завершая фазу обучения данного примера.
Фаза действия данного примера описывается в строках 21-43 в Таблице 23 и иллюстрирует последовательность действий, которая содержит действие короб-вычислительной системы. В строке 23 в Таблице 23 создается для использования переменная rslt результирующего короба, связанная с акторной частью данной фазы действия, и этой переменной rslt идентичным образом присваиваются случайные значения, все равно какие, поскольку эти значения вскоре будут переписаны. Строки 25-28 в Таблице 23 инсталлируют короб в переменной cin[0] в состояния ячеек-сенсоров. Это инициализирует ячейки-сенсоры, так что может начаться последовательность исполнения, которой подвергается короб-вычислительная система в данном примере. Строки 29-43 в Таблице 23 совершают итерации короб-вычислительной системы в количестве, равном значению константы CASES, которая, как отмечалось ранее, равна 100. Во-первых, все ячейки короб-вычислительной системы исполняются в строке 31 в Таблице 23. Во-вторых, в строках 33 -36 в Таблице 23 осуществляется доступ к ячейкам-акторам, извлекаются их значения состояния, и эти значения помещаются в переменную rslt. В-третьих, в строках 39-42 в Таблице 23 из переменной rslt загружаются ячейки-сенсоры. Эти три шага: (1) исполнение ячеек, (2) вывод данных из ячеек-акторов и (3) ввод данных в ячейки-сенсоры - составляют один цикл процесса итерации фазы действия короб-вычислительной системы.
Отметим, что между шагом (2), т.е. выводом данных из ячеек-акторов, и шагом (3), т.е. вводом данных в ячейки-сенсоры, обычно происходит действие, внешнее по отношению к самой короб-системе. Это внешнее действие может быть простым, как в данном текущем примере, где переменная rslt просто передается сенсорам, либо произвольно сложным. При работе с короб-вычислительными системами это внешнее действие часто называется родовым понятием "функция среды", чтобы описывать что угодно, что осуществляет доступ к данным ячеек-акторов короб-системы, обрабатывает их и представляет данные ячейкам-сенсорам короб-системы.
После завершения фазы действия должна исполняться строка 44 в Таблице 23. Эта строка просто печатает номер только что завершенной итерации фазы действия и значение, выданное функцией metric(), из короба, являющегося последним в начальной инициализационной цепочке и хранящегося в переменной cin[CASES], в короб, в данный момент находящийся в переменной rslt, которая только что была выработана последней итерацией фазы действия. Вот информация, печатаемая строкой 44 в Таблице 23: итерация 100: metric=0,000000
Интерпретация этого выходного значения состоит в том, что было получено нулевое метрическое расстояние от последнего короба в инициализационной цепочке до последнего результата цепочки итераций. Это может происходить только тогда, когда цепочечная последовательность успешно пройдена. На этом данный пример завершен.
Вычисления с помощью короб-вычислительных систем
Короб-вычислительные системы являются универсальными вычислительными системами с новыми возможностями. В данном разделе автор изобретения подтверждает это утверждение и описывает некоторые последствия и использования настоящего изобретения.
Хотя ячейка представляет собой фундаментальный строительный блок короб-вычислительных систем и сама по себе является новым и полезным конструктом, по-настоящему революционная сила данного изобретения достигается за счет объединений ячеек, действующих в короб-вычислительной системе по фиг.4. Путем объединения ячеек и их взаимосоединения различными способами возможно построение вычислительных конструктов, которые ассоциируют короба с коробами, как было показано выше.
Возможности взаимосоединения, обеспечиваемые отображением 52 по фиг.4, охватывают все возможные взаимосоединения между ячейками массива ячеек 50 короба по фиг.4, начиная с предельного случая, когда ни одна из ячеек не зависит ни от одной другой ячейки, вплоть до другого предельного случая, когда каждая ячейка зависит от всех остальных ячеек. Некоторые из этих конфигураций взаимосоединения возникают регулярно при применении короб-вычислительных систем к реальным задачам.
Одна из общих конфигураций взаимосоединения называется "Х-модель", поскольку расположение значений "1" или "истинно" формирует большой символ "X" на средстве 52 отображения по фиг.4, лучи этого символа "X" могут достигать всех четырех углов средства 52 отображения по фиг.4. Х-модель полезна для реализации иерархических систем распознавания образов и генерирования функций.
Еще одна общая конфигурация взаимосоединения называется "доля". Она образуется в короб-вычислительных системах по фиг.4, в которых все ячейки массива короб-ячеек 50 по фиг.4 обозначены либо как ячейки-сенсоры, либо как ячейки-акторы, но не те и другие одновременно. Доля полезна для ассоциирования пар коробов, в частности, пар, в которых два короба имеют различные размерности. Это позволяет составленной таким образом короб-вычислительной системе близко эмулировать интерполяционные характеристики традиционных нейронных сетей.
Существует способ для математического доказательства того, что вычислительная система является универсальной вычислительной системой. Это осуществляется путем доказательства того, что рассматриваемая вычислительная система эквивалентна математическому конструкту, называемому "универсальной машиной Тьюринга" (Turing), и на самом деле может реализовывать, по меньшей мере, в пределах возможностей своей памяти, этот математический конструкт. Автор изобретения не намерен формально здесь доказывать эту эквивалентность. Вместо этого он утверждает, что это в самом деле доказуемо для настоящего изобретения, и приводит следующий внушающий доверие аргумент. Автор изобретения предполагает, что читатель является специалистом по машинам Тьюринга, и переходит поэтому непосредственно к обсуждению.
Таблица состояний машины Тьюринга позволяет легко построить ее с помощью короб-вычислительной системы. Все необходимые состояния связаны с уникальными коробами, и с помощью способов по настоящему изобретению строится короб-вычислительная система, реализующая таблицу перехода состояний. Входом в таблицу состояний является символ ленты, и каждый элемент множества всех возможных символов ленты связывается с уникальным коробом с помощью способов настоящего изобретения. Подобным же образом уникальные короба соответствуют каждому элементу множества движений ленты. Все это очень просто.
Наиболее интересной частью проблемы является реализация самой ленты. Каждое положение ленты должно быть регулярно записываемым и должно сохранять то, что было записано. Чтобы выполнить это, автор изобретения сначала отмечает, что существует хорошо известный вид машины Тьюринга, в котором ни одно из положений на ленте не записывается более одного раза. Вместо этого, когда необходимо обновить ячейку, создается полностью новая копия данных ленты, содержащая обновление, и помечается как "активная", а старая копия данных состояния помечается как "неактивная" и аннулируется. Разумеется, это очень расточительно в отношении ресурсов памяти, но сама по себе машина Тьюринга полезна как математический конструкт, а не как практическая вычислительная парадигма, поэтому это не имеет значения.
Следует также отметить, что даже люди, без помощи карандаша и бумаги или их эквивалентов, способны эффективно обрабатывать в голове только очень небольшие системы машины Тьюринга. Короб-вычислительные системы эффективны там, где эффективны живые нейронные системы, и малоэффективны в тех же областях, где малоэффективны живые нейронные системы, а именно в областях традиционных вычислений, поэтому не должно являться сюрпризом то, что сложно реализовать машину Тьюринга, которая является парадигмой традиционных вычислений, в виде программы для короб-вычислительной системы, но хотя это сложно и расточительно в смысле ресурсов, важно то, что это все равно возможно.
Для создания ленты памяти автор изобретения просто реализует форму ленты с однократной записью. Используя коробы в качестве переменных состояния, можно просто маркировать ранее изученные коробы как "неактивные", и использовать только заново сохраненные коробы.
Таким образом, разобравшись со всеми компонентами машины Тьюринга, автору изобретения остается только добавить, что универсальная машина Тьюринга является программой моделирования машины Тьюринга, которая запускается на машине Тьюринга, и сделать утверждение, что запись такой программы означает кодирование только что описанной машины Тьюринга для реализации программы универсальной машины Тьюринга. Затем автор изобретения заключает, что короб-вычислительные системы могут реализовывать универсальную машину Тьюринга и потому являются завершенными по Тьюрингу, другими словами, способны реализовывать любую вычислимую функцию. Это теоретически важный результат, поскольку он означает, что короб-вычислительные системы являются универсальными вычислительными системами.
То, в чем короб-вычислительные системы являются действительно эффективными, является не эмулирование работы традиционных компьютеров, а эмулирование работы живых систем обработки информации. Устойчивая природа короба, короб-памяти, короб-ячейки и короб-вычислительной системы создает возможность написания грамматик, машин состояний, управляющих систем и широкого спектра других программных конструктов, особенно относящихся к традиционной работе в области искусственного интеллекта и распознавания образцов, посредством того, что они обобщаются путем разрешения структурам данных, которые они используют, быть коробами, что позволяет этим структурам иметь "участки фиксирования" эквивалентности, или устойчивую, терпимую к ошибкам природу, которая крайне полезна при работе с такими типами источников, как образцы, которых обычно касается дело в этих областях.
Дополнительным преимуществом короб-вычислительных систем является уникальная форма параллельной обработки. Поскольку все ячейки массива ячеек 50 короба по фиг.4 исполняются один раз в ходе каждой итерации короб-вычислительной системы по фиг.4, и поскольку эти ячейки могут, в соответствии с определениями в средстве 52 отображения по фиг.4, принимать участие в различных элементах проводимых вычислений, эти различные элементы обязательно исполняются параллельно. Это уникальное разделение параллельных задач, достигаемое путем реализации этих задач в виде процессов в короб-вычислительной системе, которое приводит к новой и полезной форме параллельного вычисления, доступной только при помощи короб-вычислительных систем.
Заключения, следствия и объем изобретения
Таким образом, представленные примеры иллюстрируют практическую природу настоящего изобретения. Были описаны новый конструкт, названный "короб", новый конструкт, названный "короб-память", новый конструкт, названный "короб-ячейка" и новый конструкт, названный "короб-вычислительная система". Каждый из этих конструктов является архитектурой для системы, которая может быть определена в широком смысле как "архитектура для основанной на коробах вычислительной системы", которая является объектом настоящего изобретения.
Была описана новая архитектура вычислительной системы, удовлетворяющая вышеназванным объектам. Настоящее изобретение обеспечивает архитектуру для вычислительных систем, вычислительные преимущества которых находятся в областях, подобных областям вычислительных преимуществ живых систем обработки информации, что резко увеличивает аналоговую функциональную возможность, сильно увеличивает устойчивость к помехам, обеспечивает компоненты, несущие преимущества коробов, обеспечивает архитектуру вычислительной системы, использующую короба, обеспечивает архитектуру основанной на коробах вычислительной системы, которая является "завершенной по Тьюрингу", обеспечивает средство для использования коробов в качестве структур данных, обеспечивает средство для выполнения обработки информации с помощью коробов и обеспечивает средство выполнения параллельной обработки с помощью коробов.
Предшествующие раскрытие и описание изобретения являются иллюстрацией и объяснением изобретения. Специалистам в области, к которой относится данное изобретение, будет понятно, что различные модификации подробностей и вариантов реализации процессов и структур, описанных здесь в целях объяснения природы изобретения, могут быть сделаны без отхода от принципов и/или сущности изобретения.
Хотя текст описания содержит множество конкретных моментов, они должны рассматриваться не в качестве ограничений объема изобретения, а в качестве примера одного предпочтительного варианта реализации изобретения. Возможно множество других вариантов реализации. Например, на протяжении данного рассмотрения программный код на языке программирования С явно использовался для определения и приведения примеров подробностей и вариантов реализации процессов и структур, описанных здесь. Среди специалистов как в области компьютерного программирования, так и в области построения электронных схем хорошо известно, что функциональные возможности любой написанной на языке С программы может быть реализована посредством специфической эквивалентной электронной схемы, и наоборот, и что выполнения, эквивалентные функционально любой написанной на языке С программе, могут быть написаны на других языках программирования, и наоборот. Короб является очень широко определяемым конструктом со специфическими свойствами, как описано здесь. Любая реализация, содержащая или использующая один или несколько коробов, следовательно, находится в пределах объема настоящего изобретения. Любая эквивалентная формулировка системы короб-памяти находится в пределах объема настоящего изобретения. Наконец, любая эквивалентная формулировка короб-вычислительной системы находится в пределах объема настоящего изобретения. Соответственно, объем изобретения должен определяться не проиллюстрированными выполнениями, а прилагаемой формулой изобретения и ее правовыми эквивалентами.
| название | год | авторы | номер документа |
|---|---|---|---|
| Архитектура для интеллектуальных вычислительных и информационно-измерительных систем с нечеткой средой вычислений | 2018 |
|
RU2680201C1 |
| СПОСОБ И СИСТЕМА КЛАССИФИКАЦИИ ДАННЫХ ДЛЯ ВЫЯВЛЕНИЯ КОНФИДЕНЦИАЛЬНОЙ ИНФОРМАЦИИ | 2019 |
|
RU2759786C1 |
| СПОСОБ И СИСТЕМА ДЛЯ ГЕНЕРАЦИИ СИНТЕТИЧЕСКИХ ДАННЫХ | 2023 |
|
RU2824524C1 |
| СПОСОБ ДИАГНОСТИРОВАНИЯ КОМПЛЕКСА БОРТОВОГО ОБОРУДОВАНИЯ ВОЗДУШНЫХ СУДОВ НА ОСНОВЕ МАШИННОГО ОБУЧЕНИЯ БЕЗ УЧИТЕЛЯ С АВТОМАТИЧЕСКИМ ОПРЕДЕЛЕНИЕМ ПАРАМЕТРОВ ОБУЧЕНИЯ МОДЕЛЕЙ | 2023 |
|
RU2818858C1 |
| Способ обнаружения аномалий в многомерных данных | 2021 |
|
RU2773010C1 |
| СПОСОБ ДИАГНОСТИРОВАНИЯ КОМПЛЕКСА БОРТОВОГО ОБОРУДОВАНИЯ ВОЗДУШНЫХ СУДОВ НА ОСНОВЕ МАШИННОГО ОБУЧЕНИЯ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2023 |
|
RU2816667C1 |
| СПОСОБ И СИСТЕМА ПОЛУЧЕНИЯ ВЕКТОРНЫХ ПРЕДСТАВЛЕНИЙ ДАННЫХ В ТАБЛИЦЕ С УЧЁТОМ СТРУКТУРЫ ТАБЛИЦЫ И ЕЁ СОДЕРЖАНИЯ | 2024 |
|
RU2839037C1 |
| СПОСОБ И СИСТЕМА ВЫЯВЛЕНИЯ КОНФИДЕНЦИАЛЬНЫХ ДАННЫХ | 2023 |
|
RU2838508C2 |
| ВИРТУАЛЬНАЯ ПОТОКОВАЯ ВЫЧИСЛИТЕЛЬНАЯ СИСТЕМА, ОСНОВАННАЯ НА ИНФОРМАЦИОННОЙ МОДЕЛИ ИСКУССТВЕННОЙ НЕЙРОСЕТИ И НЕЙРОНА | 2012 |
|
RU2530270C2 |
| СПОСОБ ДИАГНОСТИРОВАНИЯ КОМПЛЕКСА БОРТОВОГО ОБОРУДОВАНИЯ ВОЗДУШНЫХ СУДОВ НА ОСНОВЕ МАШИННОГО ОБУЧЕНИЯ | 2023 |
|
RU2809719C1 |
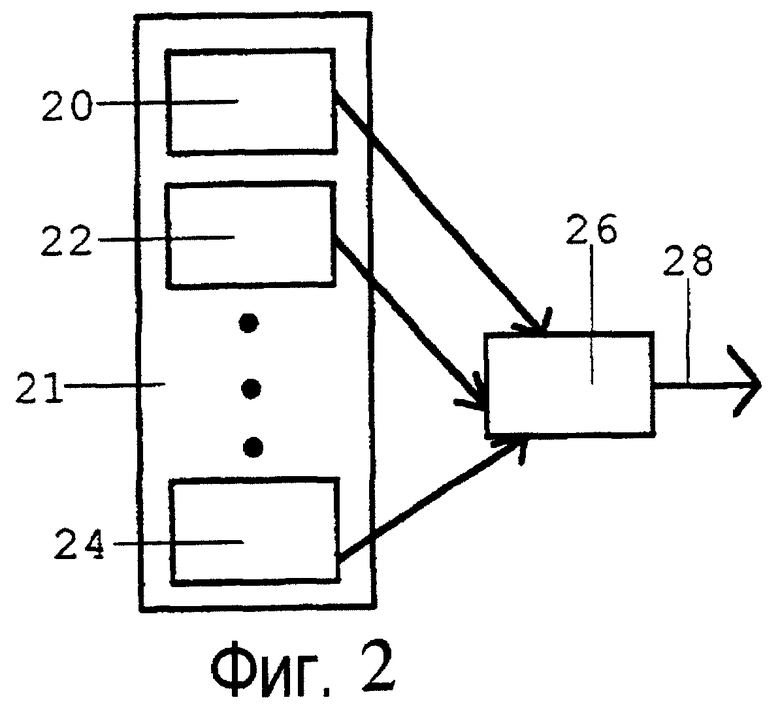
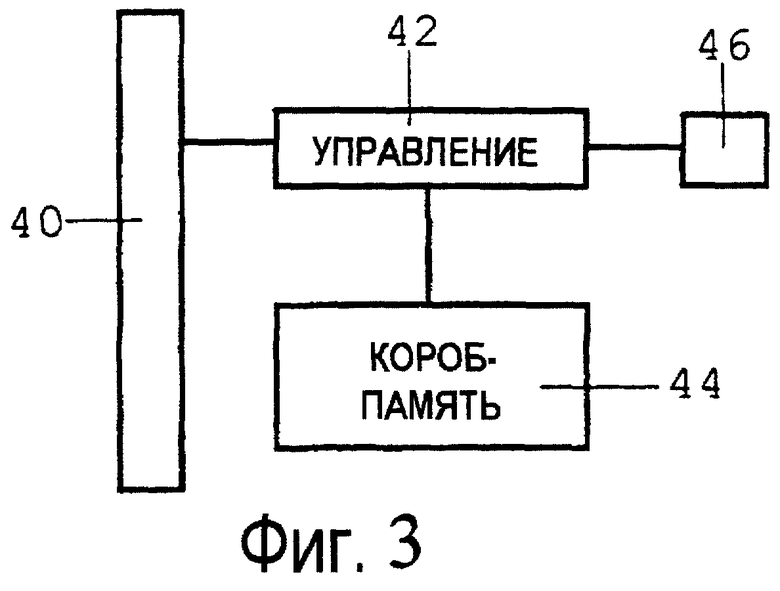
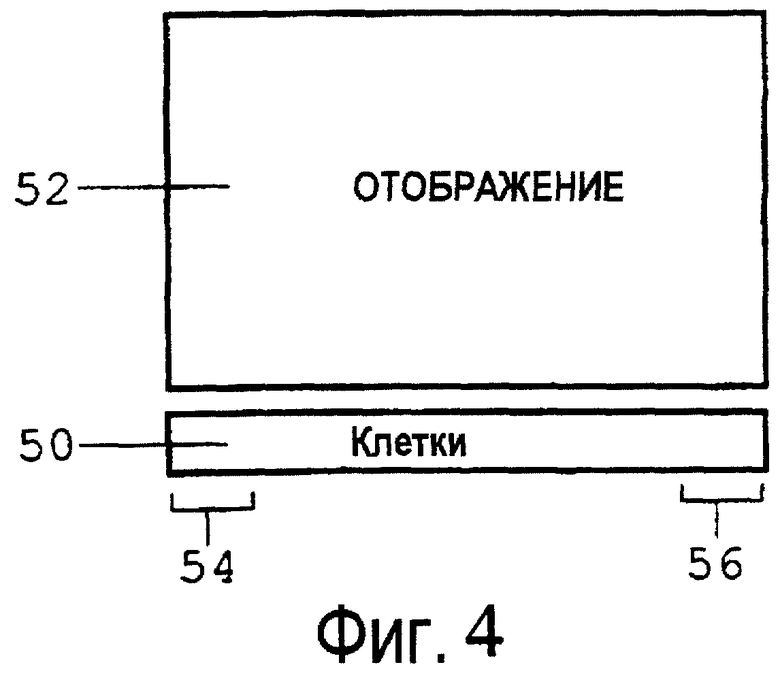
Изобретение относится к программным вычислительным системам, основанным на коробах. Техническим результатом является расширение функциональных возможностей. Система обработки данных содержит память, способную хранить данные коррелитмического объекта, представляющего точку в частном пространстве, и процессор, способный использовать метрику, которая является формулой для вычисления значений между коррелитмическим объектом и точками указанного пространства. Другой вариант системы обработки содержит память, способную хранить данные о множестве ячеек, и процессор, способный в процессе работы принимать входное значение для отдельно взятой ячейки от каждой из заданных ячеек из множества ячеек и формировать второе выходное значение, связанное с отдельно взятой ячейкой, на основании входных значений, определенных на основании данных средства отображения. Способы описывают работу указанных систем. 10 с. и 114 з.п. ф-лы, 4 ил., 23 табл.
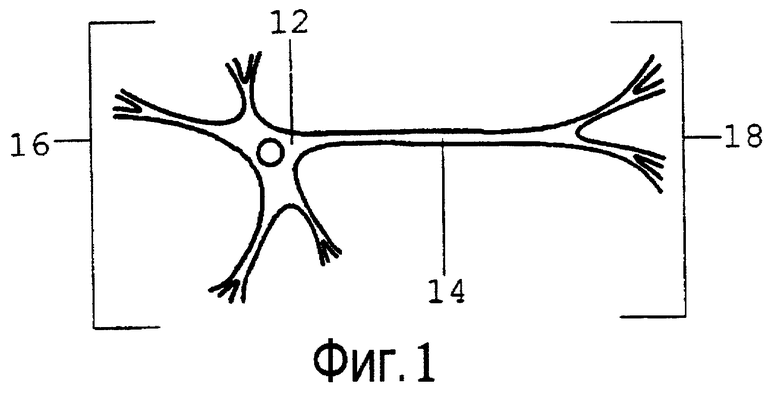
| СПОСОБ НЕПРЕРЫВНОЙ РАЗЛИВКИ СЛЯБОВ НА УСТАНОВКАХ С КРИВОЛИНЕЙНОЙ ТЕХНОЛОГИЧЕСКОЙ ОСЬЮ И УСТАНОВКА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2001 |
|
RU2206428C2 |
| RU 94045146 A1, 20.10.1996 | |||
| СПОСОБ ОБРАБОТКИ ИНФОРМАЦИИ В НЕЙРОННОЙ СЕТИ | 1991 |
|
RU2006067C1 |
| Домовый номерной фонарь, служащий одновременно для указания названия улицы и номера дома и для освещения прилежащего участка улицы | 1917 |
|
SU93A1 |
| EP 0378115 A2, 18.07.1990. | |||
Авторы
Даты
2005-04-10—Публикация
1999-03-18—Подача