Изобретение относится к области автоматики и вычислительной техники и может быть использовано при проектировании устройств преобразования цифрового кода в системе остаточных классов (СОК) в напряжение в блоках сопряжения разнотипных элементов вычислительных и информационно-измерительных систем.
Известен способ (аналог) преобразования кода СОК в напряжение [1, с.239-240], заключающийся в преобразовании кода числа в СОК в позиционную систему счисления (ПСС) и последующем формировании из полученного позиционного кода напряжения путем суммирования токов, прямо пропорциональных весам разрядов позиционного кода, на общем сопротивлении нагрузки [2, с.208-211].
Недостаток способа - низкое быстродействие, обусловленное необходимостью дополнительного преобразования кода СОК в ПСС.
Наиболее близким по технической сущности (прототипом к предлагаемому изобретению) является способ, базирующийся на известном [1, с.31; 3, с.35-39, с.77-78] способе получения позиционного кода числа А из его кода (α 1, α 2,... ,α N) в СОК:
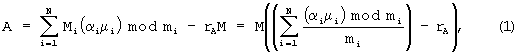
где
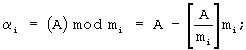
[• ] - целая часть числа; mi - совокупность взаимно простых целых положительных чисел;

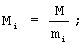
μ i - вес ортогонального базиса, получаемый из решения сравнения (μ iMi)mod 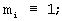
rA - ранг числа А, представляющий собой целое неотрицательное число, показывающее, во сколько раз диапазон СОК - М был превзойден при переходе от представления числа в СОК к его позиционному представлению.
Данный способ преобразования кода СОК в напряжение заключается [4, с.23-24] в вычислении по модулям mi, произведений разрядов α i кода числа А в СОК на веса ортогональных базисов μ i, этих разрядов - β i=(α i,μ i)mod mi, где mi - основания СОК i=1,2,... N, суммировании на общем сопротивлении нагрузки токов, прямо пропорциональных значениям дроби β i/mi, и вычитании из напряжения, полученного в результате прохождения суммы этих токов через сопротивление нагрузки, напряжения, прямо пропорционального рангу числа - rA.
Недостаток прототипа - низкое быстродействие, так как при преобразовании кода СОК в напряжение необходимо рассчитывать ранг числа - rA. Известные алгоритмы получения ранга числа [3, с.78-82; 4, с.23-24] требуют дополнительных затрат оборудования и выполняются только за N шагов, где N - число оснований в СОК.
Целью заявляемого способа является повышение производительности перспективных образцов вычислительных и информационно-измерительных систем различного назначения.
Технический результат выражается в повышении быстродействия выполнения преобразования кода СОК в напряжение.
Поставленная цель достигается тем, что в известном способе, включающем вычисление по модулям mi, произведений разрядов α i кода числа А в СОК на веса ортогональных базисов μ i, этих разрядов - β i=(α i,μ i)mod mi, где mi - основания СОК; i=1,2,... N, дополнительно формируют два опорных гармонических колебания u01(t)=Ucos(ω · t) и u02(t)=Usin(ω · t), где U и ω - соответственно амплитуда и частота гармонического колебания; t - время, получают из опорного колебания u01(t) гармоническое колебание u1(t) путем L сдвигов фазы на
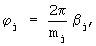
где j=1,2,... L; L - целая часть результата деления числа N на 2, а из гармонического колебания u02(t) получают гармоническое колебание u2(t) путем (N-L) сдвигов фазы на
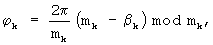
где k=(L+1), (L+2),... N, и определяют интеграл произведения этих колебаний:

причем значение uu при 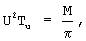 Тu>(2... 3)T и 0≤ А<<М равно величине числа А, где Тu - интервал интегрирования; Т - период гармонического колебания;
Тu>(2... 3)T и 0≤ А<<М равно величине числа А, где Тu - интервал интегрирования; Т - период гармонического колебания;

Сущность изобретения основывается на использовании свойства периодичности гармонической функции, аналогичного свойствам кольца классов вычетов по целочисленным модулям.
Поскольку в заявляемом способе отсутствует необходимость вычисления ранга числа, происходит повышение быстродействия преобразования кода СОК в напряжение.
Известно, что
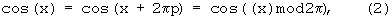
где p=1,2,3,...
Пусть формируются два гармонических колебания u01(t)=Ucos(ω t) и u02(t)=Usin(ω t) с амплитудой U и частотой ω .
Если начальную фазу гармонического колебания u01(t) сдвинуть L раз на величину

где L - целая часть результата деления числа N на 2; j=1,2,... L, а начальную фазу второго гармонического колебания u02(t) сдвинуть (N-L) раз на величину
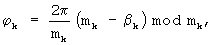
где k=(L+1), (L+2),... N, то после этих сдвигов данные гармонические колебания будут описываться соответствующими выражениями
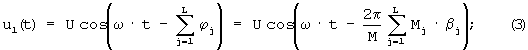
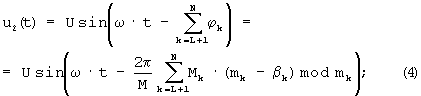
Так как
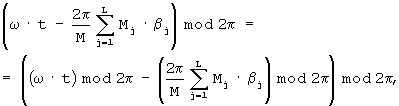
а в свою очередь
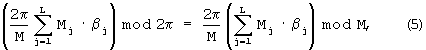
то на основании (3) и (5) получим
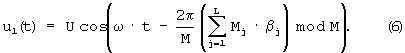
Аналогично, с учетом выражения (4) получаем формулу
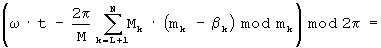
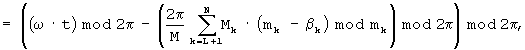
второе слагаемое в которой преобразуется к виду
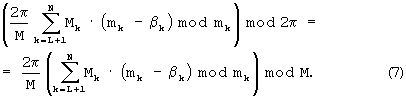
Соответственно, на основании (4) и (7) получаем
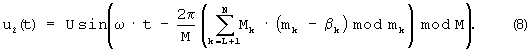
Если гармонические колебания (6) и (8) перемножить и проинтегрировать, то приходим к следующему выражению:
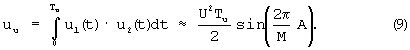
где 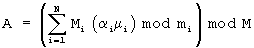 [3, с.36, формула (1.30)].
[3, с.36, формула (1.30)].
Здесь приближенное равенство в (9) вытекает из предположения, что при ω >>1 и Тu ≥(2... 3)T, где Т - период гармонических колебаний u1(t) и u2(t), интеграл от комбинационной составляющей произведения гармонических колебаний с суммарной частотой значительно меньше интеграла от комбинационной составляющей с разностной (нулевой) частотой.
Соответствующим выбором набора оснований СОК mi всегда можно обеспечить то, чтобы величина А была во много раз меньше диапазона представления чисел в СОК - М, то есть 0≤ А<<М. Тогда (9) можно представить следующим приближенным соотношением:

из которого видно, что при
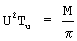
будет обеспечиваться приближенное равенство

Например, при

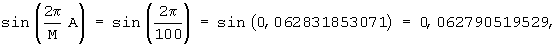
то есть аргумент sin(• ) совпадает с его значением с точностью до четвертого знака.
С учетом изложенного, время формирования из кода СОК напряжения будет равна сумме времени задержки τ ϕ гармонических колебаний (3) и (4) в L устройствах сдвига фазы и времени интегрирования Тu произведения колебаний u1(t) и u2(t), то есть tΣ ≈ τ ϕ +Тu.
Так как задержка гармонического колебания на интервал времени, равный длительности его периода, соответствует фазовому сдвигу на угол 2π , то время задержки при формировании любого из L фазовых сдвигов примем равным периоду частоты опорного гармонического колебания
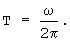
Тогда τ ϕ ≈ L· T.
Как уже отмечено выше, Тu ≥(2... 3)T. Возьмем Тu=3T. Следовательно, время получения напряжения из кода СОК равно
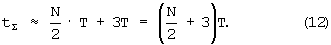
При выводе формулы (12) полагалось, что
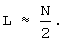
Например, при частоте опорного гармонического колебания 100 ГГц и N=8 время tΣ ≈ 7· 10-11 с, что соизмеримо с предельно возможным временем переключения цифрового логического элемента [5, с.173], и, следовательно, существенно меньше времени расчета ранга числа rA в арифметических устройствах на базе полупроводниковых логических элементов, необходимого для получения из кода СОК напряжения с использованием прототипа.
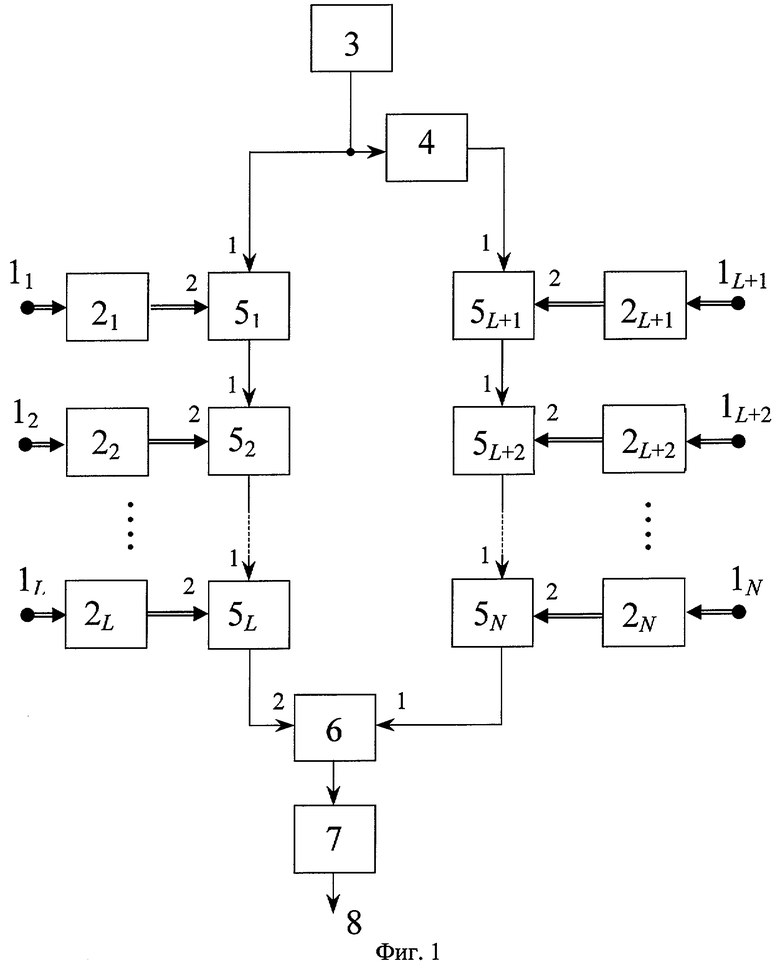
На фиг.1 приведена структурная схема устройства, реализующего предлагаемый способ преобразования кода СОК в напряжение, где 11-1N - информационные входы устройства, 21-2N - устройства отображения, 3 - генератор гармонического колебания, 4 - фазовращатель на угол 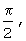 51-5N - управляемые фазовращатели, 6 - аналоговый перемножитель, 7 - интегратор, 8 - выход устройства.
51-5N - управляемые фазовращатели, 6 - аналоговый перемножитель, 7 - интегратор, 8 - выход устройства.
Информационные входы 11-1N соединены со входами соответствующих устройств отображения 21-2N, выходы которых соединены со вторыми входами соответствующих управляемых фазовращателей 51-5N, при этом выход генератора гармонических колебаний 3 соединен непосредственно с первым входом управляемого фазовращателя 5i и через фазовращатель на угол 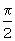 4 - с первым входом управляемого фазовращателя 5L+1, при этом выход управляемого фазовращателя 5j соединен с первым входом управляемого фазовращателя 5(j+1), где j=1,2,... L-1, а выход управляемого фазовращателя 5k соединен с первым входом управляемого фазовращателя 5(k+1), где k=(L+1),(L+2),... N-1, причем выход управляемого фазовращателя 5N подключен к первому входу аналогового перемножителя 6, второй вход которого соединен с выходом управляемого фазовращателя 5L, при этом выход аналогового перемножителя 6 соединен со входом интегратора 7, выход которого является выходом устройства 8.
4 - с первым входом управляемого фазовращателя 5L+1, при этом выход управляемого фазовращателя 5j соединен с первым входом управляемого фазовращателя 5(j+1), где j=1,2,... L-1, а выход управляемого фазовращателя 5k соединен с первым входом управляемого фазовращателя 5(k+1), где k=(L+1),(L+2),... N-1, причем выход управляемого фазовращателя 5N подключен к первому входу аналогового перемножителя 6, второй вход которого соединен с выходом управляемого фазовращателя 5L, при этом выход аналогового перемножителя 6 соединен со входом интегратора 7, выход которого является выходом устройства 8.
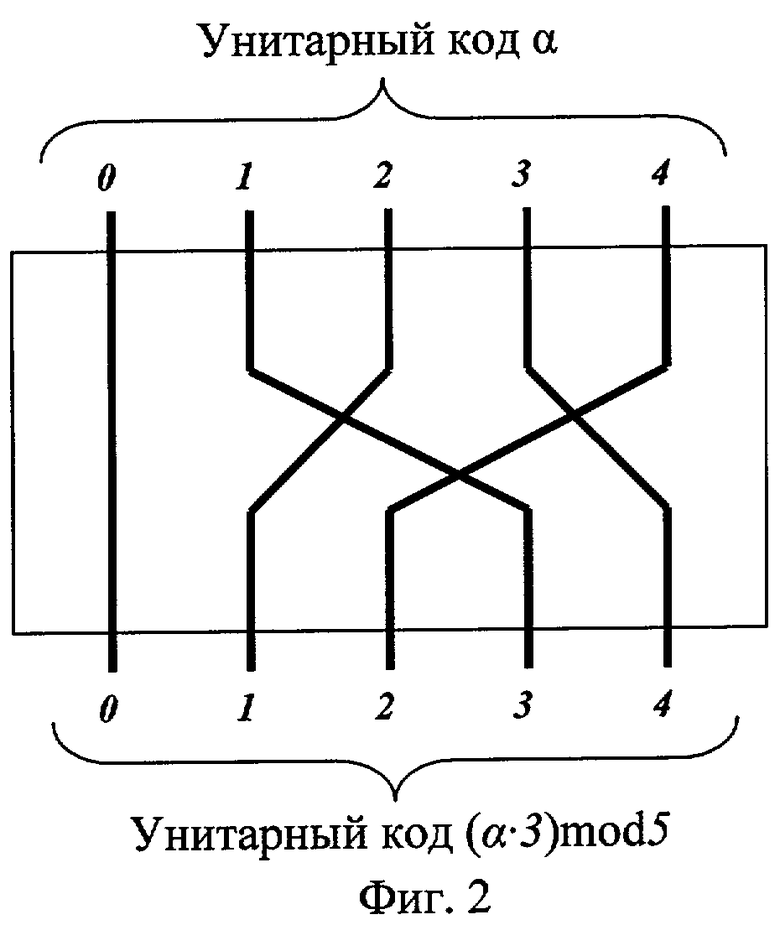
Рассмотрим работу устройства. На N информационных входов 11-1N устройства поступают унитарные коды α i соответствующих разрядов числа A в коде СОК, где i=1,2,... N. Так как веса ортогональных базисов μ i - константы, то в устройствах отображения 21-2L путем соответствующей перекоммутации входных шин данных относительно выходных осуществляется унарное преобразование α j →(α j,μ j)mod mj=β j, где j=1,2,... L, a в устройствах отображения 2L+1-2N - унарное преобразование α k →(mk-α k,μ k)mod mk=(mk-β k)mod mk, где k=(L+1),(L+2),... N.
В качестве примера устройств отображения 21-2N на фиг.2 приведена схема устройства отображения, реализующего преобразование α → (α · 3)mod5.
Унитарные коды чисел β j и (mk-β k)mod mk поступают на вторые входы соответствующих управляемых фазовращателей 5j и 5k, где j=1,2,... L; k=(L+1),(L+2),... N. В этих управляемых фазовращателях устанавливаются соответствующие сдвиги фазы
 и
и 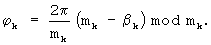
После прохождения гармонических колебаний с выхода генератора 3 через соответствующие фазовращатели, на выходе управляемого фазовращателя 5L устанавливается суммарный набег фаз
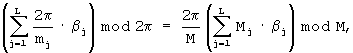
а на выходе управляемого фазовращателя 5N - набег фаз

В результате перемножения в аналоговом перемножителе 6 гармонических колебаний с этими сдвигами фаз и последующего интегрирования в интеграторе 7, на выходе 8 устройства образуется напряжение, прямо пропорциональное
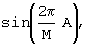
которое при 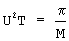 и 0≤ A<<M будет равно величине числа А.
и 0≤ A<<M будет равно величине числа А.
Пример. Пусть N=5; m1=11; m2=7; m3=5; m4=3; m5=2; A=50; 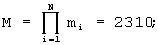 α 1=A mod m1=6; α 2=1; α 3=0; α 4=2; α 5=0 (А=(6, 1, 0, 2, 0)); μ 1=1; μ 2=1; μ 3=3; μ 4=2; μ 5=1.
α 1=A mod m1=6; α 2=1; α 3=0; α 4=2; α 5=0 (А=(6, 1, 0, 2, 0)); μ 1=1; μ 2=1; μ 3=3; μ 4=2; μ 5=1.
После преобразования унитарных кодов чисел α 1, α 2, α 3, α 4 и α 5 в устройствах отображения 21-25, на вторые входы управляемых фазовращателей 51-55 соответственно поступают следующие значения унитарных кодов (α 1,μ 1)modm1=6; (α 2,μ 2)modm2=1; (m3-α 3,μ 3)modm3=0; (m4-α 4,μ 4)modm4=2 и (m5-α 5,μ 5)modm5=0. В управляемых фазовращателях 5j и 5k, где j=1 и 2, а k=3,4 и 5, соответственно устанавливаются следующие сдвиги фазы: 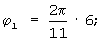
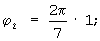

 и ϕ 5=0.
и ϕ 5=0.
После прохождения гармонического колебания с выхода генератора 3 через соответствующие фазовращатели, на выходе управляемого фазовращателя 52 установится набег фазы, равный
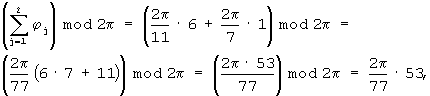
а на выходе управляемого фазовращателя 55 установится набег фазы, равный

В результате перемножения в аналоговом перемножителе 6 гармонического колебания с выхода управляемого фазовращателя 52 -
u1(t)=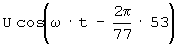
с колебанием с выхода управляемого фазовращателя 55 -
u2(t)=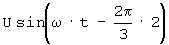
и его интегрирования в интеграторе 7, на выходе 8 сформируется напряжение

При 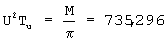 получаем
получаем
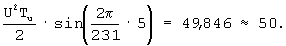
Так как в коде СОК возможно представление только целых чисел [3, с.12], то из приведенного примера видно, что однозначно может быть принято решение о значении числа А, равном 50.
Источники информации
1. Чернявский А.Ф. и др. Высокоскоростные методы и системы цифровой обработки информации. - Мн.: Белгосуниверситет, 1996. - 376 с.
2. Гитис Э.И., Пискунов Е.А. Аналого-цифровые преобразователи. - М.: Энергоиздат, 1981. - 360 с.
3. Акушский И.Я., Юдицкий Д.И. Машинная арифметика в остаточных классах. - М.: Сов. радио, 1968. - 440 с.
4. Абрамсон И.Т., Авров О.М., Лапкин Л.Я. Кодирование электрических величин в системе остаточных классов. // Автометрия, №2 (62), 1975, с.23-29.
5. Акаев А.А., Майоров С.А. Оптические методы обработки информации. - М.: Высш. шк., 1988. - 237 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПРЕОБРАЗОВАНИЯ КОДА СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ В НАПРЯЖЕНИЕ | 2005 |
|
RU2290754C1 |
| СПОСОБ ПРЕОБРАЗОВАНИЯ КОДА СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ В НАПРЯЖЕНИЕ | 2005 |
|
RU2289881C1 |
| ЦИФРОВОЙ СИНТЕЗАТОР ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ | 2003 |
|
RU2239281C2 |
| СИНТЕЗАТОР ЧАСТОТЫ | 2002 |
|
RU2237972C2 |
| УСТРОЙСТВО ДЛЯ ДЕЛЕНИЯ ЧИСЛА В МОДУЛЯРНОМ КОДЕ НА ОСНОВАНИЕ СИСТЕМЫ СЧИСЛЕНИЯ | 2002 |
|
RU2237274C2 |
| УСТРОЙСТВО ДЛЯ МАСШТАБИРОВАНИЯ ЧИСЛА В МОДУЛЯРНОЙ СИСТЕМЕ СЧИСЛЕНИЯ | 2002 |
|
RU2246753C2 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ЧИСЕЛ ИЗ КОДА СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ В ПОЛИАДИЧЕСКИЙ КОД | 2001 |
|
RU2187886C1 |
| ФОРМИРОВАТЕЛЬ ПЕРИОДИЧЕСКИХ СИГНАЛОВ ПРОИЗВОЛЬНОЙ ФОРМЫ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2003 |
|
RU2271602C2 |
| ЦИФРОАНАЛОГОВЫЙ ПРЕОБРАЗОВАТЕЛЬ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2020 |
|
RU2744337C1 |
| УСТРОЙСТВО ДЛЯ ДЕЛЕНИЯ ЧИСЛА В МОДУЛЯРНОМ КОДЕ НА ОСНОВАНИЕ СИСТЕМЫ СЧИСЛЕНИЯ | 2002 |
|
RU2231822C2 |
Изобретение относится к области автоматики и вычислительной техники и может быть использовано при проектировании устройств преобразования цифрового кода в системе остаточных классов (СОК) в напряжение в блоках сопряжения разнотипных элементов вычислительных и информационно-измерительных систем. Техническим результатом является повышение производительности вычислительных и информационно-измерительных систем различного назначения, повышение быстродействия выполнения преобразования кода СОК в напряжение. Указанный результат достигается за счет формирования двух опорных гармонических колебаний u01(t) и u02(t), где t - время получения из опорного колебания u01(t) гармонического колебания u1(t), а из гармонического колебания u02(t) – колебания u2(t), и определения интеграла произведения этих колебаний:  где Tu - интервал интегрирования. 2 ил.
где Tu - интервал интегрирования. 2 ил.
Способ преобразования кода системы остаточных классов (СОК) в напряжение, включающий вычисление по модулям mi произведений разрядов α i кода числа А в СОК на веса ортогональных базисов μ i этих разрядов - β i=(α iμ i)mod mi, где mi - основания СОК; i=1,2,...N, отличающийся тем, что дополнительно формируют два опорных гармонических колебания u01(t)=U· cos(ω · t) и u02(t)=U· sin(ω · t), где U и ω - соответственно амплитуда и частота гармонического колебания; t - время, получают из опорного колебания u01(t) гармоническое колебание u1(t) путем L сдвигов фазы на 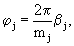 где j=1,2,...L; L - целая часть результата деления числа N на 2, а из гармонического колебания u02(t) получают гармоническое колебание u2(t) путем (N-L) сдвигов фазы на
где j=1,2,...L; L - целая часть результата деления числа N на 2, а из гармонического колебания u02(t) получают гармоническое колебание u2(t) путем (N-L) сдвигов фазы на 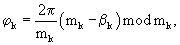 где k=(L+1), (L+2),... N, и определяют интеграл произведения этих колебаний:
где k=(L+1), (L+2),... N, и определяют интеграл произведения этих колебаний: 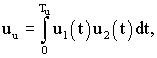 причем значение uu при
причем значение uu при 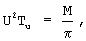 Tu>(2...3)T и 0≤ А<<М равно величине числа А, где Tu - интервал интегрирования; T- период гармонического колебания;
Tu>(2...3)T и 0≤ А<<М равно величине числа А, где Tu - интервал интегрирования; T- период гармонического колебания;
| АКУШСКИЙ И.Я | |||
| и др | |||
| Машинная арифметика в остаточных классах | |||
| - М.: Сов.радио, 1968, с.35-39, 77-82 | |||
| Преобразователь кода системы остаточных классов в напряжение | 1983 |
|
SU1175034A1 |
| Преобразователь кода числа из системы остаточных классов в напряжение | 1982 |
|
SU1069155A1 |
| Преобразователь кода системы остаточных классов в напряжение | 1989 |
|
SU1742997A1 |
| US 4963869 A, 16.10.1990. | |||
Авторы
Даты
2005-06-10—Публикация
2003-12-22—Подача