Предлагаемое изобретение относится к области, связанной с наведением космических аппаратов и космических кораблей на заданную орбиту. С помощью терминального управления обеспечиваются заданные параметры их движения в конце активного маневра. Такие способы управления используются в системах управления разгонными блоками, обеспечивающих переход с одной орбиты на другую, и космических аппаратов, выполняющих посадку на Луну или другие планеты.
Наиболее близким техническим решением является способ коррекции параметров программы изменения продольного движения при терминальном управлении наведением разгонного блока на заданную орбиту, заключающийся в том, что в процессе реализации активного маневра периодически прогнозируют параметры движения разгонного блока на момент отсечки маршевого двигателя, определяют по ним прогнозируемые отклонения радиуса и радиальной скорости от их значений на заданной орбите, вычисляют функции чувствительности отклонений радиуса и радиальной скорости к изменению параметров программы управления по углу и угловой скорости тангажа, формируют сигналы коррекции по углу и угловой скорости тангажа, обеспечивающие компенсацию отклонений по радиусу и радиальной скорости, и ограничивают сигнал коррекции по углу тангажа на заданном уровне [1].
Недостатком известного способа коррекции параметров программы изменения терминального управления является скачкообразное изменение этих параметров при каждом обновлении программы управления. При значительных скачках программы управления в контурах угловой стабилизации разгонного блока возникают дополнительные возмущения из-за колебаний жидкого топлива в баках.
Техническим результатом изобретения является снижение уровня возмущений, действующих на контур угловой стабилизации разгонного блока, путем ограничения величин корректирующих поправок и обеспечение при этих ограничениях приоритетной отработки отклонения радиальной скорости от ее значения на заданной орбите.
Указанный технический результат достигается тем, что в известном способе коррекции параметров программы изменения продольного движения при терминальном управлении наведением разгонного блока на заданную орбиту, заключающемся в том, что прогнозируют параметры движения разгонного блока на момент отсечки маршевого двигателя, определяют по ним отклонения радиуса и радиальной скорости от их значений на заданной орбите, вычисляют функции чувствительности отклонений радиуса и радиальной скорости к изменению параметров программы управления по углу и угловой скорости тангажа, формируют сигналы коррекции по углу и угловой скорости тангажа, обеспечивающие компенсацию отклонений по радиусу и радиальной скорости, ограничивают сигнал коррекции по углу тангажа на заданном уровне, дополнительно определяют превышение сигнала коррекции по углу тангажа относительно его ограниченного уровня как разность между сигналом коррекции по углу тангажа и его ограниченным значением, формируют добавку к сигналу коррекции по угловой скорости тангажа, равную произведению полученного превышения на отношение функции чувствительности радиальной скорости по углу тангажа к функции чувствительности ее к угловой скорости тангажа, формируют сигнал коррекции по угловой скорости тангажа как сумму сигнала коррекции по угловой скорости тангажа, определенного без учета ограничения, на сигнал коррекции по углу тангажа, с добавкой, определяемой при выходе сигнала коррекции по углу тангажа на ограничение.
На фиг.1 представлена структурная схема устройства коррекции параметров ориентации терминального управления по известному способу-прототипу; на фиг.2 представлено изменение угловой скорости 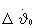 и угла
и угла 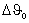 тангажа на такте терминального управления Тy; на фиг.3 показаны отклонения по радиусу ΔR и радиальной скорости ΔV прогнозируемых значений Rпp, Vr пp от их значений на заданной орбите; на фиг.4 показана фазовая плоскость параметров ΔR и ΔV в начале маневра с граничными линиями I, II, III; на фиг.5 представлены граничные линии I, II, III и изменения начальных отклонений параметров ΔR и ΔV за один такт терминального управления; на фиг.6 на фазовой плоскости параметров ΔR, ΔV показано их изменение по способу-прототипу (т. А, А', А''...) и по предлагаемому способу (т. А, С', С''...), на фиг.7 приведена структурная схема устройства коррекции параметров программы изменения продольного движения по предлагаемому способу; на фиг.8 приведен процесс отработки начальных отклонений параметров при ограничении корректирующей поправки по углу тангажа
тангажа на такте терминального управления Тy; на фиг.3 показаны отклонения по радиусу ΔR и радиальной скорости ΔV прогнозируемых значений Rпp, Vr пp от их значений на заданной орбите; на фиг.4 показана фазовая плоскость параметров ΔR и ΔV в начале маневра с граничными линиями I, II, III; на фиг.5 представлены граничные линии I, II, III и изменения начальных отклонений параметров ΔR и ΔV за один такт терминального управления; на фиг.6 на фазовой плоскости параметров ΔR, ΔV показано их изменение по способу-прототипу (т. А, А', А''...) и по предлагаемому способу (т. А, С', С''...), на фиг.7 приведена структурная схема устройства коррекции параметров программы изменения продольного движения по предлагаемому способу; на фиг.8 приведен процесс отработки начальных отклонений параметров при ограничении корректирующей поправки по углу тангажа  способа-прототипа; на фиг.9 показан процесс отработки начальных отклонений параметров при ограничении корректирующих поправок по предлагаемому способу.
способа-прототипа; на фиг.9 показан процесс отработки начальных отклонений параметров при ограничении корректирующих поправок по предлагаемому способу.
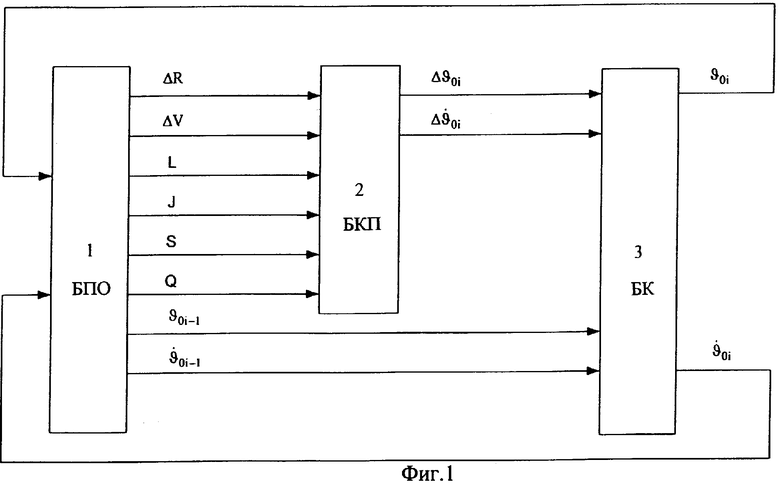
Структурная схема устройства коррекции параметров программы изменения терминального управления по известному способу-прототипу представлена на фиг.1, где: 1 - блок прогноза отклонений (БПО) от заданной орбиты и расчета функций чувствительности, 2 - блок корректирующих поправок (БКП) программного управления, 3 - блок коррекции (БК) параметров программ управления.
В блоке 1 на каждом такте терминального управления определяются отклонения по радиус-вектору ΔR и радиальной скорости ΔV от параметров заданной орбиты в прогнозируемый момент окончания маневра tf. Параметры ΔR, ΔV с первого и второго выходов блока 1 поступают на первый и второй входы блока 2, с выходов 3-6 - на соответствующие входы блока 2 - вычисленные значения функций чувствительности L, J, S, Q отклонений ΔV и ΔR к изменению параметров программы управления по углу и угловой скорости тангажа, а с выходов 7, 8 на входы 3, 4 блока 3 поступают параметры программ управления по тангажу ϑoi-1 и угловой скорости тангажа 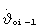 , при которых выполняется прогноз движения разгонного блока.
, при которых выполняется прогноз движения разгонного блока.
В блоке 2 на основе вычисленных функций чувствительности из условий обнуления отклонений ΔV и ΔR рассчитываются корректирующие поправки по углу тангажа Δϑoi и угловой скорости тангажа 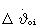 , и их значения поступают с выходов 1, 2 на соответствующие входы блока 3, где выполняется коррекция параметров программ управления и определяются их значения на интервалах времени до следующего такта терминального управления. Откорректированные параметры управления ϑoi,
, и их значения поступают с выходов 1, 2 на соответствующие входы блока 3, где выполняется коррекция параметров программ управления и определяются их значения на интервалах времени до следующего такта терминального управления. Откорректированные параметры управления ϑoi, 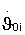 c выходов 1, 2 блока 3 поступают на 1 и 2 входы блока 1 для формирования программы управления на следующем такте терминального управления.
c выходов 1, 2 блока 3 поступают на 1 и 2 входы блока 1 для формирования программы управления на следующем такте терминального управления.
Для разгонного блока в качестве управляющих параметров терминального управления используются параметры линейных по времени программ изменения ориентации космического аппарата, определяющих направление действия тяги его маршевого двигателя.
Терминальное управление выполняется периодически с заданным интервалом Ту между его тактами.
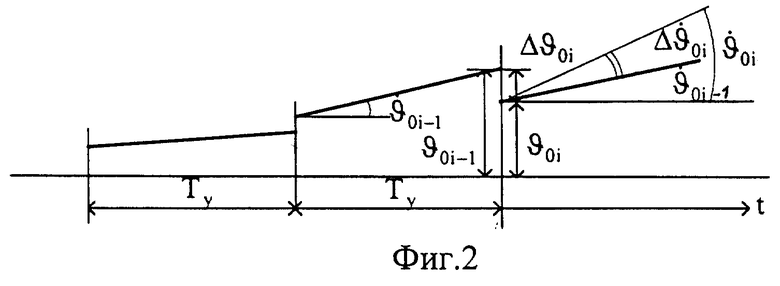
Для продольного движения программа ориентации по углу тангажа в начале i-го такта терминального управления имеет вид ϑi=ϑoi-1+ t, где время t отсчитывается от начала такта терминального управления, начальное значение угла тангажа ϑoi-1 и скорость его изменения
t, где время t отсчитывается от начала такта терминального управления, начальное значение угла тангажа ϑoi-1 и скорость его изменения 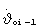 принимаются равными значениям этих параметров на конец предыдущего (i-1)-гo такта, а для первого такта - равными значениям, заданным в полетном задании.
принимаются равными значениям этих параметров на конец предыдущего (i-1)-гo такта, а для первого такта - равными значениям, заданным в полетном задании.
В процессе терминального управления движением разгонного блока на каждом его такте выполняются следующие операции:
- прогноз параметров движения на прогнозируемый момент окончания процесса управления, определяемого по времени Т, оставшемуся до отключения маршевого двигателя, выполняемого при достижении заданного значения функционала;
- определение отклонений от параметров расчетной орбиты по радиус-вектору ΔR и радиальной скорости ΔV в прогнозируемый момент окончания маневра;
- определение функций чувствительности параметров ΔR, ΔV при изменении управляющих параметров:


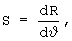
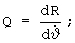
- определение корректирующих поправок Δϑoi, 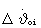 , по параметрам управления, обеспечивающих списывание отклонений ΔR, ΔV;
, по параметрам управления, обеспечивающих списывание отклонений ΔR, ΔV;
- коррекция параметров управления (фиг.2):

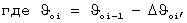

В качестве модели прогноза траекторного движения разгонного блока используется система дифференциальных уравнений:
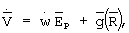
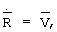
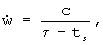
ts=t-to,
где  - радиус-вектор центра масс разгонного блока;
- радиус-вектор центра масс разгонного блока;
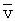 - вектор абсолютной скорости разгонного блока;
- вектор абсолютной скорости разгонного блока;
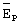 - единичный вектор тяги в геоинерциальной системе координат;
- единичный вектор тяги в геоинерциальной системе координат;
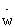 - кажущееся ускорение;
- кажущееся ускорение;
С - удельный импульс маршевого двигателя;
t - текущее время;
to - время начала прогноза;
Т - условное время сгорания массы разгонного блока, имеющейся на момент to.
Прогноз параметров движения разгонного блока (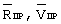 ) на момент отсечки маршевого двигателя (tf) осуществляется путем численного интегрирования уравнений модели движения методом Рунге-Кутта.
) на момент отсечки маршевого двигателя (tf) осуществляется путем численного интегрирования уравнений модели движения методом Рунге-Кутта.
Начальные значения по параметрам  ,
, 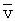 определяются по информации, поступающей из навигационной системы.
определяются по информации, поступающей из навигационной системы.
В плоскости орбиты (фиг.3) отклонения по радиусу ΔR и радиальной скорости ΔV определяются по формулам
ΔR=Rпp-R,
ΔV=Vr пр-Vr,
где Rпр, R - значения прогнозируемого и расчетного радиусов в момент отсечки маршевого двигателя соответственно;
Vr пр,Vr - значения прогнозируемой и расчетной радиальной скорости соответственно.
При изменении программы управления на малые величины Δϑ0, 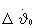 изменение ускорения движения
изменение ускорения движения 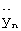 в направлении по нормали к номинальной траектории полета может быть описано уравнением
в направлении по нормали к номинальной траектории полета может быть описано уравнением
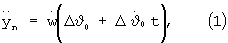
где 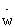 - кажущееся ускорение, определяемое как
- кажущееся ускорение, определяемое как 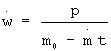
р - тяга двигателя;
m0 - масса космического аппарата в момент t=0;
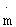 - секундный расход массы.
- секундный расход массы.
Кажущееся ускорение 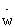 , определяемое этими параметрами, может быть записано в виде
, определяемое этими параметрами, может быть записано в виде
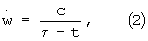
где 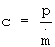 - удельный импульс;
- удельный импульс;
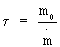 - условное время сгорания начальной массы m0 космического аппарата.
- условное время сгорания начальной массы m0 космического аппарата.
С учетом этого запишем уравнение (1) в виде
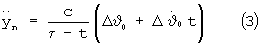
Интегрирование уравнения (3) в пределах от 0 до Т,
где Т - оставшееся время до отключения маршевого двигателя, дает
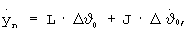
а из повторного интегрирования следует
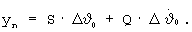
В последних уравнениях функции чувствительности имеют вид [2]:
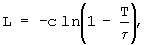
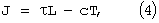
S=TL-J,
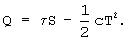
Принимая, что 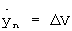 , а yn=ΔR из системы уравнений
, а yn=ΔR из системы уравнений
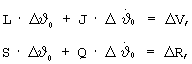
определяются корректирующие поправки по параметрам управления, компенсирующие отклонения ΔR, ΔV:
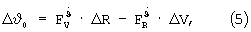

где 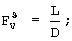
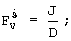
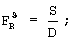
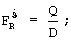
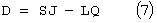
Расчеты показывают, что корректирующие поправки по угловой скорости 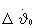 значительно меньше по величине поправок по углу Δϑ0. Так, для длительного маневра при времени, оставшемся до выключения маршевого двигателя, Т=576 с, Т=1405,3 с и значениях функций чувствительности L=2384 м/с, J=745000 м, S=629015 м, Q=133155000 мс для компенсации отклонений ΔR=10 км корректирующие поправки Δϑ0=2,8°,
значительно меньше по величине поправок по углу Δϑ0. Так, для длительного маневра при времени, оставшемся до выключения маршевого двигателя, Т=576 с, Т=1405,3 с и значениях функций чувствительности L=2384 м/с, J=745000 м, S=629015 м, Q=133155000 мс для компенсации отклонений ΔR=10 км корректирующие поправки Δϑ0=2,8°, 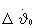 =0,009 °/c, а для ΔV=100 м/с - Δϑ0=5,4°,
=0,009 °/c, а для ΔV=100 м/с - Δϑ0=5,4°, 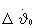 =0,024 °/c.
=0,024 °/c.
В связи с этим в системах управления накладывается жесткое ограничение только по величине корректирующей поправки по углу тангажа:
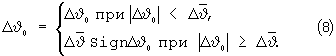
Однако эта мера в случаях, приводящих к выходу поправки Δϑo на ограничение, может приводить к значительному перерегулированию в переходном процессе по отработке отклонений ΔV, ΔR. На коротких маневрах с малой продолжительностью работы маршевого двигателя это ведет к незавершенности переходного процесса и к ошибкам выведения разгонного блока на заданную орбиту.
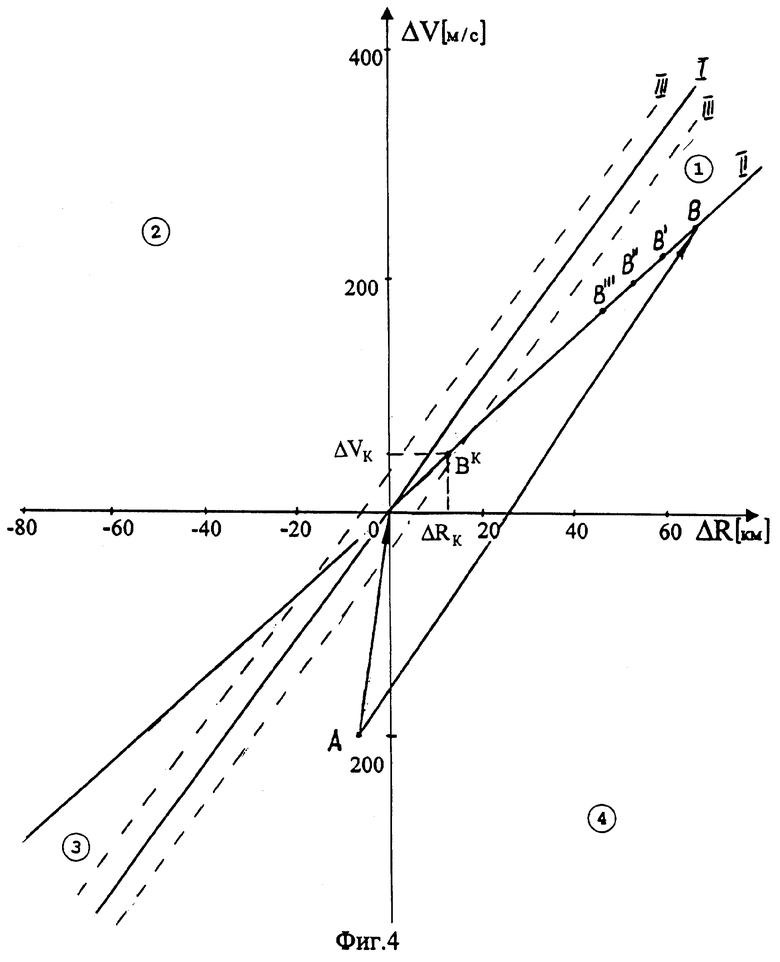
Для анализа процессов изменения отклонений в результате коррекции программы управления на фазовой плоскости параметров ΔV, ΔR (фиг.4) выделим следующие линии:
Линия I - граница, соответствующая условию 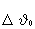 =0 и определяемая из уравнения (5):
=0 и определяемая из уравнения (5):
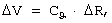
Линия II - граница, соответствующая условию 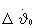 =0 и определяемая из уравнения (6):
=0 и определяемая из уравнения (6):
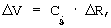
где 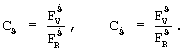
Линии III - параллельные линии I и определяющие коридор условий, соответствующих изменению корректирующей поправки 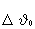 на величину
на величину 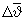 . Уравнение этих линий находится из уравнения (5) при
. Уравнение этих линий находится из уравнения (5) при 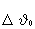 =±
=±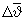 :
:
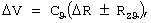
где 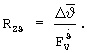
Для рассмотренных выше условий при 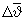 =2°, RZϑ=7,08 км (для справки: линии, аналогичные линиям III и параллельные линии II, при
=2°, RZϑ=7,08 км (для справки: линии, аналогичные линиям III и параллельные линии II, при 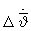 =2 °/c имели бы
=2 °/c имели бы 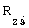 =2212 км).
=2212 км).
Линии I, II делят фазовую плоскость параметров ΔV, ΔR на области 1, 2, 3, 4.
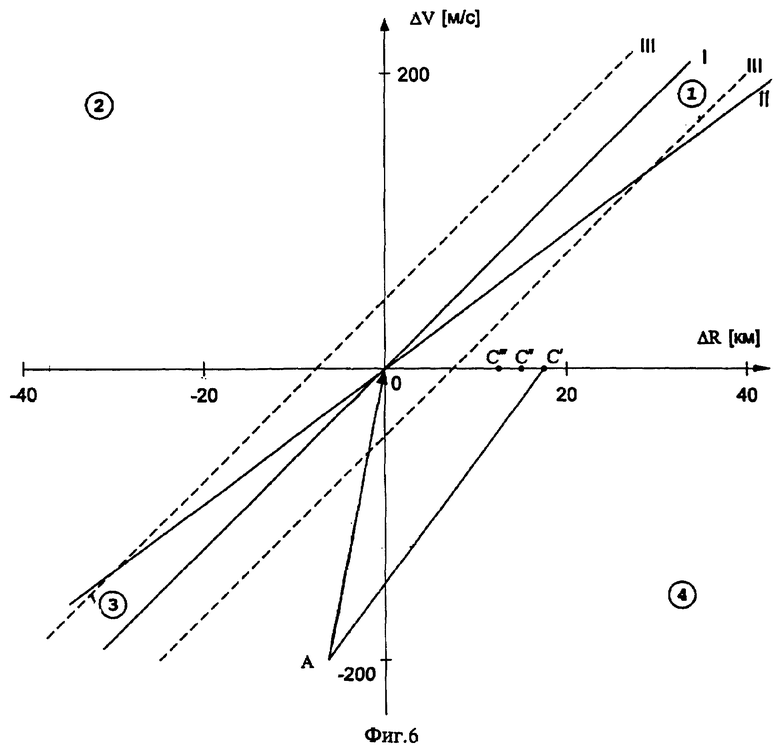
Пусть по результатам прогноза определены значения начальных отклонений, соответствующих на фиг.4 точке А, находящейся за пределами зоны, ограниченной линией III. При отсутствии ограничений по величине корректирующей поправки 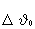 или в случае, если она не превысила установленного ограничения, то есть при нахождении точки А внутри зоны, ограниченной линиями III-III, отработка этих отклонений с новыми значениями программ управления приводит точку А в начало координат по вектору А0.
или в случае, если она не превысила установленного ограничения, то есть при нахождении точки А внутри зоны, ограниченной линиями III-III, отработка этих отклонений с новыми значениями программ управления приводит точку А в начало координат по вектору А0.
При наличии ограничения 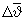 начальные отклонения ΔV0, ΔR0 к прогнозируемому моменту окончания маневра изменятся на величины ΔVC, ΔRC:
начальные отклонения ΔV0, ΔR0 к прогнозируемому моменту окончания маневра изменятся на величины ΔVC, ΔRC:
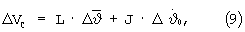
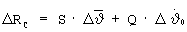
и новые значения отклонений ΔVH, ΔRH к следующему циклу терминального управления составили бы величины

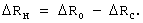
Из уравнений (10) с учетом уравнений (6) и (9) найдем:
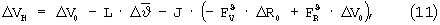

Предположим, что функции чувствительности за один цикл терминального управления не изменились, что справедливо для условий начала длительных маневров. Значения корректирующих поправок для отклонений ΔVH, ΔRH будут иметь величины
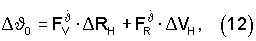
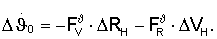
Если |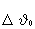 |>
|>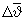 , то вычисленная поправка
, то вычисленная поправка 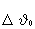 ограничивается на принятом уровне
ограничивается на принятом уровне 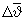 . Подставляя во второе уравнение (12) значения уравнений (11), получим
. Подставляя во второе уравнение (12) значения уравнений (11), получим

Таким образом, точка А перемещается в точку В на линию II.
При условии, что
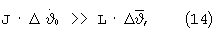
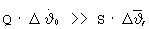
из уравнений (11) получим
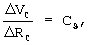
то есть при условии (14) смещение начальной точки А на фазовой плоскости в точку В на линии II происходит параллельно линии I.
Если бы функции чувствительности не изменялись, то за каждый последующий такт пересчета поправок при 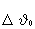 =
=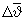 и
и 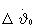 =0 точка В передвигалась бы к точке 0 в соответствии с уравнениями (9) на величины
=0 точка В передвигалась бы к точке 0 в соответствии с уравнениями (9) на величины
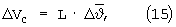
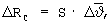
занимая положения В', В'', В'''... на линии ОВ до тех пор, пока она не войдет в зону, ограниченную линиями III-III, из которой попадет в точку 0.
На фиг.5 векторами показаны перемещения начальных отклонений ΔR0, ΔV0 в значения ΔVH, ΔRH при использовании корректирующих поправок 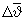 ,
, 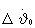 .
.
Из-за наличия ограничения по поправке 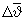 при начальных отклонениях, находящихся в областях 2, 4 (фиг.4, 5), их новые значения ΔVH, ΔRH в ряде случаев могут существенно превосходить начальные значения.
при начальных отклонениях, находящихся в областях 2, 4 (фиг.4, 5), их новые значения ΔVH, ΔRH в ряде случаев могут существенно превосходить начальные значения.
Если при определенных начальных условиях маневр формирования заданной орбиты завершается в момент, соответствующий точке Вк на фазовой плоскости (фиг.4) с остаточными отклонениями ΔVК, ΔRК, то это приведет к погрешностям по параметрам формируемой орбиты.
Из двух погрешностей ΔV и ΔR на точность формирования заданной орбиты в большей степени влияет ошибка по радиальной скорости. Чувствительности параметров орбиты к погрешностям ΔV и ΔR, выраженные в частных производных радиуса апогея Ra, радиуса перигея Rp и эксцентриситета e по ΔV и ΔR, определенные в конце маневра формируемой орбиты, представлены в таблице.
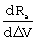
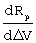
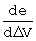
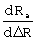
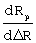
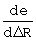
Для уменьшения погрешностей формирования орбит в предлагаемом способе формирования корректирующих поправок при ограниченной угловой поправке по углу тангажа 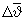 решается задача по приведению невязки по скорости ΔV к нулю путем соответствующего формирования поправки по угловой скорости тангажа
решается задача по приведению невязки по скорости ΔV к нулю путем соответствующего формирования поправки по угловой скорости тангажа 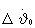 .
.
При ограниченной поправке по углу тангажа 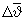 начальные отклонения ΔV, ΔR к прогнозируемому моменту окончания маневра за 1 такт терминального управления изменятся на величины
начальные отклонения ΔV, ΔR к прогнозируемому моменту окончания маневра за 1 такт терминального управления изменятся на величины
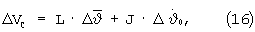
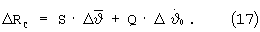
При ΔVС=ΔV поправка по угловой скорости тангажа 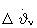 , обеспечивающая обнуление отклонения ΔV, определяется из (16) в виде
, обеспечивающая обнуление отклонения ΔV, определяется из (16) в виде
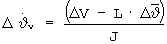
и с учетом этого из (17)
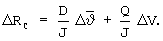
Таким образом, на первом такте терминального управления при 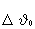 =
=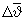 поправка по угловой скорости тангажа
поправка по угловой скорости тангажа 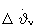 определяется из условия обнуления невязки ΔV, невязка ΔR изменяется при этом на величину ΔRс, а на последующих тактах (при ΔV=0 и
определяется из условия обнуления невязки ΔV, невязка ΔR изменяется при этом на величину ΔRс, а на последующих тактах (при ΔV=0 и 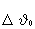 =
=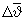 ) на величину
) на величину
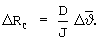
На фазовой плоскости параметров ΔR, ΔV (фиг.6) при предлагаемом способе формирования корректирующих поправок точками С', С'', С'''... обозначено изменение параметров ΔR, ΔV на каждом такте терминального управления от начальных условий, соответствующих точке А.
Корректирующая поправка по угловой скорости 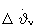 представляет собой сумму:
представляет собой сумму:
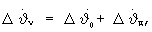
где 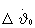 - корректирующая поправка по угловой скорости тангажа, определенная без учета ограничения на поправку по углу тангажа (17);
- корректирующая поправка по угловой скорости тангажа, определенная без учета ограничения на поправку по углу тангажа (17);
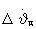 - добавка к величине
- добавка к величине 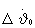 при выходе поправки по углу тангажа на ограничение.
при выходе поправки по углу тангажа на ограничение.
Величина 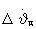 определяется как
определяется как
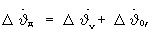
и путем использования зависимостей (18), (17) приводится к виду
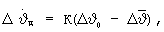
где 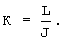
На фиг.7 приведена структурная схема устройства коррекции параметров программы изменения продольного движения по предлагаемому способу, где приняты следующие обозначения: 1 - блок прогноза отклонений (БПО) от заданной орбиты и расчета функций чувствительности, 2 - блок корректирующих поправок (БКП) программного управления, 3 - блок коррекции (БК) параметров программ управления, 4 - ограничитель угловой поправки (ОУП), 5 - блок формирования превышения (БФП) угловой поправкой уровня ограничения, 6 - множитель (М), 7 - сумматор (С).
При коррекции параметров программы изменения терминального управления по предлагаемому изобретению в блоке 1 схемы на фиг.7 определяются отклонения от заданной орбиты по радиус-вектору ΔR и радиальной скорости ΔV в прогнозируемый момент выключения маршевого двигателя и функции чувствительности L, J, S, Q по параметрам управления. Эти параметры с выходов 1-6 блока 1 поступают на соответствующие входы блока 2, а с выходов 7, 8 на входы 3, 4 блока 3 выдаются параметры программ управления по тангажу ϑ0i-1 и угловой скорости тангажа 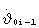 , при которых выполнен прогноз движения разгонного блока.
, при которых выполнен прогноз движения разгонного блока.
В блоке 2 определяются корректирующие поправки и сигнал К, определяющий отношение функции чувствительности радиальной скорости по углу тангажа J к функции ее чувствительности к угловой скорости тангажа L: 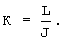 Поправка Δϑ0i c первого выхода блока 2 поступает через ограничитель угловой поправки 4 на первый вход блока 3 и на второй вход блока формирования превышения угловой поправкой уровня ограничения 5, на первый вход которого поступает поправка
Поправка Δϑ0i c первого выхода блока 2 поступает через ограничитель угловой поправки 4 на первый вход блока 3 и на второй вход блока формирования превышения угловой поправкой уровня ограничения 5, на первый вход которого поступает поправка 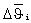 .
.
С выхода блока формирования превышения угловой поправкой уровня ограничения 5 на первый вход множителя 6 приходит сигнал превышения, представляющий собой разность между корректирующей поправкой по тангажу и ее ограниченным в блоке 4 значением:
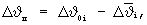
а на второй вход - сигнал К со второго выхода блока 2. Сигнал с выхода множителя 6 поступает на 2-й вход сумматора 7.
С третьего выхода блока 2 на первый вход сумматора 7 поступает корректирующая поправка по угловой скорости 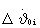 , а с выхода этого сумматора на 2-й вход блока коррекции параметров программ управления 3 поступает суммарная корректирующая поправка
, а с выхода этого сумматора на 2-й вход блока коррекции параметров программ управления 3 поступает суммарная корректирующая поправка 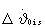 угловой скорости тангажа в виде
угловой скорости тангажа в виде
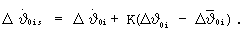
Если вычисленная в блоке 2 корректирующая поправка по углу тангажа Δϑ0i не превышает ограничения 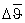 , то с выхода блока 5 на множитель 6 поступает нулевой сигнал и на 2-й вход блока 3 поступает вычисленная корректирующая поправка по угловой скорости без изменений.
, то с выхода блока 5 на множитель 6 поступает нулевой сигнал и на 2-й вход блока 3 поступает вычисленная корректирующая поправка по угловой скорости без изменений.
В блоке 3 выполняется коррекция параметров программы управления по зависимости
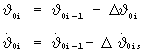
и программа ориентации разгонного блока на i-й интервал терминального управления принимается в виде
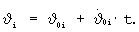
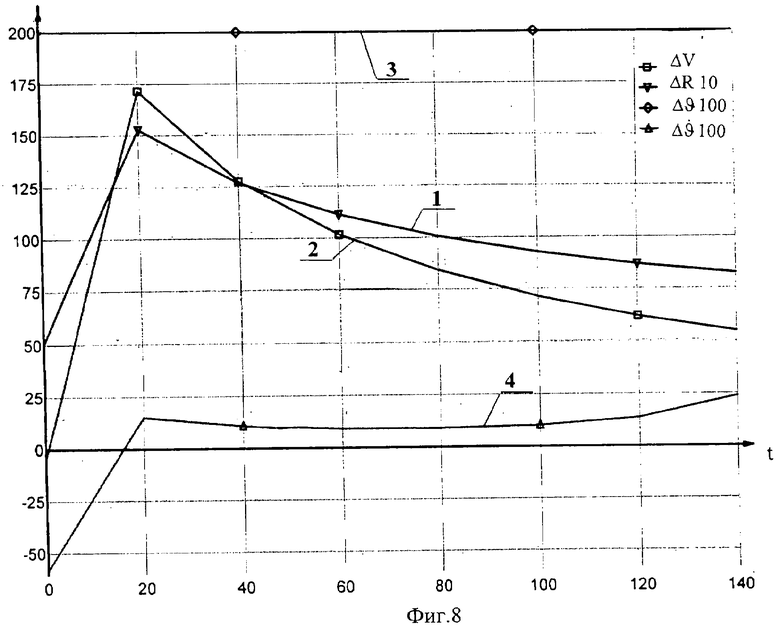
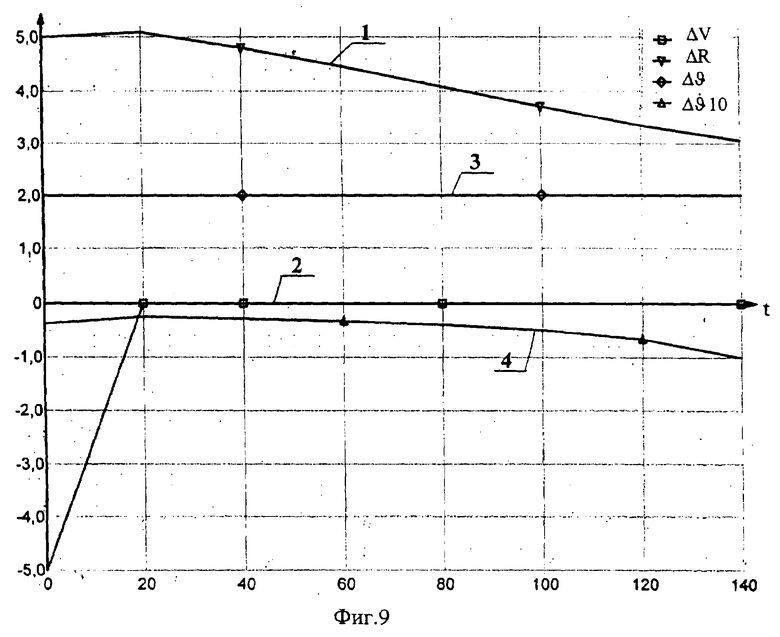
Эффективность предлагаемого способа формирования корректирующих поправок при отработке начальных отклонений ΔR=5000 км и ΔV=-5 м/с при терминальном управлении с тактом Тy=20 с видна из представленных переходных процессов на фиг.8 (по способу-прототипу) и фиг.9 (по предлагаемому способу).
На фиг.8, 9 показаны изменения следующих параметров: 1 - отклонение радиус-вектора ΔR (км), 2 - отклонение радиальной скорости ΔV (м/с), 3 - поправка по углу тангажа Δϑ (град), ограниченная на уровне 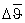 =2 град., 4 - поправка по угловой скорости тангажа
=2 град., 4 - поправка по угловой скорости тангажа 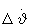 (град/с). На фиг.8 параметр ΔR увеличен в 10 раз, а параметры Δϑ и
(град/с). На фиг.8 параметр ΔR увеличен в 10 раз, а параметры Δϑ и 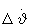 в 100 раз; на фиг.9 параметр
в 100 раз; на фиг.9 параметр 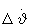 увеличен в 10 раз.
увеличен в 10 раз.
Таким образом, предложенный способ коррекции параметров программы изменения продольного движения при терминальном управлении наведением разгонного блока на заданную орбиту позволяет повысить точность формирования заданной орбиты при выполнении маневров малой продолжительности.
Источники информации
1. Сыров А.С., Соколов В.Н., Ежов В.В., Кислик Л.И. Алгоритм наведения разгонного блока с нерегулируемым маршевым двигателем и малой тяговооруженностью. Авиакосмическая техника и технология, 1998, №1, с.31-33.
2. А.П.Разыграев Основы управления полетом космических аппаратов и кораблей. М.: Машиностроение, 1977, с.366.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ КОРРЕКЦИИ ПАРАМЕТРОВ ПРОГРАММЫ ОРИЕНТАЦИИ ПРИ ТЕРМИНАЛЬНОМ УПРАВЛЕНИИ НАВЕДЕНИЕМ РАЗГОННОГО БЛОКА НА ЗАДАННУЮ ОРБИТУ | 2010 |
|
RU2454357C1 |
| СПОСОБ КОРРЕКЦИИ ПАРАМЕТРОВ ПРОГРАММЫ ОРИЕНТАЦИИ РАЗГОННОГО БЛОКА | 2010 |
|
RU2432595C1 |
| СПОСОБ УПРАВЛЕНИЯ ДВИЖЕНИЕМ РАЗГОННОГО БЛОКА НА УЧАСТКЕ ДОРАЗГОНА | 2010 |
|
RU2424954C1 |
| СПОСОБ ФОРМИРОВАНИЯ ПРОГРАММЫ ОРИЕНТАЦИИ РАЗГОННОГО БЛОКА ПРИ ТЕРМИНАЛЬНОМ УПРАВЛЕНИИ ЕГО НАВЕДЕНИЕМ НА ЗАДАННУЮ ОРБИТУ | 2005 |
|
RU2282568C1 |
| СПОСОБ УПРАВЛЕНИЯ ДВИЖЕНИЕМ РАЗГОННОГО БЛОКА В КОНЦЕ МАНЕВРА | 2010 |
|
RU2432596C1 |
| СПОСОБ ФОРМИРОВАНИЯ ТЕРМИНАЛЬНОГО УПРАВЛЕНИЯ НАВЕДЕНИЕМ РАЗГОННОГО БЛОКА НА ЗАДАННУЮ ОРБИТУ | 2002 |
|
RU2223894C1 |
| СПОСОБ УПРАВЛЕНИЯ ПРОДОЛЬНЫМ ДВИЖЕНИЕМ РАЗГОННОГО БЛОКА НА УЧАСТКЕ ДОРАЗГОНА | 2009 |
|
RU2408851C1 |
| СПОСОБ КОРРЕКЦИИ ПАРАМЕТРОВ ПРОГРАММЫ ИЗМЕНЕНИЯ ПРОДОЛЬНОГО ДВИЖЕНИЯ ПРИ ТЕРМИНАЛЬНОМ УПРАВЛЕНИИ НАВЕДЕНИЕМ РАЗГОННОГО БЛОКА НА ЗАДАННУЮ ОРБИТУ | 2002 |
|
RU2211786C1 |
| СПОСОБ УПРАВЛЕНИЯ ПРОДОЛЬНЫМ ДВИЖЕНИЕМ РАЗГОННОГО БЛОКА НА УЧАСТКЕ ДОРАЗГОНА | 2007 |
|
RU2350521C1 |
| СПОСОБ КАЛИБРОВКИ ИМПУЛЬСА ТЯГИ МАРШЕВОГО ДВИГАТЕЛЯ | 2009 |
|
RU2388665C1 |


Изобретение относится к космической технике, а более конкретно к бортовым средствам терминального управления разгонных блоков (РБ) с нерегулируемыми маршевыми ракетными двигателями. Согласно изобретению, прогнозируют параметры движения РБ на момент отсечки маршевого двигателя и определяют по ним отклонения радиуса и радиальной скорости РБ от их значений на заданной орбите. Формируют сигналы коррекции по углу и угловой скорости тангажа для компенсации указанных отклонений. Ограничивают сигнал коррекции по углу тангажа на заданном уровне и определяют его превышение над этим уровнем. При выходе данного сигнала коррекции на ограничение формируют добавку к сигналу коррекции по угловой скорости тангажа. Эта поправка равна произведению указанного превышения на отношение функций чувствительности радиальной скорости РБ к углу тангажа и к угловой скорости тангажа. Результирующий сигнал коррекции по угловой скорости тангажа формируют как сумму этого сигнала, определенного без учета указанного ограничения сигнала коррекции по углу тангажа, и указанной добавки. Тем самым обеспечивают приоритетную отработку скоростной невязки при ограниченной поправке по углу тангажа. Технический результат изобретения состоит в повышении точности формирования заданной орбиты при выполнении маневра РБ малой продолжительности путем снижения уровня возмущений на контур угловой стабилизации. 1 табл., 9 ил.
Способ коррекции параметров программы изменения продольного движения при терминальном управлении наведением разгонного блока на заданную орбиту, заключающийся в том, что прогнозируют параметры движения разгонного блока на момент отсечки маршевого двигателя, определяют по ним отклонения радиуса и радиальной скорости разгонного блока от их значений на заданной орбите, вычисляют функции чувствительности этих отклонений к изменению параметров программы управления по углу и угловой скорости тангажа, формируют сигналы коррекции по углу и угловой скорости тангажа, обеспечивающие компенсацию указанных отклонений радиуса и радиальной скорости разгонного блока, ограничивают сигнал коррекции по углу тангажа на заданном уровне, отличающийся тем, что определяют превышение сигнала коррекции по углу тангажа относительно заданного при его ограничении уровня, формируют добавку к сигналу коррекции по угловой скорости тангажа, равную произведению этого превышения на отношение функций чувствительности радиальной скорости разгонного блока к углу тангажа и к угловой скорости тангажа, формируют сигнал коррекции по угловой скорости тангажа как сумму сигнала коррекции по угловой скорости тангажа, определенного без учета ограничения сигнала коррекции по углу тангажа, и указанной добавки, определяемой при выходе сигнала коррекции по углу тангажа на его указанное ограничение.
| СЫРОВ А.С., СОКОЛОВ В.Н | |||
| и др | |||
| Алгоритм наведения разгонного блока с нерегулируемым маршевьм двигателем и малой тяговооруженностью | |||
| Авиакосмическая техника и технология | |||
| Способ и аппарат для получения гидразобензола или его гомологов | 1922 |
|
SU1998A1 |
| ЛИТВИН-СЕДОЙ М.З | |||
| Управление космическими кораблями | |||
| М.: Изд | |||
| МГУ, 1967, с.285-301 | |||
| РАЗЫГРАЕВ А.П | |||
| Основы управления полетом космических кораблей | |||
| М.: | |||
Авторы
Даты
2005-06-20—Публикация
2003-06-27—Подача