Изобретение относится к методам испытаний и может быть использовано в области испытаний автомобильной техники.
Матрица передаточных функций характеризует динамику бокового перемещения точки, принятой за полюс, и динамику угловых перемещений вокруг этого полюса. Матрицу передаточных функций можно построить, имея в распоряжении математическую модель упругой системы автомобиля в боковом движении. Известна математическая модель автомобиля в виде системы с двумя степенями свободы (см. Рокар И. Неустойчивость в механике. Автомобили. Самолеты. Висячие мосты. М. 1959, стр.115), основанная на использовании теоремы о движении центра масс и теоремы об изменении момента количества движения в относительном движении относительно центра масс:
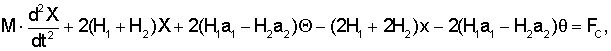
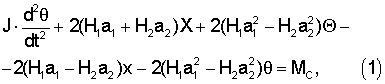
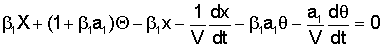
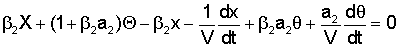
где M - масса автомобиля, J - радиус инерции автомобиля, X - поперечная координата центра тяжести автомобиля; х - поперечная координата прямоугольника, вершины которого - точки соприкосновения колес с дорожным покрытием; Θ - угол, определяющий направление автомобиля; θ - угол, определяющий направление прямоугольника вершины которого - точки соприкосновения колес с дорожным покрытием; H1, H2 - жесткость колес соответственно передней и задней оси; a1, а2 - расстояния от передней и задней оси до положения центра тяжести; FС - внешняя боковая сила; МС - внешний, изменяющий направление колес момент; β1, β2 - коэффициент деформации шин передней и задней оси; V - скорость движения автомобиля.
Преобразовав данные уравнения по Лапласу при нулевых начальных условиях, мы получаем передаточную матрицу упругой системы автомобиля в боковом движении, однако даже в простейшем случае формулы получаются весьма сложными. При учете дополнительных степеней свободы соответствующее выражение усложняется настолько, что в настоящее время известны математические модели, учитывающие не более 4 степеней свободы.
У прототипа и заявляемого изобретения имеются следующие существенные признаки: оба способа нацелены на получение математической модели автомобиля. При построении модели как системы с двумя степенями свободы фиксируются переходные процессы, по которым находят собственные частоты, коэффициенты затухания и коэффициенты статической податливости.
К причинам, препятствующим достижению указанного ниже технического результата при применении известного метода испытания, принятого за прототип, относится чрезвычайное усложнение модели при попытке учета дополнительных степеней свободы.
Способ предназначен для использования при оценке курсовой устойчивости автомобиля, а также для анализа качества переходных процессов при боковых порывах ветра, а также несимметричном воздействии со стороны дорожного профиля.
Технический результат - предложен способ построения матрицы передаточных функций упругой системы автомобиля в боковом движении, направленной на решение задачи, заключающейся в учете влияния всех существенно проявляющих себя степеней свободы, а именно мостов, рамы, кузова, двигателя и др. на курсовую устойчивость автомобиля.
Особенность заключается в том, что прикладывается гармоническое воздействие перпендикулярно продольной плоскости автомобиля в точке, принятой за полюс, и измеряют кинематические параметры колебаний - перемещения центра масс и угловые колебания, затем прикладывается пара сил, действующая относительно полюса и также меняющаяся по гармоническому закону, и также измеряют кинематические параметры - перемещения центра масс и угловое колебание относительно центра масс. Регистрируют амплитудно-фазо-частотные характеристики (АФЧХ) измеряемых кинематических параметров, в дальнейшем с помощью АФЧХ строят матрицу передаточных функций в виде:
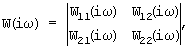
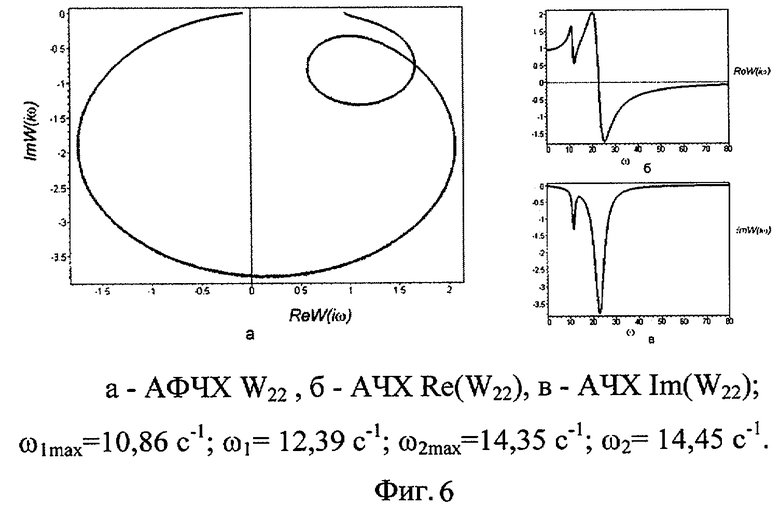
W11(iω) - АФЧХ линейного перемещения центра масс, W22(iω) - АФЧХ углового перемещения центра масс, W12(iω) и W21(iω) - перекрестные АФЧХ.
Фиксируют характеристики частоты - экстремальные точки АФЧХ, соответствующие минимальному значению мнимой составляющей ωn, максимальному значению вещественной составляющей ωnmax. По зафиксированным значениям ωn и ωnmax определяют постоянные времени:
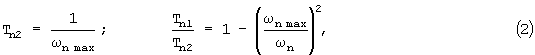
где Тn2, Tn1 - постоянные инерционная и демпфирования n-го колебательного звена. Смотри: Ю.Н.Санкин. Динамика несущих систем металлорежущих станков. - М.: Машиностроение, 1986. - 96 с.
В работе: Динамические характеристики вязкоупругих систем с распределенными параметрами. Санкин Ю.Н. Издательство Саратовского университета, 1977 г., дано теоретическое представление передаточной функции, являющейся математической моделью эквивалентной упругой системы:
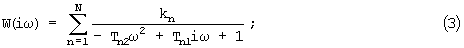
где 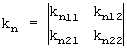 - соответствующие матрицы коэффициентов усиления n-го колебательного звена
- соответствующие матрицы коэффициентов усиления n-го колебательного звена 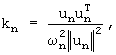 обозначая
обозначая 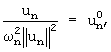 N - число существенно проявляющихся витков АФЧХ.
N - число существенно проявляющихся витков АФЧХ.
Дальнейшая оценка устойчивости осуществляется по построенным АФЧХ независимо от числа колебательных звеньев, существенно проявляющих себя на АФЧХ.
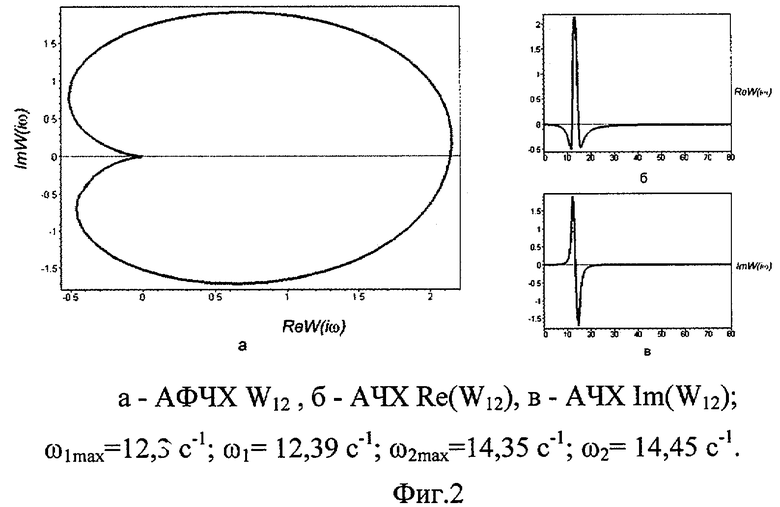
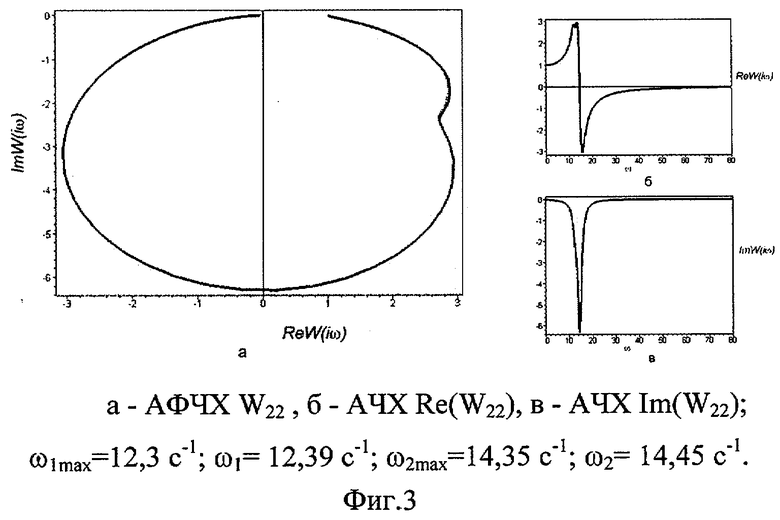
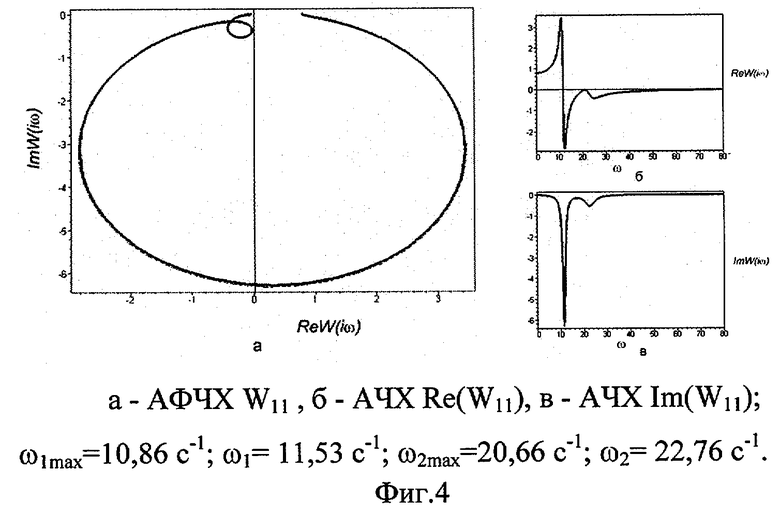
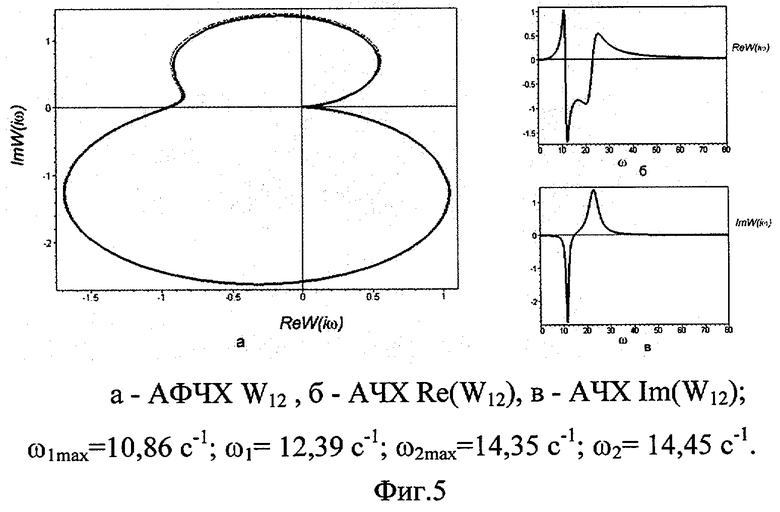
Сущность изобретения поясняется чертежами, где на Фиг.1, 2 и 3 - соответственно линейная, перекрестная и угловых колебаний АФЧХ для модели Рокара, а также соответствующие АЧХ; на Фиг.4, 5, 6 соответственно линейная, перекрестная и угловых колебаний АФЧХ для модели со многими степенями свободы.
Сущность изобретения основывается на следующих теоретических соображениях. В основу положена система линейных дифференциальных уравнений движения автомобиля, полученная авторами и которая обобщает систему дифференциальных уравнений, приведенную в работе: Рокар И. Неустойчивость в механике. Автомобили. Самолеты. Висячие мосты. М. 1959., 288 стр.:
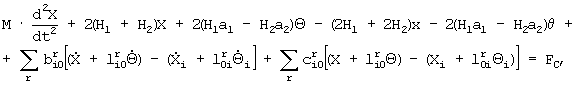
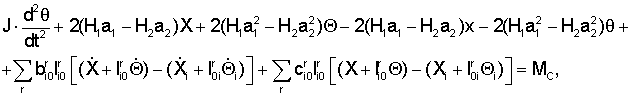
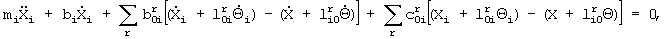
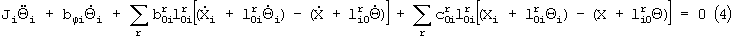

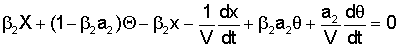
где М - масса рамы автомобиля, J - радиус инерции рамы автомобиля, mj - масса присоединенного агрегата автомобиля, Ji - радиус инерции присоединенного агрегата автомобиля, Х - поперечная координата центра тяжести рамы автомобиля; Xi - поперечная координата центра тяжести присоединенного агрегата автомобиля; х - поперечная координата прямоугольника, вершины которого - точки соприкосновения колес с дорожным покрытием; Θ - угол, определяющий направление рамы автомобиля; Θi - угол, определяющий направление присоединенного агрегата автомобиля; θ - угол, определяющий направление прямоугольника вершины которого - точки соприкосновения колес с дорожным покрытием; с - эквивалентная жесткость упругой связи рамы с присоединенным агрегатом; b - коэффициент рассеяния энергии в упругой связи рамы с присоединенным агрегатом; l - расстояние от центра тяжести присоединенного агрегата до точки крепления упругой связи; i - число присоединенных тел; r - число упругих связей.
Данное изобретение было проверено с помощью численного эксперимента. В модель Рокара были заложены следующие исходные данные: М=2530 кг, J=1,068 кг·м2; H1=H2=100800 Н/м; a1=1,314 м; а2=1,086 м; β1=β2=2,7. Модель (4), позволяющая учитывать множество степеней свободы, первоначально рассматривалась как состоящая из двух тел: рамы и кузова с параметрами: М=930 кг; m1=1600 кг; a1=1,21 м; а2=1,19 м; с=1800 кН/м; γ=0,01.
Предположим, что АФЧХ на фиг.1, 2, 3 (пунктир) получены экспериментальным путем, а на самом деле - из системы уравнений (1), АФЧХ на фиг.1, 2, 3 (сплошная линия) - в виде ряда по колебательным звеньям, используя уравнение (3). Соответствующая передаточная матрица, построенная по формуле (3), имеет вид:
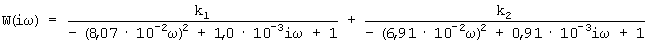
Обозначая 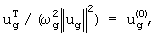 то для рассматриваемого случая:
то для рассматриваемого случая: 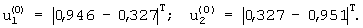
Как видно, обе кривые практически совпадают одна с другой. При увеличении числа степеней свободы в модели (4), число существенно проявляющих себя колебательных звеньев не растет. Поэтому кривая (сплошная линия), построенная по уравнению (3):
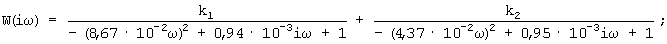
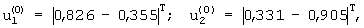
являющаяся суммой двух колебательных звеньев, с достаточной точностью аппроксимирует АФЧХ, полученную из системы уравнений (4), и мало зависит от числа учитываемых степеней свободы (пунктир).
Численные эксперименты показывают практически полное совпадение АФЧХ, построенных путем решения уравнений (1, 4) и путем моделирования в виде ряда по колебательным звеньям (3).
Изобретение относится к способам испытаний транспортных средств. Способ заключается в том, что прикладывают гармоническое воздействие перпендикулярно продольной плоскости автомобиля в точке, принятой за полюс, снимают АФЧХ (амплитудно-фазо-частотные характеристики) поперечных и угловых колебаний, затем прикладывают пару сил, действующих относительно полюса и также меняющихся по гармоническому закону, при этом также снимают АФЧХ угловых и линейных колебаний. По построенным АФЧХ строят матрицу передаточных функций, каждый элемент которой представляет собой ряд по колебательным звеньям, число которых равно числу существенно проявляющих себя витков АФЧХ. После этого полученную модель дополняют уравнениями неголономных связей шин с дорожным покрытием и используют для оценки качества переходных процессов и курсовой устойчивости, при этом эквивалентная динамическая модель автомобиля в боковом движении с учетом скорости движения получается в результате испытаний на неподвижном автомобиле. В результате предложенного способа испытания учитывается влияние всех существенно проявляющих себя степеней свободы, а именно мостов, рамы, кузова, двигателя и др. на курсовую устойчивость автомобиля. 6 ил.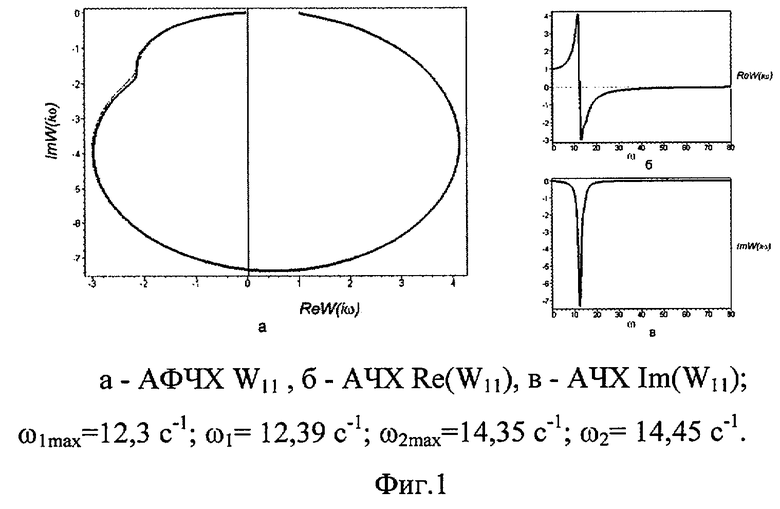
Способ построения матрицы передаточных функций автомобиля в боковом движении, заключающийся в том, что прикладывают гармоническое воздействие перпендикулярно продольной плоскости автомобиля в точке, принятой за полюс, снимают АФЧХ (амплитудно-фазочастотные характеристики) поперечных и угловых колебаний, затем прикладывают пару сил, действующих относительно полюса и также меняющихся по гармоническому закону, при этом также снимают АФЧХ угловых и линейных колебаний, отличающийся тем, что по построенным АФЧХ строят матрицу передаточных функций, каждый элемент которой представляет собой ряд по колебательным звеньям, число которых равно числу существенно проявляющих себя витков АФЧХ, после чего полученную модель дополняют уравнениями неголономных связей шин с дорожньм покрытием и используют для оценки качества переходных процессов и курсовой устойчивости, при этом эквивалентная динамическая модель автомобиля в боковом движении с учетом скорости движения получается в результате испытаний на неподвижном автомобиле.
| Рокар И | |||
| Неустойчивость в механике | |||
| Автомобили | |||
| Самолеты | |||
| Висячие мосты | |||
| - М.,1959, стр.115, 228, | |||
| Ю.Н.Санкин, Динамика несущих систем металлорежущих станков | |||
| - М., 1986, 96 с. |
Авторы
Даты
2005-11-20—Публикация
2004-04-09—Подача