Изобретение относится к адаптивным системам автоматического управления объектами с неизвестным математическим описанием и произвольными возмущающими воздействиями при наличии в задании системе управления нелинейных ограничений в форме равенств и неравенств на управляемые переменные, управляющие воздействия и траектории перехода объекта управления в требуемое состояние.
Известны системы адаптивного управления, предназначенные для автоматического управления динамическими объектами с неизвестным математическим описанием, основанные на принципе разделения и стохастической теории оптимального оценивания (Красовский А.А. Адаптивный оптимальный регулятор с переменным порядком наблюдателя и временем экстраполяции // АиТ. 1994. №11; Острем К., Виттенмарк Б. Системы управления с ЭВМ. - М.: Мир, 1987. - с.388-405; Саридис Дж. Самоорганизующиеся стохастические системы управления. - М.: Наука, 1980). В соответствии с принципом разделения эти системы формируют управляющие воздействия путем решения детерминированной задачи оптимального управления с использованием в цепи обратной связи оптимальных оценок переменных состояния вместо их реальных значений. В состав систем адаптивного управления (как и в состав заявленного изобретения) входят: блок формирования задания (БФЗ), генератор управляющих воздействий (ГУВ) с блоком сравнения (БС) и самонастраивающимся регулятором (СР) и объект управления (ОУ), которые образуют прямую цепь системы управления, а также измерительное устройство и наблюдатель переменных состояния и(или) параметров (НПС), включенные в цепь обратной связи. Кроме того, в состав систем адаптивного управления (в отличие от заявленного изобретения) входят отбеливающие фильтры, формирующие оценки возмущающих воздействий из центрированных белых гауссовских шумов (ЦБГШ). Отличаются адаптивные системы с СР друг от друга математическими моделями ОУ; моделями отбеливающих фильтров; алгоритмами оценивания переменных состояния и(или) параметров модели системы управления; алгоритмами формирования управляющих воздействий. В качестве моделей ОУ и отбеливающих фильтров используют различные авторегрессии, временные ряды, полиномы и сплайны. НПС вычисляет функции распределения условных вероятностей переменных состояния ОУ и оптимальные оценки параметров и переменных состояния указанных моделей, используя результаты измерений выходных сигналов ОУ, априорные сведения об интенсивностях ЦБГШ и значения управляющих воздействий, реализованные в предыдущие моменты времени. Для вычисления этих оценок применяют алгоритмы стохастической аппроксимации, метод наименьших квадратов, метод максимума правдоподобия либо фильтр Калмана. Алгоритмы СР синтезируют путем решения задачи минимизации используемой функции штрафа в детерминированной постановке с помощью вариационного исчисления, принципа максимума или методом динамического программирования.
Адаптивные системы автоматического управления с СР удалось реализовать только в линейных системах и в простейших нелинейных системах (если заданы траектории перехода всех управляемых переменных ОУ в требуемое конечное состояние, ограничения в форме неравенств отсутствуют, при синтезе алгоритма СР используют квадратичную функцию штрафа). Однако в реальных задачах управления эти условия одновременно выполняются редко. Многие системы управления содержат устройства с нелинейными характеристиками (например, измерительные устройства с нелинейными статическими характеристиками, различные нелинейные преобразователи и т.п.). Обычно функции распределения вероятностей возмущающих воздействий отличны от гауссовских функций, часто эти функции распределения неизвестны по априорным данным. Кроме того, траектории перехода в требуемое конечное состояние заданы только для части переменных состояния ОУ, а для другой части переменных состояния с помощью неравенств (линейных и нелинейных) задано множество допустимых траекторий перехода в требуемое конечное состояние. В этих случаях принцип максимума приводит к нелинейной двухточечной краевой задаче, а динамическое программирование - к нелинейному уравнению Беллмана, которые нельзя решить численными методами в процессе управления в реальном масштабе времени (Бар-Шалом Я., Ци Э. Концепции и методы стохастического управления // Фильтрация и стохастическое управление в динамических системах / Под ред. К.Е.Леондеса. М.: Мир, 1980. С.74-122; Фельдбаум А.А. Основы теории оптимальных автоматических систем. - М.: Наука, 1966). Кроме того, указанные адаптивные системы управления реализуют алгоритмы пропорционального регулирования оценок переменных состояния, параметров и управляющих воздействий. Поэтому они имеют статическую ошибку управления в случаях, когда возмущающие воздействия отличны от ЦБГШ.
Последний недостаток частично устранен в адаптивной системе управления с самонастраивающимся ПИД-нейроконтроллером, формирующим управляющие воздействия по алгоритму ПИД-регулирования с автоматической настройкой параметров ПИД-регулятора с помощью обучаемой нейросети (Нейроуправление и его приложения. Кн.2. / Сигеру Омату, Марзуки Халид, Рубия Юсоф. - М.: ИПРЖР, 2000; Saiful A. and S. Omatu, «Neuromorphic self-tuning PID controller», Proc. of 1993 IEEE ICNN. San Francisco, pp.552-557, 1993). Эта система (прототип изобретения) имеет (как и заявленное изобретение): блок формирования задания; генератор управляющих воздействий, содержащий блок сравнения и ПИД-регулятор, и ОУ, образующие прямую цепь системы управления, систему измерительных устройств (ИУ) и НПС, включенные в цепь обратной связи. Входы БС соединены с выходами БФЗ и НПС. Выходы БС соединены с входами ПИД-регуляторов. БФЗ формирует требуемые значения управляемых переменных в текущий момент времени, требуемые средние значения этих переменных в скользящем временном окне и требуемые скорости изменения управляемых переменных. Выходные сигналы системы измерительных преобразователей связаны с управляемыми переменными известными функциональными зависимостями (линейными или нелинейными). В отличие от изобретения адаптивная система управления с самонастраивающимся ПИД-нейроконтроллером содержит формирователь оценок параметров ПИД-регулятора, выполненный в виде обучаемой нейросети. НПС этой системы выполнен в виде еще одной обучаемой нейросети и формирует оценки управляемых переменных и матриц чувствительности управляемых переменных к изменению управляющих воздействий. Обе нейронные сети образованы из статических нейронов и обучаются по алгоритму обратного распространения ошибки.
Однако адаптивная система с самонастраивающимся ПИД-нейроконтроллером не учитывает ограничения в форме неравенств на управляемые переменные и траектории перехода переменных состояния ОУ в требуемое конечное состояние. Кроме того, при использовании в системе управления динамической нейронной сети в качестве модели объекта управления алгоритм обратного распространения ошибки порождает нелинейную краевую задачу (которую, как указывалось, нельзя решить в реальном масштабе времени в процессе управления).
Сущность изобретения как технического решения, обеспечивающего с погрешностью, асимптотически стремящейся к нулю, автоматическое управление объектами с неизвестным математическим описанием при наличии в задании системе управления нелинейных ограничений в форме равенств и неравенств на управляемые переменные, управляющие воздействия и траектории перехода объекта управления в требуемое состояние, выражается в совокупности следующих признаков:
- полезная модель выполнена в виде адаптивной системы управления с самонастраивающимися ПИД-регуляторами и формирует оценки переменных состояния и управляющие воздействия с помощью модифицированных алгоритмов фильтра Калмана, в которых в качестве априорных моделей объекта управления и генератора управляющих воздействий используется авторегрессия скользящего среднего;
- каждое измерительное устройство образовано последовательным соединением измерительного преобразователя (с линейной или нелинейной статической характеристикой) и вычислителя, выполненного в виде параллельного соединения пропорционального, интегрирующего и дифференцирующего блоков;
- БФЗ, вычислитель системы измерительных устройств и ГУВ оснащены нелинейными преобразователями (НП), обеспечивающими выполнение системой управления ограничений, заданных неравенством 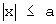 . Такие НП имеют сигмоидальные статические характеристики s(x,a), заданные сплайнами или другими непрерывными функциями, например:
. Такие НП имеют сигмоидальные статические характеристики s(x,a), заданные сплайнами или другими непрерывными функциями, например:
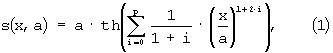
где:
s(x,a) - выходной сигнал НП;
x - входной сигнал НП;
а - заданный параметр, определяющий границы множества допустимых значений переменной x (входного сигнала НП);
p - целое число, которое выбирают из диапазона значений 0≤p≤3;
- нелинейный преобразователь БФЗ включен в дополнительный контур обратной связи и он формирует свои выходные сигналы (дополнительное задание системе управления) с учетом заданных ограничений в форме неравенств на траектории перехода переменных состояния в требуемое конечное состояние и текущих значений выходных сигналов системы измерительных устройств.
Изобретение решает задачу автоматического управления (с погрешностью, асимптотически стремящейся к нулю) многомерным динамическим объектом с неизвестным математическим описанием и произвольными возмущающими воздействиями при наличии нелинейных ограничений в виде следующих совместимых равенств и неравенств:
yj(tk)=hj(z(tk),tk)+δj(tk); j=1,2,...,n;
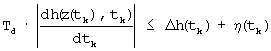 ; tk=k·Δt;
; tk=k·Δt; 

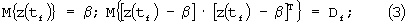
rj(tk)=ƒj(z(tk),u(tk),tk)+εj(tk); 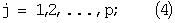
 ;
; 
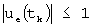 ;
; 
где:
rj(tf)=fj(β,uопт(tf),tf); γi(tf)=ϕi(β,uопт(tf),tf);
y(tk) - вектор выходных сигналов измерительных преобразователей;
z(tk) - вектор управляемых переменных (выходных сигналов ОУ);
h(z(tk),tk) - вектор нелинейных статических характеристик измерительных преобразователей;
δ(tk) - вектор погрешностей измерений;
Δt - шаг квантования времени tk;
Td - время дифференцирования;
Δh(tk) - вектор заданных функций времени tk;
η(tk) - вектор допустимых погрешностей отклонения скоростей изменения управляемых переменных от предельных значений, заданных неравенством (2);
rj(tk) - известная по априорным данным функция, с помощью которой заданы координаты траекторий перехода в требуемое конечное состояние (3) части управляемых переменных, входящих в ограничение (4);
ϕi(z(tk),tk) - функция, с помощью которой задано ограничение (5) на допустимые траектории перехода другой части управляемых переменных в требуемое конечное состояние (3);
εj(tk) - допустимая погрешность управления;
u(tk) - вектор управляющих воздействий;
uопт(tk) - вектор оптимальных управляющих воздействий.
Сущность изобретения поясняет блок-схема адаптивной системы автоматического управления, изображенная на чертеже.
Заявленная адаптивная система автоматического управления, как и системы-аналоги, использует авторегрессию скользящего среднего в качестве априорных моделей объекта управления и генератора управляющих воздействий. Она, как и прототип, содержит (см. чертеж): блок формирования задания 1; генератор управляющих воздействий, образованный БС 2 и ПИД-регулятором 3, и объект управления 4, включенные в прямую цепь системы управления, систему измерительных преобразователей 5 и НПС 6, включенные в цепь обратной связи. При этом входы БС 2 соединены с выходами БФЗ 1 и НПС 6, а выходы БС 2 соединены с входами ПИД-регулятора 3. Выходы ОУ 4 соединены с входами системы измерительных преобразователей 5. Отличается заявленная адаптивная система автоматического управления от прототипа тем, что система измерительных устройств помимо измерительных преобразователей 5 содержит вычислитель 7, образованный параллельным соединением пропорционального блока 8, интегрирующего блока 9 и дифференцирующего блока 10. Входы вычислителя 7 соединены с выходами системы измерительных преобразователей 5, а его выходы соединены с входами НПС 6. Кроме того, БФЗ 1, ПИД-регулятор 3 и дифференцирующий блок 10 оснащены нелинейными преобразователями 11, 12 и 13 с сигмоидальными статическими характеристиками (1), обеспечивающими выполнение системой управления ограничений (2), (5) и (6). ГУВ полезной модели содержит дополнительный блок сравнения 14, входы которого соединены с выходами НПС 6 и НП 12, а выходы соединены с входами ПИД-регулятора 3. Входы НП 11 соединены с выходами дифференцирующего блока 10. Входы НП 12 соединены с выходами БФЗ 1 и НПС 6. Входы НП 13 соединены с выходами ПИД-регулятора 3, а выходы соединены с входами ПИД-регулятора 3, ОУ 4 и НПС 6.
Нелинейная адаптивная система автоматического управления реализует алгоритм управления следующим образом. БФЗ 1 по известным априорным данным формирует в скользящем временном окне следующее задание системе управления:
- текущие значения вектора r(tk) (левую часть ограничений (4)), которые поступают в БС 2;
- текущие значения вектора γ(tk) (левую часть ограничений (5)), которые поступают в НПС 6 и НП 12;
- алгоритм формирования правых частей ограничений (4) и (5), который поступает в НПС 6.
Вычислитель 7 формирует выходные сигналы системы измерительных устройств по алгоритму
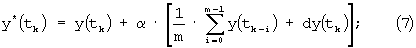
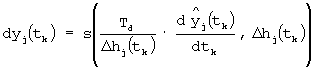 ;
; 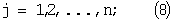
а затем передает их текущие значения в НПС 6, где:
y*(tk) - вектор выходных сигналов системы измерительных устройств;
0≤α≤1 - весовой коэффициент (параметр регуляризации);
Td - время дифференцирования;
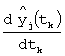 - сглаженная оценка скорости изменения выходного сигнала yj(tk) измерительного преобразователя с номером j.
- сглаженная оценка скорости изменения выходного сигнала yj(tk) измерительного преобразователя с номером j.
Нелинейный преобразователь 13 формирует вектор управляющих воздействий u(tk) по алгоритму:
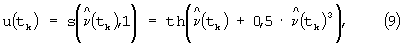
где 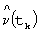 - вектор выходных сигналов ПИД-регулятора 3. Кроме того, НП 12 формирует вектор
- вектор выходных сигналов ПИД-регулятора 3. Кроме того, НП 12 формирует вектор  своих выходных сигналов (дополнительное задание системе управления) с учетом ограничений (5) по алгоритму:
своих выходных сигналов (дополнительное задание системе управления) с учетом ограничений (5) по алгоритму:
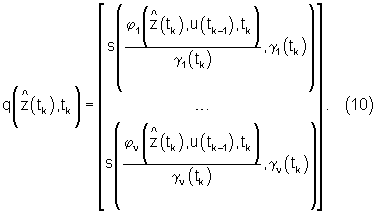
НПС 6 выполнен в виде многомерного самонастраивающегося ПИД-регулятора оценок управляемых переменных. Он реализует модифицированный алгоритм фильтра Калмана:

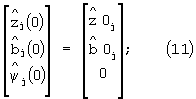
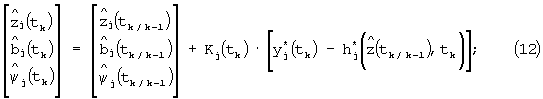
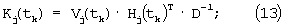

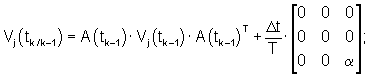


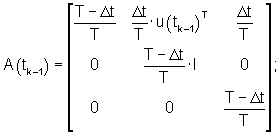
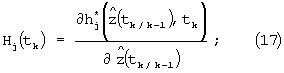

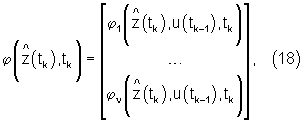
где:
bj(tk) - вектор коэффициентов чувствительности управляемой переменной zj(tk) к изменению управляющих воздействий;
ψj(tk) - вспомогательная переменная;
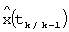 - прогноз значения переменной x(tk) в момент времени tk, вычисленный по результатам измерений, выполненных в моменты времени t1, t2,...,tk-1;
- прогноз значения переменной x(tk) в момент времени tk, вычисленный по результатам измерений, выполненных в моменты времени t1, t2,...,tk-1;
Т - постоянная времени сглаживающего фильтра (11);
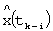 - оценка переменной x(tk), вычисленная в момент времени tk-i;
- оценка переменной x(tk), вычисленная в момент времени tk-i;
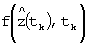 ,
,  - векторы выходных сигналов НПС 6 (векторы оценок выходных сигналов БФЗ 1 и НП 12 соответственно).
- векторы выходных сигналов НПС 6 (векторы оценок выходных сигналов БФЗ 1 и НП 12 соответственно).
НПС 6 по алгоритму (11)-(18) вычисляет текущие значения своих выходных сигналов (прогноз задания системе управления): вектор  , который поступает в БС 2, и вектор
, который поступает в БС 2, и вектор  , который поступает в НП 12 и БС 14. НПС 6 формирует свои выходные сигналы в предположении, что в момент времени tk действуют управляющие воздействия u(tk)=u(tk-1), сформированные в предыдущий момент времени tk-1. Нелинейный преобразователь 12 по алгоритму (10) формирует вектор
, который поступает в НП 12 и БС 14. НПС 6 формирует свои выходные сигналы в предположении, что в момент времени tk действуют управляющие воздействия u(tk)=u(tk-1), сформированные в предыдущий момент времени tk-1. Нелинейный преобразователь 12 по алгоритму (10) формирует вектор 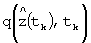 - дополнительное задание системе управления, которое передает в БС 14. Блоки сравнения 2 и 14 формируют по уравнению
- дополнительное задание системе управления, которое передает в БС 14. Блоки сравнения 2 и 14 формируют по уравнению

вектор сигналов рассогласования 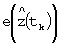 и их текущие значения передают в ПИД-регулятор 3. ПИД-регулятор 3 реализует алгоритм модифицированного фильтра Калмана
и их текущие значения передают в ПИД-регулятор 3. ПИД-регулятор 3 реализует алгоритм модифицированного фильтра Калмана
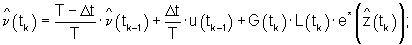
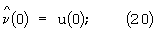


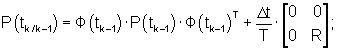
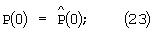
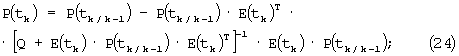
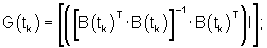
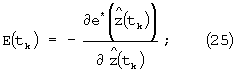
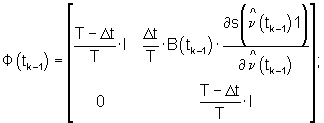
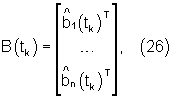
где: Q и R - положительно определенные матрицы.
Затем НП 13 из выходных сигналов 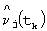 ПИД-регулятора 3 формирует по алгоритму (9) текущие значения управляющих воздействий uj(tk).
ПИД-регулятора 3 формирует по алгоритму (9) текущие значения управляющих воздействий uj(tk).
Из формулы (1) непосредственно следует, что для выходного сигнала s(x,a) нелинейного преобразователя со статической характеристикой (1) выполняется неравенство  при любых значениях его входного сигнала x и параметра а. Значит, оптимальную оценку
при любых значениях его входного сигнала x и параметра а. Значит, оптимальную оценку  переменной x, ограниченной неравенством
переменной x, ограниченной неравенством  , можно определить путем решения уравнения
, можно определить путем решения уравнения
s(x,a)-x=0.
Поэтому при синтезе алгоритмов НПС 6 и ПИД-регулятора 3 вместо неравенств (2), (5) и (6) использовались равенства (8), (10), (19) и (9).
Уравнения (11)-(18) алгоритма оценивания параметров и управляемых переменных (модифицированный фильтр Калмана) получены минимизацией функции штрафа
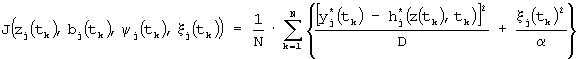
с помощью вариационного исчисления и инвариантного погружения с учетом используемой априорной модели состояния ОУ (в виде авторегрессии скользящего среднего)
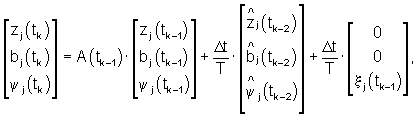
где ξj(tk) - погрешность априорной модели состояния ОУ.
Уравнения модифицированного фильтра Калмана (20)-(26), реализуемые ПИД-регулятором 3, получены минимизацией функции штрафа
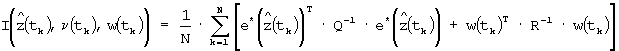
с помощью вариационного исчисления и инвариантного погружения с учетом уравнений (9), (19) и апостериорной модели состояния ОУ
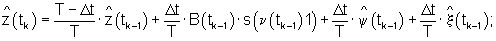
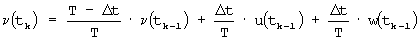 ;
; 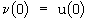 .
.
Заявленная адаптивная система автоматического управления реализует алгоритмы пропорционально-интегрально-дифференциального регулирования управляющих воздействий и оценок параметров и управляемых переменных. Поэтому она обеспечивает погрешность управления, стремящуюся асимптотически к нулю.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ АДАПТИВНОГО УПРАВЛЕНИЯ АКТИВНОЙ МОЩНОСТЬЮ ГИДРОАГРЕГАТА С ПОВОРОТНО-ЛОПАСТНОЙ ТУРБИНОЙ | 2009 |
|
RU2468246C2 |
| СПОСОБ АДАПТИВНОГО УПРАВЛЕНИЯ АКТИВНОЙ МОЩНОСТЬЮ И ЧАСТОТОЙ ГИДРОАГРЕГАТА С ПОВОРОТНО-ЛОПАСТНОЙ ТУРБИНОЙ | 2013 |
|
RU2531068C1 |
| АДАПТИВНАЯ СИСТЕМА УПРАВЛЕНИЯ | 2007 |
|
RU2339988C1 |
| САМОНАСТРАИВАЮЩАЯСЯ СИСТЕМА УПРАВЛЕНИЯ | 1992 |
|
RU2068196C1 |
| АДАПТИВНАЯ СИСТЕМА УПРАВЛЕНИЯ | 2007 |
|
RU2368934C2 |
| АДАПТИВНАЯ СИСТЕМА УПРАВЛЕНИЯ | 2007 |
|
RU2343524C1 |
| Способ автоматической настройки ПИД-регулятора для управления дизельным двигателем в составе электроагрегатов и электростанций | 2016 |
|
RU2653938C2 |
| САМОНАСТРАИВАЮЩАЯСЯ СИСТЕМА УПРАВЛЕНИЯ С ГРАДИЕНТНОЙ АДАПТАЦИЕЙ РЕГУЛЯТОРА СОСТОЯНИЯ | 2014 |
|
RU2574283C1 |
| СПОСОБ МИНИМАКСНОЙ ФИЛЬТРАЦИИ ПАРАМЕТРОВ ДВИЖЕНИЯ БЕСПИЛОТНОГО ЛЕТАТЕЛЬНОГО АППАРАТА С КОРРЕКЦИЕЙ ОТ СПУТНИКОВОЙ НАВИГАЦИОННОЙ СИСТЕМЫ | 2015 |
|
RU2625603C2 |
| АДАПТИВНАЯ СИСТЕМА УПРАВЛЕНИЯ | 2015 |
|
RU2612340C1 |
Изобретение относится к адаптивным системам автоматического управления объектами с неизвестным математическим описанием и произвольными возмущающими воздействиями при наличии в задании системе управления нелинейных ограничений в форме равенств и неравенств на управляемые переменные, управляющие воздействия и траектории перехода объекта управления в требуемое состояние. Технический результат - обеспечение погрешности, асимптотически стремящейся к нулю. В системе блок формирования задания, вычислитель выходных сигналов системы измерительных устройств и генератор управляющих воздействий оснащены нелинейными преобразователями с сигмоидальными статическими характеристиками, обеспечивающими выполнение системой управления ограничений в форме неравенств. Вычислитель системы измерительных устройств образован параллельным соединением пропорционального, интегрирующего и дифференцирующего блоков, а генератор управляющих воздействий и наблюдатель переменных состояния выполнены в виде многомерных самонастраивающихся ПИД-регуляторов, реализующих алгоритмы модифицированных фильтров Калмана. 1 ил.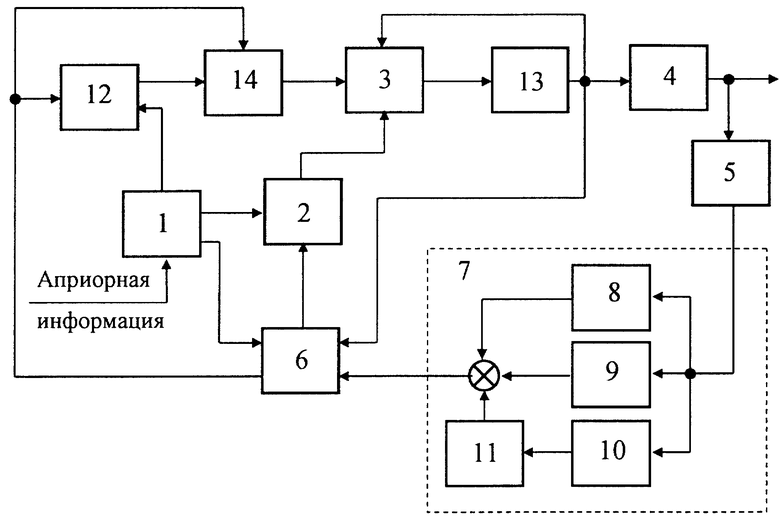
Адаптивная система автоматического управления объектами с неизвестным математическим описанием и произвольными возмущающими воздействиями при наличии в задании системе управления нелинейных ограничений в форме равенств и неравенств на управляющие воздействия и траектории перехода объекта управления в требуемое состояние, которая содержит блок формирования задания, блок сравнения, генератор управляющих воздействий и объект управления, включенные в прямую цепь системы управления, систему измерительных устройств и наблюдатель переменных состояния, включенные в цепь обратной связи, отличающаяся тем, что в контур обратной связи системы управления включены нелинейный преобразователь и дополнительный блок сравнения, входы которого соединены с выходами нелинейного преобразователя и наблюдателя переменных состояния, а выходы соединены с дополнительными входами генератора управляющих воздействий; входы этого нелинейного преобразователя соединены с выходами блока формирования задания и наблюдателя переменных состояния; в прямую цепь системы управления установлен еще один нелинейный преобразователь, входы которого соединены с выходами генератора управляющих воздействий, а выходы соединены с входами наблюдателя переменных состояния, генератора управляющих воздействий и объекта управления; вычислитель выходных сигналов системы измерительных устройств образован параллельным соединением пропорционального, интегрирующего и дифференцирующего блоков, а дифференцирующий блок оснащен нелинейным преобразователем; нелинейные преобразователи имеют сигмоидальные статические характеристики, составленные с учетом ограничений, заданных в форме неравенств; генератор управляющих воздействий и наблюдатель переменных состояния выполнены в виде модифицированных фильтров Калмана, реализующих алгоритмы ПИД-регулирования управляющих воздействий и оценок параметров и управляемых переменных.
| АДАПТИВНАЯ СИСТЕМА УПРАВЛЕНИЯ С ИДЕНТИФИКАТОРОМ И НЕЯВНОЙ ЭТАЛОННОЙ МОДЕЛЬЮ ПРИ ВРЕМЕННЫХ ЗАДЕРЖКАХ ИНФОРМАЦИИ В СИСТЕМЕ УПРАВЛЕНИЯ | 2001 |
|
RU2192031C1 |
| US 4407013 А, 27.09.1983 | |||
| КРАСОВСКИЙ А.А | |||
| Справочник по теории автоматического управления | |||
| - М.: Наука, 1987, с.480, 198, 513. | |||
Авторы
Даты
2005-12-27—Публикация
2004-03-29—Подача