Область техники.
Изобретение относится к области определения деформационных и прочностных характеристик материалов.
Уровень техники.
В настоящее время разработан большой набор математических моделей нелинейного поведения различных материалов, но при конкретном применении возникают значительные трудности в их оснащении материальными функциями и константами. Получение этих данных имеющимися инструментальными средствами при больших деформациях материала путем прямых экспериментальных измерений затруднено, поскольку в лабораторных образцах возникает неодноосное и неоднородное напряженно-деформированное состояние (НДС), проявляется влияние краевых эффектов и т.п. Обычно для получения деформационных и прочностных свойств материалов используются способы, основанные на экспериментально-аналитическом подходе:
1. ГОСТ 1497-84 «Металлы. Методы испытаний на растяжение»;
2. ГОСТ 3565-80 «Металлы. Метод испытаний на кручение»;
3. Марковец М.П. Определение механических свойств по твердости. - М.: Машиностроение, 1979, 191 с.
Применение данных способов налагает существенные ограничения на форму испытуемых образцов, вид нагружения, параметры НДС, что не всегда соответствует реальным условиям эксперимента. Особенно существенно недостатки проявляются в нелинейной области деформирования материалов и элементов конструкций при неоднородном НДС. Для исследования свойств материалов при больших деформациях целесообразно развитие экспериментально-расчетного подхода, в значительной мере свободного от ограничений экспериментально-аналитических методов. Возможности экспериментально-расчетных подходов существенно расширяются, если использовать современные численные методы для математического моделирования физических экспериментов в сочетании с методами идентификации и оптимизации. Предлагаемый способ основан на экспериментально-расчетном подходе, который предполагает проведение совместного анализа результатов эксперимента и полномасштабного (в рамках механики сплошных сред) компьютерного моделирования процессов деформирования лабораторных образцов или элементов конструкций без принятия априорных силовых и кинематических гипотез. Известные аналоги предлагаемого способа описываются в следующих работах:
1. Zhang Z.L., Odegard J., Sovik О.Р. Determining true stress-strain curve for isotropic and anisotropic materials with rectangular tensile bars: method and verifications. // Comput. Mater. Sci., 2001, 20, №1, p.77-85.
2. Бакиров М.Б., Зайцев М.А., Фролов И.В. Математическое моделирование процесса вдавливания сферы в упругопластическое полупространство // Заводская лаборатория. Диагностика материалов, №1, 2001, т.67, с.37-47.
3. Hasanov A., Seyidmamedov Z. The solution of an axisymmetric inverse elastoplastic problem using penetration diagrams. // Int. J. Non-Linear Mech., 1995, v.30, №4, p.465-477.
Применение данных способов также налагает ограничения на форму испытуемых образцов, и, как показали исследования, применение их оказалось малоэффективным при больших деформациях и неоднородном виде НДС. Деформационные и прочностные характеристики определяются с низкой точностью.
Раскрытие изобретения.
Сущность изобретения.
Целью изобретения является расширение возможностей исследования деформационных и прочностных характеристик упругопластических материалов при наиболее простых и малозатратных вариантах испытаний образцов на растяжение, сжатие, кручение и безобразцовом способе испытаний путем кинетического внедрения индентора произвольной формы в исследуемую конструкцию (испытания на твердость) с замерами интегральных параметров - нагружающего усилия (крутящего момента) и перемещения (углов закручивания). Способ определения деформационных и прочностных свойств материалов основан на идентификации результатов эксперимента с помощью численного моделирования процессов деформирования лабораторных образцов или элементов конструкций, в результате применения которого определяется истинная диаграмма деформирования при больших деформациях и неоднородном НДС. Параметрами сравнения являются значения нагружающих усилий (крутящего момента) при одинаковых смещениях (углах закручивания) в расчете и эксперименте. В дальнейшем осуществляется коррекция значений интенсивности напряжений на истинной диаграмме деформирования пропорционально отношению значений параметров сравнения до их совпадения с заданной точностью. Следует отметить, что предложенный способ, в отличие от известных ранее аналогов, позволяет строить диаграммы деформирования независимо от формы образцов и вида нагружения (растяжение, сжатие, кручение, твердость) для больших деформаций и с учетом неоднородности НДС вплоть до момента близкого к разрушению.
Решаемые задачи и технические результаты.
Входными данными для построения истинной диаграммы деформирования является экспериментальная зависимость растягивающей силы от перемещения торца до момента начала разрушения при растяжении-сжатии, или крутящего момента от угла закручивания торца до момента начала разрушения при кручении, или сжимающей силы от смещения индентора при испытаниях на твердость. Для построения истинной диаграммы деформирования проводится численное моделирование деформирования лабораторных образцов или элементов конструкций. Построение диаграммы деформирования основано на коррекции зависимости «интенсивность напряжений - интенсивность деформаций». Для этого в процессе решения задачи анализируется отношение значений нагружающих усилий (крутящего момента), полученных из эксперимента и расчета при одинаковых перемещениях (углах закручивания), и пропорционально этой разнице осуществляется итерационная процедура корректировки значения интенсивности напряжений на диаграмме деформирования, соответствующее максимальному значению интенсивности деформаций в расчете при данном перемещении. Процедура корректировки проводится до совпадения экспериментальных и расчетных значений нагружающих усилий (крутящего момента) с заданной точностью. Как показали исследования для сходимости итерационной процедуры достаточно в качестве начального приближения задать любую диаграмму деформирования упрочняющегося материала. Наиболее эффективный алгоритм заключается в корректировке диаграммы на каждом этапе нагружения образца. Можно также осуществлять корректировку сразу всей диаграммы. При этом необходимо решать задачу многократно, что более трудоемко, но позволяет воспользоваться доступной программой решения прямой задачи без каких-либо модификаций.
Осуществление изобретения.
В тестовых примерах численное моделирование процесса деформирования лабораторных образцов и элементов конструкций осуществлялось с помощью ППП «Динамика-2» [1, 2]. Эксперименты проводились на испытательных установках УРС-20/6000 и ЦДТЕ-30 [3, 4]. Построение истинных диаграмм деформирования при растяжении образцов.
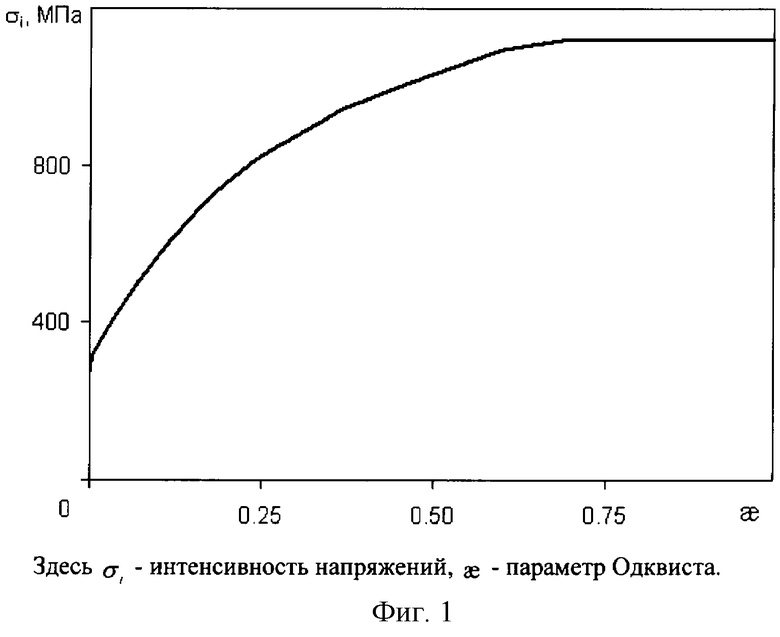
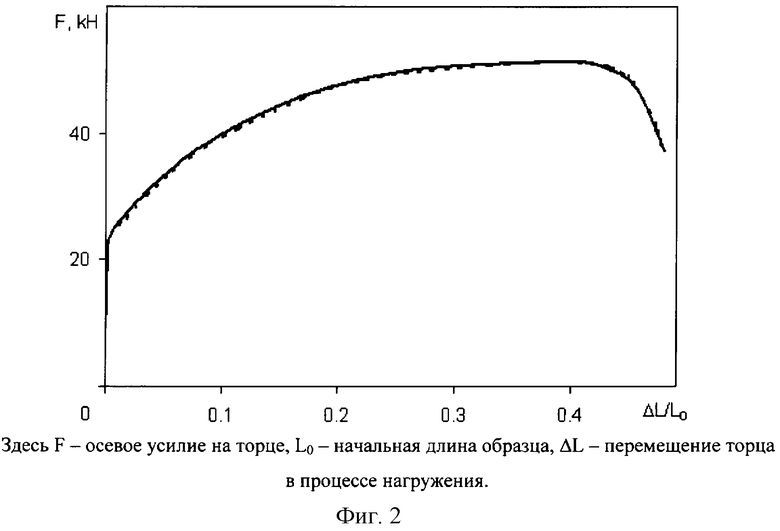
В качестве примера рассмотрим построение истинной диаграммы деформирования при квазистатическом растяжении до разрушения цилиндрического стрежня, выполненного из стали 12Х18Н10Т. Радиус рабочей части стержня 0.5 см, длина - 6 см. Упругие характеристики материала были известны: модуль объемного сжатия К=1.75×105 МПа, модуль сдвига G=0.8077×105 МПа. Плотность материала: ρ=7800 кг/м3. Экспериментальная зависимость осевых усилий от относительного перемещения торца показана на фиг.2 (сплошная линия). Для построения диаграммы деформирования проводится численное моделирование процесса растяжения образца. В расчете один торец стержня жестко закреплен, другой двигается с постоянной скоростью. В процессе решения задачи пропорционально отношению значений осевых усилий в эксперименте (Fэ) и расчете (Fρ) при одинаковых перемещениях осуществляется коррекция интенсивности напряжений (σi) на диаграмме деформирования, соответствующей максимальному значению параметра Одквиста (æ) в расчете (новое значение интенсивности напряжений 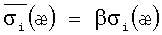 , где β=Fэ/Fp). Процедура корректировки итерационная и проводится до совпадения значений осевых усилий в эксперименте и расчете с точностью 1%. Исследования показали, что итерационный процесс сходится. Скорость сходимости - число итераций мало зависит от начального приближения. На участке до образования шейки достаточно одной итерации, после образования шейки до разрыва - пяти. Полученная в итоге диаграмма деформирования стали 12Х18Н10Т показана на фиг.1. На фиг.2 приведено сопоставление зависимостей растягивающих усилий от относительного перемещения торца, полученных из эксперимента (сплошная линия) и численного расчета (пунктирная линия).
, где β=Fэ/Fp). Процедура корректировки итерационная и проводится до совпадения значений осевых усилий в эксперименте и расчете с точностью 1%. Исследования показали, что итерационный процесс сходится. Скорость сходимости - число итераций мало зависит от начального приближения. На участке до образования шейки достаточно одной итерации, после образования шейки до разрыва - пяти. Полученная в итоге диаграмма деформирования стали 12Х18Н10Т показана на фиг.1. На фиг.2 приведено сопоставление зависимостей растягивающих усилий от относительного перемещения торца, полученных из эксперимента (сплошная линия) и численного расчета (пунктирная линия).
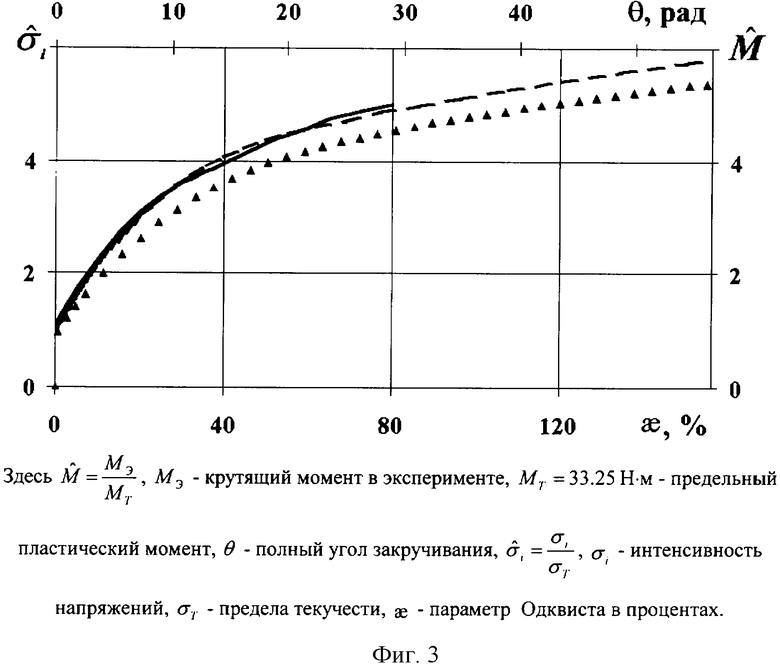
Построение истинной диаграммы деформирования при кручении образцов. В качестве примера рассмотрим построение истинной диаграммы деформирования при квазистатическом кручении цилиндрического стержня до разрушения, выполненного из стали 12Х18Н10Т. Радиус рабочей части образца R=0.5 см, длина рабочей части образца L=10 см. Упругие характеристики материала были известны: модуль объемного сжатия К=1.75×105 МПа, модуль сдвига G=0.8077×105 МПа. Плотность материала: ρ=7800 кг/м3. Экспериментальная зависимость крутящего момента от угла закручивания представлена на фиг.3 треугольниками. Для построения диаграммы деформирования осуществляется численное моделирование процесса кручения образца. В расчете один торец стержня жестко закреплен, на другом задается постоянная угловая скорость закручивания. В процессе решения задачи пропорционально отношению значений крутящего момента в эксперименте и расчете при одинаковых углах закручивания осуществляется коррекция интенсивности напряжений на диаграмме деформирования, аналогичная описанной выше. Процедура корректировки итерационная и проводится до совпадения значений крутящих моментов в эксперименте и расчете с точность 1%. В данном примере диаграмма выстраивается при одной итерации. На фиг.3 пунктирной линией изображена полученная истинная диаграмма деформирования, сплошной линией - полученная ранее при испытаниях на растяжение цилиндрического стержня (фиг.1). Наблюдается хорошее соответствие полученных диаграмм растяжения и кручения. Построение истинных диаграмм деформирования при кинетическом внедрении индентора в исследуемую конструкцию.
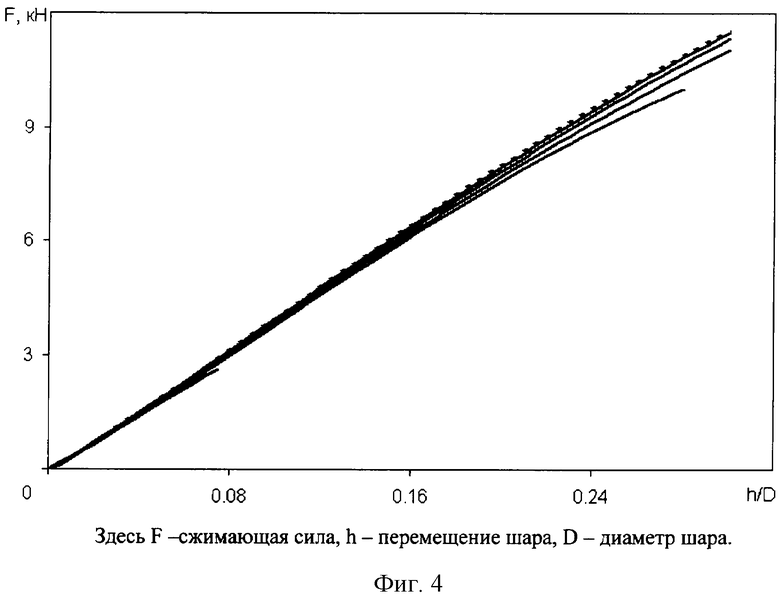
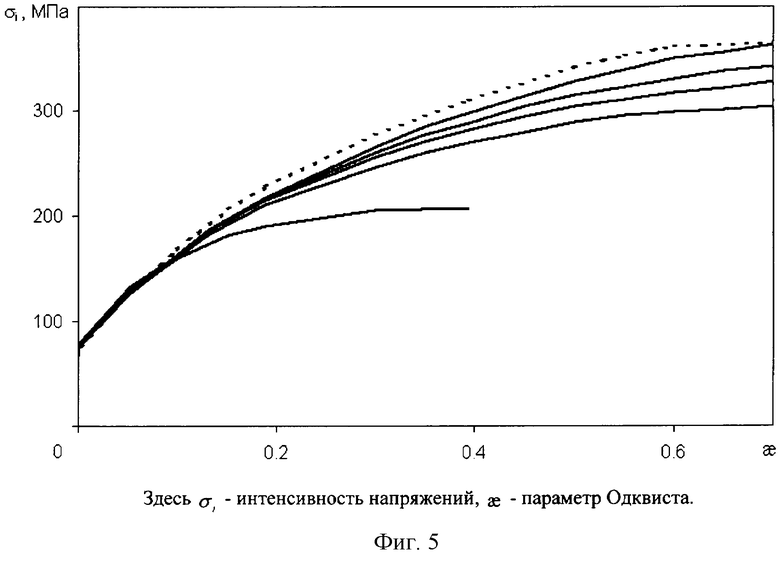
В качестве примера рассмотрим построение истинной диаграммы деформирования при кинетическом внедрении шара в пластину (проба Бринелля). Шар выполнен из высокопрочной шарикоподшипниковой стали ШХ-15. Упругие характеристики материала пластины известны: модуль объемного сжатия К=1.58×105 МПа, модуль сдвига G=0.45×105 МПа. Плотность материала: ρ=8950 кг/м3. Диаметр шара 0.5 см, диаметр пластины 4 см, толщина пластины 0.5 см. В качестве экспериментальных данных используется результат численного решения с известной диаграммой деформирования. В дальнейшем предполагается, что диаграмма неизвестна и проводится ее построение. Экспериментальная зависимость сжимающей силы от перемещения шара показана на фиг.4 (пунктирная линия). Для построения диаграммы деформирования осуществляется численное моделирование процесса внедрения шара в пластину. В расчете рассматривается только половина шара, верхняя граница шара движется с постоянной скоростью, нижняя граница пластины неподвижна в направлении движения шара. В процессе решения задачи пропорционально отношению значений сжимающих усилий в эксперименте и расчете при одинаковых перемещениях шара осуществляется коррекция интенсивности напряжений на диаграмме деформирования, аналогичная описанной выше. Процедура корректировки итерационная и проводится до совпадения значений сжимающих усилий в эксперименте и расчете с точность 1%. На фиг.4 показано сравнение экспериментальной зависимости сжимающей нагрузки от глубины внедрения шара (пунктирная линия) с расчетными (сплошные линии). На фиг.5 показано сравнение экспериментальной диаграммы деформирования (пунктирная линия) с расчетными (сплошные линии). Как видно из чертежей, итерационный процесс сходится (5 итераций), и диаграмма восстанавливается с точностью до 5% при заданной точности 1%. Но в данной задаче, скорость сходимости - число итераций сильно зависят от начального приближения. Для его выбора целесообразно воспользоваться приближенными аналитическими методами [5].
Список литературы
1. Баженов В.Г., Зефиров С. В., Кибец А.И. О численной реализации вариационно-разностной моментной схемы решения нелинейных задач динамики нетонких оболочек при импульсном воздействии // Прикл. пробл. прочности и пластичности. Методы решения: Всесоюз. межвуз. сб., Горьк. ун-т, 1988, с.66-73.
2. Баженов В.Г., Зефиров С. В., Кочетков А.В., и др. Пакет прикладных программ "Динамика-2" // Прикл. пробл. прочности и пластичности. Исследование и оптимизация конструкций. Всесоюз. межвуз. сб., Горьк. ун-т, 1987, с.4-13.
3. Крамаров Л.Н. Испытание конструкционных материалов // Прикладные проблемы прочности и пластичности: Межвуз.сб. - М.: ТНИ КМК, 1995, вып.53, с.87-93.
4. Крамарев Л.Н., Горохов А.Н., Сысоев О.В., Комбинированное нагружающее устройство для испытаний материалов на сложное нагружение // Проблемы прочности и пластичности. Н. Новгород, 2000, с.193-199.
5. Матюнин В.М. Методы твердости в диагностике материалов. Состояние, проблемы и перспективы. // Заводская лаборатория. Диагностика материалов, №6, 2004, т.70, с.37-41.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ МАКСИМАЛЬНЫХ ИСТИННЫХ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ | 2006 |
|
RU2319944C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МАКСИМАЛЬНЫХ ИСТИННЫХ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ | 2012 |
|
RU2516592C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРОЧНОСТНЫХ СВОЙСТВ МАТЕРИАЛОВ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ | 2014 |
|
RU2553425C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СОПРОТИВЛЕНИЯ ДЕФОРМАЦИИ СДВИГА МАТЕРИАЛОВ | 2018 |
|
RU2713809C1 |
| СПОСОБ И УСТРОЙСТВО ИССЛЕДОВАНИЯ ХАРАКТЕРИСТИК ЗАРЯДА ВЗРЫВЧАТОГО ВЕЩЕСТВА И СПОСОБ ИДЕНТИФИКАЦИИ СВОЙСТВ ВЗРЫВЧАТОГО ВЕЩЕСТВА | 2015 |
|
RU2634249C2 |
| СПОСОБ ИСПЫТАНИЯ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ НА ИЗГИБ С КРУЧЕНИЕМ ПРИ СТАТИЧЕСКОМ И КРАТКОВРЕМЕННОМ ДИНАМИЧЕСКОМ ВОЗДЕЙСТВИИ | 2015 |
|
RU2578662C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СВОЙСТВ ДЕФОРМИРОВАНИЯ | 2013 |
|
RU2537341C2 |
| Устройство для испытания колец на растяжение и способ испытания | 2018 |
|
RU2688590C1 |
| Способ испытаний образца алюминий-магниевого сплава при переменной жёсткости нагружающей системы и устройство для его осуществления | 2021 |
|
RU2774055C1 |
| Способ определения свойств деформирования | 1991 |
|
SU1827306A1 |
Изобретение относится к области определения деформационных и прочностных характеристик материалов. Сущность: проводят испытания на растяжение, сжатие, кручение, твердость. Строят диаграммы деформирования независимо от формы образцов (вида индентора) для больших деформаций и с учетом неоднородности НДС вплоть до момента, близкого к разрушению. Из эксперимента узнают только зависимости интегральных параметров нагружающих усилий от перемещений. Идентификация результатов экспериментов производится с помощью численного моделирования процесса деформирования лабораторных образцов или элементов конструкции. В результате определяется истинная диаграмма деформирования на основе итерационной корректировки интенсивности напряжений на диаграмме пропорционально отношению значений нагружающих усилий в расчете и эксперименте при одинаковых перемещениях до совпадения их с заданной точностью. Технический результат: расширение возможностей исследования деформационных и прочностных характеристик, уменьшение затрат и упрощение проведения испытаний. 5 ил.
Способ определения деформационных и прочностных свойств материалов при больших деформациях и неоднородном напряженно-деформированном состоянии при испытаниях на растяжение, сжатие, кручение, твердость по результатам натурных испытаний, отличающийся тем, что позволяет строить диаграммы деформирования независимо от формы образцов (вида индентора) для больших деформаций и с учетом неоднородности НДС вплоть до момента близкого к разрушению, и из эксперимента необходимо знать только зависимости интегральных параметров нагружающих усилий от перемещений, и идентификация результатов экспериментов производится с помощью численного моделирования процесса деформирования лабораторных образцов или элементов конструкции, и в результате определяется истинная диаграмма деформирования на основе итерационной корректировки интенсивности напряжений на диаграмме пропорционально отношению значений нагружающих усилий в расчете и эксперименте при одинаковых перемещениях до совпадения их с заданной точностью.
| Способ испытания на растяжение образцов материалов | 1984 |
|
SU1232994A1 |
| Способ определения прочностных характеристик разномодульного материала | 1988 |
|
SU1583732A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРЕДЕЛА ПРОЧНОСТИ МАТЕРИАЛА | 1991 |
|
RU2011182C1 |
| СПОСОБ ПОЛУЧЕНИЯ МЕРКАПТОАЛКИЛТРИАЗОЛ.ТИОНОВ ИЛИ МЕРКАПТОАЛКИЛТРИАЗОЛОНОВ | 0 |
|
SU245120A1 |
Авторы
Даты
2008-05-10—Публикация
2006-05-06—Подача