Изобретение относится к гидроакустике.
Известен способ селекции движущихся целей [1], основанный на излучении тонального сигнала, приеме отраженного эхосигнала, определении модуля спектра отраженного сигнала, определении доплеровского смещения частоты отраженного сигнала относительно излученного и селекции движущихся целей по их радиальной скорости.
При увеличении длительности излученного тонального сигнала данный способ позволяет повысить разрешение по доплеровскому сдвигу частоты и соответственно по радиальной скорости целей. Однако при увеличении длительности излученного тонального сигнала уменьшается разрешение по дистанции.
Известно, что использование в излучении сложных сигналов с гиперболическим законом модуляции частоты, инвариантных к доплеровскому сдвигу частоты при согласованной (корреляционной) обработке излученного и отраженного сигналов, позволяет получить высокое разрешение по дистанции до цели. Однако искажение модуля спектра отраженного сигнала при распространении в среде не позволяет достоверно определять доплеровский сдвиг спектра отраженного эхосигнала и оценивать радиальную скорость целей в практических случаях.
Известен способ селекции движущихся целей [2], основанный на облучении исследуемого объема пространства (исследуемой акватории) сигналом с гиперболической частотной модуляцией (ГЧМ), приеме отраженного эхосигнала цели, измерении разности фаз излученного и отраженного ГЧМ сигналов, вычислении радиальной скорости целей по известной скорости звука в среде и разности фаз и принятии решения по результатам сравнения радиальных скоростей целей.
Данный способ позволяет повысить разрешающую способность по радиальной скорости движущихся целей при излучении ГЧМ сигналов. Однако, поскольку этот способ основан на сравнении радиальных скоростей целей, в исследуемом объеме пространства (исследуемой акватории) должна быть хотя бы одна цель с априори известной нулевой радиальной скоростью. Либо должно быть известно точное значение скорости звука по пути распространения излученного и отраженного сигналов, что практически нереализуемо.
Техническим результатом изобретения является расширение области применения способа путем учета различий фазовой структуры излученного и отраженного ЧМ сигналов.
Для обеспечения указанного технического результата в способ селекции движущейся цели, основанный на облучении исследуемого объема пространства (исследуемой акватории) частотно-модулированными (ЧМ) сигналом излучения и приеме отраженного ЧМ сигнала, введены новые признаки, а именно: вычисляют комплексные частотные спектры излученного и отраженного ЧМ сигналов размерности N/k, где N=Tm/Td, Tm - длительность модуляции частоты, Тd - период дискретизации сигналов, k=2n, n=0,1,2..., определяют фазовые спектры и непрерывные фазовые функции излученного и отраженного ЧМ сигналов в доплеровской полосе частот, нормируют непрерывные фазовые функции излученного и отраженного ЧМ сигналов на свой экстремум, в полученных нормированных непрерывных фазовых функциях излученного и отраженного ЧМ сигналов определяют их максимальные значения и соответствующие им значения частот, по разности частот, соответствующих максимальным значениям нормированных непрерывных фазовых функций излученного и отраженного ЧМ сигналов, определяют доплеровское смещение спектра отраженного ЧМ сигнала и производят селекцию движущихся целей по их радиальной скорости, определяемой доплеровским смещением спектра отраженного ЧМ сигнала.
В случае ЧМ сигнала излучения, имеющего возрастающий закон модуляции частоты, непрерывную фазовую функцию излученного и отраженного ЧМ сигналов нормируют на ее минимальное значение.
В случае ЧМ сигнала излучения, имеющего спадающий закон модуляции частоты, непрерывную фазовую функцию излученного и отраженного ЧМ сигналов нормируют на ее максимальное значение.
Под фазовой структурой частотно-модулированного (ЧМ) сигнала понимается следующее.
Известно, что комплексный спектр сложного сигнала может быть представлен в виде
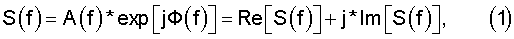
где A(f) - амплитудный спектр, 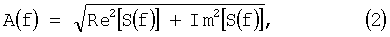
Ф(f) - фазовый спектр сигнала, определяемый как
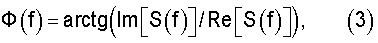
Значения Ф(f) определены в пределах ±π, т.е. фазовый спектр ЧМ сигнала имеет разрывы (скачки) при переходе фазы от -π к +π и наоборот.
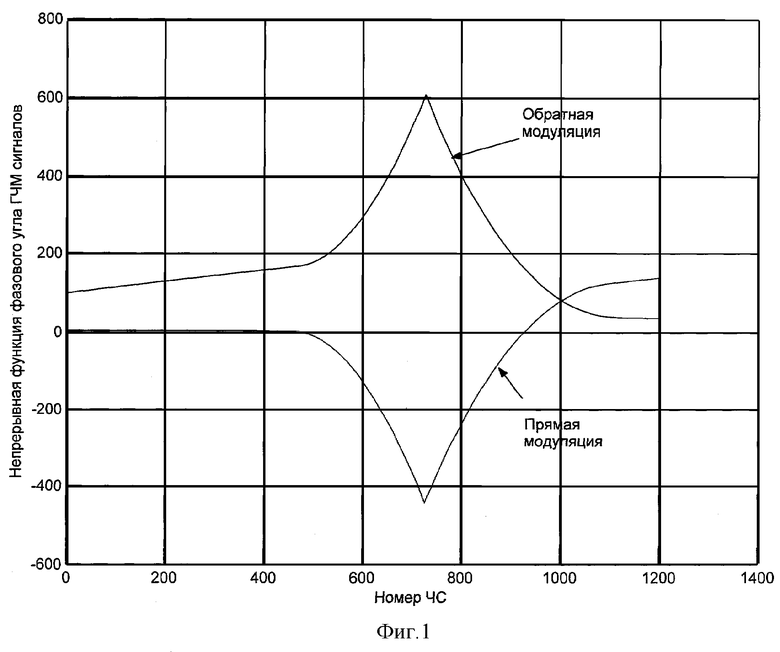
Известный алгоритм вычисления непрерывной функции фазового угла [3] устраняет скачки фазового спектра. Расчет непрерывной функции фазового угла (НФФУ) для ГЧМ сигналов с возрастающей и спадающей модуляцией частоты имеет вид, представленный на фиг.1. Как видно из графиков (см.фиг.1), для ГЧМ сигналов с возрастающей модуляцией частоты НФФУ имеет минимум в области отрицательных значений, а для ГЧМ сигналов со спадающей модуляцией частоты - НФФУ имеет максимум в области положительных значений. При этом частоты, соответствующие этим экстремальным значениям, совпадают, если законы изменения частоты дуальные.
Таким образом, под фазовой структурой спектра сложного сигнала подразумевается характер зависимости от частоты НФФУ спектра или его непрерывная фазовая функция (НФФ). Наличие выраженного экстремума НФФУ ЧМ сигнала (изменение знака производной от НФФ) и зависимость частоты этого экстремума от доплеровского смещения спектра отраженного ЧМ сигнала позволяют однозначно судить о радиальной скорости цели даже в условиях существенного искажения спектра отраженного ЧМ сигнала помехами.
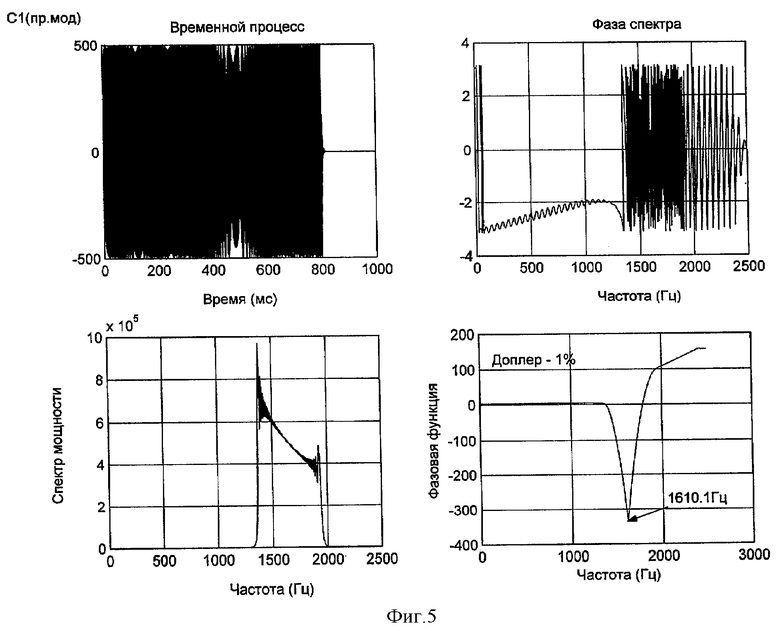
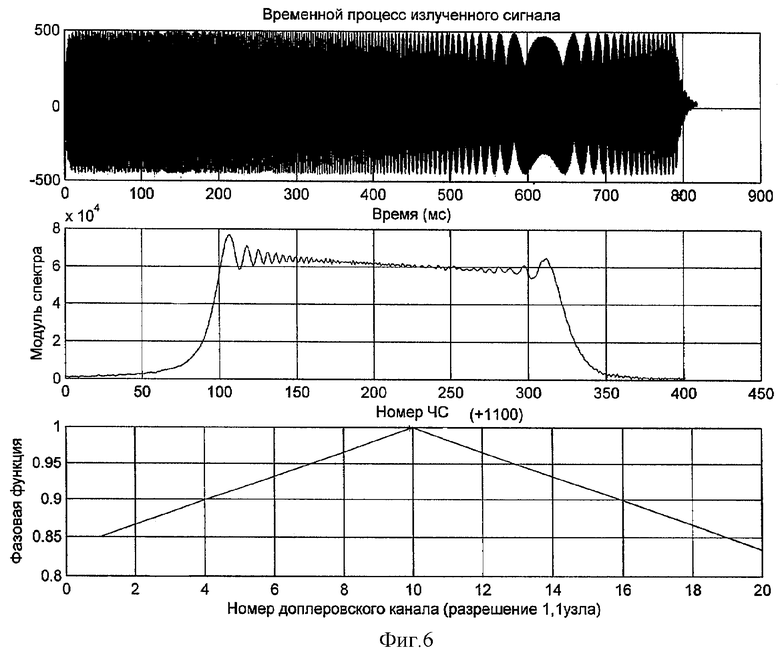
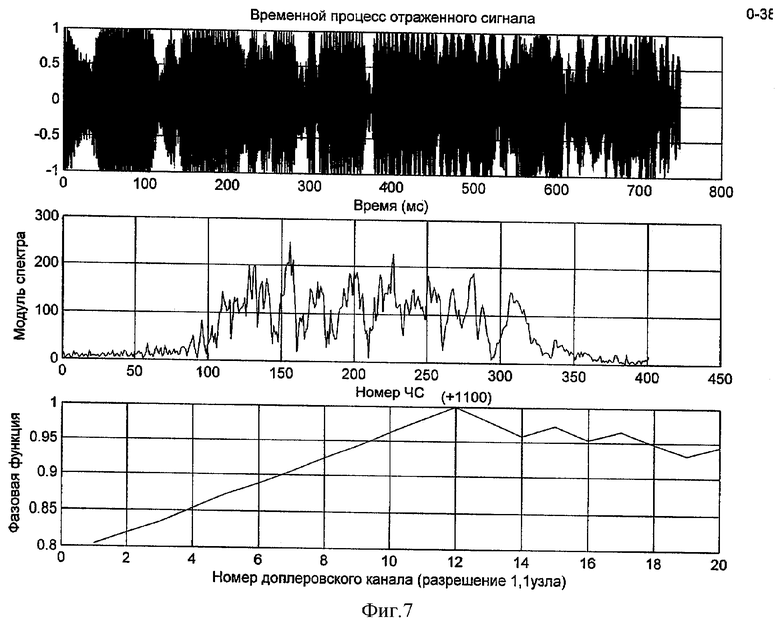
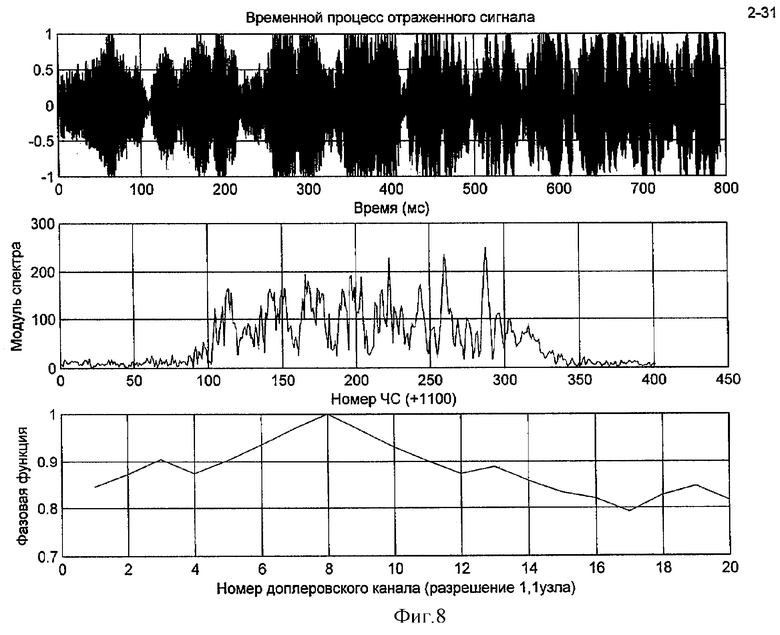
Сущность изобретения поясняется фиг.1-8, где на фиг.1 представлены графики НФФ ГЧМ сигналов с возрастающей и спадающей модуляцией частоты, на фиг.2 представлено устройство, реализующее предлагаемый способ, на фиг.3 представлены модули спектров и графики нормированных непрерывных фазовых функций (ННФФ) ГЧМ и ЛЧМ сигналов, на фиг.4 представлены временной процесс, спектр мощности, фазовый спектр и НФФУ ГЧМ сигнала с нулевым доплеровским сдвигом, на фиг.5 - то же для ГЧМ сигнала с доплеровским сдвигом спектра на 1%, на фиг.6 - временной процесс, модуль спектра и ННФФ экспериментально излученного ГЧМ сигнала, на фиг.7 - то же для ГЧМ сигнала, отраженного от цели с радиальной скоростью +2 узла, на фиг.8 - то же для ГЧМ сигнала, отраженного от цели с радиальной скоростью (-2) узла.
Устройство, реализующее способ (фиг.2), содержит генератор 1 ЧМ сигнала, излучатель 2, приемник 3, блок 4 обработки излученного сигнала (опорный канал), блок 5 обработки отраженного сигнала (приемный канал), устройство 6 индикации.
Каждый из блоков 4 и 5 содержит аналого-цифровой преобразователь 7, первое буферное запоминающее устройство 8, блок 9 вычисления преобразования Фурье, второе буферное запоминающее устройство 10, блок 11 вычисления фазового спектра, блок 12 вычисления непрерывной фазовой функции, блок 13 определения экстремума, делитель 14.
Предложенный способ имеет следующую последовательность операции.
Генератор 1 формирует ЧМ сигнал, который поступает на излучатель 2 и одновременно в блок 4 обработки излученного сигнала.
Излучатель 2 излучает ЧМ сигнал в исследуемый объем пространства.
Приемник 3 принимает отраженный сигнал от цели, находящейся в исследуемом объеме пространства. Принятый сигнал поступает через приемник 3 в блок 5 обработки отраженного сигнала. Излучатель 2 и приемник 3 могут быть выполнены как в виде одиночного пьезокерамического преобразователя, так и в виде многоэлементной гидроакустической антенны.
Структура блоков 4 и 5 одинаковая.
В первом буферном запоминающем устройстве 8 производят накопление N/К отсчетов сигнала, поступающего в блок 5(4) через АЦП 7, при этом
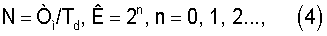
Тм - длительность модуляции частоты или длительность излученного сигнала, если они совпадают,
Тd - период дискретизации сигнала в АЦП.
Если выбрать n=0, то накапливаются N отсчетов сигнала, если n=1, то запоминается каждый 2-ой отсчет, если n=2, то запоминается каждый 4-й отсчет и т.д. Таким образом, прореживание временных отсчетов позволяет в необходимых случаях уменьшить размерность вычисления спектра.
Далее в блоке 9 производят вычисление комплексного спектра сигнала, например, с помощью преобразования Фурье размерности N/К. Из полученного спектра выбираются корректные отсчеты (от 0 до N/2K), в которых определяют доплеровскую полосу частот как разность между минимальной нижней частотой и максимальной верхней частотой спектра отраженного ЧМ сигнала, обусловленных максимально возможной радиальной скоростью предполагаемой цели и собственной скоростью излучателя (с учетом направлений векторов скоростей).
Отсчеты комплексного спектра S(f) в доплеровской полосе частот ΔfD из блока 9 передаются и запоминаются во втором буферном запоминающем устройстве 10, а затем поступают в блок 11 определения фазового спектра Ф(k) по формуле (3).
Полученный фазовый спектр поступает в блок 12 вычисления непрерывной фазовой функции [3]:
F(k)=UNWRAP(Ф(k)),
где k - номер частотной составляющей фазового спектра Ф(k) в доплеровской полосе частот.
Алгоритм вычисления функции UNWRAP(.) является встроенной процедурой - функцией библиотеки программ MATLAB и приведен в Приложении.
Далее в блоке 13 производят поиск экстремума непрерывной фазовой функции, причем, если излученный ЧМ сигнал имеет возрастающую модуляцию частоты, то определяют минимальное значение непрерывной фазовой функции F(k), а если спадающую модуляцию, то определяют максимальное значение F(k).
Далее в делителе 14 производят деление массива непрерывной фазовой функции на ее экстремум и на выходе делителя 14 получают нормированную (на экстремум) фазовую функцию сигнала, которая поступает на устройство 6 индикации.
В устройстве 6 индикации при одновременном отображении нормированных фазовых функции излученного и отраженного сигналов по максимальным значениям функции определяют значения соответствующих им частот и по разности частот определяют доплеровское смещение спектра отраженного сигнала ДР и наличие радиальной скорости цели, по которой производится селекция движущейся цели в исследуемом объеме пространства.
Таким образом, достигнутым техническим результатом изобретения является расширение области применения способа путем учета различий фазовой структуры излученного и отраженного ЧМ сигналов, так как в предлагаемом способе не требуется знание скорости звука в среде и наличие каких-либо целей с априори нулевой радиальной скоростью.
Дополнительным преимуществом предлагаемого способа является возможность учета собственной скорости излучателя. Например, путем смещения доплеровской полосы излучаемого сигнала на величину
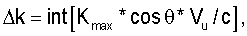
где int[.] - операция округления до целого,
Кmax - номер частотной составляющей в спектре излученного сигнала, соответствующий максимуму нормированной непрерывной фазовой функции,
θ - угол между направлением вектора скорости излучателя и направлением на исследуемый объем пространства относительно излучателя,
Vи - скорость излучателя,
с - среднее значение скорости звука в среде.
Необходимо отметить, что предлагаемый способ реализуется независимо от методов облучения исследуемого объема пространства. То есть может быть выполнено ненаправленное (или секторное) излучение и прием на направленную антенну в некотором телесном угле, в котором осуществляется селекция по времени (по дистанции). Либо может быть выполнено направленное излучение в узком телесном угле и прием на ненаправленный приемник с последующей селекцией во времени. Также может быть выполнено направленное излучение и секторный прием или наоборот.
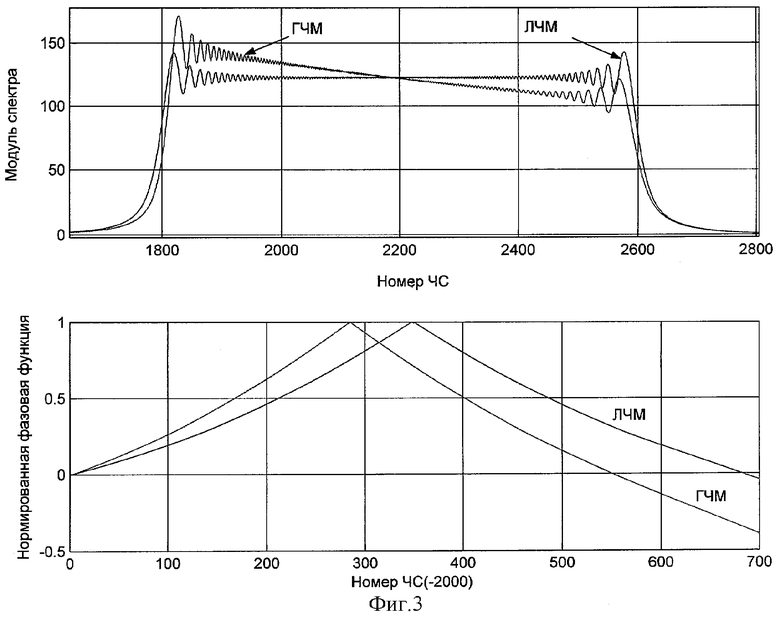
Предлагаемый способ может быть реализован как для ГЧМ сигналов, так и для сигналов с линейной частотной модуляцией (ЛЧМ). На фиг.3 приведены модули спектров и нормированные непрерывные фазовые функции ГЧМ и ЛЧМ сигналов. Как видно из фиг.3, при одинаковых полосах спектра нормированные фазовые функции имеют максимум, но на разных частотах, т.е. фазовые структуры ГЧМ и ЛЧМ сигналов различны.
Работоспособность предлагаемого способа подтверждается моделированием и практическими измерениями в реальных условиях.
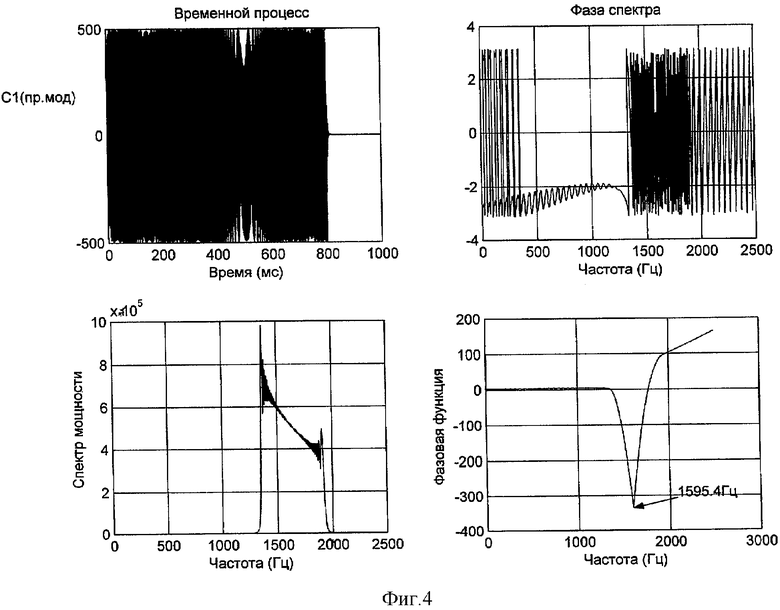
На фиг.4 и 5 показаны результаты моделирования ГЧМ сигнала с доплеровским сдвигом частоты на +1%. По результатам моделирования сдвиг непрерывной фазовой функции составил +0,92%.
На фиг.6 приведены: временной процесс, модуль спектра и нормированная фазовая функция излученного сигнала в реальных условиях.
На фиг.7 приведены: временной процесс, модуль спектра и нормированная фазовая функция отраженного сигнала от приближающейся цели с радиальной скоростью 2 узла. Сравнения фиг.6 и 7 показывают, что спектр отраженного сигнала искажается, и оценка доплеровского смещения по спектру не состоятельна. В то же время смещение частотных составляющих максимальных значений непрерывных фазовых функций излученного и отраженного сигналов равно 2(12-10), что составляет +2,2 узла.
На фиг.8 приведены аналогичные характеристики отраженного сигнала для цели, удаляющейся с радиальной скоростью -2 узла. Как следует из сравнения фиг.6 и 8 смещение частотных составляющих равно -2(8-10), т.е. -2,2 узла.
Таким образом, в данном случае ошибка оценки радиальной скорости цели составила 10%, что обусловлено дискретностью вычисления спектра сигнала.
Источники информации
1. Бакулев П.А., Степин В.М. Методы и устройства селекции движущихся целей. М., Радио и связь, 1986.
2. Патент РФ №2058033, кл. G 01 S 15/00.
3. Потемкин В.Г. Система MATLAB. Справочное пособие. - М., ДИАЛОГ-МИФИ, 1997, с.226.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОБНАРУЖЕНИЯ ДВИЖУЩИХСЯ ЦЕЛЕЙ В ГИДРОЛОКАЦИИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2007 |
|
RU2357269C2 |
| СПОСОБ И УСТРОЙСТВО ПЕРЕДАЧИ ДИСКРЕТНОЙ ИНФОРМАЦИИ ДЛЯ БЫСТРОДВИЖУЩИХСЯ ОБЪЕКТОВ | 2017 |
|
RU2658649C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СКОРОСТИ ДВИЖЕНИЯ СУДНА ОТНОСИТЕЛЬНО ДНА | 1992 |
|
RU2037847C1 |
| Способ цифровой обработки сложных широкополосных локационных сигналов | 2023 |
|
RU2832199C1 |
| Способ определения параметров движения высокоскоростного воздушного объекта | 2023 |
|
RU2807316C1 |
| УСТРОЙСТВО ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ В ИМПУЛЬСНО-ДОПЛЕРОВСКОЙ РЛС С КОМПЕНСАЦИЕЙ ЧМ ДОПЛЕРОВСКИХ СИГНАЛОВ ЗА ОДИН ПЕРИОД ИЗЛУЧЕНИЯ И ПРИЕМА ПАЧКИ РАДИОИМПУЛЬСОВ | 2021 |
|
RU2782574C1 |
| СПОСОБ КОРРЕЛЯЦИОННОЙ ОБРАБОТКИ СИГНАЛОВ, ОТРАЖЕННЫХ ОТ БЫСТРОДВИЖУЩИХСЯ ЦЕЛЕЙ | 2005 |
|
RU2293997C1 |
| Имитатор радиолокационных целей | 2021 |
|
RU2787576C1 |
| Способ определения скорости объекта в доплеровской радиолокации | 2016 |
|
RU2709626C1 |
| УСТРОЙСТВО ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ В ИМПУЛЬСНО-ДОПЛЕРОВСКОЙ РЛС С КОМПЕНСАЦИЕЙ ЧМ ДОПЛЕРОВСКИХ СИГНАЛОВ | 2017 |
|
RU2657462C1 |
Изобретение относится к гидроакустике. Технический результат заключается в повышении разрешающей способности при измерении радиальной скорости цели. Для этого излучают частотно-модулированный (ЧМ) сигнал, принимают отраженный от цели ЧМ сигнал, вычисляют комплексные частотные спектры излученного и отраженного сигналов, из полученных комплексных спектров определяют фазовые спектры и непрерывные функции фазового угла, нормируют непрерывные функции фазового угла на максимум, по нормированным непрерывным функциям фазового угла определяют частоты, соответствующие максимуму этих функций, по разности полученных частот определяют доплеровское смещение спектра отраженного ЧМ сигнала, которое и позволяет определить радиальную скорость цели. 2 з.п. ф-лы, 8 ил.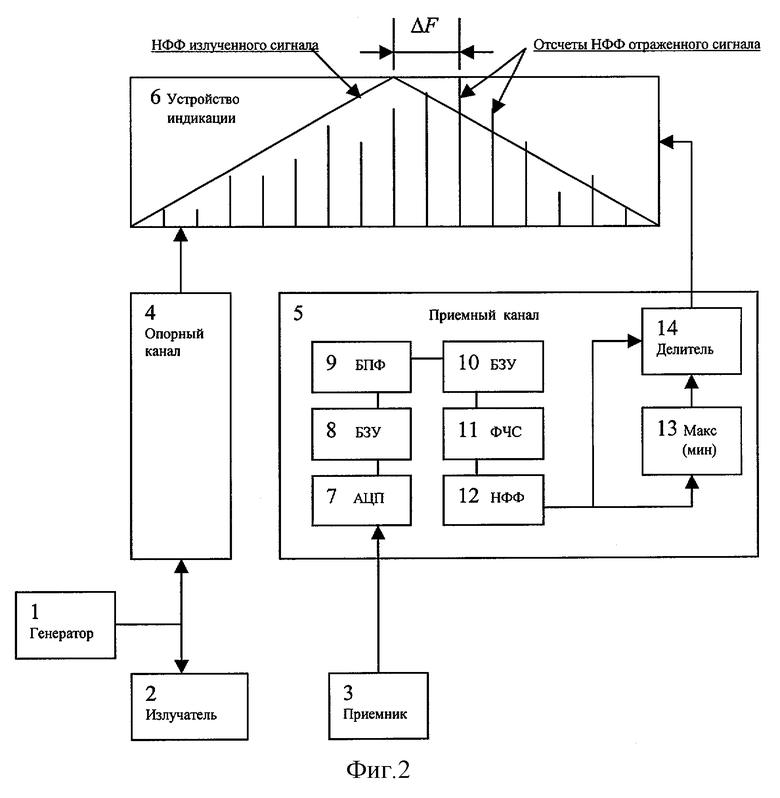
| US 5491668, 13.02.1996 | |||
| RU 2058033 C1, 10.04.1996 | |||
| US 6130857, 10.10.2000 | |||
| US 5481503, 02.01.1996 | |||
| US 3733581, 15.05.1973. |
Авторы
Даты
2007-02-10—Публикация
2004-10-18—Подача