Заявляемое изобретение относится к аналитическому приборостроению, в частности к способам создания градуировочных моделей для различного вида измерительных приборов.
Во многих отраслях промышленности и научных исследованиях определение свойств образца при помощи прямых методов измерения не обеспечивает необходимой скорости анализа или приводит к разрушению образца, а в некоторых случаях непосредственное определение требуемых свойств вообще может оказаться невозможным. В качестве примера можно привести аналитическую химию, где традиционный прямой метод химического анализа для определения концентраций образующих образец компонентов основан на проведении химических реакций, что приводит к разрушению образца, а, кроме того, требует значительных временных затрат.
В подобных случаях широкое распространение получили непрямые методы, где анализируемые свойства образцов определяют путем измерения других свойств образцов, зависящих от анализируемых, которые, однако, в отличие от анализируемых свойств могут быть легко измерены напрямую в течение короткого промежутка времени и без разрушения образца. Часто при этом непосредственно измеряемые свойства образцов называют «первичными свойствами», а анализируемые свойства образцов - «вторичными свойствами». Одним из наиболее эффективных непрямых методов исследования является спектроскопический анализ, при котором на основе измерения оптических спектров поглощения, отражения или рассеяния («первичных» свойств) определяют требуемые «вторичные» свойства образцов (например, химический состав).
После измерения множества первичных свойств необходимо найти математические соотношения, связывающие результаты измерений со значениями величин, характеризующих анализируемые вторичные свойства. Эти соотношения между измеряемыми на приборе первичными характеристиками и анализируемыми вторичными свойствами образца называются градуировочными моделями или градуировками, в результате их нахождения определяется ряд градуировочных констант. Процедура создания градуировочных моделей достаточно трудоемкая, длительная и дорогостоящая. Особенно этот процесс усложняется для случая многомерного анализа, когда для определения количественных характеристик вторичных свойств образца используется набор результатов измерения большого числа параметров, характеризующих первичные свойства. Например, в случае спектроскопического анализа для определения концентрации различных компонентов проводят измерения большого количества спектральных данных (величины поглощения, отражения или рассеяния) для разных значений волновых чисел (длин волн, частот).
Чтобы построенная градуировочная модель обеспечивала заданную точность определения параметров, характеризующих анализируемые вторичные свойства произвольного образца, необходимо провести анализ большого числа образцов, представительных к тем образцам, которые будут анализироваться на приборе в дальнейшем (градуировочный набор). Подбор образцов градуировочного набора регламентируется стандартами на различные непрямые методы анализа, например, стандартом на качественный анализ при помощи БИК спектроскопии [1]. Значения параметров, характеризующих анализируемые вторичные свойства образцов градуировочного набора, предварительно определяются при помощи стандартных методов, называемых референтными. При проведении референтных анализов следует обратить особое внимание на точность результатов анализов, так как точность референтного анализа лимитирует точность всей градуировки. Например, в рассмотренном ранее случае спектроскопического анализа химического состава образцов анализируемые свойства образцов градуировочного набора могут быть предварительно определены стандартными химическими методами с использованием химических реакций.
Образцы градуировочного набора выбираются таким образом, чтобы их вторичные свойства охватывали возможный диапазон изменений этих свойств при анализе неизвестных образцов и были равномерно распределены по этому диапазону. Выполнение данных условий повышает устойчивость градуировочной модели, благодаря чему небольшие шумовые изменения в измеряемых первичных свойствах не приводят к статистически значимым изменениям в результатах анализа вторичных свойств.
Созданная градуировочная модель должна быть подвергнута стандартной процедуре проверки, называемой валидацией [1], в результате которой определяются статистические параметры, характеризующие качество градуировочной модели, а также выпадающие из градуировки образцы. Для поиска таких образцов применяется статистический анализ выбросов, например, по расстоянию Махаланобиса [1], использующего данные измерений первичных свойств полного градуировочного набора. Для повышения устойчивости градуировки такие образцы необходимо исключить из градуировочного набора.
Чтобы оценить применимость градуировочной модели для описания неизвестного образца, измеренные первичные свойства образца также подвергают анализу по статистике определения выбросов. Эта проблема схожа с задачами, решаемыми при качественном анализе, где на основании измерения первичных свойств образца (спектральных данных) и сопоставления их с библиотечными данными делается вывод о наборе компонентов в образце. Следует заметить, что условия измерений анализируемого образца и градуировочных образцов должны быть идентичными.
На результаты измерения первичных свойств образцов, а как следствие, и на точность определения параметров, характеризующих анализируемые вторичные свойства образцов, могут существенно влиять различные свойства, например, изменения внешних условий или технических характеристик измерительного прибора. Необходимо отметить, что технические характеристики прибора могут изменяться со временем вследствие старения или при проведении ремонтных работ, а также замены отдельных типовых элементов конструкции прибора. В таком случае может потребоваться создание новой градуировочной модели, учитывающей особенности текущего состояния прибора. Как отмечалось ранее этот процесс длительный, трудоемкий и дорогостоящий. Поэтому было предложено несколько способов создания градуировочных моделей, устойчивых к изменению условий измерений, технических характеристик прибора и прочих влияющих на результаты измерений свойств, что позволяет не повторять сложный процесс построения градуировочной модели на каждом отдельном приборе после выполнения его ремонта, замены отдельных типовых элементов конструкции или изменения параметров прибора с течением времени.
В одном из подобных способов [3] рассматривается построение градуировочной модели приборов для спектроскопического анализа химического состава, которая мало восприимчива к изменению характеристик прибора. Данный подход применили Т.Scecina и др., которые основывались на том, что искусственное добавление в градуировочную модель спектров образцов, измеренных при изменении конкретного влияющего параметра (например, температура или давление) свыше ожидаемого диапазона изменения при эксплуатации, улучшает анализ с использованием подобной модели тех образцов, для которых изменение данного параметра характерно. Применяя указанную концепцию по отношению к изменению технических характеристик измеряющего прибора, был разработан алгоритм, позволяющий учесть подобные изменения. Указанный метод принимает во внимание изменчивость спектральных приборов за счет включения в градуировочную модель спектров образцов, зарегистрированных при изменении определенных параметров прибора, чтобы перекрыть весь возможный диапазон подобных изменений. Данная идея практически идентична методу, описанному в патенте [2]. Например, вводится сдвиг длины волны на определенную величину для всех точек, в которых производятся измерения, или величина данного сдвига пропорциональна положению конкретной точки на оси волновых чисел. Допускается также учет подобных изменений с помощью математической обработки спектров.
С другой стороны предлагается возможность модификации рассмотренного алгоритма, заключающаяся в создании градуировочных моделей на нескольких приборах, предпочтительно при этом, чтобы технические характеристики этих приборов охватывали возможный диапазон изменения указанных характеристик на всех приборах данной серии. Затем полученные данные объединяются в единый градуировочный набор и дополнительно искусственно вводятся изменения характеристик прибора посредством математических манипуляций над спектральными данными. Такой подход позволяет в еще большей степени учесть изменчивость параметров прибора, делая создаваемую модель более устойчивой.
Однако данный метод требует большого количества проводимых измерений, что приводит к увеличению затрат труда, времени и материальных ресурсов на стадии создания градуировочной модели. Рассмотренный алгоритм не лишен и других недостатков, а именно снижение точности модели, т.к. в модели изначально предполагается вариация результатов измерения первичных свойств, и сложность оценки правомерности применения градуировочной модели для анализа того или иного неизвестного образца, что может привести к ошибкам в анализе вторичных свойств.
Еще один способ, посвященный созданию градуировочных моделей, компенсирующих изменения параметров прибора, предложен в [4]. Согласно данному методу спектрометры характеризуются при помощи определения соответствия их спектров (спектральных характеристик) предварительно определенному ограниченному числу кластеров. Принадлежность кластеру определяется на основании подобия спектральных особенностей и рабочих характеристик. Спектральные особенности, используемые для классификации, могут быть отнесены к известным параметрам прибора или представлять собой некоторые абстрактные характерные черты, получаемые с помощью вычислительных методов. Градуировочная модель для каждого кластера компенсирует приборные изменения, она будет более простой и точной.
Предложенный алгоритм включает в себя четыре стадии: измерение, классификация, градуировка, определение аномальных образцов. На первой стадии производится измерение спектров определенных стандартов, которые могут быть использованы, например, для классификации смещений, наблюдаемых по оси длин волн или интенсивности. Вид измеряемых стандартов определяется тем, какие эффекты необходимо учесть в каждом конкретном случае. В общем случае приборные изменения могут быть классифицированы на основе спектральных данных на следующие виды: изменения интенсивности сигнала, ширины полосы, длины волны или комбинация указанных явлений. В рассматриваемом источнике дается довольно подробная их классификация. Нужно отметить, что в некоторых случаях в качестве стандартов могут выступать реальные образцы, моделирующие особенности измерений с помощью данного прибора. На второй стадии полученные спектры необходимо классифицировать. Для этого выделяют характерные спектральные особенности, используя математические преобразования полученных данных, улучшающие определенные аспекты, полезные для интерпретации, например, анализ на основе главных компонент, вычисление расстояния Махаланобиса. Также данные особенности можно получить на основе априорного знания о системе (шумовые характеристики, линейность детектора и т.п.). В дальнейшем производится классификация, то есть отнесение полученных спектров определенным кластерам, и разрабатывается классификационная модель путем нахождения некоторого закона, позволяющего определить, какому кластеру соответствует спектр измеряемого образца. На третьей стадии для каждого кластера строится градуировочная модель, учитывающая приборные изменения, характерные для этого кластера. Спектры внутри определенного кластера имеют высокую степень внутреннего постоянства и обладают схожими особенностями, определяющими не все возможные изменения параметров прибора, а лишь одно или несколько, учитываемых внутри кластера. Подобный подход позволяет упростить процедуру создания градуировки для единичного кластера. Другое его преимущество - возможность определения аномальных спектров. Поскольку каждый кластер имеет свой собственный набор классификационных требований, то если измеренный спектр им не удовлетворяет, производится попытка подобрать другой кластер, параметры которого позволяют провести анализ указанного спектра. Если это оказывается невозможным, данный спектр подвергают математической обработке, чтобы он соответствовал одному из кластеров. Если соответствия достигнуть не удается, спектр считается аномальным.
По сути, это модификация метода, описанного в предыдущих патентах с введением изменений в характеристики приборов при построении градуировочной модели. Отличие здесь в том, что рассматривают не весь возможный диапазон изменений, а разбивают его на несколько поддиапазонов (кластеров), в каждом из которых, например, изменяется только один параметр и в ограниченном диапазоне значений. Строится градуировочная модель, на основании которой вторичные свойства определяются с достаточно высокой точностью для всех приборов, первичные свойства которых характеризуются данным кластером. Для приборов из другого кластера (изменяется другой параметр или тот же параметр, но в другом диапазоне значений) строится независимая градуировочная модель или проводят перенос градуировки по известным методам.
К достоинствам данного метода относятся простота градуировочной модели и достаточно высокая точность определения вторичных свойств для конкретного кластера, а также возможность определения аномальных спектров, что позволяет оценить правомерность применения градуировочной модели для анализа того или иного неизвестного образца, и, соответственно, снизить вероятность ошибок в анализе вторичных свойств. Из недостатков можно выделить необходимость выполнения большого количества операций, связанных с определением кластеров, нахождением квалификационных алгоритмов и построением градуировочных моделей для каждого кластера, а также узкая ориентированность предложенного метода на спектрометрические приборы.
Известен способ переноса градуировочных моделей между приборами [5], который также может быть использован для переградуировки одного прибора, чтобы учесть изменения в характеристиках прибора, возникшие в процессе эксплуатации вследствие различных причин, в частности старения. Согласно данному методу, для учета подобных изменений выбирается некоторый набор образцов, например, из тех, которые использовались при создании градуировочной модели. Первичные свойства каждого образца из этого набора измеряются на приборе, характеристики которого изменились с течением времени, и производится сопоставление при помощи регрессионных методов результатов измерений первичных свойств образцов набора с результатами измерения первичных свойств тех же самых образцов, полученными на приборе в исходном состоянии, для которого создавалась градуировка. Таким образом, определяются соотношения для преобразования результатов измерений, проведенных на исходном приборе, к виду, эквивалентному измерениям на приборе в его текущем состоянии, при котором произошли некоторые изменения в характеристиках в процессе эксплуатации. В дальнейшем при помощи найденных соотношений данные для образцов градуировочного набора, измеренных на исходном приборе, преобразуются к виду, эквивалентному результатам измерений образцов градуировочного набора на приборе в текущем состоянии, и по этим преобразованным данным создается градуировочная модель.
Созданная при помощи данного способа градуировочная модель учитывает произошедшие в процессе эксплуатации изменения в характеристиках прибора, обеспечивает достаточно высокую точность определения анализируемых свойств, при этом нет необходимости повторять измерения на приборе всех образцов градуировочного набора, что снижает длительность и трудоемкость процесса градуировки. При измерении неизвестного образца допускается возможность проведения анализа выпадающих данных при помощи статистики предсказания выбросов, что позволяет оценить правомерность применения градуировочной модели. Для учета влияния мешающих факторов, таких как различия в пробоподготовке и в состоянии образцов, предложено использовать процедуру нормализации с использованием различных видов математической предобработки результатов измерений и данных по вторичным свойствам (референтных данным).
Существенный недостаток данного изобретения в том, что созданная градуировочная модель учитывает лишь текущее состояние прибора и его характеристик, а также иных свойств, оказывающих влияние на результаты измерений. Таким образом, по прошествии определенного времени эти свойства могут измениться снова вследствие различных причин, в частности, старения, выполнения ремонта прибора, замены отдельных конструктивных элементов, изменения условий эксплуатации. В результате погрешность анализа по созданной градуировочной модели может увеличиться, и в итоге возникнет необходимость построения новой градуировки, то есть повторения всех операций описанных выше в соответствии с данным методом даже в том случае, если происходит многократное изменение одних и тех же характеристик.
Известен еще один способ [2] создания многомерных градуировочных моделей, маловосприимчивых к изменению параметров прибора, на котором проводятся измерения, а также к изменению внешних условий, при которых происходят измерения, и к изменению прочих свойств образца. По совокупности существенных признаков данный способ является наиболее близким к заявляемому изобретению и выбран в качестве прототипа. В рассматриваемом методе для создания градуировочной модели выбирается необходимое количество градуировочных образцов с известными вторичными свойствами, таким образом, чтобы прочие свойства образцов изменялись в максимально возможном диапазоне ожидаемых изменений. Затем для каждого из выбранных градуировочных образцов проводят измерение на приборе, для которого определяется градуировочная модель, большого числа параметров, характеризующих первичные свойства образца, после чего проводится математическая обработка полученных результатов и определяется ряд градуировочных констант в соотношениях между значениями величин, характеризующих первичные и вторичные свойства градуировочных образцов. Особенность метода заключается в том, что в процессе измерений для одного или нескольких образцов из градуировочного набора намеренно производят изменения, как минимум, одного из параметров измерительного прибора, дополнительно при этом может вводиться изменение внешних условий. Величина изменений указанных параметров при построении градуировочной модели должна быть того же порядка или большей, чем ожидаемая величина изменений этих параметров между различными приборами в процессе эксплуатации. Изменения параметров прибора или прочих условий измерений могут также вводиться не в процессе проведения реальных измерений, а с помощью математических преобразований. Например, в случае спектрометров на основе монохроматора предлагается провести измерение одного или нескольких образцов, использующихся для градуировки, намеренно произведя сдвиг длины волны в диапазоне значений, которые могут ожидаться при эксплуатации. Этого можно достигнуть, произведя физические изменения монохроматора (в зависимости от конструкции используется сдвиг или изменение угла наклона решетки или фильтра, изменение положения отверстий на решетке, изменение наклона падающего излучения) или с помощью изменения констант, используемых для вычисления длин волн монохроматора.
Результаты анализа вторичных свойств образца, полученные с использованием многомерной градуировочной модели, созданной в соответствии с данным способом, мало зависят от условий измерений и технических параметров измерительного прибора. Намеренное введение разброса данных результатов измерения образцов градуировочного набора повышает устойчивость модели, а область ее применимости становится более широкой.
Данный метод не лишен и недостатков. Прежде всего, необходимо отметить снижение точности результатов анализа с использованием подобной градуировочной модели, что обусловлено изначально предполагаемой вариацией результатов измерения первичных свойств. Это же обстоятельство затрудняет оценку примененимости градуировки для анализа того или иного неизвестного образца. Например, если градуировочная модель для определения процентного содержания различных химических компонентов в образце будет использована для анализа неизвестного образца, состоящего из других компонентов и в значительной степени отличающегося от образцов градуировочного набора, это приведет к ошибкам определения вторичных свойств. Кроме того, построение математической модели, малочувствительной к воздействию всех факторов, влияющих на результаты измерений, не всегда возможно, вследствие большого количества подобных факторов. Поэтому процесс создания градуировочной модели, учитывающей влияние большого количества дополнительных факторов, требует проведения огромного объема измерений градуировочных образцов при различных условиях, что еще более увеличивает трудоемкость и длительность процедуры создания градуировки.
Задачей настоящего изобретения является создание многомерной градуировочной модели, которая обеспечивает высокую точность определения анализируемых свойств и является устойчивой к изменениям свойств, влияющих на результаты измерений прибора, причем даже в случае многократного изменения подобных факторов, в частности, к возможным линейным и нелинейным отличиям технических параметров прибора, возникающим вследствие старения, выполнения ремонта или замены отдельных типовых элементов конструкции, изменению условий эксплуатации, а также прочих факторов, при этом снижается трудоемкость и длительность процедуры построения подобной модели, впоследствии применяемой для определения одного или нескольких вторичных свойств неизвестного образца по результатам измерения множества первичных свойств этого образца, причем не обязательно спектральных.
Решение поставленной задачи достигается способом создания многомерных градуировочных моделей, состоящим из последовательности действий, объединенных единым изобретательским замыслом. Способ включает в себя подбор градуировочного набора образцов с известными вторичными свойствами, определенными референтными методами; измерение на приборе первичных свойств каждого из образцов градуировочного набора; искусственное внесение изменений, по крайней мере, в одно из свойств, оказывающих влияние на результаты измерений прибора; измерение на приборе в измененном таким образом состоянии первичных свойств как минимум, одного образца; создание градуировочной модели, устойчивой к указанным изменениям, путем нахождения при помощи методов многомерного регрессионного анализа с использованием данных, полученных на приборе после внесения изменений, соотношений градуировки, позволяющих определить анализируемые вторичные свойства неизвестного образца по результатам измерений множества первичных свойств этого образца, отличающийся тем, что до внесения изменений формируют набор образцов для расчета корректирующих соотношений, измеряют первичные свойства каждого образца из этого набора на приборе до и после внесения изменений, и, сопоставляя при помощи методов многомерного регрессионного анализа результаты измерений первичных свойств образцов набора, полученные на приборе до внесения изменений, с результатами измерений первичных свойств тех же самых образцов, полученными на приборе в состоянии, когда внесены изменения, определяют корректирующие соотношения, причем найденные для какого-либо одного прибора корректирующие соотношения, учитывающие влияние внесенных изменений, используются на любом другом приборе данного типа при построении устойчивой к указанным изменениям градуировочной модели; осуществляют преобразование результатов измерения первичных свойств образцов градуировочного набора при помощи полученных корректирующих соотношений к виду, соответствующему измерениям на приборе после внесения изменений; скорректированными таким образом под измененное состояние прибора результатами измерения первичных свойств образцов градуировочного набора дополняют результаты измерения первичных свойств градуировочных образцов, полученные на приборе до внесения изменений, причем проверку многомерной градуировочной модели, созданной по совокупности исходных и скорректированных результатов измерения первичных свойств образцов градуировочного набора, производят осуществляя процедуру валидации и используя определяемые на основании нее количественные параметры валидации градуировки.
Определение корректирующих соотношений на основе измерения, сформированного в соответствии с данным методом представительного набора образцов, позволяет учесть нелинейные отличия в характеристиках прибора, обусловленные изменением свойств, влияющих на результаты его измерений, т.к. для нахождения соотношений преобразования результатов измерений используется несколько зависимостей изменения первичных свойств. При этом нет необходимости проводить огромный объем измерений образцов градуировочного набора при различных условиях, что значительно снижает трудоемкость и длительность процесса создания градуировочной модели, устойчивой к изменениям факторов, влияющих на результаты измерений прибора, в соответствии с предложенным алгоритмом.
Изменения вносятся таким образом, чтобы охватить их возможный диапазон в процессе эксплуатации прибора. Поэтому построенная градуировочная модель будет устойчива даже к многократным изменениям влияющих на результаты анализа свойств, если их воздействие было учтено предложенной коррекцией градуировки на стадии ее создания. Этот факт также является существенным достоинством данного метода.
Все результаты измерений градуировочных образцов, в том числе и дополняющие градуировочный набор результаты измерения первичных свойств образцов градуировочного набора, преобразованные к виду, эквивалентному результатам измерений на приборе, когда внесены изменения по крайней мере в одно из влияющих на результаты его измерений свойств, сохраняются в компьютере данного градуируемого прибора. Это обеспечивает независимость созданной модели от измерений на приборе в исходном состоянии и позволяет оценить правомерность применения градуировки для анализа неизвестного образца на приборе в состоянии, когда изменились одно или несколько влияющих на результаты измерений свойств, а также определить выпадающие данные при помощи статистики предсказания выбросов, что гарантирует высокую точность определения анализируемых вторичных свойств.
Для оценки точности анализа вторичных свойств неизвестных образцов по рассчитанной градуировочной модели на заключительном этапе проводится ее проверка (валидация). Данная процедура осуществляется путем сравнения вторичных свойств образцов, определенных по данной градуировке на основании результатов измерений прибора, с прямыми результатами измерения вторичных свойств, полученными с использованием референтных методов.
Использование статистики предсказания выбросов и исключение из модели выпадающих образцов градуировочного набора перед определением соотношений градуировки повышает устойчивость создаваемой градуировочной модели.
Для преобразования результатов измерений и референтных данных к наиболее оптимальному виду можно использовать процедуру нормализации. Это позволяет минимизировать погрешность определения анализируемых вторичных свойств и учесть технические особенности измерительного прибора, а также различие пробоподготовки и состояния исследуемого образца. Процедура нормализации представляет собой выбор того или иного метода математической предобработки. Критерием выбора является точность анализа вторичных свойств образцов, которую обеспечивает прибор с градуировкой, при создании которой использовался данный вид математической предобработки. В качестве основных количественных критериев используются количественные параметры процедуры валидации градуировочной модели (например, стандартная ошибка валидации) [1].
Найденные корректирующие соотношения, учитывающие определенный вариант изменений свойств, влияющих на результаты измерений прибора, предлагается использовать с целью компенсации таких изменений при построении градуировки и для любого другого прибора данного типа, используя заявляемый алгоритм.
Сущность изобретения заключается в том, что предложенная совокупность признаков позволяет создать на градуируемом измерительном приборе многомерную градуировочную модель, устойчивую к возможным вариациям свойств, влияющих на результаты измерений прибора, в частности изменениям технических параметров прибора, возникающим вследствие старения, выполнения ремонта или замены отдельных типовых элементов конструкции, а также особенностям условий эксплуатации, причем даже в случае неоднократного изменения указанных факторов, при этом снижается трудоемкость и длительность процедуры построения подобной модели по сравнению с существующими известными методами. Созданная градуировочная модель предоставляет возможность с высокой точностью предсказывать вторичные свойства неизвестных образцов по результатам измерения множества первичных, не обязательно спектроскопических, свойств, причем градуировочная модель строится на основе данных по первичным свойствам образцов из градуировочного набора, измеренных на градуируемом приборе, и этих же данных, преобразованных к виду, как если бы измерения проводились на приборе, когда внесены некоторые изменения, по крайней мере, в одно из свойств, влияющих на результаты измерений прибора, например, соответствующие максимальным ожидаемым в процессе эксплуатации изменениям для приборов данного типа. Корректирующие соотношения, позволяющие преобразовать результаты измерений градуировочных образцов к виду, эквивалентному результатам измерений на приборе в измененном состоянии, определяются из измерений представительного набора образцов на приборе до и после внесения изменений, причем набор для расчета корректирующих соотношений состоит из гораздо меньшего количества образцов, чем градуировочный. Образцы из набора для расчета корректирующих соотношений обеспечивают существенные различия в результатах измерений во всем диапазоне первичных свойств на приборе, как в исходном, так и в измененном состоянии. Использование набора образцов для расчета корректирующих соотношений позволяет определить нелинейную связь между результатами измерений одних и тех же образцов на приборе до и после внесения изменений путем корреляционного анализа с использованием регрессионных методов. Найденные корректирующие соотношения, учитывающие определенный вариант изменений по крайней мере одного из факторов, влияющих на результаты измерений прибора, предлагается использовать при построении градуировочной модели с целью компенсации таких изменений и для любого другого прибора данного типа. Таким образом, существует возможность построения градуировки для любого другого прибора, устойчивой к отличиям технических параметров градуируемого прибора, возникающим вследствие старения, выполнения ремонта или замены отдельных типовых элементов конструкции, изменениям условий эксплуатации, а также прочих свойств, влияющих на результаты измерений прибора, используя корректирующие соотношения, рассчитанные только для одного прибора на основе предложенного алгоритма, что в еще большей степени упрощает процесс создания градуировочной модели. Так как при построении градуировочной модели используется совокупность результатов измерений первичных свойств образцов градуировочного набора, полученных на приборе в исходном состоянии, а также приведенных к виду прибора, когда по крайней мере в одно из влияющих на результаты измерений свойств внесены некоторые изменения, можно оценить правомерность применимости построенной градуировки для анализа неизвестного образца, используя статистические методы анализа выпадающих данных, например, по расстоянию Махаланобиса. Выполнение процедуры нормализации с использованием различных видов математической предобработки результатов измерений и данных по вторичным свойствам (референтных данных) позволяет обеспечить минимальную погрешность определения анализируемых вторичных свойств, определив, таким образом, оптимальные для данных условий соотношения градуировки.
Заявляемое изобретение поясняется чертежом, где представлено схематическое изображение заявляемого способа в виде потоковой диаграммы.
Заявляемый способ создания многомерных градуировочных моделей может быть использован для любых приборов, где анализируемые свойства образца определяются на основе многократного измерения других свойств, в частности, в спектрофотометрии для различного вида спектрометров, измеряющих поглощение светового излучения образцом на множестве различных длин волн. Данные, характеризующие результат подобных измерений, называются спектром. Рассмотрим применение заявляемого способа на примере спектрометров для анализа химического состава образца, заметив, однако, еще раз, что область применения заявляемого способа не ограничивается спектроскопией.
Спектрометр, как и любой аналитический прибор, требует предварительной градуировки, определяющей взаимосвязь между анализируемыми свойствами образца и спектральными характеристиками. Отметим, что часто с анализируемыми свойствами образца сопоставляются не непосредственно результаты измерений, а уже прошедшие процедуру нормализации (предварительную математическую предобработку) спектральные данные. Так, например, может проводиться сглаживание спектров, вычитание базовой линии или дифференцирование. Вид предварительной математической обработки выбирается исходя из критерия максимальной точности определения анализируемых вторичных свойств и сведения к минимуму влияния побочных факторов, связанных с паразитным рассеянием и особенностями пробоподготовки. Одна и та же математическая предобработка применяется ко всем спектрам образцов градуировочного набора, после проведения процедуры нормализации преобразованные спектральные данные имеют ярко выраженные характерные черты даже при незначительных изменениях анализируемых свойств [6]. В качестве критериев для оценки качества градуировочной модели используются различные статистические характеристики, например стандартная ошибка градуировки (SEC), стандартная ошибка валидации (SEV) и стандартная ошибка кросс-валидации (SECV) [1]. Наиболее распространенным видом математической предобработки при спектральном анализе является нахождение средневзвешенных значений спектральных данных [6], уменьшающее на 1 число степеней свободы в градуировочной модели. В данной предобработке находят усредненный по всему градуировочному набору спектр и вычитают его из каждого спектра градуировочных образцов. Аналогично находят средневзвешенные значения референтных данных. Тогда при анализе неизвестного образца перед применением построенной градуировочной модели из измеренного спектра также вычитается усредненный по градуировочному набору спектр.
Для проведения градуировки отбирается набор образцов, представительный к тем образцам, которые будут в дальнейшем анализироваться. При выборе градуировочных образцов для спектрального анализа используются следующие критерии [1]: а) образцы должны содержать все химические компоненты, которые планируется анализировать; б) диапазон изменения концентрации анализируемых компонентов в образцах градуировочного набора должен превышать диапазон изменения в анализируемых неизвестных образцах; в) величины изменения в концентрации химических компонентов от образца к образцу должны быть равномерно распределены по всему диапазону изменений; г) число образцов должно обеспечивать нахождение при помощи статистических методов математических соотношений между спектроскопическими данными и концентрацией отдельных химических компонентов. Образцы, выпадающие из градуировочного набора, определяются с помощью статистического анализа выбросов, например, путем вычисления расстояния Махаланобиса [1], которое определяется как:
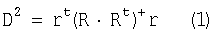
где R - матрица спектральных данных полного градуировочного набора, r - вектор, соответствующий спектру одного образца. Расстояние Махаланобиса показывает, сколько степеней свободы вносит в градуировочную модель данный образец. В среднем каждый градуировочный образец должен вносить k/m, где k - число переменных в регрессии, m - число образцов в градуировочном наборе. Образцы с D2>3k/m должны быть исключены из градуировочного набора. Большое значение расстояния Махалонобиса означает, что спектр данного образца почти полностью определяет один из регрессионных коэффициентов, что делает модель неустойчивой. Такое может произойти, когда, например, нарушена равномерность распределения анализируемых свойств градуировочных образцов по диапазону, в котором они изменяются, т.е. когда состав образца существенно отличается от остальных образцов в градуировочном наборе. Из градуировочного набора должны быть также исключены образцы, значения анализируемых свойств которых, определенные при помощи построенной модели, значительно отличаются от значений, которые дает референтный метод. Данные образцы определяются из расхождений по Стьюденту, рассчитанных по формуле:
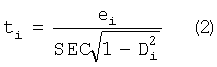
здесь еi - отличие полученной с помощью градуировочной модели величины концентрации химического компонента или анализируемого свойства от референтного значения для i-го градуировочного образца, SEC - стандартная ошибка градуировки [1], 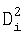 - расстояние Махаланобиса для i-го градуировочного образца. Расхождения по Стьюденту должны быть равномерно распределены по нормальному закону. Величина расхождения сравнивается с коэффициентом Стьюдента, для доверительной вероятности 0,95 и числа степеней свободы m-k. В случае если величина расхождения превышает коэффициент, образец исключается из градуировочного набора.
- расстояние Махаланобиса для i-го градуировочного образца. Расхождения по Стьюденту должны быть равномерно распределены по нормальному закону. Величина расхождения сравнивается с коэффициентом Стьюдента, для доверительной вероятности 0,95 и числа степеней свободы m-k. В случае если величина расхождения превышает коэффициент, образец исключается из градуировочного набора.
Анализируемые свойства градуировочных образцов должны быть заранее известны или определяются при помощи референтных методов. Полученные численные значения считаются реальными значениями анализируемых свойств, поэтому точность референтного анализа определяет точность всей градуировки, и к этой процедуре предъявляются достаточно высокие требования. Повысить точность референтного анализа можно, проводя многократное повторение анализов с последующим усреднением результатов.
Спектры образцов градуировочного набора регистрируются на приборе, после чего может быть создана многомерная градуировочная модель. Для этого используются мультивариантные математические методы, такие как анализ принципиальных компонентов (РСА), метод дробных наименьших квадратов (PLS) и т.п. В дальнейшем, измеряя спектр неизвестного образца на данном приборе и используя созданную градуировочную модель, можно определить анализируемые свойства, например, химический состав. Точность подобных измерений будет достаточно высокой до тех пор, пока свойства, оказывающие влияние на результаты измерений прибора, будут оставаться постоянными. Но, как уже упоминалось ранее, в процессе эксплуатации, при проведении ремонтных работ или замены отдельных типовых элементов конструкции могут изменяться, например, технические характеристики прибора, что в свою очередь может привести к снижению точности предсказаний и необходимости построения новой градуировочной модели. Следовательно, для обеспечения достаточной точности предсказания свойств неизвестных образцов на приборе при условии возможных многократных изменений, влияющих на результаты измерений факторов, необходимо иметь градуировочную модель, устойчивую к различиям в характеристиках прибора, изменениям условий эксплуатации и прочих свойств, влияющих на результаты измерений прибора, при этом дающую заданную точность анализа, позволяющую оценить применимость модели для анализа неизвестного образца, причем процесс создания подобной градуировки не должен быть чрезмерно длительным и трудоемким.
Заявляемый способ позволяет создавать многомерную градуировочную модель для градуируемого прибора, устойчивую к возможным изменениям одного или нескольких факторов, влияющих на результаты его измерений, не проводя измерения полного набора градуировочных образцов на приборе, когда указанный фактор или факторы изменились, причем это справедливо даже в случае многократных изменений. Для создания градуировки используются спектральные данные, измеренные на градуируемом приборе, дополненные спектральными данными, полученными в результате преобразования исходных данных к виду, эквивалентному измерениям на приборе в состоянии, когда изменено по крайней мере одно из влияющих на результаты измерений свойств, например, таким образом, чтобы охватить ожидаемый диапазон подобных изменений для приборов данного типа в процессе эксплуатации. Область применимости и устойчивость градуировочной модели анализируются на основании совокупности этих спектральных данных. Так как все данные сохраняются в компьютере градуируемого прибора, это позволяет производить оценку выпадающих данных при анализе неизвестных образцов, например, с помощью статистики Махаланобиса.
Для коррекции спектральных данных градуировочного набора, проводимой с целью учета изменений свойств, влияющих на результаты измерений прибора, используется специально подобранный набор образцов, именуемый в дальнейшем как набор для расчета корректирующих соотношений, число образцов в котором намного меньше, чем в полном градуировочном наборе, при этом их свойства могут быть неизвестны, важно лишь то, что этот набор образцов обеспечивает значительные вариации в измеряемых спектральных данных, позволяющие найти выражения преобразования. Для этого спектр каждого образца набора измеряется на приборе в состоянии, соответствующем измерению спектров градуировочных образцов, и этом же приборе, когда по крайней мере в одно из свойств, оказывающих влияние на результаты измерений, внесены некоторые изменения («измененном» приборе). Проводя корреляцию полученных спектральных данных, находят соотношения, позволяющие преобразовать спектры, измеренные на приборе до внесения изменений, к виду, как если бы измерения проводились на измененном приборе, и учитывающие различия в результатах измерений одних и тех же образцов, возникающие вследствие изменения одного или нескольких факторов, влияющих на результаты измерений прибора. С целью получения оптимальной градуировки спектральные данные могут быть подвергнуты нормализации, заключающейся в проведении одинаковых математических преобразований для всех измеренных спектров. Это обеспечивает выявление явных отличий в спектральных данных, измеренных на приборе до и после внесения изменений, что в свою очередь способствует более точному определению выражений для преобразования спектральных данных. Необходимо отметить, что найденные подобным образом для какого-либо одного прибора корректирующие соотношения, учитывающие влияние на результаты измерений прибора изменений определенного свойства или свойств, могут быть использованы на любом другом приборе данного типа при построении градуировочной модели, устойчивой к указанным изменениям. Совокупность перечисленных признаков позволяет снизить трудоемкость и длительность процесса создания градуировочной модели, устойчивой к изменениям свойств, влияющих на результаты измерений прибора. Градуировочную модель для градуируемого прибора создают по совокупности исходных и преобразованных спектральных данных градуировочных образцов, используя стандартные математические методы многомерного регрессионного анализа (MLR, РСА, PLS и т.п. [6]), причем из градуировки должны быть исключены выпадающие образцы, что гарантирует устойчивость созданной модели, после чего ее можно использовать для определения свойств неизвестного образца.
В качестве практического пояснения заявляемого изобретения рассмотрим пример создания многомерной градуировочной модели, устойчивой к изменениям технических параметров спектрометра ИнфраЛЮМ ФТ-10, которые могут произойти вследствие старения, выполнения ремонта или замены отдельных типовых элементов конструкции. Принцип работы данного прибора основан на Фурье спектроскопии в ближней инфракрасной области спектра (БИК). В качестве объекта исследований выбрана продовольственная пшеница, для которой с помощью построенной градуировки на данном приборе определялись основные показатели качества. Подчеркнем при этом еще раз, что данный пример используется лишь для практической иллюстрации предлагаемого способа.
Для создания градуировки отбирается представительный набор образцов, спектры которых измеряются на спектрометре. Полученные спектральные данные могут быть подвергнуты процедуре нормализации, учитывающей особенности приборов, работающих на пропускание и использующих принципы Фурье спектроскопии [6]. При построении градуировочной модели в рамках данных исследований использовались следующие предобработки: выравнивание базовой линии, нормирование спектров по среднеквадратичному отклонению, расчет средневзвешенных значений [6].
Как упоминалось ранее, вид математической обработки определяется таким образом, чтобы обеспечить минимальную погрешность определения анализируемых свойств. Если спектральные данные подвергнуты процедуре нормализации, то соотношения градуировки определяются на основе сопоставления этих данных с известными, также прошедшими нормализацию, свойствами образцов градуировочного набора, определенными референтными методами.
Для оценки качества созданной градуировочной модели используются различные статистические характеристики [1].
Одним из таких параметров является стандартная ошибка градуировки (SEC), которая служит для оценки ожидаемой согласованности между величинами, полученными, используя модель градуировки, и величинами, измеренными референтным методом.
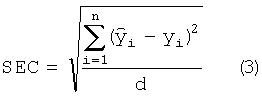
где 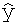 - вектор значений определяемых показателей для градуировочных образцов, полученных при применении этой градуировки; y - вектор референтных данных; d=n-k - число степеней свободы градуировочной модели, n - число градуировочных образцов, к - число переменных величин в градуировочной модели, зависящее от математического метода, использующегося для построения модели.
- вектор значений определяемых показателей для градуировочных образцов, полученных при применении этой градуировки; y - вектор референтных данных; d=n-k - число степеней свободы градуировочной модели, n - число градуировочных образцов, к - число переменных величин в градуировочной модели, зависящее от математического метода, использующегося для построения модели.
Стандартная ошибка кросс валидации (SECV) вычисляется при перекрестной проверке градуировочной модели и позволяет оценить ее устойчивость [1].
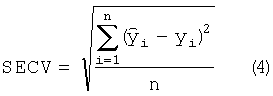
где 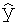 - вектор, содержащий оценки перекрестной валидации.
- вектор, содержащий оценки перекрестной валидации.
Стандартная ошибка валидации (SEV) характеризует ошибку отклонения между референтными и предсказанными по градуировочному уравнению значениями для образцов дополнительного набора, не входивших в градуировочный.
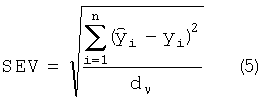
где dν - общее число референтных значений анализируемого показателя для всех спектров дополнительного набора, yi - референтные значения анализируемого показателя для i-го спектра дополнительного набора, 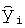 - предсказанные значения анализируемого показателя для i-го спектра дополнительного набора.
- предсказанные значения анализируемого показателя для i-го спектра дополнительного набора.
Основные статистические характеристики исходной градуировочной модели, созданной по образцам продовольственной пшеницы на исследуемом спектрометре без искусственного внесения изменений в свойства, влияющие на результаты измерений, приведены в Таб.1. Градуировки были построены на два основных показателя качества - протеин и клейковину. Для определения SEV использовался валидационный набор, который выбирался таким образом, чтобы содержание в нем соответственно протеина или клейковины было равномерно распределено по всему диапазону возможных значений концентрации этих показателей.
Чтобы создать на спектрометре многомерную градуировочную модель, учитывающую возможные изменения свойств, оказывающих влияние на результаты измерений прибора, например, отличия технических параметров прибора, возникающие вследствие старения, выполнения ремонта или замены отдельных типовых элементов конструкции, необходимо в соответствии с заявляемым изобретением сформировать набор образцов для расчета корректирующих соотношений между результатами, получаемыми на приборе в исходном состоянии, и в состоянии, когда внесены изменения. В данном случае из градуировочного набора было отобрано 10 образцов с максимальным и минимальным значениями параметра score для каждого из анализируемых показателей. Однако отметим, что образцы в наборе для расчета корректирующих соотношений в общем случае могут не принадлежать градуировочному набору.
Спектры выбранных образцов регистрировались на градуируемом приборе. Затем в конструктивные особенности данного прибора искусственно вносились некоторые изменения, например, те, которые возможны при ремонте анализатора. В частности, в приводимом примере производилась замена светоделителя в интерферометре на другой, покрытие которого отличается от исходного настолько, что вызывает максимально возможные отклонения по распределению светового пучка среди светоделителей данного класса. После этого выполнялись измерения образцов для расчета корректирующих соотношений на измененном таким образом приборе и путем корреляции спектральных данных, полученных на приборе до и после внесения изменений, находились выражения для преобразования результатов измерений на приборе в исходном состоянии к виду, соответствующему измерениям на приборе после внесения изменений. В простейшем виде эти соотношения могут быть определены методом линейной регрессии.
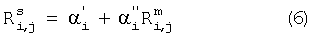
где 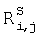 - значения спектральных данных, измеренные на приборе, когда в его конструкцию внесены изменения (i-ая длина волны, j-й образец из набора для расчета корректирующих соотношений),
- значения спектральных данных, измеренные на приборе, когда в его конструкцию внесены изменения (i-ая длина волны, j-й образец из набора для расчета корректирующих соотношений), 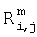 - аналогичные спектральные данные, измеренные на приборе до внесения изменений.
- аналогичные спектральные данные, измеренные на приборе до внесения изменений.
Спектральные данные могут подвергаться процедуре нормализации, при этом используемая математическая обработка должна быть одинаковой для спектров, измеряемых на приборе как до, так и после внесения изменений. Для определения корректирующих соотношений методом наименьших квадратов находятся коэффициенты регрессии.
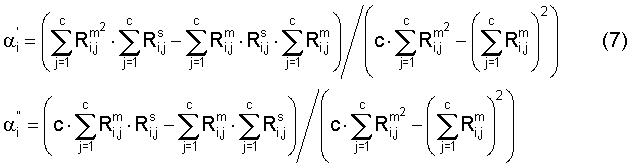
где с - количество образцов в наборе для расчета корректирующих соотношений.
После нахождения корректирующих соотношений, используя найденные регрессионные коэффициенты 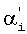 и
и 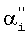 , спектральные данные для каждого образца из градуировочного набора в соответствии с формулой (6) преобразуются к виду, соответствующему измерениям на приборе после внесения изменений. Далее создается новая многомерная градуировочная модель по совокупности исходных и преобразованных данных градуировочного набора, которая проверяется с помощью стандартной процедуры валидации [1], в результате чего определяются ее основные статистические параметры.
, спектральные данные для каждого образца из градуировочного набора в соответствии с формулой (6) преобразуются к виду, соответствующему измерениям на приборе после внесения изменений. Далее создается новая многомерная градуировочная модель по совокупности исходных и преобразованных данных градуировочного набора, которая проверяется с помощью стандартной процедуры валидации [1], в результате чего определяются ее основные статистические параметры.
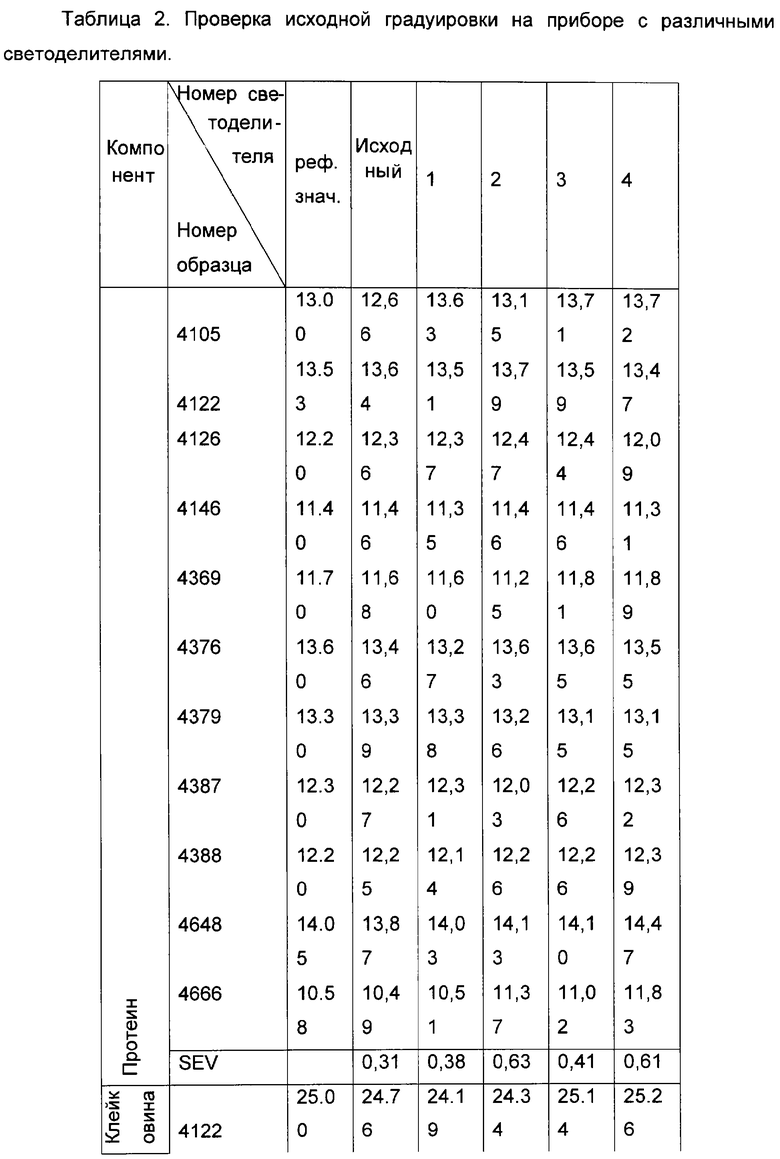
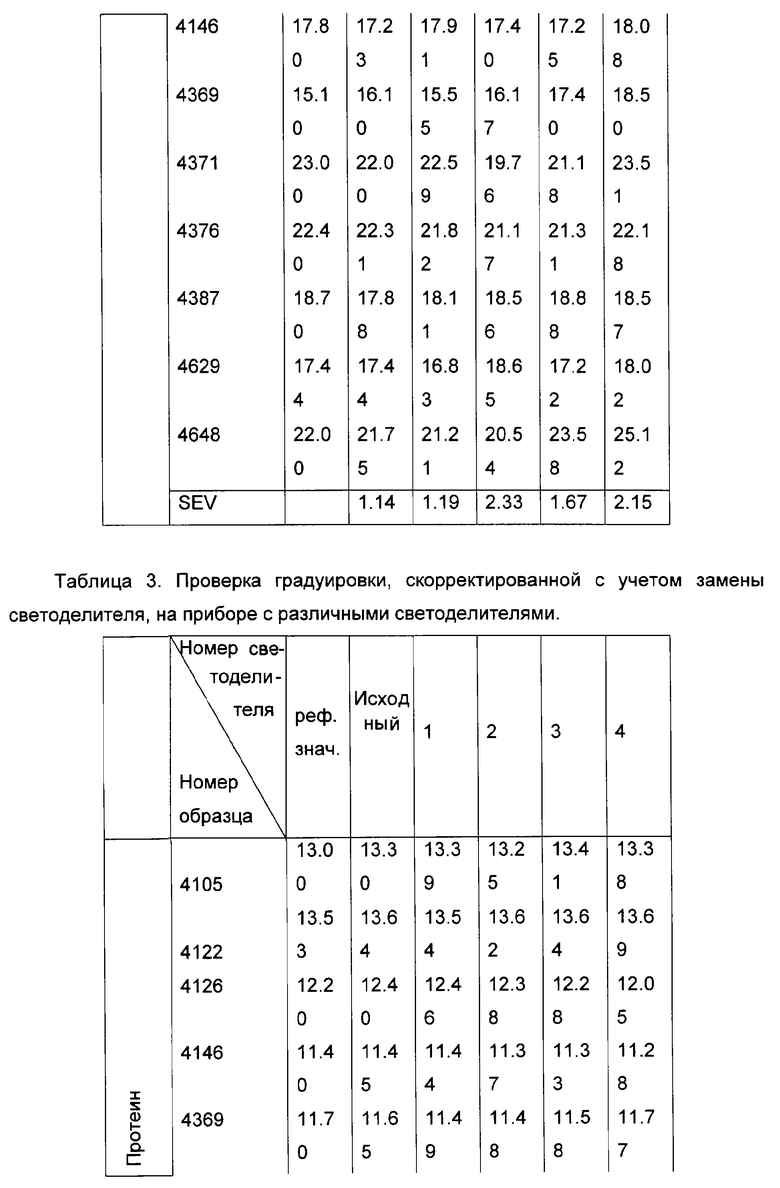
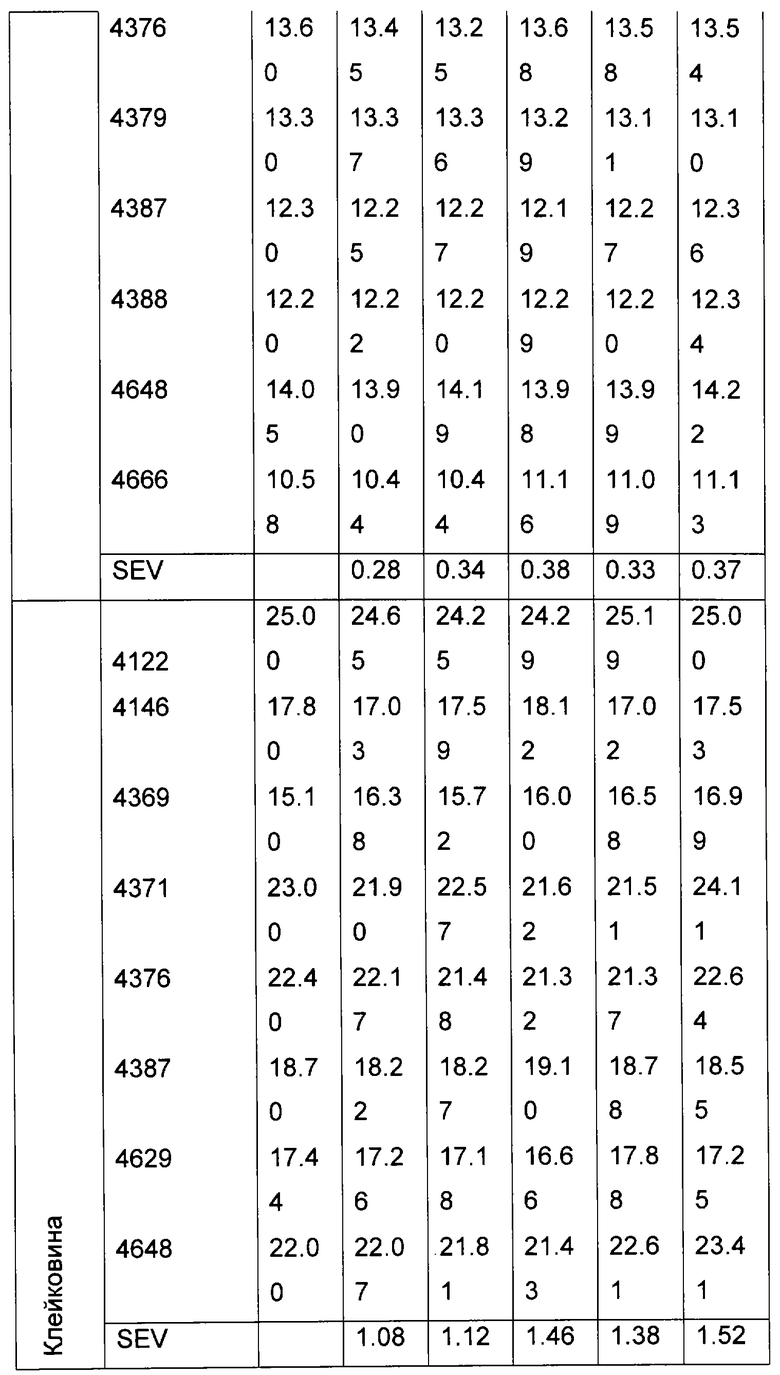
Для проверки эффективности предложенного метода на исследуемом приборе устанавливались несколько различных светоделителей, и в каждом случае регистрировались спектры валидационного набора образцов. После этого на основе стандартной процедуры валидации [1] оценивались основные статистические параметры исходной и скорректированной градуировочных моделей. В таблице 2 приведены данные для исходной градуировки, а в таблице 3 для скорректированной, устойчивой к влиянию замены светоделителя.
Из приведенных данных видно, что созданная в соответствии с заявляемым изобретением многомерная градуировочная модель позволяет с высокой точностью определять свойства неизвестных образцов и при этом значительно менее чувствительна к учтенному с помощью предложенного алгоритма возможному изменению конструкции прибора, в данном случае замене светоделителя. Подобным образом могут быть учтены любые другие изменения свойств, влияющих на результаты измерений прибора, приведенный здесь пример выбран в качестве наглядной иллюстрации заявляемого изобретения вследствие того, что подобные изменения являются одними из наиболее характерных для спектрометров данного типа и способны привести к значительному снижению точности анализа по изначально построенной градуировочной модели прибора, если не будут учтены при ее создании.
Была проведена проверка возможности использования найденных корректирующих соотношений на другом приборе той же модели. На этом приборе были зарегистрированы спектры выбранного для него градуировочного набора образцов продовольственной пшеницы и на основании этих данных построена градуировочная модель, которая не учитывает возможного изменения свойств, оказывающих влияние на результаты измерений прибора.
После этого спектральные данные, полученные при измерении на градуируемом приборе градуировочного набора образцов, были скорректированы по найденным ранее корректирующим соотношениям к виду, соответствующему прибору, для которого проведена замена светоделителя. В соответствии с предложенным алгоритмом была создана градуировочная модель по совокупности исходных и скорректированных спектральных данных градуировочных образцов прибора.
Для проверки эффективности предложенного метода на градуируемом приборе устанавливались несколько различных светоделителей, и в каждом случае регистрировались спектры валидационного набора образцов. После этого на основе стандартной процедуры валидации [1] оценивались основные статистические параметры исходной градуировочной модели, построенной для данного прибора, и градуировочной модели, устойчивой к влиянию замены светоделителя, на основе корректирующих соотношений, рассчитанных ранее для другого прибора. Полученные данные приведены соответственно в таблицах 4 и 5.
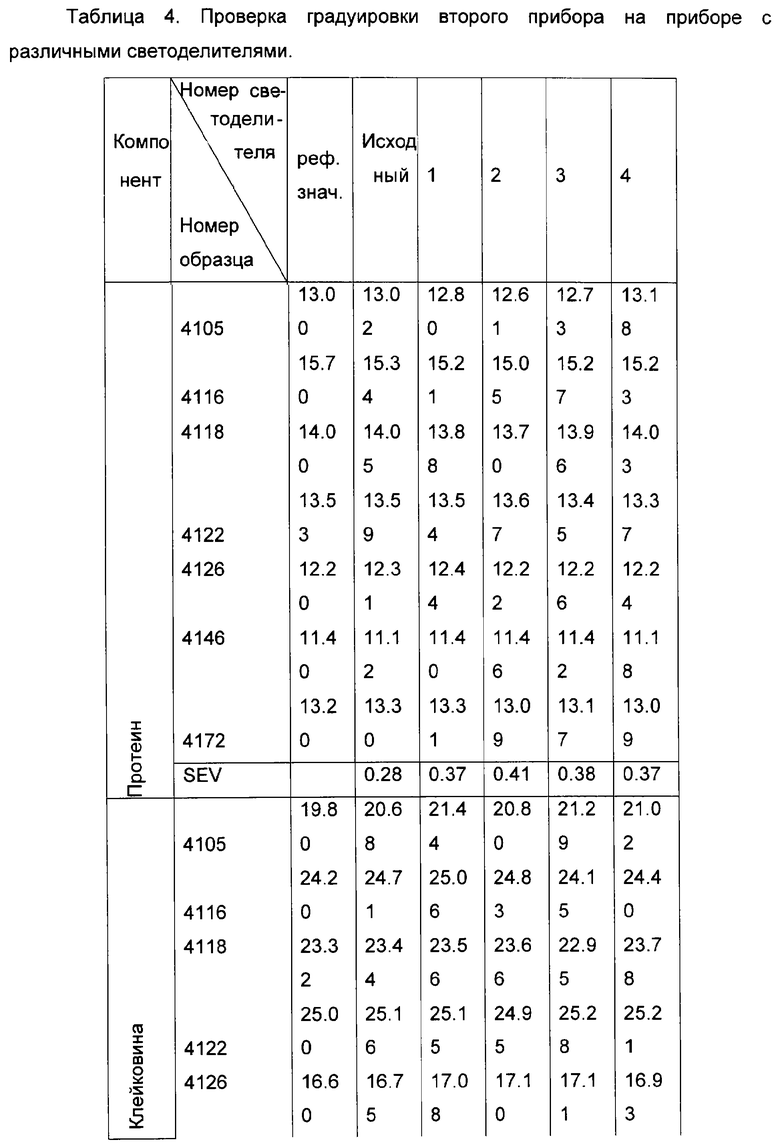
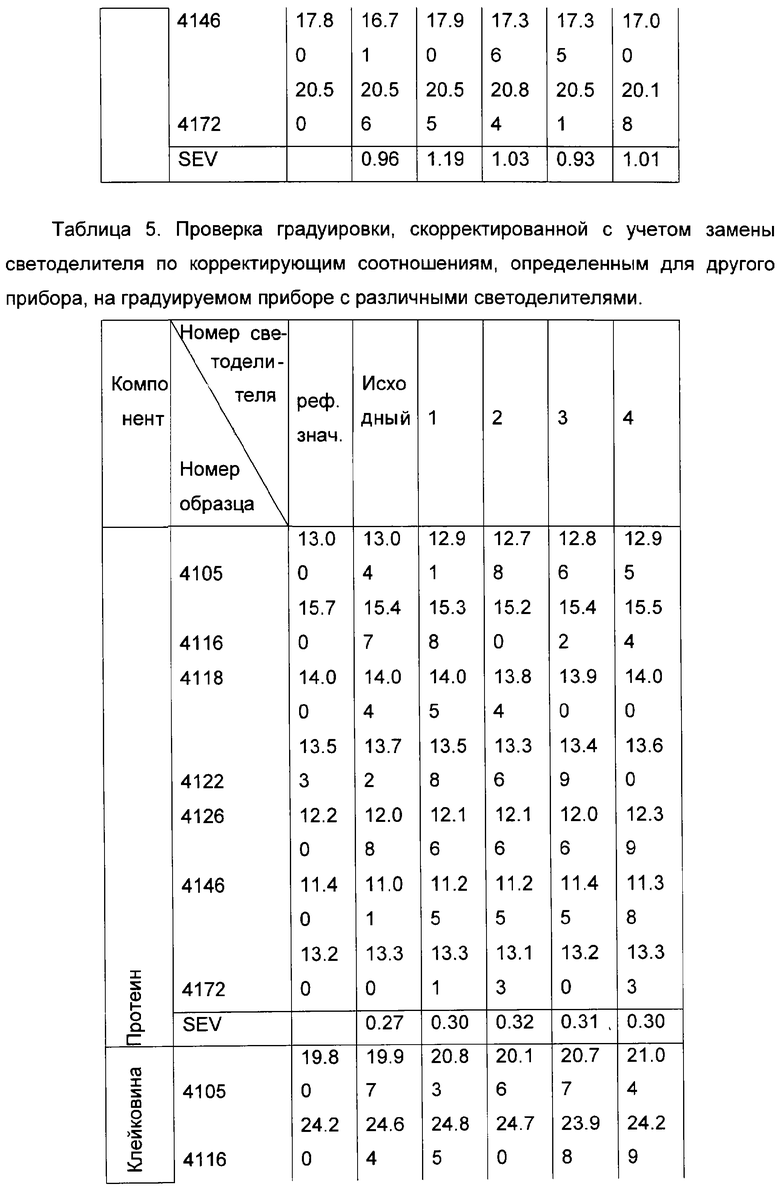
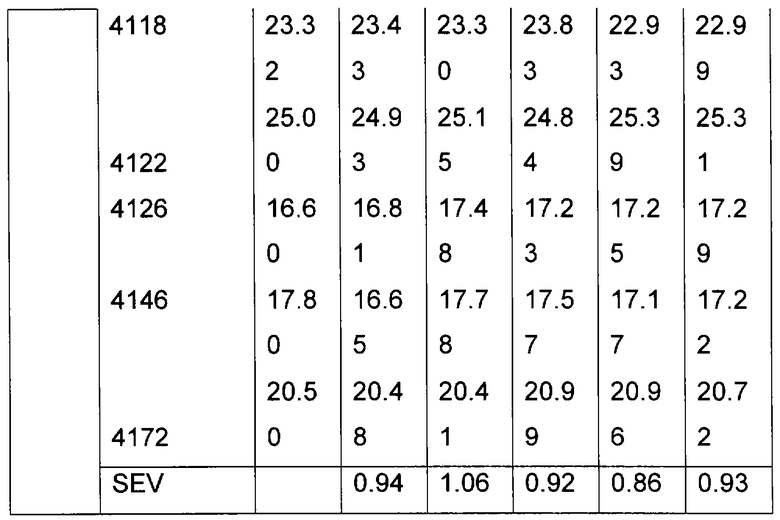
Результаты таблиц 4 и 5 подтверждают возможность использования корректирующих соотношений, определенных для какого-либо одного прибора и учитывающих влияние изменений его параметров или иных свойств, влияющих на результаты измерений, на любом другом приборе данной серии при построении устойчивой к указанным изменениям градуировочной модели. Данная особенность позволяет после создания в соответствии с предложенным способом градуировочной модели, компенсирующей отличия определенного влияющего на результаты измерений свойства или свойств, например, технических параметров прибора, изменения которых происходят вследствие старения, выполнения ремонта или замены отдельных типовых элементов конструкции, для какого-либо одного прибора, в дальнейшем использовать найденные корректирующие соотношения для всех остальных приборов данного типа при построении градуировочных моделей, учитывающих с помощью данных соотношений коррекции соответствующие изменения влияющих свойств. В таком случае нет необходимости выбирать и проводить измерения набора образцов для расчета корректирующих соотношений для всех остальных приборов, кроме первого, поскольку спектральные данные, полученные при регистрации градуировочных образцов на остальных приборах, преобразуются математически с использованием найденных корректирующих соотношений к виду, соответствующему прибору, когда внесены некоторые изменения в одно или несколько свойств, влияющих на результаты измерений.
В заключение еще раз отметим, что область применения заявляемого способа не ограничивается спектроскопией. Заявляемое изобретение может быть использовано для различных приборов, определяющих некоторые свойства образца на основе многократного измерения других свойств.
Источники информации
1. ASTM standard, E 1655-00, Practices for Infrared Multivariate Quantitative Analysis.
2. Патентная заявка США №4944589, МПК G01J 3/18, опубликована 31.07. 1990.
3. Патентная заявка США №6615151, МПК G01N 015/06, опубликована 02.09.2003.
4. Европейская патентная заявка ЕР 0225233, МПК G01N 021/27 Е публикована 28.03.2002
5. Российская патентная заявка №2266523 С1, МПК 7: G01N 021/01, опубликована 20.12.2005.
6. Руководство по эксплуатации ИнфраЛЮМ ФТ-10, 152.00.00.00.РЭ.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ СОЗДАНИЯ НЕЗАВИСИМЫХ МНОГОМЕРНЫХ ГРАДУИРОВОЧНЫХ МОДЕЛЕЙ | 2004 |
|
RU2266523C1 |
| СПОСОБ СОЗДАНИЯ МНОГОМЕРНЫХ ГРАДУИРОВОЧНЫХ МОДЕЛЕЙ АНАЛИТИЧЕСКОГО ПРИБОРА | 2013 |
|
RU2541906C1 |
| СПОСОБ ПРОВЕДЕНИЯ ИСПЫТАНИЯ ТАБЛЕТИРОВАННЫХ ЛЕКАРСТВЕННЫХ ПРЕПАРАТОВ В БЛИСТЕРНОЙ УПАКОВКЕ МЕТОДОМ БИК СПЕКТРОМЕТРИИ | 2018 |
|
RU2685758C1 |
| СПОСОБ ПРОВЕДЕНИЯ ИСПЫТАНИЯ КАПСУЛИРОВАННЫХ ЛЕКАРСТВЕННЫХ ПРЕПАРАТОВ В БЛИСТЕРНОЙ УПАКОВКЕ МЕТОДОМ БИК СПЕКТРОМЕТРИИ | 2018 |
|
RU2685756C1 |
| СПОСОБ ДИФФЕРЕНЦИАЛЬНОЙ ДИАГНОСТИКИ МИКРОБОВ И СЛОЖНЫХ АМИНОКИСЛОТ | 2007 |
|
RU2362145C2 |
| СПОСОБ РЕНТГЕНОФЛУОРЕСЦЕНТНОГО ОПРЕДЕЛЕНИЯ СОДЕРЖАНИЯ ПРИМЕСЕЙ КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ | 2014 |
|
RU2584064C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ЧАСТИЦ, ВЗВЕШЕННЫХ В ЖИДКОСТИ, ПО СПЕКТРАМ МАЛОУГЛОВОГО РАССЕЯНИЯ СВЕТА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2006 |
|
RU2321840C1 |
| УСТРОЙСТВО И СПОСОБ ДЛЯ ОПРЕДЕЛЕНИЯ ТОКСИЧНОСТИ ЖИДКИХ СРЕД | 2011 |
|
RU2514115C2 |
| СПОСОБ ПОСТРОЕНИЯ УСТОЙЧИВОЙ ГРАДУИРОВОЧНОЙ ЗАВИСИМОСТИ ПРИ ОПРЕДЕЛЕНИИ КОЛИЧЕСТВЕННОГО СОСТАВА ЭЛЕМЕНТОВ В ЦИНКОВЫХ СПЛАВАХ | 2011 |
|
RU2462701C1 |
| Способ определения суммарного содержания углеводородов в водах | 2016 |
|
RU2611413C1 |
Изобретение относится к аналитическому приборостроению, в частности к способам создания градуировочных моделей для различного вида измерительных приборов. Способ создания многомерных градуировочных моделей включает подбор градуировочного набора образцов с известными вторичными свойствами, измерение на приборе первичных свойств каждого из образцов, искусственное внесение изменений, по крайней мере, в одно из свойств, оказывающих влияние на результаты измерений прибора, измерение первичных свойств, как минимум, одного образца на приборе в измененном таким образом состоянии, причем до внесения изменений формируют набор образцов для расчета корректирующих соотношений, измеряют первичные свойства каждого образца из этого набора на приборе до и после внесения изменений, и, сопоставляя при помощи методов многомерного регрессионного анализа результаты измерений первичных свойств образцов набора, полученные на приборе до внесения изменений, с результатами измерений первичных свойств тех же самых образцов, полученными на приборе в состоянии, когда внесены изменения, определяют корректирующие соотношения. Осуществляют преобразование результатов измерения первичных свойств образцов градуировочного набора при помощи полученных корректирующих соотношений к виду, соответствующему измерениям на приборе после внесения изменений. Скорректированными таким образом под измененное состояние прибора результатами измерения первичных свойств образцов градуировочного набора дополняют результаты измерения первичных свойств градуировочных образцов, полученные на приборе до внесения изменений, рассчитывают многомерную градуировочную модель по совокупности исходных и скорректированных результатов измерения первичных свойств образцов градуировочного набора и производят ее проверку, определяя на основании ее количественные параметры валидации градуировки. Техническим результатом является создание многомерной градуировочной модели, которая обеспечивает высокую точность определения анализируемых свойств и является устойчивой к изменениям свойств, влияющих на результаты измерений прибора. 8 з.п. ф-лы, 5 табл., 1 ил.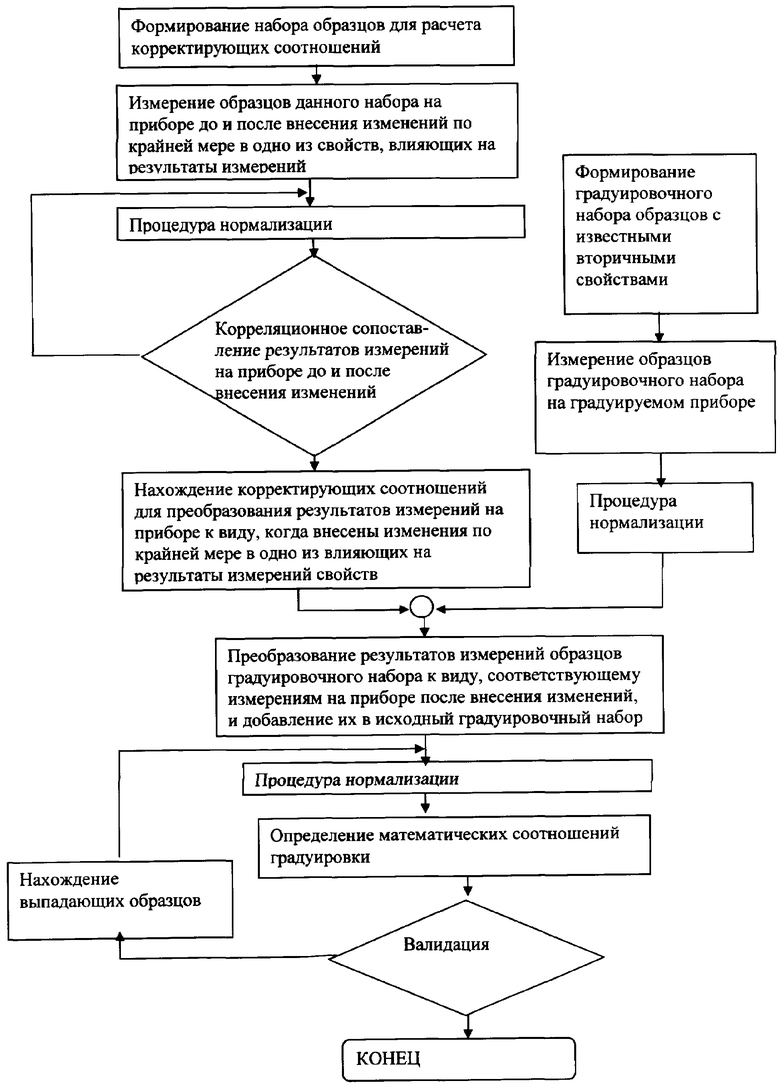
| СПОСОБ СОЗДАНИЯ НЕЗАВИСИМЫХ МНОГОМЕРНЫХ ГРАДУИРОВОЧНЫХ МОДЕЛЕЙ | 2004 |
|
RU2266523C1 |
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| US 6615151 B1, 02.09.2003 | |||
| US 4944589 А, 31.07.1990 | |||
| СПОСОБ КАЛИБРОВКИ СПЕКТРАЛЬНОГО ПРИБОРА | 1992 |
|
RU2117932C1 |
| Способ выбора градуировочных образцов для спектрального анализа | 1979 |
|
SU1109586A1 |
| US 5459677 А, 17.10.1995. | |||
Авторы
Даты
2007-10-20—Публикация
2006-06-20—Подача