Изобретение относится к спектрофотометрам, предназначенным для измерения электромагнитного излучения, в частности инфракрасного, ближнего (длинноволнового) инфракрасного, видимого излучения, рамановских спектров, рэлеевского рассеяния и т.п. Более конкретно, изобретение относится к методам калибровки, которые могут быть полезны при прогнозировании химических и физических свойств на основе наблюдаемых спектральных данных, полученных с помощью спектрофотометра. Еще более конкретно, это изобретение включает уравнения калибровки в ближней инфракрасной области спектра, пригодные для прогнозирования или оценки физических или химических свойств, например, октана.
В публикации в журнале ("J.Sci.Food Agric." 34 (1983) c. 1441-1443) Б.Г. Осборн предлагает использовать уравнение, полученное для калибровки одного типа прибора, для другого прибора.
В статье "Использование косвенной калибровки с многими переменными для контроля качества сельскохозяйственных продуктов с помощью спектроскопии в ближней инфракрасной области", Г. Пучвейн и А.Эйбелгубер (Microchim Acta (Вена), 1986, 11, 43-51) предлагает компьютерную программу для калибровки прибора. Программа отбирает соответствующие значения частоты для спектральных данных для части из серии образцов, с помощью которых осуществляется калибровка прибора, а затем осуществляет подтверждение в отношении остальных образцов.
В статье "Ограничения, существующие в ближней ИК-области спектра, относящиеся к самокалибровке кремниевого фотодиода" Ж.М. Пальмер (SPIE т.499, "Измерения оптического излучения" (1984), стр. 7-14) описывается самокалибровка кремниевых фотодиодных детекторов.
В статье "Простой способ внутренней модуляции для спектральной калибровки спектрометров с круговым переменным фильтром в ближней ИК-области спектра", Чандрасекхар, Ашок, Бхатт и Маньян (Физика инфракрасного излучения, т. 24, N 6, 1984, стр. 571-572) описывают калибровку по длинам волн телескопов, связанных с приборами ИК-излучения ближней области ИК-спектра для астрономических исследований с использованием частотно-зависимого сигнала ртутной дуговой лампы низкого давления.
Марк и Уоркман (Спектроскопия: 311, 28) разработали компьютерный алгоритм с целью нахождения изонумерационных значений длины волны. Изонумерационные значения длины волны представляют собой калибровочные длины волн, которые соответствуют одному и тому же отсчету поглощательной способности на контрольном калибре NIR и подчиненном устройстве NIR. Следовательно эти длины волн фактически не изменяются от одного прибора к другому.
Гекман, Диффи и Милхаус (Analytica Chemica Acta, 192 (1987), 197) предложили компьютерную программу, которая переносит уравнения калибровки путем подсчета поправок на систематическую погрешность и наклон для каждой длины волны в уравнении. Этот способ поправок на систематическую погрешность и наклон действительно используется в примере 3 данной заявки. В патенте США N 4761522 на имя Р.Д. Розентал заявлен политетрафторэтиленовый стандарт для ближнего ИК-излучения и способ изготовления этого стандарта. Однако данный стандарт не используется в переносе калибровки от одного прибора к другому.
В статье "Стандартизация приборов с многими переменными" Уэнга и др. (Anal. Chem., 1991, 63, 2750-2756) описываются четыре способа стандартизации или для корректирования первичной модели калибровки с целью использования на вторичном приборе или для корректирования спектров, полученных на втором приборе, чтобы определить разницы откликов для обоих приборов. Было обнаружено, что модель калибровки, построенная на основе одной группы, может оказаться не применимой для другой группы. Однако с использованием математического аппарата процедуры калибровки с многими переменными были разработаны четыре других метода с целью выбора наилучшего подмножества из имеющихся образцов для переноса калибровки. В числе названных способов известен способ корректирования спектров по способу линейного переноса одной спектральной характеристики по ее интенсивности от одного прибора на такую же характеристику другого. В этом источнике раскрыто использование расчетной зависимой переменной величины, соответствующей нужному физическому свойству и используемой для вывода коэффициентов для постоянных величин во втором уравнении калибровки.
В статье "Калибровка прибора для спектроскопии в ближней ИК-области спектра" (48 Спектроскопии, т. 4, N 4, стр. 48-55) Б.Г. Осборн детально описывает операции для установления простых закономерностей с помощью множественной линейной регрессии, а также использование производных от линейных членов. Обсуждается проверка достоверности калибровочных кривых, в частности как выбираются конкретные значения длин волн для определения членов в уравнениях множественной линейной регрессии, а также статистическая значимость конкретного калибровочного образца. Этот способ может быть использован в данном изобретении с целью определения уравнений калибровки соответственно калибруемого прибора для диапазона значений, в пределах которых может быть осуществлено успешное прогнозирование, т.е. для области, представляющей интерес.
Другие способы определения уравнений калибровки описаны в "Журнале аналитической химии" (т. 60, стр. 1193-1202 (1988)). Д.М. Хааландом и Э.В. Томасом. Представлены способы с использованием обратных наименьших квадратов, частичных наименьших квадратов, традиционных наименьших квадратов и анализ главного компонента регрессии.
В статье "Стандарты поглощения жидкости для ультрафиолетовой, видимой и ближней инфракрасной спектрофотометрии" Р.Г. Мартинека в "J.Am.Med.Technol." (июль-август, 1978, стр. 210-216) представлены стандарты поглощения жидкости, имеющие следующие желаемые характеристики: широкие пики поглощения, широкий диапазон длин волн, высокая молярная поглощательная способность, стабильность в растворе, легко определяемые характеристики чистоты и минимальные спектральные температурные коэффициенты. Целью использования таких стандартов является расчет абсолютной спектральной поглощательной способности на основе наблюдаемой поглощательной способности и использование поправочного коэффициента прибора.
В статье "Использование статистических данных при калибровке и проверке неавтономных анализаторов длинноволнового ИК-излучения" Б.Томпсона, (ISA, 1989, документ # 88-0116) описывается использование ИК-излучения длинноволновой части ИК-спектра для управления технологическим процессом, в том числе с использованием статистики.
Б. Г. Осборн в статье "Калибровка приборов для спектроскопии в длиноволновой части ИК-спектра" ("Спектроскопия", 4(4), с.48-50) описывает необходимость в мультипликативной коррекции рассеивания для твердых образцов, вызванную различием в размерах частиц твердых веществ, и компьютерный перенос комплексных уравнений. Осборн предлагает способы вывода уравнений калибровки для конкретных случаев, пригодные для использования в настоящем изобретении. Обсуждаются выбор соответствующих значений длин волн и образцов и приводятся далее относящиеся к делу статьи, поясняющие применяемую технологию. Описывается перенос уравнений калибровки от одного прибора к другому, при котором для современных приборов требуется только изменение значения захвата, при этом компьютеризованные процедуры учитывают разницу в спектральных данных, получаемых различными приборами. Эти компьютеризованные процедуры не объясняются детально, но, по-видимому, предусматривают преобразование спектральных данных одного прибора так, чтобы они были совместимыми со спектральными данными другого прибора. Это следует различать от того, что предусмотрено настоящим изобретением, согласно которому вместо преобразования спектральных данных соответствующие коэффициенты в уравнении калибровки для второго прибора изменяются в сравнении с коэффициентами, полученными для уравнения калибровки первого прибора в соответствии с новой процедурой, раскрытой в настоящем описании.
В докторской диссертации автора настоящего изобретения, озаглавленной "Хемометрический анализ устройства магнитной обработки воды" (Международный университет микропленок. Отдел диссертаций, N 8919928), обсуждается анализ линейной регрессии (простой и множественной) для построения модели линейной регрессии и преобразования данных, которые могут преобразовывать нелинейные типы данных в данные, подходящие для моделирования линейной регрессии. Представлены определения, устанавливающие степень надежности, согласно которой значение одной переменной величины (зависимой переменной величины) может быть найдено на основе значений для других переменных величин (независимых переменных величин). В принципе способы определения постоянных регрессии (или коэффициентов) для уравнений калибровки, обсуждаемых в упомянутой докторской диссертации, используются для выведения уравнения калибровки для первого или эталонного прибора в настоящем изобретении.
В статье "Новый подход к выявлению переносимых способов калибровки для количественной спектроскопии в ближней инфракрасной области спектра" (Спектроскопия, т. 3, N 11, с. 28-36, авторов Х. Марка и Д. Уоркмана) показано, что применяемость характеристик прибора осложняет перенос калибровочных данных между приборами. Однако путем выбора длин волн и соответствующих спектральных свойств для таких длин волн, так чтобы они удовлетворяли определенному критерию, можно добиться того, что некоторые отличия между приборами не приведут к существенному изменению калибровочного уравнения, полученного для одного прибора, при описании с его помощью работы другого прибора. Однако не описывается, каким образом сделать так, чтобы уравнение калибровки одного прибора было пригодно для использования в другом приоре, когда имеются существенные изменения в уравнении калибровки, пригодном для применения второго прибора.
Р.А. Гекман, Д.Т. Диффи, Л.А. Милхаус в статье "Компоненты табака, соотнесенные к приборам с отклоняющим фильтром" (Analytica Chem. Acta, 192 (1987), с. 197-203) описывают перенос монохроматической калибровки в ближней инфракрасной области для компонентов табака на прибор с отклоняющим фильтром с целью использования экспериментального уравнения калибровки для чувствительного, но не прочного лабораторного прибора с целью анализа данных в приборе, предназначенном для продукции, не требующей большой точности, чтобы прогнозировать такие свойства, как влажность, содержание глицерина, пропилен гликоля, никотина и восстанавливающего сахара. Программа под названием MTRAN не может быть непосредственно использована, пока тщательно не будет проверено, что прибор с отклоняющим фильтром снабжен соответствующими фильтрами так, чтобы он соответствовал длинам волн в первичном или эталонном уравнении калибровки лабораторного прибора. Следовательно, прежде чем можно будет преобразовать первичное уравнение калибровки, файлы монохроматических данных сжимается для моделирования условий в приборе с отклоняющим фильтром. Файл полученных данных используется для восстановления уравнения калибровки. С указанными изменениями может быть использована программа CALTRAN, которая раньше использовалась только для переноса калибровки между фильтровыми приборами с целью осуществления переноса от монохроматического прибора ближнего инфракрасного излучения к прибору с отклоняющим фильтром.
В типовом случае известные способы направлены на изменение наблюдаемых спектров (или их математического преобразования), полученных одним прибором, в соответствии с изменениями, полученными отградуированным эталонным прибором. Только после того, как спектры от некалиброванного прибора совпадут со спектрами от калиброванного прибора, можно искать пути переноса уравнения калибровки от одного прибора к другому. Опыт показывает, что при этом имеет место тенденция к возникновению ошибок, неопределенности и многочисленных вычислительных проблем, которые осложняют пользование и снижают точность, тогда как изобретение позволяет избежать этого.
Патент США N 4963745 на имя Маггарда, озаглавленный "Способ и устройство для измерения октана", раскрывает, как первоначально вывести уравнение калибровки для эталонного прибора. Конкретно описывается то, что спектральные признаки, такие как вторые производные, инфракрасных спектральных данных на частотах метиловой полосы в диапазоне около 1200-1236 нанометров (нм), значительно коррелированы с октановыми значениями для газолиноподобных веществ. В описании упомянуты многочисленные патенты и статьи в качестве ссылок, а также другие публикации, которые, включая специально упомянутые, приводятся в данном случае конкретно в виде ссылок.
Пример линейного уравнения калибровки имеет вид ϒ
Откалиброванный спектрометр может косвенно определять физическое или химическое свойство образца на основе спектральных откликов, измеренных спектрометром по отношению к конкретному образцу. Изобретение относится к способу калибровки или повторной калибровки первого спектрометра в зависимости от второго спектрометра или самого себя соответственно. При калибровке используются определенный выбор и обработка спектральных данных, полученных как от первого, так и от второго прибора. При повторной калибровке первого прибора используются определенный выбор и обработка спектральных данных от одного и того же первого прибора, полученными как до, так и после возникновения необходимости повторной калибровки первого выбора. Вместо модифицирования соответствующих характеристик первого и второго приборов или первого прибора до и после возникновения необходимости в калибровке первого прибора данное изобретение позволяет модифицировать уравнение калибровки второго или повторно откалиброванного прибора с целью получения результатов, совместимых с результатами, полученными первым прибором для того, как он выйдет из калиброванного состояния. Уравнение калибровки представляет собой уравнение, которое преобразует спектральные данные конкретного образца для множества длин волн для получения расчетного значения для какого-либо химического или химического свойства. Обычно такие уравнения калибровки имеют вид линейной комбинации значений спектральной поглощательной способности или математических преобразований значений поглощательной способности, измеренной первым и вторым приборами для каждого образца. Неожиданным результатом, подтвержденным статистически, оказалось сохранение точности калиброванного или повторно калиброванного прибора, а в некоторых случаях даже повышение этой точности.
Предлагаемые на сегодняшнем рынке приборы используют необработанные спектральные данные и преобразуют их в цифровую форму или формируют представляющий их аналоговый сигнал для использования при выполнении расчетов. Как основной этап в таких расчетах, уравнение калибровки вместе с этим сигналом определяет зависимую переменную величину. Зависимая переменная величина или равна значению, или указывает на значение какого-либо физического или химического свойства материала, необработанные спектральные данные которого измеряются. Соответствующее конкретному прибору уравнение калибровки будет изменяться в зависимости от изменений в спектрометре, который выдает необработанные спектральные данные. Чтобы калибровать спектрометр, определяют соответствующее уравнение калибровки, которое вместе с сигнальным представлением необработанных данных спектра, измеренных спектрометром для некоторого материала, должно определять для значения своей зависимой переменной значение или равное, или индуцирующее какое-либо физическое или химическое свойство измеряемого материала. На практике изменения в таком уравнении непосредственно связаны с изменениями в константах, входящих в такое уравнение. Настоящее изобретение направлено частично на то, как определить эти константы для неоткалиброванного прибора с помощью откалиброванного прибора и его уравнения калибровки. Как только такие постоянные величины определены, находится новое или перенесенное на новый прибор уравнение калибровки, которое может быть использовано совместно с преобразованным в цифровую форму сигналом или аналоговым сигналом, представляющим необработанные данные спектра, измеренные с помощью ранее неоткалиброванного прибора.
Например, если нужно определить уравнение калибровки для второго прибора (т.е. уравнение-2 калибровка для прибора-2) с помощью откалиброванного первого прибора и соответствующего ему уравнения калибровки (т.е. прибора-1 и уравнения-1), то операции, осуществляемые для достижения этого в соответствии с изобретением, включают:
а) определение из уравнения-1 калибровки значения, показательного для каждой зависимой переменной-1, соответствующей каждому члену калибровочного множества, основываясь на спектральных данных-1 для каждого члена упомянутого калибровочного множества, измеренных с помощью прибора-1, и
б) определение постоянных величин-2 в упомянутом уравнении-2 калибровки так, чтобы сумма абсолютных разниц между:
(1) упомянутым значением, показательным для каждой зависимой переменной-2 для каждого члена упомянутого множества на основе уравнения-2 калибровки и данных-2, соответствующих каждому члену, и
(2) тем соответствующим значением зависимой переменной-1, вычисленным для каждого члена на основе уравнения-1 калибровки и данных-1, соответствующих каждому члену, была минимальной.
Изобретение решает проблему, как использовать результаты калибровки одного прибора для калибровки другого прибора. Кроме того, изобретение может использоваться для повторной калибровки прибора с целью обеспечения совместимых результатов после того, как было некоторое изменение в спектральном отклике прибора, что имеет место при изменении источников света, например, при замене перегоревших ламп накаливания или из-за новых соединений, используемых для сбора данных от разных источников, таких как изменения в волоконной оптике, используемой для передачи света или электромагнитного излучения от одного места в другое, изменения длины пробега или изменения в спектроскопическом режиме, например, от прозрачности до отражения.
Изобретение в широком смысле относится к калибровке нового прибора с помощью эталонного прибора, также представлен способ постоянного контроля за прибором, чтобы с уверенностью отметить, что он не изменился настолько, что необходимо вывести новое уравнение калибровки с целью получения надежного прогнозирования для какого-либо физического или химического свойства исследуемого материала.
Изобретение описывает способы косвенного определения множества свойств-p, таких как содержание цетана, октана, ароматического нафтенолифина, коэффициент вязкости, молекулярный вес и многие другие, с помощью спектроскопических данных. Подразумевается, что спектральные данные широко включают, но не ограничиваются этим, всю интенсивность в сравнении с волновыми спектрами, которые возникают тогда, когда свет, широко захватывая обширный дипазон частот, например, от радиочастот до ультрафиолета, взаимодействует с материалом. В принципе любые спектральные признаки (как определено в этом описании), получаемые из спектральных данных, которые могут сопоставляться с целью прогнозирования значений для какого-либо определенного прямо или косвенно химического или физического свойства, входят в объем изобретения.
Некоторые из преимуществ, обеспечиваемых изобретением, заключаются в следующем:
1. Требуется только небольшое число образцов (по сравнению с числом образцов, используемых при первоначальной калибровке эталонного прибора) для определения уравнения калибровки для неоткалиброванного прибора ввиду возможности использования уравнения калибровки эталонного прибора. В примере 7 показано, что может быть использована небольшая калибровочная выборка, состоящая всего лишь из четырех элементов.
2. Калибровочное множество, выборка-с, не должно содержать каких-либо нестабильных элементов, которые могут включаться в первоначальное калибровочное множество выборок, и предпочтительно, в случае со смесями, такими как газолин или другое нефтяное топливо, может содержать незначительное их количество в виде чистых молекул или легко приготавливаемых их смесей.
Ограничение на соответствующие элементы выборки-с при определении уравнения калибровки для неотградуированного прибора на основе его спектральных откликов зависит частично от выбранной для этих данных статистической обработки. Для множественных линейных регрессий число элементов выборки-с должно быть по меньшей мере на 1 элемент больше, чем число длин волн (независимые переменны), используемых в модели, если не применяется поправка на систематическую погрешность и наклон или другая уменьшающая погрешность процедура. Например, для переноса уравнения калибровки с тремя независимыми переменными должно быть использовано по меньшей мере четыре образца.
Было обнаружено, что в дополнение к поправке на систематическую погрешность и отклонение могут быть использованы другие операции, уменьшающие погрешность, например, с использованием наименьших квадратов, обобщенной наименьшей суммы, и некоторых других приемов, которые могут еще больше уменьшить любую оставшуюся погрешность в полученном уравнении-2 калибровки.
Предпочтительно для того, чтобы эталонное множество (выборка-с) могло быть использовано для переноса дисперсии, ковариации или функции, полученной из дисперсии для откалиброванного прибора, на неоткалиброванный прибор или на тот же самый прибор к более позднему моменту времени выборка-с должна раскрывать спектральные признаки, которые изменяются по мере изменения прибора. В целях этого изобретения выборка-с должна быть определена таким образом, чтобы значения спектральных поглощательных характеристик показывали изменения на длинах волн, представляющих интерес, когда имеют место изменения в рабочих характеристиках прибора, но выборка должна оставаться постоянной (в пределах инструментальных погрешностей), когда прибор функционирует в стандартных или типовых условиях.
Особое применение одного из решений, вытекающего из настоящего изобретения, заключается в калибровке спектрофотометра ИК-излучения ближней ИК-области с помощью использования результатов, полученных от полностью или частично откалиброванного эталонного спектрофотометра ближней ИК-области излучения. В настоящем описании ссылки будут даваться на один или более спектрофотометров. Полностью или частично откалиброванный спектрофотометр или другой прибор, который будет называться здесь "эталонным прибором" или "эталонным спектрофотометром", характеризуется уравнением калибровки, которое полностью или частично определено. Прибор, который должен быть калиброван относительно эталонного прибора, будет называться здесь как "неоткалиброванный прибор" или "неоткалиброванный спектрофотометр". Эталонный прибор может стать неоткалиброванным или выйти из калиброванного состояния в результате различных изменений в самом приборе или связей между прибором и источником, от которого он получает измеренные или спектральные данные.
Изобретение обеспечивает калибровку неоткалиброванного спектрофотометра по отношению к эталонному спектрофотометру с помощью значительно меньшего множества выборок для калибровки, чем это было необходимо для полного определения уравнения калибровки для эталонного спектрофотометра в самом начале. Множество выборки для калибровки здесь названо " множеством выборки-с" или просто "выборкой-с". С целью определения уравнения калибровки для подсчета октана, ароматических соединений, олефинов, полиолов, гидроксильного числа и т.д. для прибора ближнего ИК-излучения используются такие системы, как модель 6500 NIR Systems, модель 1200 IT Jndustree, модель серии 300 Guided Wave, инфралайзер Bran-Luebbe или инфрапрувер, приблизительно 200 смесей. К несчастью, так как газолины являются смесями, содержащими компоненты с разной летучестью, то очень трудно, иногда невозможно, хранить такие образцы для обработки на неоткалиброванном спектрофотометре до более позднего срока. Другими словами, используемые для калибровки эталонного спектрофотометра образцы должны быть пригодными. Использование других материалов, не тех, которые применялись для калибровки эталонного спектрофотометра, увеличивает трудность калибровки неоткалиброванного спектрофотометра, так как каждый член множества выборки-с из приблизительно двухсот образцов должен иметь октановое число или антидетонационную характеристику, определенные в соответствии с ASTMD2699 и D2700 или т.п. Процедура определения октановых чисел требует длительного времени и множества операций на одном и том же образце с различными двигателями, прежде чем будут получены надежные результаты антидетонационных характеристик.
Из уровня техники неизвестно, могут ли быть отобраны для множества выборки-с компоненты наподобие чистого газолина, например особые молекулы углеводорода, которые легко воспроизводятся. Авторами настоящего изобретения было обнаружено применительно к ближнему инфракрасному излучению с длинами волн в диапазоне 800 - 2500 нм, что множество выборки-с, включающее в качестве образцов: бензол, метил t-бутилэфир, изо-октан, n-декан, I-октен, 2,3,4-триметилпентан, n-гептан, циклогексан, n-гексан или толуол, при измерении как на эталонном приборе, так и на неоткалиброванном приборе с целью получения спектральных данных от каждого прибора, может предоставить достаточно данных или информации для того, чтобы откалибровать неоткалиброванный прибор. Для данного описания откалиброванный прибор - это такой прибор, который представляет стабильные и воспроизводимые спектральные характеристики и имеет уравнение калибровки, с помощью которого могут быть получены необходимые значения физических или химических свойств образца с точностью, равной или превосходящей точность прямого способа испытания (например, ASTM), с целью определения такого химического или физического свойства.
В самом широком смысле, чтобы перенести уравнение калибровки для октана, могут быть использованы любые соединения, активные в ближней ИК-области спектра, т. е. поглощают ближнее инфракрасное излучение в диапазоне 800 - 2500 нм. Примерами таких соединений могут служит: n-парафины, изо-парафины, ароматические соединения (такие, как дихлорбензол или бензол), спирты (такие, как метанол или этанол), олефины (такие, как I-октен), галогенезированные алканы (такие, как трихлорэтан), кетоны (такие, как метил-этил-кетон), простые эфиры (такие, как метил- t-бутилэфир), сложные эфиры (такие, как амилацетат) и нафтены (такие, как циклогексан и метил-циклогексан). В данном описании и формуле изобретения стандартная погрешность расчета или прогнозирования составляют 68% доверительной границы, если нет другого указания. Каждая погрешность соответственно названа здесь "СПР" или "СПП".
Уравнение калибровки для конкретного прибора прогнозирует физическое или химическое свойство на основе спектральных откликов или спектральных данных. При измерении октановых чисел конкретные спектральные отклики или математические преобразования, соответствующие значениям спектральных признаков, выбираемых для прогнозирования октановых чисел для конкретного образца, детально они описаны в патенте США N 4963745. Уравнение, предпочтительно, является линейным, но могут быть также использованы нелинейные уравнения.
Спектральные признаки функционально связаны со спектральными данными, в функции каждая спектральная отличительная характеристика определяется единственно с помощью таких спектральных данных. Примером таких функциональных связей являются математические преобразования, такие как производные первого, второго и более высокого порядка; анализ Фурье, позволяющий определить частотные компоненты и их вклад; дифференцирование спектров; интегрирование по сегментам и т.п. Единственным ограничением при выборе таких функциональных связей или математических преобразований является то, что любые значения, полученные в применении их к спектральным данным, должны быть коррелируемыми как независимые переменные для точного определения значения для зависимой переменной в уравнении калибровки, которая соответствует прямо или косвенно значению физического или химического свойства.
При детальном обсуждении изобретения получены следующие определения. Для данной заявки "функция" представляет собой соответствие, которое связывает с каждым множеством значений для множества независимых переменных, единственное значение зависимой переменной. В соответствии с этим определением "уравнение калибровки" в данном изобретение представляет собой функцию, которая устанавливает соответствие между независимыми переменными, значения которых определяются спектральными признаками и зависимой переменной, которая соответствует значению для какого-либо химического и физического свойства. Любая функция, которая определяет значения для спектрального признака, которые однозначно связаны со спектральными данными или могут быть использованы в уравнении калибровки, входит в объем данного изобретения. Спектральные данные однозначно определяются по результатам измеренных спектральных откликов материала по отношению к электромагнитному излучению. Примеры электромагнитного излучения обсуждены в других частях данной спецификации. Из уровня техники известны функции, которые могут быть использованы для определения производных значений для спектральных признаков, исходя из спектральных данных. Если существует уравнение калибровки, которое содержит независимые переменные, эквивалентные спектральным признакам, определенным функцией, то отсутствуют ограничения на конкретные спектральные признаки или функции для спектральных данных, которые определяют спектральные признаки, которые могут быть использованы в данном изобретении.
Для данного описания и формулы изобретения "уравнение калибровки" обозначает уравнение, которое прогнозирует прямо или косвенно, например, путем функциональной связи количественную оценку химического или физического свойства (зависимую переменную) на основе одного или более спектральных признаков (независимых переменных) и, возможно, некоторые другие параметры, например температуру.
Модель регрессии для ИК-излучения ближней ИК-области спектра для измерений октановых значений в газолине, который содержит МТВЕ, была опубликована в книге трудов Американского химического общества, отдела топливной химии, т. 35, N 1, с. 266-275, написанной Стивеном М.Маггардом и представленной им же на 199-й конференции Американского национального химического общества в Бостоне, Массачусетс, 22-27 апреля 1990 г. В этом документе специально описано и представлено использование комбинационных полос метина t-бутила, включая цветовые тона, в модулях с целью прогнозирования октанов газолиновых соединений, содержащих МТВЕ.
В данной заявке "спектральные признаки" означают спектральную способность, прозрачность, отражательную способность (диффузное отражение, зеркальное, полное, ослабленное и т.д.), эмиссию, флуоресценцию, фосфоресценцию или трансфлектанцию, или их математические функции, такие как производные, отношения, преобразования Фурье и отличия для ультрафиолетовой части спектра, видимой части, ближней инфракрасной, средней инфракрасной, дальней инфракрасной, микроволнового или электромагнитного радиочастотного излучения.
В тексте описания упоминается использование производных от данных спектральной поглощательной способности. Будет показан пример того, что имеется в виду под термином "производная". Логика, используемая для взятия производной от данных спектральной поглощательной способности, основана на вычислении конечных разностей, так как упомянутые данные определены через регулярно расположенные интервалы, и между этими интервалами они прерывны.
Могут быть использованы спектральные данные поглощательной способности, собранные с использованием систем NIROL-6500. OL-6500 имеет спектральную полосу пропускания около 9 нм, но спектральные данные преобразованы в цифровую форму таким образом, что записанные данные отображаются с интервалами в 2 нм. В общем случае могут изменяться два элемента, когда вычисляется производная в точке, первый из них определяет сегмент, а второй - промежуток. Сегмент определяет число точек, которые используются для расчета среднего числа вправо и влево от точки, в которой вычисляется производная. С другой стороны, промежуток обозначает число точек около средней точки (непосредственно прилегающей к точке, где берется значение производной), которые исключаются из расчетов соседних сегментов (хотя общая длина сегмента не изменяется). Если обозначить среднее значение сегмента (с более высокими длинами волн) выше точки, где берется производная, точкой A, а среднее значение сегмента ниже точки, где берется производная, точкой B, тогда в соответствии с вычислением конечных разностей, первая производная в точке равна A минус B.
Например, когда сегмент равен 10 с приращениями 2 нм на сегменты, а промежуток равен 0, первая производная спектральной поглощательной способности (d1A/dw) при 1170 нм подсчитывается следующим образом:
d1A/dw1170= { (A1172+A1174+A1176+ A1178+A1180)/5} -{(A1168+A1166+A1164+ A1162+A1160)/5}
Если сегмент изменяется до 6, а промежуток - до 8, первая производная имеет вид:
d1A/dw1170={(A1176+A1178+A1180)/3}- {(A1164+A1162+A1160)/3}
Обычно для данных, полученных через интервалы, равные 2 нм, первая производная спектральной поглощательной способности при длине волны x равна:
d1A/dwx= Σi(A(x+(промежуток/2)+2i)/(сегмент/2)
- Σi(A(x+(промежуток/2)+2i)/(сегмент/2)
где x - длина волны в нанометрах, например, 1170 и i = от 1 до сегмент/2.
В пакете программ систем NIR, NSAS (пакет программ спектрального анализа ближнего ИК-излучения, NIR Systems, Inc.) по известным причинам приведенное выше уравнение строго действительно только для сегментов 2, 6, 10, 14, 18 и т. д. и для промежутков 0, 4, 8, 12, 16 и т.д. Сегмент 0 обрабатывается как сегмент 2. Точно так же сегмент 4 обрабатывается как 6 и т.д. Точно так же промежуток 6 обрабатывается как промежуток 0, а промежуток 6 - как промежуток 4 и т.д.
Производные более высокого порядка могут быть упрощены до выражений, включающих только члены первой производной, и решены по форме предыдущего уравнения. В общем случае, если порядок производной равен h, то искомая производная равна:
dhA/dwx=dh-1A/dw(x+{ (сегмент +пром ежуток)/2} +1)-dh-1A/dw(x-{ (сегмент+ пром ежуток)/2}-1)
где промежуток равен промежутку производной порядка h, а сегмент, используемый для подсчета производной порядка h-1, является таким же, как искомое значение для производной порядка h.
Например, четвертая производная 1170 нм при сегменте 10 и промежутке 4 равна:
d4A/dw1170=d3A/dw1178- d3A/dw1162
=(d2A/dw1186 - d2A/dw1170) - (d2A/dw1170 - d2A/dw1154)
= {(d1A/dw1194 - d1A/dw1178) - (d1A/dw1178 - d1A/dw1162)} - {(d1A/dw1178 - d1A/dw1162) - (d1A/dw1162-d1A/dw1146)
= { { [((A1198+A1200+. . . +A1206)/5) - ((A1190+A1188+...+A1182)/5)]- [((A1182+A1184+...+A1190)/5)- ((A1174+A1172+...+A1166)/5)]}- { [((A1182+A1184+...+A1190)/5)- ((A1174+A1172+...+A1166)/5)]- [((A1166+A1168+. ..+A1174)/5)- ((A1158+A1156+...+A1150)/5)]}}- {{[((A1182+A1184+... +A1190)/5)- ((A1174+A1172+. . .+A1166)/5)]}- {[((A1166+A1168+...+A1174)/5)- ((A1158+A1156+...+A1150)/5)]- {[((A1166+A1168+...+A1174)/5)- ((A1158+A1156+. ..+A1150)/5)]- [((A1150+A1152+...+A1158)/5)- ((A1142+A1140+...+A1134)/5]}}
где все производные более низкого порядка также взяты с использованием сегмента 10 и промежутка 4. Следует отметить, что необходимо корректировать сегмент и промежуток до действительного значения прежде, чем применить одну из обобщенных формул (например, четвертая производная сегмента 8 и промежутка 6 корректируется до сегмента 10 и промежутка 4 до применения формулы).
Следует отметить, что использовались сегменты по 2 нм, но могут быть использованы сегменты с меньшим или большим числом нм или равные частям нм. Предпочтительно выбор зависит от степени спектральной разрешающей способности, обеспечиваемой спектрометром.
Представлены примеры дифференциалов, конечных дифференциалов, но может быть принят один из многих типов конечных дифференциалов. Все доступные для использования способы фактически основаны на одной теории, однако конкретные детали вычислений могут до некоторой степени изменяться. Также необходимо отметить, что хотя обсуждаются конечные дифференциалы, возможно, что могут быть также использованы дифференциалы с разницами, приближающимися к нулю, а не к некоторому конечному числу. Например, может быть использован полиномиальный степенной ряд, такой как ряд Тейлора, основанный на ряде точек кривых зависимости интенсивности от длины волны или спектральных данных.
Это изобретение описывает средство для определения уравнения калибровки для первичного прибора, которое использует значительный объем ранее проделанной работы для получения уравнения калибровки для эталонного спектрофотометра. Действительно, первый прибор может быть эталонным спектрофотометром, который вышел из калибровочного состояния по уже названным причинам.
Чтобы легче понять описание, должны быть приняты следующие условия. Независимые переменные величины, соответствующие уравнению калибровки для первого прибора, будут обозначены -i или -I, например, независимая переменная-i или независимая переменная-I соответствует одному или нескольким членам множества независимых переменных в уравнении калибровки, уравнении-i калибровки или урвнении-I калибровки, соответственно для первого прибора, называемого здесь прибором-i или прибором-I. В большинстве примеров используются три длины волны, каждая из которых названа длина-i волны, из которых с помощью функции получены три независимых переменных-i на основе спектральных признаков выборки-c. Соответственно конкретному множеству независимых переменных-i существует зависимая переменная, названная здесь как зависимая переменная-i. Значение зависимой переменной-i обычно будет равно прогнозируемому значению свойства-p выборки-c. Зависимая переменная-i соответствует зависимой переменной, найденной в уравнении-i калибровки. Постоянные величины в уравнении-i калибровки названы здесь как константы-i. Существуют два различных вида констант-i. Один соответствует константе-i крутизны, а другой - константе-i смещения. Константы-i крутизны представляют собой коэффициенты независимых переменных-i. Ясно, что существует константа-i крутизны для каждой независимой переменной-i, которая в свою очередь зависит от числа длин-j волн, входящих в уравнение-i градуирования. Существует только одна константа-i смещения, которая не является коэффициентом какой-либо независимой переменной-i.
При определении уравнения калибровки для прибора-k (названного также прибором-2) с помощью уравнения калибровки для прибора-i главным образом определяется новое множество констант уравнения калибровки, которые соответствуют константам-k. Новые значения констант определяются по меньшей мере за один или, предпочтительно, за два этапа с учетом того, что уже имеется уравнение-i калибровки, выведенное для прибора-i.
Для успешного переноса или модификации уравнения-i калибровки в уравнении-k калибровки значения СПР или СПП для свойства-p, основанные на спектральных данных прибора-k или прибора-2 посредством уравнения-k калибровки или уравнения-2 калибровки, должны быть фактически такими же точными, как и значения, полученные прибором-i и уравнением-i калибровки или альтернативно должны быть такими же точными, как и значения, которые могли бы быть получены в том случае, если прибор-k откалиброван таким же образом, как и прибор-i, но в большинстве случаев они должны быть по меньшей мере равны или лучше, чем СПР для первичного способа испытания для непосредственного измерения значений для определения свойства-p, используемого для калибровки прибора-i. Данное изобретение обеспечивает преимущество, которое заключается в том, что число образцов, необходимых для обработки или прибором-i, или прибором-k, или обоими, оказывается значительно меньше, чем число образцов, необходимых для получения надежного уравнения калибровки для прибора-i или для полной калибровки прибора-k таким же образом, как и прибора-i. Другими словами, в любом случае значение E(k) в стандартной погрешности прогнозирование значения для определения свойства-p с помощью прибора-k и уравнения-k калибровки не должно существенно превышать значение стандартной погрешности прогнозирования, полученное в результате определения значений для свойства-p прямым или первичным способом испытания, первоначально использованном для калибровки прибора-i.
Одним, хотя и не единственным способом переноса уравнения-i калибровки на прибор-k является изменение констант уравнения-i калибровки. Эти измененные константы становятся константами-k. Предпочтительно уравнение-i калибровки превращается в уравнение-k калибровки в два этапа. Оптимальным является этап 2 (приведен ниже), но он предпочитается в зависимости от того, значительной ли является поправка, указанная этапом 2. Под символом "значительный" подразумевается, что полученное значение дисперсии в прогнозируемых значениях не превышает более, чем на 10%, значения СПР или СПП в зависимости от того, какое из них больше, определенные с помощью уравнения-k калибровки без этапа 2.
Этап I: определение уравнения-k калибровки (уравнения-2 калибровки) с помощью уравнения-i калибровки (уравнения-1 калибровки) включает следующие подэтапы:
(а) Определить уравнение-i калибровки путем измерения зависимых переменных-i непосредственно с помощью первичного способа испытания со стандартной погрешностью расчета E и корреляции данной зависимой переменной-i c множеством независимых переменных-i. Множество независимых переменных-i может состоять из одного или более элементов.
(б) Получить соответственно прибором-i и прибором-k спектральные данные-i и спектральные данные-k, соответственно для каждого элемента выборки-c, которые должны быть использованы на этапе (в) (включающем по меньшей мере один элемент с), определить с помощью функции значение-k и значение-i, соответственно (равные соответственно каждому спектральному признаку-k и -i) для каждого элемента выборки-c, соответствующего каждой независимой переменной-k и -i соответственно.
(в) Определить (в соответствии с уравнением-i калибровки) значение для данной зависимой переменной-i для каждого элемента выборки-c. Значение, определенное для зависимой переменной-i, или значение, определенной с помощью какой-то функции-f с использованием этого значения, определенного для зависимой переменной-i, вводится в уравнение-k калибровки для значения зависимой переменной-k в уравнении-k калибровки. Также вводятся в уравнение-k калибровки значения спектральных признаков-k, найденные для каждого элемента выборки-c. (Напомним, что спектральные признаки-k определяются функционально с помощью спектральных данных-k, определенных посредством замеров, выполненных прибором-k по каждому элементу выборки-c. Следовательно единственными неизвестными в уравнении-k калибровки будут константы-k). Значения для констант-k, которые должны будут подставлены в уравнение-k калибровки, образуют в результате уравнение-k калибровки, при этом сумма всех абсолютных разниц между каждым определенным значением свойства-p для образца с, соответствующим зависимой переменной-k для образца c, и определенным значением свойства-p для выборки-c, соответствующим зависимой переменной-i для выборки-c, сведена к минимуму так, что значения для свойства-p для выборки-U, величины которых для свойства-p не выходят за требуемые пределы, получаются на основе выведенного уравнения-k калибровки, причем СПП фактически не превышает значение СПР или СПП для E при определении зависимой переменной-i непосредственно с помощью какого-либо первичного способа испытания. Как только определены константы-k, что позволяет получить как следствие значение зависимых переменных-k для элементов выборки-c, имея значения для свойства-p в требуемых пределах, в пределах СПР или СПП для E при прямом или первичном способе испытания, получается уравнение-k калибровки в свете предшествующего уравнения-i калибровки. Абсолютная разность представляет собой значение разности между двумя числами, полученными в результате первого возведения в квадрат и взятия положительного квадратного корня. (Напомним, что прибор-k, первый прибор, может на деле быть эталонным прибором, который вышел из калибровочного состояния, или может быть фактически совершенно другим прибором).
Значение для зависимой переменной-i, которое должно быть подставлено в уравнении-k калибровки для зависимой переменной-k, может быть функционально связано с зависимой переменной-i с помощью функции-f такой, как, например, логарифм (log) при любом основании (например, натуральный или десятичный), такой, как ϒ
Диапазон требуемых значений ϒ
Для ясности, если ϒ
Ak= nA
где
A
B
Другими словами, какими бы ни были значения для n и m зависимая переменная -k будет функционально связана с зависимой переменной-i. Для определения значения для соответствующего физического или химического свойства, измеряемого непосредственно, нужно просто осуществить инверсное преобразование от ϒ
Прибор-k и его спектральные данные используются в этом изобретении, если прибор-k может быть откалиброван идентичным способом до такого прибора, который может быть использован для успешной калибровки прибора-i.
Предпочтительно уравнение-i и уравнение-k калибровки являются линейными. В обсужденном выше обобщенном способе для настоящего изобретения нет необходимости в том, чтобы оба уравнения-i и -k были одного и того же вида или оба были линейными. Под одной и той же формой подразумевается одна и та же функциональная зависимость от одного и того же числа независимых переменных с соответствующими константами, определяющими зависимую переменную.
Предпочтительно уравнения градуирования для прибора-i и прибора-k имеют следующую линейную форму: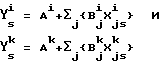
где
ϒ
Ak и Ai - каждое является соответственно константами-i и -k пересечения или смещения в уравнениях-i и -k калибровки;
X
B
Может быть бесконечное множество способов подстановки значений для констант-k, которые приводят к уравнению-k калибровки с значением СПР, фактически не превышающим значение СПР или СПП, обязательно присутствующее в прямом способе, используемом в некоторой точке для получения прямо или косвенно уравнения-i калибровки. Под "фактически не превышающим" значением подразумевается на 30% больше, предпочтительно на 20% больше и наиболее предпочтительно на 10% больше. Прямо определенные значения свойства-p должны быть по меньшей мере один раз получены с помощью какого-либо первичного или прямого способа испытания с целью калибровки прибора путем определения его уравнения калибровки для прогнозирования значений физического или химического свойства, свойства-p, для ряда материалов на основе спектральных данных для таких материалов. Однако, как только откалиброван первый прибор, его можно использовать для калибровки других приборов без необходимости повторного измерения свойства-p с помощью первичного способа испытания. Прибор-i имеет прямо определенное уравнение-i калибровки, если некоторые или все константы-i в нем определены с помощью значений, непосредственно найденных в результате первичного способа испытания. Однако, если только используемые для определения констант-k значения получаются на основе прогнозирования ранее откалиброванным прибором значений без учета значений от первичного способа испытания для свойства-p, в таком случае прибор-k калибруется косвенным образом. Во всех случаях будет по меньшей мере один прибор, уравнение калибровки которого определено первично на основе значений для его зависимой переменной, определенной посредством первичного способа испытания. Выше упоминалось о СПР или СПП этого первичного способа испытания.
Однако обнаружено, что особенно приемлемыми для определения констант-k являются следующие критерии, принимая во внимание, что уравнения-k и -i калибровки имеют линейную форму, как отмечалось выше. Согласно одному критерию требуется, чтобы соответствующие B
Альтернативно могут быть использованы значения B
B
и
Ak= Σc(ϒ
где
n = числу элементов выборки-c.
В конечном итоге также найден особенно приемлемый критерий для определения констант-k, соответствующих B
B
и
Ak= Σc(ϒ
где
n = числу элементов выборки-c.
Этап 2 влечет за собой поправку на крутизну и смещение. Требования для образцов относительно поправки на крутизну и смещение обсуждаются в примерах. Главным образом поправка на крутизну и смещение получается из определения значений для "m" и "b", которые удовлетворяют следующему выражению: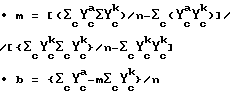
где
ϒ
n - число элементов выборки-p;
v - стандартная погрешность расчета от использования значений уравнения-k калибровки с целью определения зависимой переменной-k для элемента выборки, c, причем v незначительно превышает E.
Подставим указанные значения для m и b в следующее выражение, в результате чего получим упрощенное уравнение калибровки для зависимой переменной-k для прибора-k, которое имеет вид:
ϒ
В некоторых случаях этап 2 может быть опущен ввиду того, что поправка, предполагаемая или требуемая при использовании поправки на крутизну или смещение, не вызывает значительного изменения константы-k для уравнения-k калибровки. Но предпочтительно осуществлять этапы в соответствии с поправкой на крутизну и смещение для того, чтобы определить существует или нет значительная поправка. В большинстве случаев обнаружено, что поправка на крутизну и смещение необходима.
Относительно этапа 2 следует отметить, что когда используется поправка на крутизну или смещение, даже значительное изменение в значениях константы-k, требуемое поправкой или из-за поправки, не означает, что при осуществлении этапа 1 была совершена ошибка, Обнаружено, что ошибка, если она имеет место, на этапе 1 фактически корректируются поправкой на крутизну или смещение и наоборот (см. пример 1). Более того обнаружено, что требуемое для реализации поправки на крутизну и смещение число образцов даже если их добавить к образцам, необходимым для проведения этапа 1, гораздо меньше, чем их необходимо для определения уравнения-i градуирования для прибора-i. Это представляется совершенно неожиданным и это нельзя предвидеть заранее. Действительно, когда поправка на крутизну указывает на значительную поправку в константах, известные из уровня техники способы (см. спектральный анализ ближнего ИК-излучения, опубл. NIR Systems, Inc., Silver Spring, Maryland, 1989) предписывают, что необходимо заново откалибровать прибор-k таким же способом, который использовался для первоначальной калибровки прибора-i.
Интерес представляет более детальный анализ того, что происходит с константами-k в уравнении-k калибровки при осуществлении этапа 1 или 2. На этапе 1 каждая константа изменяется по существу независимо, чтобы удовлетворять множеству числовых критериев, указанных выше. На этапе 2 константы смещения изменяются все вместе на величину, определяемую как "m". Константа-k пересечения испытывает влияние как со стороны m, так и со стороны величины приращения b. Когда они применяются вместе, уравнение-k калибровки для прибора-k предпочтительно дает возможность определить значение СПП для зависимой переменной-k, которое оказывается точнее, и часто намного лучше, чем значение, полученное из уравнения-i калибровки с использованием данных, измеренных прибором-i или по меньшей мере СПП, которые являются равными значению E или точнее, чем это значение, при этом берется значение СПП для прямого способа испытания с целью определения величин, используемых для калибровки прибора-i. Показанный в примерах этот результат является полностью неожиданным.
Это изобретение описывает также косвенный способ определения свойства-p для выборки-u с использованием спектральных данных-k, измеренных с помощью прибора-k, дающий возможность определить такие спектральные данные-k для выборки-u. Хотя известны многие способы идентифицирования уравнения калибровки прибора, но до настоящего времени они не обеспечивали возможности простого преобразования уравнения-i калибровки, соответствующего прибору-i, в уравнение-k калибровки, соответствующего прибору-k.
Новая форма для уравнения калибровки-k или -i влечет за собой использование дифференциалов соседнего порядка в качестве спектральных признаков. Например, каждое из уравнений калибровки для прибора-k и прибора-i имеет вид: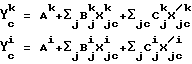
Здесь Y
X
X
С помощью уравнений калибровки в форме производных соседних порядков спектральных данных обнаружено, что неожиданно поправка на крутизну и смещение вызывает изменение в константах-k уравнения калибровки, которое приводит к получению значений для свойства-p образца, c, на основе спектральных данных, измеренных для выборки-c прибором-k, которые демонстрируют отличное совпадение с результатами, полученными от прибора-i и уравнения-i калибровки.
Пример 1. Уравнение калибровки для неоткалиброванного прибора выводится на основе уравнения калибровки, установленного для эталонного прибора. Решения для следующих уравнений определяют: B
Независимо используются три различных математических критерия. Так как используются только три длины волны, то J = 1 - 3, и так как 25 - общее число элементов выборки-c, то c = 1 - 25. Независимые переменные, X
Математический критерий 1
Σc(ϒ
при условии ϒ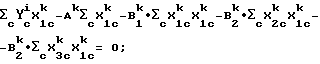
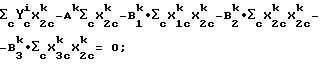
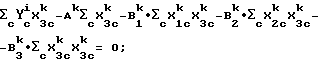
Прибор-i калибруется с использованием множественной линейной регрессии второй производной спектральной поглощательной способности при длине волны 1196, 1220 и 1236 нм путем модулирования зависимой переменной октан (R+M)/2 на 72 газолиновых образцах, заключающих октановый диапазон 86-93 с примерно равномерным распределением. Прибор представляет собой NIR Systems 6500, функционирующий в режиме отражения с использованием волоконной оптики с длиной пробега 18 мм.
Из уравнения регрессии для прибора получаются значения 25-и стандартов переноса калибровки и затем эти значения принимаются как значения октана (R+M)/2 зависимой переменной для 25-и стандартных значений переноса калибровки. Те же самые стандарты представлены в примере 2.
25 Стандартных значений переноса калибровки и 10 образцов с известным октановым числом обрабатываются прибором-k. Результаты представлены в табл. 1.
Альтернативно определено также, что возможно косвенно получить уравнение-k калибровки из перенесенного уравнения-k калибровки, когда используется этап уменьшения погрешности наименьшего квадрата вместо поправки на крутизну и смещение. Когда погрешности были смоделированы, как зависимая переменная-k с использованием спектральных данных-k, опять в качестве независимой переменной стало возможным сложить полученные контакты с константами из перенесенного уравнения-k калибровки и косвенно вывести определение методом наименьших квадратов (математический критерий I).
Математический критерий II
B
Ak= Σc(ϒ
При условии ϒ
Следует отметить, что c = 1 - 25, используются только три длины волны 1196, 1220 и 1236, и n = 25, так как число элементов в выборке-c равно 25.
Прибор-i калибруется с помощью множественной линейной регрессии второй производной спектральной поглощательной способности при 1196, 1220 и 1236 нм путем моделирования октана (R+M)/2 зависимой переменной на 72-х газолиновых образцах, заключающих октановый диапазон 86-93 при приближенно равномерном распределении. Прибор-i представляет собой тип NIR Systems 6500, функционирующий в режиме отражения с использованием волоконной оптики с длиной пробега 18 мм.
Из уравнения регрессии для прибора-i выводятся значения 25-и стандартных значений переноса калибровки, после чего эти значения принимаются как значения октана (R+M)/2 зависимой переменной для 25-и стандартных значений переноса калибровки. Те же самые стандарты представлены в примере 2.
Прибором-k обрабатываются 25 стандартных значений переноса калибровки. Константы регрессии подсчитываются следующим образом: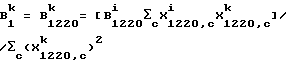
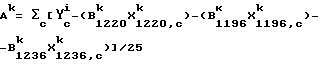
Вышеупомянутые константы в уравнении калибровки предсказывают значение 10-и образцов с известным октановым числом. Отмечается жесткое смещение октановых чисел (R+M)/2. Компьютерная программа устанавливает необходимость поправки на крутизну, равную 0,56741, и необходимость поправки на пересечение, равную 36,646. Эти поправки дают значение конечной крутизны и уравнение калибровки с поправкой на смещение для прибора-k и демонстрируют стандартную погрешность расчета, равную 0,184, и смещение 0,0265 октановых чисел (R+M)/2 для остальных 62-х образцов.
Математический критерий III.
B
Ak= Σc(ϒ
При условии ϒ
Следует отметить, что r = 1 - 3, так как используются только три значения длины волны, n = 25, так как число элементов в образце равно 25. Вышеупомянутый критерий III используется так же, как и критерий II. Результаты всех способов представлены в табл. 1.
Для демонстрации ожидаемой точности от уравнения калибровки октана, перенесенного от одного прибора, прибора-i к другому прибору-k, выполняется следующее.
Оба прибора-i и -k независимо калибруются с использованием тех же 72-х образцов. В результате калибровки выводится линейное уравнение калибровки, которое может быть использовано для прогнозирования октановых значений. Стандартная погрешность прогнозирования для каждого из этих уравнений выводится для 10-и известных образцов.
Уравнение переноса калибровки для прибора-k выводится из уравнения-i калибровки и одного из следующих критериев: I, II или III.
Каждое переносимое уравнение корректируется на крутизну и смещение с 10-ю образцами, представляющими уравнение с поправкой на крутизну и смещение.
Результаты приведенных выше этапов показаны в табл. 1. Особенно важно то, что СПП резко изменяется как результат поправки на крутизну и смещение. Однако конечная СПП после поправки на крутизну и смещение в случае критерия 1 дает СПП, идентичную значению СПП первоначального уравнения-i калибровки.
В данном случае точным расчетом наилучшего значения СПП, на который можно надеяться, будет значение СПП, равное 0,146, которое является значением СПП для прибора-k при полной калибровке с использованием 72-х образцов.
Пример 2. В этом примере используется математический критерий I примера 1 (множественной линейной регрессии), уравнение калибровки имеет линейную форму, но для независимых переменных величин используются спектральные признаки, определенные второй и третьей производными спектральных данных, соответственно каждой выбранной частоте.
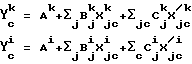
Здесь ϒ
X
X
Значения длин волн те же, что и в примере 1.
Прибором-i был проведен анализ 72 газолиновых образцов для получения их спектральных поглощающих характеристик. Кроме того, обработаны также 25 образцов стандартных значений переноса калибровки. Затем выводятся вторые и третьи производные спектров с использованием длин сегментов, равных 10, и промежутков, равных 0, посредством NSAS (пакет программ для спектрального анализа ближнего ИК-излучения, фирмы NIR Sysfems, Juc.). Композиции из 25-и стандартных значений переноса калибровки представлены в табл. 7, они выбраны специально, так как заключают в себя большинство изменчивости 72-х газолиновых образцов при длине волны, используемой для калибровки. Октановое число 72 газолиновых образцов находится в пределах 86,3 - 93,2 чисел октана (R + M)/2, образцы распределены в данном диапазоне в приблизительном равномерном распределении. Анализ каждого образца проводится 4 раза четырьмя различными лабораторными детонационного двигателя (APAL, Контрольная Лаб., Окружная контрольная лаб. и Контрольная лаб. Св. Павла) по способам ASTM 2699 и 2700 для получения точных расчетов октана (R + И)/2.
Файлы второй и третьей производной 72-х газолиновых образцов посылаются на универсальную ЭВМ и множественная линейная регрессии в соответствии с математическим критерием 1 выполняется с помощью обычных компьютерных программ с использованием статистических данных SAS (институт SAS, Inc. Кэри, Сев. Каролина) для второй производной спектральной поглощательной способности при 1196, 1220 и 1236 нм путем моделирования зависимой переменной октана (R + M)/2. Анализ данных по этому способу дает модель множественной линейной регрессии вида: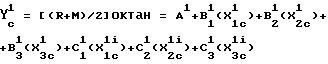
Значения членов Bi представлены в табл. 2. В табл. 2 приведены также множественный коэффициент определения (R2), множественный коэффициент корреляции (R) и стандартная погрешность расчета. Из табл. 2 может быть сделано заключение о том, что уравнение калибровки является очень точным.
Затем прогнозируются значения стандартов переноса калибровки из уравнения калибровки прибора-i и прогнозируемые значения используются как зависимая переменная октана (R+M)/2, а данные спектральной поглощательной способности для стандартов переноса калибровки на приборе-к преобразуются во вторую производную и третью производную и используются для значений независимых перменных-к для определения соответствующих констант-к по классическому методу наименьших квадратов или математическому критерию 1. Результаты приведены в табл. 3.
Затем 72 газолиновых образца обрабатывались прибором-к и получались файлы второй и третьей производных, как указывалось выше. Новое уравнение калибровки из табл. 3 используется для прогнозирования октана (R+M)/2 72 образцов (следует отметить, что эти образцы являются идентичными первоначальному калибровочному множеству, обработанному на приборе-i), используя то же самое октановое число, которое использовалось при первоначальной калибровке прибора-i. Эти расчеты выполняются на ПК с использованием программы Бейсик. Расчетные октановые значения показывают смещение -0,431 и имеют стандартную погрешность прогнозирования 0,586. Эти погрешности довольно высоки, учитывая, что первоначальная стандартная погрешность расчета на приборе-i всего лишь 0,145. Также из прогнозируемых октановых значений можно видеть, что погрешность для прогнозирования низких октановых чисел ((R+M)/2 примерно равно 86) достаточно высока, т.е. около -0,8 при сравнении с прогнозированием более высокого октанового числа ((R+M)/2 примерно равно 93), например, намного ближе к нулю, приблизительно 0,1. Этот тип поведения аналогичен дисперсии, зависящей от другой случайной величины, когда рассчитанные значения прогнозирования имеют тенденцию к погрешности на величину, которая представляет функцию расчетного октанового числа. Например, более низкие октановые числа дали высокие значения погрешности, а более высокие октановые числа дали более низкие значения погрешности. Когда наблюдается описанное выше поведение, поправка на крутизну и смещение оправдана в результате того, что график 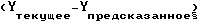 в сравнении с октановым числом приближается к прямой линии. Обычно это связано с тем, что первоначальное уравнение калибровки, линейное или нелинейное, преобразовано таким образом, чтобы получить линейную зависимость. При анализе данных ясно, что поправка на крутизну оправдана, так как зависимость стремится к прямой линии. При использовании программы ПК Бейсик показано, что необходимы поправка на крутизну для m, равная 0,86406, и поправка на смещение для b, равная 12,5590.
в сравнении с октановым числом приближается к прямой линии. Обычно это связано с тем, что первоначальное уравнение калибровки, линейное или нелинейное, преобразовано таким образом, чтобы получить линейную зависимость. При анализе данных ясно, что поправка на крутизну оправдана, так как зависимость стремится к прямой линии. При использовании программы ПК Бейсик показано, что необходимы поправка на крутизну для m, равная 0,86406, и поправка на смещение для b, равная 12,5590.
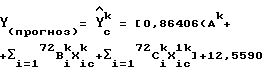
В табл. 5 приведены конечные константы регрессии для прибора-k с использованием переноса калибровки, затем следует поправка на крутизну и смещение.
Обнаружено, что это уравнение имеет стандартную погрешность расчета 0,190 на приборе-k по сравнению со стандартной погрешностью 0,145 прибора-i для 72-х газолиновых образцов.
Пример 3. Этот пример определяет поправку на крутизну и смещение, упомянутое выше в данном описании (Anal.Chem.Acta, 192 (1987) 197).
Различные члены определены ранее в описании, ϒ представляет собой расчетную или прогнозируемую зависимую переменную с учетом независимых переменных, эквивалентных одному или более спектральным признакам, определенным как члены X.
В зависимости от величины поправок на крутизну и смещение, соответствующих m и b, где m - поправка на крутизну, а b - поправка на смещение, можно принять решение не изменять уравнение калибровки для неоткалиброванного прибора. 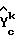 - значение с поправкой на крутизну и смещение, прогнозируемое для физического свойства, как показано далее.
- значение с поправкой на крутизну и смещение, прогнозируемое для физического свойства, как показано далее.
В особом примере ϒ
1. Представляло требуемый диапазон для конкретного свойства, например, октана. Затем образец должен иметь текущие октановые значения (измеренные в соответствии с TSTM D 2699 и D 2700) приблизительно в диапазоне интересующих октановых значений.
2. Имело октановое число, измеренное для каждого образца, и чтобы это текущее октановое значение затем коррелировалось (с помощью построенного графика) в сравнении с расчетным октановым значением для каждого образца, определенным с помощью уравнения калибровки, в котором должна быть произведена поправка на крутизну и смещение.
3. Число n образцов для внесения поправки на крутизну и смещение должно равняться 2 с целью определения как m, так и b, но в примерах обычно используется число 10. Уравнение калибровки для прибора-k имеет вид: ϒ
4. Найти m и b, решить уравнение относительно m и b, которые удовлетворяют следующим математическим критериям: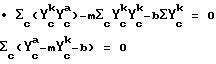
Результаты являются следующими: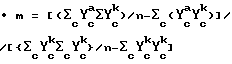
• b = 1/n{Σcϒ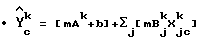
Пример 4. Математическая обработка переходит от множественной линейной регрессии к частичным наименьшим квадратам для переноса калибровки от прибора-i к прибору-k.
В данном примере прибор-i является стендовым измерительным прибором типа NIR Systems 6500, функционирующий в режиме отражения с использованием волоконной оптики. Прибор откалиброван, как показано в примере 1, с использованием 72-x образцов. Калибровка осуществляется как до моделирования октана (R + M)/2 с использованием второй производной спектральной поглощательной способности при 1220, 1196 и 1236 нм как независимых переменных уравнения калибровки множественной регрессии. Стандартные значения переноса калибровки те же 25 значений, указанные в примере 5.
Прибор-k представляет собой неоткалиброванный прибор типа NIR Systems OL-6500, функционирующий в режиме отражения с использованием волоконной оптики. На этом приборе обрабатываются 25 стандартных значений переноса калибровки с использованием расчетных значений октана от прибора-i в качестве зависимой переменной. Благодаря изобретению возможно откалибровать прибор-k, прибегая к различному математическому подходу, отличному от подхода, который был использован на приборе-i (множественной линейной регрессии). Частичные наименьшие квадраты (ЧНК) выбраны в качестве альтернативного способа калибровки для прибора-k. Принципы ЧНК хорошо известны (Гарольд Мартенз и Тормод Нэс, Многомерная калибровка, Изд-во Джон Вилей и сыновья, Нью-Йорк, 1989, ISBN 471-90979-3).
Способ ЧНК выполняется с помощью моделирования зависимой переменной расчетного значения октана для 25-и стандартных значений калибровки на уровне вторых производных спектральных поглощатеьной способности в диапазоне длин волн 1190 - 1240 нм (с интервалами в 2 нм, т.е. 1190, 1192, 1194... 1240). Перекрестная проверка результатов на достоверность осуществляется с помощью 4-х групп подмножества. Модели строятся с использованием одной, двух, трех, четырех, пяти и шести скрытых переменных. Модель четырех скрытых переменных очевидно дает наилучший расчет октанового числа возбуждения для прибора-k и корреляцию 0,9994 октановых значений, подсчитанных прибором-i. Модель ЧНК четвертой скрытой переменной используется для прогнозирования значений первых 10-и образцов из калибровочного множества для первоначальных 72-х образцов. Прогнозируемые значения показывают значительное смещение, равное 0,433, октановых чисел (R + M)/2 и стандартную погрешность, равную 0,468. Выполняются поправка на крутизну 0,940 и поправка на пересечение 5,77 октановых чисел (R + M)/2. Остальные 62 образца прогнозируются как неизвестные. 62 Образца показывают смещение 0,0156 октановых чисел и стандартную погрешность прогнозирования 0,153 для октановых чисел для неизвестных.
Следует отметить, что может быть выбрана другая область спектров, а не 1190 - 1240 при условии, что она функционально связана с октановым числом по меньшей мере с такой же надежностью, как и при его измерении прямым способом. Это также ясно показывает, что используемые в уравнении-1 длины волн необязательно должны быть теми же, что и значения в уравнении-2, что указывает на дополнительные преимущества изобретения.
Пример 5. Этот пример описывает перенос уравнения калибровки, который может быть использован при переносе от одного нефтеперерабатывающего завода к другому, от одного детонационного двигателя к другому, от одного прибора после изменения конфигурации и смены лампы к другому прибору со значительно уменьшенной погрешностью прогнозирования посредством двойного переноса калибровки.
Этот пример ярко демонстрирует преимущества настоящего изобретения, например прибор-k полностью откалиброван с использован только газолинов, которые не содержали MTBE (метил-t-бутил эфир). Недавно Конгресс передал акт о новом составе топлива, а так как прибор-k функционирует на нефтеперерабатывающем заводе, который расположен на участке, где нет CO (моноксида углерода), акт о новом составе топлива предписывает, чтобы на нефтеперерабатывающем заводе добавляли MTBE (или какое-либо другое сырье, насыщенное кислородом) к газолиновым смесям к такому-то числу. Так как прибор-k откалиброван без MTBE, следует ожидать, что это приведет к значительным погрешностям, если будет использоваться текущая калибровка прибора-k на неизвестных образцах, которые содержат MTBE. Чтобы не производить полную калибровку прибора-k заново, было бы желательно перенести уравнение калибровки, которое может учитывать поступление MTBE по мере того, как он добавляется к газолиновому сырью нефтеперерабатывающего завода на некоторую дату в будущем. В этом примере прибор-k представляет собой тип NIR Systems OL-6500, функционирующий в отражательном режиме с использованием волоконной оптики.
Тип NIR Systems OL 6500 выбран для прибора-i, так как он был однажды откалиброван на основе 226-и образцов, некоторые из которых содержали MTBE, и с его помощью можно отобрать образцы, содержащие P-15% по объему MTBE.
Проблема несколько осложняется тем, что только стандартные калибровочные значения обрабатываются прибором-i при его калибровке с MTBE, эти значения представляют собой 8 чистых смесей (и расчетные октановые числа), приведенных в табл. 6. Эти 8 смесей не обрабатываются прибором-k, поэтому прямой перенос калибровки невозможен.
Для выполнения переноса 8 стандартных калибровочных значений еще раз обрабатываются прибором-i. Так как калибровка прибора-i осуществляется с учетом MTBE, прибор-i перестраивается с измерений пропускания при длине пробега 20 мм на измерение отражения при длине пробега 18 мм с использованием волоконной оптики. Коэффициент усиления лампы и детектора также изменяется.
С учетом нового множества условий, используя 8 стандартных калибровочных значений, калибровка для MTBE переносится от прибора-i в режиме пропускания к прибору-i в отражательном режиме. Затем его уравнение без поправки на крутизну и смещение или других способов погрешности (например, способа наименьших квадратов) используется для расчета прогнозируемых значений октана для 25-и стандартных калибровочных значений, которые также обрабатываются прибором-i в отражательном режиме и прибором-k также в отражательном режиме.
Множественная линейная регрессия по 25-и стандартным значениям табл. 7 на приборе-k с использованием расчетных октановых значений в качестве зависимых переменных и второй производной спектральной поглощательной способности при 1220, 1196 и 1236 нм выдает новое уравнение калибровки для прибора-k, которое может быть использовано для прогнозирования октановых чисел газолиновых смесей, содержащих MTBE.
Новое уравнение имеет поправку на крутизну и смещение по 10-и газолиновым образцам. Четыре из этих образцов представляют собой высшие неосвинцованные газолиновые смеси ((R + M)/2 октан = 92), остальные 6 - нормальные неосвинцованные газолиновые смеси ((R + M)/2 = 87). Эти образцы показывают смещение 0,919 и стандартную погрешность 0,946 (R + M)/2 октановых чисел.
На основе этих данных выполняется поправка на крутизну, равная 0,950, и поправка на смещение, равная 5,30. Полученное в результате этого уравнение демонстрирует смещение 0,0401 и стандартную погрешность прогнозирования 0,122 для 30-и неизвестных газолиновых образцов. Некоторые соответствующие данные приведены ниже.
Сводная таблица показывает очень интересное явление, которое заключается в том, что перенесенное уравнение калибровки оказывается примерно в 2 раза более точным, чем первоначальное уравнение. Это скорее всего объясняется тем фактом, что используемые октановые значения в поправке на крутизну и смещение для прибора-k известны с большей точностью, чем калибровочные образцы, используемые на приборе-i.
Этот пример противоречит общепринятому мнению некоторых специалистов систем NIR. Эти учены считают, что уравнение, выведенное для одного нефтеперерабатывающего завода, не может быть использовано для прогнозирования на другом заводе. В этом примере калибровка для MTBE прибора-i произведена на нефтеперерабатывающем заводе Эшланда в Кэтлетсбурге. Это очень сложный нефтеперерабатывающий завод, функционирующий в соответствии с промышленными стандартами, он имеет 12 газолиновых смешивающихся компонентов. С другой стороны, прибор-k обрабатывает данные от нефтеперерабатывающего завода в Эшландском Парке Св. Павла в Миннесоте, который имеет только 6 газолиновых смешивающихся компонентов и поэтому считается менее сложным. Более того, нефтеперерабатывающие заводы в Кэтлетсбурге и Парке Св. Павла почти не имеют наложений в смысле составов сырой нефти.
Пример 6. Этот пример показывает, что если ϒk,s - линейная функция ϒi,s , то перенесенное уравнение калибровки оказывается столь же эффективным или почти таким же эффективным, как и уравнение, полученное от прямого переноса калибровки предыдущих примеров, (т.е. где ϒi,s(прогноз.)= ϒk,s(текущее) . Здесь будет рассматриваться линейная функция ϒi,s , где ϒk,s= 3(ϒi,s)прогноз.+25.
В предыдущем примере показана калибровка для октана (R + M)/2 на 226-и образцах, которое прогнозирует октановые значения (R + M)/2 8 калибровочных стандартов (изооктана, n-декана, 1-октена 2,4,3-триметилпентана, n-гептана, циклогексана, n-гексана и толуола). Эта калибровка разработана на модели 6500 NIR Systems, функционирующей в режиме трансмиссии при длине пробега 20 мм.
Впоследствие этот прибор был адаптирован для волоконной оптики с использованием отражательной способности при длине пробега 18 мм после того, как были изменены коэффициенты усиления лампы и детектора. 8 Калибровочных стандартов обрабатываются на приборе с использованием три раза октанового значения, определенного из измерений пропускания плюс 25, как значения зависимой переменной. Результаты множественной линейной регрессии являются следующими:
Ak - = 286,951
Bk,1220 - = 283,252
Bk,1196 - = 70,020
Bk,1236 - = 84,185
Затем значения прогнозируются для 10-и газолиновых образцов.
Прогнозируемые значения для 10-и газолиновых образцов корректируются с помощью трех эквивалентных способов. Способ 1 влечет за собой вычитание 25 из значения, прогнозируемого для газолиновых образцов (R + M)/2, разделив результат на 3 и осуществив поправку на крутизну и смещение. Способ 2 требует поправку на крутизну и смещение с использованием измеренного в данный момент октанового значения образца. Способ 3 требует использования три раза октанового значения газолиновых образцов плюс 25 для образцов, используемых в поправке на крутизну и смещение, и корректирования значений, предсказанных для последующих неизвестных, вычитая 25 и разделив на 3. В каждом из этих трех способов отмечается смещение 0,0281 и стандартная погрешность прогнозирования 0,240 октановых чисел (R + M)/2 с использованием неизвестного множества, состоящего из 62-х неизвестных
Следует отметить, что окончательное уравнение для прямого переноса калибровки (ϒi,sпрогноз.= ϒk,sтекущее) показывает несколько низкую погрешность и смещение, чем любой из предыдуших способов (смещение = 0,0237, СПП = 0,223 октана (R + M)/2). ϒk,sтек. , умноженное на константу и с добавлением некоторых других констант, дало значение для зависимой переменной для переноса, которое повлияло на член погрешности (ϒk,sпрогноз.-ϒi,sтек.), который не может быть удален с помощью обратной математической функции или с помощью поправки на крутизну и смещение.
Однако, если мы формируем уравнение переноса калибровки (без поправки на крутизну и смещение) и умножаем константы регрессии (Ak, Bk,1220, Bk,1196 и Bk,1236) на 3 и добавляем 25 к Ak, при точном ответе мы можем прийти к тому, что прямой способ (ϒk,sпрогноз.= ϒi,sтек.) после использования поправки на крутизну и смещение с текущими октановыми значениями (R + M)/2 10-и образцов или с помощью поправки на крутизну и смещение, выдает уравнение, использующее три раза значение октана плюс 25 и вычитающее 25 из каждого прогнозированного октанового значения и делящее его на 3.
Пример 7. Уравнение калибровки для неоткалиброванного прибора получается на основе уравнения калибровки, выведенного для опорного прибора. Решения для следующих уравнений определяют: B
Используется математический критерий I - метод классических наименьших квадратов. Но так как используются только три длины волны, то J = 1 - 3, так как 4 - общее число элементов в выборке-c, то c = 1 - 4. Независимые переменные X
Математический критерий I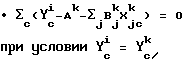
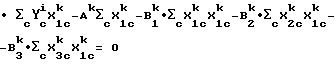
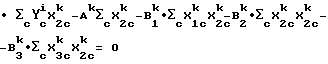
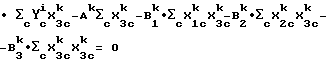
Следует отметить, что в математическом критерии I форма уравнения калибровки для эталонного прибора-i может отличаться от формы уравнения для неоткалиброванного прибора-k.
Даже после смены лампы, что обычно изменяет спектральные характеристики прибора, и адаптирования прибора к волоконной оптике, работая в отражательном режиме при различной длине пробега, было возможно заново откалибровать такой прибор с помощью этапов этого изобретения.
Калибровка осуществляется на приборе-i для октанового значения возбуждения. Калибровочное множество включает 226 образцов. Эти образцы анализируются на приборе-i и выполняется множественная линейная регрессия путем моделирования октана (R + M)/2 на уровне второй производной поглощательной способности при 1220, 1196 и 1236 нм. Прибор-i функционирует в режиме пропускания с использованием общей длины пробега в 20 мм. Полученные константы регрессии являются следующими:
Ai - = 87,925
B
B
B
Стандартная погрешность расчета для уравнения составляет 0,330. Следует отметить, что эти результаты получены от разных операторов детонационного двигателя, испытывающих образцы на одних и тех же детонационных двигателях. Считается, что эти результаты хорошие, так как допустимые предельные значения ASTM для (R + M)/2 являются стандартной погрешностью расчета, равной приблизительно 0,35. Эти образцы характеризуются приблизительно равномерным распределением от 84-94 октана (R + M)/2.
Значения уравнения калибровки, полученные на основе множественной регрессии, предсказаны для 4-х стандартов переноса калибровки. Эти стандарты и их расчетные значения октана (R + M)/2 приведены в табл. 9.
Следует отметить также, что прибор-i калибровался на протяжении четырехмесячного периода (т.е. образцы обрабатывались по мере того, как они поступали в лабораторию), а это не совсем оптимальный вариант калибровки. Не был оптимальным и тот факт, что эти калибровочные стандарты не обрабатывались на приборе сразу же или одновременно с первоначальной калибровкой, но не позже, чем спустя 1 месяц после выполнения калибровки.
После этого лампа на приборе-i перегорает и вставляется новая лампа. Прибор также адаптируется к волоконной оптике, функционируя в отражательном режиме при разной общей длине пробега (≈ 18 мм). После изменений в характере конфигурации и длины пробега должен измениться и детекторный коэффициент усиления для аккомодации новой лампы и более низкой пропускной способности конфигурации волоконной оптики (в противоположность трансмиссии).
Стандартные образцы для переноса калибровки снова обрабатываются на приборе-i и выводится уравнение переноса калибровки путем моделирования расчетного октана в виде функции второй производной спектральной поглощательной способности при 1220, 1196 и 1236 нм.
Полученные константы регрессии были следующими:
Ak - = 87,717
B
B
B
B
Затем был произведен анализ 97-и образцов для октана (R + M)/2. Все образцы отличались от предыдущих. Более того, они подвергались анализу многими операторами на разных детонационных двигателях, отличных от использованных ранее двигателей. Уравнение переноса калибровки показывает незначительное смешение, равное 0,0392 значений октана (R + M)/2 (обратите внимание, что смещение между двумя разными детонационными двигателями обычно намного выше, чем это значение) и стандартную погрешность расчета, равную 0,371 октана (R + M)/2. Поправка на смещение и крутизну была выполнена с использованием двух образцов: один с октановым числом 87,4 и другой - с октановым числом 92,5, поправка на крутизну составила 0,9402 и поправка на пересечение или поправка на смещение составила 5,297, получено конечное уравнение:
Ak - = 87,774
B
B
B
Уравнение с поправкой на крутизну и смещение имеет смещение 0,0 и стандартную погрешность прогнозирования 0,343.
Для того, чтобы показать, что это не может быть выполнено непосредственно от первоначального уравнения калибровки с учетом данных для пропускания, первоначальное уравнение калибровки используется для прогнозирования октана (R + M)/2 для каждого образца из 97-и газолиновых образцов. Результат показывает смещение 0,482 октана. Установка смещения и крутизны только с использованием всех 97-и образцов соответственно первоначальному уравнению калибровки показывает смещение 0 и стандартную погрешность расчета 1,96 (R + M)/2 октана.
Также следует отметить, что крутизна двух точек и настройка смещения могут также рассматриваться как этап, уменьшающий погрешность обобщенной наименьшей суммы, в том смысле, что он может быть выполнен эквивалентно с использованием геометрического подхода.
Например, с помощью линии, проходящей через измеренные текущие значения, можно определить константы для получения линии, проходящей между прогнозируемыми значениями, перед тем как осуществить настройку, чтобы обеспечить эквивалентность обеих линий. Следовательно это - обобщенная наименьшая сумма, так как при этом подходе не используются квадраты.
Конкретные композиции, обсужденные способы или варианты исполнения приведены в описании только для иллюстрации. Изменения этих композиций, способов или вариантов исполнения очевидны специалисту данной области и следовательно они должны быть включены в объем описываемого изобретения.
Например, способ, эквивалентный описанным в примерах способам, не выходящий за рамки заявленной области изобретения, определяет значение смещения, например, для Ak в уравнении-k калибровки для прибора-k на основе уравнения-i калибровки для прибора-i, при этом принимается во внимание, что Ai равно какому-либо произвольному значению, например нулю, или значению, определенному в зависимости от Ai и функции Ai, т.е. частично откалиброванного прибора. Правильным значением для Ak является такое значение, которое при использовании в уравнении-k калибровки определяет значение для зависимой переменной-k, которое по существу равно текущему значению нужного физического или химического свойства. Правильное значение для Ak может быть получено применением поправки на крутизну и смещение к тому уравнению, которое получается при использовании произвольного значения для A или значения, определенного какой-либо функцией A. Другой способ, эквивалентный вышеописанному, имеет место тогда, когда в конечном уравнении, которое будет выведено из уравнения крутизны и смещения, может быть использованы функции от m или b (членов, описанных в примере 6). Это четко изменит расчетное или прогнозируемое значение зависимой переменной. Однако так же, как было показано в описании для использования функции YΨ уравнения-i калибровки, может быть использована функция m или b, а затем полученная в результате этого зависимая переменная может быть преобразована обратно к значению, которое будет по существу равно текущему значению для химического или физического свойства требуемого диапазона.
Другим изменением в пределах области этого изобретения является то, каким образом значения приписываются зависимой переменной-k. Эти значения для зависимой переменной-k, которые могут быть использованы для определения констант-k в уравнении-k калибровки или для выполнения поправки на крутизну и смещение, могут быть найдены без применения первичного способа испытания, но вместо этого могут быть определены с помощью уравнения-i калибровки и спектральных данных-i, полученных от прибора-i или, возможно, любого другого откалиброванного прибора вместе с его соответствующим уравнением калибровки, которое охватывает фактически тот же требуемый диапазон и соответствующие спектральные данные.
Другим вариантом этого изобретения является использование разных спектральных признаков в уравнении-i калибровки, отличных от характеристик в уравнении-k калибровки, например разные значения длин волн или разные математические преобразования, или оба эти подхода, при условии, что каждое это отличие коррелируется с нужным физическим или химическим свойством.
В большинстве примеров используются только три длины волн. Однако это число может изменяться в зависимости от искомой или нужной статистической надежности. Если для какого-либо свойства косвенный способ имеет СПП относительно V, значение которой меньше, чем интервал надежности для прямого способа при определении такого свойства, то существует практический предел того, что насколько мало моет быть это значение V и сколько длин волн может быть необходимо.
Другая модификация относится к спектральным признакам, которые могут быть выведены из спектров поглощения. В примерах были использованы как вторая производная, так и производная более высоких порядков от интенсивности в зависимости от длин волн или поглощательной способности. Конкретно, производные более высоких порядков, такие как первая, вторая, третья, четвертая, пятая и т. д. , также предполагаются рассматриваемыми в этом изобретении. Значения спектральных признаков могут просто равняться значению, определенному для конкретной длины волны или диапазону длин волн, относительно эталонной длины волны, например, значениям поглощательной способности. Спектральные признаки не предполагают обязательных отличий от спектральных данных по своим значениям. Очевидно, что они могут быть более сложным и что использование линейной комбинации спектральных признаков или их математических преобразований также входит в объем изобретения.
Очевидной также является, как вариант этого изобретения, линейная комбинация производных более высоких порядков, например производных третьего и четвертого или более высокого порядка спектральных данных (см. пример 5).
Более того, приведенное в описании множество элементов или диапазон чисел может включать любой элемент или число в пределах такого множества или диапазона, соответственно включая любое подмножество или поддиапазон в пределах любого названного множества или диапазона.
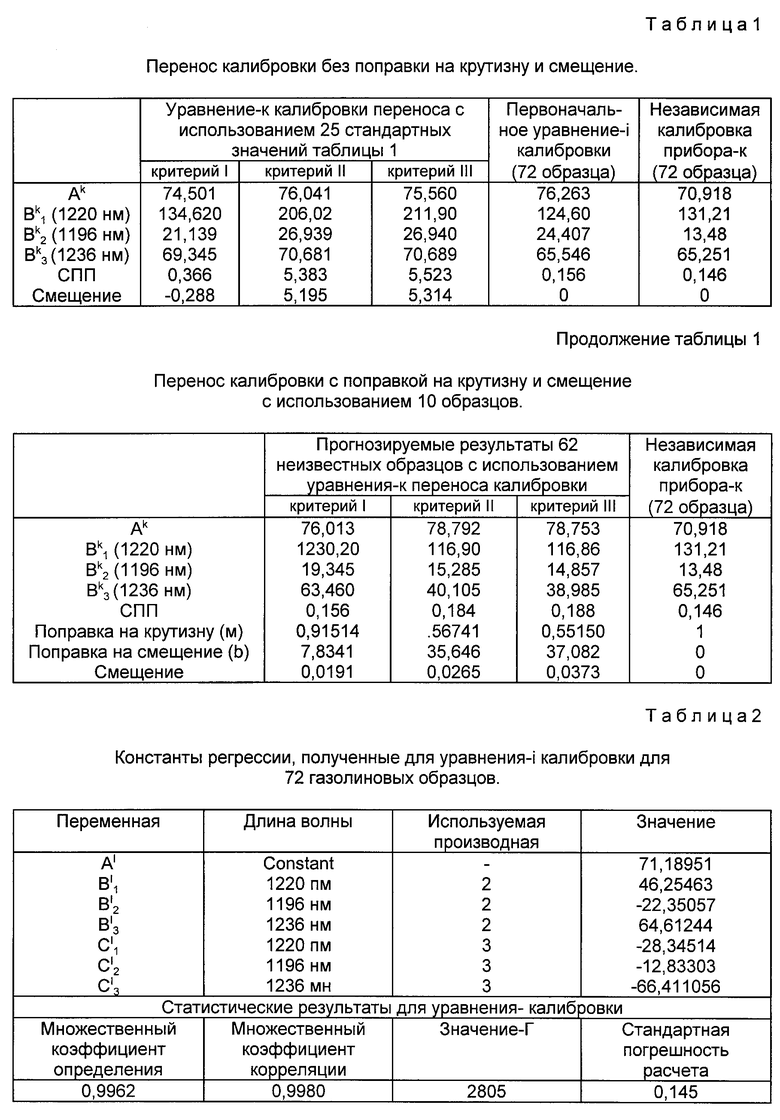
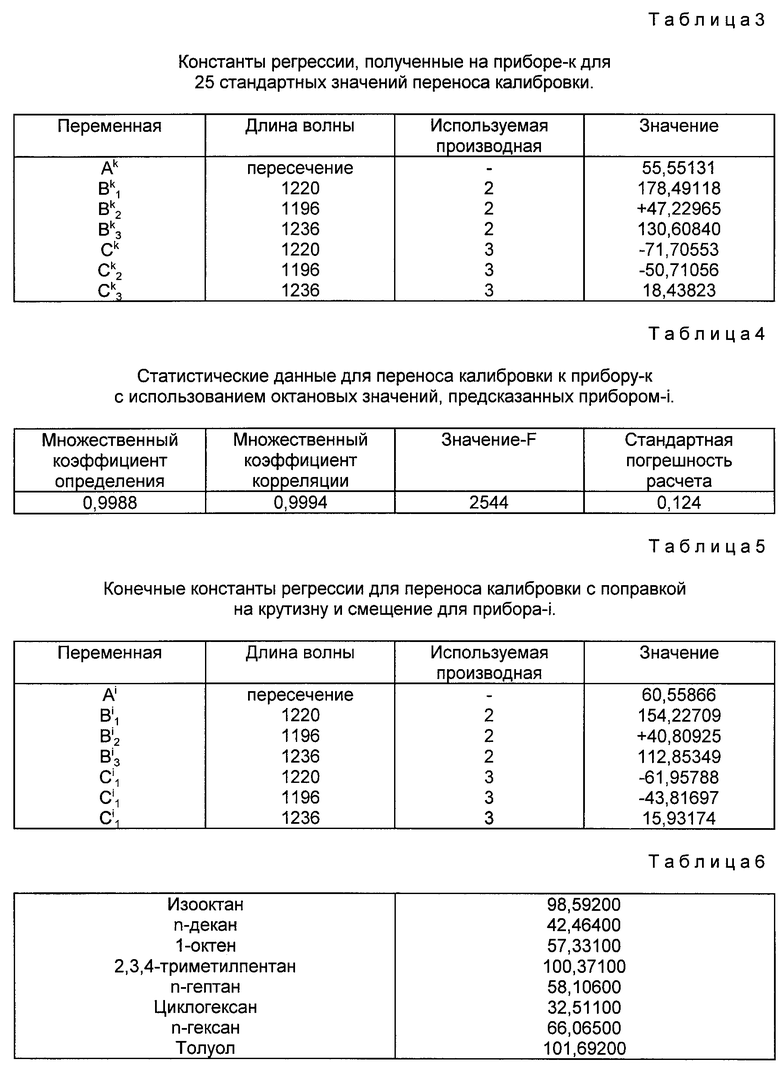
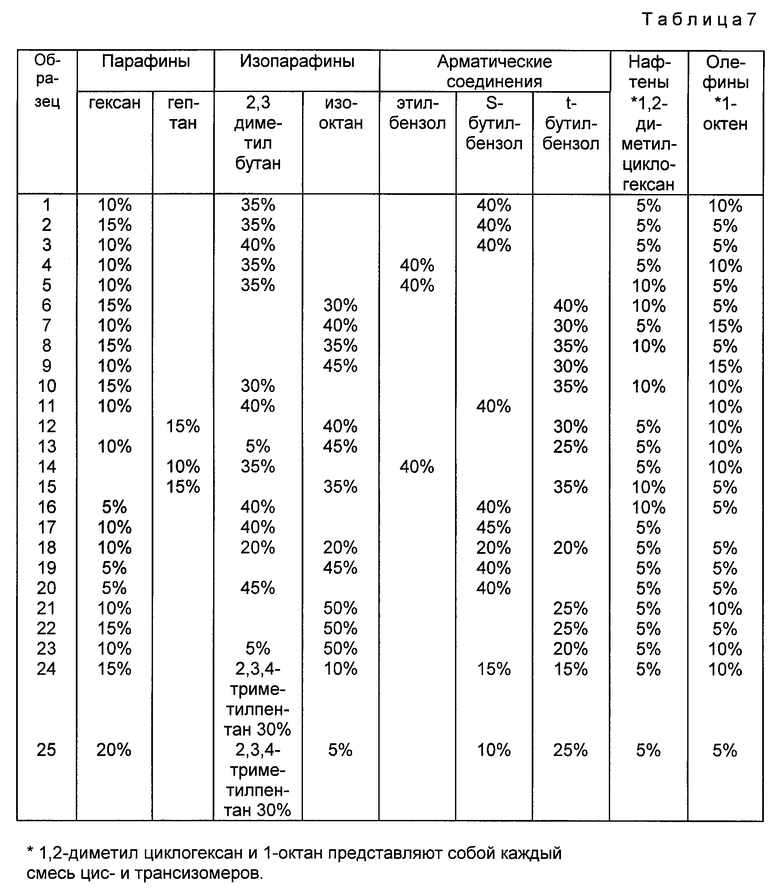
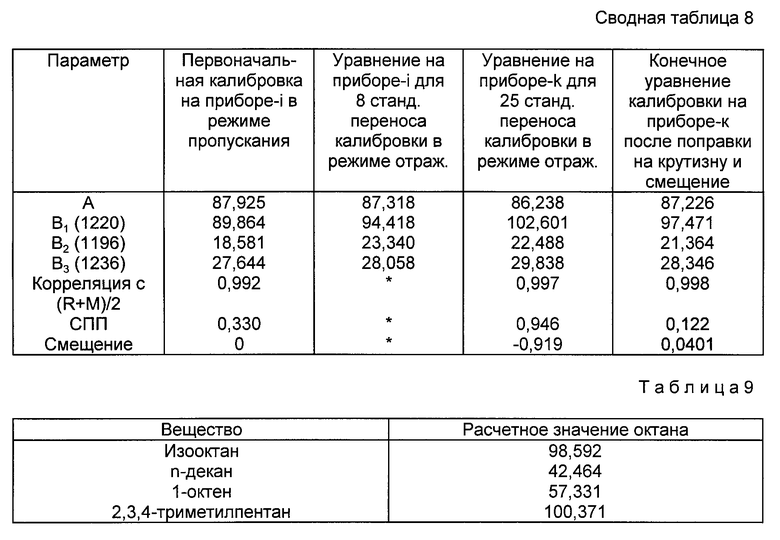
Изобретение относится к способу первоначальной калибровки или повторной калибровки второго спектрометра в свете первого спектрометра или, соответственно, его самого. При калибровке используются выбор и обработка спектральных данных, полученных как от первого, так и от второго приборов. При повторной калибровке используются выбор и обработка спектральных данных от того же первого прибора, которые получены как до, так и после того, как возникает необходимость в повторной калибровке. Вместо модификации соответствующих характеристик первого и второго приборов или первого прибора до и после возникновения необходимости в калибровке данное изобретение модифицирует уравнение калибровки второго и повторно калибруемого прибора для получения результатов согласующихся с результатами, полученными первым прибором или первым прибором для того, как он выйдет из калиброванного состояния. Уравнение калибровки - это такое уравнение, которое преобразует спектральные данные конкретного образца при множестве длин волны в соответствии с расчетным значением для какого-либо химического или физического свойства. Обычно формой таких уравнений калибровки является линейная комбинация спектральной поглощательной способности или математического преобразования значений поглощательной способности, измеренных первым и вторым приборами для каждого образца. Технический результат: точность первоначально или повторно откалиброванного прибора сохраняется и в некоторых случаях даже улучшается. 3 с. и 7 з.п.ф-лы, 9 табл.
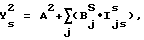
где Y
Y
A2 - константа-2 переноса;
B
I
и упомянутое сведение к минимуму абсолютных разностей обеспечивается путем минимизации следующего выражения:
Σs{Y
независимая переменная определяется на основе спектральных данных-2 путем преобразования поглощательной способности, которое включает определение дифференциала спектров поглощения.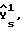 при этом осуществляется подстановка значений для m и b в следующее выражение:
при этом осуществляется подстановка значений для m и b в следующее выражение: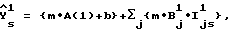
где m и b определены из следующих выражений: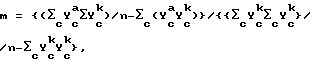
b = 1/n{ΣcY
где зависимая переменная (ас) Y
| US 4963745 A, 1990 | |||
| Способ выбора градуировочных образцов для спектрального анализа | 1979 |
|
SU1109586A1 |
| US 4864842 A, 1989 | |||
| Osborne B.G | |||
| и др | |||
| Calibr | |||
| of instrum | |||
| for near IR Spectroscopy | |||
| Spectroscopy, 1989, v.4, N 4, p.48 - 52 | |||
| Mark X | |||
| и др | |||
| A new approach to generat | |||
| traus | |||
| calibrat., etc, Spectroscopy, 1988, v.3, N 11, p.28 - 37 | |||
| Wang и др | |||
| Multivar | |||
| instrum, standar | |||
| Anal | |||
| Chem | |||
| Циркуль-угломер | 1920 |
|
SU1991A1 |
Авторы
Даты
1998-08-20—Публикация
1992-10-07—Подача