Предлагаемый способ относится к области траекторных измерений параметров орбит подвижных космических объектов (КО) на фоне звездного неба с помощью оптико-электронной аппаратуры, установленной на орбитальном измерителе (космическом аппарате-измерителе - КАИ).
Известны способы и устройства определения координат подвижных объектов (авт. свид. СССР №1019673; патенты РФ №№2081383, 2168753, 2172010, 2191407, 2197070, 2251712; патенты США №№3567163, 3700799, 6122572, 6163372; патент WO №0125722; Грязин Г.Н. Оптико-электронные системы для обзора пространства: Системы телевидения. - Л.: Машиностроение, Ленинградское отделение, 1988, с.8-9, рис.4 и другие).
Из известных способов и устройств наиболее близким к предлагаемым являются «Способ определения координат объекта и оптико-электронное устройство для его осуществления» (патент РФ №2.251.712, G01S 13/66, 2003), которые и выбраны в качестве прототипов.
Известный способ заключается в определении угловой координаты изображения объекта вместе с изменяющими образ элементами в поле зрения и последующем пересчете полученной величины в стабилизированную систему координат, определении величины и направления линейной скорости объекта в стабилизированной системе координат, формировании величины углового смещения в стабилизированной картинной плоскости, исходя из полученной величины и координат, характеризующих линейное смещение изменяющих образ элементов относительно собственной системы координат объекта, корректировке угловой координаты изображения объекта вместе с искажающими образ элементами в стабилизированной системе координат на величину углового смещения.
Оптико-электронное устройство содержит последовательно соединенные оптико-электронный пеленгатор и преобразователь из измерительной в стабилизированную систему координат, последовательно соединенные блок определения линейной скорости объекта, блок формирования величины углового смещения и сумматор, второй вход которого соединен с выходом преобразователя из измерительной в стабилизированную систему координат.
Однако известные способ и устройство не обеспечивают точного определения координат движущегося космического объекта на фоне звездного неба с помощью оптико-электронной аппаратуры, установленной на орбитальном измерителе.
Технической задачей изобретения является повышение точности определения координат движущегося космического объекта на фоне звездного неба с помощью оптико-электронной аппаратуры, установленной на орбитальном измерителе, путем привязки космического объекта к каталожным звездам, координаты которых с высокой точностью известны во второй экваториальной системе координат.
Поставленная задача решается тем, что способ определения координат космического объекта, в соответствии с ближайшим аналогом, заключающийся в определении угловой координаты изображения космического объекта вместе с изменяющими образ элементами в поле зрения и последующем пересчете полученной величины в стабилизированную систему координат, отличается от ближайшего аналога тем, что в качестве стабилизированной системы координат используют вторую экваториальную систему координат, дополнительно определяют линейные координаты xρ, yρ изображения космического объекта в приборной системе координат, жестко связанной с ПЗС-матрицей телескопа, плоскость которой устанавливают на расстоянии fп от фокуса телескопа перпендикулярно его оптической оси, прямое восхождение αо и склонение δо оптической оси телескопа во второй экваториальной системе координат и угол разворота ϕр между плоскостью круга склонения оптической оси телескопа и вертикальной плоскостью приборной системы координат, а затем переносят плоскость ПЗС-матрицы вдоль оптической оси на расстояние fп от фокуса телескопа, линейные координаты xρ, yρ пересчитывают в углы отклонения γρ, βρ проекции изображения космического объекта на оси xпр, yпр приборной системы координат от оптической оси телескопа, определяют отклонения направления вектора 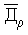 на космический объект от направления оптической оси телескопа, дальнейшие расчеты проводят на сфере единичного радиуса, используя формулы сферической тригонометрии для расчета элементов сферических треугольников, образуемых пересечением дуг больших кругов на поверхности сферы единичного радиуса, и определяют прямое восхождение αρ и склонение δρ вектора
на космический объект от направления оптической оси телескопа, дальнейшие расчеты проводят на сфере единичного радиуса, используя формулы сферической тригонометрии для расчета элементов сферических треугольников, образуемых пересечением дуг больших кругов на поверхности сферы единичного радиуса, и определяют прямое восхождение αρ и склонение δρ вектора 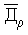 во второй экваториальной системе координат.
во второй экваториальной системе координат.
Поставленная задача решается тем, что оптико-электронное устройство, в соответствии с ближайшим аналогом, содержащее последовательно соединенные оптико-электронный пеленгатор и преобразователь из измерительной в стабилизированную систему координат, отличается тем, что в качестве оптико-электронного пеленгатора выбран телескоп, который установлен на борту орбитального измерителя, в качестве измерительной системы координат выбрана приборная система координат, жестко связанная с ПЗС-матрицей, плоскость которой установлена на расстоянии fп от фокуса телескопа перпендикулярно его оптической оси, в качестве стабилизированной системы координат выбрана вторая экваториальная система координат, а преобразователь из приборной во вторую экваториальную систему координат выполнен в виде последовательно подключенных к первому выходу ПЗС-матрицы телескопа первого квадратора, сумматора, второй вход которого через второй квадратор соединен со вторым выходом ПЗС-матрицы, блока извлечения квадратного корня, первого блока деления, первого блока вычисления арктангенса и блока вычисления элементов сферического треугольника, два выхода которого являются выходами преобразователя из приборной во вторую экваториальную систему координат, последовательно подключенных к первому выходу ПЗС-матрицы телескопа второго блока деления и второго блока вычисления арктангенса, выход которого соединен со вторым входом блока вычисления элементов сферического треугольника, последовательно подключенных к второму выходу ПЗС-матрицы телескопа третьего блока деления и третьего блока вычисления арктангенса, выход которого соединен с третьим входом блока вычисления элементов сферического треугольника, причем вторые входы блоков деления соединены с выходом блока определения расстояния fп ПЗС-матрицы от фокуса телескопа, четвертый, пятый и шестой входы блока вычисления элементов сферического треугольника соединенная с выходами блока определения угла разворота ϕρ между плоскостью круга склонения оптической оси телескопа и вертикальной плоскостью приборной системы координат и блока определения прямого восхождения αо и склонения δо оптической оси телескопа во второй экваториальной системе координат.
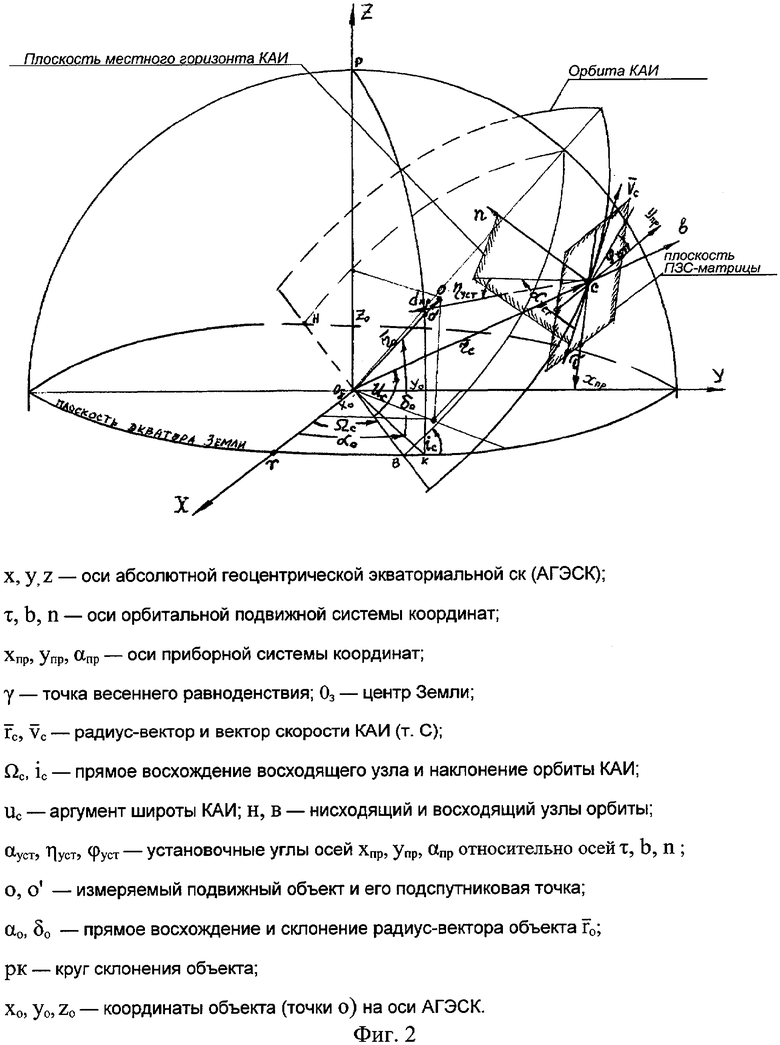
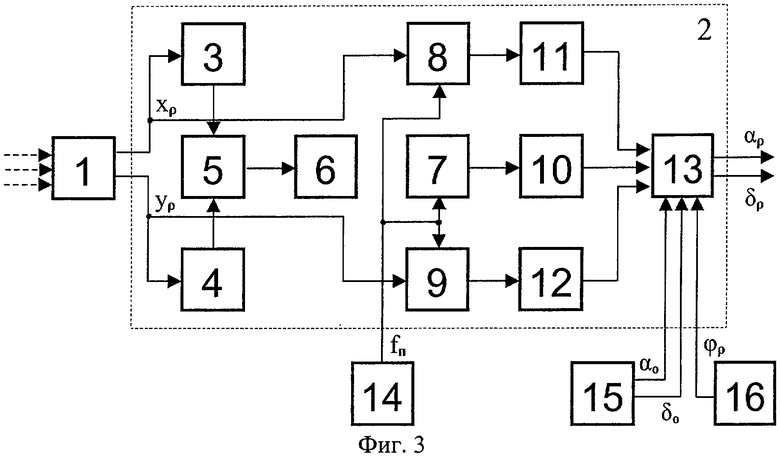
Связь между приборной и экваториальной системами координат показаны на фиг.1 и 2. Структурная схема оптико-электронного устройства, реализующего предлагаемый способ определения координат космического объекта, представлена на фиг.3.
Оптико-электронное устройство содержит последовательно соединенные оптико-электронный пеленгатор 1 и преобразователь 2 из измерительной в стабилизированную систему координат, выполненный в виде последовательно подключенных к первому выходу пеленгатора 1 (ПЗС-матрицы) первого квадратора 3, сумматора 5, второй вход которого через второй квадратор 4 соединен со вторым выходом телескопа 1 (ПЗС-матрицы), блока 6 извлечения квадратного корня, первого блока 7 деления, первого блока 10 вычисления элементов сферического треугольника, два выхода которого являются выходами преобразователя 2 из приборной во вторую экваториальную систему координат, последовательно подключенных к первому выходу ПЗС-матрицы телескопа второго блока 8 деления и второго блока 11 вычисления арктангенса, выход которого соединен со вторым входом блока 13 вычисления элементов сферического треугольника, последовательно подключенных ко второму выходу ПЗС-матрицы третьего блока 9 деления и третьего блока 12 вычисления арктангенса, выход которого соединен с третьим входом блока 13 вычисления элементов сферического треугольника. Причем вторые входы блоков 7, 8 и 9 деления соединены с выходом блока 14 определения расстояния fп ПЗС-матрицы от фокуса телескопа 1, четвертый, пятый и шестой входы блока 13 вычисления элементов сферического треугольника соединены с выходами блока 15 определения прямого восхождения αо и склонения δо оптической оси телескопа 1 во второй экваториальной системе координат и блока 16 определения угла разворота ϕρ между плоскостью круга склонения оптической оси телескопа 1 и вертикальной плоскостью приборной системы координат.
Предлагаемый способ реализуют следующим образом.
В моменты проведения измерений космический объект ρ фиксируется на фотоприемнике (ПЗС-матрице) в виде точки, линейные координаты которого (xρ, уρ) определяются в приборной системе координат OпXхр, Yпрdпр (фиг.1), жестко связанной с ПЗС-матрицей, плоскость которой устанавливается на расстоянии fп от фокуса телескопа перпендикулярно его оптической оси. Вместе с космическим объектом в моменты проведения измерений на ПЗС-матрице фиксируются изображения звезд (S1, S2, S3), в том числе и каталожных, координаты которых записаны в звездном каталоге (например, «FK-5», «Hipparcos») в виде прямого восхождения αs и склонения δs звезды с точностью долей угловых секунд во второй экваториальной системе координат х, у, z (фиг.1,2). Последняя используется в качестве стабилизированной системы координат.
Для того чтобы привязать подвижный космический объект ρ к каталожным звездам, необходимо получить его координаты также во второй экваториальной системе координат, т.е. получить прямое восхождение αρ и склонение δρ вектора 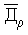 , направленного на измеряемый объект ρ (фиг.1).
, направленного на измеряемый объект ρ (фиг.1).
Поскольку направление оптической оси телескопа (оси dпр приборной системы координат) задается двумя установочными углами αуст, ηуст относительно осей орбитальной подвижной системы координат τ, ε, n, а положение осей хпр, упр определяется углом разворота ϕр относительно круга склонения оптической оси телескопа, то пересчет линейных координат подвижного космического объекта (xρ, yρ) и звезд (xsj, ysj) во вторую экваториальную систему координат производится путем последовательного перемножения матриц перехода между осями приборной и подвижной орбитальной систем координат, затем между осями подвижной орбитальной (τ, b, n) и абсолютной геоцентрической (х, у, z) системами координат в соответствии с правилами преобразования координат в пространстве (п. 2.6.5.2.3 «Справочник по математике для инженеров и учащихся ВТУЗов», авторы И.Н.Бронштейн. К.А.Семендяев, М.: Наука, 1980. - С.312-314).
Взаимное положение осей координат приборной (xпр, yпр, dпр), подвижной орбитальной (τ, b, n) и абсолютной геоцентрической (х, у, z) систем координат показано на фиг.2, а матрицы перехода между осями этих систем координат приведены в работе «Основы теории полета космических аппаратов». Под ред. Г.С.Нариманова. - М.: Машиностроение, 1972. - 608 с.
Пересчитав координаты объекта ρ из приборной в абсолютную геоцентрическую систему координат (АГЭСК) xρ, yρ, zρ, можно получить угловые координаты вектора 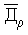 во второй экваториальной системе координат по формулам:
во второй экваториальной системе координат по формулам:
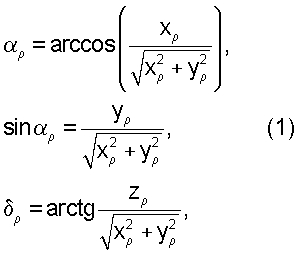
которые позволяют получить значения угла αρ в диапазоне [0, 2π], а угла δρ в пределах [-π/2, π/2].
Однако предложенный выше пересчет углов связан с большим количеством вычислений и большим риском получения ошибочных значений углов αρ, δρ, что связано, прежде всего, с допущением случайной ошибки в направляющих косинусах между осями систем координат или в результатах перемножения матриц перехода.
Предлагаемый способ пересчета линейных координат (xρ, yρ) в угловые координаты (αρ, δρ) лишен указанных выше недостатков и может использоваться в бортовой ЭВМ орбитального измерителя при условии, что известно направление оптической оси телескопа (углы αo, δo) во второй экваториальной системе координат и угол разворота ϕр вертикальной плоскости приборной системы координат, в которой лежат оси dпр, упр, относительно плоскости круга склонения оптической оси телескопа (дуга L1ρ на фиг.1).
Определение углов αо, δо и ϕр производится по разработанным алгоритмам прогноза и уточняется на момент проведения измерений путем привязки их к каталожным звездам.
Таким образом, в момент определения положения подвижного космического объекта ρ измеряются или считываются известными прямое восхождение αо и склонение δо оптической оси телескопа во второй оптической системе координат, угол разворота ϕр между плоскостью круга склонения оптической оси телескопа и вертикальной плоскостью приборной системы координат (осью упр), линейные координаты xρ, уρ изображения (проекции) объекта ρ на плоскость ПЗС-матрицы (точка ρ' на фиг.1) и расстояние fп вдоль оптической оси между фокусом телескопа (точка Оз на фиг.1) и плоскость ПЗС-матрицы (fп равно длине отрезка ОзОп).
Для определения угловых координат (αρ, δρ) вектора 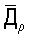 во второй экваториальной системе координат перенесем плоскость ПЗС-матрицы вдоль оптической оси на расстояние fп от фокуса телескопа, в результате чего плоскость ПЗС-матрицы в точке Оп будет касаться сферы радиусом fп с центром в точке фокуса телескопа Оз, который лежит в плоскости экватора Земли.
во второй экваториальной системе координат перенесем плоскость ПЗС-матрицы вдоль оптической оси на расстояние fп от фокуса телескопа, в результате чего плоскость ПЗС-матрицы в точке Оп будет касаться сферы радиусом fп с центром в точке фокуса телескопа Оз, который лежит в плоскости экватора Земли.
Поскольку оптическая ось телескопа перпендикулярна плоскости ПЗС-матрицы, то линейные координат xρ, yρ можно пересчитать в углы отклонения проекции точки ρ' на оси xпр, yпр (точки К и М на фиг.1) от оптической оси телескопа
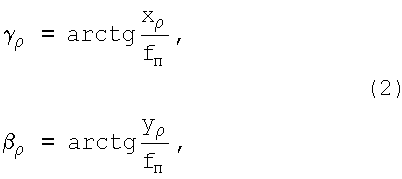
а отклонение направления вектора 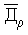 , проходящего через точку ρ', от направления оптической оси телескопа равно
, проходящего через точку ρ', от направления оптической оси телескопа равно
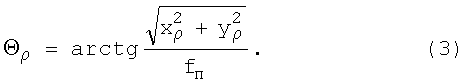
Переведя линейные координаты (xρ, yρ) в угловые значения γρ, βρ, Θρ, дальнейшие расчеты можно производить на сфере единичного радиуса, используя формулы сферической тригонометрии для расчета элементов сферических треугольников, образуемых пересечением дуг больших кругов на поверхности сферы единичного радиуса. Для этого проведем дуги больших кругов 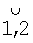 , в котором лежит вертикальная плоскость приборной системы координат (оси dпр, yпр),
, в котором лежит вертикальная плоскость приборной системы координат (оси dпр, yпр), 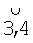 , в котором лежит горизонтальная плоскость приборной системы координат (оси dпр, xпр),
, в котором лежит горизонтальная плоскость приборной системы координат (оси dпр, xпр), 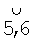 , в котором лежат векторы
, в котором лежат векторы 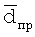 и
и 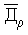 .
.
Проекция точки ρ на дугу 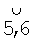 большого круга обозначена буковой ρ", а точки М и К спроецируются на дуги
большого круга обозначена буковой ρ", а точки М и К спроецируются на дуги 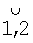 и
и 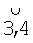 в виде точек М', К' (на фиг.1 не показаны). Точка Оп лежит на дуге
в виде точек М', К' (на фиг.1 не показаны). Точка Оп лежит на дуге 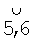 . Соединив точку ρ" с точками Оп и М' дугами больших кругов, получим прямоугольный сферический треугольник ОпМ'р", в котором известными элементами являются три стороны (Опρ"=Θρ,ОпМ'=βρ, ρ"М'=γρ) и угол ОпМρ"=π/2.
. Соединив точку ρ" с точками Оп и М' дугами больших кругов, получим прямоугольный сферический треугольник ОпМ'р", в котором известными элементами являются три стороны (Опρ"=Θρ,ОпМ'=βρ, ρ"М'=γρ) и угол ОпМρ"=π/2.
По теореме синусов в прямоугольном сферическом треугольнике OпM'ρ" имеем
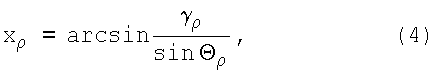
а по теореме косинусов сторон
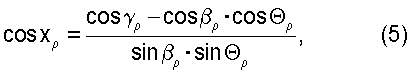
что позволяет определить угол разворота дуги ОпМρ" относительно вертикальной плоскости приборной системы координат (дуги 1,2) xρ в диапазоне [0,2π].
Из сферического треугольника ОпРρ", в котором известны две стороны (РОп=π/2-δо; Опρ"=Θρ) и угол (ϕρ+xρ), по теореме косинусов сторон имеем
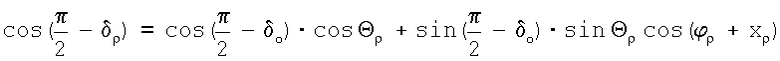 или
или
sin δρ=sinδocosΘρ+cosδosinΘρ·cos(fp+xυ),
откуда склонение вектора 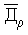 во второй экваториальной системе координат определяется по формуле
во второй экваториальной системе координат определяется по формуле
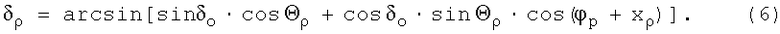
По теореме синусов в том же сферическом треугольнике получим
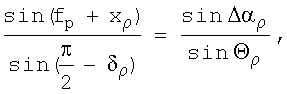 откуда
откуда
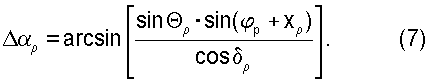
Из геометрических соотношений на фиг.1 следует, что прямое восхождение вектора 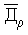 во второй экваториальной системе координат равно
во второй экваториальной системе координат равно

Таким образом, осуществлен прямой пересчет линейных координат (xρ, уρ) из приборной системы координат в угловые координаты (αρ, δρ) второй экваториальной системы координат.
Оптико-электронное устройство работает следующим образом.
В момент проведения измерений космический объект ρ фиксируется на фотоприемнике (ПЗС-матрицы) в виде точки, линейные координаты (xρ, yρ) определяются в приборной системе координат Опxпрyпрdпр (фиг.1), жестко связанной с ПЗС-матрицей, плоскость которой устанавливается на расстоянии fп от фокуса телескопа 1 перпендикулярно его оптической оси. Вместе с КО в моменты проведения измерений на ПЗС-матрице фиксируются звезды (S1, S2, S3, фиг.1), в том числе и каталожные, координаты которых известны.
Линейные координаты xρ, уρ КО с двух выходов телескопа 1 (ПЗС-матрицы) поступают на входы квадраторов 3 и 4, на первые входы блоков 8 и 9 деления соответственно. Сигналы, пропорциональные xρ 2 и yρ 2, с выхода квадраторов 3 и 4 поступают на два входа сумматора 5. Выходной сигнал последнего, пропорциональный xρ 2+yρ 2, поступает на вход блока 6 извлечения квадратного корня, выходной сигнал 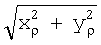 которого подается на вход блока 7 деления. На вторые входы блоков 7, 8 и 9 деления поступает сигнал, пропорциональный fп, с выхода блока 14. На выходе блоков 7, 8 и 9 деления образуются сигналы пропорциональные
которого подается на вход блока 7 деления. На вторые входы блоков 7, 8 и 9 деления поступает сигнал, пропорциональный fп, с выхода блока 14. На выходе блоков 7, 8 и 9 деления образуются сигналы пропорциональные
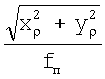 ;
; 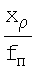 ;
; 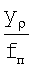 ,
,
соответственно, которые поступают на вход блоков 10, 11 и 12 вычисления арктангенса. На выходе последних образуются сигналы, пропорциональные
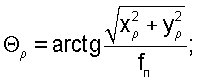
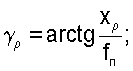
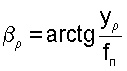
соответственно. Эти сигналы поступают на входы блока 13 определения элементов сферического треугольника, на другие входы которого подаются сигналы, пропорциональные αo, δo и ϕρ, с выходов соответствующих блоков 15 и 16.
В блоке 13 определяются угловые координаты КО во второй экваториальной системе координат:
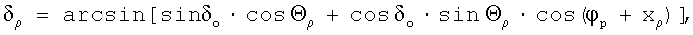
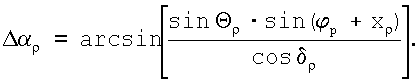
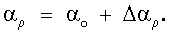
Все используемые для реализации заявленного оптико-электронного устройства блоки являются известными либо могут быть реализованы на базе известных блоков известными методами.
Таким образом, предлагаемые способ и устройство по сравнению с прототипами и другими техническими решениями аналогичного назначения обеспечивают повышение точности определения координат движущегося космического объекта на фоне звездного неба с помощью оптико-электронной аппаратуры, установленной на орбитальном измерителе. Это достигается путем привязки космического объекта к каталожным звездам, координаты которых с высокой точностью известны во второй экваториальной системе координат.
При этом для указанной привязки предложен метод прямого пересчета линейных координат, полученных в измерительной системе оптико-электронного прибора, в угловые координаты второй экваториальной системы координат.
Предлагаемый прямой метод пересчета линейных координат в угловые координаты по сравнению с классическим методом пересчета, основанным на последовательном перемножении матриц перехода в соответствии с правилами преобразования координат в пространстве, свободен от большого количества вычислений и большого риска получения ошибочных значений угловых координат в процессе перемножения матриц перехода.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ СОЗДАНИЯ КОСМИЧЕСКОЙ ГЕОДЕЗИЧЕСКОЙ СЕТИ | 2006 |
|
RU2337372C2 |
| Способ высокоточного позиционирования аппарата на поверхности Луны и устройство для его осуществления | 2018 |
|
RU2692350C1 |
| СПОСОБ АВТОНОМНОЙ НАВИГАЦИИ И ОРИЕНТАЦИИ КОСМИЧЕСКИХ АППАРАТОВ | 2021 |
|
RU2776096C1 |
| Телескоп | 1990 |
|
SU1770736A1 |
| Учебный прибор по астрономии и географии | 1987 |
|
SU1464199A1 |
| ВЫВЕРИТЕЛЬ ФОКУСИРОВКИ ТЕЛЕСКОПА | 1982 |
|
SU1839851A1 |
| Способ астрономической коррекции навигационных параметров летательного аппарата | 2021 |
|
RU2767449C1 |
| Способ спутниковой гравитационной градиентометрии | 2020 |
|
RU2745364C1 |
| Приборный отсек космического аппарата | 2015 |
|
RU2610850C1 |
| СПОСОБ И УСТРОЙСТВО УПРАВЛЕНИЯ ДВИЖЕНИЕМ КОСМИЧЕСКОГО АППАРАТА С УПРАВЛЯЕМОЙ ОРИЕНТАЦИЕЙ | 2017 |
|
RU2669481C1 |
Предлагаемый способ относится к области траекторных измерений параметров орбит подвижных космических объектов (КО) на фоне звездного неба. Достигаемым техническим результатом изобретения является повышение точности определения координат движущегося КО на фоне звездного неба. Результат достигается за счет того, что в заявленном способе определяют угловые координаты КО и пересчитывают полученные величины во вторую экваториальную систему координат путем привязки КО к каталожным звездам, координаты которых с высокой точностью известны во второй экваториальной системе координат. 3 ил.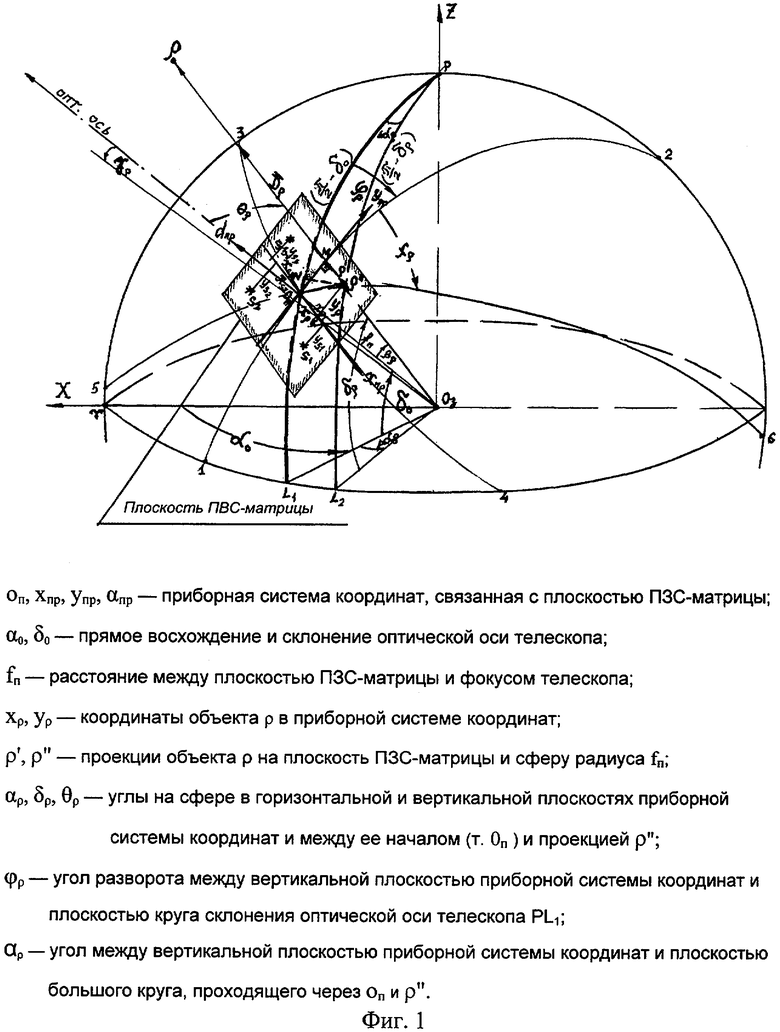
Способ определения координат космического объекта, заключающийся в определении угловой координаты космического объекта и последующем пересчете полученной величины в стабилизированную систему координат, отличающийся тем, что в качестве стабилизированной системы координат используют вторую экваториальную систему координат, дополнительно определяют линейные координаты xρ, уρ изображения космического объекта в приборной системе координат, жестко связанной с ПЗС-матрицей телескопа, плоскость которой устанавливают путем переноса вдоль оптической оси телескопа на расстоянии fп от фокуса телескопа перпендикулярно его оптической оси, прямое восхождение αо и склонение δо оптической оси телескопа во второй экваториальной системе координат и угол разворота ϕр между плоскостью круга склонения оптической оси телескопа и вертикальной плоскостью приборной системы координат, линейные координаты xρ, уρ пересчитывают в углы отклонения γρ, βρ проекции изображения космического объекта на оси xпр, упр приборной системы координат от оптической оси телескопа, определяют отклонения направления вектора 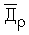 на космический объект от направления оптической оси телескопа, прямое восхождение αρ и склонение δρ вектора
на космический объект от направления оптической оси телескопа, прямое восхождение αρ и склонение δρ вектора 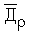 на космический объект во второй экваториальной системе координат, используя формулы сферической тригонометрии для расчета элементов сферических треугольников, образуемых пересечением дуг больших кругов на поверхности сферы единичного радиуса.
на космический объект во второй экваториальной системе координат, используя формулы сферической тригонометрии для расчета элементов сферических треугольников, образуемых пересечением дуг больших кругов на поверхности сферы единичного радиуса.
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ОБЪЕКТА И ОПТИКО-ЭЛЕКТРОННОЕ УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2003 |
|
RU2251712C1 |
| ОПТИКО-ЭЛЕКТРОННАЯ СИСТЕМА УПРАВЛЕНИЯ | 2000 |
|
RU2172010C1 |
| ПАРАЛЛАКТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ОБЪЕКТА | 1984 |
|
RU2027144C1 |
| Устройство определения направления на источник излучения | 1990 |
|
SU1764007A1 |
| US 6603539 B1, 05.08.2003 | |||
| US 6163372 A, 19.12.2000 | |||
| WO 9837434, 27.08.1998. | |||
Авторы
Даты
2008-03-10—Публикация
2006-04-19—Подача