ОБЛАСТЬ ТЕХНИКИ, К КОТОРОЙ ОТНОСИТСЯ ИЗОБРЕТЕНИЕ
Настоящее изобретение относится, в общем случае, к способам исследования подземных пластов с использованием акустических измерений, осуществляемых в буровой скважине. В частности, это изобретение направлено на создание способов определения величины, обратной скорости волны (медленности), в пласте вдоль и вокруг буровой скважины.
ПРЕДПОСЫЛКИ СОЗДАНИЯ ИЗОБРЕТЕНИЯ
Генерация и регистрация акустических волн в буровой скважине является основным способом измерений, используемым при каротаже нефтяных месторождений посредством зонда, опускаемого в буровую скважину на кабеле. В настоящее время существует множество скважинных устройств и способов для осуществления акустических измерений. Некоторые устройства содержат один источник акустических волн и два или более приемников, однако большинство устройств в настоящее время содержит множество приемников, расположенных в виде группы. Несмотря на то что существующие в настоящее время акустические устройства являются полезными для предоставления разнообразной информации о параметрах буровой скважины и соседних пластов, результаты акустических скважинных измерений используют, главным образом, для оценки величины, обратной скорости волны сжатия в пласте.
Оценку величины, обратной скорости волны сжатия в пласте, обычно осуществляют с использованием значений времени пробега волны, собранных способом обнаружения первого вступления. В предложенном из предшествующего уровня техники варианте с одним источником и двумя приемными устройствами оценку величины, обратной скорости волны в пласте, осуществляют путем вычитания значений времени вступления между двумя приемниками и деления на расстояние между приемниками. Однако такой оценке свойственны погрешности вследствие наклона скважинного устройства, размыва ствола скважины, влияния границы пласта и т.д. Для снижения погрешностей, вносимых таким влиянием окружающей среды, были использованы дополнительные источники и приемники акустических волн и более устойчивые способы, одним из которых является, например, способ STC (анализа временной когерентности величины, обратной скорости волны).
Вышеописанный способ измерения времени пробега волны для определения величины, обратной скорости волны в пласте, также имеет другие недостатки. Существующие способы обеспечивают получение только одномерных значений величины, обратной скорости волны в пласте, вдоль оси скважины и не используют имеющуюся в сигнале ценную информацию о свойствах пласта в иных направлениях, например, в радиальном и/или в азимутальном направлениях, перпендикулярных к оси скважины, которая является присущей этому сигналу.
Чтобы преодолеть затруднения при оценке распределения величины, обратной скорости волны в обоих направлениях: осевом и радиальном, может быть использовано решение обратной кинематической задачи томографическим методом (то есть "томография"). Цель решения обратной кинематической задачи томографическим методом состоит в нахождении такого решения или такой модели (то есть распределение величины, обратной скорости волны в пласте, вдоль и вокруг буровой скважины), которые минимизируют расхождение между измеренными и вычисленными значениями времени пробега для всех пар источник - приемник. Основное уравнение кинематической томографии обычно является нелинейным, но может быть решено посредством итерационного алгоритма решения, начиная с исходной модели. При каждой итерации этого процесса решения выполняют следующие две операции: решение прямой задачи и решение обратной задачи. При "решении прямой задачи" вычисляют время пробега волны для каждой пары источник - приемник для заданной модели (либо исходя из исходного предположения, либо исходя из результата предыдущей итерации). Однако, поскольку используемая модель, вероятно, не является истинной моделью подземной структуры, то вычисленные значения времени пробега обычно не соответствуют реальным измеренным значениям времени пробега. Следовательно, после этой операции "решения прямой задачи" вычисляют расхождение между реально измеренными и вычисленными значениями времени пробега, а затем минимизируют его способом оптимизации/минимизации (например, способом обратного проецирования или способом сопряженных градиентов) для исправления/корректировки предыдущей результирующей модели. Эти две операции осуществляют многократно до тех пор, пока не будет достигнуто наилучшее соответствие (то есть пока не будет получено схождение погрешностей времени пробега волны). Таким образом, получают модель окончательного решения. Успех томографического метода сильно зависит от этих операций решения прямой задачи и решения обратной задачи. Для каждой из этих двух операций более критичным и существенным фактором является численный метод, используемый для решения прямой задачи. Легко понять, что при неточном и менее устойчивом решении прямой задачи происходит генерация неправильных значений времени пробега волны, что, следовательно, приводит к неправильному окончательному решению.
Подобный способ томографии, основанный на решении обратной кинематической задачи для значений времени пробега, измеренных устройством акустического каротажа, предложен в патенте США №5,081,611 (B. Hornby, 1992 г.). Хорнби (Hornby) утверждает, что его способ обеспечивает возможность определения распределений величины, обратной скорости волны, на расстоянии от буровой скважины. Однако способ, раскрытый Хорнби (Hornby), используют редко, вероятно, потому, что ядро для решения прямой задачи, основанное на способе трассировки лучей для преломленных волн, является ненадежным. Кроме того, в способе, предложенном Хорнби (Hornby), требуется наличие неявно наложенных виртуальных слоев вдоль оси скважины, имеющих недостаточную устойчивость относительно априорной информации и геологического обоснования. Кроме того, способ, предложенный Хорнби (Hornby), ограничен только двумя измерениями, то есть направлением вдоль оси скважины и одним из радиальных направлений.
Как описано выше, необходимой операцией при решении этой обратной томографической задачи является решение прямой задачи, и его устойчивость и эффективность являются решающими факторами для успеха решения обратной задачи. Несмотря на то что трассировка лучей является хорошо известным способом численного моделирования и широко используется в акустической области для вычисления времени пробега, этот способ имеет многочисленные ограничения, препятствующие его устойчивому использованию для акустической томографии. Например, в способах трассировки лучей предполагают, что частота акустических волн является бесконечно высокой. Однако реальные волны часто имеют ограниченную полосу частот. На распространение реальных волн оказывают воздействие не только структуры вдоль траектории луча, что подразумевают в лучевом приближении, но также и среда в окрестностях траектории луча. Для акустических волн, у которых длина волны не является много меньшей, чем расстояние между источником и приемниками, такое лучевое приближение является недостаточно точным. Кроме того, вычисление способом трассировки лучей является дорогостоящим, нестабильным, и его практическое применение для трехмерной (3-D) томографии является затруднительным.
Настоящее изобретение направлено на подавление или, по меньшей мере, уменьшение влияния одной или большего количества из изложенных выше проблем.
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
Настоящее изобретение обеспечивает решение вышеописанных и иных потребностей. В частности, в настоящем изобретении предусмотрен способ определения величины, обратной скорости волны, в участках пласта, пересекаемых буровой скважиной, содержащий следующие операции: осуществляют формирование акустических волн устройством акустического каротажа, содержащим источник и, по меньшей мере, один приемник, и вычисляют путь волн во френелевском объеме для акустических волн.
В настоящем изобретении также предложен способ определения величины, обратной скорости волны, в трехмерном (3-D) пласте, расположенном вокруг буровой скважины, по данным устройства акустического каротажа, снабженного источником акустических волн и множеством приемников, содержащий следующие операции: для пласта и буровой скважины задают исходную модель величины, обратной скорости волны, вычисляют френелевский объем, отображающий путь (френелевские объемы, отображающие пути) распространения волны, для каждого приемника вычисляют теоретическое значение времени первого вступления на основании пути распространения волны во френелевском объеме, вычисляют функцию измеренного значения времени первого вступления и теоретического значения времени первого вступления для каждого приемника, при этом измеренное значение времени первого вступления для каждого приемника определяют по данным устройства акустического каротажа, осуществляют обратное проецирование функции вдоль пути волны первого вступления во френелевском объеме, производя, тем самым, модификации исходной модели величины, обратной скорости волны, для множества участков пласта, и модифицируют исходную модель величины, обратной скорости волны, как функцию произведенных модификаций.
Согласно другому аспекту изобретения предлагается способ определения величины, обратной скорости волны, в участках пласта, пройденных буровой скважиной, содержащий следующую операцию: применяют томографию зоны Френеля для данных акустического каротажа.
В настоящем изобретении также предложено устройство для определения величины, обратной скорости волны в пласте, содержащее источник акустических волн, приемник акустических волн и процессор, соединенный с источником акустических волн и с приемником акустических волн и запрограммированный таким образом, что вычисляет и корректирует зону Френеля с учетом акустических волн, генерация которых осуществлена источником акустических волн, а их прием осуществлен приемником акустических волн.
Дополнительные преимущества и существенные новые признаки настоящего изобретения сформулированы в приведенном ниже описании или могут быть понятны специалистам в данной области техники путем изучения этих материалов или практической реализации настоящего изобретения. Преимущества настоящего изобретения могут быть достигнуты средствами, изложенными в прилагаемой формуле изобретения.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
На сопроводительных чертежах представлены предпочтительные варианты осуществления настоящего изобретения, являющиеся частью описания. Вместе с приведенным ниже описанием чертежи демонстрируют и поясняют принципы настоящего изобретения.
На Фиг.1 изображен вид устройства акустического каротажа, соединенного с процессором, согласно одному из вариантов осуществления настоящего изобретения.
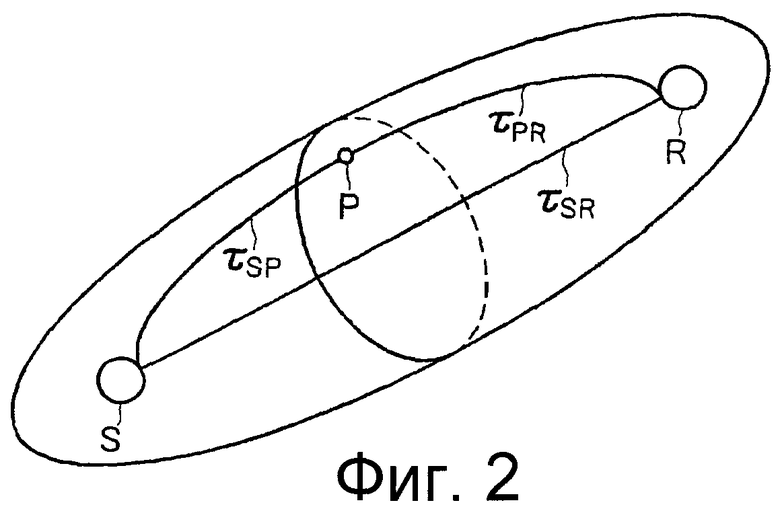
На Фиг.2 показано схематичное изображение френелевского объема, соответствующего источнику и приемнику.
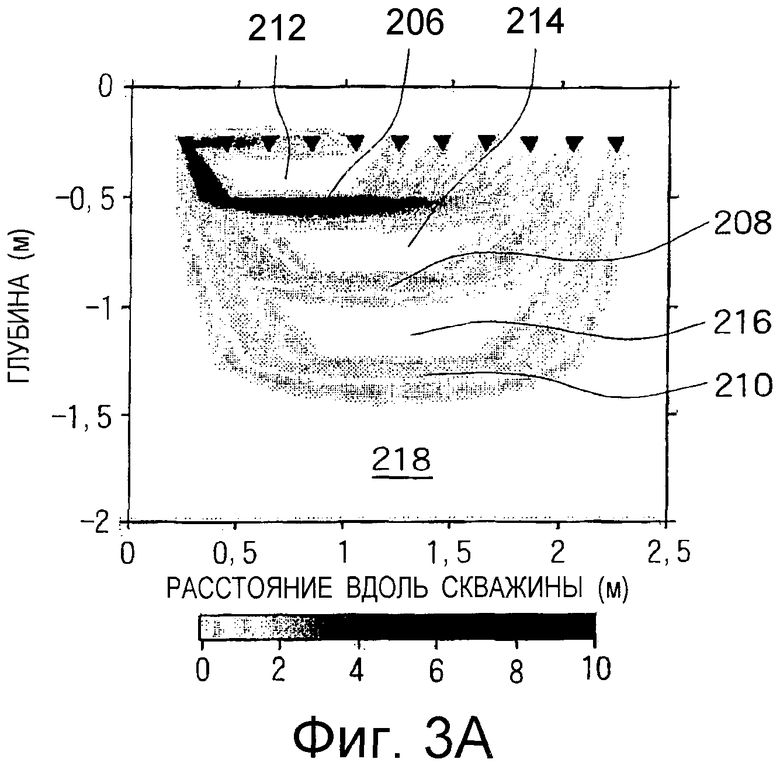
На Фиг.3А показан пример головной волны во френелевском объеме в четырехслойной среде согласно одному из вариантов осуществления настоящего изобретения.
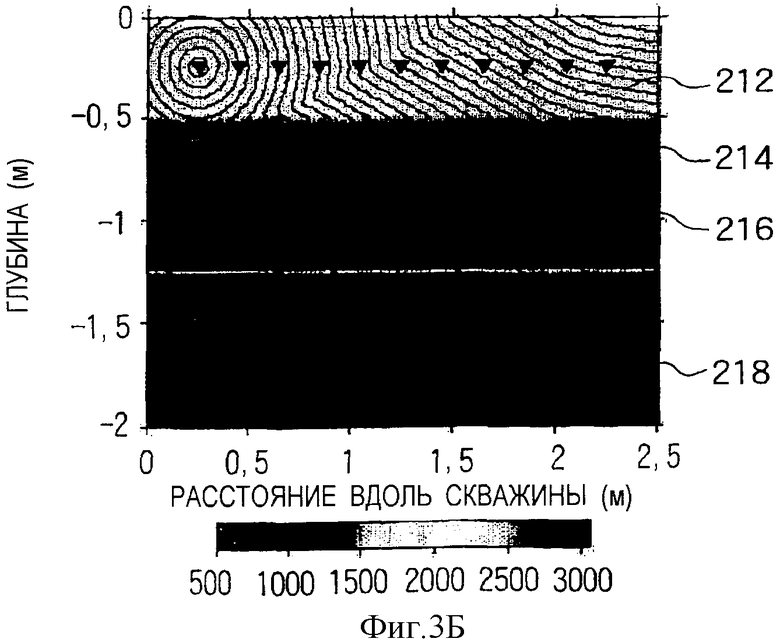
На Фиг.3Б показана диаграмма траекторий лучей первого вступления для четырехслойной среды согласно Фиг.3А.
На Фиг.4 показано схематическое объяснение алгоритма восстановления согласно одному из вариантов осуществления настоящего изобретения.
На Фиг.5 показана схема последовательности операций для определения величины, обратной скорости волны в пласте, согласно одному из объектов настоящего изобретения.
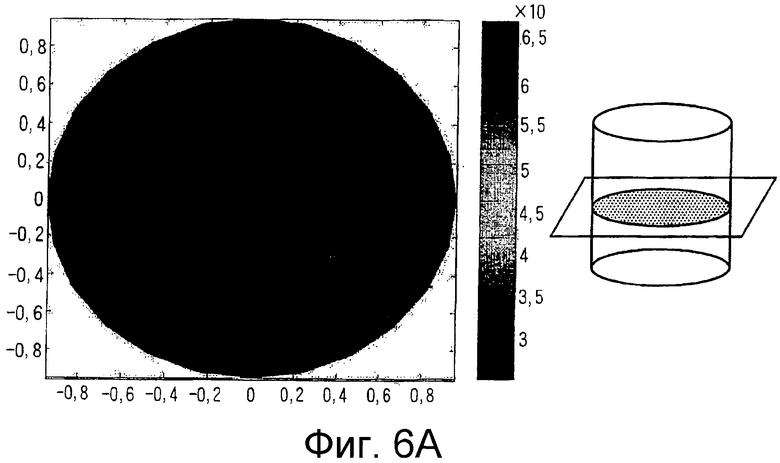
На Фиг.6А показан профиль величины, обратной скорости волны, для гипотетического пласта, полученный способом компьютерного моделирования.
На Фиг.6Б показан оценочный расчет профиля величины, обратной скорости волны, полученный путем решения обратной задачи, исходя из синтезированных значений времени пробега волны, вычисленных для гипотетического пласта.
На Фиг.6В показаны выраженные в процентах изменения разности между наблюдаемым временем пробега волны в гипотетическом поле величины, обратной скорости волны, и вычисленными значениями времени пробега в восстановленном поле величины, обратной скорости волны.
На всех чертежах идентичные элементы обозначены одинаковыми номерами позиций.
ПОДРОБНОЕ ОПИСАНИЕ ПРЕДПОЧТИТЕЛЬНЫХ ВАРИАНТОВ ОСУЩЕСТВЛЕНИЯ ИЗОБРЕТЕНИЯ
Теперь приведено описание чертежей и, в частности, чертежа Фиг.1, на котором показано устройство (100) акустического каротажа, расположенное рядом с однородным пластом (102). Устройство (100) акустического каротажа содержит источник (S) и, по меньшей мере, один приемник (R). В настоящем варианте осуществления изобретения имеется два приемника (R), однако также может быть использовано намного большее количество приемников (R) и источников (S). Показанный на чертеже вариант компоновки с одним источником (S) и двумя приемниками (R), по существу, приведен лишь в качестве примера, и может иметь место вариант с полным набором приемников и/или источников. Приемники (R) и источник (S) соединены с компьютерным процессором (104), служащим для сбора и обработки данных, поступающих из устройства (100) акустического каротажа. Также показана траектория (106) сейсмического луча, представляющая собой траекторию волны сжатия, вызванной приведением в действие источника (S). Приемники (R) могут представлять собой приемники различных типов, в том числе, пьезоэлектрические и магниторестриктивные приемники, но эти примеры не являются ограничивающим признаком. Приемники (R) способны обнаруживать вступление акустических волн.
Собранную из устройства (100) акустического каротажа информацию или данные, которые могут содержать сигналы, формирование которых осуществлено приемниками (R) в течение времени, передают в компьютерный процессор (104) через кабель (108), на котором подвешено устройство (100) акустического каротажа, или любым иным удобным способом связи. Компьютерный процессор (104) представляет собой серийно выпускаемое устройство, которое может быть приобретено у многочисленных поставщиков. Обработка данных акустического каротажа, снятых устройством (100) акустического каротажа и полученных компьютерным процессором (104), может быть реализована с использованием способа на основе френелевского объема (описание которого приведено ниже) для определения величины, обратной скорости волны в пласте, согласно способу из настоящего изобретения. Вычисление величины, обратной скорости волны в пласте, может быть выполнено компьютерным процессором (104) на буровой площадке, или же вычисления могут быть осуществлены в месте обработки вне буровой площадки с использованием данных акустического каротажа, собранных устройством (100) акустического каротажа. Кроме того, согласно некоторым способам из настоящего изобретения вычисление величины, обратной скорости волны в пласте, реализованное способом на основе френелевского объема, может быть выполнено компьютерным процессором (104) в реальном масштабе времени.
Затем, переходя к рассмотрению Фиг.2, на ней показано схематичное изображение френелевского объема (200). Согласно одному из вариантов осуществления настоящего изобретения способ на основе френелевского объема (200) для обработки данных акустического каротажа может быть реализован для определения величины, обратной скорости волны в пласте. Френелевский объем (200), соответствующий источнику (S) акустических волн и приемнику (R), изображен точкой (P), которая удовлетворяет приведенному ниже уравнению:

где  - время пробега волны от источника (S) до рассматриваемой точки (P),
- время пробега волны от источника (S) до рассматриваемой точки (P),  - время пробега волны от приемника (R) до рассматриваемой точки (P),
- время пробега волны от приемника (R) до рассматриваемой точки (P),  - кратчайшее время пробега волны от источника (S) до приемника (R), а ƒ - частота акустических волн (1/ƒ - период).
- кратчайшее время пробега волны от источника (S) до приемника (R), а ƒ - частота акустических волн (1/ƒ - период).
Следовательно, френелевский объем или зона (200) Френеля могут быть описаны как множество возможных лучей (лучи представляют собой линии, перпендикулярные к фронтам волны), имеющих задержку по времени, не превышающую половину периода. Реализация френелевского объема (200) имеет преимущество, заключающееся в том, что она устраняет потребность в способах трассировки лучей, известных из предшествующего уровня техники, которые трудно реализовать, а их практическое применение ограничено двумерной (2-D) томографией. Отсутствует необходимость в точной трассировке луча, поскольку он содержится во френелевском объеме (200) в неявном виде.
Согласно настоящему изобретению оценка френелевского объема (200) может быть осуществлена методом Видэйла (Vidale, 1988), который содержит решение уравнения эйконала посредством конечно-разностного приближения. В частности, согласно одному из способов, предложенных в настоящем изобретении, определение зоны (200) Френеля содержит объединение волновой теории, теоремы обратимости и принципа Ферма. В теории распространения волн справедлив принцип обратимости, то есть значения времени пробега волны от приемника (R) до рассматриваемой точки (P) и от этой точки (P) до приемника (R) равны 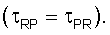 Принцип Ферма гласит, что траектория луча света между двумя точками представляет собой путь, время прохождения по которому является минимальным. Принцип Ферма также справедлив и для звуковых волн.
Принцип Ферма гласит, что траектория луча света между двумя точками представляет собой путь, время прохождения по которому является минимальным. Принцип Ферма также справедлив и для звуковых волн.
Следовательно, согласно одному из вариантов осуществления настоящего изобретения зона Френеля может быть получена путем вычисления значения времени пробега волн для всего пространства, например для ячейки (202), суммирования значений времени пробега волны как между приемником (R) и рассматриваемой точкой (P), так и между источником (S) и рассматриваемой точкой (P) 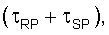 вычитания времени пробега волны между источником (S) и приемником (R)
вычитания времени пробега волны между источником (S) и приемником (R)  из суммы
из суммы 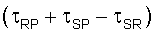 и нахождения зоны, в которой выполняется уравнение (1). Эта зона является зоной (200) Френеля по определению и представляет собой устойчивый способ "трассировки лучей", поскольку в алгоритме не находят точную траекторию луча.
и нахождения зоны, в которой выполняется уравнение (1). Эта зона является зоной (200) Френеля по определению и представляет собой устойчивый способ "трассировки лучей", поскольку в алгоритме не находят точную траекторию луча.
Однако траектории, определяемые зоной (200) Френеля, могут быть уточнены путем присвоения значений весовых коэффициентов в отдельных узловых точках сетки. Для уточнения траекторий путем присвоения значений весовых коэффициентов выбирают надлежащую весовую функцию. Например, может быть выбрано экспоненциальное значение весового коэффициента, уменьшающееся от 1 до 0 по экспоненте при увеличении измеренной временной задержки распространения волны согласно приведенному ниже уравнению:

где 
На Фиг.3 показан пример френелевского объема головных волн, отображенных как значения весовых коэффициентов с использованием весовой функции из уравнения (2). На фигуре показано множество зон (206, 208 и 210) Френеля, характеризующих наличие множества слоев (212, 214, 216, 218) в пласте. Аналогичным образом, на Фиг.3Б показаны траектории лучей первого вступления к множеству приемников при одном положении источника для четырехслойного пласта. На Фиг.3Б ясно видны преломленные волны от второго (214), третьего (216) и четвертого (218) слоев.
Томография френелевского объема отличается от стандартных способов томографии, основанных на точной трассировке лучей, в которых рассматривают траекторию одного луча. В томографии френелевского объема траекторию луча рассматривают как пучок, а не как одиночную линию. Эти траектории лучей реализованы посредством значений весовых коэффициентов на сетке. Следовательно, ядро решения обратной томографической задачи содержит значения весовых коэффициентов. Время пробега волны от источника до приемника в высокочастотном приближении может быть выражено следующим интегральным уравнением:

где  обозначает траекторию k-го луча,
обозначает траекторию k-го луча, 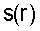 - величина, обратная скорости волны, на сетке, а
- величина, обратная скорости волны, на сетке, а  - длина дуги. С учетом реализованных здесь значений
- длина дуги. С учетом реализованных здесь значений  весовых коэффициентов уравнение перезаписано в следующем виде:
весовых коэффициентов уравнение перезаписано в следующем виде:
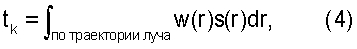
Путем выбора надлежащей весовой функции френелевский объем может отображать распространение волн с конечной частотой, полученное из волновой теории. Преимущество подхода на основе френелевского объема состоит в том, что он не требует большого времени вычисления по сравнению с другими подходами на основе волновой теории. Подход на основе френелевского объема является промежуточным между лучевым приближением и волновой теорией.
Согласно решению обратной задачи для всех волн на основе волнового уравнения для акустических волн, минимизируемая функция ошибок определяется как полная мощность разностей формы волны. Вычисляют градиент функции ошибок относительно скорости путем корреляции разностей волнового поля, распространяющегося в прямом направлении, и волнового поля, распространяющегося в обратном направлении. Путем выбора надлежащей весовой функции френелевский объем может отображать распространение волн с конечной частотой, полученное из волновой теории. Преимущество подхода на основе френелевского объема состоит в том, что он не требует большого времени вычисления по сравнению с другими подходами на основе волновой теории. Подход на основе френелевского объема является промежуточным между лучевым приближением и волновой теорией.
Как описано выше, вычисление траектории волн в зоне Френеля осуществляют путем простых вторичных вычислений времени пробега волны и выражают путем значений весовых коэффициентов на сетке. Затем может быть получено решение обратной задачи для зоны Френеля для восстановления сетки поля величины, обратной скорости волны, на той же самой сетке, которая была использована для вычисления времени пробега и френелевских объемов. Например, в однородном поле S величины, обратной скорости волны, где T - время пробега волны для пары источник - приемник, которые расположены на расстоянии L друг от друга, зависимость между величиной, обратной скорости волны, и временем пробега может быть математически описана как:


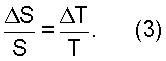
Скорректированная величина 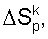 обратная скорости волны, в р-й узловой точке сетки при k-й итерации и погрешность
обратная скорости волны, в р-й узловой точке сетки при k-й итерации и погрешность  времени пробега i-х лучей выражаются следующими уравнениями:
времени пробега i-х лучей выражаются следующими уравнениями:
 и
и

где 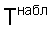 и
и 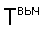 - наблюдаемое время пробега и вычисленное время пробега для текущей модели.
- наблюдаемое время пробега и вычисленное время пробега для текущей модели.
Если 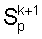 задано таким образом, что является истинным значением
задано таким образом, что является истинным значением  величины, обратной скорости волны, и использовано уравнение (4), то может быть получена следующая зависимость между величиной, обратной скорости волны, и временем пробега, связанная со значениями весовых коэффициентов в каждой узловой точке сетки:
величины, обратной скорости волны, и использовано уравнение (4), то может быть получена следующая зависимость между величиной, обратной скорости волны, и временем пробега, связанная со значениями весовых коэффициентов в каждой узловой точке сетки:

где  - значения весовых коэффициентов в каждой узловой точке сетки, вычисленные посредством уравнения (2). Учитывая все лучи, скорректированная величина, обратная скорости волны, для каждой узловой точки сетки может быть выражена следующим образом:
- значения весовых коэффициентов в каждой узловой точке сетки, вычисленные посредством уравнения (2). Учитывая все лучи, скорректированная величина, обратная скорости волны, для каждой узловой точки сетки может быть выражена следующим образом:

Наконец, из уравнений (4) и (6) получают параметр корректировки в следующем виде:
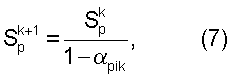
где 
Уравнение (7) является развитием обычного способа одновременного итерационного восстановления (SIRT), примененного к зоне Френеля, в котором корректировку величины, обратной скорости волны, осуществляют после учета всех траекторий лучей. На Фиг.4 показано объяснение алгоритма восстановления, например алгоритма, подробное описание которого приведено выше. Способ SIRT представляет собой один из пригодных способов обратного проецирования; понятно, что может быть использован иной способ обратного проецирования.
Способ томографии зоны Френеля был первоначально разработан для сейсмических прикладных задач (например, Ватанабе (Watanabe) и др. 1999), однако согласно настоящему изобретению способ на основе зоны Френеля приспособлен для применения к данным акустического каротажа. Сбор данных акустического каротажа обычно осуществляют при небольшом расстоянии между источником и приемником с несколькими смещениями, покрывающими сотни футов длины буровой скважины. Однако восстановленная область охватывает собой только лишь несколько футов от буровой скважины. Следовательно, применение томографии зоны Френеля для данных акустического каротажа согласно настоящему изобретению может содержать конкретные варианты ее адаптации.
Согласно одному из способов, предложенных в настоящем изобретении, применение томографии зоны Френеля для данных акустического каротажа может содержать следующую операцию: для пласта задают исходную модель величины, обратной скорости волны, в виде многослойной структуры. Как описано выше, вычисление величины, обратной скорости волны, с использованием томографии зоны Френеля представляет собой итерационный процесс, поэтому "наилучшая предполагаемая" модель может быть задана на основании анализа подобия данных акустического каротажа и использования данных кавернограммы (при их наличии). Однако итерационный процесс определения величины, обратной скорости волны, с использованием зон Френеля является устойчивым и поэтому менее чувствительным к неточной исходной модели. На Фиг.5 продемонстрирован один из способов вычисления величины, обратной скорости волны, с использованием томографии зоны Френеля согласно настоящему изобретению.
Исходная модель (500) величины, обратной скорости волны, может быть построена путем дельта-t обработки и с использованием данных кавернограммы. Модель может быть отображена на координатной сетке, а способ вычисления величины, обратной скорости волны, может содержать следующую дополнительную операцию: соответствующие координаты из координатной сетки модели присваивают данным о времени пробега акустических волн, собранных устройством (100, Фиг.1) акустического каротажа, что показано в блоках (504 и 505), подробное описание которых приведено ниже. Для создания координатной сетки модели выбирают сигналы первого вступления из сигналов от акустических волн (504), а затем выбранные данные о времени пробега акустических волн могут быть упорядочены по координатам модели (505). Координатная сетка может быть разделена на дискретные интерпретационные блоки (502) на основании исходной модели (500), что в предпочтительном варианте осуществляют таким образом, чтобы блок содержал однородный участок пласта. Относительно малый интерпретационный блок обеспечивает возможность более удобного применения процесса решения обратной задачи. Кроме того, может быть задана (506) начальная полоса частотного фильтра.
Затем может быть осуществлено оценочное вычисление френелевского объема путем решения прямой/обратной задачи для значений времени пробега (508) волны описанным выше способом, после чего путем решения обратной задачи восстанавливают величину, обратную скорости волны в пласте, согласно способу обратного проецирования (также описанному выше). Для преодоления проблемы, связанной с чрезвычайно большим соотношением между длиной и шириной для данных акустического каротажа, согласно одному из способов, предложенных в настоящем изобретении, для вычисления времени пробега волны в прямом направлении может быть взят прямоугольный элемент. Вычисление значений времени пробега волны для прямоугольных сеток может быть выполнено, например, способом быстрой прогонки или способом линейной интерполяции времени пробега. Способ быстрой прогонки был недавно разработан Сетианом (Sethian, 1996) для анализа и вычисления движения границы раздела сред при множестве установочных параметров. Этот алгоритм является быстрым и применимым для геометрической конфигурации общего вида, сохраняя при этом реальную точность.
Ключевые моменты способа быстрой прогонки могут содержать следующие операции: осуществляют построение решения уравнения эйконала, вытекающий из наименьших значений времени пробега волны, отходят от граничного условия в направлении постепенного уменьшения, и повторно вычисляют значения времени пробега волны в соседних точках в направлении постепенного уменьшения, которые не могут выдать меньшее значение, чем любая из известных точек. При использовании этого способа отсутствует какая-либо необходимость возврата и повторного посещения точки с известным значением, поскольку известные значения остаются неизменными при всех последующих вычислениях.
Кроме того, оценочное вычисление френелевского объема содержит следующие операции: присваивают значения весовых коэффициентов (510) описанным выше способом, осуществляют корректировку величины, обратной скорости волны в пласте, на основании обратного проецирования (512), а затем осуществляют проверку погрешностей между измеренными и модельными значениями времени пробега (514) волны. На основании измеренных погрешностей регулируют и переназначают полосу частотного фильтра (516), а также интерпретационные блоки (518); и производят итерационное оценочное вычисление величины, обратной скорости волны, путем повторения операций, обозначенных блоками (508-514), до тех пор, пока погрешности не сойдутся. Когда получено схождение погрешностей, способ завершают (520).
Томограммы величины, обратной скорости волны, восстановленные с использованием способа обратного проецирования, также могут быть использованы в конфигурации для получения трехмерной томограммы. Для облегчения трехмерного восстановления может быть использовано средство решения уравнения эйконала. Полезным является средство решения цилиндрического уравнения эйконала, поскольку данные акустического каротажа измерены вокруг буровой скважины. Известный из предшествующего уровня техники способ быстрой прогонки был реализован в декартовых и в сферических координатах. В настоящем изобретении способ быстрой прогонки, представленный в виде формул, был распространен на трехмерные (3-D) цилиндрические координаты. Описание формул приведено ниже.
Средство решения трехмерного цилиндрического уравнения эйконала
Ниже приведено описание формульного представления уравнения эйконала в цилиндрических координатах на основании алгоритма быстрой прогонки. Средства решения уравнения эйконала представляют собой примеры того, каким образом следует решать использованные математические выражения согласно некоторым аспектам настоящего изобретения, однако также может быть использован иной способ решения соответствующих математических уравнений. Выражение для уравнения эйконала в цилиндрических координатах имеет следующий вид:
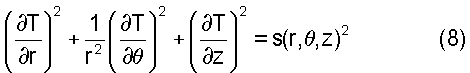
Однако, как описано ниже, логика вычислений меняется для различных случаев.
Общий случай 1: вычисляемая точка имеет шесть соседних точек, по две в каждом направлении
Сначала задают операторы правой и левой пространственных производных в следующем виде:
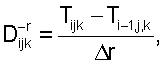



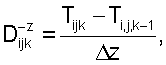
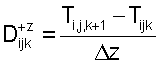
Таким образом, уравнение эйконала может быть аппроксимировано приведенной ниже формулой:

Если в одном заданном направлении две соседних точки уже были вычислены, то в приближении уравнения эйконала окажется точка, имеющая минимальное значение. Если известна только одна соседняя точка, то другая равна бесконечности, и, следовательно, в приближении уравнения эйконала окажется только известное значение. Если не была вычислена ни одна из соседних точек, то обе из них имеют значение, равное бесконечности, и, следовательно, в приближении уравнения эйконала соответствующий член исчезает.
Случай 1a - в каждом направлении уже была вычислена, по меньшей мере, одна точка
Для решения этого уравнения выбраны следующие условные обозначения:
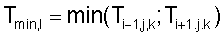
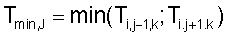

Следовательно, уравнение эйконала может быть записано в следующем виде:

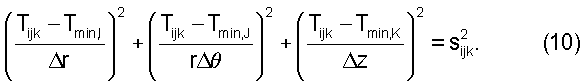
Это приводит к квадратному уравнению (11):
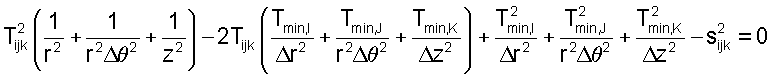
и получаем:
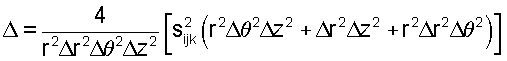
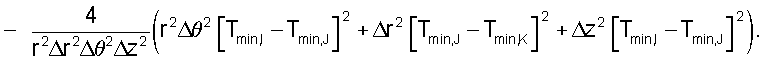
Беря решение, которое дает большее значение времени пробега, чем уже вычисленные значения:
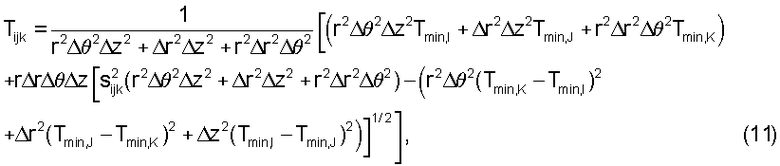
И, используя следующие условные обозначения:

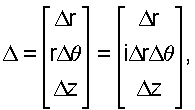

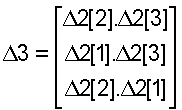
получают приведенное ниже уравнение (12):

Случай 1b - две соседние точки в одном направлении являются неизвестными
Когда неизвестны две соседние точки в одном направлении, имеется только два минимума, возникающие в приближении уравнения эйконала. Эти два минимума обозначают как T1 и T2, а соответствующие расстояния между узлами сетки (расстояние между узлами сетки в том направлении, в котором уже была вычислена, по меньшей мере, одна соседняя точка) как Δ1 и Δ2. Таким образом, приближение уравнения эйконала имеет следующий вид:

Это приводит к квадратному уравнению:


И, следовательно,
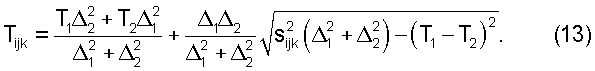
Случай 1с - Две соседние точки в двух направлениях являются неизвестными
Когда неизвестны две соседние точки в двух направлениях, то уравнение эйконала дает только одно минимальное время пробега волны. Именуя этот минимум как T, а соответствующее расстояние между узлами сетки как Δ, решение является тривиальным и дает следующий результат:


Случай 2 - Особый случай: вычисляемая точка расположена на вертикальной оси на цилиндрической решетке
Случай 2а - Соседние точки расположены на вертикальной оси
На вертикальной оси местоположение не играет никакой роли. Следовательно, рассматривают соседнюю точку с наименьшим временем вступления, точно так же, как и в общем случае.
Случай 2b - Соседние точки расположены в плоскости (r, θ)
В плоскости (r, θ) вычисляемая точка имеет более двух соседних точек. Если точка имеет положение (0, j, k) (j может принимать любое значение), то соседними точками являются m точек с координатами (1, j, k), где j∈{1..m}. Соответственно, определяют, какая именно точка имеет наименьшее значение времени вступления, и наименьшее значение времени вступления используют для решения приближения уравнения эйконала. Поэтому в данном случае приближение уравнения эйконала имеет только два члена.
Если T1 - минимальное время пробега в вертикальном направлении, а T2 - соседняя точка в плоскости (r, θ) с минимальным временем пробега, то Δ1 равно Δz, а Δ2 равно Δr. Следовательно, приближение уравнения эйконала записывается в следующем виде:
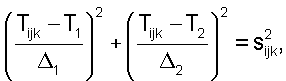
что приводит к квадратному уравнению:
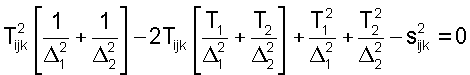

И, следовательно,
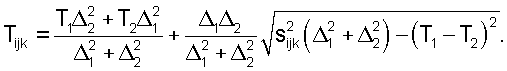
Согласно одному из способов, предложенных в настоящем изобретении, алгоритмы ориентации скважинного устройства способны распознавать положение источника (S) и приемника (R) и объединять информацию о положении с решениями обратной томографической задачи для создания трехмерных томограмм величины, обратной скорости волны.
Используя вышеописанный способ, может быть выполнено компьютерное моделирование для трехмерной (3-D) томографии. Например, было проведено экспериментальное испытание, описание которого приведено ниже. Были предусмотрены следующие варианты: гипотетический пласт с буровой скважиной, поврежденная зона в пласте и невскрытый пласт. На Фиг.6А показан график величины, обратной скорости волны, для гипотетического пласта. Исследование гипотетического пласта было проведено при помощи имитационного моделирования скважинного устройства, имеющего восемь приемников, расположенных в азимутальном направлении через каждые 45 градусов, и тринадцать уровней, расположенных вдоль оси на расстоянии шесть дюймов один от другого, на расстоянии от двенадцати до восемнадцати футов от источника. Значения времени пробега, смоделированные посредством такого скважинного устройства, были вычислены средством решения трехмерного цилиндрического уравнения эйконала. Значения времени пробега волны, полученные в местах расположения приемников, были введены в средство томографической обработки для решения обратной задачи для профиля величины, обратной скорости волны. Результаты восстановления величины, обратной скорости волны, для гипотетического пласта показаны на Фиг.6Б.
На Фиг.6В показаны выраженные в процентах изменения разности между наблюдаемым временем пробега волны в гипотетическом поле величины, обратной скорости волны, и вычисленными значениями времени пробега волны в восстановленном поле величины, обратной скорости волны. После сорока итераций разность между наблюдаемыми и вычисленными значениями времени пробега волны составляла приблизительно три процента. Сравнение Фиг.6А и Фиг.6Б показало, что способом осуществлено успешное восстановление профиля величины, обратной скорости волны, для гипотетического пласта.
Вышеизложенное описание было приведено только лишь для пояснения и описания изобретения. Подразумевают, что оно не является исчерпывающим или ограничивающим изобретение каким-либо точным его вариантом осуществления, который был раскрыт. Вышеизложенная концепция изобретения предусматривает возможность множества его модификаций и вариантов.
Предпочтительный вариант осуществления изобретения был выбран и описан для наилучшего пояснения принципов настоящего изобретения и его практического применения. Приведенное выше описание предназначено для того, чтобы специалисты в данной области техники могли наилучшим образом использовать настоящее изобретение в различных вариантах его осуществления и с различными его модификациями, подходящими для конкретного предполагаемого его использования. Подразумевают, что объем патентных притязаний настоящего изобретения определяется приведенной ниже формулой изобретения.




Предложены способ и устройство для определения величины, обратной скорости волны в пласте, расположенном вокруг буровой скважины. Концепция френелевского объема применена для кинематической томографии. Френелевский объем отображает путь распространения акустической волны вблизи от буровой скважины. Применение френелевского объема для данных акустического каротажа обеспечивает устойчивое решение обратной задачи и возможность практической реализации трехмерной (3-D) томографии. Решение обратной задачи получают способом итерационного обратного проецирования. 4 н. и 38 з.п. ф-лы, 6 ил.
осуществляют формирование акустических волн устройством акустического каротажа, содержащим источник и, по меньшей мере, один приемник, и
вычисляют путь волн во френелевском объеме для акустических волн, при этом задают исходную модель для пути волн во френелевском объеме, причем указанная исходная модель является не однородной по меньшей мере в направлении оси буровой скважины.
вычисление значения времени пробега волны для полного пространства;
суммируют значения времени пробега волны от мест расположения источника и приемника до рассматриваемой точки;
вычитают наименьшее время пробега волны от источника до приемника; и находят зону, в которой сумма значений времени пробега волны от мест расположения источника и приемника до рассматриваемой точки за вычетом наименьшего времени пробега волны от источника до приемника является меньшей или равной половине периода волны.
a) задают исходную модель величины, обратной скорости волны, для пласта и буровой скважины; при этом исходная модель является не однородной по меньшей мере в направлении оси буровой скважины;
b) вычисляют френелевский объем или объемы, отображающие путь распространения волны;
c) вычисляют теоретическое значение или значения времени первого вступления на основании пути распространения волны во френелевском объеме для каждого приемника;
d) вычисляют функцию измеренного значения времени первого вступления и теоретического значения времени первого вступления для каждого приемника, при этом измеренное значение времени первого вступления для каждого приемника определяют по данным устройства акустического каротажа;
e) осуществляют обратное проецирование функции вдоль пути волны первого вступления во френелевском объеме, производя, тем самым, модификации исходной модели величины, обратной скорости волны, для множества участков пласта; и
f) модифицируют исходную модель величины, обратной скорости волны, как функцию произведенных модификаций.
вычисление значения времени пробега для полного пространства;
суммирование значения времени пробега волны от мест расположения источника и приемника до рассматриваемой точки;
вычитание наименьшего времени пробега волны от источника до приемника; и
нахождение зоны, в которой сумма значений времени пробега волны от мест расположения источника и приемника до рассматриваемой точки за вычетом наименьшего времени пробега волны от источника до приемника является меньшей или равной половине периода волны.
формирование акустических волн источником акустических волн для
обеспечения данных акустического каротажа; и
вычисление пути волн во френелевском объеме для акустических волн.
вычисление значений времени пробега волны для полного пространства;
суммирование значений времени пробега волны от мест расположения источника и приемника до рассматриваемой точки;
вычитание наименьшего времени пробега волны от источника до приемника; и
нахождение зоны, в которой сумма значений времени пробега волны от мест расположения источника и приемника до рассматриваемой точки за вычетом наименьшего времени пробега волны от источника до приемника является меньшей или равной половине периода волны.
источник акустических волн;
приемник акустических волн;
процессор обработки, соединенный с упомянутым источником акустических волн и с упомянутым приемником акустических волн и запрограммированный таким образом, что осуществляет вычисление и корректировку зоны Френеля с учетом акустических волн, формирование которых осуществлено источником акустических волн, а их прием осуществлен приемником акустических волн в буровой скважине, при этом исходная модель задается для пути волн во френелевском объеме, причем указанная исходная модель является не однородной по меньшей мере в направлении оси буровой скважины.
| Приспособление для разматывания лент с семенами при укладке их в почву | 1922 |
|
SU56A1 |
| US 5081611 А | |||
| Паровоз для отопления неспекающейся каменноугольной мелочью | 1916 |
|
SU14A1 |
| СПОСОБ РЕНТГЕНОРАДИОМЕТРИЧЕСКОГО АНАЛгл*к:но-!4;х<<«-:;;-кдя1О'-^ | 0 |
|
SU296987A1 |
| US 4543648 А, 24.09.1985 | |||
| Способ скважинной сейсморазведки | 1985 |
|
SU1347740A1 |
| Устройство для акустического каротажа скважин | 1982 |
|
SU1065800A1 |
Авторы
Даты
2008-08-10—Публикация
2003-12-18—Подача