Изобретение относится к области электроизмерительной техники и может быть использовано в средствах измерений комплексных величин переменного тока, например в мостах переменного тока.
Известен способ измерения параметров многоэлементных двухполюсников путем уравновешивания разветвленной мостовой измерительной цепи при одновременном действии нескольких тестовых воздействий с разными частотами, разделяемых с помощью аналоговых фильтров [Шеремет Л.П. Принципы построения мостовых измерительных цепей для одновременного уравновешивания на нескольких частотах. //Проблемы технической электродинамики, вып.54, Киев: Наукова думка, 1975. - С.14-19].
Обеспечиваемая этим способом возможность производить измерения одновременно на нескольких частотах позволяет получать информацию о быстроизменяющихся сложных объектах измерения и протекающих в них процессах. Однако применяемые для разделения тестовых воздействий с разными частотами аналоговые фильтры, от избирательности которых зависит точность измерения, обладают инерционностью и сложностью реализации, возрастающими по мере повышения их избирательности, что является недостатком способа.
Известен также способ измерения основной (первой) гармоники периодического сигнала, принятый автором за прототип, согласно которому измерение синусной и косинусной составляющих этой гармоники, т.е. ее проекций на два ортогональных, т.е. сдвинутых относительно друг друга по фазе на 90° опорных сигнала, осуществляют в реальном масштабе времени путем неравномерной дискретизации данного сигнала на множестве моментов времени, являющихся линейными комбинациями полупериодов его гармоник с номерами, равными простым числам: 1, 2, 3, 5, 7, 11,…, и суммирования множества полученных на этом множестве времени дискрет [Пат. Р.246351, Польша, МКИ G01R, Sposob i uklad do pomiaru wektora harmonicznej podstawowej przebiegu odksztalconego / Sawicki J. - Warszawa: Biuletyn Urzedu Patentowego. - 1985. - Nr 19 (307). - P.39].
Недостатком этого способа является возможность измерения лишь одного из совместно действующих сигналов, причем строго конкретного вида, а именно первой гармоники периодического сигнала, что не позволяет решать ряд измерительных задач, например, указанной выше задачи измерения сложных объектов с быстроизменяющимися параметрами, требующих одновременного выполнения измерений на нескольких частотах, задачи измерения сигналов на фоне детерминированных гармонических помех и др.
Целью изобретения является обеспечение возможности измерения любого из М совместно действующих гармонических сигналов, если его частота не кратна частотам других сигналов, причем в реальном масштабе времени и с высокой точностью, а также одновременного измерения нескольких сигналов путем увеличения числа измерительных каналов пропорционально числу измеряемых сигналов.
Поставленная цель достигается тем, что в способе измерения вектора гармонического сигнала, действующего вместе с М-1 другими гармоническими сигналами и имеющего, как и они, известный период Tj и неизвестные амплитуду Aj и начальный фазовый сдвиг φ0j, при котором проекции 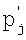 и
и 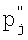 измеряемого сигнала
измеряемого сигнала
Sj(t)=Ajsin(2πt/Tj+φ0j)
на два ортогональных вектора опорных сигналов, связанные с Aj и φ0j, например, соотношениями
 и
и 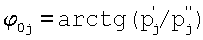 ,
,
измеряют путем выборки и суммирования дискрет суммарного сигнала

с помощью мгновенных импульсов, действующих в моменты времени, образующие множества {ti '} и {ti ''=ti '+Tj/4}j, причем {ti '}j формируют так, чтоб
 и
и 
где Kj - коэффициент, зависящий от процедуры формирования
{ti'}j, a N - число ti ', в качестве измеряемого выбирают любой из совместно действующих сигналов, частота следования которого 1/Tj не кратна частотам других сигналов, а множество {ti '}j моментов времени действия мгновенных импульсов выборки дискрет суммарного сигнала σ(t) формируют с помощью пошаговой процедуры из начального множества, состоящего из одного произвольного начального момента t0, путем получения на первом шаге дополнительного множества, состоящего также из одного момента, посредством сдвига начального множества на нечетное число полупериодов первого сигнала, затем получения на втором шаге дополнительного множества, состоящего уже из двух моментов, посредством сдвига двух моментов суммарного множества, полученного на первом шаге, на нечетное число полупериодов второго сигнала и продолжают эту процедуру с образованием на каждом m-м шаге дополнительного множества посредством сдвига суммарного множества, сформированного на предыдущем шаге, на нечетное число nm полупериодов очередного подавляемого сигнала, и удвоением числа моментов выборки дискрет сигнала σ(t), до тех пор, пока число шагов не станет равным М-1, а амплитуду Aj и фазовый сдвиг φ0j сигнала Sj(t) определяют по соотношениям
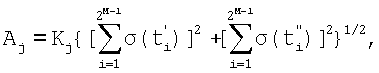
 при
при 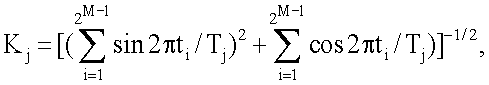
где ti '=ti+t0, t1=0, t2=t1+n1T1/2,
t3=t1+n2T2/2, t4=t2+n2T2/2, t5=t1+n3T3/2, t6=t2+n3T3/2, t7=t3+n3T3/2, t8=t4+n3T3/2,……, 
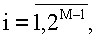
 m≠j.
m≠j.
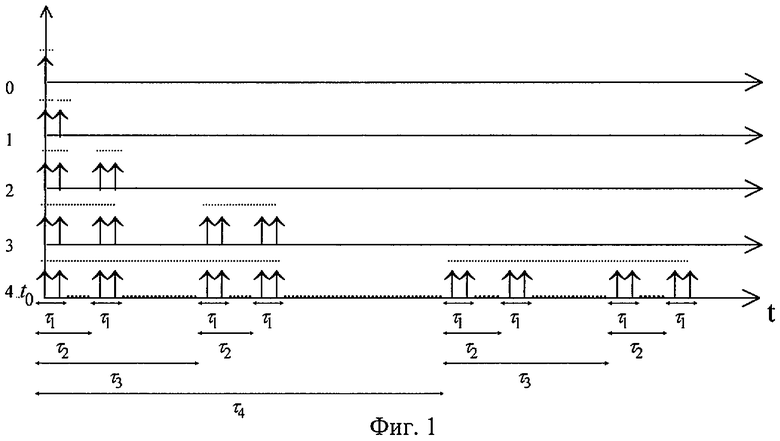
Изобретение поясняется графическим материалом: на фиг.1 отражена процедура формирования множества моментов времени {ti'}j выборки дискрет суммарного сигнала

а фиг.2 поясняет методику получения математического выражения для Kj.
Сущность изобретения состоит в том, что предлагаемая процедура формирования множества моментов времени {ti'}j позволяет точно и быстро (в реальном масштабе времени) измерить проекции на ортогональные векторы опорных сигналов любого из входящих в σ(t) сигналов, в частности, проекции p' j и р'' j сигнала Sj(t), если его частота не кратна частотам других сигналов, инвариантно по отношению к остальным, т.е. исключить влияние всех этих сигналов на точность измерения p' j и р'' j, а значит и Aj и
φoj.
Достигается это тем, что множество моментов времени, в которые действуют обозначенные стрелками мгновенные единичные импульсы, производящие выборку дискрет суммарного сигнала σ(t), формируют с помощью процедуры пошагового исключения влияния (подавления) всех сигналов, действующих вместе с измеряемым. В результате на m-м шаге оказываются подавленными m сигналов, а на (М-1)-м все, кроме измеряемого. Степень подавления сигналов пропорциональна точности информации об их частотах.
Согласно данной процедуре на каждом очередном шаге осуществляется раздвоение (и удвоение) полученного на предшествующем шаге множества моментов времени путем его сдвига относительно самого себя на интервал времени, равный нечетному числу полупериодов подавляемого на данном шаге сигнала.
Поясним это математически. Пусть имеется исходное множество {ti} моментов времени выборки дискрет (подавляемого) гармонического сигнала, сформированное на (m-1)-м шаге. И пусть образовано дополнительное множество {ti*} путем сдвига исходного на интервал времени, равный nmTm/2, где nm - нечетное число. Покажем, что сумма дискрет гармонического сигнала с периодом Тm, полученных на суммарном множестве моментов времени, состоящем из исходного и дополнительного множеств, равна нулю. Для этого пронумеруем в произвольном порядке моменты времени ti исходного множества. Тогда моментами времени дополнительного множества будут ti*=ti+nmTm/2. Но сдвиг на интервал времени nmТm/2, если nm - нечетное число, эквивалентен сдвигу по фазе на π, а sin(φ+π)=-sinφ и значит суммы всех пар дискрет подавляемого сигнала с одинаковыми номерами моментов времени ti и ti* будут равны нулю, что и требовалось доказать.
Заметим, что равенство сдвига нечетному числу полупериодов, а не одному, нужна для исключения возможного совпадения моментов времени выборки дискрет при сдвигах множеств {ti} и {ti*}, например, в случае Т3=Т2+Т1 и ему подобных исключениях.
Итак, вне зависимости от того, какие сигналы были подавлены на предыдущих шагах, благодаря такой процедуре формирования множеств времени выборки дискрет на каждом очередном шаге будет подавлен очередной гармонический сигнал.
Остается доказать, что окончательное множество моментов времени выборки дискрет суммарного сигнала позволяет подавить, за исключением измеряемого, все сигналы.
Для этого рассмотрим множество, сформированное на очередном шаге, в частности, на следующем шаге по отношению к описанному выше. Оно также состоит из двух одинаковых множеств, основного (исходного) и дополнительного, сдвинутых во времени на nmТm+1/2, и благодаря этому позволяет подавить сигнал с периодом
Tm+1. Но из приведенного выше доказательства следовало, что первое из этих множеств (исходное) позволяет подавить сигнал с периодом Тm. Сдвиг же этого множества на произвольный отрезок времени Δt не влияет на его свойство подавления этого сигнала, так как sin(φ+2πΔt/Tm+π)=-sin(φ+2πΔt/Tm). Таким образом, дополнительное множество, как и исходное, тоже обладает свойством подавления сигнала с периодом
Тm, а значит и суммарное множество будет обладать этим свойством. Отсюда получаем, что суммарное множество будет обладать свойством подавления сигналов с периодами и Тm, и Tm+1.
Применив теперь метод математической индукции, получим, что первое множество моментов времени выборки дискрет суммарного сигнала, включающее в себя два момента времени, позволяет подавить один из суммы совместно действующих сигналов
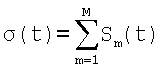
с периодом Т1, второе - два с периодами
Т1 и Т2, m-е - m с периодами Т1, Т2,…, Тm, а окончательное - (М-1) сигналов соответственно с периодами Т1, Т2,…, Тm, ТM, где m≠j, a j - номер измеряемого сигнала, что и требовалось доказать.
Проиллюстрируем эту процедуру графически с помощью фиг.1, соответствующей случаю М=5, где на верхней строке показано исходное (начальное) множество, состоящее из одного изображенного стрелкой импульса выборки дискреты, инициирующего формирование всего множества дискрет и соответствующего произвольному начальному моменту времени t0. Таким образом, отсчет времени t осуществляется относительно t0, т.е. ti'=ti+t0. На второй строке показано первое множество, состоящее из двух импульсов выборки дискрет, соответствующих множеству из двух моментов времени, отстоящих друг от друга на интервал τ1=n1Т1/2, и значит позволяющее подавить сигнал с периодом Т1.
На третьей строке показано второе множество, состоящее из двух подмножеств, а именно изображенного на второй строке и сдвинутого относительно него на τ2=n2T2/2 того же самого множества. Согласно вышеизложенному это множество содержит четыре дискреты, соответствующие четырем моментам времени, т.е. вдвое большему числу моментов, чем у предыдущего, и позволяет подавить сигналы с периодами Т1 и
Т2. Подтвердим это численно подстановкой имеющих место значений моментов времени в математические выражения сигналов S1(t)=A1sin(2πt/T1+φ01) и S2(t)=A2sin(2πt/T2+φ02) и суммированием полученных дискрет, приняв для упрощения выкладок ni=1
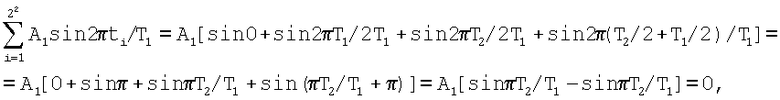
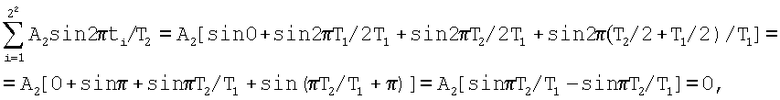
На четвертой строке показано третье множество, состоящее из двух изображенных на третьей строке множеств, сдвинутых относительно друг друга на τ3=n3Т3/2, и позволяющее подавить сигналы с периодами Т1, T2 и T3. Убедиться в этом легко путем подстановки моментов времени ti в выражения для сигналов S1(t), S2(t) и S3(t) аналогично тому, как это было сделано выше для третьей строки.
Наконец, на пятой строке показано окончательное множество из 24 моментов времени и соответствующих им импульсов выборки дискрет, состоящее из двух изображенных на четвертой строке множеств, сдвинутых относительно друг друга на
τ4=n4Т4/2, и позволяющее подавить четыре сигнала с периодами Т1, T2, Т3 и Т4. Пары формируемых на очередных шагах множеств отмечены штриховыми линиями над стрелками.
Доказав, что полученные множества времен выборки дискрет позволяют исключить влияние на точность измерения сигнала Sj(f) действующих вместе с ним сигналов, отметим, что пара сумм
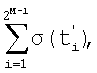

при  будет составлять пару его проекций (p' j и p'' j) на оси ортогональной системы координат, так как в силу периодичности синусоиды значения входящих в данные суммы дискрет приводятся к одному периоду Sj(t), a Δtj=Тj/4 означает фазовый сдвиг сигналов на 90°. Найдем теперь формулу для коэффициента Kj.
будет составлять пару его проекций (p' j и p'' j) на оси ортогональной системы координат, так как в силу периодичности синусоиды значения входящих в данные суммы дискрет приводятся к одному периоду Sj(t), a Δtj=Тj/4 означает фазовый сдвиг сигналов на 90°. Найдем теперь формулу для коэффициента Kj.
Чтобы найти математическое выражение для Кj, воспользуемся векторной моделью гармонических сигналов, а для упрощения выкладок преобразуем форму представления сигнала Sj(t)=Ajsin(2πt/Tj+φ0j) к удобному для анализа виду с учетом инвариантности Kj по отношению к амплитуде Aj и фазовому сдвигу φ0j сигнала Sj(t), положив Aj=1 и φ0j=0
Sj(t)⇒s(t)=sin2πt/Tj=sinωjt,
а поскольку процедура формирования {ti}j одинакова для всех сигналов, опустим индекса и запишем {ti}j в виде {ti},
где 
а также положим
Kj=К, Tj=Т и ωj=ω.
Кроме этого учтем, что, как отмечалось выше, благодаря периодичности синусоиды множество {ti} преобразуется в  , где
, где 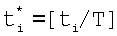 - дробная часть частного от деления ti на T=2π/ω, т.е. моменты времени выборки дискрет сигнала Sj(t) приводятся к одному периоду синусоиды Sj(t). В результате множество дискрет {si=s(ti)} преобразуется в множество дискрет
- дробная часть частного от деления ti на T=2π/ω, т.е. моменты времени выборки дискрет сигнала Sj(t) приводятся к одному периоду синусоиды Sj(t). В результате множество дискрет {si=s(ti)} преобразуется в множество дискрет  , приведенных к одному периоду синусоиды s(t), а множество фазовых углов {φ(ti)=ωti}, соответствующих дискретам Sj(ti), преобразуется в множество
, приведенных к одному периоду синусоиды s(t), а множество фазовых углов {φ(ti)=ωti}, соответствующих дискретам Sj(ti), преобразуется в множество  , приведенных к четырем квадрантам декартовой системы координат. При этом каждому из фазовых углов
, приведенных к четырем квадрантам декартовой системы координат. При этом каждому из фазовых углов 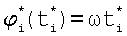 соответствует дискрета
соответствует дискрета  и наоборот.
и наоборот.
Воспользуемся теперь формулой Эйлера, имеющей в данном случае вид: ejωt=cosωt+jsinωt, согласно которой комплексное число выступает как единичный вектор  в полярной системе координат, а дискрета
в полярной системе координат, а дискрета  - как проекция единичного вектора
- как проекция единичного вектора  на мнимую ось комплексной плоскости
на мнимую ось комплексной плоскости  .
.
Связанные с применением этой формулы построения приведены на фиг.2, на которой показано множество единичных векторов  , где ω=2π/Tj, с действительными и мнимыми составляющими (проекциями на оси координат) s*ix, s*iy и их сумма
, где ω=2π/Tj, с действительными и мнимыми составляющими (проекциями на оси координат) s*ix, s*iy и их сумма  , полученная по правилам векторной алгебры. Поворот
, полученная по правилам векторной алгебры. Поворот  на любой угол
на любой угол  не приводит к изменению его модуля
не приводит к изменению его модуля

где N=2M-1, т.е. (в отличие от проекций
SΣx и SΣy) он является инвариантом по отношению к 
Далее, поскольку математическое выражение для  получено для случая единичного вектора, т.е. для синусоиды с единичной амплитудой (Aj=1), то выражение
получено для случая единичного вектора, т.е. для синусоиды с единичной амплитудой (Aj=1), то выражение

где N=2M-1 выступает в качестве нормирующего множителя.
Учитывая произведенные выше упрощения обозначений величин, а именно ωj=ω, получим

Таким образом, все соотношения между параметрами измеряемого сигнала и суммами дискрет определены.
Изобретение относится к области электроизмерительной техники. Способ может быть применен в средствах измерений пассивных и активных комплексных величин переменного тока, например в мостах переменного тока для измерения параметров многоэлементных двухполюсников, путем уравновешивания разветвленной мостовой измерительной цепи одновременно при нескольких тестовых воздействиях с разными частотами, а также при измерениях в случае действия нескольких гармонических помех. Способ состоит в том, что проекции 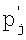 и
и  измеряемого сигнала Sj(t)=Ajsin(2πt/Tj+φ0j) на два ортогональных опорных сигнала получают путем сложения дискрет суммы совместно действующих сигналов σ(t), моменты выборки которых составляют соответственно множества {ti'}j и {Ti ''=ti '+Tj/4}, которые формируют с помощью пошаговой процедуры из начального множества, состоящего из одного произвольного начального момента времени t0, путем получения на первом шаге дополнительного множества, состоящего тоже из одного момента, посредством сдвига начального множества на нечетное число полупериодов первого сигнала, затем получения на втором шаге дополнительного множества, состоящего уже из двух моментов, посредством сдвига двух моментов суммарного множества, полученного на первом шаге, на нечетное число полупериодов второго сигнала и продолжают эту процедуру с образованием дополнительного множества на каждом шаге посредством сдвига суммарного множества, сформированного на предыдущем шаге, на нечетное число полупериодов очередного подавляемого сигнала и с удвоением на каждом шаге числа моментов времени выборки дискрет суммы совместно действующих сигналов до тех пор, пока число шагов не станет равным М-1, а амплитуду Aj и фазовый сдвиг φ0j сигнала Sj(t) определяют по соотношениям
измеряемого сигнала Sj(t)=Ajsin(2πt/Tj+φ0j) на два ортогональных опорных сигнала получают путем сложения дискрет суммы совместно действующих сигналов σ(t), моменты выборки которых составляют соответственно множества {ti'}j и {Ti ''=ti '+Tj/4}, которые формируют с помощью пошаговой процедуры из начального множества, состоящего из одного произвольного начального момента времени t0, путем получения на первом шаге дополнительного множества, состоящего тоже из одного момента, посредством сдвига начального множества на нечетное число полупериодов первого сигнала, затем получения на втором шаге дополнительного множества, состоящего уже из двух моментов, посредством сдвига двух моментов суммарного множества, полученного на первом шаге, на нечетное число полупериодов второго сигнала и продолжают эту процедуру с образованием дополнительного множества на каждом шаге посредством сдвига суммарного множества, сформированного на предыдущем шаге, на нечетное число полупериодов очередного подавляемого сигнала и с удвоением на каждом шаге числа моментов времени выборки дискрет суммы совместно действующих сигналов до тех пор, пока число шагов не станет равным М-1, а амплитуду Aj и фазовый сдвиг φ0j сигнала Sj(t) определяют по соотношениям 
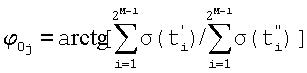 при
при  где ti '=ti+t0, t1=0, t2=t1+n1T1/2, t3=t1+n2T2/2, t4=t2+n2T2/2, t5=t1+n3T3/2, t6=t2+n3T3/2, t7=t3+n3T3/2, t8=t4+n3T3/2,……,
где ti '=ti+t0, t1=0, t2=t1+n1T1/2, t3=t1+n2T2/2, t4=t2+n2T2/2, t5=t1+n3T3/2, t6=t2+n3T3/2, t7=t3+n3T3/2, t8=t4+n3T3/2,……, 

 m≠j. Технический результат - обеспечение возможности точного измерения в реальном масштабе времени любого из совместно действующих гармонических сигналов с известными периодами, а также возможность одновременного измерения нескольких сигналов при условии, что частота измеряемого сигнала не кратна частотам действующих совместно с ним сигналов. 2 ил.
m≠j. Технический результат - обеспечение возможности точного измерения в реальном масштабе времени любого из совместно действующих гармонических сигналов с известными периодами, а также возможность одновременного измерения нескольких сигналов при условии, что частота измеряемого сигнала не кратна частотам действующих совместно с ним сигналов. 2 ил.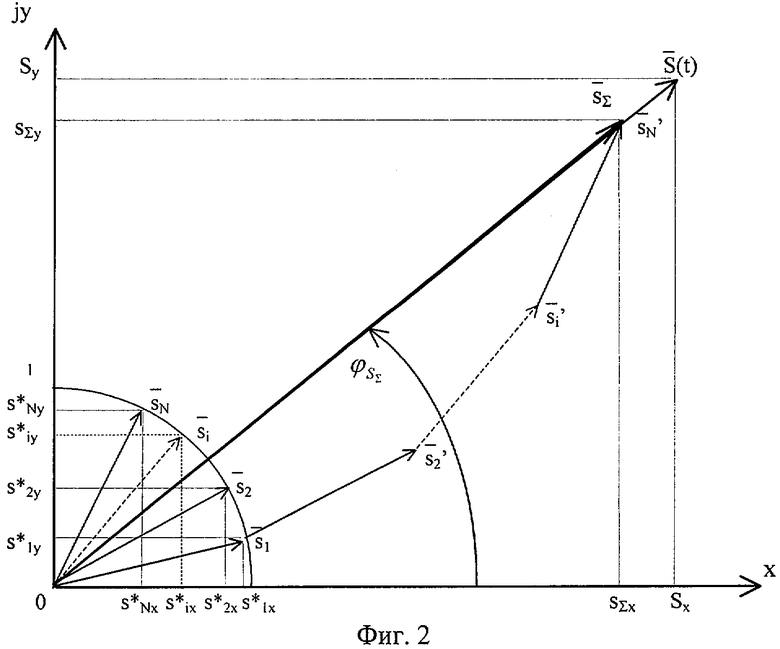
Способ измерения вектора гармонического сигнала, действующего вместе с М-1 другими гармоническими сигналами и имеющего, как и они, известный период Тj и неизвестные амплитуду Aj, и начальный фазовый сдвиг φ0j, при котором проекции  и
и
 измеряемого сигнала
измеряемого сигнала
Sj(t)=Ajsin(2πt/Tj+φ0j) на два ортогональных вектора опорных сигналов, связанные с Aj и φ0j, например, соотношениями 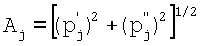 и
и  измеряют путем выборки и суммирования дискрет суммарного сигнала
измеряют путем выборки и суммирования дискрет суммарного сигнала  с помощью мгновенных импульсов, действующих в моменты времени, образующие множества {ti '} и {tj ''=ti '+Tj/4}j, причем {tj '}j, формируют так, чтоб
с помощью мгновенных импульсов, действующих в моменты времени, образующие множества {ti '} и {tj ''=ti '+Tj/4}j, причем {tj '}j, формируют так, чтоб  и
и 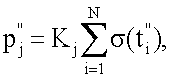
где Kj - коэффициент, зависящий от процедуры формирования {ti '}, а N - число ti ', отличающийся тем, что в качестве измеряемого выбирают любой из совместно действующих сигналов, частота следования которого 1/Tj не кратна частотам других сигналов, а множество {ti '} моментов времени действия мгновенных импульсов выборки дискрет суммарного сигнала σ(t) формируют с помощью пошаговой процедуры из начального множества, состоящего из одного произвольного начального момента t0, путем получения на первом шаге дополнительного множества, состоящего также из одного момента, посредством сдвига начального множества на нечетное число полупериодов первого сигнала, затем получения на втором шаге дополнительного множества, состоящего уже из двух моментов, посредством сдвига двух моментов суммарного множества, полученного на первом шаге, на нечетное число полупериодов второго сигнала и продолжают эту процедуру с образованием на каждом m-ом шаге дополнительного множества посредством сдвига суммарного множества, сформированного на предыдущем шаге, на нечетное число nm полупериодов очередного подавляемого сигнала и с удвоением числа моментов выборки дискрет сигнала σ(t) до тех пор, пока число шагов не станет равным М-1, а амплитуду Aj и фазовый сдвиг φ0j сигнала Sj(t) определяют по соотношениям:

 при
при 
где ti '=ti+t0, t1=0, t2=t1+n1T1/2,
t3=t1+n2T2/2, t4=t2+n2T2/2, t5=t1+n3T3/2,
t6=t2+n3T3/2, t7=t3+n3T3/2, t8=t4+n3T3/2,……,
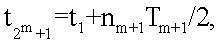


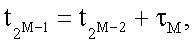

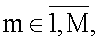 m≠j.
m≠j.
| ДРОБЕМЁТНЫЙ АППАРАТ | 0 |
|
SU246351A1 |
| СПОСОБ ИЗМЕРЕНИЯ ПОСТОЯННОЙ СОСТАВЛЯЮЩЕЙ СИГНАЛА | 2003 |
|
RU2239842C1 |
| СПОСОБ ИЗМЕРЕНИЯ ПОСТОЯННОЙ СОСТАВЛЯЮЩЕЙ ГАРМОНИЧЕСКОГО СИГНАЛА | 2000 |
|
RU2196998C2 |
| Способ поверки и градуировки приборов для измерения коэффициента несимметрии многофазной системы напряжений | 1979 |
|
SU924646A1 |
| ШЕРЕМЕТ Л.П | |||
| Принципы построения мостовых измерительных цепей для одновременного уравновешивания на нескольких частотах // Проблемы технической электродинамики, вып.54 | |||
| - Киев: Наукова думка, 1975, с.14-19. | |||
Авторы
Даты
2009-12-27—Публикация
2008-10-27—Подача