Изобретение относится к области электроизмерительной техники и может быть использовано в средствах измерений пассивных и активных комплексных величин, например, в мостах и компенсаторах переменного тока или в измерителях параметров электрических цепей, а также в векторных вольтметрах.
Известен способ измерения параметров двухполюсников, имеющих сложные схемы замещения, с помощью разветвленной мостовой измерительной цепи при воздействии на нее нескольких тестовых гармонических сигналов с разными частотами, разделяемых в процессе уравновешивания цепи с помощью аналоговых фильтров [Шеремет Л.П. Принципы построения мостовых измерительных цепей для одновременного уравновешивания на нескольких частотах // Проблемы технической электродинамики, вып.54, Киев: Наукова думка. 1975. - С.14-19].
Данный способ позволяет производить измерения сложных объектов исследования одновременно на нескольких частотах, обеспечивая тем самым возможность получения информации о быстроизменяющихся параметрах таких объектов и/или о протекающих в них процессах. Однако аналоговые фильтры, которые применяют для разделения сигналов с разными частотами и от избирательности которых зависят помехоустойчивость и точность измерения, обладают инерционностью и сложностью реализации, возрастающими по мере повышения их избирательности, что является недостатком способа.
Известен также принятый автором за прототип способ измерения вектора любого из М совместно действующих гармонических сигналов Sj(t)=Ajsin(2πt/Tj+φ0j), в том числе помех, с заданными и не кратными друг другу значениями периодов Tm, имеющего, как и они, известный период Tj и неизвестные начальный фазовый сдвиг φ0j и амплитуду Aj, при которой проекции 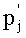 и
и 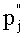 сигнала Sj(t) на два ортогональных вектора опорных сигналов, связанные с Aj и φ0j, например, соотношениями
сигнала Sj(t) на два ортогональных вектора опорных сигналов, связанные с Aj и φ0j, например, соотношениями 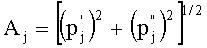 и
и 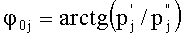 , измеряют путем выборки и суммирования дискрет суммарного сигнала
, измеряют путем выборки и суммирования дискрет суммарного сигнала 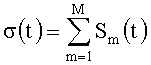 с помощью мгновенных импульсов, действующих в моменты времени, образующие множества
с помощью мгновенных импульсов, действующих в моменты времени, образующие множества 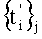 и
и 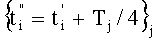 , а значения
, а значения 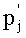 и
и 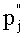 определяют по соотношениям
определяют по соотношениям 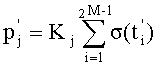 и
и 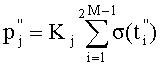 , где
, где 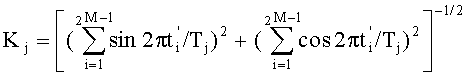 - нормирующий множитель, причем
- нормирующий множитель, причем 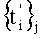 формируют с помощью пошаговой процедуры, начинающейся с исходного множества в виде произвольного начального момента t0 и раздвоения его на первом шаге путем получения дополнительного множества посредством сдвига исходного на нечетное число полупериодов первого (подавляемого) сигнала или гармонической помехи, и далее получения на каждом последующем шаге дополнительного множества посредством сдвига полученного на предыдущем шаге (суммарного) множества на нечетное число nm полупериодов m-го (подавляемого) сигнала до тех пор, пока число шагов не станет равным М-1 [1. Патент РФ на изобретение №2377577, МКИ G01R 17/10. Способ измерения вектора гармонического сигнала / Агамалов Ю.Р // Изобретения - 2009 - №26. - Опубл. 27.12.09. 2. Агамалов Ю.Р. Метод измерения векторов совместно действующих гармонических сигналов на основе их дискретизации и суммирования дискрет // Метрология. - 2010. - №12. - С.26-35].
формируют с помощью пошаговой процедуры, начинающейся с исходного множества в виде произвольного начального момента t0 и раздвоения его на первом шаге путем получения дополнительного множества посредством сдвига исходного на нечетное число полупериодов первого (подавляемого) сигнала или гармонической помехи, и далее получения на каждом последующем шаге дополнительного множества посредством сдвига полученного на предыдущем шаге (суммарного) множества на нечетное число nm полупериодов m-го (подавляемого) сигнала до тех пор, пока число шагов не станет равным М-1 [1. Патент РФ на изобретение №2377577, МКИ G01R 17/10. Способ измерения вектора гармонического сигнала / Агамалов Ю.Р // Изобретения - 2009 - №26. - Опубл. 27.12.09. 2. Агамалов Ю.Р. Метод измерения векторов совместно действующих гармонических сигналов на основе их дискретизации и суммирования дискрет // Метрология. - 2010. - №12. - С.26-35].
Недостатком данного способа являются погрешности измерения, связанные с действием аддитивных периодических помех несинусоидального вида, которые возникают в измерительной аппаратуре, в частности, в цифровых мостах и компенсаторах переменного тока или анализаторах электрических цепей, а также в векторных вольтметрах благодаря функционированию разного рода генераторов с известными частотами, как внутренних, например, в цепях индикации и других узлах, так и внешних.
Техническим результатом изобретения является повышение точности измерения в реальном времени вектора гармонического сигнала S(t)=Asin(2πt/T+φ0) с известным периодом Т, действующего совместно с сигналами помех Pn(t), где 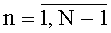 , в том случае, когда помехами являются периодические сигналы Pn(t)=Pn(t-Tn), где Pn(t) - непрерывные функции с известными периодами Tn, не кратными Т. При этом в качестве измеряемого может выступать любой из гармонических сигналов, входящих в число N-1 периодических помех, так что все гармонические сигналы из σ(t) могут быть поочередно измерены, а при соответствующем увеличении числа каналов - и параллельно.
, в том случае, когда помехами являются периодические сигналы Pn(t)=Pn(t-Tn), где Pn(t) - непрерывные функции с известными периодами Tn, не кратными Т. При этом в качестве измеряемого может выступать любой из гармонических сигналов, входящих в число N-1 периодических помех, так что все гармонические сигналы из σ(t) могут быть поочередно измерены, а при соответствующем увеличении числа каналов - и параллельно.
Технический результат достигается тем, что в способе измерения вектора гармонического сигнала S(t)=Asin(2πt/T+φ0) с известным периодом Т, действующего совместно с сигналами помех Pn(t), где, 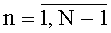 , при котором амплитуду А и начальный фазовый сдвиг φ0 сигнала S(t) определяют, например, по соотношениям A=[(p')2+(p”)2]1/2 и φ0=arctg(p'/p”), где р' и р” - проекции вектора сигнала S(t) на два ортогональных вектора опорных сигналов, а значения р' и р” получают путем неравномерной дискретизации суммарного сигнала
, при котором амплитуду А и начальный фазовый сдвиг φ0 сигнала S(t) определяют, например, по соотношениям A=[(p')2+(p”)2]1/2 и φ0=arctg(p'/p”), где р' и р” - проекции вектора сигнала S(t) на два ортогональных вектора опорных сигналов, а значения р' и р” получают путем неравномерной дискретизации суммарного сигнала 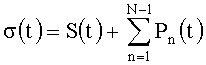 и суммирования его дискрет, выборку которых производят мгновенными импульсами, действующими в моменты времени, образующие соответственно для р' и р” множества
и суммирования его дискрет, выборку которых производят мгновенными импульсами, действующими в моменты времени, образующие соответственно для р' и р” множества 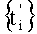 и
и 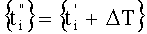 , где ΔТ=(2r±1)T/4. r=0, 1, 2,…, при этом в том случае, когда помехами являются периодические сигналы Pn(t)=Pn(t-Tn), где Tn - периоды сигналов помех, a Pn(t) - непрерывные функции, проекции р' и р” сигнала S(t) измеряют путем неравномерной дискретизации суммарного сигнала σ(t) на множестве моментов времени
, где ΔТ=(2r±1)T/4. r=0, 1, 2,…, при этом в том случае, когда помехами являются периодические сигналы Pn(t)=Pn(t-Tn), где Tn - периоды сигналов помех, a Pn(t) - непрерывные функции, проекции р' и р” сигнала S(t) измеряют путем неравномерной дискретизации суммарного сигнала σ(t) на множестве моментов времени 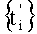 , которое формируют пошагово согласно условию
, которое формируют пошагово согласно условию 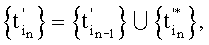 где
где 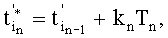 kn=1, 2,…, a
kn=1, 2,…, a 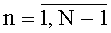 - номер шага, совпадающий с номером сигнала помехи Pn(t), так что
- номер шага, совпадающий с номером сигнала помехи Pn(t), так что 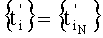 , и знакопеременного суммирования дискрет σ(t) с коэффициентами a
i, причем модули a
i принимают равными единице, а знаки определяют в зависимости от номеров дискрет согласно условию
, и знакопеременного суммирования дискрет σ(t) с коэффициентами a
i, причем модули a
i принимают равными единице, а знаки определяют в зависимости от номеров дискрет согласно условию 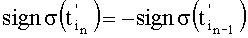 , по соотношениям:
, по соотношениям: 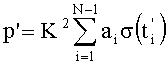 ,
, 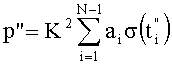 ,
, 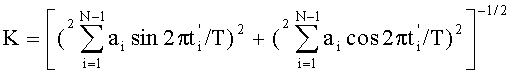 и
и 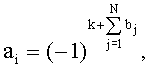 где bj=0,1 - значение j-го разряда представленного в двоичной системе счисления номера
где bj=0,1 - значение j-го разряда представленного в двоичной системе счисления номера 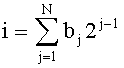 момента времени выборки i-й дискреты суммарного сигнала σ(t), a
момента времени выборки i-й дискреты суммарного сигнала σ(t), a 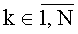 - номер младшего значащего разряда bj, при этом определяют k как номер элемента b1 множества {b1}, где b1=1, согласно условию k=inf1.
- номер младшего значащего разряда bj, при этом определяют k как номер элемента b1 множества {b1}, где b1=1, согласно условию k=inf1.
Изобретение поясняется чертежом, на котором отображена пошаговая процедура формирования множества 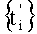 моментов времени выборки дискрет суммарного сигнала σ(t), а также единичных коэффициентов a
i, определяющих знаки суммирования этих дискрет.
моментов времени выборки дискрет суммарного сигнала σ(t), а также единичных коэффициентов a
i, определяющих знаки суммирования этих дискрет.
На первой строке чертежа изображено порождающее множество импульсов выборки дискрет, состоящее из одного (начального) импульса с положительной амплитудой, знак которой, как и всех других импульсов, соответствует знаку коэффициента a i суммирования сформированной начальным импульсом дискреты, т.е. в данном случае коэффициента а 1.
На второй строке изображено множество импульсов, сформированное на множестве моментов времени выборки дискрет 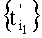 , соответствующем первому шагу формирования
, соответствующем первому шагу формирования 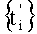 и состоящем из двух импульсов, где второй согласно условию
и состоящем из двух импульсов, где второй согласно условию 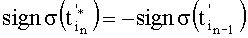 при n=1, имеет отрицательную амплитуду, знак которой совпадает со знаком а
2 суммирования формируемой им (второй) дискреты.
при n=1, имеет отрицательную амплитуду, знак которой совпадает со знаком а
2 суммирования формируемой им (второй) дискреты.
На последующих строках чертежа изображены множества импульсов выборки дискрет, сформированные на множествах моментов времени 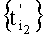 ,
, 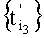 ,
, 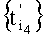 , т.е. на втором, третьем и четвертом шагах процедуры формирования
, т.е. на втором, третьем и четвертом шагах процедуры формирования 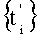 , и имеющие знаки амплитуд, соответствующие соотношению
, и имеющие знаки амплитуд, соответствующие соотношению 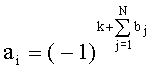 .
.
Сущность изобретения состоит в том, что предлагаемая (пошаговая) процедура формирования множества моментов времени 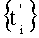 выборки дискрет суммарного сигнала σ(t), т.е. их расстановки во времени, а также знаков их суммирования позволяет точно и быстро (в реальном времени) измерять проекции р' и р” гармонического сигнала S(t) инвариантно по отношению к действующим вместе с ним N-1 периодическим помехам Pn(t), в том числе полезным гармоническим сигналам, выступающим в процессе измерения S(t) в качестве помех, при условии, что их периоды не кратны периоду S(t), т.е. исключить или минимизировать в зависимости от точности информации о периодах сигналов Pn(t) и S(t) влияние сигналов Pn(t) на точность измерения проекций р' и р” сигнала S(t), а значит, и на точность измерения А и φ0.
выборки дискрет суммарного сигнала σ(t), т.е. их расстановки во времени, а также знаков их суммирования позволяет точно и быстро (в реальном времени) измерять проекции р' и р” гармонического сигнала S(t) инвариантно по отношению к действующим вместе с ним N-1 периодическим помехам Pn(t), в том числе полезным гармоническим сигналам, выступающим в процессе измерения S(t) в качестве помех, при условии, что их периоды не кратны периоду S(t), т.е. исключить или минимизировать в зависимости от точности информации о периодах сигналов Pn(t) и S(t) влияние сигналов Pn(t) на точность измерения проекций р' и р” сигнала S(t), а значит, и на точность измерения А и φ0.
Достигают этого тем, что множество моментов времени действия обозначенных на чертеже мгновенных импульсов, с помощью которых производят выборку дискрет суммарного сигнала σ(t), а также знаки этих импульсов, в соответствии с которыми производят знакопеременное, или алгебраическое, суммирование дискрет этого сигнала, формируют с помощью процедуры пошагового подавления, т.е. исключения или минимизации в зависимости от точности информации о значениях периодов S(t) и Pn(t) влияния на точность измерения S(t) всех сигналов, действующих вместе с ним, согласно условию 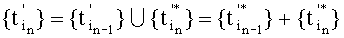 , где
, где 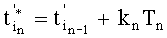 , kn=1, 2, …, а
, kn=1, 2, …, а 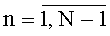 - номер шага, совпадающий с номером сигнала помехи Pn(t), и знакопеременного суммирования дискрет σ(t) с коэффициентами a
i, причем модули a
i принимают равными единице, а знаки определяют в зависимости от номеров дискрет согласно условию
- номер шага, совпадающий с номером сигнала помехи Pn(t), и знакопеременного суммирования дискрет σ(t) с коэффициентами a
i, причем модули a
i принимают равными единице, а знаки определяют в зависимости от номеров дискрет согласно условию 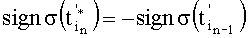 , по соотношениям:
, по соотношениям: 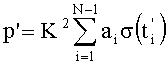 ,
, 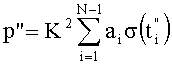 ,
, 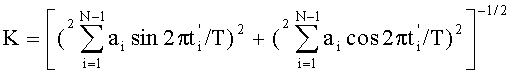 и
и 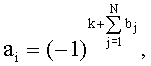 где bj=0,1 - значение j-го разряда представленного в двоичной системе счисления номера
где bj=0,1 - значение j-го разряда представленного в двоичной системе счисления номера 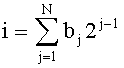 момента времени выборки i-й дискреты суммарного сигнала σ(t), а
момента времени выборки i-й дискреты суммарного сигнала σ(t), а 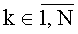 - номер младшего значащего разряда, bj, при этом определяют k как номер элемента b1 множества {b1}, где b1=1, согласно условию k=inf1.
- номер младшего значащего разряда, bj, при этом определяют k как номер элемента b1 множества {b1}, где b1=1, согласно условию k=inf1.
Поясним математически механизм подавления сигналов, сопутствующих измеряемому, и выведем фигурирующие в формуле изобретения соотношения.
Согласно определению периодического сигнала Pn(t)=Pn(t-Tn). Из этого соотношения непосредственно следует, что верно и более общее соотношение: Pn(t)=Pn(t-knTn), или Pn(t)-Pn(t-knTn)=0. Таким образом, P1(t)-P1(t-k1T1)=0, т.е., если импульсы выборки первых двух дискрет расставить друг относительно друга на расстоянии k1T1, то разность, или алгебраическая сумма, дискрет сигнала P1(t), полученных с помощью этих импульсов, изображенных на чертеже на второй строке и действующих в моменты времени 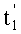 и
и 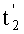 , будет равна нулю. При этом согласно условию некратности периода P1(t) периоду измеряемого сигнала S(t) разность дискрет последнего, полученных на моментах времени
, будет равна нулю. При этом согласно условию некратности периода P1(t) периоду измеряемого сигнала S(t) разность дискрет последнего, полученных на моментах времени 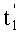 и
и 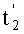 , равна нулю не будет. Заметим также, что, если в дальнейшем производить дискретизацию σ(t) с помощью пар импульсов выборки, отстоящих друг от друга на интервал k1T1 и имеющих при этом разные знаки, то алгебраические суммы этих дискрет для сигнала P1(t) будут равны нулю вне зависимости от числа и расстановки во времени этих пар. Далее, если расставить эти пары на расстоянии k2T2 и при этом с противоположными знаками, то согласно [1, 2] они будут эквивалентны двум дискретам P2(t), имеющим разные знаки и, следовательно, будут иметь место соотношения:
, равна нулю не будет. Заметим также, что, если в дальнейшем производить дискретизацию σ(t) с помощью пар импульсов выборки, отстоящих друг от друга на интервал k1T1 и имеющих при этом разные знаки, то алгебраические суммы этих дискрет для сигнала P1(t) будут равны нулю вне зависимости от числа и расстановки во времени этих пар. Далее, если расставить эти пары на расстоянии k2T2 и при этом с противоположными знаками, то согласно [1, 2] они будут эквивалентны двум дискретам P2(t), имеющим разные знаки и, следовательно, будут иметь место соотношения: 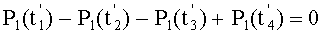 и
и 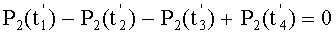 . Иначе говоря, алгебраическая сумма (четырех) дискрет сигнала σ(t), сформированных в моменты времени
. Иначе говоря, алгебраическая сумма (четырех) дискрет сигнала σ(t), сформированных в моменты времени  ,
, 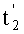 ,
, 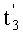 ,
, 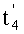 и изображенных на третьей строке чертежа, будет инвариантна (нечувствительна), опять таки в меру точности информации о периодах всех сигналов, уже к двум сигналам P1(t) и Р2(t).
и изображенных на третьей строке чертежа, будет инвариантна (нечувствительна), опять таки в меру точности информации о периодах всех сигналов, уже к двум сигналам P1(t) и Р2(t).
Множество импульсов выборки дискрет, сформированное на третьем шаге и изображенное на четвертой строке чертежа, состоит из двух множеств: 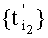 , сформированного на втором шаге, и
, сформированного на втором шаге, и 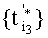 , образованного путем сдвига
, образованного путем сдвига 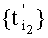 на интервал k3T3, с общим шагом четверка дискрет инвариантна сигналам P1(t) и Р2(t), а множества
на интервал k3T3, с общим шагом четверка дискрет инвариантна сигналам P1(t) и Р2(t), а множества 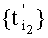 и
и 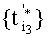 сдвинуты друг относительно друга на интервал k3T3, суммарное множество
сдвинуты друг относительно друга на интервал k3T3, суммарное множество 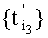 будет инвариантно трем сигналам помех: P1(t), P2(t) и Р3(t).
будет инвариантно трем сигналам помех: P1(t), P2(t) и Р3(t).
Продолжая подобную пошаговую процедуру, с помощью метода математической индукции получим, что сформированное на n-м шаге множество 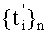 будет обеспечивать инвариантность суммы дискрет σ(t) к
будет обеспечивать инвариантность суммы дискрет σ(t) к 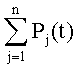 при числе дискрет, равном 2N, а на N-1-м шаге будет иметь место инвариантность суммы дискрет σ(t) к
при числе дискрет, равном 2N, а на N-1-м шаге будет иметь место инвариантность суммы дискрет σ(t) к 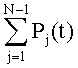 при общем числе дискрет, равном 2N-1.
при общем числе дискрет, равном 2N-1.
Выведем теперь соотношение, связывающее знаки алгебраического суммирования дискрет σ(t) с характеризующими номера дискрет параметрами. Для этого запишем номер i дискреты σ(t) в двоичной системе счисления: 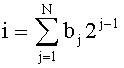 и представим его в показательной форме:
и представим его в показательной форме: 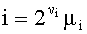 , где νi - число нулевых bj перед первым значащим разрядом i, a µi - нечетное число, начинающееся и оканчивающееся единицами, а также учтем, что моменты выборки дискрет σ(t) расставляют, а знаки их суммирования определяют согласно условиям:
, где νi - число нулевых bj перед первым значащим разрядом i, a µi - нечетное число, начинающееся и оканчивающееся единицами, а также учтем, что моменты выборки дискрет σ(t) расставляют, а знаки их суммирования определяют согласно условиям: 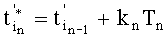 при
при 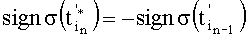 , где n - номер шага, откуда следует,
, где n - номер шага, откуда следует, 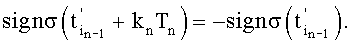 При этом, учтем также, что смещение на n-м шаге момента выборки дискреты с номером i на интервал knTn означает изменение его номера на 2n единиц.
При этом, учтем также, что смещение на n-м шаге момента выборки дискреты с номером i на интервал knTn означает изменение его номера на 2n единиц.
Таким образом, если в двоичном числе µi исключить последнюю единицу, то полученное число 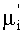 будет означать номер дискреты с знаком, противоположным знаку дискреты с номером µi. Если теперь в числе
будет означать номер дискреты с знаком, противоположным знаку дискреты с номером µi. Если теперь в числе 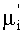 тоже исключить последнюю единицу, то получится число
тоже исключить последнюю единицу, то получится число 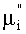 , представляющее собой номер дискреты со знаком, противоположным знаку дискреты с номером
, представляющее собой номер дискреты со знаком, противоположным знаку дискреты с номером 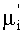 . Продолжая эту процедуру до того момента, когда µi станет равным единице, получим число
. Продолжая эту процедуру до того момента, когда µi станет равным единице, получим число 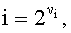 при этом
при этом 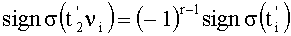 , где r - количество единичных разрядов в числе µi. Но количество единичных разрядов в числе µi равно количеству единиц в числе i. В результате окончательно будем иметь
, где r - количество единичных разрядов в числе µi. Но количество единичных разрядов в числе µi равно количеству единиц в числе i. В результате окончательно будем иметь 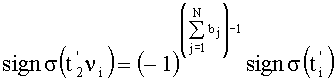 , или
, или 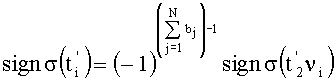 .
.
Установим теперь связь знака дискреты с номером 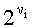 со знаком первой дискреты, который по определению является плюсом.
со знаком первой дискреты, который по определению является плюсом.
Для этого примем во внимание то, что множества 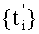 формируют пошагово согласно соотношению
формируют пошагово согласно соотношению 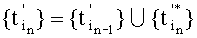 , что знаки полученных на этих множествах дискрет определяют по условию
, что знаки полученных на этих множествах дискрет определяют по условию 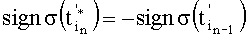 и что при этом число моментов выборки дискрет на каждом шаге увеличивается в два раза, поскольку множество
и что при этом число моментов выборки дискрет на каждом шаге увеличивается в два раза, поскольку множество 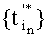 образуют путем сдвига
образуют путем сдвига 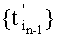 относительно самого себя на интервал knTn.
относительно самого себя на интервал knTn.
Учитывая все это, получим, что на первом шаге последняя дискрета множества 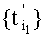 суммируется со знаком минус. На втором шаге последняя дискрета множества
суммируется со знаком минус. На втором шаге последняя дискрета множества 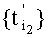 будет суммироваться со знаком, противоположным знаку суммирования последней дискреты множества, полученного на предыдущем (первом) шаге, и т.д. Таким образом, на каждом последующем шаге знак суммирования последней дискреты, имеющей номер 2n, будет противоположным знаку суммирования дискреты с номером 2n-1, а следовательно, если в номере дискреты i перед первым значащим разрядом имеют место νi нулей, то знак ее по отношению к положительному знаку первой дискреты будет измененным νi раз, т.е. столько раз, сколько нулей имеет место перед первым значащим разрядом числа i, или k-1 раз, где k - номер первого значащего разряда числа i, представленного в двоичной системе счисления. Таким образом, знак i-й дискреты будет измененным по отношению к первой
будет суммироваться со знаком, противоположным знаку суммирования последней дискреты множества, полученного на предыдущем (первом) шаге, и т.д. Таким образом, на каждом последующем шаге знак суммирования последней дискреты, имеющей номер 2n, будет противоположным знаку суммирования дискреты с номером 2n-1, а следовательно, если в номере дискреты i перед первым значащим разрядом имеют место νi нулей, то знак ее по отношению к положительному знаку первой дискреты будет измененным νi раз, т.е. столько раз, сколько нулей имеет место перед первым значащим разрядом числа i, или k-1 раз, где k - номер первого значащего разряда числа i, представленного в двоичной системе счисления. Таким образом, знак i-й дискреты будет измененным по отношению к первой 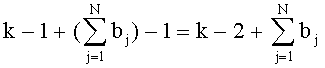 раз, откуда следует, что
раз, откуда следует, что 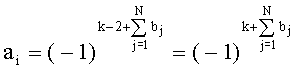 .
.
Итак, все соотношения, входящие в формулу изобретения, математически обоснованы.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ИЗМЕРЕНИЯ ВЕКТОРА ГАРМОНИЧЕСКОГО СИГНАЛА | 2014 |
|
RU2578742C1 |
| СПОСОБ ИЗМЕРЕНИЯ ВЕКТОРА ГАРМОНИЧЕСКОГО СИГНАЛА | 2013 |
|
RU2528274C1 |
| СПОСОБ ИЗМЕРЕНИЯ ВЕКТОРА ГАРМОНИЧЕСКОГО СИГНАЛА | 2008 |
|
RU2377577C1 |
| Способ измерения векторов гармонических сигналов с постоянной составляющей | 2015 |
|
RU2611256C1 |
| СПОСОБ НЕКОГЕРЕНТНОГО НАКОПЛЕНИЯ СВЕТОЛОКАЦИОННЫХ СИГНАЛОВ | 2011 |
|
RU2455615C1 |
| УСТРОЙСТВО ДЛЯ НАСТРОЙКИ КОРРЕКТОРА МЕЖСИМВОЛЬНОЙ ИНТЕРФЕРЕНЦИИ | 1991 |
|
RU2034404C1 |
| СПОСОБ ПОСТРОЕНИЯ СЕЙСМИЧЕСКОГО ДИНАМИЧЕСКОГО ГЛУБИННОГО И/ИЛИ ТОТАЛЬНОГО ВРЕМЕННОГО РАЗРЕЗА | 2011 |
|
RU2454682C1 |
| СПОСОБ КРИПТОГРАФИЧЕСКОГО ПРЕОБРАЗОВАНИЯ БЛОКОВ ДАННЫХ | 1997 |
|
RU2106753C1 |
| СПОСОБ И УСТРОЙСТВО ФОРМИРОВАНИЯ ОПОРНОГО СИГНАЛА ВЫЧИСЛИТЕЛЬНЫМИ СРЕДСТВАМИ В СИСТЕМАХ ЧАСТОТНОЙ И ФАЗОВОЙ СИНХРОНИЗАЦИИ ШИРОКОПОЛОСНЫХ СИСТЕМ СВЯЗИ | 2013 |
|
RU2535198C1 |
| СПОСОБ БЛОЧНОГО ШИФРОВАНИЯ ДАННЫХ | 1997 |
|
RU2103828C1 |
Способ может быть применен в средствах измерений пассивных и активных комплексных величин, например, в мостах и компенсаторах переменного тока или в измерителях параметров электрических цепей, а также в векторных вольтметрах, путем измерения вектора гармонического сигнала в случае действия нескольких периодических помех. Техническим результатом является повышение точности измерения в реальном времени вектора гармонического сигнала с известным периодом, действующего совместно с периодическими сигналами помех, описываемыми непрерывными функциями, при условии, что периоды их тоже известны и не кратны периоду измеряемого сигнала, а также возможность измерения полезных гармонических сигналов из числа сигналов помех. Способ состоит в том, что проекции р' и р” измеряемого сигнала S(t)=Asin(2πt/T+φ0) на два ортогональных вектора опорных сигналов, связанные с его амплитудой А и начальным фазовым сдвигом φ0, получают путем неравномерной дискретизации суммарного сигнала 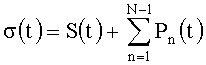 и суммирования его дискрет, выборку которых производят мгновенными импульсами, действующими в моменты времени, образующие соответственно для р' и р” множества
и суммирования его дискрет, выборку которых производят мгновенными импульсами, действующими в моменты времени, образующие соответственно для р' и р” множества 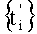 и
и 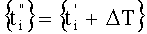 ,
,
где ΔТ=(2r±1)Т/4. r=0, 1, 2,…, которые формируют пошагово согласно условию 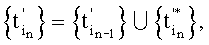 где
где 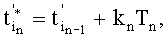 kn=1, 2,…, a
kn=1, 2,…, a 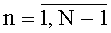 - номер шага, совпадающий с номером сигнала помехи Pn(t), так что
- номер шага, совпадающий с номером сигнала помехи Pn(t), так что 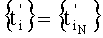 , и знакопеременного суммирования дискрет σ(t) с коэффициентами ai, причем модули аi принимают равными единице, а знаки определяют в зависимости от номеров дискрет согласно условию
, и знакопеременного суммирования дискрет σ(t) с коэффициентами ai, причем модули аi принимают равными единице, а знаки определяют в зависимости от номеров дискрет согласно условию 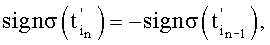 по соотношениям:
по соотношениям: 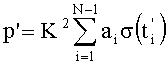
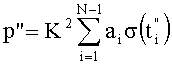
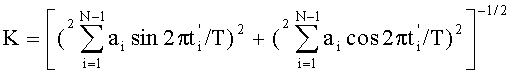 и
и 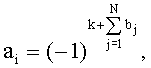 где bj=0,1 - значение j-го разряда представленного в двоичной системе счисления номера
где bj=0,1 - значение j-го разряда представленного в двоичной системе счисления номера 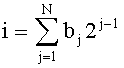 момента времени выборки i-й дискреты суммарного сигнала σ(t), а
момента времени выборки i-й дискреты суммарного сигнала σ(t), а 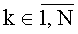 - номер младшего значащего разряда, bj, при этом определяют k как номер элемента b1 множества {b1}, где b1=1, согласно условию k=inf1. 1 ил.
- номер младшего значащего разряда, bj, при этом определяют k как номер элемента b1 множества {b1}, где b1=1, согласно условию k=inf1. 1 ил.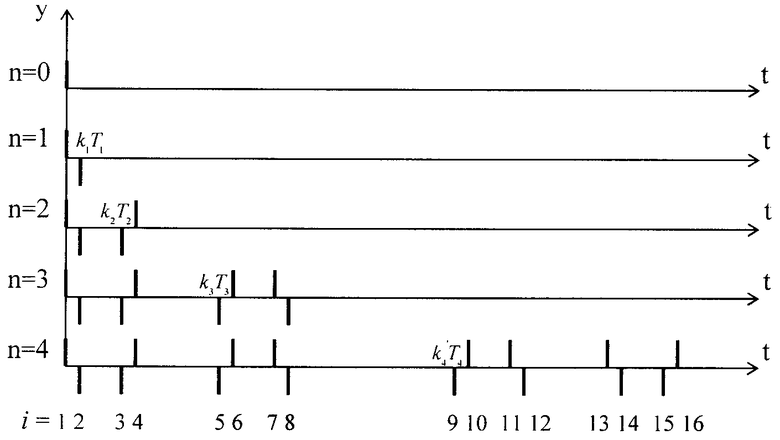
Способ измерения вектора гармонического сигнала S(t)=Asin(2πt/T+φ0) с известным периодом Т, действующего совместно с сигналами помех Pn(t), где 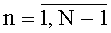 , а N - число сигналов помех, при котором амплитуду А и начальный фазовый сдвиг φ0 сигнала S(t) определяют, например, по соотношениям A=[(p')2+(p″)2]1/2 и φ0=arctg(p'/p″), где р' и р″ - проекции вектора сигнала S(t) на два ортогональных вектора опорных сигналов, а значения р' и р″ получают путем неравномерной дискретизации суммарного сигнала
, а N - число сигналов помех, при котором амплитуду А и начальный фазовый сдвиг φ0 сигнала S(t) определяют, например, по соотношениям A=[(p')2+(p″)2]1/2 и φ0=arctg(p'/p″), где р' и р″ - проекции вектора сигнала S(t) на два ортогональных вектора опорных сигналов, а значения р' и р″ получают путем неравномерной дискретизации суммарного сигнала 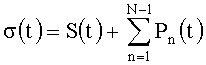 и суммирования его дискрет, выборку которых производят мгновенными импульсами, действующими в моменты времени, образующие соответственно для р' и р″ множества
и суммирования его дискрет, выборку которых производят мгновенными импульсами, действующими в моменты времени, образующие соответственно для р' и р″ множества 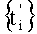 и
и 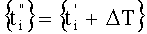 , где ΔТ=(2r±1)Т/4, r=0, 1, 2,…, отличающийся тем, что в том случае, когда помехами являются периодические сигналы Pn(t)=Pn(t-Tn), где Tn - известные периоды сигналов помех, a Pn(t) - непрерывные функции, проекции р' и р″ сигнала S(t) измеряют путем неравномерной дискретизации суммарного сигнала σ(t) на множестве моментов времени
, где ΔТ=(2r±1)Т/4, r=0, 1, 2,…, отличающийся тем, что в том случае, когда помехами являются периодические сигналы Pn(t)=Pn(t-Tn), где Tn - известные периоды сигналов помех, a Pn(t) - непрерывные функции, проекции р' и р″ сигнала S(t) измеряют путем неравномерной дискретизации суммарного сигнала σ(t) на множестве моментов времени 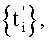 которое формируют пошагово согласно условию
которое формируют пошагово согласно условию
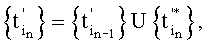 где
где 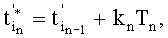 kn=1, 2,…, a
kn=1, 2,…, a 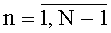 - номер шага, совпадающий с номером сигнала помехи Pn(t), так что
- номер шага, совпадающий с номером сигнала помехи Pn(t), так что 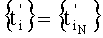 , и знакопеременного суммирования дискрет σ(t) с коэффициентами ai, причем модули ai принимают равными единице, а знаки определяют в зависимости от номеров дискрет согласно условию
, и знакопеременного суммирования дискрет σ(t) с коэффициентами ai, причем модули ai принимают равными единице, а знаки определяют в зависимости от номеров дискрет согласно условию 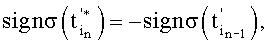 по соотношениям:
по соотношениям: 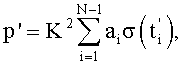
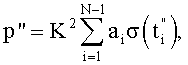
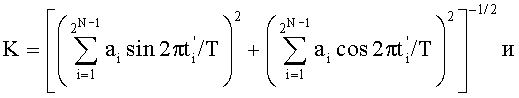
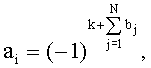
где bj=0,1 - значение j-го разряда, представленного в двоичной системе счисления номера 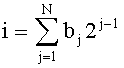 момента времени выборки i-й дискреты суммарного сигнала σ(t), a
момента времени выборки i-й дискреты суммарного сигнала σ(t), a 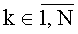 - номер младшего значащего разряда bj, при этом определяют k как номер элемента b1 множества {b1}, где b1=1, согласно условию k=inf1.
- номер младшего значащего разряда bj, при этом определяют k как номер элемента b1 множества {b1}, где b1=1, согласно условию k=inf1.
| US 2007063753 A1, 22.03.2007 | |||
| СПОСОБ ИЗМЕРЕНИЯ ПОСТОЯННОЙ СОСТАВЛЯЮЩЕЙ СИГНАЛА | 2003 |
|
RU2239842C1 |
| Способ измерения постоянной составляющей периодического сигнала | 1983 |
|
SU1126888A1 |
| US 4642564 A, 10.02.1987 | |||
| СПОСОБ ИЗМЕРЕНИЯ ВЕКТОРА ГАРМОНИЧЕСКОГО СИГНАЛА | 2008 |
|
RU2377577C1 |
| Агамалов Ю.Р | |||
| Метод измерения векторов совместно действующих гармонических сигналов на основе их дискретизации и суммирования дискрет | |||
| Метрология, 2010. | |||
Авторы
Даты
2012-11-10—Публикация
2011-06-22—Подача