Изобретение относится к области магнитного разделения. Оно может быть использовано в различных отраслях промышленности для анализа магнитовосприимчивой фракции примесей текучих сред, т.е. примесей, склонных к магнитному осаждению. В их числе, например, такие ферропримеси, как частицы, образующиеся вследствие коррозии оборудования, его износа (особенно при осуществлении процессов дробления и размола технологических сред), частицы окалины, различные металлические включения (последствия металлообработки, термообработки и сварки при ремонте и обслуживании оборудования).
Снижая качество сред, эти примеси к тому же становятся серьезным дестабилизирующим фактором производства, уменьшая надежность и долговечность работы оборудования: они интенсифицируют износ, приводят к повреждениям, поломкам оборудования, провоцируют аварийные остановки производства и т.д. Поэтому достоверная информация об этой фракции примесей, для удаления которой используются магнитные очистные аппараты, например, информация о доле λ такой фракции примесей в общем балансе всех примесей, является крайне важной. Прежде всего, она позволяет объективно судить о потенциальном уровне данного (магнитного) метода очистки применительно к той или иной среде, подлежащей очистке.
Из уровня техники известен способ анализа магнитовосприимчивой фракции примесей в текучей среде [1].
Способ основан на многократном пропускании пробы анализируемой среды через лабораторный образец магнитного очистного аппарата, который выступает здесь базовым элементом анализатора магнитовосприимчивой фракции примесей.
В результате такой полицикличной операции, проводимой с целью принудительной многократной «выборки» магнитовосприимчивых примесей из анализируемой среды по мере увеличения числа циклов (n), концентрация (с) примесей, измеряемая в этой среде, уменьшается [1]. Из этой иллюстрации следует, что необходимое для реализации способа-аналога число циклов достигает здесь, в частности, n=6-8, когда концентрация примесей в анализируемой среде минимизируется до практически стабильного значения Сост, которое тем самым свидетельствует о том, что из анализируемой среды магнитовосприимчивые частицы уже практически полностью «выбраны». А это дает возможность находить значение доли магнитовосприимчивой фракции примесей в анализируемой среде как результат вычисления относительной разницы между значениями исходной (с0) и остаточной (сост) концентрациями:
 ,
,
где 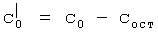 - концентрация активной (магнитовосприимчивой) фракции примесей.
- концентрация активной (магнитовосприимчивой) фракции примесей.
О необходимом для достижения этого результата числе циклов (n) свидетельствует появление и дальнейшее сохранение автомодельного, «горизонтального» участка получаемой опытной зависимости (с) от (n).
Данный способ, являющийся одним из надежных способов анализа магнитовосприимчивой фракции примесей, тем не менее, имеет недостатки, заключающиеся в следующем.
Для его реализации в ряде случаев требуется проведение достаточного (иногда значительного) количества циклов (n) - такого, при котором действительно отчетливо прослеживается появление и дальнейшее сохранение упоминаемого выше автомодельного («горизонтального») участка получаемой экспериментальной зависимости, т.е. достижение практически стабильного, почти постоянного минимального значения концентрации (сост). А это повышает трудоемкость опытов.
К тому же, при реализации данного способа все же допускается определенная погрешность, так как сами понятия «горизонтального» участка и стабильного значения остаточной концентрации являются здесь не в полной мере строгими. Так, при увеличенном числе циклов (n) все же может наблюдаться некоторое, хотя и незначительное, дальнейшее понижение значения (Сост), что, естественно, вынуждает вносить уточнение в итоговый результат определения λ.
Известен экспериментально-расчетный способ (вариант 1) анализа магнитовосприимчивой фракции примесей в текучей среде [2] (стр.96-97).
Суть данного способа, при реализации которого используют магнитный фильтр (анализатор) с фильтр-матрицей, выполняющей роль поглощающего экрана примесей при прохождении сквозь нее текучей среды, заключается в выполнении трех описанных ниже действий.
1. Получают экспериментальные данные эффективности ψ=(с0-с)/с0 удаления примесей из анализируемой среды в зависимости от рабочей длины L фильтр-матрицы [2 (стр.52)].
2. Выбирают из этих экспериментальных данных (для последующего использования в вычислениях) два или три конкретных значения эффективности ψ1, ψ2, и/или ψ3.
Первое значение эффективности, т.е. ψ1, выбирают при произвольном значении длины фильтр-матрицы L1, исходя из возможности беспрепятственного осуществления последующих условий реализации данного способа.
Второе значение эффективности, т.е. ψ2, должно соответствовать строго увеличенной длине фильтр-матрицы, а именно L2=2L1.
В качестве второго значения эффективности ψ2 может быть использовано также отличное от предыдущего значение эффективности ψ2 (ψ3), которое соответствует длине фильтр-матрицы L3, (L3)=3L1. Для четкого разграничения с предыдущей точкой, удобно пользоваться не символикой ψ2 и L2, а символикой ψ3 и L3.
3. Используют указанные в п.2 выбранные (или специально полученные) экспериментальные данные ψ1, ψ2 и/или ψ3 для вычисления доли магнитовосприимчивой фракции λ по следующим формулам [2]:
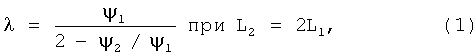

полученным вследствие решения обратной задачи с использованием базового уравнения магнитно-фильтрационной очистки [2], т.е. общего выражения для эффективности такой очистки (с коэффициентом поглощения примесей α):

Недостатком этого способа является то, что он применим для ограниченного круга сред - тех, которые подчиняются модели экспоненциального поглощающего экрана, т.е. уравнению (3). К их числу относятся среды, содержащие относительно «односортные» магнитовосприимчивые примеси, т.е. обладающие сравнительно узким спектром крупности (в пределах одного порядка) и восприимчивости.
Проверка же на соответствие или несоответствие анализируемой среды такой модели представляет самостоятельный вопрос, нуждающийся в дополнительном разъяснении.
Так, с математической точки зрения тест анализируемой среды на ее соответствие или несоответствие модели экспоненциального поглощающего экрана может быть легко и наглядно продемонстрирован, если экспериментальные данные ψ от L представить в координатах ξ от L, где кси-параметр вычисляют как

В связи с этим базовое уравнение (3) преобразуется к такому виду:

показывающему, что зависимость ξ от L - прямая пропорциональная.
Значит, если экспериментальные данные ψ преобразовать в ξ, то они линеаризуются, начиная с центра избранной системы координат (ξ, L). И действительно, целый ряд промышленных сред, как это следует из публикаций [2 (стр.52)] и [3 (стр.19]), подчиняется модели экспоненциального поглощающего экрана.
Однако не все анализируемые среды подчиняются модели экспоненциального поглощающего экрана. Получаемая зависимость ξ и L не является, как ранее прямой пропорциональной, а содержит два выраженных участка. Один из них (начальный, относительно короткий), ограничивающийся некоторым, сравнительно малым значением длины фильтр-матрицы Lξ - круто восходящий, а второй (хвостовой, удлиненный) - более пологий, представляющий собой практически прямую линию.
Если экстраполировать именно хвостовой участок зависимости ξ от L в область малых значений L вплоть до пересечения с осью ординат, то можно получить некоторую, на первый взгляд формальную, «стартовую» ординату ξ0. Тогда зависимость ξ от L для подобного рода сред, не являясь прямой пропорциональной, имея выраженный «скачок» в области сравнительно малых значений L<Lξ, лишь при L≥Lξ линеаризуется, указывая на такой аналитический вид:

отличный от выражения (5), причем он становится понятным и объяснимым с позиций концепции «разносортности» магнитовосприимчивых примесей [2, 3], состоящих, по меньшей мере, из двух подфракций - с ослабленной и повышенной склонностью к магнитному осаждению («трудноосаждаемой» А и «легкоосаждаемой» В).
Так, если принять во внимание, что эти подфракции характеризуются исходными концентрациями c0A и c0B 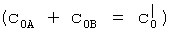 , выходными концентрациями cA и cB
, выходными концентрациями cA и cB  и индивидуальными коэффициентами поглощения αA и αB, то в этом случае справедливой становится модель двухэкспоненциального поглощающего экрана [3], в соответствии с которой
и индивидуальными коэффициентами поглощения αA и αB, то в этом случае справедливой становится модель двухэкспоненциального поглощающего экрана [3], в соответствии с которой

где: 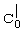 и
и  - концентрация именно магнитовосприимчивой фракции примесей среды до и после ее очистки.
- концентрация именно магнитовосприимчивой фракции примесей среды до и после ее очистки.
Для (хвостового) участка зависимости ξ от, который характеризуют как технологически принципиальную стадию доочистки, т.е. очистки от «трудноосаждаемой» подфракции λA (мелких частиц и частиц, обладающих сравнительно небольшой магнитной восприимчивостью), выражение (7) упрощается до вида:
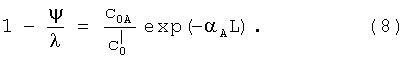
так как процесс протекает уже практически в отсутствие подфракции λB, (cB→0).
Логарифмируя левую и правую части уравнения (8) и принимая во внимание определение (4), получают выражение для ξ-параметра [3]:

в том числе с учетом вводимого обозначения:
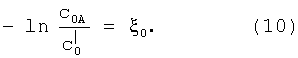
Таким образом, уравнение (9), полученное на основании модели двухэкспоненциального поглощающего экрана, согласуется с эмпирической зависимостью (6), а это подтверждает справедливость данной модели и вытекающих из нее следствий.
Тогда и выражение для определения ψ, которое можно получить из формул (6) или (9) после обратного перехода от ξ к ψ посредством формулы (4), принимает вид:
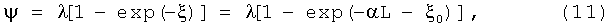
отличающийся, от базового выражения (3) наличием (в экспоненте) еще
одного, ранее не фигурировавшего, параметра: ξ0.
А это значит, что и расчетные формулы (1) и (2), полученные без учета данного параметра, здесь как результативные использованы быть не могут (заметим - для рассматриваемого случая отклонения экранной характеристики анализируемой среды от модели экспоненциального поглощающего экрана).
Формальное же их использование (повторим - для сред, не подчиняющихся классической модели экспоненциального поглощающего экрана) приведет к ошибкам и получению недостоверных данных определяемой доли магнитовосприимчивой фракции примесей λ.
Именно в этом, собственно, и заключается уже упомянутый выше недостаток описанного способа определения доли магнитовосприимчивой фракции примесей λ.
Более того, описанному способу присущ и такой принципиальный недостаток, который не только повышает риск ошибки, но и серьезно препятствует его применению, даже при наличии специально полученной экранной экспериментальной зависимости - типа одной из зависимостей.
По сути, при реализации данного способа создается тупиковая ситуация, своеобразный «порочный круг». Действительно, намерение применить формулы (1) и (2) для определения λ сдерживается отсутствием информации о гарантированной принадлежности анализируемой среды к кругу сред, подчиняющихся модели экспоненциального поглощающего экрана, а получение такой информации, в свою очередь, невозможно без знания конкретной величины λ.
Известен способ анализа магнитовосприимчивой фракции примесей в текучей среде (модернизированный вариант 2), который принят нами в качестве прототипа [2 (с.97-98)]. Суть данного способа тоже заключается в выполнении трех основных действий.
1. Получают экспериментальные данные эффективности ψ удаления примесей из анализируемой среды (магнитным фильтром-анализатором) в зависимости от рабочей длины L фильтр-матрицы, т.е. получают типичную для такого анализа экранную зависимость.
2. Выбирают из этих экспериментальных данных обязательно три конкретных значения эффективности: ψ1, ψ2 и ψ3.
Первое значение эффективности, т.е. ψ1, выбирают при произвольном (но не слишком малом) значении длины фильтр-матрицы L1 магнитного очистного устройства. Второе и третье значения эффективности, т.е. ψ2 и ψ3, соответствуют строго увеличенным значениям длины фильтр-матрицы L2 и L3, с соблюдением условия: L3-L2=L2-L1, т.е. значения L1, L2 и L3 подчиняются арифметической прогрессии.
3. Используют указанные в п.2 выбранные (или специально полученные) экспериментальные данные ψ1, ψ2 и ψ3 для вычисления доли магнитовосприимчивой фракции λ по известной из [2] формуле:
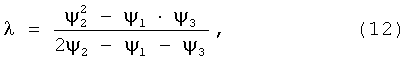
полученной путем решения обратной задачи с использованием уравнения магнитно-фильтрационной очистки (11) [2, 3] для указанного выше частного случая, когда L2-L1=L3-L2.
Кроме того, данный способ позволяет также определять значения долей подфракций λA и λB - с ослабленной и повышенной склонностью к магнитному осаждению. Так, из введенного обозначения (10) следуют известные из [2, 3] формулы, по которым можно определить доли подфракций λA и λB:


пользуясь значениями ξ0, получаемыми графическим путем.
Между тем, данный модернизированный способ также обладает присущим ему недостатком. Он заключается в том, что формула (12) справедлива лишь при L≥Lξ, т.е. строго для участка доочистки: хвостового (заметим - сравнительно длинного) участка зависимости ξ от L, который отчетливо просматривается лишь на этой (ξ от L) зависимости, благодаря ее характерному «излому», приходящемуся на переходное значение Lξ.
Но такая зависимость (ξ от L) недоступна экспериментатору до определения значения λ.
А на доступной экспериментатору зависимости ψ от L четко указать на переходное значение Lξ, начиная с которого следует выбирать первое результативное значение L1, не представляется возможным.
Другими словами, реализация данного способа в отсутствие указания на «местонахождение» переходного значения Lξ осложнена. Так, проблематично гарантировать использование всех значений эффективности, т.е. ψ1, ψ2 и ψ3, полученных для длин фильтр-матрицы L1, L2 и L3 (прежде всего стартовых значений ψ1, L1) исключительно из хвостового участка экспериментальной экранной зависимости, причем желательно - в пределах практически всей протяженности этого участка. Причина этому уже указана: лишь на зависимости ξ от L этот участок (после «излома» этой зависимости) становится явным, а на зависимости ψ от L он - неявный.
Следовательно, при реализации этого способа экспериментатор всегда объективно испытывает затруднение, прежде всего в выборе стартового значения L1 (и соответствующего ему значения ψ1), так как неправильный выбор этого значения (а именно L<Lξ) повлечет погрешность при вычислении λ по формуле (12).
Ориентировать же экспериментатора на выбор значения L1 «с запасом» приведет (с учетом последующего соответствующего выбора L2 и L3) к использованию лишь концевой части хвостового участка опытной зависимости ψ от L, т.е. к ограничению поля («шкалы») привлекаемых для использования здесь экспериментальных данных. К тому же, используемые для расчета λ значения ψ1, ψ2 и ψ3, будут в этом случае нежелательно близкими друг к другу по величине. В итоге все это тоже негативно скажется на точности определения λ.
Что же касается определения долей подфракций λA и λB (в составе λ) по формулам (13) и (14), то такой подход - с предшествующим графическим нахождением параметра ξ0 - тоже обладает недостатком, связанным именно с графическим (а не более объективным аналитическим) определением этого параметра.
Задачей предлагаемого способа анализа магнитовосприимчивой фракции примесей текучей среды является повышение точности определения магнитовосприимчивой фракции примесей.
Технический результат - повышение точности определения доли магнитовосприимчивой фракции примесей и ее подфракций в конкретной производственной среде, их активности к магнитному осаждению - достигается следующим образом.
Производят отбор предназначенной для анализа пробы среды (разумеется, заранее не поддающейся идентификации на принадлежность или непринадлежность к средам, подчиняющимся модели экспоненциального поглощающего экрана).
Затем проводят эксперименты для получения данных эффективности ψ удаления примесей этой среды магнитным очистным устройством (фильтром лабораторной производительности) в зависимости от рабочей длины его фильтр-матрицы L. Получают три значения эффективности, т.е. ψ1, ψ2 и ψ3, для трех кратных друг другу значений длин, т.е. L1, L2=2L1 и L3=3L1.
Располагая полученными данными, формально (несмотря на отсутствие информации о принадлежности или непринадлежности анализируемой среды к средам, подчиняющимся модели экспоненциального поглощающего экрана) все же производят вычисление значения доли магнитовосприимчивой фракции примесей λ по формулам (1), (2) и (12).
Вычисление по этим формулам может дать два принципиальных результата.
Первый: полученные значения λ оказались одинаковыми (весьма близкими друг к другу). Этот однозначный результат - сам по себе важный. Он означает, что имеют дело со средой, подчиняющейся модели экспоненциального поглощающего экрана. При этом полученное значение λ является вполне достоверным. И дальнейшие шаги в рамках способа определения доли магнитовосприимчивой фракции примесей λ приостанавливаются как завершенные.
Второй: полученные значения λ оказались различными. Такой результат тоже является важным промежуточным результатом. Это свидетельствует о том, что имеют дело со средой, не подчиняющейся модели экспоненциального поглощающего экрана, т.е. со средой, в которой магнитовосприимчивая фракция примесей содержит подфракции примесей, характеризующиеся ослабленной и повышенной склонностью к магнитному осаждению.
Автоматически это означает, что параметр λ исполняет две информативные функции. Одна из которых, соответствует прямому определению этого параметра λ - как характеристики доли магнитовосприимчивых примесей в общем содержании примесей. Вторая - для определения долей подфракции λA и λB, магнитовосприимчивых примесей: с ослабленной и повышенной склонностью к магнитному осаждению.
Итак, после квалификации анализируемой среды как не подчиняющейся модели экспоненциального поглощающего экрана значение доли магнитовосприимчивой фракции λ, вычисленное по формуле (12), принимают в качестве значения, более близкого к достоверному, но нуждающемуся в уточнении.
Для совершения этих действий необходимо удостовериться в том, что все три точки (ψ1, ψ2 и ψ3) принадлежат участку доочистки (неявному хвостовому участку полученной первичной зависимости ψ от L, который может стать явным лишь после преобразования зависимости ψ от L в зависимость ξ от L, а это возможно только после нахождения λ). При этом всегда существует сомнение, что, по меньшей мере, значение эффективности ψ1 получено при неблагоприятном значении длины фильтр-матрицы L1<Lξ.
Для того чтобы опровергнуть или подтвердить это сомнение, эксперимент повторяют с получением данных эффективности ψ4 при увеличенной длине L4=4L1 фильтр-матрицы магнитного очистного устройства и опять определяют значение λ по формуле, аналогичной (12):
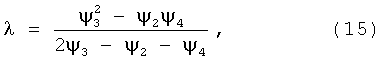
но с использованием экспериментальных данных эффективности ψ2, ψ3 и ψ4. Такое смещение (вправо по графику зависимости ψ от L) обновленной тройки данных ψ (данных ψ2, ψ3, и ψ4 вместо данных ψ1, ψ2, и ψ3) осуществляют с целью обязательного выхода за пределы области «излома», где вполне могли оказаться стартовые значения L1 и ψ1.
И если полученное по формуле (15) значение λ соответствует предыдущему значению λ, то это означает, что высказанное сомнение не имеет оснований. В этом случае результат определения λ (как точный) считается достигнутым.
В случае же расхождения значения λ с предыдущим значением λ эксперимент еще раз повторяют - для получения данных эффективности ψ5 при дополнительно увеличенной длине L5=5L1 фильтр-матрицы магнитного очистного устройства с последующим определением значения λ по формуле, аналогичной (12) и (15):
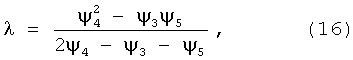
но с использованием экспериментальных данных эффективности ψ3, ψ4 и ψ5. (эта, вновь обновленная тройка данных ψ, опять отражает факт очередного дискретного смещения вправо по графику зависимости ψ от L). Полученное же по формуле (16) значение λ, как и ранее, сравнивается с предыдущим.
Подобные действия по проведению экспериментов с дальнейшим увеличением L фильтр-матрицы магнитного очистного устройства, получению соответствующих данных эффективности ψ удаления примесей и определению значения доли магнитовосприимчивой фракции примесей λ в текучей среде продолжают до тех пор, когда сравниваемые значения λ станут одинаковыми. Это и будет свидетельствовать о факте достижения истинного, достоверного значения доли магнитовосприимчивой фракции примесей.
При этом результат, достигаемый за счет таких оправданных дискретных смещений, отвечает обоим необходимым условиям реализации способа. Это - условие L1≥Lξ и условие более полного использования участка доочистки.
После определения доли магнитовосприимчивой фракции примесей λ становится возможным также определение по формулам (13) и (14) доли каждой из подфракций (λА и λB) - с ослабленной («трудноосаждаемой» А) и повышенной («легкоосаждаемой» В) склонностью к магнитному осаждению.
Для этого необходимо располагать значением входящего в эти формулы параметра ξ0. Для нахождения ξ0 требуются всего лишь два числовых значения ψ из уже использованных (для нахождения λ) трех значений ψ (ψn-2, ψn-1, ψn), явившихся завершающими результативными значениями ψ среди всех установленных ранее экспериментальных значений ψ (ψ1, ψ2, ψ3, ψ4…ψn).
При этом возможны три комбинации пар из указанных трех значений ψ. Первая: ψn-1 и ψn. Вторая: ψn-2 и ψn-1. Третья: ψn-2 и ψn.
Используя сначала первую из возможных комбинаций, т.е. такие два значения эффективности удаления примесей как ψn-1 и ψn, полученные при значениях рабочей длины Ln-1 и Ln, фильтр-матрицы магнитного очистного устройства, получают применительно к этим значениям систему двух уравнений, адекватных уравнению (11):

Полученную систему уравнений (содержащую два неизвестных параметра, а именно ξ0 и α, заметим - при уже известном параметре λ) решают относительно параметра ξ0. При этом формулу для расчета ξ0 получают в следующем виде:

при соответствующих значениях Ln=nL1 и ψn, Ln-1=(n-1)L1 и ψn-1.
Точно так же поступают и с двумя другими комбинациями пар значений эффективности ψ (в рамках тех же трех результативных значений эффективности: ψn-2, ψn-1, ψn).
Так, при выборе значений ψn-2 и ψn-1, полученных при значениях рабочей длины Ln-2 и Ln-1, решением дополнительно составленной (для этого случая) системы, аналогичной системе уравнений (17), только с соответствующей индексацией, являются выражения, подобные (18), а именно:

А при выборе значений ψn-2 и ψn, полученных при значениях рабочей длины Ln-2 и Ln, используя такой же подход, можно также получить еще и такие выражения, подобные (18) и (19):

Примечательно, что выражения (18)-(20) для ξ0, которые изначально внешне сходны, тем не менее, строго индивидуальны - в зависимости от конкретных значений эффективности ψ удаления примесей магнитным очистным устройством в зависимости от рабочей длины его фильтр-матрицы L.
Использование полученных выражений в качестве расчетных формул может быть продемонстрировано на частном примере (с «укороченной процедурой» выполнения экспериментальной части реализации способа).
Так, пусть при проведении экспериментальной части предлагаемого способа экспериментатору понадобилось получить (выбрать) всего лишь четыре значения эффективности, т.е. ψ1, ψ2, ψ3, ψ4, из которых последние три, т.е. ψ2, ψ3, ψ4, - итоговые, результативные.
Тогда, используя сначала значения ψ3 и ψ4, полученные при значениях L3=3L1 и L4=4L1, на основании формулы (18) применяют к рассматриваемому случаю формулу для расчета ξ0:
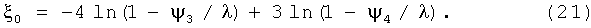
Используя далее значения ψ2 и ψ3, полученные при значениях L2=2L1 и L3=3L1, и на основании формулы (19), для расчета ξ0, применяют к данному рассматриваемому случаю следующую формулу:

А используя значения ψ2 и ψ4, полученные при значениях L2=2L1 и L4=4L1, и на основании формулы (20) для расчета ξ0, применяют к данному рассматриваемому случаю следующую формулу:
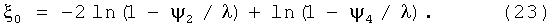
Достоверная же информация о параметре ξ0, которая при наличии соответствующих данных становится доступной благодаря приведенным выше формулам, как уже оговорено, дает возможность в соответствии с формулами (13) и (14) получать и информацию о значениях долей «трудноосаждаемой» λА и «легкоосаждаемой» λB подфракций всей магнитовосприимчивой фракции примесей.
Таким образом, реализация предлагаемого способа позволяет устранить отмеченные выше недостатки способа-прототипа и получить объективную информацию как о доле магнитовосприимчивой фракции примесей λ в анализируемой среде, так и о долях входящих в нее основных подфракций этих примесей: «трудноосаждаемой» λA и «легкоосаждаемой» λB.
Предложенный способ поясняется соответствующими графиками, на которых изображено следующее.
На фиг.1a изображен график, иллюстрирующий экспериментальную экранную характеристику (незатемненные точки) анализируемой среды.
При этом из выделенных (затемненных) четырех точек на этой зависимости (ψ1, ψ2, ψ3 и ψ4) в расчетах по формуле (15) должны использоваться последние три, а именно ψ2, ψ3 и ψ4, полученные при L2=2L1, L3=3L1 и L4=4L1. В расчетах же по формулам (13) и (14), которые требуют применения формул (18)-(20), а для проиллюстрированной здесь «укороченной процедуры» - формул (21)-(23), из указанных трех значений ψ используется лишь пара значений (по выбору).
На фиг.1б изображен график, иллюстрирующий ту же характеристику, но после преобразования данных эффективности ψ в данные ξ-параметра в соответствии с определением (4).
При этом здесь явно выделяющейся особенностью является то, что эта характеристика не подчиняется прямой пропорциональной зависимости. Она содержит два заметных участка, разграничивающиеся некоторым, сравнительно малым значением длины фильтр-матрицы Lξ. Экстраполяция второго (хвостового) участка зависимости ξ от L в область малых значений L вплоть до пересечения с осью ординат дает «стартовую» ординату ξ0 (графический прием, используемый в способе-прототипе). Однако эту же ординату ξ0 целесообразнее получить расчетно-эмпирическим путем, используя уже имеющиеся (фиг.1а) экспериментальные значения ψ2, ψ3 и ψ4 (точнее - два из них в любой из возможных трех комбинаций) с последующим применением, в частности, расчетных формул (21)-(23).
Предлагаемый способ реализуется путем выполнения следующих действий.
1. Получают экспериментальные данные эффективности ψ удаления примесей из анализируемой среды (магнитным фильтром-анализатором) в зависимости от рабочей длины L фильтр-матрицы (см. фиг.1а, незатемненные точки), т.е. получают типичную для такого анализа экспериментальную экранную зависимость.
2. Выбирают из этих экспериментальных данных три конкретные значения эффективности: ψ1, ψ2, ψ3 (см. фиг.1а, затемненные точки).
Первое значение эффективности ψ1 выбирают при произвольном (но не слишком малом) значении длины фильтр-матрицы L1, исходя из возможности беспрепятственного осуществления последующих условий реализации предлагаемого способа.
Второе и третье значения эффективности, т.е. ψ2, ψ3 (а возможно, четвертое и другие значения эффективности ψ4 … ψn→λ) должны соответствовать строго увеличенным значениям длины фильтр-матрицы L магнитного очистного устройства с соблюдением условия: L2=2L1, L3=3L1 (L4=4L1 … Ln=nL1). В этом случае, разумеется, выполняется также частное условие способа-прототипа: L3-L2=L2-L1, когда значения L1, L2 и L3 должны подчиняться арифметической прогрессии.
При этом во внимание могут быть приняты следующие обстоятельства:
- если экспериментатор обладает полнообъемной «многоточечной» экранной зависимостью (см. фиг.1а, незатемненные точки), то для выбора значений ψ1, ψ2, ψ3 (а возможно и ψ4…ψn) необходимо пользоваться аппроксимирующей кривой, усредняющей локальные опытные значения ψ;
- для повышения объективности результата последующего определения λ экспериментатор варьирует значением ψ1 (и соответственно значениями ψ2, ψ3 и т.д.), варьируя при этом значением L1 (и соответственно значениями L2, L3, L4 и т.д.) таким образом, чтобы использовать максимум поля экспериментальных данных («шкалы») имеющейся экспериментальной зависимости (ее хвостовой части);
- упоминаемые конкретные значения эффективности ψ1, ψ2, ψ3 получают целенаправленно, без обязательного получения всей «многоточечной» экспериментальной зависимости ψ от L (см. фиг.1a).
3. Используют указанные в предыдущем п.2 выбранные экспериментальные данные ψ1, ψ2 и ψ3 для вычисления доли магнитовосприимчивой фракции λ - сначала по формулам (1), (2), (12), после чего производят сравнительный анализ полученных конкретных данных λ.
4. В случае если полученные данные λ оказались одинаковыми, то анализируемую среду квалифицируют как подчиняющуюся модели экспоненциального поглощающего экрана. При этом полученное значение λ является вполне достоверным и, стало быть, дальнейшие шаги в рамках способа определения доли магнитовосприимчивой фракции примесей λ приостанавливаются как завершенные.
В случае же если полученные данные λ оказались неодинаковыми, то анализируемую среду квалифицируют как не подчиняющуюся модели экспоненциального поглощающего экрана, т.е. содержащую подфракции λA и λB примесей, характеризующиеся ослабленной и повышенной склонностью к магнитному осаждению. При этом параметр λ исполняет две информативные функции, одна из которых соответствует прямому определению этого параметра, характеризуя долю магнитовосприимчивых примесей в общем содержании примесей, а вторая выполняет роль одного из параметров, необходимых для определения долей подфракций магнитовосприимчивых примесей: с ослабленной и повышенной склонностью к магнитному осаждению. И в данном случае более достоверным, но нуждающимся в уточнении, принимают значение λ, вычисленное по формуле (12).
5. Эксперимент повторяют для получения нового конкретного значения эффективности: ψ4, при увеличенной длине L4=4L1.
6. Опять определяют значение λ - по формуле (15) с использованием экспериментальных данных эффективности ψ2, ψ3 и ψ4.
7. В случае расхождения значения λ с предыдущим значением λ эксперимент повторяют для получения данных эффективности ψ5 при дополнительно увеличенной длине L5=5L1.
8. Опять определяют значение λ - по формуле (16) с использованием экспериментальных данных эффективности ψ3, ψ4 и ψ5.
9. Подобные действия по проведению экспериментов с дальнейшим увеличением L длины фильтр-матрицы магнитного очистного устройства, получению соответствующих данных эффективности ψ удаления примесей и определению значения λ продолжают до тех пор, когда значения доли магнитовосприимчивой фракции примесей λ станут одинаковыми, что свидетельствует о достоверности достигнутого результата.
10. Полученный результат определения доли магнитовосприимчивой фракции примесей λ используют для пересчета значений эффективности ψ удаления примесей (фиг.1а) в значения ξ (фиг.1б) по выражению (4), последующего построения зависимости ξ-параметра от L (см. фиг.1б) и получения наглядной картины в виде двух выраженных участков этой зависимости, которые разграничиваются значением L=Lξ (используемым для самоконтроля).
11. Полученное значение λ, а также два из трех последних экспериментальных значений ψ (ψn-2, ψn-1 и ψn), полученных при соответствующих значениях Ln-2=(n-2)L1, Ln-1=(n-1)L1 и Ln=nL1, используют для определения доли подфракций λA и λB.
При этом входящий в расчетные формулы (13) и (14), а именно λA=ехр(-ξ0) и λB=1-λA, параметр ξ0 находится по одному из трех выражений (18)-(20):
а) при использовании значений ψn-1 и ψn, полученных при Ln-1=(n-1)L1 и Ln=nL1, применяется выражение (18),
б) при использовании значений ψn-2 и ψn-1, полученных при Ln-2=(n-2)L1 и Ln-1=(n-1)L1, применяется выражение (19),
в) при использовании значений ψn-2 и ψn, полученных при Ln-2=(n-2)L1 и Ln=nL1, применяется выражение (20).
12. В частности, при «укороченной процедуре» реализации предлагаемого способа, ограничивающейся получением четырех экспериментальных значений эффективности, т.е. ψ1, ψ2, ψ3, ψ4, согласно п.11 описания способа, для определения искомых долей подфракций λA и λB используют любые два из трех последних (результативных) экспериментальных значений ψ, здесь - из значений ψ2, ψ3 и ψ4, полученных при соответствующих значениях L2=2L1, L3=3L1 и L4=4L1. При этом входящий в упомянутые расчетные формулы λA=ехр(-ξ0) и λB=1-λA параметр ξ0 находят по одному из трех выражений (21)-(23):
а) при использовании значений ψ3 и ψ4, полученных при L3=3L1 и L4=4L1, применяется выражение (21),
б) при использовании значений ψ2 и ψ3, полученных при L2=2L1 и L3=3L1, применяется выражение (22),
в) при использовании значений ψ2 и ψ4, полученных при L2=2L1 и L4=4L1, применяется выражение (23).
Использование предлагаемого способа в лабораторной практике позволяет оперативно и точно определять долю магнитовосприимчивой фракции примесей в конкретной производственной среде, а также количественно квалифицировать эту долю по подфракциям с точки зрения их активности (более выраженной и менее выраженной) к магнитному осаждению. Все это представляет собой весьма ценную информацию для разработчиков и эксплуатационников магнитных очистных аппаратов, способствующих удалению «везде и всегда» присутствующих в различных производственных средах магнитовосприимчивых примесей, образующихся вследствие коррозии оборудования, его износа (особенно при осуществлении процессов дробления и размола технологических сред), металлообработки, термообработки и сварки (при ремонте и обслуживании оборудования) и пр.
Источники информации
1. Патент США №4492921, G01N 15/06, 1985.
2. Сандуляк А.В. Магнитно-фильтрационная очистка жидкостей и газов. М.: Химия, 1988, стр.95-96.
3. Сандуляк А.В. и др. Особенности модели поглощающего экрана магнитного фильтра. - Тяжелое машиностроение, 2004, №10, с.18-23.
| название | год | авторы | номер документа |
|---|---|---|---|
| СИСТЕМА ОТКАЗОУСТОЙЧИВОГО УПРАВЛЕНИЯ ДВИЖЕНИЕМ КОРАБЛЯ | 2013 |
|
RU2536011C2 |
| СЕПАРАТОР | 2005 |
|
RU2305598C2 |
| Многолучевая стрелковая мишень | 2024 |
|
RU2840640C1 |
| СПОСОБ ИЗГОТОВЛЕНИЯ ТЕНЗОРЕЗИСТОРНОГО ДАТЧИКА ДАВЛЕНИЯ С ВЫСОКОЙ ВРЕМЕННОЙ И ТЕМПЕРАТУРНОЙ СТАБИЛЬНОСТЬЮ НА ОСНОВЕ ТОНКОПЛЕНОЧНОЙ НАНО- И МИКРОЭЛЕКТРОМЕХАНИЧЕСКОЙ СИСТЕМЫ | 2015 |
|
RU2594677C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОНЦЕНТРАЦИИ МАГНИТОВОСПРИИМЧИВЫХ ПРИМЕСЕЙ В ТЕКУЧЕЙ СРЕДЕ | 2009 |
|
RU2409425C1 |
| МАГНИТНЫЙ СЕПАРАТОР | 2007 |
|
RU2346748C1 |
| МАГНИТНЫЙ СЕПАРАТОР | 2005 |
|
RU2305008C2 |
| СПОСОБ МАГНИТОКОНТРОЛЯ ФЕРРОПРИМЕСЕЙ СЫПУЧЕЙ СРЕДЫ ТОНКОГО КЛАССА | 2014 |
|
RU2580853C1 |
| МАГНИТНЫЙ СЕПАРАТОР | 2004 |
|
RU2277017C1 |
| СПОСОБ ФОРМИРОВАНИЯ ТРЕХМЕРНОГО ИЗОБРАЖЕНИЯ ЗЕМНОЙ ПОВЕРХНОСТИ В БОРТОВОЙ ЧЕТЫРЕХКАНАЛЬНОЙ ДОПЛЕРОВСКОЙ РЛС | 2014 |
|
RU2572357C1 |
Изобретение относится к области магнитного разделения и может быть использовано в различных отраслях промышленности для анализа магнитовосприимчивой (склонной к магнитному осаждению) фракции примесей текучих сред. Получают три экспериментальных значения эффективности удаления примесей магнитным очистным устройством для трех кратных друг другу значений длин фильтр-матрицы с вычислением доли А этой фракции по трем ключевым формулам. Производят тестирование анализируемой среды на соответствие модели экспоненциального поглощающего экрана (для односортной среды) или квалифицируют ее как не подчиняющуюся этой модели (содержащую подфракции, характеризующиеся ослабленной и повышенной склонностью к магнитному осаждению). Путем последовательных приближений (повторением эксперимента при кратно увеличивающейся длине) уточняют результат вплоть до достижения истинного значения λ. Определяют доли подфракции примесей, дополнительно устанавливая для этого значение кси-параметра расчетно-эмпирическим путем с использованием специально полученных формул и соответствующих взаимосвязанных пар найденных экспериментальных значений эффективности. Способ позволяет оперативно и точно определять долю магнитовосприимчивой фракции примесей в производственной среде, а также количественно квалифицировать эту долю по подфракциям, конкретизируя и облегчая задачу оптимизации разработки и эксплуатации магнитных очистных аппаратов. 3 з.п. ф-лы, 1 ил.
1. Способ анализа магнитовосприимчивой фракции примесей текучей среды, заключающийся в отборе анализируемой текучей среды, получении экспериментальных данных эффективности ψ удаления примесей магнитным очистным устройством в зависимости от рабочей длины L его фильтр-матрицы, вычислении доли магнитовосприимчивой фракции примесей λ в текучей среде по формулам:

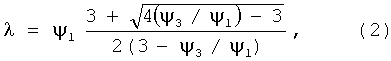
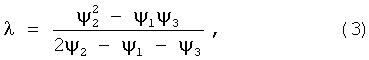
где ψ1, ψ2 и ψ3 - значения эффективности удаления примесей, полученные при L1, L2=2L1 и L3=3L1, и с последующим тестированием анализируемой среды на соответствие модели экстюненциального поглощающего экрана, отличающийся тем, что после вычисления доли магнитовосприимчивой фракции примесей λ в общем содержании примесей, дополнительно вычисляют доли магнитовосприимчивых подфракций примесей λA и λB, для чего, после тестирования анализируемой среды, при наличии в магнитовосприимчивой фракции λ подфракций примесей, характеризующихся ослабленой и повышенной склонностью к магнитному осаждению в магнитном очистном устройстве, более достоверным, нуждающимся в уточнении, принимают значение доли магнитовосприимчивой фракции λ, вычисленное по формуле (3), затем при увеличенной длине Ln=L4=4L1 фильтр-матрицы магнитного очистного устройства эксперимент дополнительно повторяют для получения данных эффективности ψn=ψ4 и опять определяют значение доли магнитовосприимчивой фракции λ по формуле:

где ψ1, …, ψn-2, ψn-1, ψn - последовательный ряд значений эффективности удаления примесей, при L1, …, Ln-2=(n-2)L1, Ln-1=(n-1)L1, Ln=nL1, адаптированной к измененным параметрам, т.е. с использованием обновленной тройки экспериментальных данных эффективности ψ2, ψ3 и ψ4, причем подобные действия по проведению экспериментов с дальнейшим увеличением рабочей длины L фильтр-матрицы магнитного очистного устройства, получению соответствующих данных эффективности ψ и описанному поэтапному определению значения λ продолжают до тех пор, пока значения доли магнитовосприимчивой фракции примесей λ станут одинаковыми, что будет свидетельствовать о достижении истинного значения λ, выступающего в виде самостоятельного параметра, характеризующего долю магнитовосприимчивых примесей в общем содержании примесей, при этом доли подфракций примесей λA=ехр(-ξ0) и λB=1-λA, характеризующихся ослабленной и повышенной склонностью к магнитному осаждению в магнитном очистном устройстве, устанавливают расчетно-эмпирическим путем, при дополнительно устанавливаемом значении кси-параметра ξ0.
2. Способ по п.1, отличающийся тем, что доли подфракций магнитовосприимчивых примесей, характеризующихся ослабленной и повышенной склонностью к магнитному осаждению λA=ехр(-ξ0) и λB=1-λA, устанавливают с использованием найденного значения λ и двух из трех завершающих экспериментальных значений эффективности, а именно: ψn-2, ψn-1, ψn, явившихся итоговыми результативными значениями ψ среди всех найденных экспериментальных значений ψ1, ψ2, ψ3, ψ4, …, ψn.
3. Способ по п.1, отличающийся тем, что в общем случае, предусматривающем получение (n) экспериментальных значений эффективности ψ (ψ1, ψ2, ψ3, ψ4, …, ψn-2, ψn-1, ψn) для (n) значений рабочей длины L (L1, L2=2L1, L3=3L1, L4=4L1, …, Ln-2=(n-2)L1, Ln-1=(n-1)L1, Ln=nL1), кси-параметр ξ0 определяют по любой из трех формул (5), (6), (7) в зависимости от выбранной комбинации пар значений эффективности ψ, входящих в число завершающих трех результативных значений эффективности (ψn-2, ψn-1, ψn), а именно:

т.е. при использовании пары ψn-1 и ψn, полученной при Ln-1=(n-1)L1 и Ln=nL1;
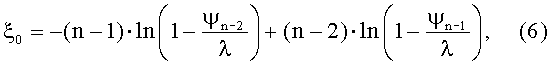
т.е. при использовании пары ψn-2 и ψn-1, полученной при Ln-2=(n-2)L1 и Ln-1=(n-1)L1;
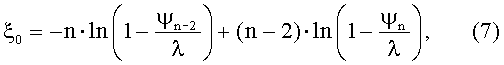
т.е. при использовании пары ψn-2 и ψn, полученной при Ln-2=(n-2)L1 и Ln=nL1.
4. Способ по п.1, отличающийся тем, что в частном случае «короткой процедуры» реализации способа, ограничивающемся получением четырех экспериментальных значений эффективности ψ (ψ1, ψ2, ψ3, ψ4) для четырех значений рабочей длины L (L1, L2=2L1, L3=3L1, L4=4L1), кси-параметр ξ0 определяют по любой из трех формул (8), (9), (10) в зависимости от выбранной комбинации пар значений эффективности ψ2, ψ3, ψ4, а именно:

т.е. при использовании пары ψ3 и ψ4, полученной при L3=3L1 и L4=4L1;
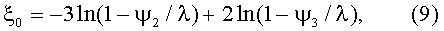
т.е. при использовании пары ψ2 и ψ3, полученной при L2=2L1 и L3=3L1;
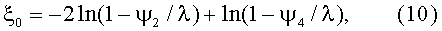
т.е. при использовании пары ψ2 и ψ4, полученной при L2=L1 и L4=L1.
| САНДУЛЯК А.В | |||
| Магнито-фильтрационная очистка жидкостей и газов | |||
| - М.: Химия, 1988, с.95-98 | |||
| Способ качественного анализа примесей в среде при ее очистке от магнитовосприимчивых частиц | 1988 |
|
SU1659784A1 |
| Способ определения содержания магнитовосприимчивой фракции примеси в среде | 1988 |
|
SU1632170A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕЛКОДИСПЕРСНОЙ ФЕРРОМАГНИТНОЙ ФРАКЦИИ ЖЕЛЕЗОСОДЕРЖАЩИХ ПРИМЕСЕЙ ПРОМЫШЛЕННЫХ ВЫБРОСОВ | 1991 |
|
RU2030216C1 |
| СПОСОБ МАГНИТНОЙ СЕПАРАЦИИ СУСПЕНЗИЙ И МАГНИТНЫЙ ФИЛЬТР ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1999 |
|
RU2165285C2 |
| US 4492921 A, 08.01.1985. | |||
Авторы
Даты
2011-07-10—Публикация
2009-04-22—Подача