Область техники, к которой относится изобретение
Настоящее изобретение относится к способу характеризации частотной зависимости линейных свойств электрического компонента, а также и к устройству, содержащему средства для осуществления такого способа.
Уровень техники
Значение широкополосного моделирования линейных электрических компонентов (таких, как устройства и системы) из результатов измерений возрастает для проектирования и проверки электрических систем. Моделирование обычно базируется на «подгонке» линейной модели варьированием набора параметров, которые описывают поведение модели, таких как адмиттанс (у), импеданс (z) и параметры рассеяния (s) в частотной области или временной области. Модель обычно основана на отношении полиномов [1], [2] или ортогональных полиномных функций [3]. В последнее время стала широко применимой технология [4] векторной аппроксимации с перемещением полюса, и были предложены некоторые улучшения [5], [6]. Моделирование завершается тогда, когда найденные параметры описывают табличные данные с заданным уровнем точности. Аппроксимация, описанная в литературе, основана на подгонке отдельных элементов матрицы полной комплексной проводимости. Это значит, что результирующая модель хорошо подходит для вычисления токов, если заданы приложенные напряжения. Однако нет гарантии, что модель будет вести себя удовлетворительно с другими граничными условиями. Например, совпадение может быть неудовлетворительным для случая, когда заданы токи, а напряжения должны быть определены. Такие результаты обычно имеют место в случаях, когда матрица полной комплексной проводимости содержит большой разброс собственных значений, что означает, что отношение между наибольшим и наименьшим собственным значением велико.
Раскрытие изобретения
Задача, которая решается настоящим изобретением, состоит в том, чтобы разработать способ для аппроксимации характеристик в частотной области с повышенной точностью, в частности для случаев с большим разбросом собственных значений.
Эта задача решается способом по пункту 1.
В соответствии с этим задача решается путем переформулирования общепринятого метода векторной аппроксимации (см. ниже) для аппроксимации модальной характеристики, а не матричных элементов, и весовой коэффициент выбирается равным обратной величине соответствующего собственного значения, для того чтобы достичь относительного точного критерия для аппроксимации с помощью собственных значений. Процедура дает улучшение точности для случаев с большим разбросом собственных значений.
Изобретение также относится к устройству, содержащему средства для выполнения этапов предложенного способа. Такое устройство обычно будет содержать соответствующие программные компоненты, используемые компьютером, но также могут использоваться специализированные аппаратные средства.
Краткое описание чертежей
Далее варианты воплощения, преимущества и применение настоящего изобретения даны в зависимых пунктах, а также и в следующем описании, которое делается со ссылкой на приложенные чертежи, где:
фиг.1 - пример электрического устройства (компонента) с примененным внешним устройством,
фиг.2 - надземная линия с отдельным проводом,
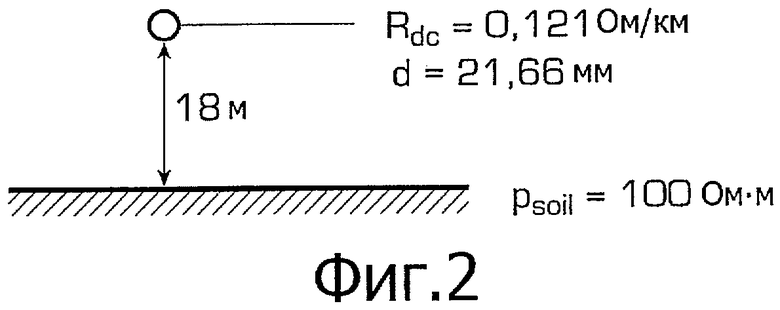
фиг.3 - собственные значения Y для случая на фиг.2,
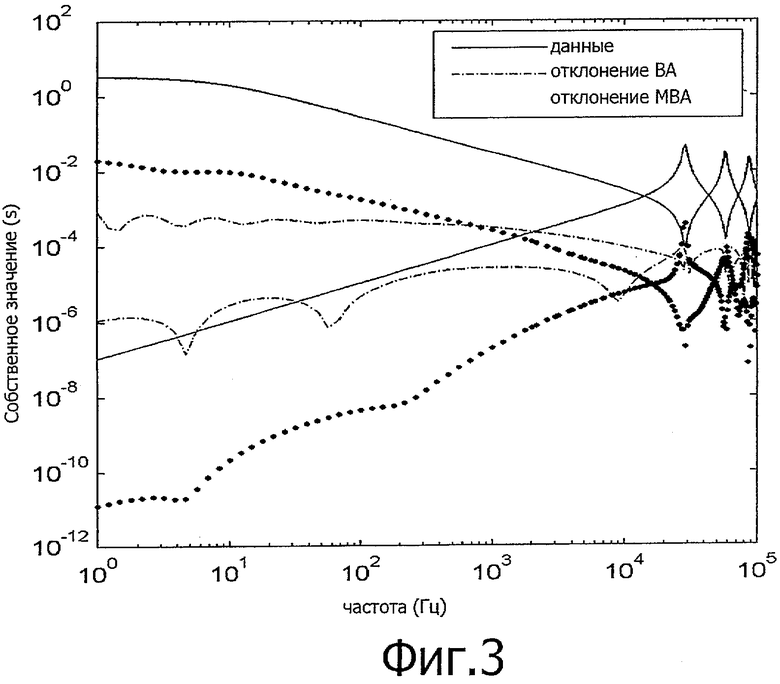
фиг.4 - элементы Y для случая на фиг.2,
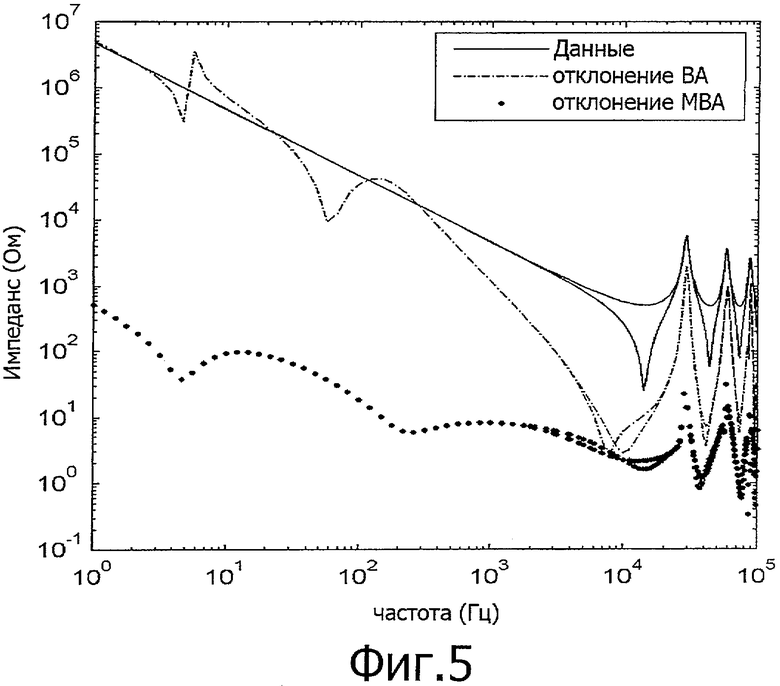
фиг.5 - собственные значения элементов Z=Y-1 для случая на фиг.2,
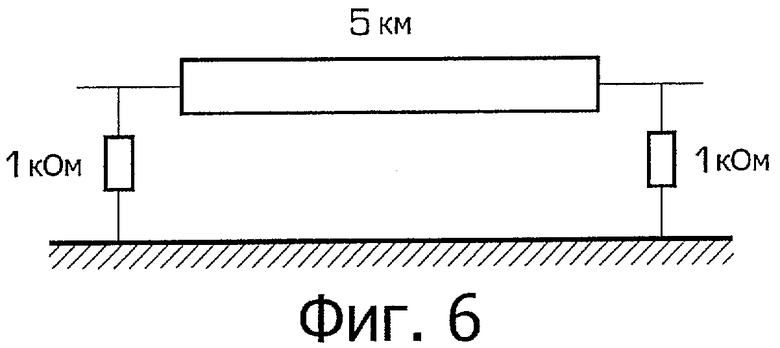
фиг.6 - электрический компонент (линии передачи с ответвлениями), соединенный с внешней сетью,
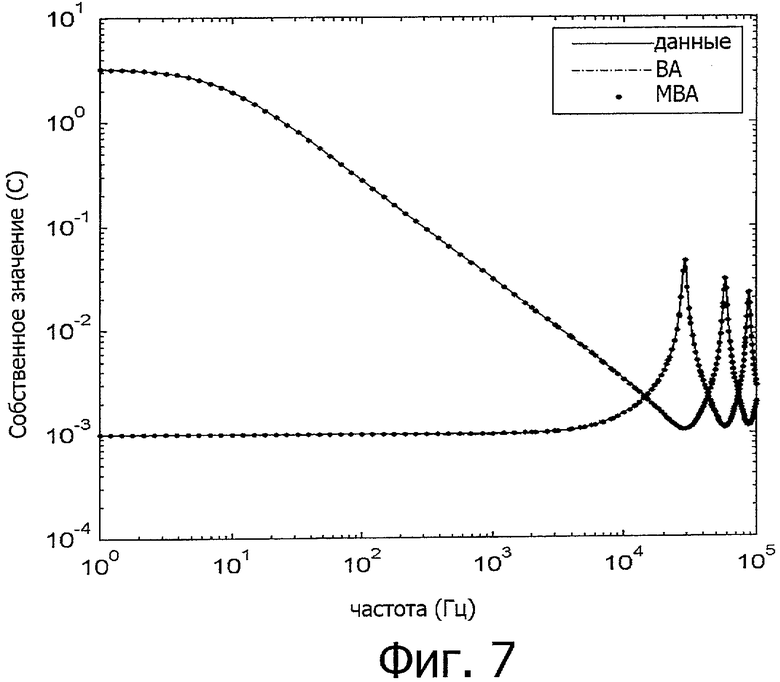
фиг.7 - собственные значения Yустройства для случая на фиг.6,
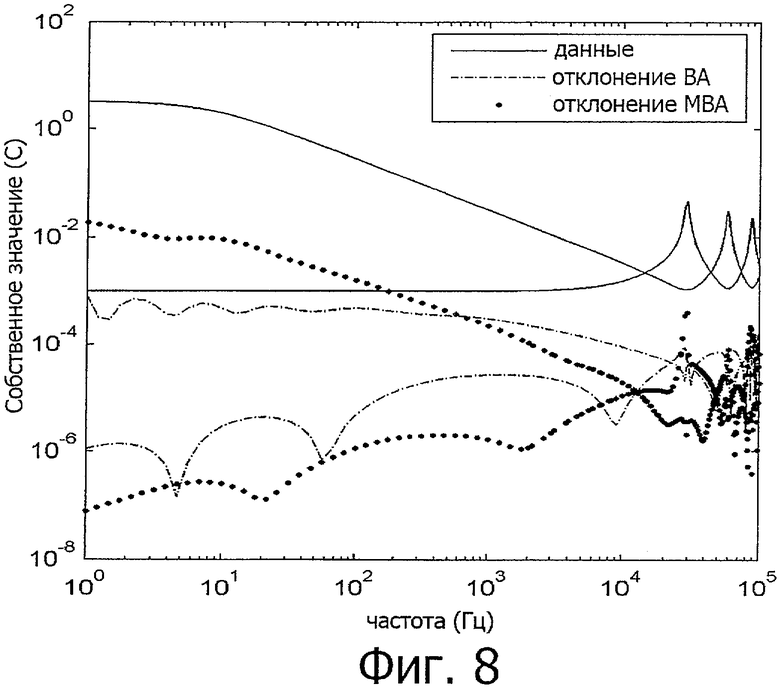
фиг.8 - элементы Yустройства для случая на фиг.6, и
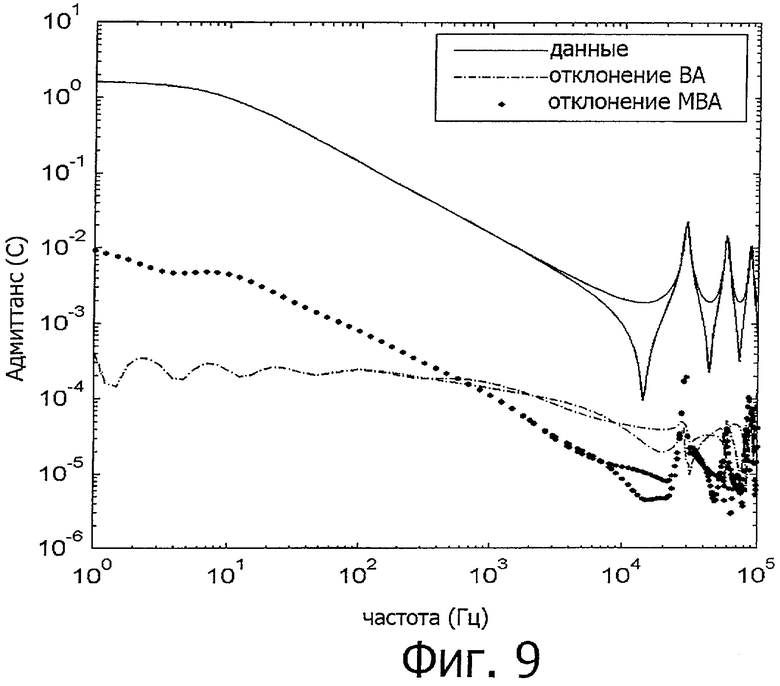
фиг.9 - собственные значения элементов Z=(Yустройства+Yвнеш)-1 для случая на фиг.6.
Осуществление изобретения
Определения
В представленном тексте заглавные буквы, набранные жирным шрифтом (такие как Y), обозначают матрицы, а строчные буквы, набранные жирным шрифтом (такие как v), обозначают векторы.
Термин «электрический компонент» должен пониматься широко и может относиться к индивидуальному устройству, такому как трансформатор, или совокупности нескольких устройств, такой как система преобразователей, электродвигателей и т.п., связанных линией электропитания. Однако это ограничивается линейными электрическими системами, которые полностью описываются матрицей полной комплексной проводимости, имеющей зависимость от частоты.
Введение
В качестве примера мы рассматриваем электрический компонент, имеющий n>1 входов. Его линейные электрические свойства описываются матрицей полной комплексной проводимости Y, определяющей характеристику тока i, проходящего через входы, когда к входам приложено напряжение v:

где s обозначает комплексную круговую частоту iω токов и напряжений.
Если источники тока приложены к клеммам, характеристика напряжения при любой частоте есть
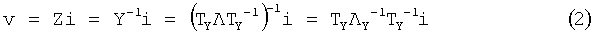
где Т или TY - зависящая от частоты матрица преобразований, а Λ или ΛY - диагональная матрица из собственных значений Y.
Согласно (2) небольшие собственные значения Y соответствуют большим собственным значениям в Z. Если Y содержит как большие, так и небольшие собственные значения, аппроксимация элементов Y, вероятно, приведет к неудовлетворительному представлению небольших собственных значений. Таким образом, аппроксимация элементов Y приводит к модели, которая лучше всего подходит для воспроизведения входных токов, если заданы напряжения. Однако модель не очень подходит для воспроизведения напряжений при заданных токах. Аналогично, если бы аппроксимировалась матрица импеданса, это лучше всего подходило бы для воспроизведения напряжений при заданных токах, но привело бы к неудовлетворительным результатам в случае, когда приложены напряжения, а токи должны быть определены.
Для того чтобы подобрать модель, которая равно хорошо подходит для всех возможных применений, нужно удостовериться, что все собственные векторы матрицы полной комплексной проводимости (или импеданса) представляются с одинаковой точностью.
Поэтому желательно подобрать модель таким образом, чтобы ошибка модели в отношении собственных значений λi относительно величины собственного значения, приводила к относительному критерию,
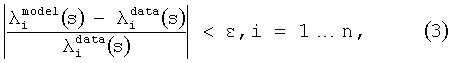
где верхний индекс «model» относится к собственным значениям, вычисленным из модели (путем приведения к диагональному виду), а верхний индекс «data» относится к собственным значениям, полученным непосредственно из матрицы Y.
Использование относительного критерия типа ур.(3) будет «балансировать» точность модели в отношении применения напряжения и применения тока соответственно и в отношении любого другого (гибридного) граничного условия, так что относительная ошибка модели для всех применений будет иметь один и тот же порядок величины.
Главной проблемой, рассматриваемой в этой заявке, является определение модели с вычетом полюсов согласно ур. (4), приведенному ниже, с D и Е возможно нулевыми, таким образом, чтобы точность собственных значений Y сохранялась в относительном смысле за счет критерия (3). Модель с вычетом полюсов может быть выражена как
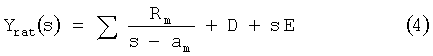
где Rm с m=1 до N - матрицы, независящие от частоты (N - число учитываемых полюсов или резонансов), D и Е - матрицы, независящие от частоты, или нули, а am с m=1 до N - комплексная круговая частота полюсов или резонансов.
Настоящее изобретение предполагает, что элементы матрицы Y(s) известны на множестве дискретных частот s, например, из прямых измерений токов i при заданных напряжениях Y на этих частотах и из ур.(1) с применением обычных методов. Аппроксимация Yrat согласно ур.(4) теперь должна быть приближена к известным величинам Y(s) путем варьирования априори неизвестных параметров Rm, am и D и Е (если предполагается, что они не раны нулю).
Векторная аппроксимация (известный уровень техники)
Ур.(4) может быть записано как множество n2 уравнений для всех элементов i, j матриц с i=1, …n и j=1, …n. Эти уравнения связаны общим множеством am полюсов.
Ниже мы описываем стандартную рациональную аппроксимацию скалярной частотной характеристики y(s).
Рациональная аппроксимация частотной характеристики y(s) посредством обычной векторной аппроксимации (ВА) [4] представляет собой итерационный процесс. Это сводится к решению линейной задачи (5) с первым множеством частот полюса {am}:
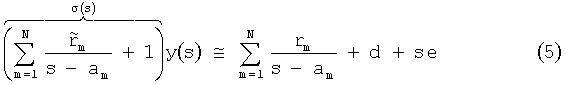
где 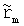 - частотно независимый скаляр с m=1-N, у - любой элемент с индексами i, j в матрице Y, rm - соответствующий элемент в матрице Rm, d - соответствующий элемент в матрице D, и е - соответствующий элемент в матрице Е.
- частотно независимый скаляр с m=1-N, у - любой элемент с индексами i, j в матрице Y, rm - соответствующий элемент в матрице Rm, d - соответствующий элемент в матрице D, и е - соответствующий элемент в матрице Е.
После решения (5) уточненное второе множество частот полюса вычисляется как нули σ(s), которые получают путем решения задачи с собственными значениями (6)
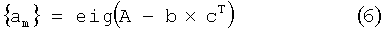
где А - диагональная матрица, содержащая первое множество полюсов am в качестве диагональных элементов, b - единичный вектор, с - вектор, содержащий 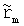 для m=1-N, полученные путем решения ур. (5) на предыдущем этапе, eig - оператор, возвращающий вектор, содержащий собственные значения матричнозначного аргумента.
для m=1-N, полученные путем решения ур. (5) на предыдущем этапе, eig - оператор, возвращающий вектор, содержащий собственные значения матричнозначного аргумента.
Новое, второе множество (перемещенных) частот полюсов, полученных с помощью (6), теперь повторно используется в (5) в итерационной процедуре. Эта процедура с перемещенным полюсом обычно сходится через несколько итераций.
При применении этой процедуры к матрице полной комплексной проводимости с более чем одним элементом второй шаг (перемещение полюса) должен быть изменен. Это осуществляется путем размещения матричных элементов Y в одном векторе, что означает, что y(s) в (5) становится вектором-столбцом. Также правая часть (5) становится вектором-столбцом. Так как σ(s) в (5) является по-прежнему скалярной величиной, все элементы в векторе у (и, таким образом, элементы Y) становятся аппроксимируемыми с общим множеством полюсов.
Итерация продолжается до тех пор, пока не выполнено условие прерывания, например, пока первое и второе множество частот полюсов не отличаются на величину, меньшую, чем заданная, или пока не удовлетворено условие ур. (3) для заданного предела ε. При первоначальной ВА итерация обычно прерывается после заранее определенного числа итераций или когда критерий ошибки приближения (например, среднеквадратическое отклонение) более не меняется между двумя итерациями. Много альтернативных критериев может использоваться, и это, очевидно, зависит от конкретного применения.
На последнем шаге вычеты Rm вычисляются путем решения ур. (5) с σ(s)=1.
Модальная векторная аппроксимация
Матрица Y может быть приведена к диагональному виду с помощью матрицы преобразований Т (частотно зависимой)
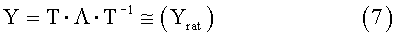
Умножение в обычном порядке (7) на Т дает для каждой собственной пары (λi, ti)

Относительная точность собственных значений λi сохраняется в решении задачи наименьшего квадратичного отклонения при масштабировании равенства с коэффициентом, равным обратной величине собственного значения, т.е.
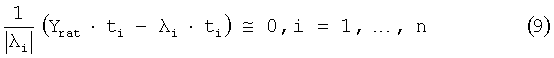
Отметим, что этот масштабный коэффициент является частотно зависимой величиной.
Комбинирование (9) с ВА приводит к подходу, который мы в дальнейшем называем Модальной Векторной Аппроксимацией (МВА).
МВА в основном проводится так же, как и обычный ВА процесс, но отличается от него тем, что ур. (5) заменено на
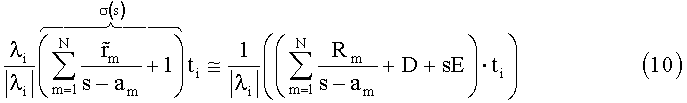
Уравнение (10) составляется для всех мод i=1, …n и объединяется в общее уравнение. Новое второе множество (перемещенных) полюсов получается из σ(s) в (10) путем подстановки (6), как в первоначальной ВА. Окончательно, как в обычной ВА, вычеты определяются путем решения (10) с σ(s)=1.
Использование характеристик внешней цепи
В некоторых случаях рассматриваемое устройство должно быть связано с внешней сетью с известными характеристиками импеданса, см. фиг.1. Если адмиттанс, определенный на выходах устройства, - Yвнеш, то полный адмиттанс
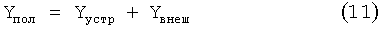
Теперь выходные характеристики определяет скорее Yпол, а не Yустр. Это может быть использовано в МВА процессе аппроксимации путем вычисления собственных пар из Yпол. Уравнение (10) тогда становится
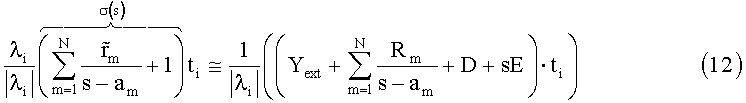
Окончательное вычисление вычетов (с известными полюсами) выполняется с σ(s) в (12), равным единице.
Пример:
В качестве примера мы рассматриваем проводник с потерями над поглощающей средой длиной 5 км, см. фиг.2. Это дает 2×2 матрицу Y.
Модель с вычетами полюсов для Y была просчитана в частотном диапазоне 1-1000 кГц с применением ВА и МВА. В обоих случаях в процессе аппроксимации использовалось пять итераций с 14 полюсами и ненулевым D.
На фиг.3 приведены собственные значения Y. Замечено, что когда разброс собственных значений велик (низкие частоты), небольшие собственные значения представляются неточно, когда Y аппроксимируется с помощью ВА. При использовании МВА все собственные значения точно представляются при всех частотах благодаря сравнительному критерию (3).
На фиг.4 (сплошные линии) приведены элементы Y. Такая же кривая показывает отклонение результатов рациональных моделей от точного решения. Видно, что с МВА кривые отклонения хорошо коррелируют с величиной элемента, что приводит близко к постоянной относительной точности, тогда как ВА обнаруживает сильные отклонения.
На фиг.5 приведены результаты для Z=Y-1, которые соответствуют характеристике напряжения при приложении токов к концам линии. Видно, что результат, полученный при МВА, остается точным, тогда как результат, полученный с помощью ВА, неудовлетворительный. Последний результат обусловлен невозможностью ВА точно представить небольшие собственные значения, как было показано на фиг.3. Так как небольшие собственные значения Y становятся большими собственными значениями Z, происходит очень большое увеличение ошибки. При МВА относительная точность собственных значений сохраняется, и поэтому точный результат обеспечивается также и для Z.
Результат в случае присоединения внешней сети
Мы продолжаем рассматривать тот же пример, но предполагаем, что линия нагружена на обоих концах сопротивлением в 1 кОм, см. фиг.6. Аппроксимация Yустр посредством МВП теперь выполнена с использованием (12).
Собственные значения Yустр+Yвнеш приведены на фиг.7. Разброс собственных значений много меньше, чем на фиг.3, благодаря заземлению через сопротивления в 1 кОм. Использование ВА и МВА, как видно, дает аналогичный результат. Однако проверка кривых отклонения показывает, что результат, полученный с применением МВА, более точный для небольших собственных значений, см. фиг.8, 9.
Как и в предыдущем примере, подходы с использованием как ВА, так и МВА, дают удовлетворительный результат для аппроксимируемых элементов Yустр (фиг.8). Но для элементов Z=(Yустр+Yвнеш)-1 (фиг.9) МВА дает более точный результат, благодаря лучшему представлению небольшого собственного значения.
Обсуждение
В некоторых случаях может быть допустима постоянная вещественная матрица преобразований TY, например, когда Y является сбалансированной матрицей (которая была в качестве примера в этом описании). Это позволяет приводить Y к диагональному виду и непосредственно подбирать собственные значения. Использование затем весового коэффициента с обратной величиной дает результат, похожий с МВА. Однако во многих случаях предположение о постоянной TY не применимо, и поэтому должно быть использована МВА.
В случае прямого применении ВА к матричным элементам, можно увеличить порядок приближения при контроле собственных значений Yмодель в зависимости от Yустр, чтобы достичь потенциально такого же хорошего результата, как при МВА, за счет более высокого порядка аппроксимации, но такая аппроксимация может быть более подвержена шуму, созданию искажений и усложнению соблюдения требований.
Иная ситуация возникает, когда модель строится на основе измерений с помехами. Было предложено измерять множество вольт-амперных векторных пар, которые соответствуют собственным парам системы. Объединенное с рациональной аппроксимацией и пассивным наблюдением это привело к разработке программных средств [7]. Здесь предпочтительно использование МВА, так как уровень шума обычно много ниже для собственных пар, соответствующих малым собственным значениям. Прямое применение ВА к матричным элементам может легко привести к тому, что наименьшие собственные значения потеряются в шуме. В практических применениях измеряемый электрический элемент может иметь большой разброс собственных значений, тогда как собственные значения примыкающей сети и объекта имеют значительно меньший разброс. Если эта информация не используется, аппроксимация будет чрезмерно ограниченной. Эта проблема легко преодолевается с помощью учета в явном виде внешней сети при вычислении собственных пар, как было продемонстрировано выше.
Заключение
Алгоритм переформулированной векторной аппроксимации (МВА) был разработан для обеспечения высокой точности полученной модели при произвольных граничных условиях. Это достигается путем явного введения собственных пар в моделирование, позволяя тем самым обеспечить высокую относительную точность для всех собственных значений. Применение к примеру с большим разбросом собственных значений наглядно показывает превосходную точность по сравнению с традиционным подходом к аппроксимации матричных элементов. МВА подход также позволяет учитывать характеристики импеданса присоединенной сети.
Описанный способ позволяет характеризовать частотную зависимость линейных свойств электрического компонента, имеющего n>1 входов, линейные свойства которого описываются в матрице Y, которая связывает напряжение, приложенное к входам и ток через входы. Как правило, Y - матрица полной комплексной проводимости, хотя и другие матрицы, такие как матрица импеданса, также могут быть использованы. Частотная зависимость Y аппроксимируется уравнением (4).
Способ включает в себя следующие этапы:
а) Получение множества величин Y(s) матрицы Y при дискретных частотах s и для каждой величины Y(s) получение собственных значений λi и собственных векторов ti с I=1-n. Как правило, величины Y(s) могут быть получены из результатов измерений на электрическом компоненте при требуемых частотах.
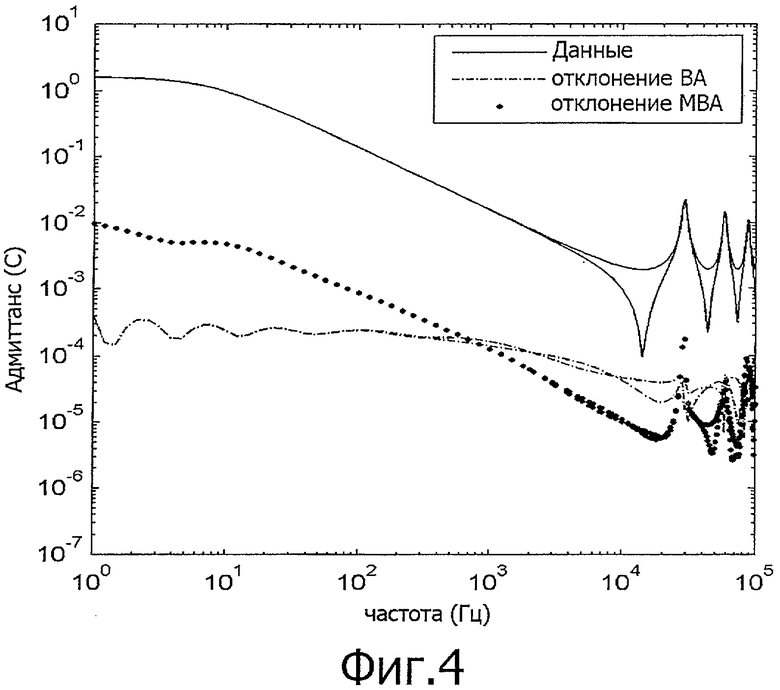
б) Аппроксимация множества n векторных уравнений (10) путем использования первого множества частот полюса am и варьирования следующих величин: 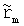 , Rm и, если предполагаются не нулевыми, D и Е.
, Rm и, если предполагаются не нулевыми, D и Е.
в) Вычисление второго множества частот полюса из ур. (6).
г) Многократное повторение этапов б) и в) с использованием второго множества частот полюса am, полученного на этапе в), в качестве первого множества частот полюса на последующем этапе б), до тех пор, пока не выполнено специальное условие прерывания.
В большинстве случаев желательно знать Rm, а также, не обязательно, D и Е. Эти величины могут быть найдены на дополнительном этапе д) путем подставки σ(s)=1 в ур. (10) и решения уравнения.
Когда электрический компонент соединен с внешним устройством, ур. (10) на этапе б) может быть заменено на ур. (12).
Необходимо отметить, что член D+sE в ур. (4), (10) и (12) может быть заменен на любую частотно зависимую матричнозначную функцию F({bj}, s), которая линейно зависит от множества (неизвестных, но частотно-независимых) параметров {bj}. Параметры могут быть определены на последнем этапе г) МВА процедуры, если имеется достаточное число измеренных величин Y.
ЛИТЕРАТУРА
[1] Е.С.Levy, "Complex curve fitting", IRE Trans. Automatic Control, vol.4, pp.37-44, May 1959.
[2] C.K.Sanathanan and J.Koerner, "Transfer function synthesis as a ratio of two complex polynomials", IEEE Trans. Automatic Control, vol.8, pp.56-58, 1963.
[3] C.P.Coelho, J.R.Phillips, and L.M.Silveira, "Generating high-accuracy simulation models using problem-tailored orthogonal polynomials basis", IEEE Trans. Circuits and Systems-1, vol.53, no. 12, pp.2705-2714, Dec. 2006.
[4] В.Gustavsen, and A.Semlyen, "Rational approximation of frequency domain responses by vector fitting", IEEE Trans. Power Delivery, vol.14, no.3, pp.1052-1061, July 1999.
[5] S.Grivet-Talocia, "Package macromodeling via timedomain vector fitting", IEEE Microwave and Wireless Components Letters, vol.13, no.11, pp.472-474, Nov.2003.
[6] В.Gustavsen, "Improving pole relocating properties of vector fitting", IEEE Trans. Power Delivery, vol.21, no. 3, pp.1587-1592, July 2006.
[7] M.Tiberg, O.Hoenecke, С.Heitz, and В.Gustavsen, "New simulation methodology for power systems-assumption free analysis entirely based on measurement", EMTP-RV Newsletters, vol.1, no.3. Dec. 2006, pp.20-26.
Настоящее изобретение относится к способу характеризации частной зависимости линейных свойств электрического компонента. Заявленное устройство предлагает новый метод для рационального макромоделирования многополюсников, который обеспечивает высокую точность при произвольных граничных условиях. Это достигается путем переформулирования метода векторной аппроксимации для аппроксимации собственных пар, а не матричных элементов, при этом весовой коэффициент выбирается равным обратной величине собственного значения, с тем чтобы получить критерий относительной точности для подбора собственного значения. Метод дает существенное улучшение точности для случаев с большим разбросом собственных значений. Также показано, как использовать импедансные характеристики присоединенной сети для уменьшения сложности аппроксимации и дополнительного улучшения ее точности. Технический результат заключается в повышении точности. 4 н. и 8 з.п. ф-лы, 9 ил.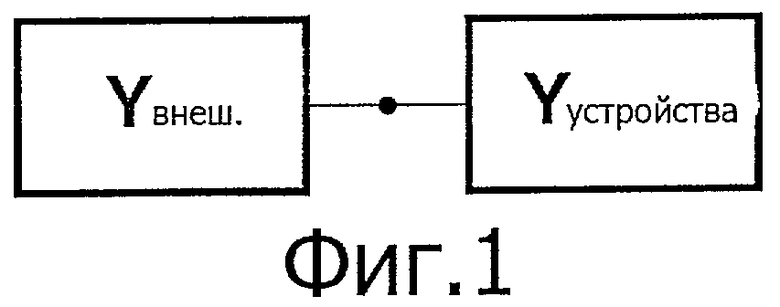
1. Устройство для характеризации линейных свойств электрического компонента, имеющего n>1 портов, причем линейные свойства электрического компонента описываются матрицей Y, связывающей напряжение, приложенное к портам, с током, проходящим через порты, причем частотная зависимость Y аппроксимируется выражением 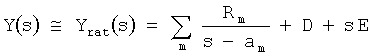 , где m от 1 до N, N - число полюсов, Rm - частотно независимые матрицы, m равно от 1 до N, D и Е - частотно независимые матрицы или нули, s - комплексная круговая частота iω, аm - комплексные круговые частоты полюсов, m равно от 1 до N, характеризующееся тем, что содержит средства для выполнения этапов, на которых: а) получают множество значений Y(s) матрицы Y при дискретных частотах s и для каждого значения Y(s) получают собственные значения λi и собственные векторы ti, i равно от 1 до n; б) подгоняют множество из n векторных уравнений
, где m от 1 до N, N - число полюсов, Rm - частотно независимые матрицы, m равно от 1 до N, D и Е - частотно независимые матрицы или нули, s - комплексная круговая частота iω, аm - комплексные круговые частоты полюсов, m равно от 1 до N, характеризующееся тем, что содержит средства для выполнения этапов, на которых: а) получают множество значений Y(s) матрицы Y при дискретных частотах s и для каждого значения Y(s) получают собственные значения λi и собственные векторы ti, i равно от 1 до n; б) подгоняют множество из n векторных уравнений 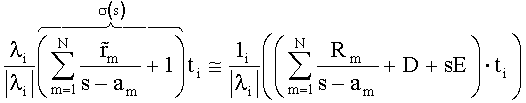
для полученных собственных значений λi и собственных векторов ti, где 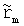 - частотно независимая скалярная величина, m равно от 1 до N, путем использования первого множества полюсных частот аm и варьирования
- частотно независимая скалярная величина, m равно от 1 до N, путем использования первого множества полюсных частот аm и варьирования 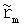 , Rm и, если предполагаются ненулевыми, D и Е; в) вычисляют второе множество полюсных частот из {am}=eig(A-b·cT), где А - диагональная матрица, содержащая первое множество полюсных частот am в качестве диагональных элементов, b - единичный вектор, с - вектор, содержащий
, Rm и, если предполагаются ненулевыми, D и Е; в) вычисляют второе множество полюсных частот из {am}=eig(A-b·cT), где А - диагональная матрица, содержащая первое множество полюсных частот am в качестве диагональных элементов, b - единичный вектор, с - вектор, содержащий 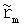 для m от 1 до N, полученные на этапе б), и eig - оператор, возвращающий в прежнее состояние вектор, содержащий собственные значения матрицы; г) повторяют этапы б) и в) с использованием второго множества полюсных частот аm, полученных на этапе в), в качестве первого множества полюсных частот на последующем этапе б), до тех пор, пока не удовлетворено условие остановки.
для m от 1 до N, полученные на этапе б), и eig - оператор, возвращающий в прежнее состояние вектор, содержащий собственные значения матрицы; г) повторяют этапы б) и в) с использованием второго множества полюсных частот аm, полученных на этапе в), в качестве первого множества полюсных частот на последующем этапе б), до тех пор, пока не удовлетворено условие остановки.
2. Устройство по п.1, в котором матрица Y описывает соотношение между напряжением v, приложенным к портам компонента, током i, протекающим через компоненты, выражением i=Yv.
3. Устройство по п.1, в котором D+sE заменяются матричнозначной функцией F({bi}, s), которая линейно зависит от множества параметров {bi}.
4. Устройство для характеризации линейных свойств электрического компонента, имеющего n>1 портов, причем линейные свойства электрического компонента описываются матрицей Y, связывающей напряжение, приложенное к портам, с током, проходящим через порты, причем частотная зависимость Y аппроксимируется выражением 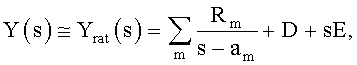 где m от 1 до N, N - число полюсов, Rm - частотно независимые матрицы, m равно от 1 до N, D и Е - частотно независимые матрицы или нули, s - комплексная круговая частота iω, аm - комплексные круговые частоты полюсов, m равно от 1 до N, характеризующееся тем, что содержит средства для выполнения этапов, на которых: а) получают множество значений Y(s) матрицы Y при дискретных частотах s и для каждого значения Y(s) получают собственные значения λi и собственные векторы ti, i равно от 1 до n; б) подгоняют множество из n векторных уравнений
где m от 1 до N, N - число полюсов, Rm - частотно независимые матрицы, m равно от 1 до N, D и Е - частотно независимые матрицы или нули, s - комплексная круговая частота iω, аm - комплексные круговые частоты полюсов, m равно от 1 до N, характеризующееся тем, что содержит средства для выполнения этапов, на которых: а) получают множество значений Y(s) матрицы Y при дискретных частотах s и для каждого значения Y(s) получают собственные значения λi и собственные векторы ti, i равно от 1 до n; б) подгоняют множество из n векторных уравнений 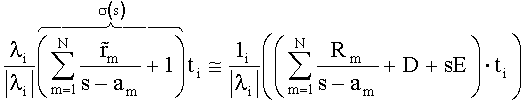
для полученных собственных значений λi и собственных векторов ti, где 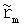 - частотно независимая скалярная величина, m равно от 1 до N, σ(s)=1, путем использования первого множества полюсных частот am, варьирования
- частотно независимая скалярная величина, m равно от 1 до N, σ(s)=1, путем использования первого множества полюсных частот am, варьирования 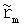 и вычисления Rm и, если предполагаются ненулевыми, D и Е; в) вычисляют второе множество полюсных частот из {am}=eig(A-b·cT), где А - диагональная матрица, содержащая первое множество полюсных частот аm в качестве диагональных элементов, b - единичный вектор, с - вектор, содержащий
и вычисления Rm и, если предполагаются ненулевыми, D и Е; в) вычисляют второе множество полюсных частот из {am}=eig(A-b·cT), где А - диагональная матрица, содержащая первое множество полюсных частот аm в качестве диагональных элементов, b - единичный вектор, с - вектор, содержащий 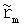 для m от 1 до N, полученные на этапе б), и eig - оператор, возвращающий в прежнее состояние вектор, содержащий собственные значения матрицы; г) повторяют этапы б) и в) с использованием второго множества полюсных частот аm, полученных на этапе в), в качестве первого множества полюсных частот на последующем этапе б), до тех пор, пока не удовлетворено условие остановки.
для m от 1 до N, полученные на этапе б), и eig - оператор, возвращающий в прежнее состояние вектор, содержащий собственные значения матрицы; г) повторяют этапы б) и в) с использованием второго множества полюсных частот аm, полученных на этапе в), в качестве первого множества полюсных частот на последующем этапе б), до тех пор, пока не удовлетворено условие остановки.
5. Устройство по п.4, в котором матрица Y описывает соотношение между напряжением v, приложенным к портам компонента, током i, протекающим через компоненты, выражением i=Yv.
6. Устройство по п.4, в котором D+sE заменяются матричнозначной функцией F({bi}, s), которая линейно зависит от множества параметров {bi}.
7. Устройство для характеризации линейных свойств электрического компонента, имеющего n>1 портов, при этом линейные свойства электрического компонента описываются матрицей Y, связывающей напряжение, приложенное к портам, с током, проходящим через порты, причем частотная зависимость Y аппроксимируется выражением 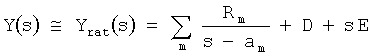 , где m от 1 до N, N - число полюсов, Rm - частотно независимые матрицы, m равно от 1 до N, D и Е - частотно независимые матрицы или нули, s - комплексная круговая частота iω, аm - комплексные круговые частоты полюсов, m равно от 1 до N, а электрический компонент подключен к внешнему устройству, линейные свойства которого описываются матрицей Yext, характеризующееся тем, что содержит средства для выполнения этапов, на которых: а) получают множество значений Y(s) матрицы Y при дискретных частотах s и для каждого значения Y(s) получают собственные значения λi и собственные векторы ti, i равно от 1 до n; б) подгоняют множество из n векторных уравнений
, где m от 1 до N, N - число полюсов, Rm - частотно независимые матрицы, m равно от 1 до N, D и Е - частотно независимые матрицы или нули, s - комплексная круговая частота iω, аm - комплексные круговые частоты полюсов, m равно от 1 до N, а электрический компонент подключен к внешнему устройству, линейные свойства которого описываются матрицей Yext, характеризующееся тем, что содержит средства для выполнения этапов, на которых: а) получают множество значений Y(s) матрицы Y при дискретных частотах s и для каждого значения Y(s) получают собственные значения λi и собственные векторы ti, i равно от 1 до n; б) подгоняют множество из n векторных уравнений 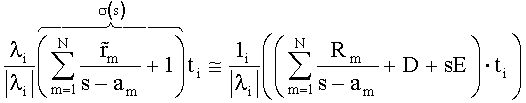
для полученных собственных значений λi и собственных векторов ti, где 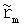 - частотно независимая скалярная величина, m равно от 1 до N, путем использования первого множества полюсных частот аm и варьирования
- частотно независимая скалярная величина, m равно от 1 до N, путем использования первого множества полюсных частот аm и варьирования 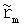 , Rm и, если предполагаются ненулевыми, D и Е; в) вычисляют второе множество полюсных частот из {am}=eig(A-b·сT), где А - диагональная матрица, содержащая первое множество полюсных частот аm в качестве диагональных элементов, b - единичный вектор, с - вектор, содержащий
, Rm и, если предполагаются ненулевыми, D и Е; в) вычисляют второе множество полюсных частот из {am}=eig(A-b·сT), где А - диагональная матрица, содержащая первое множество полюсных частот аm в качестве диагональных элементов, b - единичный вектор, с - вектор, содержащий 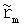 для m от 1 до N, полученные на этапе б), и eig - оператор, возвращающий в прежнее состояние вектор, содержащий собственные значения матрицы; г) повторяют этапы б) и в) с использованием второго множества полюсных частот am, полученных на этапе в), в качестве первого множества полюсных частот на последующем этапе б), до тех пор, пока не удовлетворено условие остановки.
для m от 1 до N, полученные на этапе б), и eig - оператор, возвращающий в прежнее состояние вектор, содержащий собственные значения матрицы; г) повторяют этапы б) и в) с использованием второго множества полюсных частот am, полученных на этапе в), в качестве первого множества полюсных частот на последующем этапе б), до тех пор, пока не удовлетворено условие остановки.
8. Устройство по п.7, в котором матрица Y описывает соотношение между напряжением v, приложенным к портам компонента, током i, протекающим через компоненты, выражением i=Yv.
9. Устройство по п.7, в котором D+sE заменяются матричнозначной функцией F({bi}, s), которая линейно зависит от множества параметров {bi}.
10. Устройство для характеризации линейных свойств электрического компонента, имеющего n>1 портов, при этом линейные свойства электрического компонента описываются матрицей Y, связывающей напряжение, приложенное к портам, с током, проходящим через порты, причем частотная зависимость Y аппроксимируется выражением 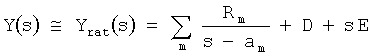 , где m от 1 до N, N - число полюсов, Rm - частотно независимые матрицы, m равно от 1 до N, D и Е - частотно независимые матрицы или нули, s - комплексная круговая частота iω, аm - комплексные круговые частоты полюсов, m равно от 1 до N, а электрический компонент подключен к внешнему устройству, линейные свойства которого описываются матрицей Yext, характеризующееся тем, что содержит средства для выполнения этапов, на которых: а) получают множество значений Y(s) матрицы Y при дискретных частотах s и для каждого значения Y(s) получают собственные значения λi и собственные векторы ti, i равно от 1 до n; б) подгоняют множество из n векторных уравнений
, где m от 1 до N, N - число полюсов, Rm - частотно независимые матрицы, m равно от 1 до N, D и Е - частотно независимые матрицы или нули, s - комплексная круговая частота iω, аm - комплексные круговые частоты полюсов, m равно от 1 до N, а электрический компонент подключен к внешнему устройству, линейные свойства которого описываются матрицей Yext, характеризующееся тем, что содержит средства для выполнения этапов, на которых: а) получают множество значений Y(s) матрицы Y при дискретных частотах s и для каждого значения Y(s) получают собственные значения λi и собственные векторы ti, i равно от 1 до n; б) подгоняют множество из n векторных уравнений 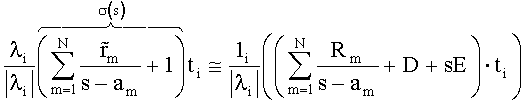
для полученных собственных значений λi и собственных векторов ti, где 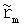 - частотно независимая скалярная величина, m равно от 1 до N, σ(s)=1, путем использования первого множества полюсных частот аm, варьирования
- частотно независимая скалярная величина, m равно от 1 до N, σ(s)=1, путем использования первого множества полюсных частот аm, варьирования 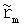 и вычисления Rm и, если предполагаются ненулевыми, D и Е; в) вычисляют второе множество полюсных частот из {аm}=eig(А-b·сT), где А - диагональная матрица, содержащая первое множество полюсных частот аm в качестве диагональных элементов, b - единичный вектор, с - вектор, содержащий
и вычисления Rm и, если предполагаются ненулевыми, D и Е; в) вычисляют второе множество полюсных частот из {аm}=eig(А-b·сT), где А - диагональная матрица, содержащая первое множество полюсных частот аm в качестве диагональных элементов, b - единичный вектор, с - вектор, содержащий 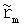 для m от 1 до N, полученные на этапе б), и eig - оператор, возвращающий в прежнее состояние вектор, содержащий собственные значения матрицы; г) повторяют этапы б) и в) с использованием второго множества полюсных частот аm, полученных на этапе в), в качестве первого множества полюсных частот на последующем этапе б), до тех пор, пока не удовлетворено условие остановки.
для m от 1 до N, полученные на этапе б), и eig - оператор, возвращающий в прежнее состояние вектор, содержащий собственные значения матрицы; г) повторяют этапы б) и в) с использованием второго множества полюсных частот аm, полученных на этапе в), в качестве первого множества полюсных частот на последующем этапе б), до тех пор, пока не удовлетворено условие остановки.
11. Устройство по п.10, в котором матрица Y описывает соотношение между напряжением v, приложенным к портам компонента, током i, протекающим через компоненты, выражением i=Yv.
12. Устройство по п.10, в котором D+sE заменяются матричнозначной функцией F({bi}, s), которая линейно зависит от множества параметров {bi}.
| Устройство для сварки термопластов | 1989 |
|
SU1684081A1 |
| Пломбировальные щипцы | 1923 |
|
SU2006A1 |
| US 2008042659 А1, 21.02.2008 | |||
| KR 20060129500 A, 15.12.2006 | |||
| US 2007035309 А1, 15.02.2007. | |||
Авторы
Даты
2011-07-10—Публикация
2007-04-02—Подача