Область техники, к которой относится изобретение
Изобретение относится к способу моделирования линейных свойств электрического компонента с принудительным осуществлением пассивности.
Уровень техники
Остаточное возмущение (OB) (RP) часто используется в качестве средства для принудительного осуществления пассивности в моделях, описывающих линейные свойства электрических компонентов. Один известный подход ОВ использует квадратичное программирование (КП) (QP) для решения задачи по методу наименьших квадратов с ограничениями.
В качестве примера рассмотрим модель с вычетами в полюсах для матрицы полных Y проводимостей
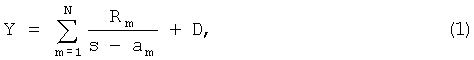
где s есть угловая частота, Rm при m=1 до N являются матрицами, независимыми от s (N представляет собой число полюсов или резонансов, принятых во внимание), D есть матрица, независимая от s, а am при m=1 до N являются комплексными угловыми частотами полюсов или резонансов.
Параметры модели должны быть возмущены таким образом, чтобы возмущенная модель удовлетворяла критерию пассивности в том, что действительная часть собственных значений Y является положительной для всех частот, т.е.
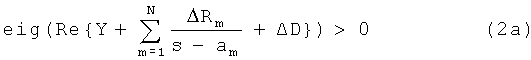
Возмущение должно быть сделано так, чтобы минимизировать изменение в исходной модели, т.е.
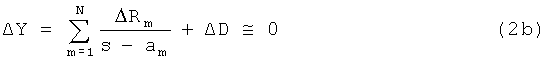
Традиционный путь обращения с уравнением (2b) состоит в минимизации изменения для ΔY в смысле наименьших квадратов.
Сущность изобретения
Задача, решаемая настоящим изобретением, состоит в обеспечении способа, имеющего более высокую точность.
Эта задача решается способом по п.1 формулы изобретения. Данное изобретение основано на понимании того, что слабость подхода в уровне техники заключается в том, что малые собственные значения Y могут легко исказиться за счет возмущения (ΔY). Изобретение преодолевает эту проблему путем «модального возмущения», т.е. путем нахождения приближенного решения для этой задачи:
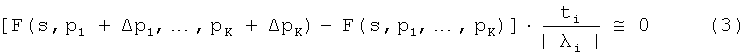
где F есть функция, описывающая зависимость матрицы Y от независимой переменной s, тогда как p1,…,pK являются параметрами (которые должны возмущаться) модели. ti есть число независимых портов электрического компонента (устройства).
Для модели с вычетами в полюсах функция F выражается уравнением (1), а параметры p1,…, pK могут, к примеру, соответствовать элементам матриц Rm и D.
В дополнение к уравнению (3) требуется ограничение, гарантирующее пассивность матрицы Y, аналогичное уравнению (2а). Согласно настоящему изобретению обобщенный вариант уравнения (2а) можно выразить за счет требования, чтобы возмущенный набор параметров p1+Δp1,…, pK+ΔpK соответствовал подходящей функции C условия в булевых значениях:
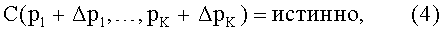
Приближенное решение для n векторных уравнений (3) преимущественно находят путем минимизации суммы квадратов каждой координаты векторов каждого из упомянутых уравнений при условии уравнения (4).
Ограничение, выраженное функцией С условия, может быть, например, ограничением согласно уравнению (2а). Но оно может также быть и другим подходящим ограничением, таким, к примеру, какое получается при использовании собственных значений матрицы гамильтониана, как, к примеру, описано в работе S.Grivet-Talocia, "Passivity enforcement via perturbation of Hamiltonian matrices" («Принудительное осуществление пассивности посредством возмущения матриц гамильтониана»), IEEE Trans. Circuit and Systems I, vol.51, no. 9, pp.1755-1769, Sept. 2004.
Дальнейшие варианты, преимущества и применения находятся в зависимых пунктах формулы изобретения и нижеследующем подробном описании.
Варианты осуществления изобретения
Моделирование устройства
Как упомянуто, настоящее изобретение относится к моделированию линейных электрических свойств в электрическом компоненте с n портами.
Термин «электрический компонент» следует понимать в широком смысле, и он может относиться к отдельному устройству, такому как трансформатор, или к узлу из нескольких устройств, такому как система трансформаторов, двигателей и т.п., взаимно соединенных линиями питания.
Линейные электрические свойства такого устройства могут быть выражены матрицей Y размером n×n, которая в общем относится к напряжению, приложенному к порту для протекающего через него тока. Матрица Y может быть матрицей полных проводимостей, как описано во введении, но она может быть, например, также матрицей импедансов (обычно называемой Z) или матрицей рассеяния (обычно называемой S) устройства. Следовательно, даже хотя матрица Y является преимущественно матрицей полных проводимостей, она также может быть описана иным типом линейного отклика устройства.
Модель описывает зависимость матрицы Y от независимой переменной s, которая может быть частотой, но она может быть также, например, временем или дискретной z-областью. Следовательно, даже хотя эта независимая переменная s является преимущественно частотой, она также может быть любой иной независимой переменной, зависимость от которой описывается моделью.
Зависимость матрицы Y от независимой переменной s может быть, к примеру, описана моделью с вычетами в полюсах по уравнению (1). Эта модель имеет несколько параметров, которые должны быть возмущены, чтобы обеспечить пассивность. В примере уравнения (1) эти параметры являются матричными элементов матриц Rm и D. Альтернативно, эти параметры могут также быть, к примеру, собственными значениями матриц Rm и D. Кроме того, возможно также возмущать полюсные частоты аi.
Следует отметить, тем не менее, что уравнение (1) не является единственной моделью, которую можно использовать для описания матрицы Y в контексте настоящего изобретения. В частности, уравнение (1) можно уточнить добавлением дополнительного выражения, а именно s·E с матрицей E размера n×n, описывающей линейную зависимость матрицы Y от независимой переменной s.
В более общих терминах зависимость матрицы Y от s можно описать матрицей-функцией F, определенной выше, т.е.
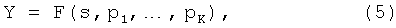
при p1,…,pK, являющихся теми параметрами модели, которые должны быть возмущены для принудительного осуществления пассивности.
Функция F преимущественно является полиномиальной функцией, рациональной функцией или суммой полиномиальных и (или) рациональных функций.
Функция F преимущественно является рациональной функцией, преимущественно заданной как отношение между двумя полиномами в s, модель с вычетами в полюсах, модель пространства состояний или любая их комбинация.
Принудительное осуществление пассивности
Параметры подлежат возмущению таким образом, чтобы матрица Y стала пассивной. «Возмущение» в данном контексте означает, что параметры p1,…,pK (слегка) скорректированы, чтобы стать возмущенным набором параметров p1+Δp1,…, pK+ΔpK.
Если, например, матрица Y является матрицей полных сопротивлений, пассивности можно достичь для возмущенного набора параметров, если удовлетворяются следующие условия:
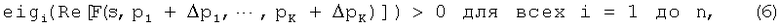
где eigi() есть оператор, выдающий собственное значение i от его матричнозначного аргумента. Если функция F есть модель с вычетами в полюсах уравнения (1) и если возмущение изменяет только матрицы Rm и D, это дает:
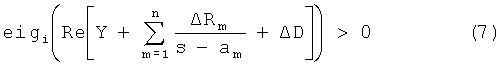
где ΔRm и ΔD являются изменениями, введенными в матрицы R и D вследствие возмущения.
В случае уравнения (1) это эквивалент условия по уравнению (2а). Следует отметить, тем не менее, что имеются и другие условия, которые обеспечивают пассивность матрицы Y, такие как ограничения, полученные из собственных значений матрицы гамильтониана, как упомянуто выше. Таким образом, в более общем виде условие того, что матрица Y возмущенного набора параметров p1+Δp1,…, pK+ΔpK пассивна, можно выразить функцией С условия в булевых значениях, зависящей от возмущенного набора параметров p1+Δp1,…, pK+ΔpK. А именно, при подходящем определении функции C условия, пассивность достигается, если:
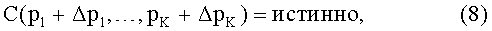
Алгоритм возмущения
Цель описанного здесь алгоритма состоит в том, чтобы найти возмущенный набор параметров p1+Δp1,…, pK+ΔpK, который удовлетворяет уравнению (6) или, в более общих терминах, уравнению (8) при том условии, что возмущение поддерживается «как можно меньшим».
Принятый в настоящем изобретении подход мотивируется тем фактом, что матрицу Y можно сделать диагональной путем преобразования ее в матрицу ее собственных векторов T. А именно:

где Λ есть диагональная матрица с собственными значениями Y в качестве ее ненулевых элементов, а Т есть матрица размером n×n, образованная размещением n собственных векторов ti матрицы Y в ее столбцы. Перемножение справа уравнения (9) с T и взятие производных первого порядка при игнорировании выражений, включающих в себя ΔT, дает для каждой пары (λi, ti):

Иными словами, возмущение матрицы Y приводит к соответствующему линейному возмущению каждой моды и собственного пространства.
Настоящее изобретение основано на понимании того, что возмущение следует поддерживать «как можно меньшим» в смысле того, что возмущение каждой моды взвешивается обратным преобразованием элементов ее собственного значения.
Для случая модели с вычетами в полюсах по уравнению (7) это означает, что можно минимизировать ошибку в следующих уравнениях:
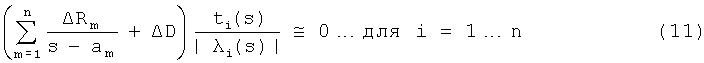
В более общем случае уравнение (5) это соответствует уравнению
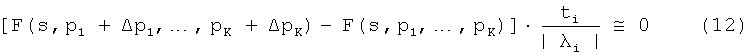
Следовательно, назначение данного алгоритма состоит в нахождении приближенного решения для уравнений (12) или - например, для модели с вычетами в полюсах - решения для уравнений (11) для всех i=1 до n. Поскольку для каждого i имеется векторнозначное уравнение, это означает, что нужно аппроксимировать всего n×n скалярных уравнений при наблюдении одного из условий (6)-(8).
Такое приближение, как правило, выполняется за счет минимизации суммы квадратов ошибок всех уравнений с помощью алгоритмов квадратичного программирования.
Многие из этих алгоритмов минимизации предполагают, что подлежащие аппроксимации уравнения являются линейными по параметрам, которые должны подвергаться возмущению. Это уже случай для уравнения (11). Для общего случая уравнения (12) это не обязательно может быть необходимо. Например, если используется модель с вычетами в полюсах для уравнения (1), но меняются и частоты am полюсов, уравнение (11) становится нелинейным по возмущаемым параметрам Δam. В этом случае уравнения следует линеаризировать перед тем, как они будут введены в стандартные алгоритмы квадратичного программирования. Для общего случая уравнения (12) эту линеаризацию можно выразить как:
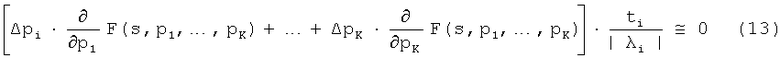
Перед введением данных в алгоритм квадратичного программирования можно вычислить производные в уравнении (13). Кроме того, значения собственных векторов ti и собственных значений λi, которые относятся к невозмущенной матрице Y, вычисляются до оптимизации.
Вместо минимизации ошибок уравнения (12) в среднеквадратичном смысле можно использовать любую подходящую меру (норму) каждого векторного элемента уравнений (13). Такие меры известны специалистам.
Способ согласно настоящему изобретению в значительной степени снижает проблемы возмущений, искажающие поведение модели при применении в моделировании с произвольными граничными условиями, в частности, если матрица Y имеет большой разброс собственных значений. Это достигается путем формулирования части наименьших квадратов в проблеме ограниченной оптимизации, так что размер возмущения собственных значений полных проводимостей обратно пропорционален размеру собственных значений. Благодаря этому можно обойти тот факт, что малые собственные значения становятся искаженными. Применение к моделям, имеющим большое нарушение пассивности, показывает, что новый подход сохраняет поведение исходной модели, тогда как большие отклонения приводят к альтернативным подходам. Подход модальных возмущений является в вычислительном плане более дорогим, чем альтернативные способы, и преимущественно используется редкими решателями для задачи квадратичного программирования.
Изобретение относится к средствам моделирования линейных свойств электрического компонента. Техническим результатом является повышение точности предсказания технически релевантных линейных электрических свойств электрического компонента. Электрический компонент, имеющий порты и обладающий линейными электрическими свойствами, которые охарактеризованы в матрице, являющейся матрицей импедансов, матрицей полных проводимостей или матрицей рассеяния электрического компонента и связывающей напряжение, приложенное к портам, с током, проходящим через эти порты. Электрический компонент обладает пассивностью, определяемой путем возмущения параметров до возмущенного набора параметров при обеспечении того, что этот возмущенный набор параметров соответствует функции условия в булевых значениях. 15 з.п. ф-лы.
1. Электрический компонент, имеющий n>1 портов и обладающий линейными электрическими свойствами, которые охарактеризованы в матрице Y, являющейся матрицей импедансов, матрицей полных проводимостей или матрицей рассеяния электрического компонента и связывающей напряжение, приложенное к портам, с током, проходящим через эти порты, причем зависимость Y от независимой переменной s, являющейся частотой, временем или дискретной z-областью, аппроксимируется моделью
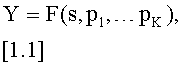
где р1,…, pK являются параметрами модели, a F представляет собой матричнозначную функцию, описывающую зависимость Y от переменной s,
при этом электрический компонент обладает пассивностью, определяемой путем возмущения упомянутых параметров р1,…, рK до возмущенного набора параметров р1+Δр1,…, pK+ΔрK при обеспечении того, что этот возмущенный набор параметров соответствует функции условия в булевых значениях
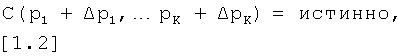
и путем нахождения приближенного решения для уравнений
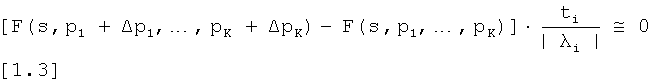
для i=1…n, причем ti и λi являются собственными векторами и собственными значениями матрицы Y.
2. Электрический компонент по п.1, причем уравнение 1.3 линеаризуют посредством выражения
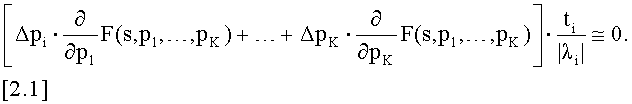
3. Электрический компонент по п.1, причем функция С условия представляет собой выражение
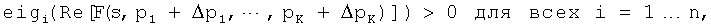
где eigi() есть оператор, возвращающий собственное значение i своего матричнозначного аргумента.
4. Электрический компонент по п.2, причем функция С условия представляет собой выражение
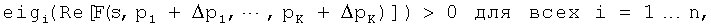
где eigi() есть оператор, возвращающий собственное значение i своего матричнозначного аргумента.
5. Электрический компонент по любому из пп.1-4, причем упомянутая функция F является функцией из группы рациональных функций, отношением полиномов, функциями вычета в полюсе, моделями в пространстве состояний или их комбинациями.
6. Электрический компонент по п.4, причем уравнение 1.1 представляет собой
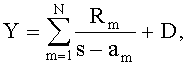
причем Rm при m=1…N являются матрицами, не зависимыми от s (где N является числом полюсов или резонансов, принимаемых во внимание), D есть матрица, не зависимая от s, а аm при m=1…N представляют собой комплексные угловые частоты полюсов или резонансов, причем упомянутые матрицы Rm и/или D и/или упомянутые полюса аm зависят от упомянутых параметров p1,…, рK.
7. Электрический компонент по п.5, причем каждый элемент упомянутых матриц Rm и D является одним из упомянутых параметров Р1,…,РK.
8. Электрический компонент по п.5, причем каждое собственное значение упомянутых матриц Rm и D является одним из упомянутых параметров p1,…,рK.
9. Электрический компонент по п.5, причем упомянутое уравнение 1.3 представляет собой
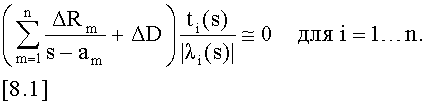
10. Электрический компонент по любому из пп.1-4, причем приближенное решение уравнения 1.3 находят путем минимизации меры каждого векторного элемента каждого из уравнений 1.3.
11. Электрический компонент по п.7, причем приближенное решение уравнения 1.3 находят путем минимизации меры каждого векторного элемента каждого из уравнений 1.3.
12. Электрический компонент по п.8, причем приближенное решение уравнения 1.3 находят путем минимизации меры каждого векторного элемента каждого из уравнений 1.3.
13. Электрический компонент по п.9, причем приближенное решение уравнения 1.3 находят путем минимизации меры каждого векторного элемента каждого из уравнений 1.3.
14. Электрический компонент по любому из пп.1-4, причем приближенное решение уравнения 1.3 находят путем минимизации суммы квадратов каждого векторного элемента каждого из уравнений 1.3.
15. Электрический компонент по п.9, причем приближенное решение уравнения 1.3 находят путем минимизации суммы квадратов каждого векторного элемента каждого из уравнений 1.3.
16. Электрический компонент по любому из пп.1-4, причем электрический компонент является отдельным устройством, в частности трансформатором, или узлом из нескольких устройств, в частности системой трансформаторов или двигателей, взаимно соединенных линиями питания.
| RU 94046063 A1, 10.09.1996 | |||
| КОММУТАТОР ЦИФРОВЫХ ДИФФЕРЕНЦИАЛЬНЫХ СИГНАЛОВ | 2003 |
|
RU2257005C1 |
| Способ обработки целлюлозных материалов, с целью тонкого измельчения или переведения в коллоидальный раствор | 1923 |
|
SU2005A1 |
| ИССЛЕДОВАТЕЛЬСКАЯ РАКЕТА | 1977 |
|
SU669814A1 |
| Устройство для горячей навивки пружин | 1979 |
|
SU797830A1 |
Авторы
Даты
2012-05-10—Публикация
2007-05-11—Подача