СПОСОБ ГАРМОНИЧЕСКОГО АНАЛИЗА ПЕРИОДИЧЕСКОГО МНОГОЧАСТОТНОГО СИГНАЛА Российский патент 2011 года по МПК G01R23/16 

Изобретение относится к измерительной технике и предназначено для гармонического анализа периодических колебательных процессов, в частности электрических сигналов.

В измерительной технике известны различные способы гармонического (спектрального) анализа периодического многочастотного сигнала, заключающиеся в определении гармонического состава периодического многочастотного сигнала y(t) и оценивании частот, амплитуд и фаз входящих в сигнал гармоник.

Известен способ (варианты) оценивания несущей частоты сигнала [1], заключающийся в предварительной дискретизации принятого сигнала в пределах полосы частот поиска в первую последовательность дискретных отсчетов P₁, вычислении компонент спектральной плотности мощности с максимальной концентрацией мощности сигнала и вычислении оценки несущей частоты в выделенной области, дополнительном сдвигании сигнала на π/2 и дискретизации его во вторую последовательность P₂, формировании нескольких дополнительных последовательностей дискретных отсчетов и преобразовании их методом дискретного преобразования Фурье, оценивании несущей частоты сигнала по частоте пика (экстремума основного лепестка) спектра.

Недостаток цитированного способа заключается в большой погрешности оценивания несущей частоты коротких отрезков сигнала, содержащего от нескольких периодов до нескольких десятков периодов. Спектры таких коротких отрезков сигнала широкие и получение дополнительных последовательностей сигнала, выполняемых с применением преобразования Гильберта, сопряжено с большими искажениями, что и приводит в итоге к большим погрешностям.

Известен способ спектрального анализа периодического многочастотного сигнала a(t_j) [2], включающий формирование опорного синусоидального сигнала b₀(t_j)=B_msin(ω₀t_j+φ₀), который многократно сдвигают по фазе один относительно другого. Для анализируемого периодического многочастотного сигнала и опорного сигнала с амплитудой B_m, представленных отсчетами мгновенных значений для одних и тех же моментов времени t_j=t₁, t₂, …, t_N, где N - число разбиений на периоде Т, находят точки совместного решения а(b₀) при различных круговых частотах опорного сигнала ω₀ и фазах опорного сигнала φ₀, строят вольт-амперные характеристики и определяют их площадь F_BAXmin, причем вывод о присутствии гармонической составляющей с круговой частотой ω_K и фазой φ_K в анализируемом сигнале a(t_j) делают исходя из условия f_BAX=0, затем определяют максимальную площадь вольт-амперной характеристики F_BAXmaxK при φ_K±90° и находят амплитуду К-й спектральной составляющей по формуле

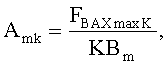
где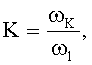

ω₁ - основная круговая частота,

далее по значениям ω_K, φ_K и A_mk судят о спектральном составе анализируемого сигнала a(t_j).

Этот способ обладает недостаточной точностью определения параметров составляющих сигнала с близкими частотами, не кратными основной гармонике.

Известен способ спектрального анализа электрического сигнала [3], заключающийся в получении цифровых отсчетов y_ц(m) электрического сигнала y(t) через равные интервалы времени Δt и формировании полиномиальных интерполирующих функций между соседними отсчетами сигнала, получении приближенной функции, аппроксимирующей сигнал, и нахождении Фурье-образа этой функции.

Указанный способ обладает низкой точностью определения частот и амплитуд спектральных составляющих анализируемого сигнала из-за дискретности спектра, погрешностей аппроксимации сигнала, влияния боковых лепестков слагаемых спектра и низкой разрешающей способности.

Известен способ спектрального анализа сигнала [4] на основе дискретного преобразования Фурье, в котором для снижения погрешности оценки частоты, вызванной дискретностью спектра, искусственно увеличена длительность периода повторения реализации сигнала путем добавления нулевых отсчетов к исходной реализации. Предельным случаем этого способа является использование дискретно-временного преобразования Фурье, эквивалентного обработке реализации сигнала с бесконечным периодом и исключающего погрешности оценки частоты и амплитуды сигнала за счет дискретности спектра.

Однако в этом способе не исключено влияние боковых лепестков слагаемых спектра на точность определения частот, фаз и амплитуд составляющих анализируемого сигнала.

Для уменьшения погрешности, обусловленной влиянием боковых лепестков слагаемых спектра на положения спектральных пиков, широко используется способ гармонического анализа сигнала y(t) [5], включающий получение отсчетов y(m) сигнала через равные интервалы времени Δt, перемножение отсчетов y(m) сигнала с отсчетами весовой функции w(m), вычисление спектра путем нахождения Фурье-образа полученного произведения и оценку частот слагаемых сигнала.

Практическое осуществление этого способа выполняют методами цифровой обработки сигналов.

Известен способ гармонического анализа сигнала y(t) [6], являющийся прототипом, включающий получение цифровых отсчетов y_ц(m) сигнала через равные интервалы времени Δt, перемножение цифровых отсчетов y_ц(m) сигнала с отсчетами весовой функции w_ц(m), вычисление спектра путем нахождения Фурье-образа полученного произведения и оценку частот слагаемых сигнала [6, стр.129, 273-274].

Известно, что обработка сигналов с помощью ВФ позволяет ослабить влияние боковых лепестков слагаемых спектра, но лишь за счет ухудшения спектрального разрешения. Считается, что в результате этих противоречий при использовании спектрального анализа на основе преобразования Фурье погрешность оценки частоты и амплитуды сигнала, с относительно широким спектром, не может быть низкой [7, стр.102]. Причем минимумы погрешности оценки частоты совпадают с максимумами погрешности оценки амплитуды.

Таким образом, известно, что для многих случаев этот способ также обладает недостаточной точностью определения частот, амплитуд и фаз спектральных слагаемых анализируемого сигнала из-за взаимного влияния боковых лепестков слагаемых спектра и низкой разрешающей способности.

Технический результат, на достижение которого направлено изобретение способа, заключается в одновременном уменьшении погрешности измерения частот амплитуд и фаз гармонических составляющих периодического многочастотного сигнала.

Указанный технический результат достигается тем, что в способе гармонического анализа периодического многочастотного сигнала y(t), цикл которого включает получение цифровых отсчетов y_ц(m) сигнала через равные интервалы времени Δt, генерирование весовой функции w_ц(m) в форме цифровых отсчетов, перемножение цифровых отсчетов y_ц(m) сигнала с цифровыми отсчетами весовой функции w_ц(m), вычисление спектра путем нахождения Фурье-образа полученного произведения, оценивание частот пиков спектра, превышающих уровень боковых лепестков наиболее интенсивного слагаемого спектра, и оценивание частот, амплитуд и фаз гармонических составляющих сигнала по частотам, амплитудам и фазам Фурье-образа, полученного произведения, на частотах пиков спектра, многократно выполняют дополнительные циклы гармонического анализа. В каждом дополнительном цикле гармонического анализа по результатам выполненного цикла гармонического анализа изменяют форму весовой функции генерированием новых цифровых отсчетов весовой функции, повторяя циклы гармонического анализа до получения на частоте каждого из анализируемых гармонических составляющих сигнала допустимых значений слагаемых спектра от заданного количества других гармонических составляющих сигнала и допустимых значений заданного количества производных слагаемых спектра от заданного количества других гармонических составляющих сигнала.

Дополнительные циклы гармонического анализа выполняют до получения на частоте каждого из анализируемых гармонических составляющих сигнала нулевых значений слагаемых спектра от заданного количества других гармонических составляющих сигнала и нулевых значений заданного количества производных слагаемых спектра от заданного количества других гармонических составляющих сигнала.

Цифровые отсчеты весовой функции w_ц(m) генерируют по отсчетам дискретной весовой функции, определенной одним из двух выражений. Первое выражение имеет вид

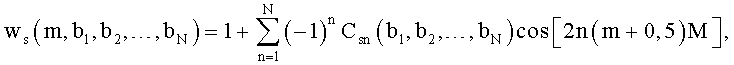
где m - номер текущего отсчета сигнала;

b_i=ω_iT/2π - нормированная частота, на которой задается равенство нулю спектр весовой функции или его производная;

ω_i - круговая частота;

T - период;

N - число варьируемых тригонометрических слагаемых весовой функции;

n - номер тригонометрического слагаемого;

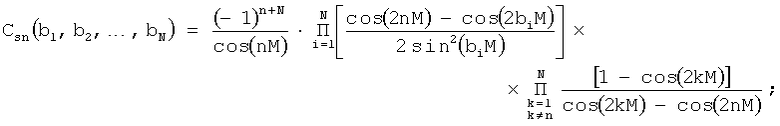
M=π/M₀;

M₀ - число отсчетов сигнала.

Второе выражение имеет вид

где

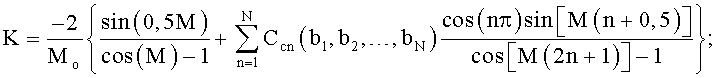
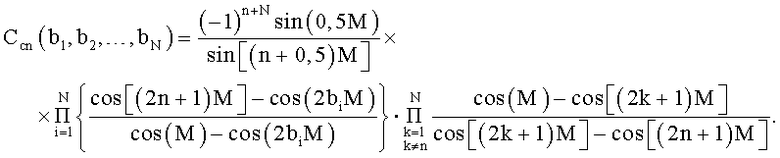
Изменение формы весовой функции задают изменением положений нулей b_i спектра весовой функции

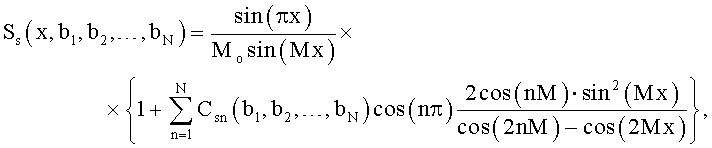
или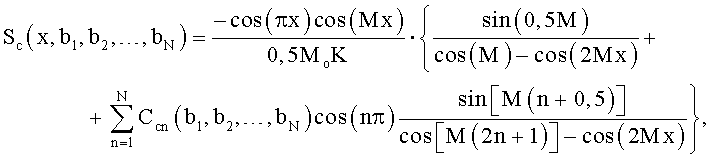

где x=ωT/2π;

ω - текущая угловая частота.

При выполнении (n) цикла гармонического анализа по оцененным частотам пиков спектра в (n-1) цикле гармонического анализа 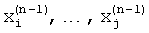, которые превышают уровень боковых лепестков наиболее интенсивного слагаемого спектра, вычисляют взаимные разности между частотами пиков спектра 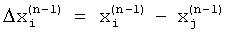и корректируют форму весовой функции путем задания частот нулей спектра или нулей его производных 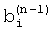равными модулям взаимных разностей между частотами пиков спектра 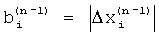. Затем используют весовую функцию со скорректированной формой в (n) цикле гармонического анализа, при этом за частоты гармонических составляющих принимают оценки на последнем цикле гармонического анализа.

Изменение формы весовой функции выполняют до снижения абсолютного значения разности между вновь полученными значениями оценок частот пиков спектра 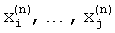и их предыдущими значениями 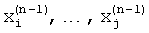, ниже контрольного уровня Δ_x:

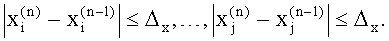
Амплитуду и фазу каждого составляющего сигнала оценивают после уточнения частот пиков спектра.

Для оценки частот гармонических составляющих многочастотного сигнала в первом цикле применяют весовую функцию такой формы, при которой для минимальной разности частот между гармоническими составляющими сигнала не происходит перекрытие основных лепестков слагаемых спектра сигнала, а уровень боковых лепестков спектра весовой функции не превышает заданного. При этом основной лепесток слагаемого спектра, соответствующий наиболее слабому из анализируемых составляющему сигнала, превышает уровень боковых лепестков слагаемого спектра наиболее интенсивного составляющего сигнала, которые определяют на основе априорных сведений о возможном гармоническом составе сигнала.

Целесообразно для оценки частот составляющих многочастотного сигнала в первом цикле гармонического анализа применять весовые функции, которые имеют минимально возможный уровень боковых лепестков спектра при заданной ширине основного лепестка, заданной скорости уменьшения уровня боковых лепестков и минимальной эквивалентной шумовой полосе.

Такими функциями являются

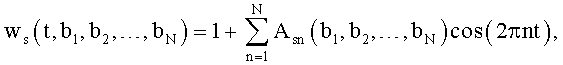
или

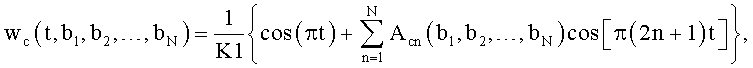
где t - текущее время внутри периода Т;

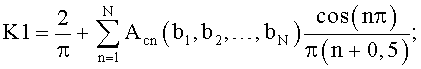
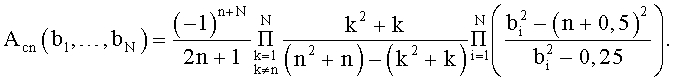
Задавая частоты b_i, получают требуемые уровень боковых лепестков (УБЛ) и ширину основного лепестка ΔF₆ по уровню -6 дБ, приведенные в таблицах 1-5.

Таблица 1. Положения нулей b_i спектра весовой функции w_s(*) со скоростью уменьшения уровня боковых лепестков спектра 6 дБ/окт N Частоты b_i УБЛ, дБ ΔF₆ 2 1,4; 2,0632 -27,09 1,486 4 1,4; 2,0444; 2,94; 3,9281 -27,637 1,4794 2 1,6; 2,2083 -32,9795 1,6058 4 1,6; 2,1788; 3,0232; 3,9739 -33,4899 1,6021 2 1,8; 2,4041 -38,2672 1,7165 4 1,8; 2,3216; 3,1144; 4,0246 -39,387 1,7123 2 2; 2,6491 -43,1875 1,8188 4 2; 2,4758; 3,2257; 4,1180 -45,1383 1,8153 2 2,25; 3,0493 -49,421 1,9368 4 2,25; 2,6825; 3,3926; 4,3057 -52,0279 1,9371 2 2,5; 3,7226 -56,6824 2,0518 4 2,5; 2,8995; 3,5797; 4,5672 -58,6678 2,0521 3 3; 3,3524; 5,3290 -71,4828 2,2638 3 3,5; 4,0150; 6,0405 -85,2222 2,4257 4 4; 4,2803; 5,0893; 8,7183 -98,1739 2,6243 4 4,5; 4,858; 6,093; 10,661 -110,903 2,7799

Таблица 2. Положения нулей b_i спектра весовой функции w_c(*) со скоростью уменьшения уровня боковых лепестков спектра 12 дБ/окт N Частоты b_i УБЛ, дБ ΔF₆ 3 1,4; 2,1577; 3,1993 -24,1852 1,5265 4 1,4; 2,1212; 3,1065; 4,2018 -25,1503 1,5138 2 1,6; 2,3355 -28,3002 1,6731 4 1,6; 2,2518; 3,1872; 4,2475 -30,6118 1,6249 2 1,8; 2,4514; -34,1185 1,7843 4 1,8; 2,3911; 3,2759; 4,2984 -36,1187 1,7591 2 2; 2,2573 -40,2450 1,8816 4 2; 2,5377; 3,3720; 4,3540 -41,657 1,8647 2 2,25; 2,7549 -47,9658 1,9905 4 2,25; 2,7292; 3,5013; 4,4294 -48,7074 1,9845 2 2,5; 3,0309 -54,3019 2,0959 3 2,5; 2,9301; 3,6503 -55,8631 2,0936 4 2,5; 2,9281; 3,6396; 4,5107 -55,9594 2,0929 2 3; 3,8862 -67,8151 2,2880 3 3; 3,3765; 4,1783 -69,1854 2,2941 4 3; 3,3540; 3,9742; 4,8074 -70,2846 2,2912 4 3,5; 3,8116; 4,3845; 5,4297 -83,5472 2,4769 3 4; 4,4703; 6,3214 -95,412 2,6368 4 4; 4,2709; 4,7753; 6,6762 -97,3896 2,6480

Таблица 3. Положения нулей b_i спектра весовой функции w_s(*) со скоростью уменьшения уровня боковых лепестков спектра 18 дБ/окт N Частоты b_i УБЛ, дБ ΔF₆ 2 1,4; ∞ -15,2021 1,6404 3 1,4; 2,3781; ∞ -19,4416 1,5921 4 1,4; 2,5597; 3,4181; ∞ -21,6597 1,5630 2 1,6; ∞ -20,2787 1,7814 3 1,6; 2,4833; ∞ -24,4934 1,7314 4 1,6; 2,3763; 3,4836; ∞ -26,7767 1,7000 2 1,8; ∞ -25,6387 1,8992 3 1,8; 2,5968; ∞ -29,6241 1,8534 4 1,8; 2,5055; 3,5558; ∞ -31,9046 1,8223 2 2; ∞ -31,4675 1,9968 3 2; 2,7172; ∞ -34,9113 1,9609 4 2; 2,6421; 3,6343; ∞ -37,0854 1,9323 2 2,25; ∞ -39,8149 2,0955 3 2,25; 2,8754; ∞ -41,8540 2,0782 4 2,25; 2,8217; 3,7401; ∞ -43,7389 2,0550 2 2,5; ∞ -48,3422 2,1736 4 2,5; 3,0090; 3,8531; ∞ -50,6284 2,1657 2 3; ∞ -56,9301 2,2854 4 3; 3,4009; 4,0956; ∞ -65,4938 2,3535 3 3,5; 4,2408; ∞ -77,8590 2,5183 4 3,5; 3,8430; 4,5397; ∞ -79,7031 2,5236 4 4; 4,3053; 5,3763; ∞ -93,3265 2,6844 4 4,5; 4,9137; 6,4222; ∞ -106,385 2,8295

Таблица 4. Положения нулей b_i спектра весовой функции w_c(*) со скоростью уменьшения уровня боковых лепестков спектра 24 дБ/окт N Частоты b_i УБЛ, дБ ΔF₆ 3 1,4; 2,5186; ∞ -16,9138 1,63 4 1,4; 2,3497; 3,6235; ∞ -19,5694 1,5941 3 1,6; 2,6206; ∞ -21,5749 1,7793 4 1,6; 2,4664; 3,6876, ∞ -24,3922 1,7383 2 1,8; ∞ -20,9957 1,9811 3 1,8; 2,7313; ∞ -26,2490 1,9110 4 1,8; 2,5923; 3,7586; ∞ -29,1913 1,8673 2 2; ∞ -25,7154 2,0954 3 2; 2,8493; ∞ -31,0002 2,0277 4 2; 2,7258; 3,8359; ∞ -34,0162 1,9835 2 2,25; ∞ -32,1222 2,2133 3 2,25; 3,0056; ∞ -37,1299 2,1556 4 2,25; 2,9020; 3,9407; ∞ -40,1406 2,1141 2 2,5; ∞ -39,2954 2,3083 3 2,5; 3,1698; ∞ -43,5669 2,2669 4 2,5; 3,0865; 4,0536; ∞ -46,4269 2,2309 3 3; 3,5142; ∞ -57,8497 2,4494 4 3; 3,4748; 4,2986; ∞ -59,7249 2,4313 2 3,5; ∞ -65,8373 2,5407 3 3,5; 3,9224; ∞ -73,5867 2,5965 4 3,5; 3,8805; 4,5613; ∞ -74,4692 2,5961 3 4; 4,6415; ∞ -87,4466 2,7375 4 4; 4,3221; 4,9686; ∞ -89,2459 2,7441 3 4,5; 5,3713; ∞ -98,4647 2,8422 4 4,5; 4,7890; 5,7069; ∞ -103,2239 2,8862

Таблица 5. Положения нулей b_i спектра весовой функции w_s(*) со скоростью уменьшения уровня боковых лепестков спектра 30 дБ/окт N Частоты b_i УБЛ, дБ ΔF₆ 4 1,4; 2,6507; ∞; ∞ -14,8566 1,6612 5 1,4; 2,4395; 3,8175; ∞; ∞ -17,7969 1,6209 3 1,6; ∞; ∞ -13,5562 1,8962 4 1,6; 2,7495; ∞; ∞ -19,2307 1,8194 5 1,6; 2,5529; 3,8801; ∞; ∞ -22,3852 1,7717 3 1,8; ∞; ∞ -17,6367 2,0452 4 1,8; 2,8572; ∞; ∞ -23,5757 1,9598 5 1,8; 2,6755; 3,9497; ∞; ∞ -26,9252 1,9068 3 2; ∞; ∞ -21,8068 2,1738 4 2; 2,9726; ∞; ∞ -27,9496 2,0847 5 2; 2,8061; 4,0257; ∞; ∞ -31,4647 2,0289 3 2,25; ∞; ∞ -27,2552 2,3090 4 2,25; 3,1262; ∞; ∞ -33,5265 2,2225 5 2,25; 2,9788; 4,1291; ∞; ∞ -37,1911 2,1662 3 2,5; ∞; ∞ -32,1000 2,4199 4 2,5; 3,2884; ∞; ∞ -39,2966 2,3429 5 2,5; 3,1604; 4,2408; ∞; ∞ -43,0251 2,2892 3 3; ∞; ∞ -46,7412 2,5855 4 3; 3,6327; ∞; ∞ -51,723 2,5420 5 3; 3,5443; 4,4857; ∞; ∞ -55,203 2,5011 4 3,5; 3,9933; ∞; ∞ -65,9912 2,6978 5 3,5; 3,9479; 4,7522; ∞; ∞ -68,3842 2,6766 3 4; ∞; ∞ -74,3238 2,7778 4 4; 4,3846; ∞; ∞ -82,6031 2,8231

Сущность способа заключается в том, что многократные оценки частот гармонических составляющих периодического многочастотного сигнала используют для итерационного процесса определения необходимой формы весовой функции. В результате форма весовой функции подбирается такой, чтобы на частоте любого из анализируемых составляющих сигнала слагаемые спектра от других составляющих сигнала по амплитуде были равны нулю, причем кратность нуля, определяемая порядком производных, может быть заданной степени. При этом, независимо от фазовых и амплитудных соотношений между составляющими периодического многочастотного сигнала, исключается их взаимное влияние при оценке параметров в спектральной области.

Сразу задать требуемую форму весовой функции невозможно, т.к. пока не достигнуто условие отсутствия взаимного влияния слагаемых спектра на положения пиков (экстремумов) основных лепестков каждого из анализируемых слагаемых спектра, частоты вычисляются с погрешностями. Эти погрешности постепенно уменьшаются по мере приближения весовой функции к нужной форме.

Проведенный анализ уровня техники, включающий поиск по патентным и научно-техническим источникам информации и выявление источников, содержащих сведения об аналогах заявляемого изобретения, позволяет установить, что заявителем не обнаружены технические решения, характеризующиеся признаками, идентичными всем существенным признакам заявленного изобретения. Выделение из перечня найденных аналогов прототипа позволило выявить совокупность существенных (по отношению к усматриваемому заявителем техническому результату) отличительных признаков в заявляемом объекте, изложенных в формуле изобретения. Следовательно, заявляемое изобретение соответствует требованию "новизна" по действующему законодательству. Сведений об известности отличительных признаков в совокупностях признаков известных технических решений с достижением такого же, как у заявляемого способа, положительного эффекта не имеется. На основании этого сделан вывод, что предлагаемое техническое решение соответствует критерию "изобретательский уровень".

Сущность предлагаемого способа поясняется с помощью одного из возможных устройств, схематично изображенного на фиг.1, спектрами, изображенными на фиг.2, фиг.4, графиками, изображенными на фиг.3.

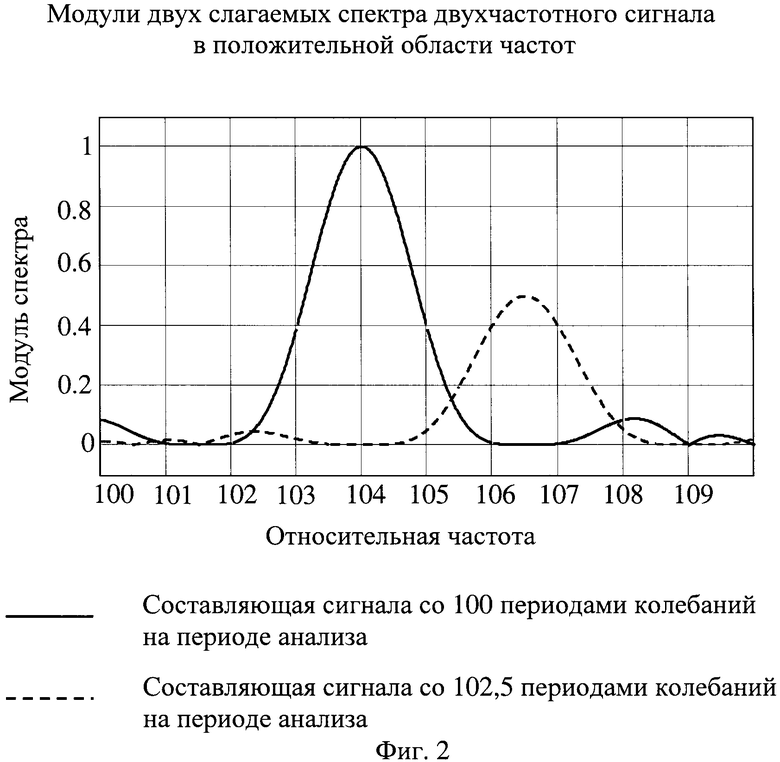
На фиг.2 изображены два слагаемых спектра двухчастотного сигнала в положительной области частот.

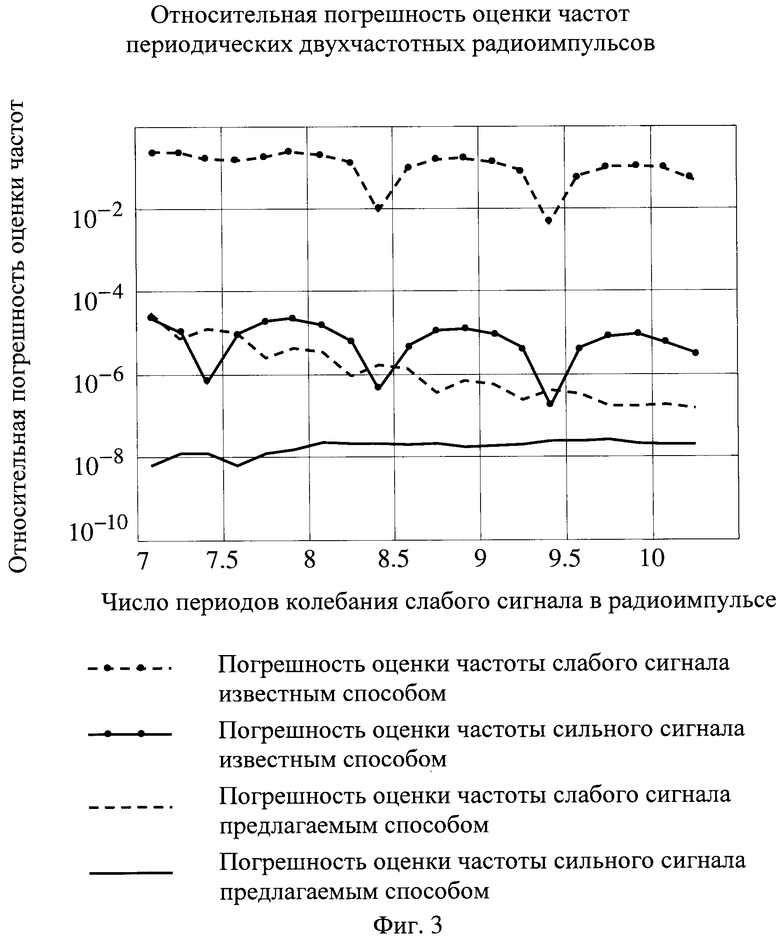
На фиг.3 приведена относительная погрешность оценки частот периодических двухчастотных радиоимпульсов.

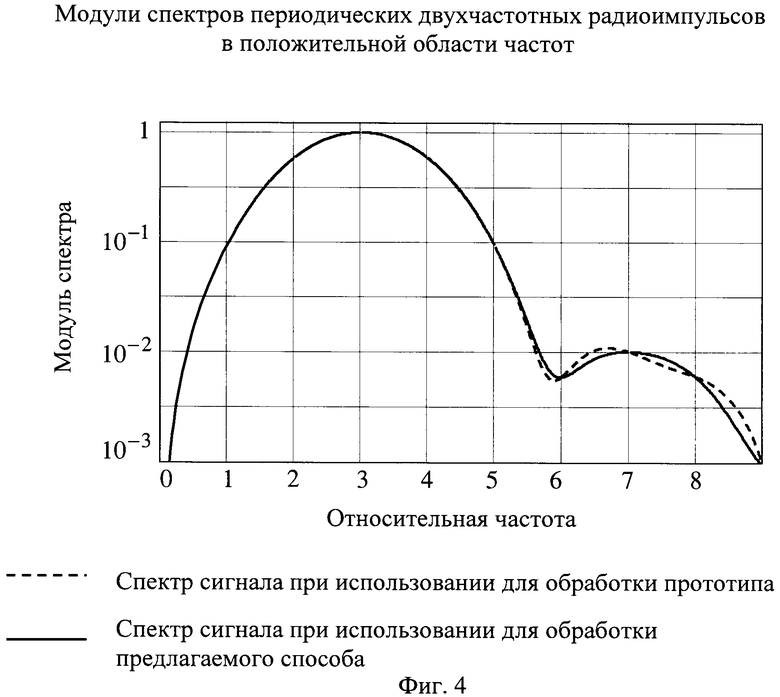
На фиг.4 изображены спектры периодических двухчастотных радиоимпульсов в положительной области частот.

Устройство (фиг.1) содержит датчик электрического сигнала 1 (ДЭС) с двумя выходами, аналого-цифровой преобразователь 2 (АЦП) с двумя входами и одним выходом, схему цифровой обработки сигналов 3 (СЦОС) с двумя входами и двумя выходами, формирователь импульсов начала и окончания периода 4 (ФИНОП).

Первый выход ДЭС 1 через АЦП 2 соединен с первым входом СЦОС 3. Второй выход ДЭС 1 соединен со вторым входом СЦОС 3 через ФИНОП 4. Первый выход СЦОС 3 соединен со вторым входом АЦП 2. Второй выход СЦОС 3 является выходом устройства. СЦОС 3 может быть выполнена стандартной, содержащей генератор импульсов синхронизации и цифровой процессор, включающий устройство памяти и арифметическое устройство.

Практическая реализация устройства не представляет сложности и осуществляется на основе широко распространенных электронных элементов и приборов.

Способ гармонического анализа периодического многочастотного сигнала осуществляют следующим образом. Аналоговый периодический многочастотный электрический сигнал y(t), формируемый ДЭС 1, поступает в АЦП 2, с выхода которого цифровые отсчеты y_ц(m) (где m=0, …, М₀-1) сигнала поступают на первый вход СЦОС 3. Одновременно с ДЭС 1 через ФИНОП 4 на второй вход СЦОС 3 поступает синхронизирующая последовательность импульсов, соответствующая началам и окончаниям периодов периодического многочастотного сигнала.

С применением СЦОС 3 выполняют все действия над сигналами и синхронизируют работу АЦП 2.

В течение первого периода одновременно с поступлением цифровых отсчетов анализируемого сигнала с помощью СЦОС 3 генерируют цифровые отсчеты весовой функции по отсчетам весовой функции

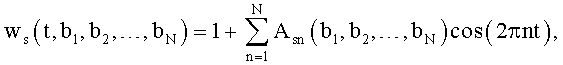
или

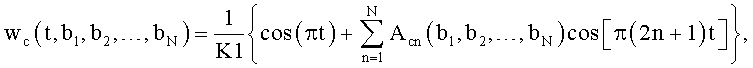
и перемножают их с цифровыми отсчетами y_ц(m) периодического многочастотного сигнала. Затем вычисляют спектр, определяют максимум и принимают уровень наиболее интенсивного слагаемого спектра равным уровню максимума, а уровень боковых лепестков наиболее интенсивного слагаемого спектра принимают равным уровню боковых лепестков примененной весовой функции. Определяют пики спектра, превышающие уровень боковых лепестков наиболее интенсивного слагаемого спектра на заданную величину, например на 10 дБ. Оценивают частоты 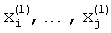модулей всех спектральных пиков, которые превышают на заданную величину, например на 10 дБ, уровень боковых лепестков наиболее интенсивного слагаемого спектра и записывают их в память. Вычисляют взаимные разности между частотами пиков спектра .

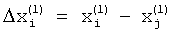Получают цифровые отсчеты y_ц(m) второго периода периодического многочастотного сигнала и генерируют цифровые отсчеты весовой функции уже по отсчетам дискретной весовой функции

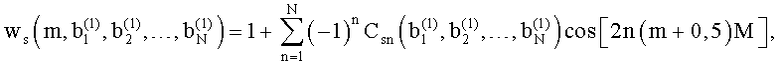
или

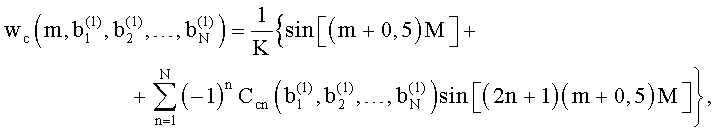
с формой огибающей заданной частотами 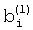, равными модулям взаимных разностей между частотами пиков спектра 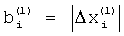, определенным в первом цикле гармонического анализа. Оценивают частоты 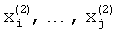модулей всех спектральных пиков, которые превышают уровень боковых лепестков наиболее интенсивного слагаемого спектра на заданную величину, и записывают их в память. Вычисляют разницу оценок частот, полученных в первом и втором циклах гармонического анализа 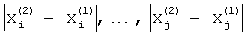. Если разница результатов оценки частот не снижена ниже контрольного уровня Δ_x, определенного допустимой погрешностью измерений, производится следующий цикл гармонического анализа путем перемножения вновь генерируемых цифровых отсчетов весовой функции с вновь измененной формой по результатам второго цикла на вновь получаемые цифровые отсчеты сигнала и оценивания частот гармонических слагаемых сигнала по частотам Фурье-образа, вновь полученного произведения на частотах спектральных пиков.

Аналогично в (n) цикле гармонического анализа получают цифровые отсчеты y_ц(m) (n)-го периода периодического многочастотного сигнала. По оцененным частотам пиков спектра в (n-1) цикле гармонического анализа 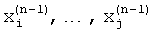, которые превышают уровень боковых лепестков наиболее интенсивного слагаемого спектра, вычисляют взаимные разности между частотами пиков спектра 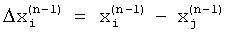, корректируют форму ВФ путем задания частот 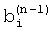, на которых приравнивается нулю спектр весовой функции или его производная, модулям взаимных разностей между частотами пиков спектра 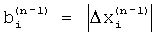и используют весовую функцию со скорректированной формо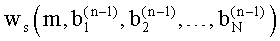й или 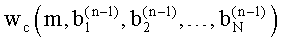в (n) цикле гармонического анализа. Итерационную процедуру циклов гармонического анализа с последовательным изменением формы весовой функции выполняют до снижения абсолютного значения разности между вновь полученными значениями оценок частот пиков спектра 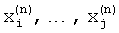и их предыдущими значениями 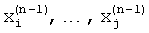, ниже контрольного уровня Δ_x:

.

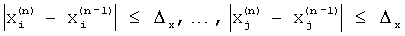При этом за частоты гармонических составляющих принимают оценки, полученные на последнем цикле гармонического анализа, а амплитуду и фазу каждого составляющего сигнала оценивают после уточнения частот пиков спектра.

В результате итерационной процедуры на частоте каждого из анализируемых гармонических составляющих сигнала получают нулевые или близкие к нулевым значения от всех слагаемых спектра, которые на заданную величину (например, на 10 дБ, как было приведено выше) превышают уровень боковых лепестков наиболее интенсивного слагаемого спектра, а также нулевые или близкие к нулевым значения заданного количества производных от этих слагаемых спектра. При этом спектральные пики, соответствующие анализируемым гармоническим составляющим сигнала, не смещаются ни по частоте, ни по амплитуде и отсутствует смещение фазы пика спектра. На фиг.2 приведены модули двух слагаемых спектра сигнала с относительными частотами 100 и 102,5 (на периоде анализа Т составляющие сигнала имеют 100 и 102,5 периодов колебаний) и с амплитудами 1 и 0,5. При обработке сигнала использована весовая функция, у которой сформированы нулевые значения спектра вместе с тремя производными на частоте 2,5. В результате в спектрах каждого из слагаемых на частотах, отличных от частоты максимума на 2,5, также формируются нулевые значения спектра вместе с тремя начальными производными и из-за отсутствия взаимного влияния слагаемых спектра положения максимумов не смещаются по частоте и на частотах максимумов амплитуды и фазы спектра определяются без погрешности.

При снижении разницы результатов оценки частоты ниже контрольного уровня СЦОС 3 производит вывод результатов оценки частот, амплитуд и фаз гармонических слагаемых многочастотного периодического сигнала на выход устройства.

На фиг.3 приведена относительная погрешность оценки частот периодических двухчастотных радиоимпульсов длительностью Т. Каждый радиоимпульс состоит из отрезка гармонического колебания единичной амплитуды с тремя периодами (х₁=3) и отрезка гармонического колебания с амплитудой на 40 дБ меньше с варьируемым числом от 7 до 10,5 периодов колебаний (х₂=7…10,5). Сплошной и пунктирной линиями с точечными маркерами показана погрешность оценки частот, соответственно, сильного и слабого составляющего сигнал известным способом (прототипом) при использовании весовой функции Блэкмана [5]. Сплошной и пунктирной линиями без маркеров показана погрешность оценки частот, соответственно, сильного и слабого составляющего сигнала предлагаемым способом при использовании весовой функции

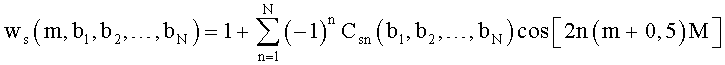
с числом варьируемых слагаемых N=8 и нормированными частотами, на которых задаются нулевые значения спектра весовой функции и его производных b₁=b₂=b₃=b₄=х₂-x₁, b₅=b₆=x₂-(-x₂)=2х₂, b₇=b₈=x₂-(-x₁)=x₂+x₁, определяемыми в циклах гармонического анализа.

Из сопоставления полученных результатов следует, что применение предлагаемого способа позволяет снизить погрешность оценки частот гармонических составляющих периодического многочастотного сигнала более чем на три порядка. Во столько же раз снижается погрешность оценки фаз составляющих сигнала, а погрешность оценки амплитуд определяется уровнем шума, в частности, при использовании в качестве СЦОС 3 персонального компьютера с уровнем шума квантования минус 192 дБ снижение погрешности оценки амплитуд составляет 8 порядков.

На фиг.4 изображены модули спектров указанных выше периодических двухчастотных радиоимпульсов в положительной области частот при x₁=3 и x₂=7. Сплошной тонкой линией изображен спектр сигнала при использовании для обработки прототипа, а сплошной толстой линией - при использовании предлагаемого способа. При использовании для обработки известного способа спектральный пик, соответствующий слабому составляющему сигнала, искажен боковыми лепестками спектра сильного составляющего сигнала настолько, что это видно при графическом представлении, и оценка его частоты, амплитуды и фазы выполняется с большими погрешностями. Обработка сигнала предлагаемым способом практически исключает искажения спектральных пиков.

ИСТОЧНИКИ ИНФОРМАЦИИ

1. Патент РФ 2137143, G01R 23/16, 1999.09.10.

2. Патент РФ 2229725, G01R 23/16. Опубликовано 2004.05.27.

3. Патент РФ 2133041, G01R 23/16, 10.07.1999.

4. Марпл.-мл. С.Л. Цифровой спектральный анализ и его приложения: Пер. с англ. М.: Мир, 1990. 584 с.

5. Хэррис Ф. Дж. Использование окон при гармоническом анализе методом дискретного преобразования Фурье // ТИИР. 1978. Т.66, №1. С.60-96.

6. Сергиенко А.Б. Цифровая обработка сигналов: Учебное пособие для вузов. - СПб.: Питер, 2002. - 608 с.

7. Иванов Ю.Е. О наивысшей точности спектрального оценивания гармонических сигналов дискретным преобразованием Фурье // Проблемы управления и информатики. - 1998. - №2. - С.102.

Изобретение относится к измерительной технике и предназначено для гармонического анализа периодических колебательных процессов, в частности электрических сигналов. Способ гармонического анализа периодического многочастотного сигнала заключается в итерационном процессе определения необходимой формы весовой функции. В результате многократных оценок частот составляющих периодического многочастотного сигнала форма весовой функции подбирается такой, чтобы на частоте любого из анализируемых составляющих сигнала слагаемые спектра от других составляющих сигнала по амплитуде были равны нулю, причем кратность нуля, определяемая порядком производных модуля спектра, может быть заданной степени. При этом, независимо от фазовых и амплитудных соотношений между составляющими периодического многочастотного сигнала, исключается их взаимное влияние при оценке параметров в спектральной области. Амплитуду и фазу каждого составляющего сигнала оценивают после определения точных значений частот. Технический результат заключается в уменьшении погрешности измерения частот амплитуд и фаз гармонических составляющих периодического многочастотного сигнала. 11 з.п. ф-лы, 5 табл., 4 ил.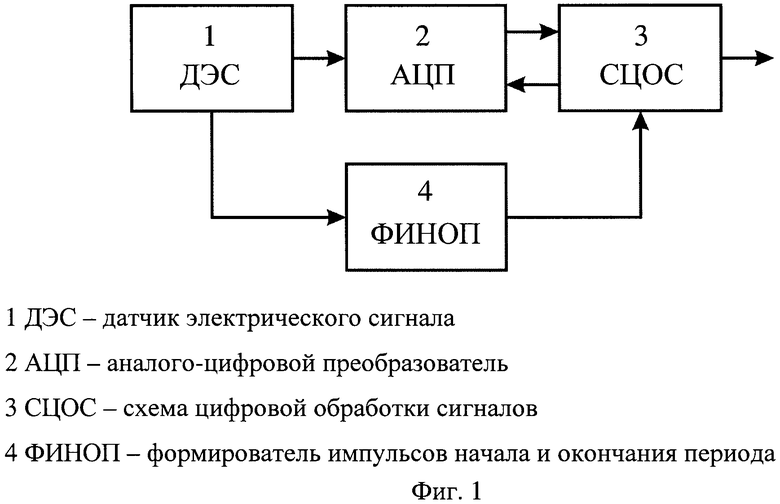

1. Способ гармонического анализа периодического многочастотного сигнала y(t), цикл которого включает получение цифровых отсчетов y_ц(m) сигнала через равные интервалы времени Δt, генерирование весовой функции w_ц(m) в форме цифровых отсчетов, перемножение цифровых отсчетов y_ц(m) сигнала с цифровыми отсчетами весовой функции w_ц(m), вычисление спектра путем нахождения Фурье-образа полученного произведения, оценивание частот пиков спектра, превышающих уровень боковых лепестков наиболее интенсивного слагаемого спектра и оценивание частот, амплитуд и фаз гармонических составляющих сигнала по частотам, амплитудам и фазам Фурье-образа полученного произведения на частотах пиков спектра, отличающийся тем, что многократно выполняют дополнительные циклы гармонического анализа, в каждом из которых по результатам выполненного цикла гармонического анализа изменяют форму весовой функции генерированием новых цифровых отсчетов весовой функции, повторяя циклы гармонического анализа до получения на частоте каждого из анализируемых гармонических составляющих сигнала допустимых значений слагаемых спектра от заданного количества других гармонических составляющих сигнала и допустимых значений заданного количества производных слагаемых спектра от заданного количества других гармонических составляющих сигнала.

2. Способ по п.1, отличающийся тем, что дополнительные циклы гармонического анализа выполняют до получения на частоте каждого из анализируемых гармонических составляющих сигнала нулевых значений слагаемых спектра от заданного количества других гармонических составляющих сигнала и нулевых значений заданного количества производных слагаемых спектра от заданного количества других гармонических составляющих сигнала.

3. Способ по п.1, отличающийся тем, что цифровые отсчеты весовой функции w_ц(m) генерируют по отсчетам дискретной весовой функции, определенной выражением

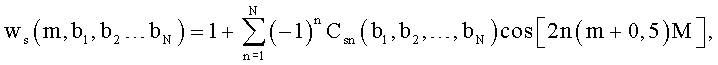
где m - номер текущего отсчета сигнала; b_i=ω_iT/2π - нормированная частота, на которой задается равенство нулю спектр весовой функции или его производная; ω_i - круговая частота; Т - период; N - число варьируемых тригонометрических слагаемых весовой функции; n - номер тригонометрического слагаемого;

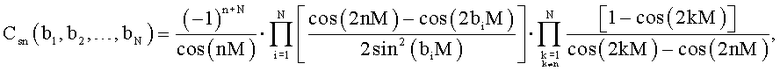
M=π/M₀; M₀ - число отсчетов сигнала.

4. Способ по п.1, отличающийся тем, что цифровые отсчеты весовой функции w_ц(m) генерируют по отсчетам дискретной весовой функции, определенной выражением

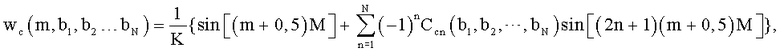
где ;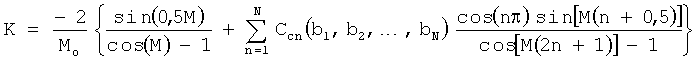

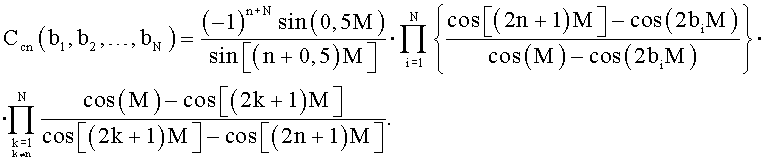
5. Способ по п.1, отличающийся тем, что изменение формы весовой функции задают изменением положений нулей b_i спектра весовой функции

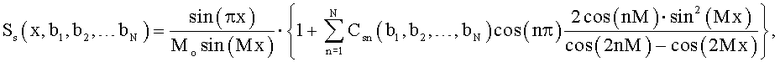
или

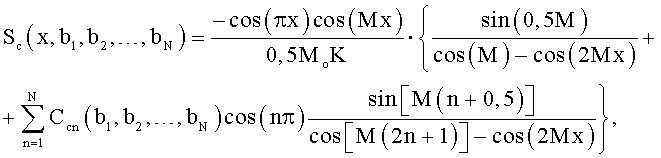
где х=ωТ/2π; ω - текущая угловая частота.

6. Способ по п.1, отличающийся тем, что при выполнении (n) цикла гармонического анализа по оцененным частотам пиков спектра в (n-1) цикле гармонического анализа 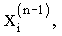…, 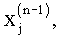которые превышают уровень боковых лепестков наиболее интенсивного слагаемого спектра, вычисляют взаимные разности между частотами пиков спектра 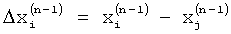и корректируют форму весовой функции путем задания частот нулей спектра или нулей его производных 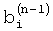равными модулям взаимных разностей между частотами пиков спектра 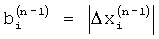и используют весовую функцию со скорректированной формой в (n) цикле гармонического анализа, при этом за частоты гармонических составляющих принимают оценки на последнем цикле гармонического анализа.

7. Способ по п.1, отличающийся тем, что изменение формы весовой функции выполняют до снижения абсолютного значения разности между вновь полученными значениями оценок частот пиков спектра 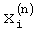, …, и их предыдущими значениями 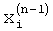, …, , 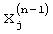ниже контрольного уровня Δх,
.

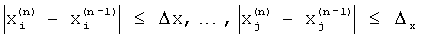8. Способ по п.1, отличающийся тем, что амплитуду и фазу каждого составляющего сигнала оценивают после уточнения частот пиков спектра.

9. Способ по п.1, отличающийся тем, что для оценки частот гармонических составляющих многочастотного сигнала в первом цикле применяют весовую функцию такой формы, при которой для минимальной разности частот между гармоническими составляющими сигнала не происходит перекрытие основных лепестков слагаемых спектра сигнала, а уровень боковых лепестков спектра весовой функции не превышает заданного.

10. Способ по п.9, отличающийся тем, что в первом цикле гармонического анализа применяют весовую функцию такой формы, при которой основной лепесток слагаемого спектра, соответствующий наиболее слабому из анализируемых составляющему сигнала, превышает уровень боковых лепестков слагаемого спектра наиболее интенсивного составляющего сигнала, которые определяют на основе априорных сведений о возможном гармоническом составе сигнала.

11. Способ по п.9, отличающийся тем, что в первом цикле гармонического анализа применяют весовые функции, имеющие минимально возможный уровень боковых лепестков спектра при заданной ширине основного лепестка, заданной скорости уменьшения уровня боковых лепестков и минимальной эквивалентной шумовой полосе.

12. Способ по п.11, отличающийся тем, что в первом цикле гармонического анализа применяют весовую функцию

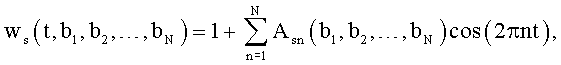
или

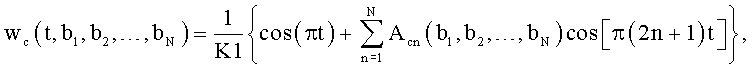
где t - текущее время внутри периода Т;



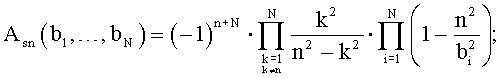
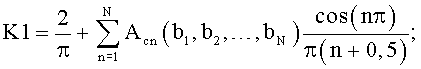
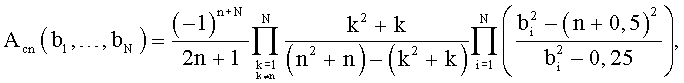
с заданием частот b_i и получаемыми при этом уровнем боковых лепестков (УБЛ) и шириной основного лепестка ΔF₆ по уровню -6 дБ.