Изобретение относится к области обработки информации и измерительной техники и может быть использовано для контроля работоспособности электротехнических и электромеханических устройств. Способ может быть применен для определения математической модели мультисинусоидального сигнала на основе дискретной информации о нем.
Известен способ частотно-временного корреляционного анализа цифровых сигналов (патент РФ №2405163, МПК G01R 23/16, опубл. 27.11.2010), использующий быстрое преобразование Фурье входных сигналов. Определяют комплексно-сопряженное значение прямого преобразования одного из сигналов, попарно умножают полученные комплексные сигналы прямого преобразования Фурье с комплексно-сопряженными значениями прямого преобразования Фурье второго сигнала, определяют частотно-временную корреляционную функцию, на основании графиков которой оценивают частоты гармонических составляющих.
Данный способ имеет следующие недостатки, снижающие быстродействие и точность метода:
- большое количество операций для осуществления быстрого преобразования Фурье, вследствие чего громоздкость расчетов и неточность вычислений;
- для реализации метода необходимо большое количество измерений сигнала (более 8000) и малый шаг дискретизации (менее 10-4);
- визуальный анализ графиков частотно-временной корреляционной функции для определения частот сигнала, не позволяющий произвести автоматизацию расчетов.
- нет возможности оценить амплитуды и начальные фазы гармонических составляющих.
Известен способ определение наличия гармонических составляющих и их частот в дискретных сигналах (патент РФ №2498324, МПК G01R 23/00, опубл. 10.11.2013), использующий быстрое преобразование Фурье входных сигналов. Определяют комплексно-сопряженные значения прямого преобразования Фурье анализируемого дискретного сигнала, попарно умножают полученные комплексные сигналы прямого преобразования Фурье анализируемого дискретного сигнала, тем самым формируют m сигналов и подвергают их обратному преобразованию Фурье, определяют частотно-временную автокорреляционную функцию и строят ее график, по которому судят о наличии гармонических составляющих и их частотах.
Данный способ имеет следующие недостатки, снижающие быстродействие и точность метода:
- большое количество операций для осуществления быстрого преобразования Фурье, формирование большого количества дополнительных сигналов (более 1000), вследствие чего громоздкость расчетов и неточность вычислений;
- для реализации метода необходимо большое количество измерений сигнала (более 16000) и малый шаг дискретизации (менее 10-4);
- визуальный анализ графиков частотно-временной корреляционной функции для определения количества гармоник и частот сигнала, не позволяющий произвести автоматизацию расчетов;
- нет возможности оценить амплитуды и начальные фазы гармонических составляющих.
Известен способ гармонического анализа периодического многочастотного сигнала (патент РФ №2435168, МПК G01R 23/16, опубл. 27.11.2011), использующий итерационный процесс определения необходимой формы весовой функции. В результате многократных оценок частот периодического сигнала форма весовой функции подбирается такой, чтобы на частоте любого из анализируемых составляющих сигнала слагаемые спектра от других составляющих сигнала по амплитуде были равны нулю, причем кратность нуля, определяемая порядком производных модуля спектра, может быть заданной степени. Амплитуду и фазу каждого составляющего сигнала оценивают после определения точных значений частот.
Данный способ имеет следующие недостатки, снижающие быстродействие и точность метода:
- итерационная процедура подбора весовой функции и проведение дополнительных циклов гармонического анализа требуют значительного числа операций, поэтому обладают недостаточным быстродействием и наличием погрешности расчетов;
- громоздкость и неточность нахождения Фурье-образа спектра;
- визуальный анализ лепестков спектра значительно затрудняет процедуру оценки частот сигнала и не позволяет автоматизировать расчеты;
- для реализации метода необходимо большое количество измерений сигнала (более 100 периодов колебаний сигнала).
Наиболее близким к предлагаемому изобретению является способ выявления скрытых периодичностей многочастотного сигнала (патент РФ 2399060, МПК G01R 23/16, опубл. 10.09.2010), использующий измерения сигнала в равноотстоящие промежутки времени и непрерывные цепные С-дроби для определения структуры и неизвестных параметров математической модели сигнала. В идентификаторе непрерывной цепной С-дроби последовательно проводят обработку значения сигнала х(k) по формуле:

до выполнения правила останова, где α-1(n)=δ(n) - дельта функция Дирака, α0(n)=х(n) - измерения сигнала, m=1,2,3, … n=0,1,2, …, с последующим восстановлением прогнозирующей модели сигнала в форме скрытой периодичности.
Этот способ имеет следующие недостатки:
- для многочастотных сигналов, содержащих начальные фазы в периодических составляющих, приводит к получению ошибочной модели сигнала;
- не предусмотрена процедура проверки наличия смещения в сигнале, что может также привести к получению ошибочной модели сигнала.
Предлагаемым изобретением решается задача идентификации мультисинусоидального цифрового сигнала, позволяющая автоматически определить наличие смещения в сигнале с помощью идентификатора непрерывной цепной С-дроби, оценить начальные фазы периодических составляющих сигнала, исключая при этом визуальный анализ реализации сигнала, и, тем самым, расширяя область применения метода идентификации для различных типов мультисинусоидальных сигналов, значительным образом повышая степень автоматизации, точность, достоверность и быстродействие процесса идентификации, что позволяет использовать данный метод как способ текущей идентификации в реальном масштабе времени, определять изменение структуры модели и, тем самым, повышать точность, надежность и качество результатов моделирования.
Предлагаемый способ идентификации мультисинусоидальных цифровых сигналов обладает рядом преимуществ, которые выражаются в том, что обеспечивается быстродействие, универсальность реализации способа, простота и высокая точность вычислений.
Изобретение иллюстрируется фиг. 1-4.
Структурная схема системы, изображенная на фиг. 1 и реализующая предлагаемый способ, содержит датчик анализируемого сигнала (ДАС), к которому последовательно подсоединены блок 1 - идентификатор непрерывной цепной С-дроби, который включает в себя 2 подблока: подблок оценивателя наличия смещения 1.1, аппроксиматор модели сигнала в форме дискретной передаточной функции (ДПФ) объекта-идентификатора 1.2; блок 2 - восстановитель модели сигнала, который включает в себя 3 подблока: подблок оценивателя круговых частот 2.1, подблок оценивателя смещения и амплитуд 2.2, подблок оценивателя начальных фазовых сдвигов 2.3; блок 3 - восстановитель модельных значений сигнала.
С выхода ДАС анализируемый сигнал x(kΔt) поступает на вход блока 1 - идентификатора непрерывной цепной С-дроби. В блоке 1 рассчитывается матрица-идентификатор до выполнения правила останова (появления нулевой строки), по номеру нулевой строки в блоке 1.1 определяется наличие смещения в сигнале, в блоке 1.2 строится непрерывная цепная С-дробь и определяется модель сигнала в форме дискретной передаточной функции (ДПФ) объекта-идентификатора. Далее в блоке 2 - восстановителя модели сигнала определяют параметры сигнала (подблок 2.1 - круговые частоты; подблок 2.2 - смещение при его наличии и амплитуды; подблок 2.3 - начальные фазы) и его прогнозирующую модель. Затем прогнозирующая модель поступает на вход блока 3 - восстановителя модельных значений сигнала, в котором определяется модельный сигнал хм(kΔt).
Предлагаемый способ осуществляется следующим образом. С ДАС результаты измерений сигнала x(kΔt) (k=0,1,2,..) в равноотстоящие промежутки времени с шагом дискретизации Δt поступают на вход блока 1, вносятся во 2-ую строку матрицы-идентификатора:

Последующие строки матрицы-идентификатора определяются с помощью формулы

где 1=3,4,..; k=1,2,.. Заполнение матрицы происходит до появления в ней нулевой строки, что является критерием останова вычислений. По номеру нулевой строки определяется количество гармоник в сигнале и наличие (или отсутствие) постоянного смещения в нем. Если (m-4) (где m - номер нулевой строки) кратно четырем, то идентифицируемый сигнал имеет смещение и представим в виде модели
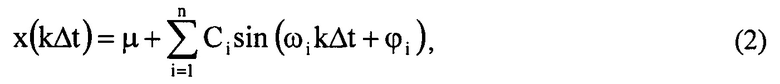
где μ - постоянное смещение, n - число гармоник, ωi - круговая частота i-ой гармоники, Ci - амплитуда i-ой гармоники, ϕi - начальная фаза i-ой гармоники, k=0,1,2,.. Если (m-2) кратно четырем, то сигнал не имеет постоянного смещения (μ=0). Иначе сигнал не является суммой n гармоник, не может быть представлен в виде (2) и не является мультисинусоидальным.
Первый столбец матрицы-идентификатора позволяет построить непрерывную цепную С-дробь в виде:
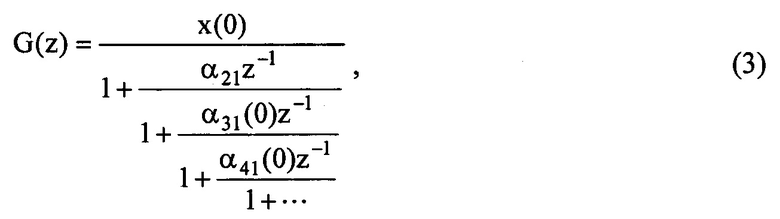
сворачивая которую, определяют модель формирующего объекта-идентификатора в форме ДПФ.
Полученная ДПФ (3) поступает на вход блока 2, в котором определяются постоянное смещение и параметры гармоник - круговые частоты, амплитуды, начальные фазы. Для нахождения круговых частот определяются комплекснозначные полюса ДПФ Zi

где zi=ui±jvi - полюса ДПФ (3). Кроме того, у ДПФ (3) может появляться дополнительный полюс z=1, который характеризует наличие смещения μ в (2).
Для нахождения амплитуд Ci (2) записывается в следующем виде:
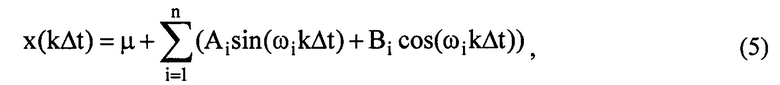
где Ai=Cicos ϕi, Bi=Cisin ϕi. Решив систему, состоящую из 2n+1 линейных уравнений

определим значения постоянного смещения μ, коэффициентов Ai и Bi, на основании которых далее определяются амплитуды Q и фазы ϕi по формулам


В случае отсутствия смещения μ в сигнале (2) составляется система из 2n линейных уравнений:
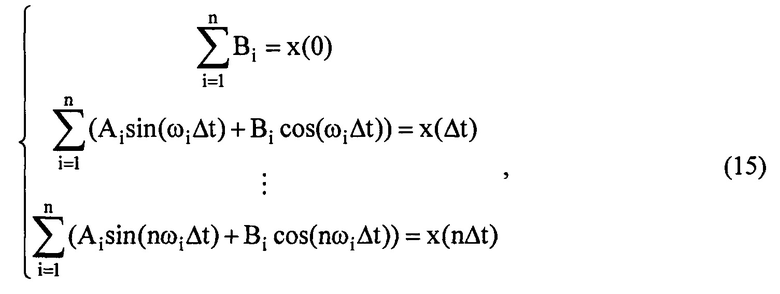
из которой определяются значения коэффициентов Ai и Bi и далее находятся амплитуды Q и фазы ϕi по формулам (10) и (11).
В виде (2) идентифицированная модель мультисинусоидального сигнала поступает на вход блока 3, который восстанавливает значения модельного сигнала.
Таким образом, предлагаемый способ идентификации мультисинусоидальных цифровых сигналов, отличается от известного тем, что при обработке значений сигнала в идентификаторе непрерывной С-дроби на основе правила останова судят о наличии смещения сигнала, а при его наличии (выявлении) выполняют последующее восстановление (последующую оценку) его значения и далее с учетом полученных результатов судят (определяют) о начальных фазовых сдвигах в гармониках сигнала. Способ позволяет оценивать структуру и параметры для большего класса сигналов (периодических и почти периодических, при наличии постоянного смещения и без него, с начальным фазовым смещением) на основе минимального количества наблюдений.
В конечном итоге, предлагаемый способ позволяет достоверно прогнозировать значения анализируемых физических процессов различных типов, принимать адекватные решения по их контролю, управлению и диагностике.
Примеры сигналов: электромагнитные волны в радиосвязи; изменение электрического напряжения в электронике; звуковая волна в акустике; механические колебания земной коры в сейсмологии; изменение давления в гидравлической системе; последовательность дискретных отсчетов в ЭВМ.
Пример 1.
Мультисинусоидальный сигнал в системе вибрационного контроля имеет вид (график сигнала приведен на фиг. 2)

С выхода ДАС поступают измерения анализируемого сигнала (шаг дискретизации Δt=0.5), в блоке 1 заполняется матрица-идентификатор:


Ее 10-ая строка обращается в нулевую. В подблоке 1.1 определяется отсутствие смещения в сигнале. В подблоке 1.2 находят ДПФ объекта-идентификатора
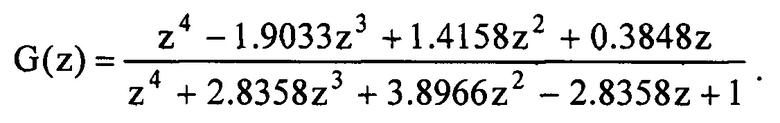
Число гармоник мультисинусоидального сигнала (16) равно n=(10-2)/4=2. Значения параметров ДПФ обрабатывают в блоке 2 и в соответствующих подблоках определяют параметры сигнала: в подблоке 2.1 - круговые частоты ω1=2.0000, ω2=1.000, в подблоке 2.2 - амплитуды C1=20.0000, С2=10.0000. После этого в блоке 2 восстанавливают прогнозирующую модель сигнала:
хМ(kΔt)=10sin(kΔt+2)+20sin(2kΔt+1).
Максимальная абсолютная погрешность оценки параметров составила 0.2⋅10-8, структура мультисинусоидального сигнала (16) восстановлена верно. Результаты расчетов модельных значений сигнала в блоке 3 приведены в Таблице 1, где хм(kΔt) - модельные значения сигнала, рассчитанные с помощью предлагаемого способа, e(kΔt)=x(kΔt) - хм(kΔt) - погрешности модельных значений. Сравнение экспериментальных и модельных значений сигнала в системе вибрационного контроля, позволяет сделать заключение о точном (с точностью до вычислительных погрешностей) модельном его восстановлении.

Пример 2.
Возмущающее воздействие, действующее на беспилотный летательный аппарат, описывается мультисинусоидальным сигналом (фиг. 3)
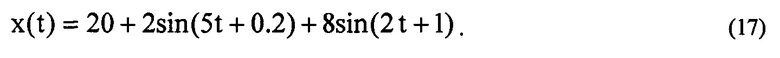
С ДАС замеры сигнала производились с шагом дискретизации Δt=0.25 на вход блока 1 - идентификатора непрерывной цепной С-дроби. В блоке 1 измерения преобразовываются в непрерывную дробь путем расчета матрицы-идентификатора:
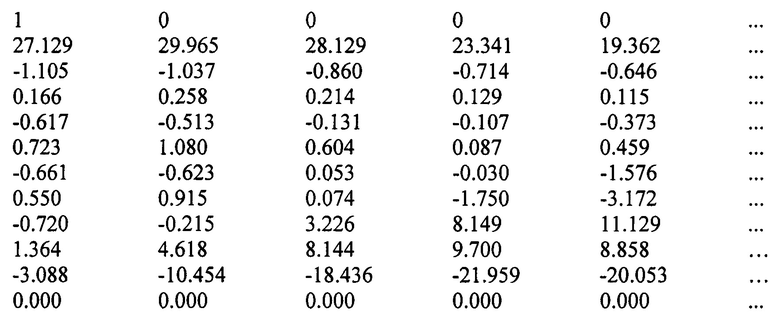
12-ая строка обращается в нулевую, что определяет в подблоке 1.1 наличие смещения в сигнале. В подблоке 1.2 находят ДПФ объекта-идентификатора

Число гармоник в сигнале (16) равно n=(12-4)/4=2. Полученные результаты подаются на вход блока 2 - восстановителя модели сигнала, который включает в себя 3 подблока: 2.1 - подблок оценивателя круговых частот, 2.2 - подблок оценивателя смещения и амплитуд, 2.3 - подблок оценивателя начальных фазовых сдвигов, блок 3 - восстановитель модельных значений сигнала.
На выходе подблока 2.1 оценивателя круговых частот имеем следующие значения: ω1=5, ω2=2. В подблоке 2.2 оцениваются смещение и амплитуды: μ=20, С1=2, С2=8. На выходе подблока 2.3 имеем оценки начальных фаз: ϕ1=0.2, ϕ2=1,. Максимальная абсолютная погрешность оценки параметров составила 0.8⋅10-5.
На выходе блока 2 снимают прогнозирующую модель сигнала
хм(kΔt)=20+2sin(5kΔt+0.2)+8sin(2kΔt+1)
и передают ее на вход блока 3 - восстановителя модельных значений сигнала, на выходе которого снимают модельный сигнал хм(k). Результаты вычислений приведены в Таблице 2, где хм(kΔt) - модельные значения сигнала, рассчитанные с помощью предлагаемого способа, e(kΔt)=x(kΔt)-хм(kΔt) - погрешности модельных значений.
Таким образом, по предлагаемому способу точно восстановлена прогнозирующая модель сигнала, что в конечном итоге позволяет получить наилучший прогноз значений сигнала возмущения на беспилотный летательный аппарат.

Пример 3.
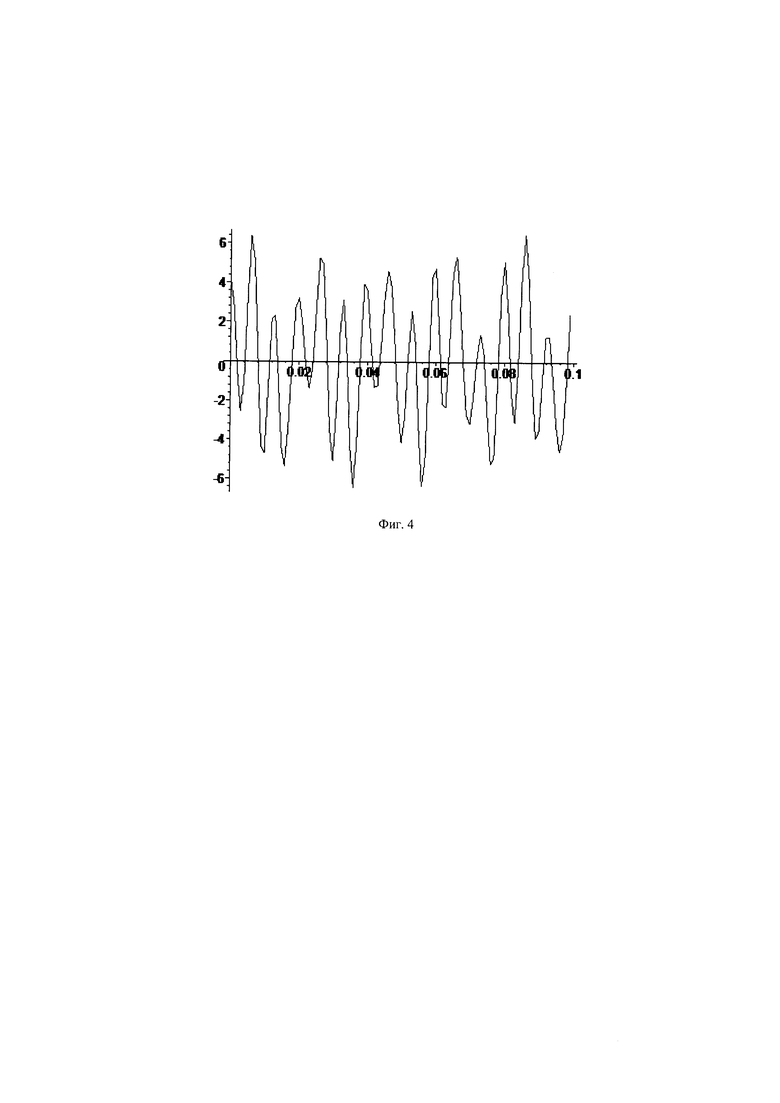
Измерения многочастотного сигнала напряжения на выходе электрического генератора с шагом Δt=0.001 (график сигнала приведен на фиг. 4)
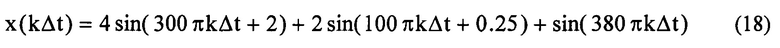
поступают с ДАС на вход блока 1, в котором рассчитывается матрица-идентификатор. 14-ая строка в матрице нулевая, что определяет в подблоке 1.1 отсутствие смещения в сигнале. В подблоке 1.2 находят ДПФ объекта-идентификатора

Число гармоник в сигнале (17) равно n=(14-2)/4=3. Полученные результаты подаются на вход блока 2 - восстановителя модели сигнала. На выходе подблока 2.1 оценивателя круговых частот имеем следующие значения: ω1=942.4783, ω2=314.1588, ω3=1193.8060. В подблоке 2.2 оцениваются амплитуды: C1=4, С2=2, С3=1. На выходе подблока 2.3 имеем оценки начальных фаз: ϕ1=2, ϕ2=0.25, ϕ3=0. Максимальная абсолютная погрешность оценки параметров составила 8⋅10-4.
На выходе блока 2 прогнозирующая модель мультисинусоидального сигнала имеет вид:
хм(kΔt)=4sin(942.4783kΔt+2)+2sin(314.1588kΔt+0.25)+sin(1193.8060kΔt).
Результаты вычислений модельного сигнала напряжения на выходе блока 3 приведены в Таблице 3, где хм(kΔt) - модельные значения сигнала, рассчитанные с помощью предлагаемого способа, e(kΔt)=x(kΔt)-хм(kΔt) - погрешности модельных значений. Сравнение экспериментальных и модельных значений сигнала напряжения, позволяет сделать заключение о точном (с точностью до вычислительных погрешностей) модельном его восстановлении.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ идентификации мультисинусоидальных цифровых сигналов | 2022 |
|
RU2787309C1 |
| СПОСОБ АНАЛИЗА МНОГОЧАСТОТНЫХ СИГНАЛОВ, СОДЕРЖАЩИХ СКРЫТЫЕ ПЕРИОДИЧНОСТИ | 2009 |
|
RU2399060C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕЙНОГО ОБЪЕКТА | 2001 |
|
RU2189622C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕЙНОГО ОБЪЕКТА | 1999 |
|
RU2146063C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕЙНОГО ОБЪЕКТА | 2002 |
|
RU2233480C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕЙНОГО ОБЪЕКТА | 2001 |
|
RU2189621C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕАРИЗОВАННОГО ДИНАМИЧЕСКОГО ОБЪЕКТА | 2003 |
|
RU2256950C2 |
| РАДИОМОДЕМ | 2010 |
|
RU2460215C1 |
| УСТРОЙСТВО И СПОСОБ ОПРЕДЕЛЕНИЯ МНОЖЕСТВА ЛОКАЛЬНЫХ ЧАСТОТНЫХ ЦЕНТРОВ ТЯЖЕСТИ В СПЕКТРЕ АУДИОСИГНАЛА | 2010 |
|
RU2490729C2 |
| СПОСОБ ВОССТАНОВЛЕНИЯ ИСХОДНЫХ СИГНАЛОВ | 2003 |
|
RU2259591C2 |


Изобретение относится к области обработки информации и измерительной техники и может быть использовано для контроля работоспособности электротехнических и электромеханических устройств. Способ может быть применен для определения математической модели мультисинусоидального сигнала на основе дискретной информации о нем. Способ идентификации мультисинусоидальных цифровых сигналов основан на использовании непрерывных цепных дробей путем измерения сигнала в равноотстоящие промежутки времени, подачи их на идентификатор непрерывной С-дроби с последующим восстановлением числа гармоник, круговых частот, амплитуд, прогнозирующей модели и модельных значений сигнала. При обработке значений сигнала в идентификаторе непрерывной С-дроби на основе правила останова судят о наличии смещения сигнала. При выявлении такого смещения выполняют последующее восстановление значения сигнала и с учетом полученных результатов судят о начальных фазовых сдвигах в гармониках сигнала. 4 ил., 3 табл.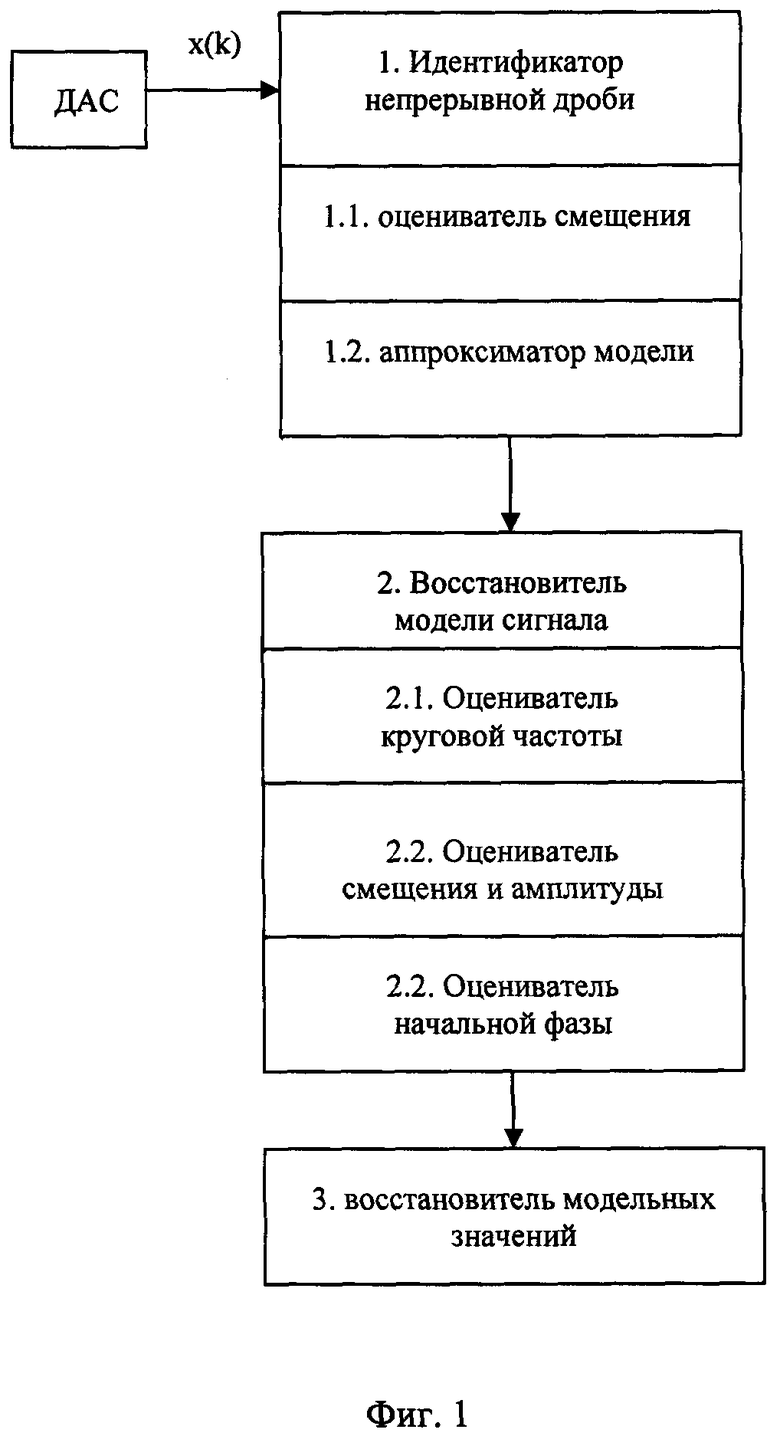
Способ идентификации мультисинусоидальных цифровых сигналов, включающий использование непрерывных цепных дробей путем измерения сигнала в равноотстоящие промежутки времени, подачи их на идентификатор непрерывной С-дроби с последующим восстановлением числа гармоник, круговых частот, амплитуд, прогнозирующей модели и модельных значений сигнала, отличающийся тем, что при обработке значений сигнала в идентификаторе непрерывной С-дроби на основе правила останова судят о наличии смещения сигнала, а при его выявлении выполняют последующее восстановление его значения и далее с учетом полученных результатов судят о начальных фазовых сдвигах в гармониках сигнала.
| СПОСОБ АНАЛИЗА МНОГОЧАСТОТНЫХ СИГНАЛОВ, СОДЕРЖАЩИХ СКРЫТЫЕ ПЕРИОДИЧНОСТИ | 2009 |
|
RU2399060C1 |
| СПОСОБ ЧАСТОТНО-ВРЕМЕННОГО КОРРЕЛЯЦИОННОГО АНАЛИЗА ЦИФРОВЫХ СИГНАЛОВ | 2009 |
|
RU2405163C1 |
| СПОСОБ ГАРМОНИЧЕСКОГО АНАЛИЗА ПЕРИОДИЧЕСКОГО МНОГОЧАСТОТНОГО СИГНАЛА | 2010 |
|
RU2435168C1 |
| WO 2003046586 A1, 05.06.2003 | |||
| US 7107306 B2, 12.09.2006 | |||
| US 10080026 B2, 18.09.2018. | |||
Авторы
Даты
2019-10-22—Публикация
2018-11-08—Подача