Изобретение относится к технической кибернетике и предназначено для идентификации линейных динамических объектов со случайным входным воздействием. Способ может быть применен для определения математической модели объекта на основе дискретной информации о сигналах на его входе и выходе и реализован с использованием ЭВМ в автоматическом режиме, в реальном масштабе времени.
Известен способ идентификации линейного динамического объекта (Дейч А.М. Методы идентификации динамических объектов. - М.: Энергия, 1979, с. 158) со стационарным случайным входным воздействием, в котором задают пробную модель дискретной передаточной функции (ДПФ) в виде:
где n ≥ m-1, а ai, bi - параметры математической модели объекта.
Идентификация заключается в том, что по результатам измерений вход-выходных случайных сигналов x(t) и y(t) объекта в дискретные моменты времени kΔt где k = 0, 1, 2, ...N, а Δt - шаг дискретизации, аппроксимируют взаимную корреляционную функцию входного и выходного сигналов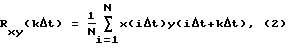
корреляционную функцию входного сигнала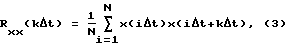
а затем неизвестные параметры ai, bi из выражения (1) оценивают путем составления системы линейных алгебраических уравнений, записав выражение
для n = 0, 1, 2, ...n+m. Далее решают эту систему уравнений относительно параметров ai, bi.
Данный способ, в связи с необходимостью правильного задания порядка модели исследуемого объекта, а при каждой замене порядка выполнения значительного числа операций, обладает недостаточной точностью и быстродействием.
Наиболее близким к предлагаемому способу является способ идентификации линейного объекта при детерминированном входном воздействии (патент РФ N 2097818, МПК G 05 B 17/02, опубл. 27.11.97, БИ N 33), сущность которого состоит в следующем: по результатам измерений входных и выходных сигналов объекта в равноотстоящие промежутки времени строят ДПФ объекта как отношение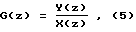
где Y(z) - z-преобразование выходного сигнала, X(z) - z-преобразование входного сигнала.
Для получения ДПФ (5) идентифицируемого объекта используется аппарат непрерывных дробей, порождающих множество пробных моделей объекта, что позволяет с помощью идентификатора непрерывной дроби автоматически определить структуру и неизвестные параметры модели по заранее заданной точности идентификации. ДПФ G(z) аппроксимируют последовательностью конечных непрерывных дробей, выделяют 1-ое дробно-рациональное выражение и переходят от полученного выражения G(z) к разностному уравнению вида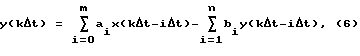
где x(kΔt) - величина сигнала на входе объекта в k-м такте; y(kΔt) -величина сигнала на выходе объекта в k-м также; ai, bi - параметры математической модели объекта; Δt - шаг дискретизации.
Уравнение вида (6) позволяет восстановить значение модельного сигнала на выходе пробной модели. Если максимальная разница между экспериментальным значением сигнала и модельным значением меньше наперед заданной точности, то уравнение (6) является искомой математической моделью идентифицируемого объекта порядка, равного порядку соответствующей конечной непрерывной дроби. В противном случае, получают новую аппроксимацию G(z), взяв конечную непрерывную дробь на порядок выше, находят соответствующее ей разностное уравнение вида (6) и проверяют выполнение заданной точности идентификации.
Этот способ имеет следующие недостатки:
применяется только для детерминированных вход-выходных сигналов x(t) и y(t);
необходимость последовательного перебора подходящих непрерывных дробей и итерационная процедура определения математической модели идентифицируемого объекта снижает быстродействие процесса идентификации.
Предлагаемым изобретением ставится задача структурно-параметрической идентификации линейного объекта со случайным сигналом на входе, позволяющая автоматически определить структуру и неизвестные параметры математической модели объекта, исключая итерационную процедуру корректировки порядка модели, значительным образом упрощая и ускоряя процесс идентификации, что дает возможность использовать данный метод как метод текущей идентификации в реальном масштабе времени, определять изменение структуры модели и, тем самым, повышать точность и достоверность результатов моделирования.
Поставленная задача решается новым способом идентификации линейного объекта путем определения значений входного и выходного сигналов объекта, подачи их на идентификатор непрерывной дроби с последующим восстановлением прогнозирующей модели объекта и определением модельных значений выходного сигнала объекта, в котором предполагается обработку значений случайного входного и выходного сигналов в идентификаторе непрерывной дроби и восстановление прогнозирующей модели объекта проводить последовательно, что становится возможным за счет того, что в идентификаторе непрерывной дроби значения входного и выходного сигналов преобразуют в детерминированные характеристики корреляции значений входного и вход-выходного сигналов объекта и последующую их обработку выполняют по формуле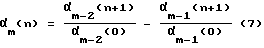
до выполнения правила останова, где α-1(n) = Rxx(n) - детерминированная характеристика корреляции значений входного сигнала объекта, α0(n) = Rxy(n) - детерминированная характеристика корреляции значений вход-выходного сигналов объекта, m = 1,2,3,..., n = 0,1,2,...
Изобретение поясняется на фиг.1-6.
Структурная схема системы, реализующей предлагаемый способ, изображена на фиг. 1.
Случайный входной сигнал x(k) поступает одновременно на вход блока 1 - объекта идентификации и на вход блока 2 - идентификатора непрерывной дроби, на блок 2 также поступает выходной сигнал y(k). Блок 2 преобразовывает значения входного и выходного сигналов объекта в детерминированные характеристики корреляции значений входного и вход-выходного сигналов, производит их обработку с помощью формулы (7) до выполнения правила останова, строит непрерывную дробь по преобразованным значениям сигналов и определяет ДПФ идентифицируемого объекта. Далее в блоке 3 - восстановления модели объекта определяют прогнозирующую модель идентифицируемого объекта. Затем параметры прогнозирующей модели идентифицируемого объекта поступают на вход блока 4 - восстановления модельных значений выходного сигнала объекта, в котором определяют модельный входной сигнал ym(k). Процесс идентификации заканчивается, так как получена модель идентифицируемого объекта.
Предлагаемый способ осуществляется следующим образом: по результатам измерений входных и выходных сигналов в равноотстоящие промежутки времени с шагом дискретизации Δt вычисляют взаимную корреляционную функцию входного и выходного сигналов Rxy(kΔt) по формуле (2) и корреляционную функцию входного сигнала Rxx(kΔt) по формуле (3). Далее строят ДПФ объекта как соотношение z-преобразований взаимной корреляционной функции входного и выходного сигналов и корреляционной функции входного сигнала по формуле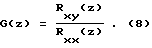
Для получения ДПФ идентифицируемого объекта пользуются представлениями (8) в виде соответствующей правильной C-дроби, применив модифицированный алгоритм B. Висковатова.
На основании (8) расчетным путем определяется следующая матрица: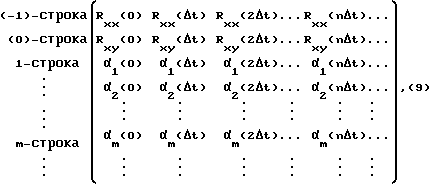
в которой (-1)-строка и (0)-строка содержат значения корреляционной функции входного сигнала Rxx(kΔt) и взаимной корреляционной функции входного и выходного сигналов 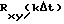 в моменты времени
в моменты времени 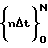 и они являются начальными условиями при построении матрицы, а элементы αm(mΔt) последовательно определяются с помощью соотношений:
и они являются начальными условиями при построении матрицы, а элементы αm(mΔt) последовательно определяются с помощью соотношений:
где α-1(nΔt) = Rxx(nΔt), α0(nΔt) = Rxy(nΔt), m = 1,2,,,..., а n = 0,1,2, ...
Тогда элементы первого столбца матрицы (9) порождают частные числители правильной C-дроби и ДПФ будет иметь вид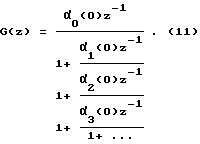
При аппроксимации дробно-рационаьлной функции в матрице (9) наблюдается появление нулевой строки, номер которой позволяет идентифицировать порядок функции. Если в некоторой i-й строке (i = 0,1,2,...) матрицы (9) конечное число ki первых элементов равны нулю, а последующие элементы отличны от нуля, то необходимо осуществить сдвиг влево на ki элементов до появления в нулевом столбце ненулевого элемента и далее продолжить определение других элементов матрицы (9) по правилу (10). Для i-й строки при восстановлении правильной C-дроби (11) элемент α1 (0) умножается на z-k. Существенным для данного правила является то, что 1-й элемент (-1)-строки был отличен от нуля, то есть входное воздействие в начальный момент времени t0 = x(0) ≠ 0.
Получив ДПФ в виде (11), свернув ее в дробно-рациональную функцию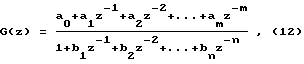
переходят от данного выражения к разностным уравнениям вида (6), позволяющим восстанавливать значения модельного сигнала yм(kΔt) на выходе модели.
Таким образом, предлагаемый способ идентификации объекта отличается от известного тем, что используют последовательную процедуру выполнения операций и математическую формулу вида (7), которые позволяют автоматически определять структуру и параметры объекта идентификации, исключая при этом задание точности идентификации и итерационную процедуру перебора пробных моделей объекта. Предлагаемый способ приводит к существенному упрощению и ускорению процесса идентификации за счет исключения большого объема вычислительных операций, что позволяет в конечном итоге достоверно прогнозировать состояние объекта идентификации, принимать адекватные решения по контролю, управлению и диагностике объекта. Также с помощью предлагаемого способа может производиться идентификация линейного объекта и при подаче на его вход детерминированного сигнала, при этом не требуется преобразование значений входного и выходного сигналов в детерминированные характеристики корреляции значений входного и вход-выходного сигналов объекта.
Пример 1.
Аналоговый объект идентификации - измерительное устройство температуры в виде биметаллической пластины. Известно, что данный объект описывается колебательным звеном с передаточной функцией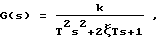
где k - коэффициент усиления, T - постоянная времени, ξ - коэффициент демпфирования. Помеха на входе измерительного устройства может быть принята в виде белого шума с корреляционной функцией Rxx(t) = δ(t) .
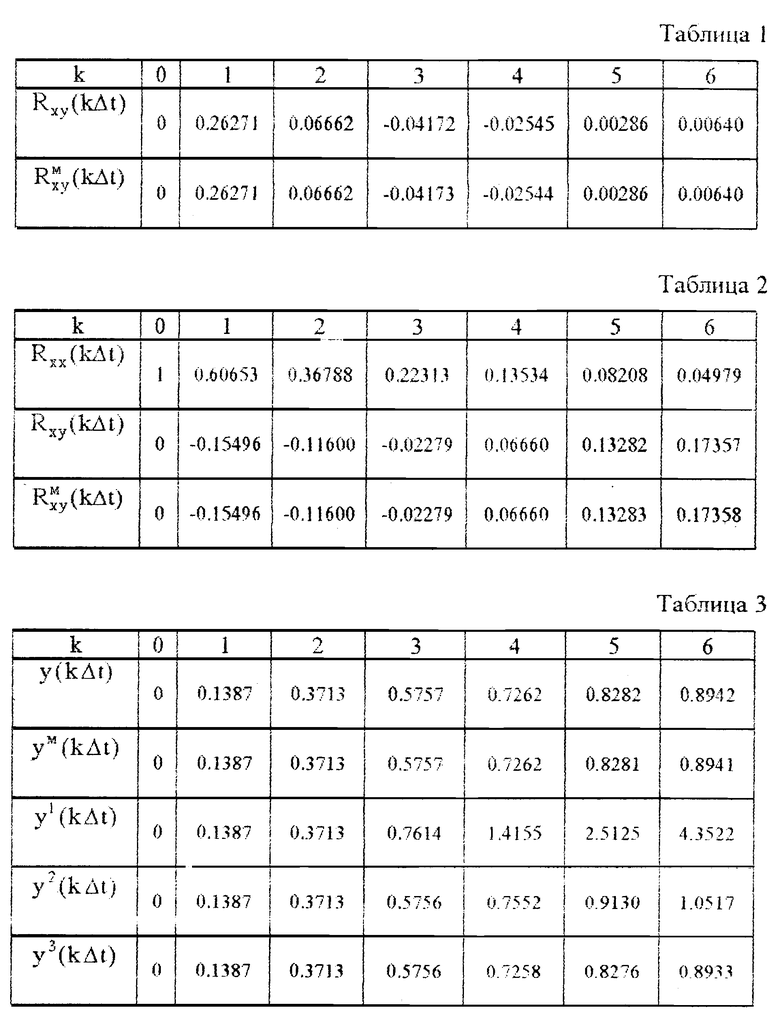
Задают для определенности k = 1, T = 2 с, ξ = 0,5, тогда взаимная корреляционная функция входного и выходного сигналов Rxy(t), изображенная на фиг. 2, будет иметь вид
Rxy(t) = kCe-νtsinλt,
где 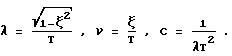
Задают шаг дискретизации Δt = 3 с.
Составляют матрицу вида (9), где (-1)- и (0)-строки содержат значения корреляционной функции входного сигнала Rxx(kΔt) и взаимной корреляционной функции входного и выходного сигналов Rxy(kΔt) , а остальные элементы матрицы вычисляются с помощью соотношения (10). Она будет иметь вид
С учетом того, что в нулевой строке осуществлен сдвиг влево на один элемент, обусловленный начальным значением Rxy(0) = 0, получают конечную правильную C-дробь:
Переходя к дробно-рациональному выражению, определяют ДПФ G(z) объекта соотношением: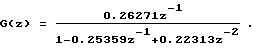
Тогда модельные значения взаимной корреляционной функции входного и выходного сигналов восстанавливаются разностным уравнением вида (4):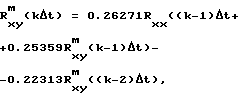
а дискретная математическая модель объекта в форме конечно-разностного уравнения (6) имеет вид: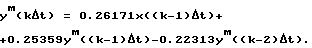
Результаты вычислений приведены в табл. 1, где Rxy(kΔt) - экспериментальные значения взаимной корреляционной функции, R
Таким образом, по предлагаемому способу точно восстановлена прогнозирующая модель измерительного устройства в виде биметаллической пластины, что в конечном итоге позволяет минимизировать среднеквадратическую ошибку прогноза и, тем самым, получить наилучший прогноз значений выходного случайного сигнала.
Пример 2.
Объект идентификации - аппарат каталитической конверсии метана. Известно, что процесс расхода кислорода описывается точной функцией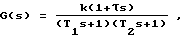
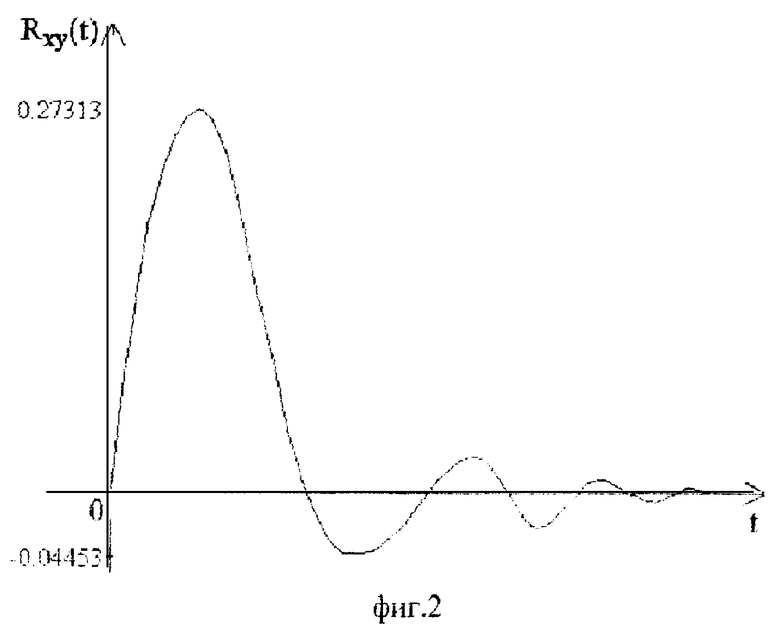
где τ T1, T2 - постоянные времени, k - коэффициент передачи. На вход объекта поступает случайный сигнал с корреляционной функцией Rxx(t) = e-t (фиг. 3). Первоначальная подача кислорода понижает температуру в зоне катализа, так как подаваемый кислород имеет сравнительно низкую температуру, и происходит отбор тепла, поэтому объект на начальном этапе приобретает свойства неминимально-фазовости. Передаточная функция объектов с неминимально-фазовой характеристикой имеет вид: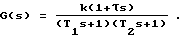
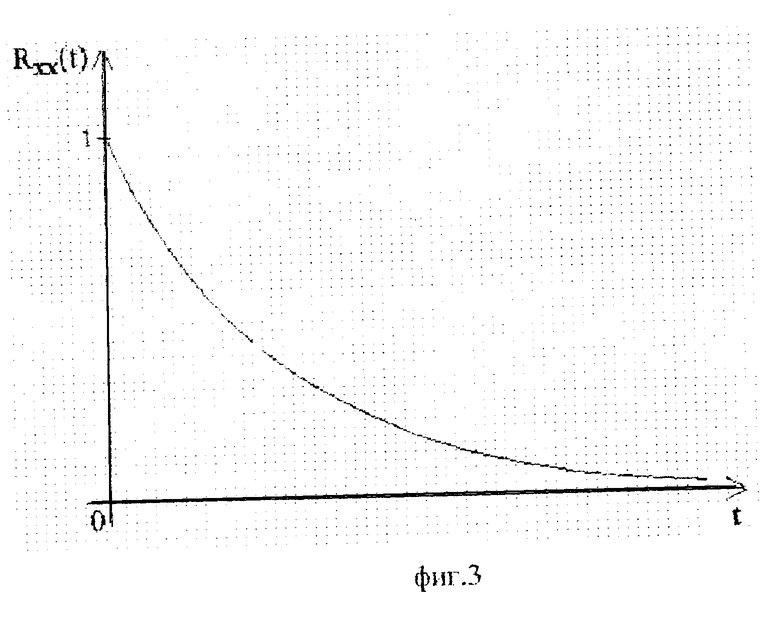
Пусть k = 1, τ = 2 с, T1 = 3 с, T2 = 1 с. Тогда взаимная корреляционная функция входного и выходного сигналов (фиг. 4) будет иметь вид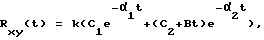
где 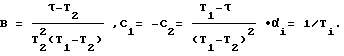
Для шага дискретизации Δt = 0,5 с матрица (9) имеет вид:
С учетом того, что в нулевой строке осуществлен сдвиг влево на один элемент, обусловленный начальным значением Rxy(0) = 0, получают конечную правильную C-дробь:
Тогда ДПФ G(z) идентифицируемого объекта равна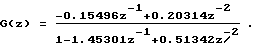
Дискретная математическая модель взаимной корреляционной функции входного и выходного сигналов согласно (4) имеет вид: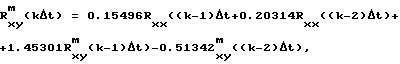
а дискретная математическая модель объекта согласно (6) восстанавливается конечно-разностным уравнением:
Результаты вычислений приведены в табл. 2, где Rxx(kΔt) - экспериментальные значения корреляционной функции входного сигнала, Rxy(kΔt) - экспериментальные значения взаимной корреляционной функции входного и выходного сигнала, R
Пример 3.
Сравнительный анализ предлагаемого способа с прототипом.
Предлагаемый способ идентификации может использоваться для идентификации линейного объекта с детерминированным входным воздействием. В этом случае в идентификаторе непрерывной дроби не требуется получение детерминированных характеристик корреляции значений входного и вход-выходного сигалов объекта, а начальными условиями при построении матрицы (9) являются значения входного x(kΔt) и выходного y(kΔt) сигналов.
Пусть объекта идентификации - парогенератор электростанции, передаточная функция которого описывается апериодическим звеном 2-го порядка: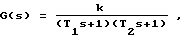
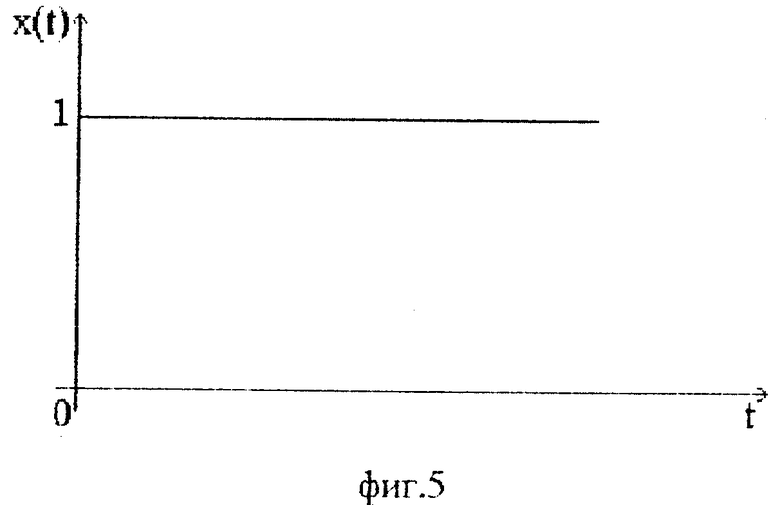
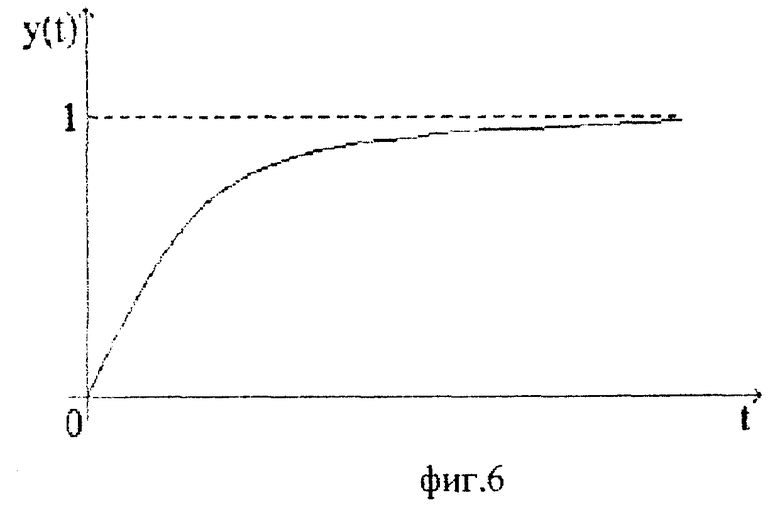
где k - коэффициент передачи, T1, T2 - постоянные времени, причем k = 1, T1 = 7,5 с, T2 = 5 с. На входе объекта имеют сигнал (фиг. 5)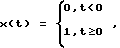
где t - время, а на выходе получают сигнал (фиг. 6)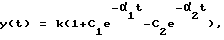
где 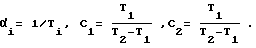
Шаг дискретизации Δt = 4 с.
Задают требуемую точность идентификации ε = 0,001.
Тогда z-преобразования: входного сигнала выходного сигнала
выходного сигнала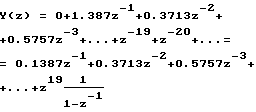
позволяет построить ДПФ объекта: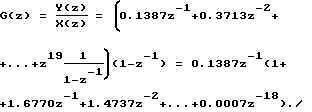
Разлагая ДПФ G(z) в непрерывную дробь, получают
Берут непрерывную дробь 2-го порядка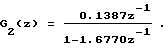
По найденной ДПФ G2(z) записывают разностное уравнение вида (6) 1-й пробной модели:
где y1(kΔt) - восстановленные значения выходной величины парогенератора электростанции в k-й момент времени. Результаты вычислений приведены в табл. 3, где y(kΔt) - экспериментальные значения выходной величины, yм(kΔt) - модельные значения выходной величины, полученные с помощью предлагаемого способа, y1(kΔt) - значения выходной величины 1-й пробной модели, рассчитанные по прототипу, y2(kΔt) - значения выходной величины 2-й пробной модели, рассчитанные по прототипу, y3(kΔt) - значения выходной величины 3-й пробной модели, рассчитанные по прототипу.
Из табл. 3 видно, что максимальная разница между экспериментальными y(kΔt) и полученными с помощью 1-й пробной модели y1(kΔt) значениями больше заданной точности: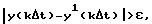
следовательно, 1-ая пробная модель не является искомой математической моделью идентифицируемого объекта.
Берут непрерывную дробь 3-го порядка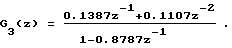
По ДПФ G3(z) записывают разностное уравнение вида (6) 2-й пробной модели: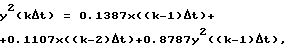
где y2(kΔt) - восстановленные значения выходной величины парогенератора электростанции в k-й момент времени.
Из табл. 3 видно, что максимальная разница между экспериментальными y(kΔt) и полученными с помощью 2-й пробной модели y2(kΔt) значениями больше заданной точности, следовательно, 2-ая пробная модель не является искомой математической моделью идентифицируемого объекта.
Берут непрерывную дробь 4-го порядка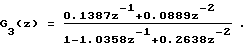
По ДПФ G4(z) записывают разностное уравнение вида (6) 3-й пробной модели:
где y3(kΔt) - восстановленные значения выходной величины парогенератора электростанции в k-й момент времени.
Из табл. 3 видно, что максимальная разница между экспериментальными y(kΔt) и полученными с помощью 3-й пробной модели y3(kΔt) значениями меньше заданной точности: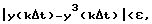
следовательно, 3-я пробная модель является искомой математической моделью идентифицируемого объекта.
Восстановим математическую модель идентифицируемого объекта с помощью предлагаемого способа. Составим матрицу вида (9), в которой (-1)-строка и (0)-строка содержат измерения значений входного x(kΔt) и выходного y(kΔt) сигналов, а остальные элементы матрицы вычисляются с помощью соотношения (10). Она будет иметь вид
С учетом того, что в нулевой строке матрицы осуществлен сдвиг влево на один элемент ввиду равенства нулю начального значения выходного сигнала y(0) = 0, получают конечную правильную C-дробь: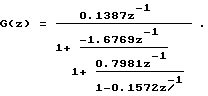
Переходя к дробно-рациональному выражению, определяют ДПФ G(z) объекта: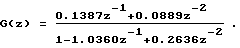
Тогда дискретная математическая модель объекта имеет вид:
Таблица 3 показывает, что предлагаемый способ идентификации позволяет более точно восстановить значения выходной величины парогенератора электростанции по сравнению со способом-прототипом, что на практике дает возможность более достоверного предсказания состояния парогенератора электростанции с последующим улучшением процесса управления, контроля и диагностики данного объекта идентификации.
Этот пример иллюстрирует следующий факт: предлагаемый способ позволяет исключить задание точности идентификации и итерационную процедуру перебора подходящих непрерывных дробей для получения модели объекта идентификации, что, в конечном итоге, повышает точность и быстродействие процесса идентификации за счет исключения большого количества вычислений, а также дает преимущества по простоте реализации предлагаемого способа идентификации.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕЙНОГО ОБЪЕКТА | 2001 |
|
RU2189622C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕЙНОГО ОБЪЕКТА | 1995 |
|
RU2097818C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕЙНОГО ОБЪЕКТА | 2001 |
|
RU2189621C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕЙНОГО ОБЪЕКТА | 2002 |
|
RU2233480C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕАРИЗОВАННОГО ДИНАМИЧЕСКОГО ОБЪЕКТА | 2003 |
|
RU2256950C2 |
| СПОСОБ АНАЛИЗА МНОГОЧАСТОТНЫХ СИГНАЛОВ, СОДЕРЖАЩИХ СКРЫТЫЕ ПЕРИОДИЧНОСТИ | 2009 |
|
RU2399060C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ МУЛЬТИСИНУСОИДАЛЬНЫХ ЦИФРОВЫХ СИГНАЛОВ | 2018 |
|
RU2703933C1 |
| Способ идентификации мультисинусоидальных цифровых сигналов | 2022 |
|
RU2787309C1 |
| СПОСОБ ПАРАМЕТРИЧЕСКОЙ ИДЕНТИФИКАЦИИ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СУДНА | 2010 |
|
RU2444043C1 |
| СПОСОБ НАСТРОЙКИ СИСТЕМЫ УПРАВЛЕНИЯ СУДНОМ ПО КУРСУ | 2024 |
|
RU2828164C1 |
Изобретение относится к технической кибернетике и предназначено для идентификации линейных динамических объектов со случайным входным воздействием. Технический результат заключается в упрощении и ускорении процесса идентификации, что достигается путем исключения процедуры перебора пробных моделей объекта до выполнения заданной точности. На объект идентификации подают случайный сигнал, определяют значения входного и выходного сигналов объекта, подают их на идентификатор непрерывной дроби, в котором эти значения преобразуют в детерминированные характеристики корреляции значений входного и вход-выходного сигналов объекта с последующей их обработкой, после чего непосредственно получают прогнозирующую модель объекта и определяют модельные значения выходного сигнала объекта идентификации. 6 ил., 3 табл.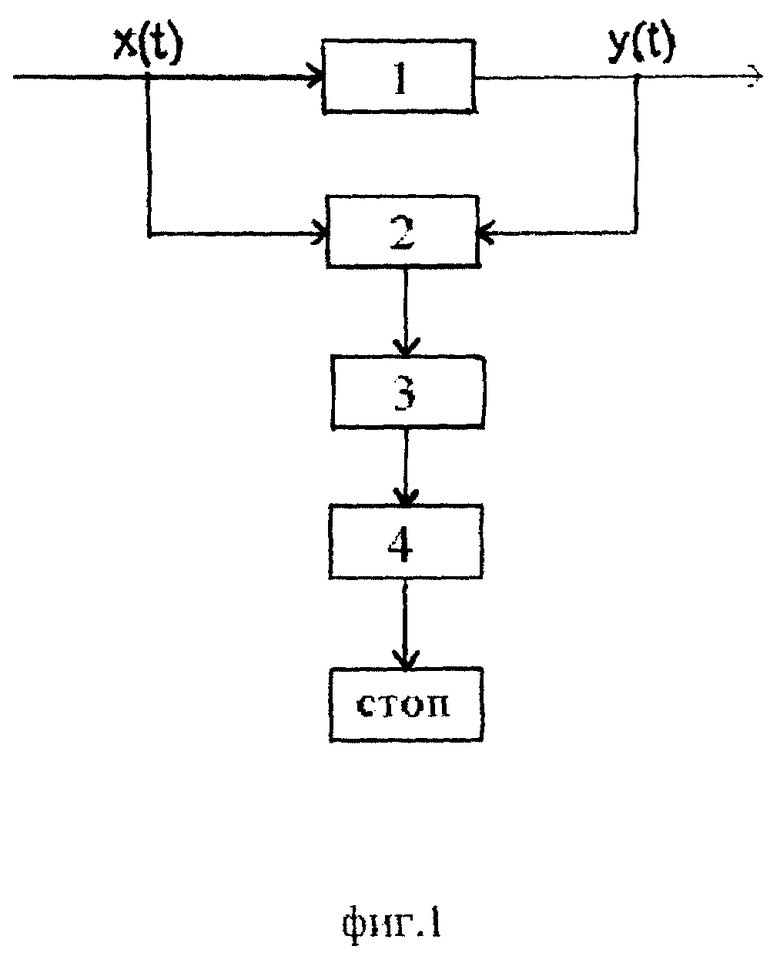
Способ идентификации линейного объекта путем определения значений входного и выходного сигналов объекта, подачи их на идентификатор непрерывной дроби с последующим восстановлением прогнозирующей модели объекта и определением модельных значений выходного сигнала объекта, отличающийся тем, что обработку значений случайного входного и выходного сигналов в идентификаторе непрерывной дроби и восстановление прогнозирующей модели объекта ведут последовательно, при этом значения входного и выходного сигналов в идентификаторе непрерывной дроби преобразуют в детерминированные характеристики корреляции значений входного и вход-выходного сигналов объекта с последующей их обработкой по формуле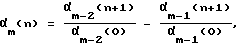
до выполнения правила останова,
где α-1(n) = Rxx(n) - детерминированная характеристика корреляции значений входного сигнала объекта;
αo(n) = Rxy(n) - детерминированная характеристика корреляции значений вход-выходного сигналов объекта;
m = 1, 2, 3, ...;
n = 0, 1, 2, ... .
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕЙНОГО ОБЪЕКТА | 1995 |
|
RU2097818C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕЙНОГО ОБЪЕКТА | 0 |
|
SU361456A1 |
| Дейч А.М | |||
| Методы идентификации динамических объектов | |||
| - М.: Энергия, 1979, с.158 | |||
| СПОСОБ МОДЕЛИРОВАНИЯ ПЕРЕХОДНОГО ПРОЦЕССА В ЯДЕРНОМ РЕАКТОРЕ | 1991 |
|
RU2044347C1 |
| RU 2064194 C1, 20.07.96 | |||
| УСТРОЙСТВО ДЛЯ МОДЕЛИРОВАНИЯ СИСТЕМЫ ДВИГАТЕЛЬ - НАСОС - ТРУБОПРОВОД | 1992 |
|
RU2065196C1 |
Авторы
Даты
2000-02-27—Публикация
1999-04-05—Подача