Предлагаемое изобретение относится к изготовлению композиционно-волокнистых материалов и может найти широкое применение в ракетно-космической технике, авиастроении, химическом машиностроении, а также в других отраслях народного хозяйства.
Известен способ определения коэффициентов внутреннего трения для тканей гладкого переплетения, предложенный в патенте России №2228524, кл. В29D 23/12. Сущность этого изобретения состоит в том, что на первом этапе из неотвержденного композиционно-волокнистого материала (препрега) вырезают полоску ткани, прикладывают к ней внешнюю растягивающую нагрузку и определяют удлинение первого семейства нитей (основы) исходя из зависимости
 ,
,
где h0, h0 и l0 - толщина, ширина и длина полосы ткани;
(EF)1 - жесткость на растяжение препрега;
γ1 - относительное неупругое удлинение препрега при растяжении;
Т - усилие при растяжении полосы ткани.
Затем препрег укладывают между двумя жесткими поверхностями, создают давление внутри препрега, разрезают одну нить, прикладывают к ней растягивающее усилие и определяют связь между длиной нити и усилием вытягивания ее из препрега исходя из зависимости
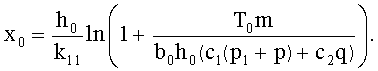
Здесь
 ;
;  ;
;
µ1, k12, k11 - статические коэффициенты трения;
p - давление внутри препрега;
р1 - условное давление внутри препрега, которое обусловлено необходимостью преодоления сил трения сопротивления, возникающих из-за переплетения семейства нитей;
q - напряжение растяжения поперечных нитей препрега;
m - количество нитей в полосе ткани препрега шириной b0.
Затем препрег укладывают между двумя жесткими поверхностями, создают давление внутри препрега, на всю глубину вставляют две гребенки и при их параллельном движении определяют перемещение первого семейства нитей (основы) препрега исходя из зависимости
 ,
,
где
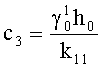 ;
;  ;
;
 ;
;
 .
.
γ-1 - относительное неупругое сжатие препрега;
(EF)-1 - жесткость на сжатие препрега;
σ0 - напряжение при растяжении препрега в районе приложения внешней нагрузки.
На втором этапе аналогичным способом определяют характеристики второго семейства нитей (утка).
Используется это изобретение для определения характеристик препрегов, имеющих наполнители в виде взаимно перпендикулярных связанных между собой двух семейств нитей - ткани гладкого переплетения. Однако он неприемлем для мультиаксиальных тканей, так как для таких тканей в расчетах необходимо использовать другие функциональные зависимости.
С целью устранения перечисленных выше недостатков методики определения коэффициентов внутреннего трения предложен вариант, содержащийся в предлагаемом изобретении. Сущность изобретения состоит в том, что из неотвержденного композиционно-волокнистого материала (препрега) вырезают полоску из мультиаксиальной ткани, укладывают ее между двумя жесткими поверхностями (нагруженными давлением Р), разрезают одну нить, прикладывают к ее концу растягивающее усилие и определяют связь между длиной нити и усилием вытягивания ее из препрега исходя из зависимости

где i - номер эксперимента;
j=0 при внешней нагрузке Р=0 и j=1 при Р≠0;
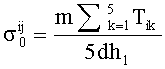 ;
; 
m - количество нитей, расположенных в ткани шириной d;
Р - сила, сдавливающая полосу ткани размером d×l;
Tik - сила, необходимая для выдергивания нити из полосы ткани;
k - номер повтора испытания в i-ом эксперименте;
h1 - толщина семейства одинаково направленных нитей;
 - длина нити;
- длина нити;
 , µ1,
, µ1,  - постоянные, подлежащие определению из эксперимента.
- постоянные, подлежащие определению из эксперимента.
Здесь необходимо отметить, что технологический процесс изготовления изделий из композиционно-волокнистых материалов состоит из следующих стадий: формование основных и свободных поверхностей заданной геометрии, т.е. получение полуфабрикатов в виде слоистой структуры семейств нитей, пропитанных связующим; отверждение связующего; механическая обработка поверхностей изделия до требуемой точности. Особый интерес представляет стадия получения полуфабриката. Здесь можно производить некоторые дополнительные операции, позволяющие заменить механическую обработку после отверждения связующего. В этой связи альтернативой просверленным отверстиям является формование их методом прокалывания (патент Японии №57-137114, кл. В29D 3/02, 1981 и патент Великобритании №149292, кл. В29D 22/14, 1976) в еще неотвержденном полимерно-волокнистом материале конструкции. В процессе формования таких отверстий происходит раздвигание нитей и перемещение их на конечные расстояния.
Другой, не менее важной областью использования свойств неупругих перемещений является формование изделий на гибких оправках, например торовых оболочек. Для этого на круглую оправку наматывается цилиндрическая оболочка. Дальнейшая трансформация оболочки происходит путем ее изгиба совместно с оправкой. Гибкие оправки могут быть разной конфигурации. Это зависит, скорее всего, от поставленной задачи, которую она должна выполнять. Например, имеются разнообразные конструкции оправок, которые состоят из кольцевых конических дисков со сквозными профильными отверстиями. Через эти отверстия протянуты гибкие канаты. Система натяжения канатов позволяет обеспечить плотную стыковку дисков и жесткость собираемой под любым углом оправки. В частном случае оправка может быть и прямолинейной (Оправка для изготовления изогнутых трубчатых изделий из композиционных материалов: а.с. / Б.П.Муленков и др. - №2177877; заявл. №2001111145/22, опубл. 12.04.2001). В результате торовая оболочка не должна иметь утяжек и разрывов армирующего материала, складок на ее поверхности и внутренних расслоений.
Исследуемые здесь препреги представляют собой слоистые композиты, армированные под углом ±φ0, т.е. не имеют регулярной структуры и, следовательно, обладают четко выраженной анизотропией каждого слоя. Такие препреги изготавливаются на основе тканей гладкого переплетения либо с использованием мультиаксиальных тканей. Тканые материалы, являющиеся, в основном, двумерными структурами, проявляют хорошую стабильность свойств в направлениях основы и утка. Кроме того, тканые материалы характеризуются более сбалансированными свойствами в плоскости ткани. На этом основании, если рассматривать задачи, которые приводят к деформациям, не выходящим за рамки слоев, то такую систему можно рассматривать как плоскую. Это может служить оправданием применения в испытаниях плоских образцов, изготовленных из тканого материала.
Процесс прокалывания отверстий, изгиб оболочки в состоянии препрега и многие другие подобные операции, проводимые с препрегами, сопровождаются возникновением растягивающих напряжений в нитях, усилий сжатия нитей в поперечном направлении, взаимным смещением нитей одного семейства по нитям второго семейства. При этом в плоскости их соприкосновения возникает сила сопротивления их относительному скольжению, т.е. сила трения скольжения. Величина этой силы, конечно, зависит от многих факторов, основными из которых являются: способ переплетения семейств нитей, вязкость связующего, а следовательно, температура композиционного материала, давление внутри слоев пакета. Сила трения скольжения между семействами нитей может принимать любые значения от нуля до значения τпр, называемого предельной силой трения скольжения.
При установлении функциональной зависимости для компонент предельной силы трения были приняты следующие гипотезы и предположения.
1. Гипотеза об абсолютной гибкости нитей, формирующих ткани.
2. В каждом поперечном сечении, мысленно проведенном внутри препрега, имеет место взаимодействие распределенных по поверхности сил.
3. В своем начальном состоянии препрег свободен от напряжений, имеет постоянную температуру и находится в термодинамическом равновесии со средой.
4. Рассматриваются только статические задачи в условиях равновесия.
5. Армирующий материал препрегов имеет возможность перемещаться со скольжением на конечные расстояния под действием внешней нагрузки. При этом сопротивлением такому движению являются силы трения.
При установлении величины силы трения, прежде всего, следует выяснить его природу и основные свойства (Крагельский И.В. Трение и износ / И.В.Крагельский. - М.: Машиностроение, 1962. - 370 с.). Для этого необходимо установить, каково оно - внутреннее или внешнее? Различие между внешним и внутренним трением является количественным или качественным? Это важно, так как в первом случае закономерности внешнего трения могли бы быть распространены на внутреннее трение, а во втором случае следует ожидать иных закономерностей.
Исследование механизма внутреннего трения показывает, что оно принципиально отлично от внешнего трения. Единственным сходством между ними будет то, что оба вида трения являются диссипативными процессами. Их различие, во-первых, в геометрии взаимодействия трущихся поверхностей. При внешнем трении соприкосновение двух тел происходит в отдельных точках. При внутреннем трении поверхность касания непрерывна и не зависит от нагрузки. Во-вторых, внутреннее трение характеризуется ламинарным перемещением материала в направлении вектора относительной скорости. При внешнем трении материал перемещается в направлении, перпендикулярном к вектору относительной скорости. В-третьих, при внешнем трении возникновение и разрушение связей должно локализоваться в тонком поверхностном слое, при внутреннем трении деформативная зона охватывает весь объем.
Все признаки внутреннего трения имеют место при движении армирующего материала в препрегах. Таким образом, силы трения, возникающие в препрегах при деформации, являются внутренними. С другой стороны, если рассматривать препреги в виде многослойных структур, состоящих из нескольких слоев однонаправленных нитей, то при деформации силы трения возникают на поверхности соприкосновения этих семейств нитей, а это является внешним видом трения. Пояснения, сделанные ниже, показывают, что это одно и то же.
Физическое или Ван-дер-Ваальсово взаимодействие универсально и существует между любыми контактирующими телами. При этом различают пять видов нарушения фрикционных связей: скол - срез материала (бугорков); пластическое оттеснение; упругое деформирование; разрушение пленок (адгезионное разрушение); разрушение основного материала (когезионное разрушение). В общем случае могут иметь место все пять видов. Таким образом, трение представляет собой смешанный процесс. В отдельных случаях превалируют некоторые из этих видов. Для приработанных поверхностей или при наличии смазки обычно преобладает упругое деформирование (Крагельский И.В. Трение волокнистых веществ / И.В.Крагельский. - М.: Гизлегпром, 1941). В этом случае остальными видами сопротивления можно пренебречь. Связующее, которое присутствует в препрегах, обладает всеми свойствами смазки. Таким образом, если будем считать, что трение в препреге является внутренним, то оно должно быть обусловлено упругими деформациями. С другой стороны, считая трение в препрегах внешним, мы приходим к выводу, что оно тоже обусловлено упругим деформированием.
Однако из сказанного необходимо сделать вывод, что трение, возникающее в препрегах при перемещении армирующего материала, сильно зависит от доли присутствия в препрегах связующего. Уменьшение толщины слоя связующего, обволакивающего стеклянные волокна, увеличивает влияние волнистости и шероховатости стекловолокнистой арматуры на коэффициенты трения. Увеличение наноса связующего приводит к утолщению его слоя и к постепенному увеличению влияния связующего на силу трения. Иными словами, трение от граничного (внешнего) постепенно переходит к смешанному (полужидкостному), которое при полном разделении прослойкой связующего смежных слоев арматуры переходит в жидкостное (внутреннее) трение.
Внутреннее трение, при котором предотвращается непосредственный контакт и взаимодействие волокон стеклоарматуры, полностью характеризуется взаимодействием между молекулами связующего и, следовательно, определяется его вязкостью, которая проявляется механически в виде касательных усилий сопротивления изменению его формы. Характерным для вязкости является ее зависимость от скорости деформации. Функционально эта зависимость задается в виде аналитической связи между касательным напряжением τ и градиентом скорости скольжения по толщине слоя связующего.
В общем случае деформация среды (трение, скольжение) начинается лишь после того, как напряжение достигает некоторого предельного τпр, выше которого τ определяется лишь функцией от градиента скорости сдвига (Цыплаков О.Г. Основы формирования стеклопластиковых оболочек / О.Г.Цыплаков. - Л.: Машиностроение, 1965. - 183 с.)
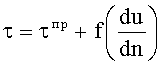 ,
,
где u - скорость сдвига;
τ - трение скольжения;
τпр - предельное значение трения скольжения.
Если сдвиг происходит с постоянной скоростью, то  и в этом случае предельное напряжение сдвига тоже всегда будет постоянным.
и в этом случае предельное напряжение сдвига тоже всегда будет постоянным.
Что касается решения задачи об определении предельных сил трения, то она должна решаться в случае предельного равновесия, когда нити находятся на грани срыва. Рассматривая эту задачу, когда нити не находятся на пороге равновесия, силы трения, вообще говоря, не максимальны. Однако при малых скоростях движения максимальные силы трения покоя и силы трения движения практически совпадают (Дерягин Б.В. Что такое трение? / Б.В.Дерягин. - М.: Изд. АН СССР, 1963. - 270 с.).
Работа сил упругого оттеснения может быть легко определена как произведение деформируемого объема V на среднее напряжение оттеснения στ. В соответствии с этим работа будет равна
W=V·στ.
Следует указать, что в этой формуле фигурирует фактическое удельное давление. Таким образом, если пользоваться контурными или нормальными давлениями, то можно сделать вывод, что сила внутреннего трения имеет линейную зависимость от удельного давления. Из изложенного следует, что сила трения неоднородного фрикционного контакта в препрегах равна сумме произведений частных значений коэффициентов трения на долю нагрузки, приходящуюся на тот или другой вид нагружения.
Необходимо учесть, что в тех местах, где нити соприкасаются, между ними возникает контактное давление. Заменим в этих местах распределенную нагрузку равнодействующей силой P и приложим в точке соприкосновения силы трения F1 и F2. Сила F1 имеет направление вдоль нити утка, а сила F2 - вдоль нити основы. Они возникают всегда, когда имеют место перемещения нитей вдоль соответствующих направлений. В этом случае предполагается не только растяжение нитей семейств, но и сжатие их в поперечном направлении. Таким образом, внешняя нагрузка на препрег может вызвать сдвиговые деформации со смещением одного семейства нитей по отношению к другому. Сдвиговые деформации могут привести к изменению угла между нитями. Будем рассматривать случай, когда препреги армированы тканями гладкого переплетения, а при деформации угол между нитями семейств становится равным α.
Вырежем ячейку ткани после деформации, состоящую из двух фрагментов нитей, принадлежащих нитям разных семейств. Полученные фрагменты нитей представляют собой прямоугольники в плане размером  для уточной нити и
для уточной нити и  - для нитей основы. На фигуре 1 показан этот фрагмент. Здесь
- для нитей основы. На фигуре 1 показан этот фрагмент. Здесь
AB и AC - касательные в точке A к поверхности нити i-го (i=1, 2) семейства;
AD - линия, вдоль которой располагаются нити второго семейства;
αi - угол, характеризующий нормальное сечение нити i-го семейства;
αi2 - угол, который характеризует сечение i-ой нити, проведенное под углом α к образующей поверхности нити.
Линия AD представляет собой элемент дуги эллипса с полуосями R1 и 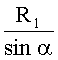 для нити утка и R2,
для нити утка и R2, 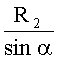 для нити основы. Радиусы кривизны этой дуги в точке D для нити утка и для нити основы соответственно равны
для нити основы. Радиусы кривизны этой дуги в точке D для нити утка и для нити основы соответственно равны
 ,
, 
Существуют три причины, от которых зависит величина контактного давления. Во-первых, под действием внешних усилий могут возникнуть силы взаимодействия между слоями ткани. Такое взаимодействие, приложенное к типичной ячейке ткани, выражается величиной

где p - удельное давление сжатия слоев препрега в рассматриваемой точке;
a и b - размеры в плане типичной ячейки ткани;
a - ширина уточной нити;
b - ширина нити основы.
Вторая компонента давления Р2 связана с растягивающей нагрузкой в нити утка. Растянутая нить утка соприкасается с поверхностью нити основы. Считая нити абсолютно гибкими, можно утверждать, что нить утка в таких соприкосновениях приобретает форму, в точности повторяющую поверхность нити основы. Рассматриваются многоволоконные нити. Для таких нитей характерно то, что в тканях они занимают такое положение, которое обеспечивает им сильную расплющенность сечения. Практически такое сечение можно сравнить с вытянутой луночкой (Василевич Ю.В. Модель деформирования препрегов в условиях равновесия / Ю.В.Василевич, В.М.Сахоненко, С.В.Сахоненко // Межведомственный научно-технический сборник «Машиностроение». - 2007. - №22. - С.134-142).
С достаточной степенью точности можно предположить, что граница луночки (сечение нити основы) сформирована двумя дугами окружности радиуса R1. Угол между этими дугами в точке их пересечения достаточно мал. Это позволяет утверждать: радиус R1 намного больше толщины ткани, поэтому давление нити утка по поверхности нити основы распределено практически равномерно. Напряжения в гибкой ленте, опирающейся на цилиндрическую поверхность, пропорциональны давлению, оказываемому лентой на эту поверхность (Прочность, устойчивость, колебания. Справочник в трех / Под общ. ред. И.А.Биргера и Я.Г.Пановко. - М.: Машиностроение, 1968. - Т.1. - 831 с.). Таким образом, если принять за основу зависимость
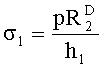 ,
,
где σ1 - напряжения в нити основы;
p - удельное давление, оказываемое нитью на опорную поверхность;
h1 - толщина нити основы, то искомое давление Р2 можно определить по формуле

Здесь N1 - усилие, растягивающее нить основы;
F1 - площадь сечения нити основы.
Третья компонента Р3 давления Р имеет линейную зависимость от давления нити основы на нить утка и поэтому
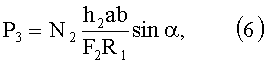
где F2 - площадь сечения нити утка;
R1 - радиус поверхности основы;
h2 - толщина нити утка;
N2 - усилие, растягивающее нить утка.
Каждой компоненте давления Р соответствует своя сила трения. Поэтому
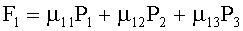 ,
,

Здесь µij (i=1, 2; j=1, 2, 3) - некоторые постоянные коэффициенты;
F1 - величина силы трения, которая является силой сопротивления при движении нити утка по поверхности нити основы;
F2 - величина силы сопротивления движению нити основы по поверхности нити утка.
Введем в рассмотрение величины:
σ11 и σ22 - распределенные растягивающие усилия для первого (нити утка) и второго (нити основы) семейств нитей, действующие параллельно нейтральной плоскости ткани;
 и
и  - компоненты силы трения, которые определяют распределенную предельную силу трения скольжения между нитями семейств ткани и лежащие в ее нейтральной плоскости (здесь индекс указывает нить, вдоль которой действует сила).
- компоненты силы трения, которые определяют распределенную предельную силу трения скольжения между нитями семейств ткани и лежащие в ее нейтральной плоскости (здесь индекс указывает нить, вдоль которой действует сила).
Введенные величины согласно определению выражаются равенствами

Здесь h - толщина ткани;
α1 и α2 определяют величину половинного угла в вершинах луночек соответствующего сечения нити.
Подставим (8) в (7), в результате, считая постоянными h, h1, h2, a, b, α1, α2, F0, F1, F2, R1, R2, получим
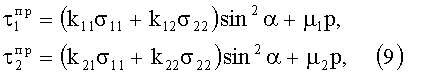
где k11, k22, k12, k21, µ1, µ2 - постоянные числа, отождествляемые с коэффициентами внутреннего трения;
α - угол между нитями семейств нитей.
Пусть теперь в препрегах в качестве наполнителя используются мультиаксиальные стеклоткани. Для таких тканей тоже можно ставить вопрос о нахождении предельной силы трения. Мультиаксиальная ткань - это текстильный нетканый материал, состоящий из нескольких слоев нитей, прошитых полиэфирной нитью. Каждый слой состоит из однонаправленных нитей, ориентированных в направлении в соответствии с требуемой схемой армирования. Если многоволоконная стеклонить является некрученой или слабо крученой, то под действием внешней нагрузки она может двигаться в продольном направлении, несмотря на присутствие прошивной нити, которая находится в натянутом состоянии и окаймляет ячейками слой стеклонитей.
Так как прошивная нить в результате ткачества находится в натянутом состоянии, то нити основных слоев в каждой ячейке испытывают действие внешнего давления совершенно аналогичное, как и в случае с тканями гладкого переплетения. Таким образом, к каждому семейству нитей основных слоев можно применить закон (9). В результате получим
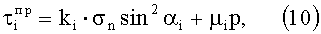
где i - номер слоя;
αi - угол, который составляет i-ый слой стеклонитей с прошивной нитью;
σn - напряжение растяжения в прошивной нити;
k1 и µi - постоянные числа, отождествляемые с коэффициентами внутреннего трения.
Тканый препрег расположим между двумя жесткими поверхностями, создающими давление внутри препрега равное р. Перерезанную нить на расстоянии х0 от края образца выдергиваем силой Т из ткани. Нагруженная таким образом нить сдвигается со смещением относительно других семейств нитей. Между вытягиваемой нитью и другими нитями возникает сила трения скольжения τ, которая может принимать любое значение от нуля до  , причем, если нить сдвигается со скольжением, то имеет место
, причем, если нить сдвигается со скольжением, то имеет место  . В нагруженной нити возникают напряжения растяжения, которые можно вычислить, руководствуясь дифференциальным уравнением
. В нагруженной нити возникают напряжения растяжения, которые можно вычислить, руководствуясь дифференциальным уравнением
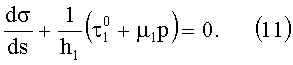
Это дифференциальное уравнение получено в результате рассмотрения условий равновесия элемента нити длиной ds (см. фигуру 2).
На фигуре 2
Т=ah1b; b - ширина нити;
 - сила трения.
- сила трения.
Основной признак установления направления действия силы  заключается в том, чтобы направить ее по касательной к нити в сторону, противоположную перемещению нити.
заключается в том, чтобы направить ее по касательной к нити в сторону, противоположную перемещению нити.
Учитывая, что для мультиаксиальной ткани
 ,
,
решение уравнения (11) с учетом граничного условия σ|s=0=σ0 имеет вид

Представление (12) является той функциональной зависимостью, с помощью которой можно производить сравнение этой зависимости с результатами экспериментальных исследований.
При проведении испытаний использовались образцы, вырезанные из биаксиальной ткани. Ширина такого образца составляет d=40 мм, а длина l=250 мм. Направление длины образца совпадает с направлением испытываемого семейства нитей. Край образца, представляющий собой длину, параллелен испытываемому семейству нитей. Для испытаний была выбрана биаксиальная ткань ВХ-470. Слои нитей у такой ткани расположены под углом ±45° к прошивной нити. Толщина этой ткани h=0,52 мм. Таким образом, толщина семейства однонаправленных нитей h1=0,26 мм. Количество нитей в полосе шириной d=40 мм равно 114 шт. Перед вырезом намеченные края образцов промазывались клеем, так как ткань очень подвижна и без этого невозможно сохранить целостность вырезанного образца. Учитывая симметричность расположения семейств нитей у ткани ВХ-470, испытаниям подвергался только один слой. Через  и
и  (i=1, 2, 3, 4; j=0, 1) обозначены результаты проведенного испытания. Напряжения
(i=1, 2, 3, 4; j=0, 1) обозначены результаты проведенного испытания. Напряжения 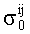 и давление pi вычислялись по формулам (2). Здесь
и давление pi вычислялись по формулам (2). Здесь  является средним значением из пяти проведенных испытаний.
является средним значением из пяти проведенных испытаний.
Предполагаем, как и в случае с тканями гладкого переплетения, что в точке разреза нити напряжение 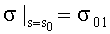 , не исключая при этом, что σ01=0, так как в точке s=s0 сделан разрез нити (пояснения к этому замечанию будут сделаны ниже). В этом случае из (12) имеем расчетную формулу
, не исключая при этом, что σ01=0, так как в точке s=s0 сделан разрез нити (пояснения к этому замечанию будут сделаны ниже). В этом случае из (12) имеем расчетную формулу

Результаты проведенных испытаний представлены в табл.1.
 и величины внешней нагрузки Р
и величины внешней нагрузки Р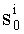 , мм
, мм
Пусть вначале Р=0. Путем вычитания правых и левых частей в соответствующих равенствах (13) исключим из рассмотрения напряжение σ01
 .
.
Полученная формула позволяет найти напряжение  . Для этого воспользуемся методом наименьших квадратов. В результате найдем
. Для этого воспользуемся методом наименьших квадратов. В результате найдем
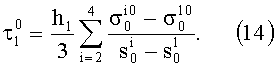
Постоянную µ1 определим тем же способом, используя данные испытаний при Р≠0. Для этого расчетную формулу представим в виде
 .
.
Аналогично, используя предыдущую формулу и результаты испытаний, найдем

Физический смысл напряжения  состоит в том, что это то сопротивление сдвигу нитей армирующего материала, которое обусловлено присутствием прошивной нити. Прошивная нить в какой-то мере способствует сжатию пакета нитей, в результате чего напряжение
состоит в том, что это то сопротивление сдвигу нитей армирующего материала, которое обусловлено присутствием прошивной нити. Прошивная нить в какой-то мере способствует сжатию пакета нитей, в результате чего напряжение  можно считать как результат сжатия давлением p01 и поэтому имеем связь
можно считать как результат сжатия давлением p01 и поэтому имеем связь
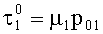 .
.
Отсюда зная  и µ, найдем давление p01, которое своим присутствием в мультиаксиальной ткани обеспечивает ее целостность
и µ, найдем давление p01, которое своим присутствием в мультиаксиальной ткани обеспечивает ее целостность

Для расчета минимального напряжения растяжения 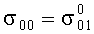 воспользуемся зависимостями (13) и результатами испытаний №1-№4 при Р=0
воспользуемся зависимостями (13) и результатами испытаний №1-№4 при Р=0

Здесь и в других расчетных формулах напряжения  рассчитаны по формулам (2) с использованием данных из таблицы 1 в виде средних значений из пяти однородных испытаний. Расчеты для биаксиальной ткани ВХ-470 по формулам (14)-(17) приведены в табл.2.
рассчитаны по формулам (2) с использованием данных из таблицы 1 в виде средних значений из пяти однородных испытаний. Расчеты для биаксиальной ткани ВХ-470 по формулам (14)-(17) приведены в табл.2.
 , МПа
, МПа
Анализ проведенных расчетов показывает, что напряжение σ01 в пограничной точке (если Р=0, то 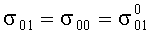 ) нельзя считать равным нулю (погрешность вычислений этого параметра намного меньше его среднего значения), хотя, на первый взгляд, это напряжение все-таки должно быть равным нулю, так как оно вычисляется в точке, где нить разрезана. Такой парадокс можно объяснить путем согласования его с понятием предсдвигового состояния в точке разреза.
) нельзя считать равным нулю (погрешность вычислений этого параметра намного меньше его среднего значения), хотя, на первый взгляд, это напряжение все-таки должно быть равным нулю, так как оно вычисляется в точке, где нить разрезана. Такой парадокс можно объяснить путем согласования его с понятием предсдвигового состояния в точке разреза.
Пусть нить имеет достаточно большую длину. Если конец этой нити нагрузить растягивающей нагрузкой σ0, то на какой-то длине во всех ее точках произойдет сдвиг со смещением. Другие точки нити будут находиться или в упругом равновесии, или в состоянии покоя. Таким образом, между этими множествами существует граничная точка. Пусть в этой точке напряжение в нити равно σ01, которое назовем предсдвиговым напряжением. Очевидно, напряжение σ01 в некоторой мере зависит от давления p. Непрерывное увеличение напряжения σ0 приведет к тому, что граничная точка совпадет с координатой s=s0. Следовательно, мы попадаем в точку s=s0, где произведен разрез нити, который фиксирует конец предсдвигового состояния. Ответ на поставленный вопрос будет таким - напряжение σ0 должно быть таким, чтобы в точке разреза нити s=s0 напряжения в нити были равными s=s01. Здесь правомочно провести сравнение с поведением функции в точке разрыва: односторонний предел и значение функции в точке разрыва могут не совпадать. Для напряжения σ0 точка s=s0 является точкой разрыва. Разрез служит только для фиксирования максимальной силы Т в эксперименте. Другими словами, если бы не было разреза, то под действием максимальной силы Т сдвиг со смещением остановился бы в точке s=s0. При этом в точках, где s>s0, имеет место упругий сдвиг.
Для установления σ01 рассмотрим напряженное состояние участка нити, где отсутствует сдвиг со смещением. Для этого воспользуемся уравнением (11). В результате, с учетом того, что
τ=Gγ=µ0(p+p01)γ; 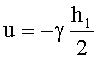 ;
; 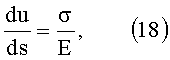
уравнение (11) преобразуем к виду
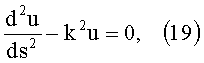
где  ;
;
G - модуль сдвига;
E - модуль упругости нити;
γ - относительная деформация сдвига.
Отметим, что модуль сдвига G для препрегов принципиально другой по сравнению с той же характеристикой для твердых упругих тел. Модуль сдвига напрямую зависит от созданного давления между слоями. Чем больше давление, тем сильнее сцепление между слоями, так как одновременно расширяется поверхность соприкосновения слоев армирующего материала и поэтому увеличивается объем упругого деформирования. Такое обстоятельство повышает жесткость на сдвиг между слоями, даже если при этом отсутствует смещение. Упругий сдвиг тесно связан с понятием трения покоя, которое имеет прямую пропорциональную зависимость от давления (Крагельский И.В. Трение и износ / И.В.Крагельский. - М.: Машиностроение, 1962. - 370 с.). В таком случае в первом приближении функциональная зависимость между модулем сдвига и давлением должна быть установлена в виде
G=µ0(p+p01),
где µ0 - некоторая постоянная, зависящая от состояния соприкасающихся поверхностей;
р - давление между слоями препрега;
p01 - давление внутри мультиаксиальной ткани, созданное прошивной нитью.
Разрешив дифференциальное уравнение (19), получим
u=c1e-ks+c2eks.
Здесь c1 и с2 - некоторые постоянные, причем с2=0, так как
u|s=+∞=0.
Воспользуемся равенствами (18) для нахождения σ и τ. В результате найдем
u=c1e-ks,
σ=-Ekc1e-ks,

Установим теперь функциональные зависимости для  когда Р≠0. Для этого приравняем это значение напряжения и силу трения их же значениям, определяемым по формулам (20)
когда Р≠0. Для этого приравняем это значение напряжения и силу трения их же значениям, определяемым по формулам (20)
 ,
,

Из системы (21) найдем
 .
.
Параметр µ0 не должен зависеть от p, следовательно, полагая в предыдущей формуле р=0, a  , найдем
, найдем

В результате для  имеем следующую зависимость
имеем следующую зависимость
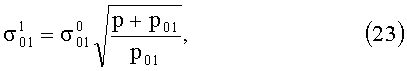
где р=0, если Р=0;
 , если Р≠0.
, если Р≠0.
Выражения (22) и (23) для µ0 и 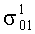 могут быть использованы в вычислительных операциях, связанных с задачами о препрегах, а также в теоретических исследованиях при построении математической модели препрегов. Полученные функциональные зависимости для компонент предельных сил трения могут применяться для препрегов, армированных мультиаксиальными тканями. Эти же зависимости могут быть использованы и для тканей, не пропитанных связующим. Следует подчеркнуть, что коэффициенты внутреннего трения постоянны при условии неизменности параметров внешней среды.
могут быть использованы в вычислительных операциях, связанных с задачами о препрегах, а также в теоретических исследованиях при построении математической модели препрегов. Полученные функциональные зависимости для компонент предельных сил трения могут применяться для препрегов, армированных мультиаксиальными тканями. Эти же зависимости могут быть использованы и для тканей, не пропитанных связующим. Следует подчеркнуть, что коэффициенты внутреннего трения постоянны при условии неизменности параметров внешней среды.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ НЕУПРУГОЙ СОСТАВЛЯЮЩЕЙ ПРИ СЖАТИИ НЕОТВЕРЖДЕННОГО КОМПОЗИЦИОННО-ВОЛОКНИСТОГО МАТЕРИАЛА | 2011 |
|
RU2452951C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ НЕОТВЕРЖДЕННЫХ КОМПОЗИЦИОННО-ВОЛОКНИСТЫХ МАТЕРИАЛОВ | 2002 |
|
RU2228524C2 |
| Армированное волокном 3D ткацкое переплетение и способ его изготовления | 2018 |
|
RU2767839C2 |
| СПОСОБ ПОЛУЧЕНИЯ РЕЗЬБЫ В НЕОТВЕРЖДЕННОМ КОМПОЗИЦИОННО-ВОЛОКНИСТОМ МАТЕРИАЛЕ | 2018 |
|
RU2680513C1 |
| СПОСОБ СОЗДАНИЯ КОМПОЗИТНОГО УГЛОВОГО СОЕДИНИТЕЛЬНОГО ЭЛЕМЕНТА НА БАЗЕ ЦЕЛЬНОТКАНОЙ 3D ПРЕФОРМЫ С ПЕРЕМЕНОЙ СТРУКТУРЫ АРМИРОВАНИЯ | 2023 |
|
RU2818055C1 |
| ТКАНЕВАЯ БРОНЕПАНЕЛЬ, ТКАНЕВЫЙ БРОНЕМОДУЛЬ И БРОНЕЗАЩИТНАЯ ТКАНЬ | 1999 |
|
RU2155313C1 |
| Композиционная баллистическая структура | 2018 |
|
RU2677059C1 |
| УГЛЕРОДНЫЙ КОМПОЗИТНЫЙ РЕЗЬБОВОЙ СОЕДИНИТЕЛЬНЫЙ ЭЛЕМЕНТ НА БАЗЕ ЦЕЛЬНОТКАНОЙ 3D ПРЕФОРМЫ | 2023 |
|
RU2801427C1 |
| ДЛИННОМЕРНЫЙ СИЛОВОЙ КОНСТРУКЦИОННЫЙ ЭЛЕМЕНТ ТИПА СТРОИТЕЛЬНОЙ БАЛКИ ИЗ ПОЛИМЕРНОГО КОМПОЗИЦИОННОГО МАТЕРИАЛА | 2013 |
|
RU2542294C2 |
| МАТЕРИАЛ ОСНОВЫ ИЗ ПРОШИТОГО УГЛЕРОДНОГО ВОЛОКНА И ВЛАЖНЫЙ ПРЕПРЕГ С ЕГО ИСПОЛЬЗОВАНИЕМ | 2013 |
|
RU2601761C2 |


Изобретение относится к изготовлению композиционно-волокнистых материалов (КВМ) и может найти широкое применение в ракетно-космической технике, авиастроении, химическом машиностроении, а также в других отраслях народного хозяйства. Сущность способа: из неотвержденного КВМ (препрега) вырезается полоска из мультиаксиальной ткани и укладывается между двумя жесткими поверхностями, нагруженными давлением Р. Затем разрезается одна нить, к ее концу прикладывается растягивающее усилие и определяется связь между длиной нити и усилием вытягивания ее из препрега исходя из указанной зависимости. Используя результаты испытаний, определяют коэффициенты внутреннего трения путем сравнения результатов испытаний с найденной зависимостью. 2 табл., 2 ил.
Способ определения параметров функциональной зависимости силы внутреннего трения  для мультиаксиальных тканей, заключающийся в том, что из неотвержденного композиционно-волокнистого материала (препрега) вырезается полоска из мультиаксиальной ткани и укладывается между двумя жесткими поверхностями, нагруженными давлением Р, затем разрезается одна нить, к ее концу прикладывается растягивающее усилие и определяется связь между длиной нити и усилием вытягивания ее из препрега, исходя из зависимости
для мультиаксиальных тканей, заключающийся в том, что из неотвержденного композиционно-волокнистого материала (препрега) вырезается полоска из мультиаксиальной ткани и укладывается между двумя жесткими поверхностями, нагруженными давлением Р, затем разрезается одна нить, к ее концу прикладывается растягивающее усилие и определяется связь между длиной нити и усилием вытягивания ее из препрега, исходя из зависимости
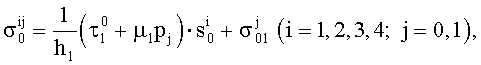
где i - номер эксперимента;
j=0 при внешней нагрузке Р=0 и j=1, при Р≠0;

m - количество нитей, расположенных в ткани шириной d;
Р - сила, сдавливающая полосу ткани размером d×1;
Tik - сила, необходимая для выдергивания нити из полосы ткани;
k - номер повтора испытания в i-м эксперименте;
h1 - толщина семейства одинаково направленных нитей;
 - длина нити;
- длина нити;
 и µ1 - параметры, описывающие величину силы внутреннего трения
и µ1 - параметры, описывающие величину силы внутреннего трения 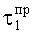 ;
;
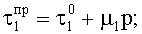
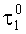 - сила сопротивления сдвигу нитей армирующего материала, обусловленная присутствием прошивной нити;
- сила сопротивления сдвигу нитей армирующего материала, обусловленная присутствием прошивной нити;
µ1 - коэффициент пропорциональности (коэффициент трения), выражающий долю участия нагрузки Р в усилии вытягивания нити;
 - напряжение растяжения в нити на расстоянии
- напряжение растяжения в нити на расстоянии  , при Р=0;
, при Р=0;
 - напряжение растяжения в нити на расстоянии
- напряжение растяжения в нити на расстоянии  , при Р≠0;
, при Р≠0;
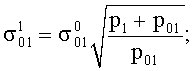
p01 - давление сжатия семейства нитей, вызванное присутствием прошивной нити;

pj (J=0,1) - удельное давление сжатия семейства нитей, вызванное внешним давлением Р;
р0 =0, если Р=0;

 , µ1,
, µ1, 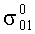 - параметры, подлежащие определению из эксперимента по формулам:
- параметры, подлежащие определению из эксперимента по формулам:



| СПОСОБ ОПРЕДЕЛЕНИЯ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ НЕОТВЕРЖДЕННЫХ КОМПОЗИЦИОННО-ВОЛОКНИСТЫХ МАТЕРИАЛОВ | 2002 |
|
RU2228524C2 |
| RU 2002118772 А, 20.01.2004 | |||
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ТРЕНИЯ ПОКОЯ ПОВЕРХНОСТНЫХ СЛОЕВ МАТЕРИАЛА | 1998 |
|
RU2150688C1 |
| L.J.BREDELL et al | |||
| Teaming measurement of the coefficient of frictioh and of contact resistance as a tool for the investigation of sliding interfaces | |||
| Wear, v.120, N 2, 1987, р.161-173. | |||
Авторы
Даты
2012-11-20—Публикация
2011-07-20—Подача