Предлагаемое изобретение относится к изготовлению изделий из композиционно-волокнистых материалов с отверстиями и может найти широкое применение в ракетно-космической технике, авиастроении, химическом машиностроении, а также в других отраслях народного хозяйства.
Известен способ изготовления отверстий в изделиях из композиционных материалов (Булановский П.И. и др. Механическая обработка стеклопластиков. - Л.: Машиностроение, 1969, с.133).
Как правило, отверстия и вырезы в изделиях из композиционно-волокнистых материалов (КВМ) получают сверлением и фрезерованием на последней стадии технологического процесса. Это приводит к существенной потере прочности, что объясняется разрывом несущих волокон и необходимостью для сил менять свое направление по матрице связующего.
Известны также способы получения отверстий в неотвержденном композиционно-волокнистом материале (патент Японии № 57-137114, кл. В 29 D 3/02, 1981 и патент Великобретании № 149292, кл. В 29 D 22/14, 1976). Сущность известных способов заключается в том, что отверстия получают еще в препреге (неотвержденном КВМ) путем раздвижения нитей наполнителя, что в какой-то мере позволяет снизить влияние вышеперечисленных факторов на прочность.
Однако все вышеперечисленные способы не обеспечивают получения высококачественных изделий с отверстиями, т.к. в зоне отверстий в процессе отверждения возникают значительные остаточные напряжения, которые в итоге приводят к разрушению изделий.
Наиболее оптимальным способом изготовления отверстий в изделиях из КВМ является способ по А.с. СССР № 1599219, МКИ В 29 С 43/20, B 29 L 9/00.
Суть известного способа заключается в следующем: к стенке заготовки изделия из КВМ, находящегося в неотвержденном состоянии, подводят заостренный стержень, а с противоположной стороны стенки располагают опору с соосной стержню втулкой. К стержню прикладывают силу Р и прокалывающий стержень под действием силы Р оформляет отверстие диаметром dc. Под действием той же силы Р стержень продолжает движение и фиксируется в положении, когда верхняя часть стержня диаметром d будет располагаться в отверстии КВМ. Образовавшийся зазор (dc>d) заполняется полуотвержденным материалом, отверстие вследствие упругих деформаций материала уменьшается в размере до диаметра d. В результате напряжения в нитях композиционно-волокнистого материала уменьшаются и таким способом можно снизить их уровень практически до нуля. При известном диаметре d необходимо знать только размер dc.
Зазор Δ=dc-d характеризует напряженно-деформированное состояние неотвержденных, а затем и отвержденных КВМ вокруг отверстия.
Все вышеперечисленные аналоги не обеспечивают определение (Δ) напряженно-деформированного состояния неотвержденных КВМ вокруг отверстия.
Авторы, проводя многочисленные экспериментальные исследования получения отверстий в неотвержденном КВМ, пришли к выводу о необходимости определения напряженно-деформированного состояния (Δ) неотвержденных КВМ с целью управления и корректировки остаточных напряжений в отвержденных КВМ.
Сущность изобретения состоит в том, что на первом этапе из неотвержденного КВМ (препрега) вырезают полоску ткани, прикладывают к ней внешнюю растягивающую нагрузку и определяют удлинение первого семейства нитей (основы), исходя из зависимости
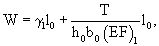
где h0, b0 и l0 - толщина, ширина и длина полосы ткани;
(EF)1 - жесткость на растяжение препрега;
γ - относительное неупругое удлинение препрега при растяжении;
Т - усилие при растяжении полосы ткани.
Затем препрег укладывают между двумя жесткими поверхностями, создают давление внутри препрега, разрезают одну нить, прикладывают к ней растягивающее усилие и определяют связь между длиной нити и усилием вытягивания ее из препрега, исходя из зависимости
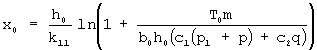
где

μ1, k12, k11 - статические коэффициенты трения;
р - давление внутри препрега;
р1 - условное давление внутри препрега, которое обусловлено необходимостью преодоления сил сопротивления, возникающих из-за переплетения семейства нитей;
q - напряжение растяжения поперечных нитей препрега;
m - количество нитей в полосе ткани препрега шириной b0.
Затем препрег укладывают между двумя жесткими поверхностями, создают давление внутри препрега, на всю глубину вставляют две гребенки и при их параллельном движении определяют перемещение первого семейства нитей (основы) препрега, исходя из зависимости
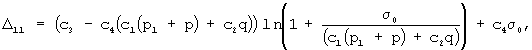
где

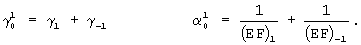
γ-1 - относительное неупругое сжатие препрега;
(EF)-1 - жесткость на сжатие препрега;
σ0 - напряжение при растяжении препрега в районе приложения внешней нагрузки,
а на втором этапе аналогичным способом определяют характеристики второго семейства нитей (утка).
Из научно-технической литературы и патентной документации неизвестно использование заявляемых зависимостей для определения напряженно-деформированного состояния неотвержденных композиционных материалов.
Технический результат заключается в том, что появляется возможность:
- определения характеристик препрега и соответственно напряженно-деформированного состояния неотвержденного КВМ;
- управления и корректировки остаточных напряжений в отвержденном КВМ.
Пусть имеется набор (пакет) слоев пропитанного связующим композиционно-волокнистого материала (препрега). При этом для предрега будем отличать два вида наполнителей. Это:
1. Взаимно перпендикулярные, не связанные между собой два семейства нитей.
2. Взаимно перпендикулярные, связанные между собой два семейства нитей - это тканые наполнители, структура и способы переплетения нитей у которых могут быть разные.
Рассмотрим гипотезы и предложения, касающиеся препрега, находящегося в напряженном состоянии.
1. Тканые наполнители - это взаимно перепендикулярные, связанные между собой два семейства нитей. Рассмотрим напряженное состояние тех зон препрега, в которых под действием внешней нагрузки происходят сдвиговые деформации со смещением одного семейства нитей по отношению ко второму. Что происходит в других зонах препрега? Вне “зоны” имеют место только упругие деформации, которые значительно меньше неупругих. Проведенные испытания показали, что неупругие деформации на порядок и более отличаются от упругих. Кроме того, отмечено: наличие вне этой “зоны” упругих деформаций не имеет существенного влияния на картину напряженно-деформированного состояния. Поэтому, не ограничивая общности, будем считать, что по контуру “зоны” препрег защемлен (очевидно, кроме участков внешнего нагружения).
2. Нити препрега являются абсолютно гибкими, т.е. имеют малую жесткость на изгиб. В связи с этим нить работает только на растяжение (отсутствие изгибной жесткости приводит к потере устойчивости при появлении сжимающих усилий). Усилие, растягивающее нить, всегда направлено по касательной к нити. Таким образом, растягивающие усилия в препреге воспринимают нити, расположенные вдоль линии действия силы, а сжимающие - семейство нитей, расположенных перпендикулярно линии действия силы.
3. При действии сжимающих усилий они передаются от одной нити к другой только при непосредственном контакте между нитями одного семейства, причем на нити другого семейства эти сжимающие усилия не оказывают никакого воздействия. При сжатии препрега происходит сдвиг нитей семейства до полного уплотнения. Дальнейшее увеличение усилий сопровождается упругими деформациями.
4. Касательные напряжения в препреге имеют место, если произошло смещение одного семейства нитей относительно второго. Таким образом, касательные усилия являются ничем иным как усилиями трения скольжения.
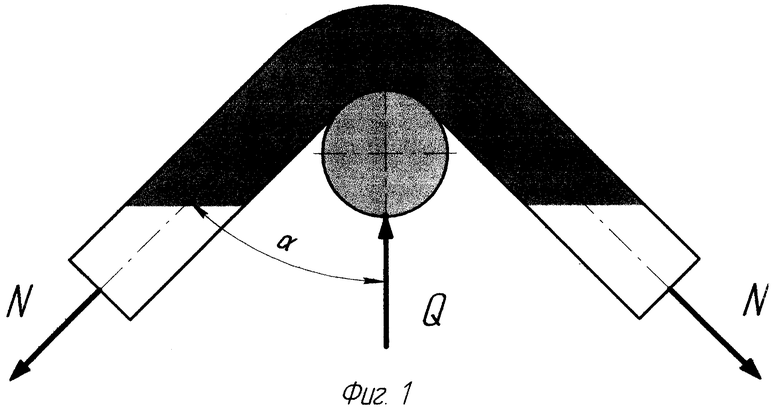
5. Переплетение нитей в тканом материале вызывает их искривление в виде вытянутой синусоиды, поэтому растягивающие усилия N в одной из них приводят к взаимному давлению одного семейства нитей ткани на другое Q (см. фиг.1).
Таким образом, предельные силы трения скольжения между семействами нитей численно будут равны
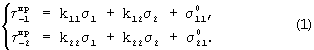
Здесь 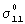 и
и 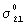 определяются по формулам
определяются по формулам
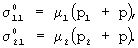
Статические коэффициенты трения μ1, μ2, k11, k12, k21, k22 - безразмерные величины. Они определяются опытным путем. Параметр р определяет давление связующего внутри препрега. Параметры р1, р2 эквивалентны таким давлениям внутри препрега, которые обусловлены необходимостью преодоления сил сопротивления (соответствующего направления), возникающих из-за переплетения семейства нитей (при отсутствии давления внутри препрега и растягивающих усилий в нитях). Величины σ1 и σ2 - растягивающие напряжения в семействах нитей. Если семейства нитей не имеют взаимного переплетения, то в формуле (1) следует положить
p1=p2=k11=k12=k21=k22=0.
6. Силы трения скольжения 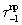 и
и 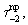 определяемые по формуле (1), возникают при перемещении семейств нитей вдоль линий действия внешних сил, приложенных к этим семействам соответственно. Очевидно, что эти линии действия внешних сил направлены по нормали к нитям семейств. Это следует из того, что нити являются абсолютно гибкими. Сила трения
определяемые по формуле (1), возникают при перемещении семейств нитей вдоль линий действия внешних сил, приложенных к этим семействам соответственно. Очевидно, что эти линии действия внешних сил направлены по нормали к нитям семейств. Это следует из того, что нити являются абсолютно гибкими. Сила трения 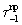 приложена к первому семейству нитей, а
приложена к первому семейству нитей, а 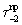 - ко второму. Первое семейство нитей испытывает также действие силы
- ко второму. Первое семейство нитей испытывает также действие силы 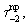 причем ее действие имеет направление, противоположное по сравнению с действием этой же силы на второе семейство. Аналогично
причем ее действие имеет направление, противоположное по сравнению с действием этой же силы на второе семейство. Аналогично 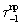 действует на второе семейство нитей при имеющих место перемещениях.
действует на второе семейство нитей при имеющих место перемещениях.
7. При перемещении одного семейства нитей тканого полотна вдоль второго семейства у последнего возникают растягивающие напряжения, а первое семейство нитей сжимается в том же направлении. Таким образом, получается, что в одном и том же материале в одном направлении возникают и растягивающие, и сжимающие усилия. Это изменяет привычные представления о напряженно-деформированном состоянии. Чтобы устранить такое противоречие, предлагается рассматривать равновесие отдельно каждого семейства нитей ткани. При этом следует учитывать, что касательные усилия, приложенные к этим семействам, равны по модулю, но имеют противоположные направления. Отметим также, что эти касательные усилия не оказывают никакого влияния на нити соседних слоев тканого материала.
Становится очевидным, что для изучения свойств препрега необходимо в первую очередь выяснить значения коэффициентов трения μ1, μ2, k11, k12, k21, k22 и давлений р1, p2. Для этого проводятся испытания и затем путем сравнения усилий и перемещений, полученных опытным путем, с усилиями и перемещениями, вычисленными аналитически, определяются искомые величины. Таким видам испытаний подвергаются нити основы и утка.
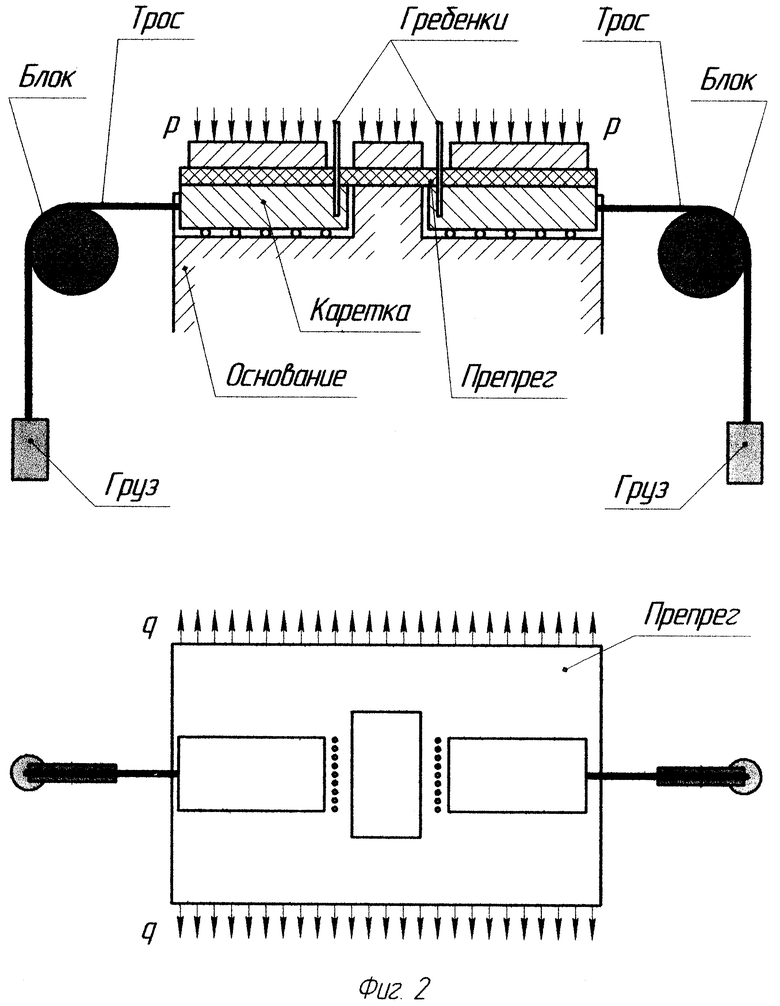
Пусть теперь препрег расположен между двумя жесткими поверхностями, которые создают давление внутри препрега, равное р. В препреге на всю его глубину вставлены две гребенки. Их параллельное смещение позволяет сдвигать поперечные нити вдоль продольных. Схема нагружения показана на фиг.2.
При такой схеме нагружения груз через трос передает усилие на гребенку, которая давит на семейство поперечных нитей препрега, заставляя их перемещаться. Нагружение осуществляется через две гребенки, перемещающиеся в разные стороны. Одновременно поперечные нити растягиваются усилиями q. При установлении равновесия после нагружения замеряются усилия, приложенные к гребенкам, и смещения гребенок, т.е. изменение расстояния между ними.
Найдем теперь аналитические зависимости между указанными усилиями и перемещениями.
Расположим систему координат Oxyz так, чтобы ось Ох была направлена вдоль семейства нитей, по которому происходит перемещение, ось Oz - вдоль второго семейства нитей, а ось Оу - перпендикулярно слоям препрега.
Необходимо отметить, что изучение равновесия с учетом сил трения скольжения можно свести к рассмотрению предельного равновесия нитей каждого семейства одного слоя ткани, которое имеет место, когда сила трения равна предельному значению. Кроме того, напряженное состояние препрега характеризуется отсутствием какого-либо перемещения в направлении осей Оу и Oz, т.е. имеет место одноосное напряженное состояние препрега. Причем нити первого семейства растягиваются, а нити второго семейства кроме растяжения равномерными усилиями q еще и сжимаются в поперечном направлении.
Связь между семействами нитей осуществляется посредством сил трения скольжения, которые определяется по формуле
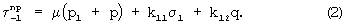
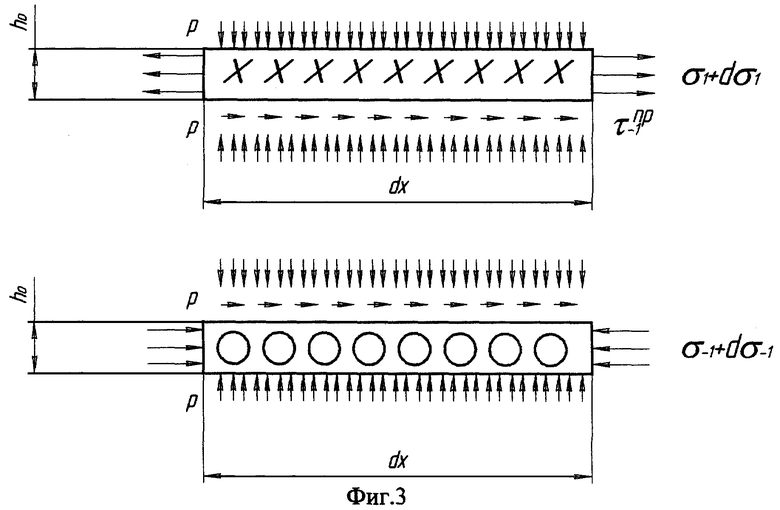
Рассмотрим (фиг.3) сечение препрега плоскостью, параллельной плоскости Оху. Возьмем в этом сечении на расстоянии х от начала координат один слой ткани длиной dx и рассмотрим равновесие каждого семейства нитей в отдельности.
На фиг.3 р - это давление, которое получает рассматриваемый элемент со стороны верхних и нижних слоев ткани; σ1 и σ1+dσ1 - усилия взаимодействия материала препрега с левой стороны и с правой стороны на рассматриваемое семейство нитей вырезанного элемента; соответственно σ-1+dσ-1 - усилия взаимодействия материала препрега на второе семейство нитей вырезанного элемента; 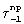 - предельные усилия трения скольжения, определяемые формулой (2).
- предельные усилия трения скольжения, определяемые формулой (2).
Рассмотрим равновесие каждого рассматриваемого семейства нитей. Сумма всех сил на ось Ох равна нулю. Таким образом:
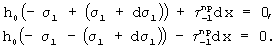
Подставляя в полученные уравнения значения для  и поделив правые и левые части равенств на dx, получим
и поделив правые и левые части равенств на dx, получим

Здесь
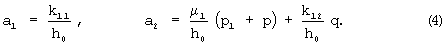
Уравнения (3) представляют собой систему линейных дифференциальных уравнений первого порядка с постоянными коэффициентами.
Решение этой системы дифференциальных уравнений с учетом граничных условий
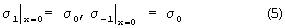
имеет вид
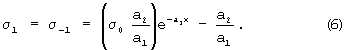
Очевидно, что граница зоны, где под действием внешней нагрузки происходит смещение со скольжением одного семейства нитей относительно другого, может быть определена из условия
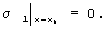
Таким образом
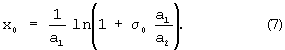
Пусть Δ1 - удлинение нитей, расположенных вдоль оси Ох, а Δ2 - величина уплотнения второго семейства нитей. Тогда перемещение гребенки будет равно
Δ11=Δ1+Δ2, причем
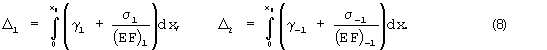
Здесь γ1 - относительное неупругое удлинение нитей за счет их распрямления; γ-1 - относительное неупругое сжатие второго семейства нитей за счет уплотнения; (EF)1 - жесткость на растяжение единичного сечения препрега в направлении первого семейства нитей; (EF)-1 - соответственно жесткость на сжатие второго семейства нитей.
Произведя несложные преобразования, получим

В этом равенстве под параметрами с1-с4 следует понимать
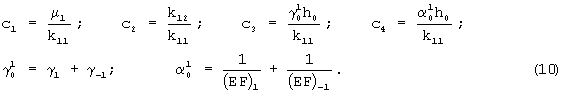
Итак, уравнение (9) устанавливает зависимость между внешней нагрузкой и соответствующими перемещениями нитей препрега. Эта зависимость содержит в совокупности четыре параметра с1-с4 и поэтому есть определенная свобода, чтобы сильно отличаться от достоверных результатов. В этом случае для конкретного препрега существует четыре конкретных значения для названных параметров, которые с наибольшим приближением описывают результаты испытаний препрега. Эти параметры с помощью соотношений (10) выражаются однозначно через восемь определенных ранее характеристик препрега
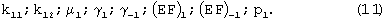
Однако должно быть и наоборот, т.е. между указанными группами параметров необходимо установление взаимно однозначного соответствия. Пока такое невозможно. Количество параметров в этих группах не совпадает. Отсюда следует вывод о необходимости проведения дополнительных испытаний.
Пусть из пакета ткани, пропитанной связующим, вытягивается одна нить усилиями, приложенными к ее концу. При этом поверхности препрега пусть будут ограничены жесткими плоскостями, которые давят на препрег с удельным давлением р. Нагруженная таким образом нить сдвигается со смещением относительно нитей, расположенных к ней перпендикулярно. Следовательно, между вытягиваемой нитью и семейством нитей, перпендикулярных к ней, возникает распределенная сила трения скольжения, которая может принимать любые значения от нуля до 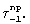 Причем там, где нить сдвигается со скольжением, имеет место
Причем там, где нить сдвигается со скольжением, имеет место 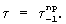
При этом
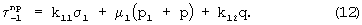
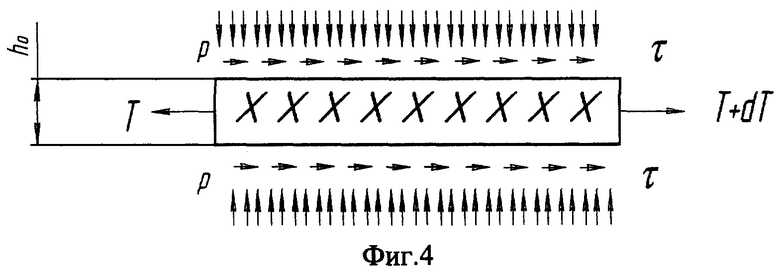
Расположим ось Ox вдоль нити. На расстоянии х вырежем элемент нити длиной dx. Не ограничивая общности, условимся считать нить в сечении прямоугольником размером h0xb0, где h0 - толщина полотна ткани; b0=b/m; m - количество нитей семейства, размещенных на полосе ткани шириной b. Рассмотрим равновесие этого элемента (фиг.4).
Суммируя все эти силы на ось Ох, получим
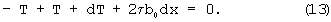
Уравнение равновесия (13) имеет место, если 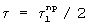 и Т=σ1b0h0, тогда
и Т=σ1b0h0, тогда
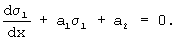
Параметры a1 и a2 определяются равенствами (4).
Необходимо отметить, что полученное уравнение для σ1 имеет такое же выражение, как и первое уравнение системы (3), поэтому с учетом граничных условий (5) выражение для σ1 имеет вид (6). Длина нити x0 определяется по формуле (7).
Полученные результаты дают возможность установить зависимость между длиной нити x0 и максимальным усилием Т при выдергивании этой нити из полотна ткани, если воспользоваться зависимостью (7). При этом следует учесть, что
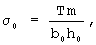
где m - количество нитей в полосе ткани шириной b0.
Как будет показано ниже, если проведем соответствующие испытания по выдергиванию нитей, то определим следующие характеристики препрега:
μ1, k11, k12, p1,
а следовательно, и параметры с1 и с2.
После подстановки этих данных в соотношение (9) и в результате проведения соответствующих испытаний определим постоянные с3 и с4. Следовательно, на основании зависимостей (10) найдем параметры
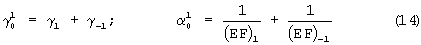
Далее воспользуемся известными методиками и проведем испытания по определению жесткости на растяжение тканого материала в соответствующем направлении. В результате определим параметры γ1 и (EF)1. Параметры γ-1 и (EF)-1 определим на основании соотношений (14). Таким образом, все восемь характеристик препрега, перечисленные в (11), найдены.
Наконец, определим остальные характеристики препрега:
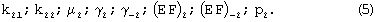
Для этого все рассмотренные выше исследования повторяются в направлении второго семейства нитей. При сравнении результатов испытаний с аналитическими зависимостями следует произвести соответствующую замену параметров (11) на параметры (15).
Суть способа определения напряженно-деформированного состояния неотвержденного КВМ продемонстрируем на примере препрега, изготовленного на основе непропитанной ткани Т-13 (ГОСТ-19170).
На первом этапе исследований определим следующие характеристики препрега:
γ1; γ2; (EF)1; (ЕF)2.
Для этого проведем испытания на растяжение образцов стеклоткани в виде полосок шириной 25 мм и длиной 100 мм. Толщина такой полоски равна 0,25 мм. Это установлено путем набора статистических данных по результатам замера толщин и слоев ткани в изделиях из стеклопластика, полученных путем намотки или прессования.
Данные по удлинению полосок (Wij) при проведении испытаний нагрузками (Тi) приведены в таблице 1.
Как известно, между удлинениями полосок и нагрузками при испытаниях имеет место приближенная зависимость
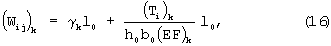
где b0 - ширина полоски; l0 - длина рабочей части полоски. При k=1 определяются характеристики основы, а при k=2 определяются характеристики в направлении утка.
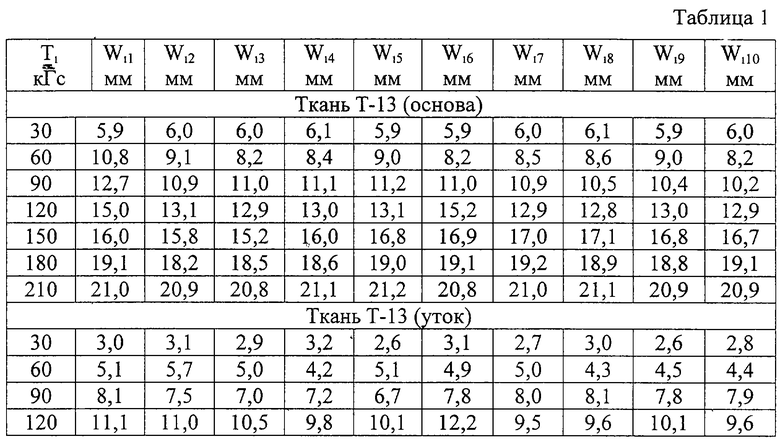
Установленная зависимость (16) является приближенной, если иметь в виду сопоставление по этой зависимости результатов испытаний. Поставим задачу определить коэффициенты γk и (EF)k так, чтобы зависимость (16) при подстановке в них результатов испытаний имела наименьшее отклонение. Для этого воспользуемся методом наименьших квадратов.
Пусть имеем
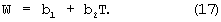
Решаем задачу минимума функции
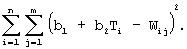
Как известно, оптимальные величины параметров b1 и b2 могут быть найдены из системы

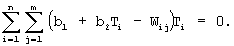
Подставим в эту систему данные таблицы 1 и, сопоставляя результаты вычислений с соответствующими коэффициентами соотношений (16) и (17), найдем
γ1=0,0343; γ2=0,0073;
(EF)1=190,099 кгс/мм2;
(EF)2=211,4537 кгс/мм2.
Здесь необходимо заметить, что упругая составляющая в направлении основы несколько меньше упругой составляющей в направлении утка несмотря на то, что соотношение нитей основы и утка составляет 1,6. Это объясняется тем, что деформация полоски ткани при ее нагружении состоит из двух составляющих: деформации нитей и деформации искривления нитей в виде синусоиды из-за их переплетения. Причем обе эти составляющие являются упругими. Доля второй составляющей при растяжении нитей основы намного больше, чем у нитей утка, так как нити утка меньше искривлены по сравнению с нитями основы.
Определим теперь коэффициенты р1 и р2. Для этого воспользуемся соотношением (7), с помощью которого можно определить усилия выдергивания нити из ткани, если длина ее равна x0.
Действительно
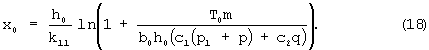
Это равенство получено из (7) после подстановки в него значений а1, а2 и
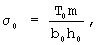
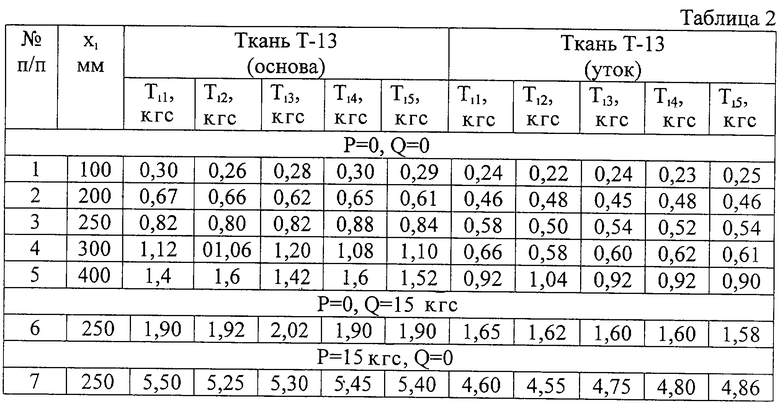
где m - количество нитей в полоске ткани шириной b0 (для полоски шириной 40 мм m=64 для нитей основы и m=40 для нитей утка); T0 - максимальное усилие при выдергивании из ткани нити длиной x0. Результаты таких испытаний приведены в таблице 2.
При этом необходимо учесть, что
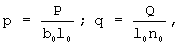
где Р - сила давления на пакет стеклоткани размером b0·l0; Q - растягивающее усилие на полоску ткани шириной l0.
Воспользуемся данными таблицы по результатам испытаний № 3 и 7.
Отметим, что при проведении этих испытаний x0 одинаково в обоих случаях и равно 250 мм.
На основании соотношения (18) получим
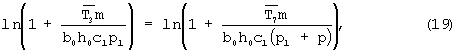
где 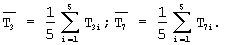
Равенство (19) будет верным, если
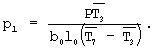
Подставим в эту формулу исходные данные из таблицы 2 и учитывая, что b0=40 мм, l0=250 мм, найдем
p1=2,74·10-4 кгc/мм2; р2=1,91·10-4 кгс/мм2.
Согласно данным таблицы 2 имеем равенство
x5-x2=x4-x1.
В таком случае на основании условия (18) получим, что
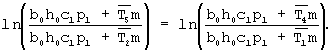
Откуда после несложных вычислений найдем

Произведем расчеты по формулам (20) с использованием данных таблицы 2. Тогда получим:
для направления нитей основы:
с1p1=45,2048 кгс/мм2, с1=1,6438·105;
k11=0,000108, μ1=17,82;
для направления нитей утка:
c1p2=2,6786 кгс/мм2; c1=1,4024·104;
к22=0,00066, μ2=9,2558.
Далее, учитывая, что х3=х6, получим
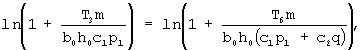
откуда найдем

Расчеты, проведенные по этой формуле, дают:
для направления нитей основы
c2=248,57, k12=c2·k11=0,0268;
для направления нитей утка:
c2=22,68, k21=c2·k22=0,015.
Рассмотрим теперь условия, при которых можно определить оставшиеся ненайденными коэффициенты γ-1 и (EF)-1.
Учитывая, что зависимость (9) устанавливает связь между нагрузкой и соответствующими поперечными перемещениями нитей препрега, проведем характерные этому случаю испытания согласно схеме нагружения, показанной на фигуре 2. Результаты измерения усилий Sk, приложенных к гребенкам, и изменение расстояния между ними Wijk представлены в таблице 3.
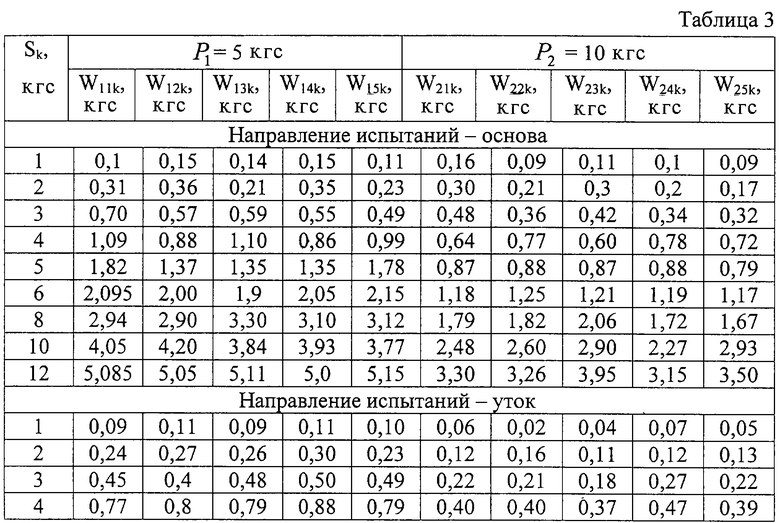
Здесь в таблице под параметром Sk следует понимать усилие на гребенку при k-ом нагружении; P1 и Р2 - нормальная суммарная нагрузка на испытываемый слой стеклоткани, равномерно распределенная по площади размером b0·l0=40·100 мм2, Wijk - изменение расстояния между гребенками при соответствующем нагружении. Отметим, что при указанных испытаниях препрег представляет собой один слой непропитанной стеклоткани.
Формула (9) представляет собой параметрическую зависимость между нагрузкой и соответствующими перемещениями нитей препрега, причем под параметрами следует понимать коэффициенты с1-с4 , из которых два уже определены: это c1 и с2. Коэффициенты с3 и с4 определим из условия наибольшего согласования результатов испытаний, представленных в таблице 3, с аналитической зависимостью (9). Для этого воспользуемся методом наименьших квадратов.
В условиях предложенных обозначений формулу (9) следует переписать в виде 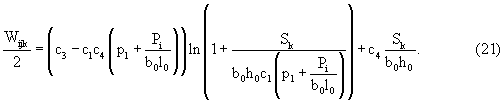
Очевидно, что зависимость (21) будет приближенной, если под переменными Wijk и Sk будем понимать результаты испытаний. Варьируя с3 и с4, можно добиться, чтобы приближение (21) было наилучшей аппроксимацией или наилучшим приближением. Для этого потребуем, чтобы функция
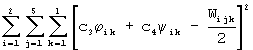
имела наименьшее значение. Здесь
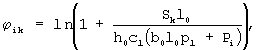
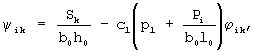
l - количество нагружений. Минимум рассматриваемой функции достигается, если
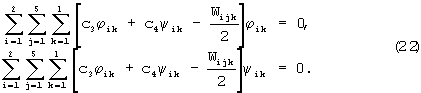
Решение этой системы относительно параметров с3 и с4 дает окончательное решение поставленной задачи. Подставим в (22) исходные данные из таблицы 3 и тогда после проведения вычислительных действий получим:
для направления нитей основы
c3=246,85 мм; c4=546,18 мм3/кгс;
для направления утка
c3=5,64 мм; с4=76,56 мм3/кгс.
Учитывая, что
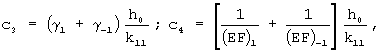
окончательно найдем
γ-1=0,0723; (EF)-1=4,21 кгс/мм2;
γ-2=0,0759; (EF)-2=5,067 кгс/мм2.
Теперь, когда известно, как связать конкретный материал препрега с его математической моделью, можно делать постановку соответствующих задач и решать уравнения равновесия, связывать полученные решения с граничными условиями и находить то единственное решение, которое удовлетворяет всем требованиям, сформулированным в условии задачи. Полученные в результате экспериментальных исследований характеристики материала позволяют определить напряженно-деформированное состояние КВМ, вычислить Δ, спроектировать и изготовить инструмент и оснастку для прокалывания и оформления отверстий.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ НЕУПРУГОЙ СОСТАВЛЯЮЩЕЙ ПРИ СЖАТИИ НЕОТВЕРЖДЕННОГО КОМПОЗИЦИОННО-ВОЛОКНИСТОГО МАТЕРИАЛА | 2011 |
|
RU2452951C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ФУНКЦИОНАЛЬНОЙ ЗАВИСИМОСТИ СИЛЫ ВНУТРЕННЕГО ТРЕНИЯ ДЛЯ МУЛЬТИАКСИАЛЬНЫХ ТКАНЕЙ | 2011 |
|
RU2467327C1 |
| СПОСОБ ПОЛУЧЕНИЯ РЕЗЬБЫ В НЕОТВЕРЖДЕННОМ КОМПОЗИЦИОННО-ВОЛОКНИСТОМ МАТЕРИАЛЕ | 2018 |
|
RU2680513C1 |
| СПОСОБ ПОЛУЧЕНИЯ ПРЕПРЕГА ДЛЯ НАМОТКИ ТЕПЛОЗАЩИТНЫХ И/ИЛИ АНТИСТАТИЧЕСКИХ ВНУТРЕННИХ ОБЕЧАЕК СТЕКЛОПЛАСТИКОВЫХ ТРУБ-ОБОЛОЧЕК РАЗЛИЧНОГО КЛАССА И НАЗНАЧЕНИЯ | 2002 |
|
RU2206582C1 |
| СПОСОБ ПОЛУЧЕНИЯ ПРЕПРЕГА | 1977 |
|
SU1840610A1 |
| ЛЕНТА БАНДАЖНАЯ ДЛЯ АРМИРОВАНИЯ ДЕФЕКТНЫХ УЧАСТКОВ ТРУБОПРОВОДА | 2001 |
|
RU2187743C1 |
| СПОСОБ ИСПЫТАНИЯ ТЕКСТИЛЬНЫХ МАТЕРИАЛОВ ПРИ ОДНОЦИКЛОВОМ РАСТЯЖЕНИИ | 2010 |
|
RU2472151C2 |
| Способ изготовления слоистого композиционного материала | 1990 |
|
SU1788062A1 |
| ЭПОКСИДНОЕ СВЯЗУЮЩЕЕ ДЛЯ АРМИРОВАННЫХ ПЛАСТИКОВ (ВАРИАНТЫ) И СПОСОБ ЕГО ПОЛУЧЕНИЯ (ВАРИАНТЫ) | 2002 |
|
RU2260022C2 |
| Способ изготовления слоистых трубчатых изделий из композиционных материалов на основе неотвержденного полимерного связующего | 2021 |
|
RU2778930C1 |
Заявленное изобретение относится к изготовлению изделий из композиционно-волокнистых материалов с отверстиями и может найти широкое применение в рекетно-космической технике, авиастроении, химическом машиностроении, а также в других отраслях народного хозяйства. Способ определения напряженно-деформируемого состояния неотвержденного композиционно-волокнистого материала заключается в том, что на первом этапе из неотвержденного КВМ (препрега) вырезают полоску ткани, прикладывают к ней внешнюю растягивающую нагрузку и определяют удлинение первого семейства нитей (основы). Технический результат - возможность определения характеристик препрега и соответственно напряженно-деформируемого состояния в неотвержденном КВМ, управления и корректировки остаточных напряжений в отвержденном КВМ. 3 табл., 4 ил.
Способ определения напряженно-деформируемого состояния неотвержденного композиционно-волокнистого материала, заключающийся в том, что на первом этапе из неотвержденного КВМ (препрега) вырезают полоску ткани, прикладывают к ней внешнюю растягивающую нагрузку и определяют удлинение семейства нитей (основы), исходя из зависимости
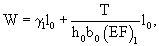
где h0, b0, l0 - толщина, ширина и длина полосы ткани;
(EF)1 - жесткость на растяжение препрега;
γ1 - относительное неупругое удлинение препрега при растяжении;
Т - усилие растяжения полосы ткани,
затем препрег укладывают между двумя жесткими поверхностями, создают давление внутри препрега, разрезают одну нить, прикладывают к ней растягивающее усилие и определяют связь между длиной нити и усилием вытягивания ее из препрега, исходя из зависимости
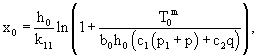
где 
μ1, k12, k11 - статические коэффициенты трения;
р - давление связующего внутри препрега;
p1 - условное давление внутри препрега, которое обусловлено необходимостью преодоления сил сопротивления, возникающих из-за переплетения семейства нитей;
q - напряжение растяжения поперечных нитей препрега;
m - количество нитей в полосе ткани препрега шириной b0,
затем предмет укладывают между двумя жесткими поверхностями, создают давление внутри препрега, на всю глубину вставляют две гребенки и при их параллельном движении определяют перемещение первого семейства нитей (основы) препрега, исходя из зависимости
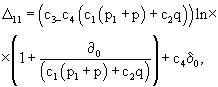
где 
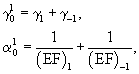
γ - относительное неупругое сжатие препрега;
(EF)-1 - жесткость на сжатие препрега;
δ0 - напряжение при растяжении препрега в районе приложения внешней нагрузки,
а на втором этапе аналогичным способом определяют характеристики второго семейства нитей (утка).
| Способ изготовления отверстий в изделиях из композиционных материалов | 1988 |
|
SU1599219A1 |
| Устройство для сборки деталей цилиндрической формы | 1961 |
|
SU149292A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДЕФОРМАЦИОННЫХ СВОЙСТВ ТЕКСТИЛЬНЫХ МАТЕРИАЛОВ ПРИ РАСТЯЖЕНИИ | 1992 |
|
RU2040792C1 |
Авторы
Даты
2004-05-10—Публикация
2002-07-16—Подача