Изобретение относится к компьютерной обработке цифровых данных, точнее к способам сжатия массивов цифровой информации путем нахождения совпадающих фрагментов последовательности данных. Изобретение может быть использовано для нахождения максимальных повторяющихся фрагментов в последовательностях цифровых данных при компьютерной обработке цифровых данных, например, с целью сжатия файлов.
Как указано в описании патента США 6400289 (раздел «Уровень техники»), существует три типа способов сжатия последовательности цифровых данных без потери информации, а именно статистическое кодирование, словарное кодирование и грамматическое кодирование. Наиболее известными алгоритмами словарного кодирования являются алгоритмы Лемпеля-Зива и их варианты. Методы словарного кодирования обеспечивают сжатие информации за счет использования избыточности данных через некоторый механизм сопоставления строк еще не закодированных данных с данными, которые уже закодированы. При этом объем вспомогательных данных, необходимых для организации эффективного поиска совпадений еще не закодированных данных с уже закодированными данными, может в несколько раз превышать объем собственно закодированных данных. В случае сжатия очень больших файлов это приводит к тому, что область поиска приходится ограничивать только самыми последними закодированными данными, используя так называемое скользящее окно поиска, длина которого может составлять десятки или сотни килобайт. Различные варианты такого поиска приведены в следующих патентах.
В патенте США 4464650 (п.123 формулы в части сжатия) предложен способ сжатия цифровых данных, в котором разбивают последовательность данных на отрезки, каждый из которых включает в себя префикс и следующий за этим префиксом символ. Префикс представляет собой самое длинное совпадение с более ранним отрезком, причем указанное разбиение определяет дерево поиска, имеющее узлы и ветви, выходящие из указанных узлов. Каждый узел имеет самое большее одну входящую ветвь. Выходящие из узла ветви представляют соответствующие символы указанного алфавита, узлы имеют соответствующие связанные с ними метки и адреса, причем дерево поиска имеет единственный коревой узел без входящих ветвей и листовые узлы без выходящих ветвей. При этом каждому узлу дерева приписывается виртуальный адрес, соответствующий номеру данного узла дерева в полном дереве поиска, частью которого является указанное дерево. Меткой узла является порядковый номер появления узла в дереве в процессе его построения. Таблица меток является массивом F, выдающим для каждого виртуального адреса метку узла, приписанную узлу с этим виртуальным адресом. Поскольку в общем случае имеется намного больше адресов, чем меток, большая часть таблицы меток является пустой, и для экономного хранения используют хеширование части массива с большими адресами. Таким образом, метка может записываться прямо в массив F по самому виртуальному адресу, или виртуальные адреса могут использоваться как входной ключ к хеш-функции, которая вычисляет реальный адрес в F, по которому записывается метка. Память, выделенная для меток узлов в массиве F, разбивается в начале кодирования на прямую и хешированную части. При этом начальная (верхняя) часть таблицы меток F записывается прямо, чтобы сэкономить время, поскольку обращение к ней происходит часто. Более поздние части таблицы меток хешируются, чтобы сэкономить память, поскольку обращение к ним происходит реже. Для обратного преобразования используется таблица адресов - массив G, выдающий для каждой метки узла виртуальный адрес узла. Массив G является обратным к массиву F и для каждой метки узла содержит приписанный ему виртуальный адрес. Поскольку таблица адресов G имеет размер, равный числу внутренних узлов, она не требует хеширования.
Как указано в абзаце 2 колонки 22 описания патента США 4464650, в программной реализации этого способа секция 4 программы кодирования выполняет корректировку дерева поиска до тех пор, пока не будет достигнут максимальный размер дерева КМ. Данная программа сохраняет дерево в статическом состоянии, когда исчерпана выделенная память. В другом варианте память под дерево поиска может быть освобождена и начат рост нового дерева. Счетчик К внутренних узлов увеличивается, и метка К внутреннего узла записывается по надлежащему адресу в массив таблицы меток F. Таким образом, недостатком этого способа является ограниченная длина поиска.
В патенте США 4558302 (п.107 формулы изобретения) предложен способ сжатия потока сигналов символов данных в сжатый поток кодовых сигналов, содержащий шаги:
запись в ячейки памяти строк сигналов символов данных, встречающихся в указанном потоке, где записанные строки имеют связанные с ними сигналы кодов, указанные ячейки памяти доступны по множеству сигналов адресов, каждая из строк сигналов символов данных включает в себя префиксную строку сигналов символов данных и сигнал символов расширения, причем префиксная строка соответствует строке, записанной в указанной памяти;
поиск в указанном потоке сигналов символов данных путем сравнения указанного потока с указанными записанными в память строками, чтобы определить самое длинное соответствие между ними;
вставка в указанную память для хранения в ней расширенной строки, включающей в себя указанное самое длинное соответствие с указанным потоком данных, продолженной следующим сигналом символа данных, следующим за указанным самым длинным соответствием;
назначение кодового сигнала, соответствующего указанной расширенной строке;
выдача кодового сигнала, связанного с указанным самым длинным соответствием, для получения указанного сжатого потока кодовых сигналов.
Как указано в абзаце 2 колонки 7 описания США 4558302, данный способ использует ограниченную длину поиска, т.е. ему присущ тот же недостаток, что и предыдущему способу.
В патенте США 4906991 предложен способ сжатия цифровых данных, в котором для поиска совпадающих фрагментов используются дерево поиска и скользящее окно поиска, причем согласно абзацу 1 колонки 25 описания максимальный размер окна может выбираться в пределах от 1000 до 63000. При этом реализация дерева поиска в виде так называемого суффиксного дерева позволяет провести весь поиск за время, линейно зависящее от длины массива цифровых данных.
В патенте США 6292115 предложен способ реализации дерева поиска в виде словаря кодовых слов, причем подробно описаны несколько вариантов словаря, содержащего 1024 кодовых слова, и отмечено, что словарь может содержать и 512, 2048, 4096 или больше кодовых слов (колонка 7 описания, 3-й абзац снизу).
Все вышеуказанные способы реализуются так называемыми «жадными» алгоритмами, когда каждый раз при кодировании оставшейся незакодированной части последовательности данных в ней производится поиск максимального фрагмента, совпадающего с некоторым фрагментом уже закодированной части данных и начинающегося с начала оставшейся незакодированной части. Недостатком этих способов является то, они не позволяют находить ситуации, когда более предпочтительной является добавление литерала, хотя существует длинный повторяющийся фрагмент, начинающийся непосредственно с начала оставшейся незакодированной части. Пример такой ситуации показан на фиг.1. На этой фигуре горизонтальной прямой условно показана строка данных, заштрихованная часть 1 которой уже закодирована. Сверху и снизу от этой прямой длинными узкими прямоугольниками показаны максимальные фрагменты, совпадающие с некоторыми фрагментами в уже закодированной части.
Символами "а" и "b" показаны реальные символы "а" и "b", присутствующие в строке данных. Позиции 2, 3, 4 указывают на фрагменты, выделяемые «жадным» алгоритмом. Позиции 5 и 6 указывают на другие максимальные фрагменты, совпадающие с некоторыми фрагментами в уже закодированной части. «Жадный» алгоритм кодирования предложит закодировать оставшуюся незакодированной часть последовательности путем кодирования фрагментов 2, 3 и 4 как копий ранее частей ранее закодированной начальной части 1 последовательности. В то же время имеется возможность закодировать оставшуюся незакодированной часть последовательности путем кодирования символов "а" и "b" в виде литералов и фрагментов 5 и 4 в виде копий частей ранее закодированной начальной части 1 последовательности. Таким образом, вместо двух копий фрагментов последовательности можно использовать одну копию фрагмента и два литерала. В большинстве схем кодирования типа Лемпеля-Зива второй вариант является более экономным. Тем самым предпочтительно использовать «нежадные» алгоритмы кодирования.
В патенте США 5883588 (описание второй реализации изобретения) предложена модификация этого подхода, не являющаяся «жадной». При кодировании последовательности данных x(i) после того как закодирована строка из первых s-1 символов, находят самое длинную подстроку x(s), … x(s+j), совпадающую с ранее закодированными данными, и если она является недостаточно длинной, то находят самую длинную совпадающую подстроку x(s+1), … x(s+j′) символов из подстрок символов, начинающихся с символа x(s+1). Сравнивают длину совпадения j с длиной совпадения j′, и если j′ больше, то x(s) кодируют в режиме литерала, a x(s+1), … x(s+j′) кодируют в режиме копирования. С другой стороны, когда длина совпадения j больше или равна длине совпадения j′, то x(s), … x(s+j) кодируют в режиме копирования. Далее процесс переходит к кодированию строк символов, начинающихся соответственно с x(s+j′+1) или с x(s+j+1). Недостатком этого способа является то, что он обеспечивает выявление литералов только длиной в один символ, т.е. отличается от «жадного» способа весьма незначительно.
В патенте США 6226628 (п.1 формулы изобретения) предложен способ предобработки файла данных для последующего сжатия, где файл данных имеет множество упорядоченных элементов данных, где соответствующие элементы данных начинают строки разных длин, включающий в себя:
создание множества указателей смещений для разных длин совпадений, где указатели смещения для определенной длины совпадения указывают смещения от соответствующих элементов данных до предыдущих строк этой длины совпадения, которые совпадают со строками этой длины совпадения, начинающимися с соответствующих элементов данных;
запоминание индексов смещений в ассоциации с файлом данных.
Как видно из фиг.6 и соответствующего описания в патенте США 6226628, объем данных, необходимых для хранения таких указателей, в несколько раз превышает объем исходного файла, что делает возможным применение этого способа только для файлов умеренного объема или только на очень мощных серверах.
Исходя из изложенного, актуальной является разработка способа нахождения всех максимальных участков в конечной последовательности символов x[i] (0≤i<N) конечного алфавита, являющихся повторениями ранее встречавшихся участков, который требовал бы дополнительную память для размещения результата, объем которой не превосходит объема исходной последовательности данных.
При этом в обоих способах достигается технический результат, состоящий в уменьшении количества памяти, требующейся для представления всех максимальных повторяющихся участков, до 2N бит (N/4 байт, т.е. ¼ от объема исходной последовательности).
Первый способ нахождения всех максимальных участков в конечной последовательности символов x[i] (0≤i<N) конечного алфавита, являющихся повторениями ранее встречавшихся участков, двумя битовыми массивами памяти, каждый из которых имеет длину N/8, состоит в том, что:
создают в памяти компьютера два битовых массива beg[i] и end[i] (0≤i<N);
заполняют все элементы указанных битовых массивов нулями;
вычисляют последовательность s1[i] по всем N значениям индексов i (0≤i<N), где s1[i] - максимальная длина линейного участка указанной последовательности данных, индекс начального элемента которого совпадает с данным индексом i, совпадающего с некоторым другим участком той же последовательности данных x[i], начало которого расположено ближе к началу последовательности данных x[i], чем начало указанного линейного участка,
определяют все указанные максимальные участки как все отрезки x[m,n] последовательности x[i], для которых начальный индекс m удовлетворяет условию s1[m]>s1[m-1]-11, а конечный индекс n равен m+s1[m]-1, для чего для каждого значения i проверяют выполнение условия s1[i]>s1[i-1]-1, и в случае выполнения этого условия устанавливают в битовых массивах beg[i] и end[i] значения beg[i]=1 и end[i+s1[i]]=1;
совокупность всех указанных максимальных участков восстанавливают по двум битовым массивам beg[i] и end[i], где единичное значение i-го элемента означает, что i-я позиция в указанной последовательности является, соответственно, началом и концом некоторого максимального указанного участка.
Второй способ нахождения всех максимальных участков в конечной последовательности символов x[i] (0≤i<N) конечного алфавита, являющихся повторениями ранее встречавшихся участков, двумя битовыми массивами памяти, каждый из которых имеет длину N/8, состоит в том, что
создают в памяти компьютера два битовых массива beg[i] и end[i] (0≤i<N);
заполняют все элементы указанных битовых массивов нулями;
вычисляют последовательность s2[i] по всем N значениям индексов i (0≤i<N), где s2[i] - максимальная длина линейного участка указанной последовательности данных, индекс конечного элемента которого совпадает с данным индексом i, совпадающего с некоторым другим участком той же последовательности данных x[i], конец которого расположен ближе к началу последовательности данных x[i], чем конец указанного линейного участка,
определяют все указанные максимальные участки как все отрезки x[m,n] последовательности x[i], для которых конечный индекс n удовлетворяет условию s2[n]>s2[n+1]-1, а начальный индекс n равен n-s2[n]+1, для чего для каждого значения i проверяют выполнение условия s2[i]>s2[i+1]-1, и в случае выполнения этого условия устанавливают в битовых массивах beg[i] и end[i] значения end[i]=1 и beg[i-s2[i]+1]=1;
совокупность всех указанных максимальных участков восстанавливают по двум битовым массивам beg[i] и end[i], где единичное значение i-го элемента означает, что i-я позиция в указанной последовательности является, соответственно, началом и концом некоторого максимального указанного участка.
Изобретение поясняется графическими материалами.
Фиг.1. Пример неоптимальности «жадного» алгоритма.
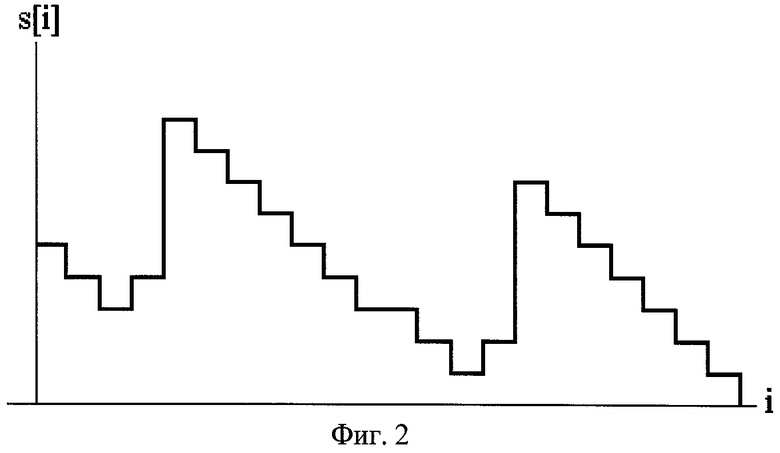
Фиг.2. Типичный вид графика функции s1[i].
Осуществление изобретения
1. Основные понятия
Прежде чем перейти к подробному описанию осуществления вышеизложенных способов, необходимо ввести некоторые понятия, связанные с поиском повторяющихся фрагментов в последовательности символов. Для заданной последовательности символов x[i] (0≤i<N) конечного алфавита через х[m,n] (0≤m≤n<N) обозначим последовательность символов x[m], х[m+1], …,х[n]. Поиск повторяющихся фрагментов в заданной последовательности символов x[i] (0≤i<N) конечного алфавита можно производить путем прохождения последовательности символов x[i] в двух направлениях: вперед и назад. В первом случае последовательность символов x[i] рассматривают в порядке возрастания значений индекса i: x[0], x[1], …, x[N-1]. Во втором случае последовательность символов x[i] рассматривают в порядке убывания значений индекса i: x[N-1], x[N-2], …, x[0].
В случае прохождения последовательности вперед для заданного фрагмента х[m,n] (0≤m≤n<N) производят поиск фрагментов x[m-d,n-d] (d>0), совпадающих с фрагментом х[m,n], т.е. пытаются найти такое d>0, что x[i]=x[i-d] для всех i, где m≤i≤n. В случае прохождения последовательности назад для заданного фрагмента х[m,n] (0≤m≤n<N) производят поиск фрагментов x[m+d,n+d] (d>0), совпадающих с фрагментом х[m,n], т.е. пытаются найти такое d>0, что x[i]-x[i+d] для всех i, где m≤i≤n. Другими словами, при любом порядке прохождения последовательности для фрагмента х[m,n] пытаются найти совпадающий с ним фрагмент х[m1,n1], расположенный в уже пройденной части последовательности. В этом случае независимо от направления прохождения последовательности такой фрагмент x[m1,n1] будем называть предыдущим появлением фрагмента х[m,n].
Информация о том, для каких фрагментов х[m,n] существует предыдущее появление, представляет значительный интерес для исследования избыточности информации в заданной последовательности символов и для ее сжатия, поскольку наличие предыдущего появления для заданного фрагмента х[m,n] говорит о том, что весь этот фрагмент может быть задан всего тремя числами: границами m, n и смещением данного фрагмента относительно его предыдущего появления. В то же время возможно задание такой информации, не требующее двумерного массива. Определим две функции
s1[i]=max{0≤j<N-i| для x[i,i+j] существует предыдущее появление},
s2[i]=max{0≤j<N-i| для x[i-j,i] существует предыдущее появление}.
Другими словами, s1[i] - максимальная длина линейного участка указанной последовательности данных, индекс начального элемента которого совпадает с данным индексом i, совпадающего с некоторым другим участком той же последовательности данных x[i], начальный элемент которого расположен ближе к началу прохождения последовательности данных x[i], чем начальный элемент указанного линейного участка. Аналогично, s2[i] - максимальная длина линейного участка указанной последовательности данных, индекс конечного элемента которого совпадает с данным индексом i, совпадающего с некоторым другим участком той же последовательности данных x[i], начальный элемент которого расположен ближе к началу прохождения последовательности данных x[i], чем начальный элемент указанного линейного участка.
Очевидно, что для фрагмента х[m,n] существует предыдущее появление тогда и только тогда, когда n-m≤s1[m]. Таким образом, знание функции s1[i] позволяет для любого фрагмента х[m,n] сразу сказать, существует ли для него предыдущее появление.
Отметим следующие важнейшие свойства функции s1[i]:
А1. s1[i+1]≥s1[i]-1 (см. фиг.2). В самом деле, пусть s1[i]=s. Тогда по определению для фрагмента x[i,i+s] существует предыдущее появление, т.е. найдется такое Δ, что x[i,i+s] совпадает с x[i+Δ,i+s+Δ], где Δ<0 в случае прохождения последовательности данных x[i] вперед и Δ<0 в случае прохождения последовательности данных x[i] назад. Тем более x[i+1,i+s] совпадает с x[i+1+Δ,i+s+Δ], причем x[i+1,i+s]=x[i+1,i+1+(s-1)] и x[i+1+Δ,i+s+Δ]=x[i+1+Δ,i+1+(s-1)+Δ]. Следовательно, для фрагмента x[i+1,i+1+(s-1)] существует предыдущее появление, откуда по определению s1[i+1]≥s-1.
Б1. Для m>0 фрагмент х[m,n] является максимальным фрагментом, для которого существует предыдущее появление, тогда и только тогда, когда n=m+s1[m] и s1[m]>s1[m-1]-1. В самом деле, пусть х[m,n] - максимальный фрагмент, для которого существует предыдущее появление. Тогда х[m,n]=х[m,m+(n-m)] является максимальным фрагментом, для которого существует предыдущее появление, откуда по определению s1[m]=n-m, т.е. n=m+s1[m]. Кроме того, поскольку фрагмент х[m-1,n] строго содержит фрагмент х[m,n], являющийся максимальным фрагментом, для которого существует предыдущее появление, то для фрагмента х[m-1,n]=х[m-1,m-1+(n-m+1)] уже не существует предыдущего появления. Следовательно, n-m+1>s1[m-1]. Таким образом, s1[m-1]-1<n-m, причем уже доказано, что n-m=s1[m], т.e. s1[m-1]-1<s1[m].
Обратно, пусть n=m+s1[m] и s1[m]>s1[m-1]-1. Предположим, что фрагмент х[m,n] содержится во фрагменте x[m1,n1], для которого также существует предыдущее появление. Если m1<m, то фрагмент x[m1,n1] содержит фрагмент х[m-1,n], откуда для фрагмента х[m-1,n] также существует предыдущее появление, являющееся частью предыдущего появления фрагмента х[m,n]. Но тогда n≤m-1+s1[m-1]. По предположению имеет место n=m+s1[m], откуда m+s1[m]≤m-1+s1[m-1], т.е. s1[m]≤s1[m-1]-1, что противоречит второму предположению. Таким образом, предположение, что m1<m, приводит к противоречию, откуда ml=m. Поскольку для фрагмента х[m1,n1] существует предыдущее появление, то по определению n1<ml+s1[ml]=m+s1[m]=n, откуда n1=n. Таким образом, фрагмент х[m,n) является максимальным фрагментом, для которого также существует предыдущее появление, и утверждение полностью доказано.
B1. Пусть m1<m2<…<mk - последовательность индексов, соответствующих началам максимальных фрагментов, для которых существует предыдущее появление, упорядоченная по возрастанию. Тогда последовательность индексов, соответствующих концам этих максимальных фрагментов, также является упорядоченной по возрастанию, т.е. m1+s1[m1]<m2+s1[m2]<…<mk+s1[mk]. To, что конец i-го максимального фрагмента имеет индекс mi+s1[mi], вытекает из свойства В. Предположим, что mi<mj, но ni=mi+s1[mi]>=nj=mj+s1[mj]. Тогда фрагмент x[mj,nj] строго содержится внутри фрагмента х[mi,ni], что противоречит максимальности фрагмента x[mj,nj].
Для функции s2[i] имеют место свойства, соответствующие свойствам функции s1[i], которые доказываются аналогично:
А2. s2[i-1]≥s2[i]-1.
Б2. Для n<N-1 фрагмент х[m,n] является максимальным фрагментом, для которого существует предыдущее появление, тогда и только тогда, когда m=n-s2[n] и s2[n]>s2[n+1]-1.
В2. Пусть n1<n2<…<nk - последовательность индексов, соответствующих концам максимальных фрагментов, для которых существует предыдущее появление, упорядоченная по возрастанию. Тогда последовательность индексов, соответствующих началам этих максимальных фрагментов, также является упорядоченной по возрастанию, т.е. n1-s2[n1]<n2-s2[n2]<…<nk-s2[mk].
2. Осуществление способа хранения значений функций s1[i] и s2[i]
Для хранения функции si[i] создают два битовых массива beg[i] и end[i], 0<=i<N. Сначала заполняют все элементы обоих массивов нулями. Последовательно вычисляют значения функции s1[i], начиная с i=0. В том случае, если ненулевое значение s1[i] для текущего значения i оказывается не меньше значения s1[i-1], т.е. если s1[i]>s1[i-1]-1, в элементы массивов beg[i] и end[i+s[i]] (только при i+s[i]<N) заносят значение 1. В результате выполнения этих действий для всех i=0, …, N-1 получают два битовых массива, которые кодируют функцию s1[i]. Заметим, что согласно свойству Б1 совокупность значений индекса i, для которых beg[i]=1, - это в точности совокупность начал максимальных фрагментов, для которых существует предыдущее появление, а совокупность значений индекса j, для которых end[j]=1, - это в точности совокупность концов таких фрагментов.
Совокупность значений функций s1[i] и s2[i] может быть восстановлена по значениям битовых массивов beg[i] и end[i], 0≤i<N следующим образом. Ясно, что s1[0]=s2[0]=0. Находят самое первое значение i0, для которого beg[i0]=1 и самое первое значение j0, для которого end[j0]=1. В этом случае согласно предыдущему абзацу s1[i0]=s2[j0]=j0-i0. Все предыдущие значения s1[i] и все предыдущие значения s2[j] равны нулю. Далее находят следующее значение i1, для которого beg[ii]=1 и самое первое значение j1, для которого end[j1]=1. В этом случае i1 - начало второго максимального фрагмента, для которого существует предыдущее появление, a j1 - конец некоторого максимального фрагмента, для которого существует предыдущее появление. В силу свойств B1, B2 этот фрагмент также является вторым. Поэтому s1[i1]=s2[j1]=j1-i1. Для всех i, таких что i0<i<i1, последовательно имеет место s1[i0+1]=s1[i0]-1, …, s1[i+1]=s1[i]-1, … Аналогично, для всех j, таких что j0<j<j1, последовательно имеет место s2[j0+1]=s2[j0]-1, …, s2[j+1]=s2[j]-1, … Далее находят следующую пару индексов i2, j2 и т.д.
3. Вычисление массива всех значений функции s2[i] для 0≤i<N
Вычисление массива всех значений функции s2[i] для 0≤i<N может быть выполнено за время O(N) с использованием дополнительной памяти объемом O(N). Для доказательства этого утверждения используется построение суффиксного дерева. Суффиксное дерево для строки символов x[0,N-1] может быть построено за время O(N) и занимает память величиной O(N) [Ukkonen E. On-line construction of suffix trees // Algorithmica, Vol.14, No 3, 1995, pp.249-260]. Ниже приводится алгоритм Укконена в интерпретации [Moritz Maab. Suffix Trees and Their Applications. Technische Universitat Munchen. October 26, 1999 // http://www.informatics.ru/?page=lib_viewarticle&article_id=27 ]. Предлагаемое нами дополнение в алгоритм Укконена позволяет вычислить весь массив значений функции s2[i] для 0≤i<N за время O(N). Ниже мы приводим только те сведения относительно алгоритма Укконена, которые необходимы для понимания производимого нами дополнения; полное описание см. в указанной работе Мааба.
Для заданного слова x1 … xN в алфавите ∑ алгоритм Укконена последовательно строит суффиксные деревья для подслов x1 … xi, i=1, …, N. На шаге i+1 алгоритм преобразует суффиксное дерево Ti для слова x1 … xi в суффиксное дерево Ti+1 слова x1 … xi+1. Важнейшим понятием для алгоритма Укконена является понятие активного суффикса слова х1 … xi. Активным суффиксом слова называется самый длинный суффикс данного слова, для которого существует предыдущее появление. Тем самым значение s2[i] совпадает с длиной активного суффикса слова x1 … xi. Таким образом, все, что надо сделать - это дополнить алгоритм Укконена операторами, позволяющими выдавать длину активного суффикса на каждом шаге.
Напомним, что суффиксное дерево Ti является поддеревом в атомарном суффиксном дереве asti для слова х1 … xi. В атомарном суффиксном дереве asti каждому суффиксу w слова соответствует узел w дерева, называемое положением w, такой, что 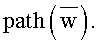 Здесь
Здесь 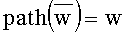 - слово, получающееся конкатенацией всех символов алфавита ∑, являющихся метками ребер, составляющих путь из корня дерева в узел
- слово, получающееся конкатенацией всех символов алфавита ∑, являющихся метками ребер, составляющих путь из корня дерева в узел  Если узел
Если узел 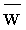 входит в суффиксное дерево Ti, то положение называется явным, в противном случае - неявным.
входит в суффиксное дерево Ti, то положение называется явным, в противном случае - неявным.
Если w=uv и 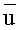 является узлом в суффиксном дереве Ti, то пара
является узлом в суффиксном дереве Ti, то пара 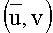 называется ссылочной парой строки w относительно Ti. Если u - самый длинный префикс в w, такой, что является
называется ссылочной парой строки w относительно Ti. Если u - самый длинный префикс в w, такой, что является  ссылочной парой, то
ссылочной парой, то  называется канонической ссылочной парой. В алгоритме Укконена ссылочная пара задается парой (s,k), где s - узел суффиксного дерева, k - число символов в слове v. Этой информации вполне достаточно, чтобы полностью задать положение узла атомарного суффиксного дерева asti, соответствующего суффиксу w.
называется канонической ссылочной парой. В алгоритме Укконена ссылочная пара задается парой (s,k), где s - узел суффиксного дерева, k - число символов в слове v. Этой информации вполне достаточно, чтобы полностью задать положение узла атомарного суффиксного дерева asti, соответствующего суффиксу w.
Алгоритм Укконена имеет вид:
 root
root
Для нас существенным является то, что в основном цикле построения суффиксного дерева (операторы 10-13) для каждого i в операторе 12 производится вычисление канонической ссылочной пары (s,k) активного суффикса слова t1 … ti. Знание (s,k) позволяет вычислить длину активного суффикса. Действительно, в узле s суффиксного дерева хранится позиция j начала суффикса слова x1 … xi, соответствующего узлу s суффиксного дерева. Значение длины активного суффикса вычисляют как s2[i]=i-j-k+1. Добавление этого действия позволяет вычислить весь массив значений s2[i] за время O(N).
4. Осуществление способа нахождения достаточно длинных повторяющихся фрагментов
Нахождение максимальных участков в конечной последовательности символов x[i] (0≤i<N) конечного алфавита, являющихся повторениями ранее встречавшихся участков, состоит в том, что сначала вычисляют последовательность s1[i] по всем N значениям индексов i (0≤i<N), где s1[i] - максимальная длина линейного участка указанной последовательности данных, индекс начального элемента которого совпадает с данным индексом i, совпадающего с некоторым другим участком той же последовательности данных x[i], начало которого расположено ближе к началу последовательности данных x[i], чем начало указанного линейного участка. Возможность вычисления последовательности s1[i] (0≤i<N) за время, линейно зависящее от N, вытекает из изложенного выше в п.п.1-3. Далее определяют все указанные максимальные участки как все отрезки x[m,n] последовательности x[i], для которых начальный индекс m удовлетворяет условию s1[m]>s1[m-1]-1, а конечный индекс n равен m+s1[m]-1. To, что при этом получаются именно все максимальные участки в конечной последовательности символов x[i] (0≤i<N) конечного алфавита, являющиеся повторениями ранее встречавшихся участков, следует из Свойства Б1 (см. п.1).

Изобретение относится к компьютерной обработке цифровых данных, точнее к способам сжатия массивов цифровой информации путем нахождения совпадающих фрагментов последовательности данных. Техническим результатом является уменьшение количества памяти, требующейся для представления всех максимальных повторяющихся участков. Для нахождения максимальных участков в конечной последовательности символов x[i] (0≤i<N) конечного алфавита, являющихся повторениями ранее встречавшихся участков, создают в памяти компьютера два битовых массива beg[i] и end[i]. Заполняют все элементы указанных битовых массивов нулями. Вычисляют последовательность sl[i] по всем N значениям индексов i, где sl[i] - максимальная длина линейного участка указанной последовательности данных. Определяют все указанные максимальные участки как все отрезки x[m,n], для которых начальный индекс m удовлетворяет условию sl[m]>sl[m-1]-1, а конечный индекс n равен m+sl[m]-1, для чего для каждого значения i проверяют выполнение условия sl[i]>sl[i-1]-1, и в случае выполнения этого условия устанавливают в битовых массивах beg[i] и end[i] значения beg[i]=1 и end[i+sl[i]]=1. Совокупность всех указанных максимальных участков восстанавливают по двум битовым массивам beg[i] и end[i]. 2 н. и 1 з.п. ф-лы, 2 ил.
1. Способ нахождения всех максимальных участков в конечной последовательности символов x[i] (0≤i<N) конечного алфавита, являющихся повторениями ранее встречавшихся участков, с целью сжатия файлов, при котором:
создают в памяти компьютера два битовых массива beg[i] и end[i] (0≤i<N);
заполняют все элементы указанных битовых массивов нулями;
вычисляют последовательность s1[i] по всем N значениям индексов i (0≤i<N), где s1[i] - максимальная длина линейного участка указанной последовательности данных, индекс начального элемента которого совпадает с данным индексом i, совпадающего с некоторым другим участком той же последовательности данных x[i], начало которого расположено ближе к началу последовательности данных x[i], чем начало указанного линейного участка,
определяют все указанные максимальные участки как все отрезки x[m,n] последовательности x[i], для которых начальный индекс m удовлетворяет условию s1[m]>s1[m-1]-1, а конечный индекс n равен m+s1[m]-1, для чего для каждого значения i проверяют выполнение условия s1[i]>s1[i-1]-1 и в случае выполнения этого условия устанавливают в битовых массивах beg[i] и end[i] значения beg[i]=1 и end[i+s1[i]]=1;
совокупность всех указанных максимальных участков восстанавливают по двум битовым массивам beg[i] и end[i], где единичное значение i-го элемента означает, что i-я позиция в указанной последовательности является соответственно началом и концом некоторого максимального указанного участка.
2. Способ нахождения всех максимальных участков в конечной последовательности символов x[i] (0≤i<N) конечного алфавита, являющихся повторениями ранее встречавшихся участков, с целью сжатия файлов, при котором:
создают в памяти компьютера два битовых массива beg[i] и end[i] (0≤i<N);
заполняют все элементы указанных битовых массивов нулями;
вычисляют последовательность s2[i] по всем N значениям индексов i (0≤i<N), где s2[i] - максимальная длина линейного участка указанной последовательности данных, индекс конечного элемента которого совпадает с данным индексом i, совпадающего с некоторым другим участком той же последовательности данных x[i], конец которого расположен ближе к началу последовательности данных x[i], чем конец указанного линейного участка,
определяют все указанные максимальные участки как все отрезки x[m,n] последовательности x[i], для которых конечный индекс n удовлетворяет условию s2[n]>s2[n+1]-1, а начальный индекс n равен n-s2[n]+1, для чего для каждого значения i проверяют выполнение условия s2[i]>s2[i+1]-1 и в случае выполнения этого условия устанавливают в битовых массивах beg[i] и end[i] значения end[i]=l и beg[i-s2[i]+1]=1;
совокупность всех указанных максимальных участков восстанавливают по двум битовым массивам beg[i] и end[i], где единичное значение i-го элемента означает, что i-я позиция в указанной последовательности является соответственно началом и концом некоторого максимального указанного участка.
3. Способ по п.2, в котором для вычисления массива всех значений функции s2[i] для всех N значений индексов i (0<i<N) используют компьютерную реализацию алгоритма Укконена, причем дополнительно для каждой i-й фазы алгоритма Укконена после определения канонической ссылочной пары (s,k) активного суффикса вычисляют s2[i] как длину активного суффикса, равную s2[i]=i-j-k+1, где j - позиция начала активного суффикса, хранящаяся в узле s суффиксного дерева, которое построено для префикса строки x[i], включающего в себя первые i символов указанной последовательности.
| US 6226628 В1, 01.05.2001 | |||
| US 5883588 А, 16.03.1999 | |||
| Соединение труб | 1959 |
|
SU129439A1 |
| СЖАТИЕ ДАННЫХ | 2005 |
|
RU2377670C2 |
| СПОСОБ ОБЪЕКТНО-ОРИЕНТИРОВАННОЙ ИНТЕРАКТИВНОЙ ОБРАБОТКИ ВИДЕОИНФОРМАЦИИ | 2002 |
|
RU2212709C1 |
Авторы
Даты
2013-01-27—Публикация
2010-05-26—Подача