Изобретение относится к области приборостроения и может быть использовано для компенсации погрешностей твердотельного волнового гироскопа в составе систем ориентации и навигации.
Известны способы моделирования погрешностей твердотельного волнового гироскопа для их последующей алгоритмической компенсации (см., например, книгу М.А.Басараб, В.Ф.Кравченко, В.А.Матвеева «Математическое моделирование физических процессов в гироскопии», М., 2005, стр.69-74), обусловленных конструктивными факторами, работой системы возбуждения резонатора, вибрациями основания, которые представлены математическими моделями.
За прототип взят способ компенсации погрешностей в показаниях твердотельного волнового гироскопа (см. книгу В.А.Матвеева, В.И.Липатникова, А.В.Алехина «Проектирование волнового твердотельного гироскопа». М., 1998, стр.140).
В этом способе для выделения из показаний твердотельного волнового гироскопа измеряемой входной угловой скорости предварительно определяют коэффициенты (Ωo, Ωm, φo) математической модели скорости дрейфа твердотельного волнового гироскопа, а в рабочем режиме алгоритмически компенсируют его скорость дрейфа, используя следующую модель выходного сигнала твердотельного волнового гироскопа
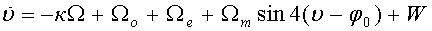 ,
,
где К - масштабный коэффициент;
Ω - измеряемая входная угловая скорость (полезный сигнал);
Ωо - постоянная составляющая скорости дрейфа;
Ωm - амплитудное значение переменной составляющей скорости дрейфа;
φ0 - положение оси резонатора с максимальной добротностью;
W - случайная составляющая скорости дрейфа;
Ωe - тепловая составляющая скорости дрейфа, которую также определяют предварительно.
Математическая модель тепловой составляющей скорости дрейфа в известном способе представлена в виде экспоненты, постоянную времени Т которой выбирают такой, чтобы наилучшим образом математическая модель показаний воспроизводила взятую для аппроксимации реализацию скорости дрейфа.
В известном способе учет температурной скорости дрейфа производится с помощью фиксированной экспоненциальной составляющей Ωe, параметры которой, постоянная времени Т и амплитуда Ωe0, выбираются неизменными для рабочего режима по результатам предварительных калибровочных испытаний.
При таком способе температурная компенсация может происходить со значительными погрешностями и даже может увеличивать собственную погрешность твердотельного волнового гироскопа.
Погрешность твердотельного волнового гироскопа зависит от угловой ориентации υ волны резонатора относительно корпуса прибора.
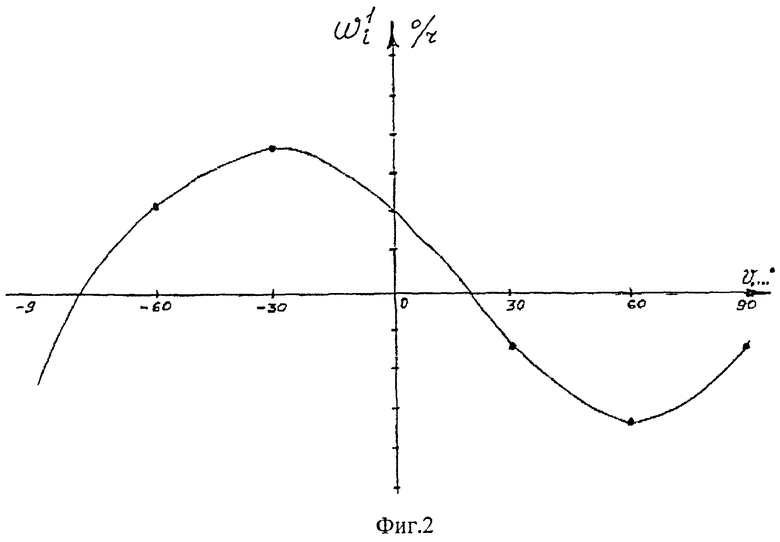
Типичная экспериментальная зависимость от угла волны резонатора переменной скорости дрейфа твердотельного волнового гироскопа представлена на фиг.2.
Из зависимости на фиг.2 видно, что переменная скорость дрейфа образца ТВГ имеет синусоидальный характер ω=ωmsin2(υ+φ1), с двойной частотой изменения в диапазоне углов υ=±180°.
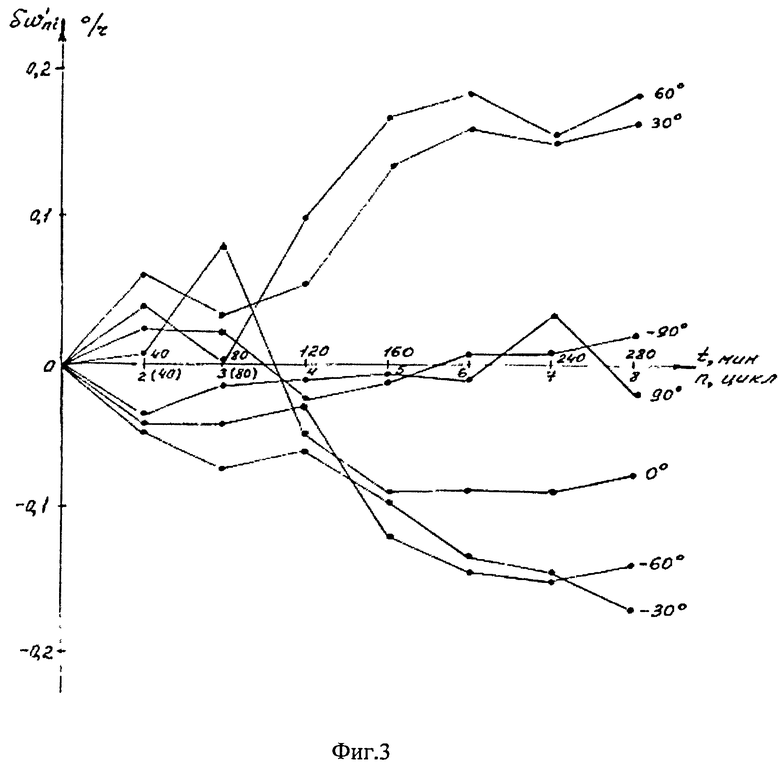
Типичная экспериментальная зависимость изменения во времени при запуске переменной скорости дрейфа твердотельного волнового гироскопа на разных углах волны резонатора показана на фиг.3.
Характер зависимостей на фиг.3 говорит о том, что переменная составляющая систематической скорости дрейфа изменяется в запуске не только от угла волны резонатора, но и во времени (от цикла к циклу последовательных измерений на одних и тех же углах волны).
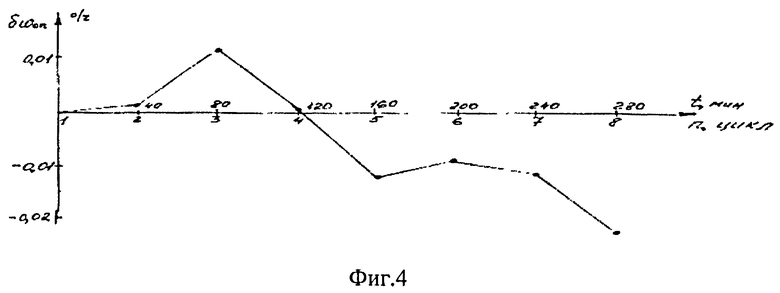
При этом изменения имеют экспоненциальный характер и зависят от угла волны. Конечное изменение в запуске переменной составляющей скорости дрейфа твердотельного волнового гироскопа на разных углах волны резонатора представлено на фиг.4.
Конечное изменение характеризует разность значений скоростей дрейфа в конечных циклах измерений и в первом цикле измерений.
Величина конечного изменения переменной скорости дрейфа имеет синусоидальный характер с частотой изменения одинаковой с частотой изменения переменной скорости дрейфа от угла волны.
На зависимости, представленной на фиг.4, видны зоны максимального и минимального изменения переменной скорости дрейфа в запуске. При этом периодически меняется знак изменения переменной скорости дрейфа в запуске.
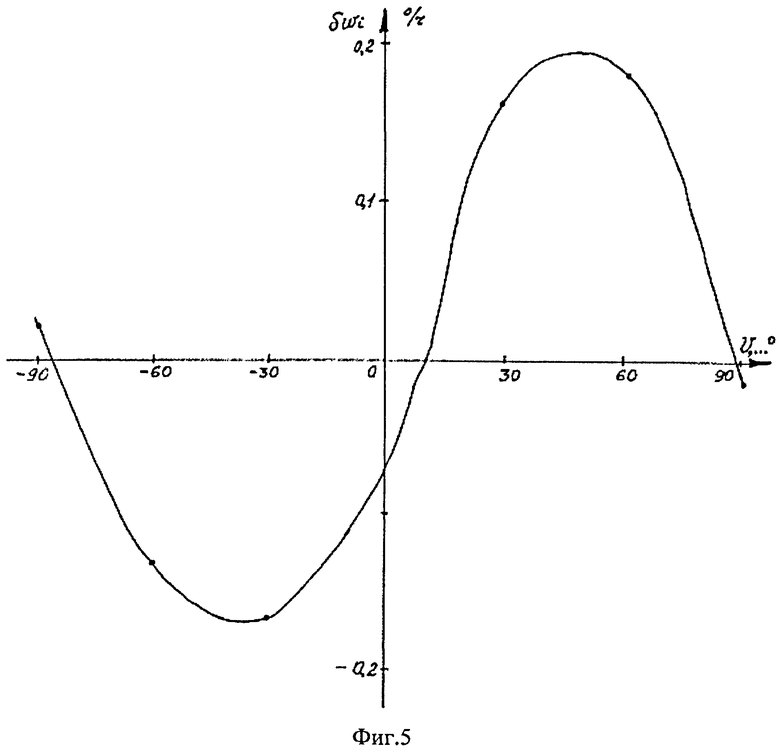
Типичная экспериментальная зависимость изменения во времени при запуске постоянной систематической составляющей скорости дрейфа твердотельного волнового гироскопа показана на фиг.5.
Постоянная составляющая скорости дрейфа не зависит от угла волны, но изменяется в запуске по закону, близкому к экспоненциальному.
Изменения в запуске переменной скорости дрейфа и постоянной скорости дрейфа имеют тепловую природу.
При работе ТВГ происходят колебания его резонатора с частотой порядка 3000 Гц. Из-за этих колебаний в результате внутреннего трения в материале резонатора происходит выделение тепла. Выделение тепла вызывает изменение температуры резонатора и температурные изменения его физических и конструктивных характеристик, что обуславливает температурную скорость дрейфа.
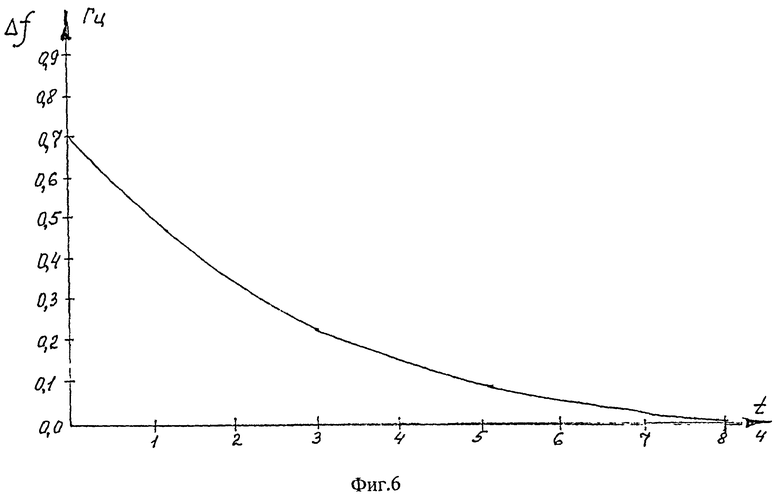
Изменение в запуске резонансной частоты резонатора, измеренное для твердотельного волнового гироскопа, показано на фиг.6.
Экспериментальная зависимость резонансной частоты резонатора твердотельного волнового гироскопа изменяется в запуске по экспоненциальному закону, что характерно для тепловых процессов.
В известном способе скорость дрейфа твердотельного волнового гироскопа компенсируют с помощью одной экспоненциальной зависимости, параметры которой постоянные в рабочем режиме и выбираются предварительно по результатам аппроксимации реализации скорости дрейфа в калибровочных испытаниях.
Применение известного способа компенсации накладывает ограничения на использование твердотельного волнового гироскопа. Длительность запуска должна быть небольшой и он должен происходить на неподвижном относительно Земли основании. В этих условиях волна резонатора находится на квазипостоянном угле и переменная составляющая скорости дрейфа будет иметь изменяющийся характер, как представлено на фиг.3. Такой характер переменной составляющей скорости дрейфа можно скомпенсировать, применяя экспоненциальную зависимость, как предлагается в известном способе. Однако при длительном запуске на неподвижном относительно Земли основании изменяется угловое положение волны резонатора за счет вращения Земли относительно инерциального пространства. При выставке оси чувствительности по оси Мира изменение относительно корпуса гироскопа углового положения волны за 12 часов составит Δυ=54°(Δυ=-кΔψ, где Δψ - угол поворота основания, к - масштабный коэффициент, Δψ=Ω3t, Ω3=15°/ч - угловая скорость вращения Земли, t=12 ч, к=0,3). Еще более значительное и быстрое изменение угла волны резонатора может происходить при установке твердотельного волнового гироскопа на высокоманевренном объекте, например самолете, имеющем угловые скорости до 400°/c.
Таким образом, на подвижном основании вследствие изменения угла волны будет изменяться характер скорости дрейфа, в том числе и температурной составляющей. Так изменение положения волны резонатора может изменять не только величину температурной скорости дрейфа, но и знак этого изменения, что будет приводить к снижению точности известного способа компенсации вплоть до отрицательного действия этой компенсации в случае изменения знака.
Таким образом, проведенный анализ показал, что при компенсации температурной скорости дрейфа твердотельного волнового гироскопа с применением известного способа могут быть значительные погрешности компенсации особенно при установке гироскопа на высокоманевренный объект вплоть до ее отрицательного действия.
Техническим результатом, который может быть получен при осуществлении настоящего изобретения, является повышение точности компенсации температурной скорости дрейфа твердотельного волнового гироскопа.
Технический результат достигается тем, что в известном способе алгоритмической компенсации температурной скорости дрейфа твердотельного волнового гироскопа, включающем предварительное определение параметров математической модели температурной скорости дрейфа твердотельного волнового гироскопа, а в рабочем режиме определение углового положения волны резонатора υ относительно корпуса гироскопа и алгоритмическую компенсацию его температурной скорости дрейфа в соответствии с этой моделью, дополнительно в предварительной калибровочной операции при нормальной температуре окружающей среды твердотельный волновой гироскоп устанавливают на неподвижное основание осью чувствительности вертикально, выдерживают его при этой температуре до момента достижения температуры резонатора Θp температуры окружающей среды, производят запуск твердотельного волнового гироскопа в нулевом угловом положении волны резонатора относительно его корпуса, при достижении времени готовности твердотельного волнового гироскопа устанавливают волну резонатора в угловое положение минус 90°, используя режим управления прецессией волны резонатора, и в интегрирующем режиме измеряют скорость дрейфа твердотельного волнового гироскопа в течение 3 минут и резонансную частоту колебаний резонатора, аналогичным образом выполняют измерения скорости дрейфа волны резонатора и резонансной частоты на углах минус 60°, минус 30°, 0°, 30°, 60°, 90° в первом цикле измерений, после завершения первого цикла выполняют еще семь таких циклов до момента стабилизации резонансной частоты резонатора, а затем в рабочем режиме твердотельного волнового гироскопа измеряют текущее значение частоты резонатора f и производят с помощью вычислителя алгоритмическую компенсацию температурной скорости дрейфа твердотельного волнового гироскопа, используя следующую математическую модель температурной скорости дрейфа.
ω∂(υ,Θp)=ω01+ωmsin k(υ+φ1)+δω0(f-f0)(fy-fo)-1+δω(υ)(f-f0)(fy-f0)-1,
где 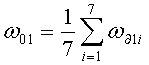 - постоянная составляющая скорости дрейфа в первом цикле измерений;
- постоянная составляющая скорости дрейфа в первом цикле измерений;
ω∂1i - скорость дрейфа в первом цикле измерений на i-м угле волны резонатора;
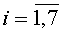 - нумерация углового положения волны резонатора;
- нумерация углового положения волны резонатора;
ωm - амплитуда переменной скорости дрейфа, определяемая с использованием измеренных значений ω1i;
φ1 - начальный фазовый угол переменной скорости дрейфа, определяемый с использованием измеренных значений ω1i;
k - номер гармоники, определяемый с использованием измеренных значений φ1i;
ω1i=ω∂1i-ω01;
δω0=ω08-ω01;
ω08 - постоянная скорость дрейфа в восьмом цикле измерений;
f0 - резонансная частота резонатора в первом цикле измерений на угле волны резонатора минус 90°;
fy - установившаяся частота резонатора в восьмом цикле измерений на угле волны резонатора 90°;
δω(υ)=δωmsin k(υ+φ2);
δωm - амплитуда зависимости конечного температурного изменения переменной скорости дрейфа от угла волны резонатора, определяемая с использованием измеренных значений δωi;
φ2 - начальный фазовый угол зависимости конечного температурного изменения переменной скорости дрейфа от угла волны резонатора, определяемая с использованием измеренных значений δωi;
δωi=ω8i-ω1i;
ω8i - значения переменной скорости дрейфа в восьмом цикле измерений на i-x углах волны резонатора.
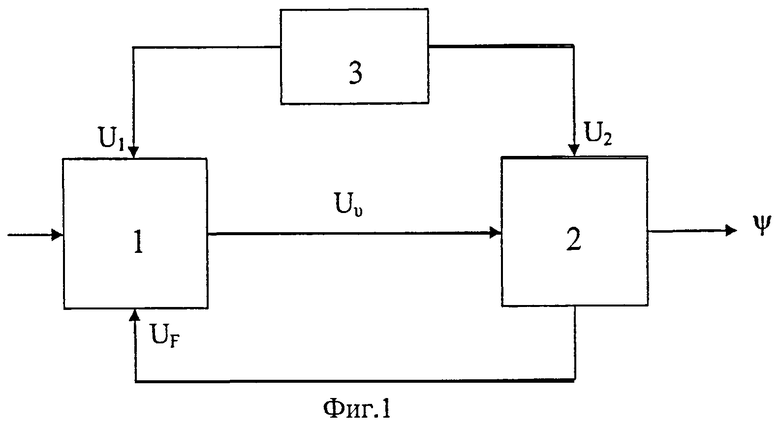
Блок-схема твердотельного волнового гироскопа представлена на фиг.1.
Датчик твердотельного волнового гироскопа 1 содержит чувствительный элемент - полусферический кварцевый резонатор; емкостные датчики перемещения для определения угла волны резонатора; емкостные датчики силы для управления параметрами волны резонатора; предварительные усилители для усиления сигналов, поступающих с емкостных датчиков.
Блок электроники 2 обрабатывает первичные сигналы с датчиков твердотельного волнового гироскопа, вырабатывает сигналы управления параметрами волны резонатора, вырабатывает текущие значения резонансной частоты резонатора, формирует математическую модель компенсационного сигнала, с помощью которого алгоритмически компенсирует погрешности твердотельного волнового гироскопа и вырабатывает приращения угла поворота корпуса.
Система электропитания 3 питает систему емкостных датчиков и электроники твердотельного гироскопа напряжениями U1, электронных схем блока электроники напряжениями U2.
По сигналам Uυ, снимаемых с датчиков сигналов твердотельного гироскопа в электронном блоке формируются сигналы UF, управляющие параметрами волны резонатора, а также могут вырабатываться управляющие сигналы, реализующие режим управляемой прецессии гироскопа.
В результате обработки показаний твердотельного волнового гироскопа, полученных на i-x углах волны резонатора в n-циклах определяют значения систематических составляющих скоростей дрейфа:
ω∂ni=ωcni-ωз,
где n - нумерация циклов измерений, 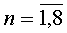 ;
;
i - нумерация угловых положений волны резонатора в цикле, 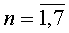 ;
;
ωз - составляющая угловой скорости Земли, направленная по оси чувствительности гироскопа;
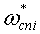 - средняя скорость прецессии гироскопа (показание гироскопа) для n-го цикла на i-м угле;
- средняя скорость прецессии гироскопа (показание гироскопа) для n-го цикла на i-м угле;
ω∂ni - скорость дрейфа гироскопа для n-го цикла на i-м угле.
Находят постоянную составляющую систематической скорости дрейфа в каждом n-ом цикле для измерений на i-x углах волны резонатора:
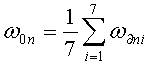 .
.
Определяют значения переменной составляющей систематической скорости дрейфа на i-м угле волны n-го цикла:
ωni=ω∂ni-ωon.
Экспериментальные исследования показывают, что скорость дрейфа твердотельного волнового гироскопа является функцией угла волны и температуры ротора резонатора:
ω∂=ω∂(υ,Θp),
Базовое состояние гироскопа характеризуется параметрами υ0, Θo0, где υ0 - исходный нулевой угол волны резонатора, Θp0 - исходная температура резонатора в момент запуска гироскопа.
Отклонения этих параметров от базовых значений обозначим как Δυ и ΔΘp. Тогда скорость дрейфа представим в виде:
ω∂=ω∂(υ0+Δυ,Θp0+ΔΘp)
Представим скорость дрейфа ω∂ в виде первых членов разложения в ряд Тейлора:
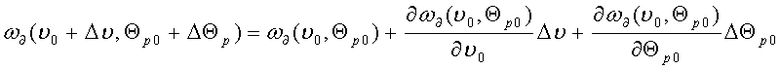 .
.
Тогда математическая модель скорости дрейфа с учетом влияния температуры и угла волны резонатора:
ω∂(υ,Θp)=k0+k1Δυ+k2ΔΘp,
где k0=ω∂(υ0,Θp0); 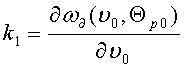 ;
; 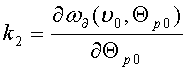 .
.
Определим составляющие этой модели. Базовым значением скорости дрейфа является измеренное предварительно значение скорости дрейфа в нулевом угловом положении волны резонатора (i=4) для первого цикла измерения (n=1):
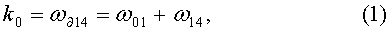
где 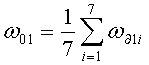 , ω14=ω∂14-ω01.
, ω14=ω∂14-ω01.
Определим составляющую скорости дрейфа, обусловленную изменением угла волны резонатора.
Измеренные значения ω1i характеризуют экспериментальную зависимость переменной составляющей скорости дрейфа в первом цикле измерений для i-x значений углов волны, которая имеет синусоидальный характер.
Аппроксимируя эту зависимость методом наименьших квадратов, определяем ее аналитическое выражение:
ω1(υ)=ωmsin k(υ+φ1),
где ωm - амплитуда переменной скорости дрейфа, определяемая с использованием измеренных значений ω1i;
φ1 - начальный фазовый угол, определяемый с использованием измеренных значений ω1i;
k - номер гармоники, определяемый с использованием измеренных значений ω1i.
Скорость дрейфа на текущем угле волны резонатора:
ω∂1(υ)=ω01+ωmsin k(υ+φ1).
Тогда скорость дрейфа, обусловленная изменением угла волны резонатора:
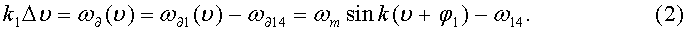
Составляющая скорости дрейфа, обусловленная изменением температуры резонатора гироскопа:
k2ΔΘp=δω0+δω(υ).
Эта составляющая складывается из температурных изменений постоянной скорости дрейфа δω0 и переменной скорости дрейфа δω(υ).
Температурное изменение постоянной составляющей скорости дрейфа в запуске за 8 циклов (см. фиг.5):
δω0=ω08-ω01,
где 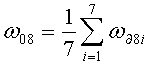 .
.
Температурное изменение резонансной частоты в запуске за 8 циклов (см. фиг.6):
Δf=fy-f0,
где f0 - измеренное значение резонансной частоты резонатора в первом цикле измерений (n=1) на угле волны минус 90° (i=1);
fy - измеренное значение резонансной частоты резонатора в восьмом цикле измерений (n=8) на угле волны 90° (i=7).
Коэффициент влияния изменения резонансной частоты резонатора (температуры резонатора) на постоянную составляющую скорости дрейфа:
k1=δω0(fy-f0)-1.
Текущее температурное изменение в запуске постоянной составляющей скорости дрейфа:
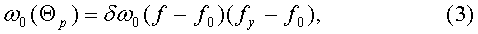
где f - текущее значение в запуске резонансной частоты ротора;
Θp - текущая температура ротора.
Определяют температурное изменение переменной составляющей скорости дрейфа.
Конечные температурные изменения переменной составляющей скорости дрейфа в запуске за 8 циклов (см. фиг.3)
δωi=ω8i-ω1i,
где
ω1i - значения переменной составляющей скорости дрейфа на i-x углах волны резонатора в первом цикле измерений;
ω8i - значения переменной составляющей скорости дрейфа на i-x углах волны резонатора в восьмом цикле измерений.
Конечные температурные изменения δωi переменной составляющей скорости дрейфа в запуске в зависимости от угла волны резонатора имеют синусоидальный характер (см. фиг.4).
Аппроксимируя эту зависимость методом наименьших квадратов определяют ее аналитическое выражение:
δω(υ)=δωmsin k(υ+φ2),
где
δωm - амплитуда зависимости конечного температурного изменения переменной скорости дрейфа от угла волны резонатора, определяемая с использованием значений δωi;
φ2 - начальный фазовый угол зависимости конечного температурного изменения переменной скорости дрейфа от угла волны резонатора, определяемого с использованием измеренных значений δωi.
Коэффициент влияния температурного изменения резонансной частоты (температуры) на переменную составляющую скорости дрейфа:
k2=δω(υ)(fy-f0)-1.
Текущее температурное изменение в запуске переменной составляющей скорости дрейфа:
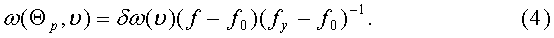
Тогда, складывая соотношения (1), (2), (3), (4) получим предлагаемую математическую модель температурной скорости дрейфа твердотельного волнового гироскопа
ω(Θp,υ)=ω01+ωmsin k(υ+φ1)+δω0(f-f0)(fy-fo)-1+δω(υ)(f-f0)(fy-f0)-1.
Таким образом, предлагаемый способ алгоритмической компенсации температурной скорости дрейфа твердотельного волнового гироскопа имеет следующие отличия от известного способа:
- в предварительной калибровочной операции по определению параметров математической модели температурной скорости дрейфа вводятся новые действия, связанные с измерением скоростей дрейфа на разных углах ориентации его волны и резонансной частоты колебаний резонатора с исходной температуры в момент запуска до установившейся температуры в конце запуска, длительность которого определена выбранным количеством циклов измерений;
- в операции алгоритмического компенсирования температурной скорости дрейфа в рабочем режиме получено новое качество компенсации, связанное с ее обеспечением при произвольных углах ориентации упругой волны резонатора гироскопа;
- алгоритмическая компенсация температурной скорости дрейфа происходит по новой аналитической зависимости, в которой введен новый член температурного изменения постоянной составляющей скорости дрейфа, и новый член, учитывающий изменение температурной скорости дрейфа переменной составляющей скорости дрейфа от угла волны.
На фиг.1 представлена блок-схема твердотельного волнового гироскопа.
На фиг.2 показана типичная экспериментальная зависимость от угла волны резонатора переменной скорости дрейфа твердотельного волнового гироскопа.
На фиг.3 представлена типичная экспериментальная зависимость изменения во время запуска переменной составляющей скорости дрейфа твердотельного волнового гироскопа на разных углах волны резонатора.
На фиг.4 показано конечное изменение в запуске переменной составляющей скорости дрейфа твердотельного волнового гироскопа на разных углах волны резонатора.
На фиг.5 показано изменение постоянной скорости дрейфа в запуске.
На фиг.6 представлена зависимость изменения в запуске резонансной частоты резонатора твердотельного волнового гироскопа.
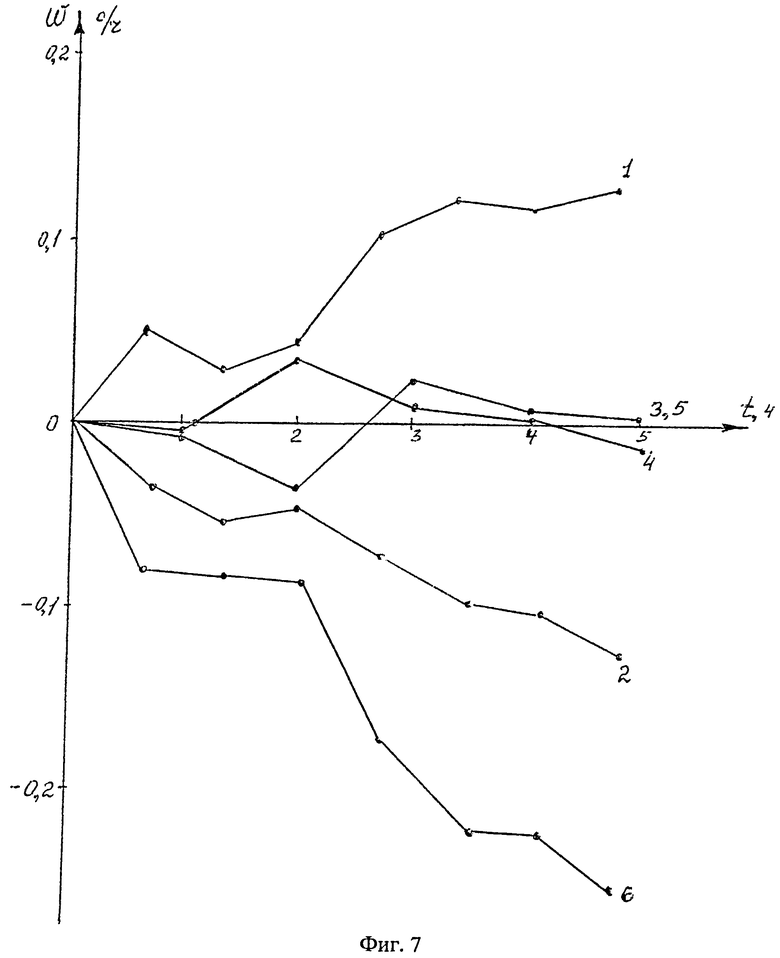
На фиг.7 показано изменение переменной составляющей скорости дрейфа твердотельного волнового гироскопа в запуске без компенсации и с алгоритмической компенсацией.
Проводились расчеты по экспериментальным данным точности алгоритмической компенсации температурной скорости дрейфа твердотельного волнового гироскопа с применением предлагаемого способа. Используя экспериментальные значения изменения частоты резонатора твердотельного волнового гироскопа (см. фиг.6) в запуске определяли изменение частоты Δf=fy-f0. Рассматривали изменения переменной скорости дрейфа на углы волны 30° и минус 30° (см. фиг.3). Используя экспериментальные значения конечных изменений скорости дрейфа в запуске (см. фиг.4), определяли изменения скоростей дрейфа δω(υ) для этих углов и находили коэффициенты температурного влияния на переменную составляющую скорости дрейфа для углов 30° и минус 30° δω(υ)(fy-f0)-1. Компенсационную зависимость в соответствии с предлагаемым способом находили как произведение коэффициента температурного влияния на разность резонансных частот начальной и текущей δω(υ)(f-f0)-1(fy-fo), где текущую частоту брали из экспериментального графика, представленного на фиг.6.
На фиг.7 зависимостями 1, 2 представлены экспериментальные значения изменения скорости дрейфа твердотельного гироскопа соответственно на углах волны резонатора 30° и минус 30° без применения компенсации. Зависимости 3 и 4 характеризуют остаточную скорость дрейфа соответственно на углах 30° и минус 30° с применением предлагаемой компенсации.
Зависимость 5 показывает остаточную скорость дрейфа после применения известного способа компенсации на угле волны резонатора 30° и предварительного определения коэффициентов модели компенсационного сигнала на этом угле. Зависимость 6 показывает остаточную скорость дрейфа после применения известного способа компенсации, когда параметры математической модели компенсации определены предварительно как предполагается в этом способе на каком-то конкретном угле волны резонатора, в данном случае на угле 30°, а компенсация была выполнена при работе гироскопа, когда положение волны характеризовалось углом минус 30°.
Из сравнения зависимостей, представленных на фиг.7, видно, что применение предлагаемого способа позволяет значительно повысить точность гироскопа, компенсируя температурные изменения скорости дрейфа при любом угловом расположении волны резонатора. Известный способ обеспечивает компенсацию в пределах угла волны резонатора, на котором предварительно были определены параметры математической модели компенсации. Зависимость 6 показывает, что в известном способе применения компенсации на другом угле волны резонатора может не только уменьшать точность компенсации, но и приводить к дополнительной погрешности.
Таким образом, использование предлагаемого способа компенсации температурной скорости дрейфа твердотельного волнового гироскопа позволяет повысить точность гироскопа при наличии изменяющейся в запуске скорости дрейфа, обусловленной изменением температуры его резонатора.
Повышение точности твердотельного волнового гироскопа расширяет область его применения, например появляется возможность их использования в инерциальных навигационных системах и системах ориентации авиационного, морского и космического применения.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ и система компенсации дрейфа твердотельного волнового гироскопа | 2016 |
|
RU2619815C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МАСШТАБНОГО КОЭФФИЦИЕНТА ТВЕРДОТЕЛЬНОГО ВОЛНОВОГО ГИРОСКОПА НА ПОВОРОТНОМ СТОЛЕ | 2012 |
|
RU2579768C2 |
| Способ измерения угловой скорости с помощью волнового твердотельного гироскопа | 2020 |
|
RU2738824C1 |
| СПОСОБ ГИРОКОМПАСИРОВАНИЯ С ПРИМЕНЕНИЕМ ГИРОСКОПИЧЕСКОГО ДАТЧИКА УГЛОВОЙ СКОРОСТИ И КОМБИНИРОВАННОЙ КОМПЕНСАЦИИ ЕГО ДРЕЙФА | 2001 |
|
RU2189564C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УГЛА ОРИЕНТАЦИИ СТОЯЧЕЙ ВОЛНЫ В ТВЕРДОТЕЛЬНОМ ВОЛНОВОМ ГИРОСКОПЕ | 2012 |
|
RU2526585C2 |
| Способ считывания и управления колебаниями волнового твердотельного гироскопа | 2019 |
|
RU2704334C1 |
| СПОСОБ ИЗМЕРЕНИЯ НАПРЯЖЕННОСТИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ | 2015 |
|
RU2626065C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УГЛОВОЙ СКОРОСТИ С ИСПОЛЬЗОВАНИЕМ ВОЛНОВОГО ТВЕРДОТЕЛЬНОГО ГИРОСКОПА | 2020 |
|
RU2750428C1 |
| Способ компенсации температурных погрешностей инерциального измерительного блока систем ориентации и навигации | 2020 |
|
RU2758339C1 |
| Способ считывания и управления колебаниями волнового твердотельного гироскопа | 2018 |
|
RU2670245C1 |
Изобретение относится к области точного приборостроения, преимущественно гироскопического, и может быть использовано при создании твердотельных волновых гироскопов и систем ориентации и навигации на их основе. Предварительно для определения параметров математической модели температурной скорости дрейфа производят запуск гироскопа при исходной температуре его резонатора, равной температуре окружающей среды, выполняют цикл измерений скорости дрейфа и частоты резонатора гироскопа при различных угловых положениях упругой волны резонатора относительно корпуса в диапазоне углов от минус 90° до плюс 90°, повторяют эти циклы измерений до практической стабилизации частоты резонатора, а в рабочем режиме гироскопа измеряют текущее значение частоты резонатора и производят с помощью вычислителя алгоритмическую компенсацию температурной скорости дрейфа волнового твердотельного гироскопа, используя математическую модель температурной скорости дрейфа, параметры которой определены по результатам измерений в предварительном калибровочном запуске. Изобретение позволяет повысить точность компенсации. 7 ил.
Способ алгоритмической компенсации температурной скорости дрейфа твердотельного волнового гироскопа, включающий предварительное определение математически параметров модели температурной скорости дрейфа твердотельного волнового гироскопа, а в рабочем режиме определение углового положения волны резонатора υ относительно корпуса гироскопа и алгоритмическую компенсацию его температурной скорости дрейфа в соответствии с этой моделью, отличающийся тем, что в предварительной калибровочной операции при нормальной температуре окружающей среды твердотельный волновой гироскоп устанавливают на неподвижное основание осью чувствительности вертикально, выдерживают его при этой температуре до момента достижения температуры резонатора Θр температуры окружающей среды, производят запуск твердотельного волнового гироскопа в нулевом угловом положении волны резонатора относительно его корпуса, при достижении времени готовности твердотельного волнового гироскопа устанавливают волну резонатора в угловое положение минус 90°, используя режим управления прецессией волны резонатора, и в интегрирующем режиме измеряют скорость дрейфа твердотельного волнового гироскопа в течение 3 мин и резонансную частоту колебаний резонатора, аналогичным образом выполняют изменения скорости дрейфа волны резонатора и резонансной частоты на углах минус 60°, минус 30°, 0, 30°, 60°, 90° в первом цикле измерений, после завершения первого цикла выполняют еще семь таких циклов до момента стабилизации резонансной частоты резонатора, а затем в рабочем режиме твердотельного волнового гироскопа измеряют текущее значение частоты резонатора f и производят с помощью вычислителя алгоритмическую компенсацию температурной скорости дрейфа твердотельного волнового гироскопа, используя следующую математическую модель температурной скорости дрейфа:
ω∂(υ,Θp)=ω01+ωmsink(υ+φ1)+δω0(f-f0)(fy-fo)-1+δω(υ)(f-f0)(fy-f0)-1, где
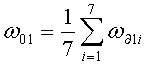 - постоянная составляющая скорости дрейфа в первом цикле измерений;
- постоянная составляющая скорости дрейфа в первом цикле измерений;
ω∂1i - скорость дрейфа в первом цикле измерений на i-м угле волны резонатора;
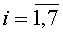 - нумерация углового положения волны резонатора;
- нумерация углового положения волны резонатора;
ωm - амплитуда переменной скорости дрейфа, определяемая с использованием измеренных значений ω1i;
φ1 - начальный фазовый угол переменной скорости дрейфа, определяемый с использованием измеренных значений ω1i;
k - номер гармоники, определяемый с использованием измеренных значений ω1i;
ω1i=ω∂1i-ω01;
δω0=ω08-ω01;
ω08 - постоянная скорость дрейфа в восьмом цикле измерений;
f0 - резонансная частота резонатора в первом цикле измерений на угле волны резонатора минус 90°;
fy - установившаяся частота резонатора в восьмом цикле измерений на угле волны резонатора 90°;
δω(υ)=δωmsink(υ+φ2);
δωm - амплитуда зависимости конечного температурного изменения переменной скорости дрейфа от угла волны резонатора, определяемая с использованием измеренных значений δωi;
φ2 - начальный фазовый угол зависимости конечного температурного изменения переменной скорости дрейфа от угла волны резонатора, определяемая с использованием измеренных значений δφi;
δφi=ω8i-ω1i;
ω8i - значения переменной скорости дрейфа в восьмом цикле измерений на i-x углах волны резонатора.
| МАТВЕЕВ В.А | |||
| и др | |||
| Проектирование волнового твердотельного гироскопа | |||
| - М.: изд-во МГТУ им | |||
| Н.Э.Баумана, 1998, с.140 | |||
| KR 20030084386 А, 01.11.2003 | |||
| Пломбировальные щипцы | 1923 |
|
SU2006A1 |
| US 7801694 B1, 21.09.2010 | |||
| JP 2006194701 A, 27.07.2006 | |||
| СПОСОБ АЛГОРИТМИЧЕСКОЙ КОМПЕНСАЦИИ ПОГРЕШНОСТИ ГИРОКОМПАСИРОВАНИЯ С ПРИМЕНЕНИЕМ ГИРОСКОПИЧЕСКОГО ДАТЧИКА УГЛОВОЙ СКОРОСТИ | 2001 |
|
RU2194948C1 |
Авторы
Даты
2013-04-27—Публикация
2011-09-21—Подача