Изобретение относится к области измерений электрических величин в беспроводных системах передачи информации, в частности, к способам оценки отношения сигнал-шум на входе приемного устройства для радиосигнала с цифровой амплитудной модуляцией и может быть применено, например, в телевизионных и прочих системах передачи видеоданных для оценки качества передачи цифровых изображений.
Известен аналогичный способ оценки отношения сигнал-шум на входе приемного устройства для радиосигнала с цифровой амплитудной модуляцией, описанный в источнике «Методика измерения отношения сигнал/шум каналов с аналоговой и цифровой модуляцией приборами серии ИТ-08 и мини-ИТ», имеющемся в сети «Интернет» по электронному адресу: http://www.planarchel.ru/Products/Measurement%20instrument/izmeritelnye-pribory-2/seriya-priborov-mini-it/paper_c-n_ratio_measuremant.pdf, а также на сайте: https://docplayer.ru/30553899-Metodika-izmereniya-otnosheniya-signal-shum-kanalov-s-analogovoy-i-cifrovoy-modulyaciey-priborami-serii-it-08-i-mini-it.html и состоящий в следующем: сначала на входе приемного устройства в частотной полосе полезного сигнала с помощью высокочувствительного шумомера со встроенным полосовым фильтром измеряют уровень сигнала, далее в частотной полосе с наименьшим содержанием полезного сигнала аналогичным образом замеряют уровень шума, после этого рассчитывают отношение сигнал-шум с учетом ширины полосы канала, ширины полосы фильтра, а также коэффициента прямоугольности фильтра, при этом отношение сигнал-шум рассчитывают либо по уровням напряжения сигнала и шума, либо по их мощности, а оба измерения проводят во входном тракте приемного устройства до резонансного фильтра.
Недостатком указанного аналога является низкая точность оценки сигнал-шум на входе приемного устройства для радиосигнала с цифровой амплитудной модуляцией, что является следствием усредненного характера замера уровня сигнала по всему ансамблю амплитуд без выделения временного отрезка сигнала с минимальным значением амплитуды.
В качестве прототипа выбран способ оценки отношения сигнал-шум на входе приемного устройства для радиосигнала с цифровой амплитудной модуляцией, описанный в источнике «Методика измерения отношения сигнал/шум каналов с аналоговой и цифровой модуляцией приборами серии ИТ-08 и мини-ИТ» имеющемся в сети «Интернет» по электронному адресу: http://www.planarchel.ru/Products/Measurement%20instrument/izmeritelnye-pribory-2/seriya-priborov-mini-it/paper_c-n_ratio_measuremant.pdf, а также на сайте: https://docplayer.ru/30553899-Metodika-izmereniya-otnosheniya-signal-shum-kanalov-s-analogovoy-i-cifrovoy-modulyaciey-priborami-serii-it-08-i-mini-it.html и состоящий в следующем: сначала на входе приемного устройства в частотной полосе полезного сигнала с помощью высокочувствительного шумомера со встроенным полосовым фильтром измеряют уровень сигнала, далее в частотной полосе с наименьшим содержанием полезного сигнала аналогичным образом замеряют уровень шума, после этого рассчитывают отношение сигнал-шум с учетом ширины полосы канала, ширины полосы фильтра, а также коэффициента прямоугольности фильтра, при этом отношение сигнал-шум рассчитывают либо по уровням напряжения сигнала и шума, либо по их мощности, а оба измерения проводят во входном тракте приемного устройства до резонансного фильтра.
Недостатком прототипа является низкая точность оценки сигнал-шум на входе приемного устройства для радиосигнала с цифровой амплитудной модуляцией, что является следствием усредненного характера замера уровня сигнала по всему ансамблю амплитуд без выделения временного отрезка сигнала с минимальным значением амплитуды.
Задачей технического решения является повышение точности оценки отношения сигнал-шум на входе приемного устройства для радиосигнала с цифровой амплитудной модуляцией.
Поставленная задача решается благодаря тому, что в способе оценки отношения сигнал-шум на входе приемного устройства для радиосигнала с цифровой амплитудной модуляцией, содержащем следующую последовательность действий: сначала на входе приемного устройства в частотной полосе полезного сигнала с помощью высокочувствительного шумомера со встроенным полосовым фильтром измеряют уровень сигнала, далее в частотной полосе с наименьшим содержанием полезного сигнала аналогичным образом замеряют уровень шума, после этого рассчитывают отношение сигнал-шум с учетом ширины полосы канала, ширины полосы фильтра, а также коэффициента прямоугольности фильтра, при этом отношение сигнал-шум рассчитывают либо по уровням напряжения сигнала и шума, либо по их мощности, а оба измерения проводят во входном тракте приемного устройства до резонансного фильтра; предусмотрены следующие отличия: перед вычислением отношения сигнал-шум с помощью шумомера с перестраиваемым полосовым пропускающим частотным фильтром, настроенным предварительно на полосу с минимальным содержанием полезного сигнала, в выходном тракте передающего устройства после конечного каскада усиления, но перед антенной, оценивают максимальный уровень напряжения собственных шумов передающего устройства, а при отсутствии такой возможности данный уровень напряжения задают приближенно, далее при тех же настройках фильтра шумомера во входном тракте приемного устройства после антенны, но перед резонансным фильтром оценивают максимальный уровень напряжения внешних помех, затем измеряют или оценивают приближенно расстояние между антеннами приемного и передающего устройств, после чего при известных максимумах напряжений внешних помех и собственных шумов передающего устройства, а также при известном расстоянии между антеннами, рассчитывают требуемое отношение сигнал-шум с помощью решения комплексного уравнения в частных производных второго порядка вида
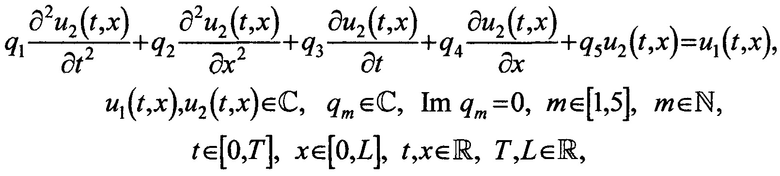
u1(t,x) - функция внешних возмущений;
u2(t,x) - искомая функция, эквивалент напряжения распространения;
q1,q2,q3,q4,q5 - коэффициенты, учитывающие свойства среды;
m - индекс коэффициентов уравнения с частными производными;
Im qm - мнимая часть m-го коэффициента;
t - время;
х - координата;
Т - максимальное значение времени;
L - максимальное значение координаты;
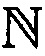 - множество натуральных чисел;
- множество натуральных чисел;
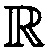 - множество действительных чисел;
- множество действительных чисел;
 - множество комплексных чисел;
- множество комплексных чисел;
с краевыми и начальными условиями
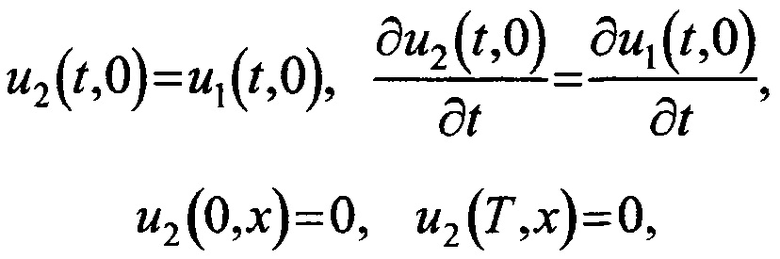
при этом за счет предварительного подбора значений действительных частей комплексных коэффициентов q1,q2,q3,q4,q5 учитывают свойства среды распространения радиосигнала, для нахождения решения уравнения в частных производных водят прямоугольную декартову систему координат с осями времени t и координаты х, начало системы координат совмещают с фазовым центром передающей антенны, ось х направляют таким образом, чтобы она проходила через фазовый центр приемной антенны, уравнение в частных производных решают с помощью высокопроизводительного вычислительного устройства, все двумерные действительные параметры математической модели на основе записанного уравнения и двумерные части комплексных функций в памяти вычислительного устройства представляют числовыми матрицами, а все одномерные действительные параметры и одномерные части комплексных параметров задают одномерными числовыми массивами, в зависимости от свойств среды коэффициенты q1,q2,q3,q4,q5 задают постоянными или переменными по одному или обоим аргументам t и х, далее для действительных и мнимых частей функций u1(t,x), u2(t,x) вводят двумерную дискретную решетку, количество узлов решетки и размер постоянных приращений по времени t и координате х подбирают предварительно в зависимости от максимального значения несущей частоты полезного сигнала и максимального расстояния его передачи, возмущающие воздействия располагают в действительной части функции u1(t,x), которую в начале координат ассоциируют с передающей антенной и задают с помощью формулы

Re u1(t,0) - действительная часть u1(t,0);
Im u1(t,0) - мнимая часть u1(t,0);
s(t) - полезный сигнал;
e1(t) - собственный шум передающего устройства;
k1 - коэффициент поправки сигнала в ближней зоне;
в остальной части области определения и действительную, и мнимую составляющие u1(t,x) задают нулевыми значениями, после этого для согласования краевых и начальных условий значения u1(0,0) и u1(Т,0) обнуляют, за счет коэффициента пропорциональности k1 корректируют уровень полезного сигнала в ближней зоне, значение k1 подбирают предварительно и задают положительным числом, массив для s(t) задают эталонным фрагментом полезного сигнала с цифровой амплитудной модуляцией, в котором присутствует как минимум один временной отрезок с минимальной ненулевой амплитудой сигнала и как минимум один временной отрезок с максимальным значением этой амплитуды, при этом указанные минимум и максимум для амплитуды полезного сигнала в модели задают значениями, характерными для реального передающего устройства, эталонный фрагмент полезного сигнала подготавливают заранее и сохраняют в памяти вычислительного устройства, массив для e1(t) формируют генератором случайных чисел вычислительного устройства, при этом максимальный уровень e1(t) задают оцененным ранее максимальным значением напряжения собственных шумов передающего устройства, уравнение в частных производных решают на основе метода Фурье с разложением функций u1(t,x) и u2(t,х) по временному базису с несколькими гармониками
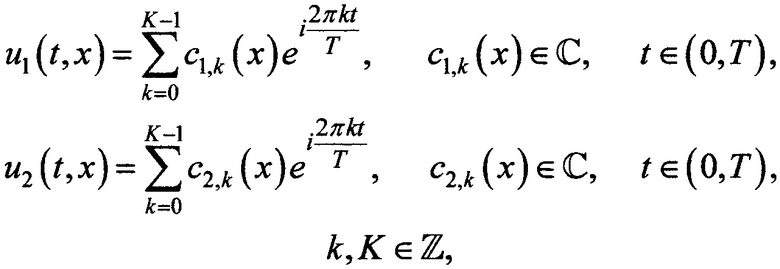
c1,k(x) - k-й коэффициент разложения Фурье функции u1(t,х);
с2,k(x) - k-й коэффициент разложения Фурье функции u2(t,x);
i - мнимая единица;
π - константа, равная 3.14;
k - индекс коэффициентов разложения Фурье;
K - количество коэффициентов разложения Фурье;
 - множество целых чисел;
- множество целых чисел;
причем количество коэффициентов разложения K задают предварительно числом большим или равным одной четвертой от количества узлов дискретной решетки по оси времени t и меньшим или равным этому количеству, далее, согласно записанным формулам разложения, находят выражения для комплексных частных производных u2(t,х), подставляют их вместе с разложениями u2(t,х) и u1(t,x) в исходное уравнение в частных производных, приводят подобные слагаемые и получают множество комплексных обыкновенных дифференциальных уравнений второго порядка вида
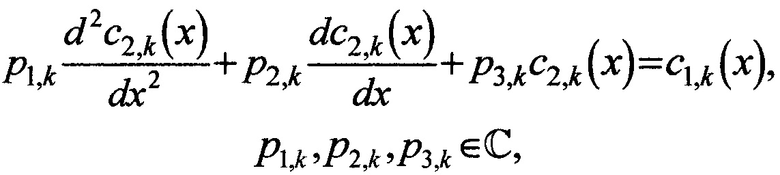
p1,k,р2,k,р3,k - комплексные коэффициенты обыкновенного дифференциального уравнения для k-го коэффициента с2,k(х);
после этого коэффициенты разложения с1,k(х) функции внешних возмущений u1(t,x) в правых частях этих уравнений получают с помощью постолбцового одномерного прямого комплексного дискретного преобразования Фурье, применяемого к u1(t,x) в каждой координатной отметке поочередно, а значения p1,k,р2,k,р3,k задают с помощью формулы
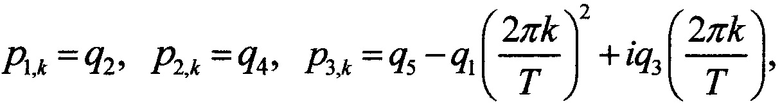
причем в случае переменных коэффициентов q1,q2,q3,q4,q5 значения p1,k,р2,k,р3,k пересчитывают каждый раз, когда меняется значение хотя бы одного из коэффициентов q1,q2,q3,q4,q5, значения q1,q2,q3,q4,q5 задают предварительно таким образом, чтобы обеспечить устойчивость решения обыкновенного дифференциального уравнения при всех возможных сочетаниях q1,q2,q3,q4,q5, далее поочередно вычисляют коэффициенты разложения с2,k(х), при этом действительные и мнимые части с2,k(х) в первом координатном узле с учетом краевых условий сразу приравнивают соответствующим значениям с1,k(х), то есть
Re c2,k,1=Re c1,k,1, Im с2,k,1=Im с1,k,1,
с2,k,1 - значение k-го коэффициента c2,k(x) в первом координатном узле;
с1,k,1 - значение k-го коэффициента c1,k(x) в первом координатном узле;
Re - обозначение действительных частей коэффициентов;
Im - обозначение мнимых частей коэффициентов;
в остальных координатных узлах, начина со второго, значения с2,k(х) находят по формуле
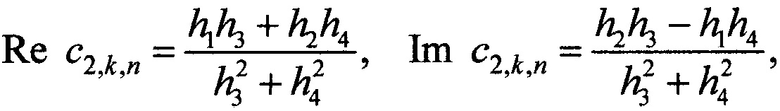
с2,k,n - значение k-го коэффициента с2,k(х) в n-ом координатном узле;
n - индекс координатного узла;
h1,h2,h3,h4 - вспомогательные параметры;
Re - обозначение действительных частей коэффициентов;
Im - обозначение мнимых частей коэффициентов;
при вспомогательных обозначениях
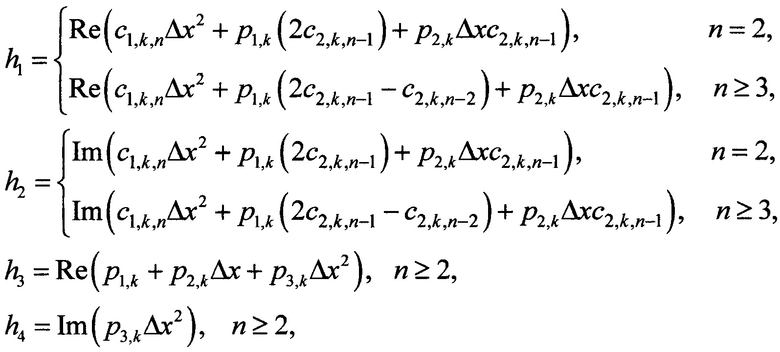
с1,k,n - значения k-го коэффициента с1,k(х) в n-ом координатном узле;
Δх - величина приращения (постоянный дискретный шаг) по оси х;
Re - обозначение действительных частей выражений в скобках;
Im - обозначение мнимых частей выражений в скобках;
после вычисления всех коэффициентов с2,k(х) возвращаются к разложению искомой функции и получают ее в комплексной форме путем постолбцового одномерного обратного комплексного дискретного преобразования Фурье, применяемого к u2(t,x) в каждой координатной отметке поочередно, эквивалент напряжения распространения извлекают из действительной части u2(t,x), далее накладывают внешние помехи согласно формуле
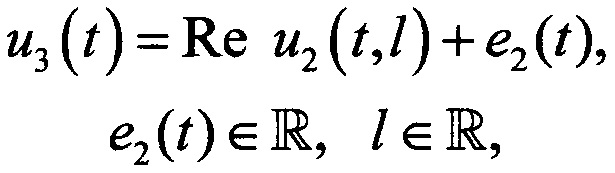
u3(t) - общее напряжение принятого радиосигнала вместе с помехами;
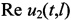 - действительная часть u2(t,x) на расчетном расстоянии;
- действительная часть u2(t,x) на расчетном расстоянии;
 - расчетное расстояние;
- расчетное расстояние;
e2(t) - внешние помехи на расчетном расстоянии;
при этом расчетное расстояние  между антеннами в модели задают предварительно и равным действительному, оцененному ранее, расстоянию между антеннами, массив для e2(t) формируют генератором случайных чисел вычислительного устройства, максимальный уровень e2(t) принимают равным, оцененному ранее, максимальному уровню напряжения внешних помех, после наложения помех получают выходной сигнал модели u3(t), уравнение в частных производных решают дважды, уровень сигнала S рассчитывают по выборке u3(t) на выходе модели как среднее арифметическое для квадратов напряжений сигнала при отсутствии шумов и помех, то есть при нулевых e1(t),e2(t), уровень шума Е рассчитывают по выборке u3(t) на выходе модели как среднее арифметическое для квадратов напряжений шума при отсутствии полезного сигнала, то есть при нулевом s(t), после этого вычисляют отношение сигнал-шум по формуле
между антеннами в модели задают предварительно и равным действительному, оцененному ранее, расстоянию между антеннами, массив для e2(t) формируют генератором случайных чисел вычислительного устройства, максимальный уровень e2(t) принимают равным, оцененному ранее, максимальному уровню напряжения внешних помех, после наложения помех получают выходной сигнал модели u3(t), уравнение в частных производных решают дважды, уровень сигнала S рассчитывают по выборке u3(t) на выходе модели как среднее арифметическое для квадратов напряжений сигнала при отсутствии шумов и помех, то есть при нулевых e1(t),e2(t), уровень шума Е рассчитывают по выборке u3(t) на выходе модели как среднее арифметическое для квадратов напряжений шума при отсутствии полезного сигнала, то есть при нулевом s(t), после этого вычисляют отношение сигнал-шум по формуле
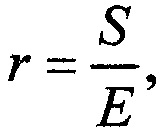
r - отношение сигнал-шум на антенне приемного устройства;
S - уровень сигнала на выходе модели;
Е - уровень шума на выходе модели;
при этом оценку минимального значения отношения сигнал-шум на выходе модели проводят на временном отрезке эталонного сигнала с минимальным уровнем амплитуды, оценку максимального значения отношения сигнал-шум на выходе модели проводят на временном отрезке эталонного сигнала с максимальным уровнем амплитуды, а в качестве итогового отношения сигнал-шум выбирают его минимальное значение.
Кроме того, если в частном случае действительная часть коэффициента q3 равна нулю, то в ходе моделирования каждый из коэффициентов с2,k(х) в координатных узлах дискретной решетки рассчитывают по упрощенной формуле
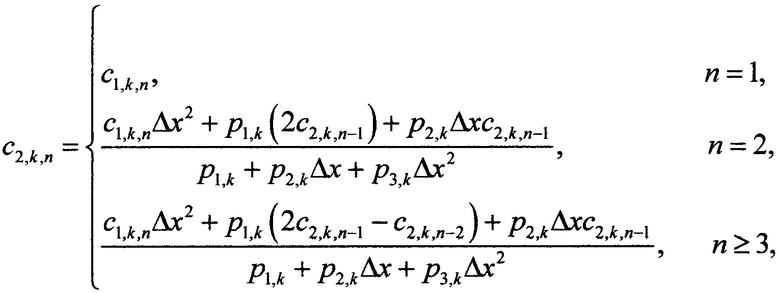
с последовательным вычислением действительной и мнимой частей с2,k,n, при этом условие равенства действительной части q3 нулю проверяют до применения основной расчетной формулы с параметрами h1,h2,h3,h4.
Сущность заявляемого технического решения поясняется следующими дополнительными материалами:
ФИГ. 1. Схема для пояснения осуществления способа;
ФИГ. 2. Пример полезного сигнала с амплитудной цифровой модуляцией;
ФИГ. 3. Пример графика шума;
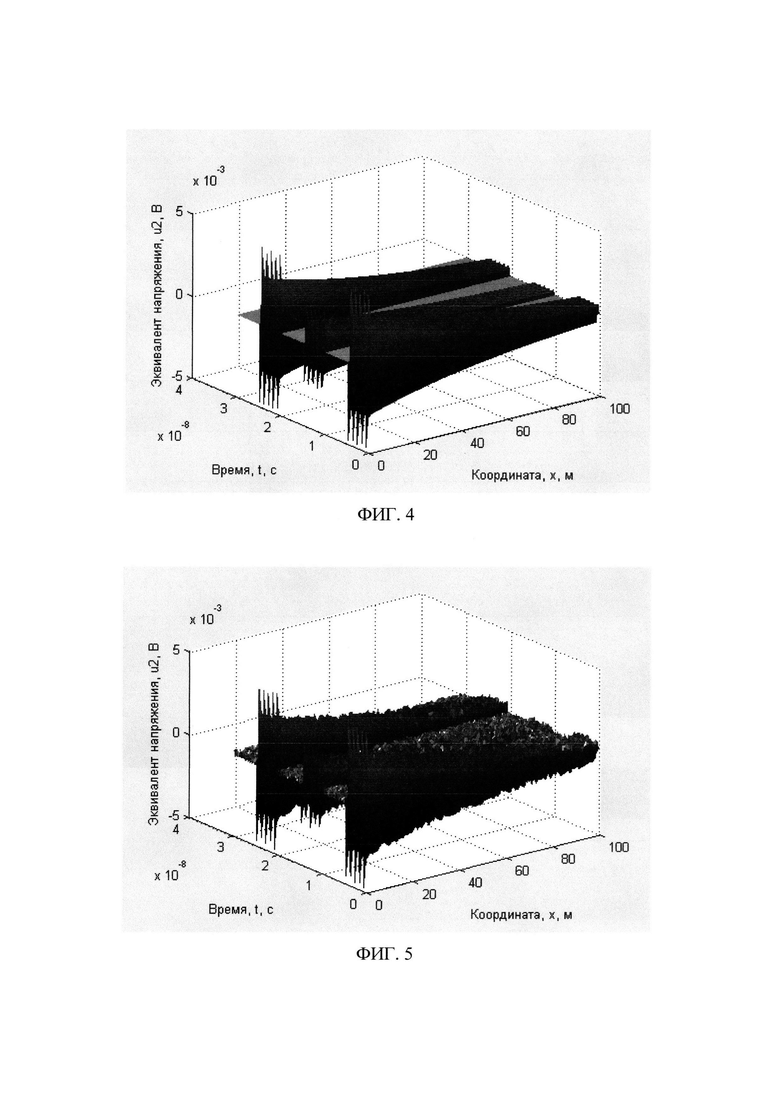
ФИГ. 4 Пример графика эквивалента напряжения распространения сигнала с амплитудной цифровой модуляцией без учета шумов и помех;
ФИГ. 5. Пример графика эквивалента напряжения распространения сигнала с амплитудной цифровой модуляцией и учетом шумов и помех;
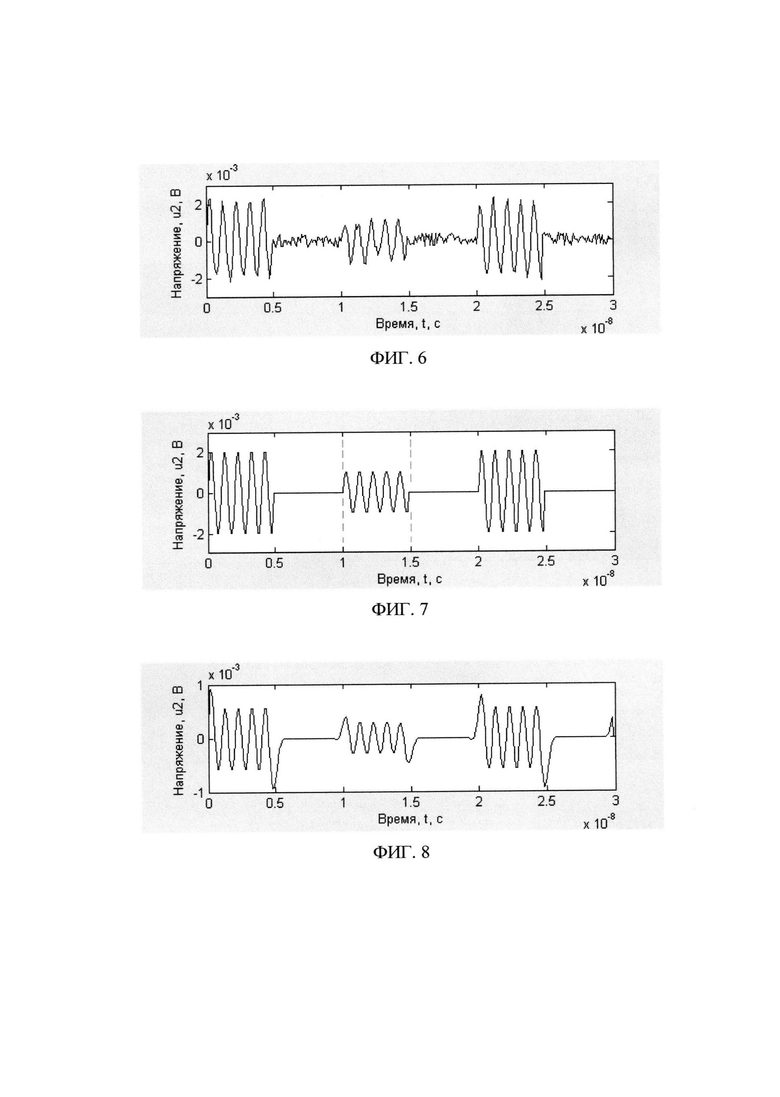
ФИГ. 6. Пример графика напряжения на приемной антенне с учетом шумов и помех;
ФИГ. 7. Пояснение к выбору временного отрезка сигнала для подсчета минимального значения отношения сигнал-шум;
ФИГ. 8. Пример сильного влияния сходимости рядов Фурье.
Осуществление способа опишем, ориентируясь на ФИГ. 1. Перед осуществлением способа передающее устройство 3 и приемное устройство 4 находятся во включенном состоянии. При этом по радиоканалу от антенны 5 передающего устройства 3 к антенне 6 приемного устройства 4 посредством радиосигнала с цифровой амплитудной модуляцией непрерывным во времени потоком передаются бинарные коды цифровых видеоизображений.
При осуществлении способа оператор 1 с помощью шумомера 2 сначала оценивает максимальный уровень напряжения собственных шумов на выходе передающего устройства 3, а в случае отсутствия такой возможности задает этот уровень приближенно. Далее оператор 1 с помощью шумомера 2 оценивает максимальный уровень напряжения внешних помех на входе приемного устройства 4. После этого оператор 1 измеряет, либо приближенно оценивает расстояние между передающей 5 и приемной 6 антеннами.
Далее при известных максимумах напряжений собственных шумов на выходе передающего устройства 3, внешних помех на входе приемного устройства 4, а также при известном расстоянии между антеннами 5 и 6 оператор 1 с помощью вычислительного устройства 7 на основе моделирования и решения уравнения в частных производных, характеризующего распространение радиосигнала, рассчитывает отношение сигнал-шум на входе приемного устройства 4.
При этом в ходе моделирования свойства среды распространения радиосигнала оператор 1 учитывает через коэффициенты исходного уравнения, а полезный сигнал в модели оператор 1 подготавливает заранее в виде эталонного расчетного фрагмента таким образом, чтобы он содержал как минимум один временной отрезок с минимальным ненулевым значением амплитуды сигнала и как минимум один временной отрезок с максимальным значением этой амплитуды. Причем указанные минимум и максимум для амплитуды полезного сигнала в модели оператор 1 задает значениями, характерными для реального передающего устройства 3.
Уровень сигнала в ходе расчета отношения сигнал-шум оператор 1 рассчитывает с помощью вычислительного устройства 7 при нулевых функциях собственных шумов передающего устройства 3 и внешних помех на входе приемного устройства 4. Уровень шума в ходе расчета отношения сигнал-шум оператор 1 рассчитывает с помощью вычислительного устройства 7 при нулевой амплитуде полезного сигнала.
Оценку минимального значения отношения сигнал-шум на выходе модели оператор 1 в ходе моделирования проводит на временном отрезке эталонного сигнала с минимальным уровнем амплитуды, а оценку максимального значения на временном отрезке эталонного сигнала с максимальным уровнем амплитуды. В качестве итогового отношения сигнал-шум оператор 1 выбирает минимальное значение этого отношения.
Возможность получения при осуществлении изобретения заявленного технического результата и наличие причинно-следственной связи между совокупностью существенных признаков заявляемого объекта и достигаемым техническим эффектом подтверждается результатами математического моделирования процесса распространения радиосигнала с цифровой амплитудной модуляцией и оценки отношения сигнал-шум на входе приемного устройства при передаче бинарных кодов цифровых видеоизображений.
Общие параметры моделирования представлены в таблице 1. В таблице 2 дана смысловая интерпретация значений амплитуд используемого ансамбля. Посредством изменения амплитуды сигнала передается логическая последовательность из трех информационных символов вида «1»,«0»,«1», каждый из которых сопровождается неинформационным символом записи. Таблица 3 содержит сведения о максимальных уровнях шума передающего устройства и внешних помех.



На ФИГ. 2 - ФИГ. 6 представлены результаты моделирования. Для функции u2(t,x) на двумерных графиках используется понятие эквивалент напряжения распространения, поскольку некорректно говорить о «напряжении электромагнитного поля». Под эквивалентом напряжения распространения понимается то значение напряжения, которое возникло бы на приемной антенне при ее размещении «в точке» с заданной координатой x. При этом геометрическими размерами антенн пренебрегаем. Графики напряжения в отдельной точке в представленном случае соответствуют расчетному расстоянию 25 м.
Отметим, что разница между соседними уровнями амплитуды необязательно должна быть равна минимальному значению амплитуды (как на ФИГ. 2). К примеру, можно использовать минимальный ненулевой уровень амплитуды в 1 В, а шаг по амплитуде задать равным 0,25 В (а не 1 В как на графиках). Но, тем не менее, между минимальным и максимальным уровнем амплитуды в сигнале с амплитудной цифровой модуляцией всегда будет какая-то разница. И чем больше эта разница, тем большую погрешность в оценке сигнал-шум будет давать усредненный замер, характерный для прототипного способа.
Так, к примеру, если использовать ансамбль амплитуд с 4-мя ненулевыми уровнями амплитуды, то при усредненном замере получаем ошибку в оценке минимального отношения сигнал-шум примерно в 2-4 раза (в зависимости от шага по амплитуде). В современных системах передачи видеоизображений может использоваться 8 и более уровней амплитуды.
Согласно результатам моделирования и автоматизированному программному подсчету переход к заявляемому способу дает как минимум 10-15% выигрыш в точности оценки сигнал-шум уже при малом шаге между уровнями амплитуды в полезном сигнале, а при значительном количестве уровней амплитуд и большом шаге между ними данный показатель возрастает в разы.
Прочие пояснения, раскрывающие сущность изобретения более детально, представлены ниже:
- прототипный и предложенный способы допускают оценку отношения сигнал-шум при работающем передатчике, однако прототипный способ при оценке отношения сигнал-шум дает в результате замера некоторое усредненное значение уровня амплитудно-модулированного сигнала (поскольку наперед неизвестно, как и сколько раз во время замера меняется амплитуда сигнала);
- между тем, очевидно, что наиболее важное значение на практике имеет минимальное значение сигнала, поскольку при нем будет минимальным и отношение сигнал-шум (то есть, с наихудшим качеством передаются коды изображений с которыми ассоциируется минимальный ненулевой уровень амплитуды полезного сигнала);
- обычно рекомендуется брать за основу оценки именно минимальное отношение сигнал-шум (иными словами, если выдержать требуемое отношение сигнал-шум для минимального значения амплитуды, то для остальных уровней амплитуды оно выдержится и подавно);
- предложенный способ в этом смысле «работает» с минимальным ненулевым уровнем амплитуды полезного сигнала (на ФИГ. 7 такой временной отрезок выделен пунктирами), но уже не в реальной схеме, а на уровне модели (причем наличие подобного отрезка сигнала является обязательным требованием при моделировании);
- точность модели, в свою очередь, обеспечивается за счет выбранного уравнения распространения радиосигнала (в том числе за счет учета свойств среды и характера затухания сигнала посредством задания коэффициентов этого уравнения), а также за счет предварительной оценки собственных максимумов напряжений шумов передатчика и внешних помех.
Далее приведем также ряд пояснений, касающихся в основном математического аппарата предложенного способа:
- в математической модели используется два основных типа «вредоносных» воздействий: собственный шум передатчика e1(t), а также внешние помехи e2(t) (берутся в расчетной точке с координатой  ), причем максимумы напряжений для этих параметров измеряются предварительно в реальной схеме (если нет возможности измерить максимум e1(t) для передатчика, то он задается приближенно);
), причем максимумы напряжений для этих параметров измеряются предварительно в реальной схеме (если нет возможности измерить максимум e1(t) для передатчика, то он задается приближенно);
- собственный шум передатчика e1(t) вовлекается в правую часть уравнения в частных производных изначально (поскольку уже содержится в общем сигнале передающей антенны вместе с полезным сигналом);
- внешние помехи e2(t) «накладываются» (добавляются) после получения решения уравнения и по принципу суперпозиции в расчетной точке приема (поскольку речь идет уже не о напряжении, а об электромагнитном распространении сигнала);
- на ближних расстояниях (до нескольких десятков метров) e1(t) может вносить ощутимый вклад в общий шумовой фон, на дальних расстояниях (от 200 м и более) преобладает в основном e2(t);
- переход именно к комплексному уравнению в частных производных потребовался вследствие того, что в поле действительных чисел при указанном составе слагаемых аналогичное уравнение в частных производных решить по методу Фурье не удалось (то есть нужно было либо сократить количество слагаемых, либо переходить в поле комплексных чисел);
- кроме того, комплексная модель допускает использование полезных сигналов произвольной формы (а не только четных или только нечетных как в аналогичной действительной модели), это особенно важно для сигналов с цифровой модуляцией и аппроксимации собственных шумов передатчика;
- как следствие, функции u1(t,x), u2(t,x) изначально представляются комплексными, но для задания воздействий вначале и извлечения принятого сигнала в конце используются действительные части указанных функций;
- к небольшим недостаткам способа следует отнести недостаточно хорошую сходимость рядов Фурье (ФИГ. 8), которая может проявиться в виде выбросов в местах резких изменений амплитуды сигнала при слабом сигнале на значительных расчетных расстояниях;
- чтобы избавиться от этого недостатка, можно повышать степень дискретизации решения (то есть наращивать количество узлов дискретной решетки) и увеличивать количество коэффициентов разложения Фурье.
Дадим также краткое пояснение к решению исходного комплексного уравнения в частных производных. Перепишем исходное уравнение:
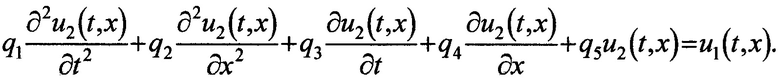
Перепишем разложения возмущающей и искомой функции:
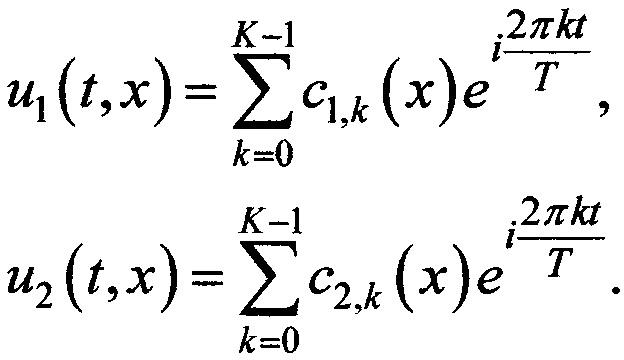
Теперь, для простоты зафиксируем одну гармонику с коэффициентом под номером k и, используя введенное разложение, запишем уравнения для частных производных искомой функции, фигурирующих в исходном уравнении:
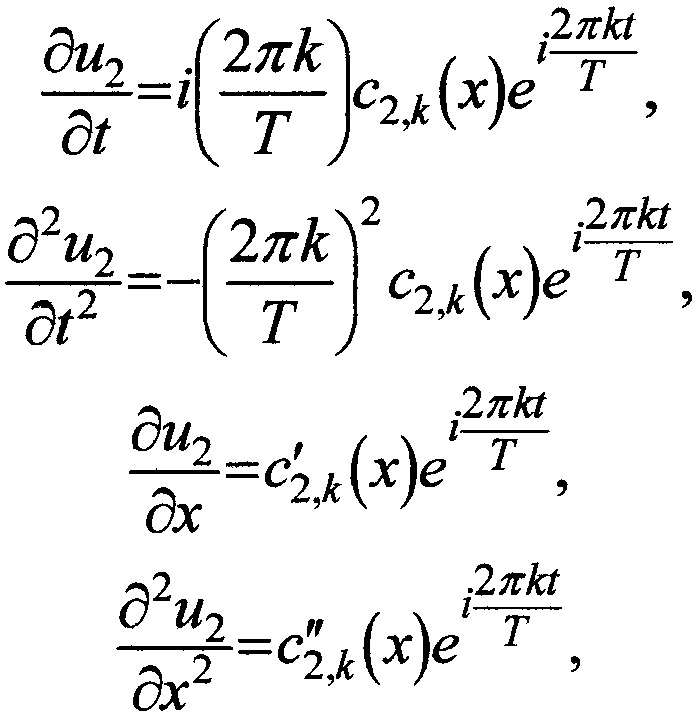
где штрихами обозначены производные по координате х.
Подстановка последних выражений производных искомой функции u2(t,x) вместе с разложениями u1(t,x), u2(t,x) в исходное уравнение с частными производными приводит для одного коэффициента разложения к обыкновенному дифференциальному уравнению:
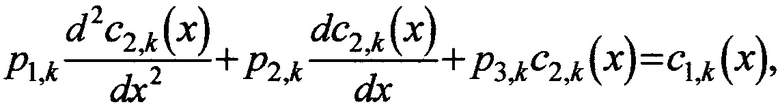
с коэффициентами:
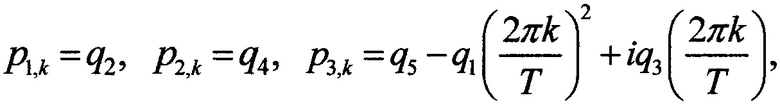
Если заменить производные в этом уравнении разностными отношениями и выразить текущее значение c2,k,n, то получаем общую расчетную формулу вида:
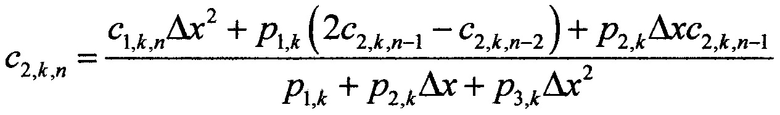
и здесь, учитывая, что мнимые части коэффициентов q1,q2,q3,q4,q5 равны нулю изначально, для отдельно взятого коэффициента с2,k,n с индексом k возможны два варианта.
В первом (частном) случае действительная часть коэффициента q3 равна нулю и, следовательно, равны нулю мнимые части сразу всех коэффициентов p1,k,р2,k,р3,k, в том числе, равна нулю и мнимая часть р3,k. Здесь можно сразу по очереди вычислять значения действительной и мнимой части с2,k,n, поэтому получаем более простую расчетную зависимость, указанную в зависимом пункте формулы изобретения.
Во втором (общем) случае действительная часть коэффициента q3 не равна нулю и, следовательно, коэффициент р3,k в знаменателе дроби имеет ненулевую мнимую часть. Здесь сразу вычислять значения действительной и мнимой части с2,k,n нельзя, а следует сначала обособить действительную и мнимую части знаменателя формулы, домножив и числитель, и знаменатель дроби на число, комплексно сопряженное знаменателю. Отсюда возникает более сложное общее решение с параметрами h1,h2,h3,h4, указанное в основной части формулы изобретения.
Технико-экономическое обоснование заявляемого способа и его практическая ценность состоят в том, что за счет высокой точности оценки отношения сигнал-шум, открывается возможность оптимизировать энергетические затраты на передачу сигала (причем как в результате предварительной оценки на этапе пусконаладочных работ, так и непосредственно на этапе эксплуатации).
К примеру, для телевизионных систем широкого вещания можно подбирать (в том числе в режиме реального времени) оптимальные значения амплитуд сигнала с цифровой модуляцией. Если минимальный ненулевой уровень амплитуды по итогам оценки можно снизить, то это выразится в снижении энергетических затрат на передачу сигнала (10-15% выигрыша в точности оценки сигнал-шум для максимально отдаленной точки приема «конвертируется» в экономию 10-15% энергозатрат).
Кроме того, на этапе проектирования и пуско-наладочных работ, для телевизионных систем широкого вещания достоверная оценка качества принимаемого изображения (посредством оценки отношения сигнал-шум) способствует рациональному выбору оборудования передающей станции (например, нет смысла использовать дорогостоящее оборудование с повышенным энергопотреблением и требованиями по техническому обслуживанию, если по результатам предварительной оценки имеется возможность использовать экономически менее затратную элементную базу).
В свою очередь, для локальных видеосистем (особенно для систем передачи цифровых видеоизображений с помощью электрических беспилотных летательных аппаратов) на первый план выходят массово-габаритные показатели передатчика. Их можно минимизировать за счет повышения точности предварительной оценки отношения сигнал-шум на заданном максимальном расстоянии. Как следствие, аккумуляторные батареи аппарата разряжаются медленнее, а время активного полета и передачи информации возрастает.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ беспроводной передачи цифровых панорамных аэровидеоизображений | 2018 |
|
RU2707139C1 |
| Устройство пространственной селекции сигналов с компенсацией преднамеренных помех | 2018 |
|
RU2677931C1 |
| МНОГОМЕРНЫЙ СИГНАЛ С УМЕНЬШЕННЫМ ОТНОШЕНИЕМ ПИКОВОЙ К СРЕДНЕКВАДРАТИЧЕСКОЙ АМПЛИТУДЕ | 2009 |
|
RU2488229C2 |
| Адаптивная антенная решетка для бистатической радиолокационной системы | 2020 |
|
RU2731875C1 |
| СПОСОБ ОБНАРУЖЕНИЯ СВЕРХМАЛЫХ РАДИОСИГНАЛОВ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2006 |
|
RU2359406C2 |
| Способ пространственной компенсации прямого и отраженных сигналов при обнаружении отраженного сигнала от воздушной цели бистатической радиолокационной системой | 2020 |
|
RU2739938C1 |
| СПОСОБ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЙ В МНОГОКАНАЛЬНЫХ РТЛС И РЛС | 2007 |
|
RU2368917C1 |
| МОНОИМПУЛЬСНЫЙ ПЕЛЕНГАТОР | 2005 |
|
RU2297645C1 |
| СПОСОБ ОБНАРУЖЕНИЯ ИСТОЧНИКОВ ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ В ПРЕДЕЛАХ КОНТРОЛИРУЕМОЙ ЗОНЫ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2002 |
|
RU2206101C1 |
| СПОСОБ ПЕЛЕНГАЦИИ УЗКОПОЛОСНЫХ РАДИОСИГНАЛОВ КВ ДИАПАЗОНА | 2009 |
|
RU2407026C1 |


Изобретение относится к области измерений электрических величин. Отношение сигнал-шум рассчитывают с помощью решения комплексного уравнения в частных производных второго порядка вида
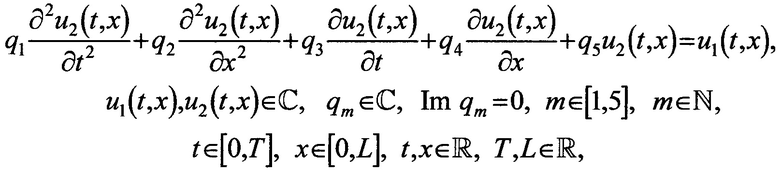
u1(t,x) - функция внешних возмущений; u2(t,x) - искомая функция, эквивалент напряжения распространения; q1,q2,q3,q4,q5 - коэффициенты, учитывающие свойства среды; m - индекс коэффициентов уравнения с частными производными; Im qm - мнимая часть m-го коэффициента; t - время; х - координата; Т- максимальное значение времени; L - максимальное значение координаты; 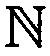 - множество натуральных чисел;
- множество натуральных чисел;  - множество действительных чисел;
- множество действительных чисел;  - множество комплексных чисел; с краевыми и начальными условиями
- множество комплексных чисел; с краевыми и начальными условиями
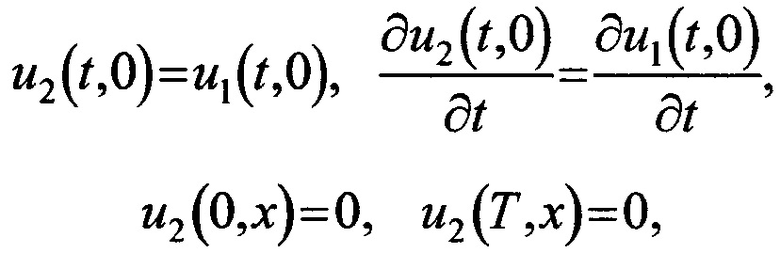
которое решают приближенно с помощью высокопроизводительного вычислительного устройства на основе метода Фурье разделения переменных с комплексным временным базисом разложения искомой функции и функции внешних возмущений. В модели используют один полезный сигнал s(t) и два «вредоносных» компонента: собственный шум передатчика e1(t) и внешние помехи e2(t). При этом полезный сигнал s(t) и собственный шум передатчика e1(t) располагают в действительной части u1(t,x) перед вычислением u2(t,x). Внешние помехи e2(t) добавляют в расчетной точке к действительной части u2(t,x) после ее получения. Оценку минимального значения отношения сигнал-шум на выходе модели проводят на временном отрезке эталонного сигнала с минимальным уровнем амплитуды. Оценку максимального значения отношения сигнал-шум на выходе модели проводят на временном отрезке эталонного сигнала с максимальным уровнем амплитуды. В качестве итогового отношения сигнал-шум выбирают его минимальное значение на выходе модели. Технический результат заключается в повышении точности оценки отношения сигнал-шум на входе приемного устройства для радиосигнала с цифровой амплитудной модуляцией. 1 з.п. ф-лы, 8 ил., 3 табл.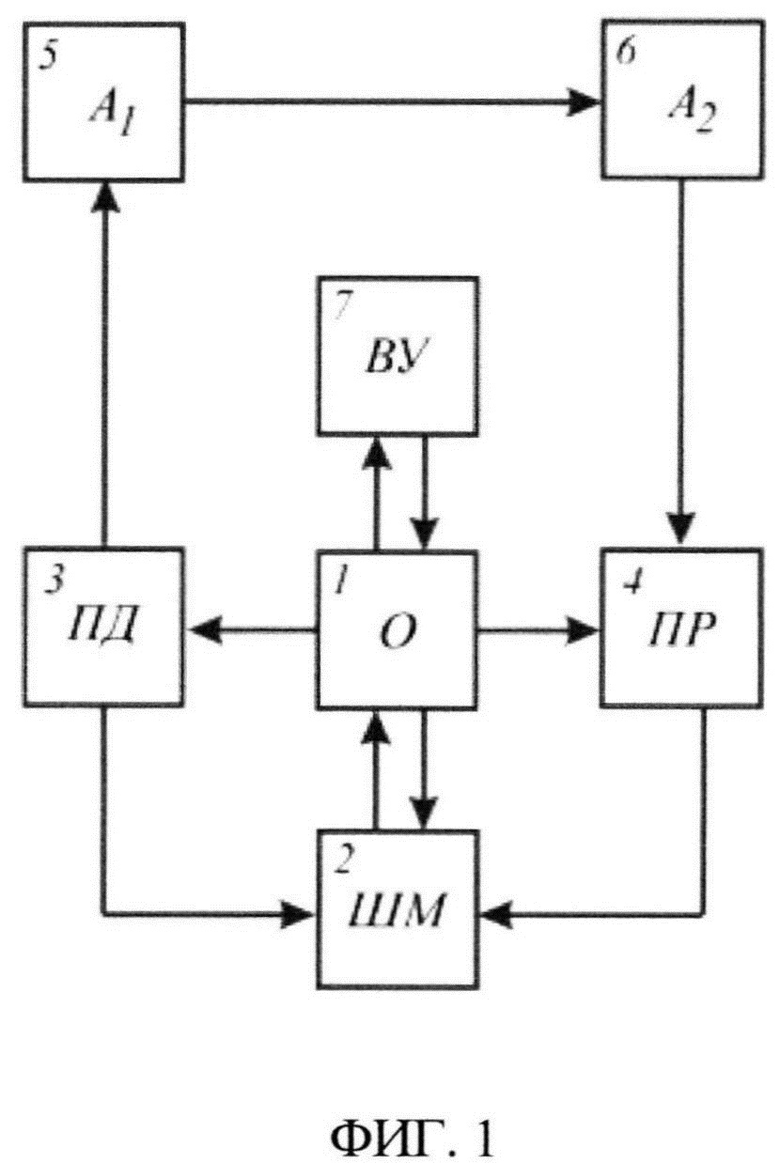
1. Способ оценки отношения сигнал-шум на входе приемного устройства для радиосигнала с цифровой амплитудной модуляцией, состоящий в следующем: сначала на входе приемного устройства в частотной полосе полезного сигнала с помощью высокочувствительного шумомера со встроенным полосовым фильтром измеряют уровень сигнала, далее в частотной полосе с наименьшим содержанием полезного сигнала аналогичным образом замеряют уровень шума, после этого рассчитывают отношение сигнал-шум с учетом ширины полосы канала, ширины полосы фильтра, а также коэффициента прямоугольности фильтра, при этом отношение сигнал-шум рассчитывают либо по уровням напряжения сигнала и шума, либо по их мощности, а оба измерения проводят во входном тракте приемного устройства до резонансного фильтра, отличающийся тем, что перед вычислением отношения сигнал-шум с помощью шумомера с перестраиваемым полосовым пропускающим частотным фильтром, настроенным предварительно на полосу с минимальным содержанием полезного сигнала, в выходном тракте передающего устройства после конечного каскада усиления, но перед антенной оценивают максимальный уровень напряжения собственных шумов передающего устройства, а при отсутствии такой возможности данный уровень напряжения задают приближенно, далее при тех же настройках фильтра шумомера во входном тракте приемного устройства после антенны, но перед резонансным фильтром оценивают максимальный уровень напряжения внешних помех, затем измеряют или оценивают приближенно расстояние между антеннами приемного и передающего устройств, после чего при известных максимумах напряжений внешних помех и собственных шумов передающего устройства, а также при известном расстоянии между антеннами рассчитывают требуемое отношение сигнал-шум с помощью решения комплексного уравнения в частных производных второго порядка вида
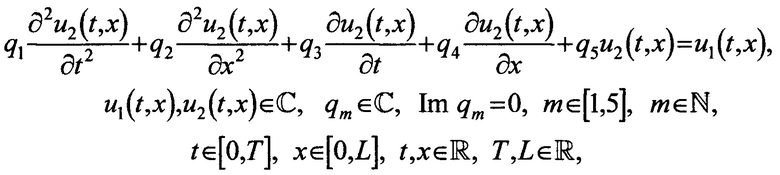
u1(t,x) - функция внешних возмущений;
u2(t,x) - искомая функция, эквивалент напряжения распространения;
q1,q2,q3,q4,q5 - коэффициенты, учитывающие свойства среды;
m - индекс коэффициентов уравнения с частными производными;
Im qm - мнимая часть m-го коэффициента;
t - время;
х - координата;
Т - максимальное значение времени;
L - максимальное значение координаты;
 - множество натуральных чисел;
- множество натуральных чисел;
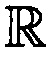 - множество действительных чисел;
- множество действительных чисел;
 - множество комплексных чисел;
- множество комплексных чисел;
с краевыми и начальными условиями
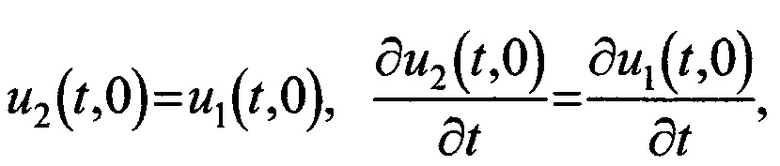
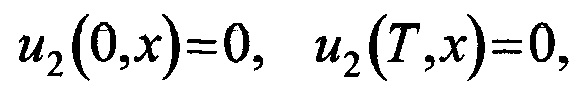
при этом за счет предварительного подбора значений действительных частей комплексных коэффициентов q1,q2,q3,q4,q5 учитывают свойства среды распространения радиосигнала, для нахождения решения уравнения в частных производных вводят прямоугольную декартову систему координат с осями времени t и координаты х, начало системы координат совмещают с фазовым центром передающей антенны, ось х направляют таким образом, чтобы она проходила через фазовый центр приемной антенны, уравнение в частных производных решают с помощью высокопроизводительного вычислительного устройства, все двумерные действительные параметры математической модели на основе записанного уравнения и двумерные части комплексных функций в памяти вычислительного устройства представляют числовыми матрицами, а все одномерные действительные параметры и одномерные части комплексных параметров задают одномерными числовыми массивами, в зависимости от свойств среды коэффициенты q1,q2,q3,q4,q5 задают постоянными или переменными по одному или обоим аргументам t и х, далее для действительных и мнимых частей функций u1(t,x), u2(t,x) вводят двумерную дискретную решетку, количество узлов решетки и размер постоянных приращений по времени t и координате x подбирают предварительно в зависимости от максимального значения несущей частоты полезного сигнала и максимального расстояния его передачи, возмущающие воздействия располагают в действительной части функции u1(t,x), которую в начале координат ассоциируют с передающей антенной и задают с помощью формулы
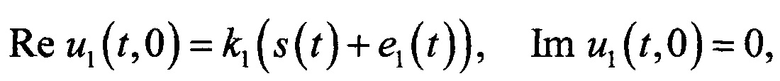
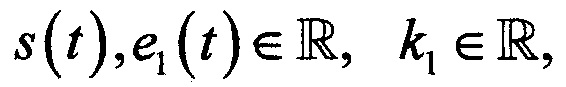
Re u1(t,0) - действительная часть u1(t,0);
Im u1(t,0) - мнимая часть u1(t,0)
s(t) - полезный сигнал;
e1(t) - собственный шум передающего устройства;
k1 - коэффициент поправки сигнала в ближней зоне;
в остальной части области определения и действительную, и мнимую составляющие u1(t,x) задают нулевыми значениями, после этого для согласования краевых и начальных условий значения u1(0,0) и u1(Т,0) обнуляют, за счет коэффициента пропорциональности k1 корректируют уровень полезного сигнала в ближней зоне, значение k1 подбирают предварительно и задают положительным числом, массив для s(t) задают эталонным фрагментом полезного сигнала с цифровой амплитудной модуляцией, в котором присутствует как минимум один временной отрезок с минимальной ненулевой амплитудой сигнала и как минимум один временной отрезок с максимальным значением этой амплитуды, при этом указанные минимум и максимум для амплитуды полезного сигнала в модели задают значениями, характерными для реального передающего устройства, эталонный фрагмент полезного сигнала подготавливают заранее и сохраняют в памяти вычислительного устройства, массив для e1(t) формируют генератором случайных чисел вычислительного устройства, при этом максимальный уровень e1(t) задают оцененным ранее максимальным значением напряжения собственных шумов передающего устройства, уравнение в частных производных решают на основе метода Фурье с разложением функций u1(t,x) и u2(t,x) по временному базису с несколькими гармониками
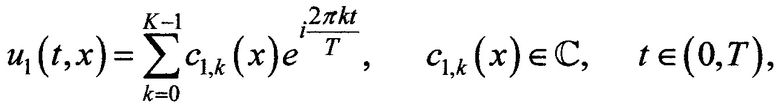
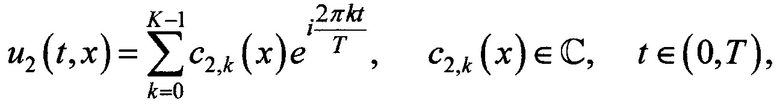

с1,k(x) - k-й коэффициент разложения Фурье функции u1(t,x);
с2,k(x) - k-й коэффициент разложения Фурье функции u2(t,x);
i - мнимая единица;
π - константа, равная 3.14;
k - индекс коэффициентов разложения Фурье;
K - количество коэффициентов разложения Фурье;
 - множество целых чисел;
- множество целых чисел;
причем количество коэффициентов разложения K задают предварительно числом большим или равным одной четвертой от количества узлов дискретной решетки по оси времени t и меньшим или равным этому количеству, далее, согласно записанным формулам разложения, находят выражения для комплексных частных производных u2(t,x), подставляют их вместе с разложениями u2(t,x) и u1(t,x) в исходное уравнение в частных производных, приводят подобные слагаемые и получают множество комплексных обыкновенных дифференциальных уравнений второго порядка вида
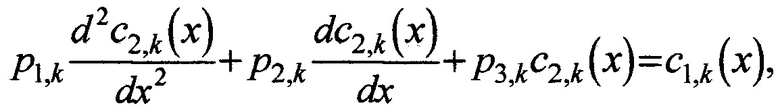

p1,k,p2,k,p3,k - комплексные коэффициенты обыкновенного дифференциального уравнения для k-го коэффициента с2,k(х);
после этого коэффициенты разложения с1,k(x) функции внешних возмущений u1(t,x) в правых частях этих уравнений получают с помощью постолбцового одномерного прямого комплексного дискретного преобразования Фурье, применяемого к u1(t,x) в каждой координатной отметке поочередно, а значения p1,k,p2,k,p3,k задают с помощью формулы
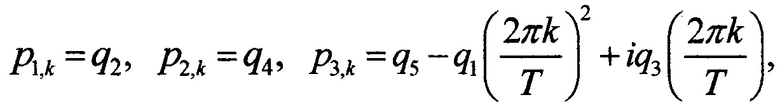
причем в случае переменных коэффициентов q1,q2,q3,q4,q5 значения p1,k,p2,k,p3,k пересчитывают каждый раз, когда меняется значение хотя бы одного из коэффициентов q1,q2,q3,q4,q5, значения q1,q2,q3,q4,q5 задают предварительно таким образом, чтобы обеспечить устойчивость решения обыкновенного дифференциального уравнения при всех возможных сочетаниях q1,q2,q3,q4,q5, далее поочередно вычисляют коэффициенты разложения с2,k(х), при этом действительные и мнимые части c2,k(x) в первом координатном узле с учетом краевых условий сразу приравнивают соответствующим значениям c1,k(x), то есть
Re c2,k1=Re c1,k,1, Im c2,k,1=Im c1,k,1,
c2,k,1 - значение k-го коэффициента c2,k(x) в первом координатном узле;
c1,k,1 - значение k-го коэффициента c1,k(x) в первом координатном узле;
Re - обозначение действительных частей коэффициентов;
Im - обозначение мнимых частей коэффициентов;
в остальных координатных узлах, начина со второго, значения с2,k(х) находят по формуле
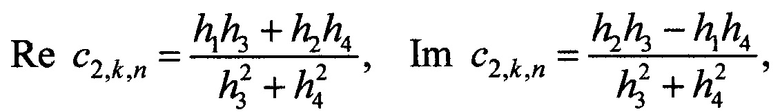
c2,k,n - значение k-го коэффициента c2,k(x) в n-м координатном узле;
n - индекс координатного узла;
h1,h2,h3,h4 - вспомогательные параметры;
Re - обозначение действительных частей коэффициентов;
Im - обозначение мнимых частей коэффициентов;
при вспомогательных обозначениях
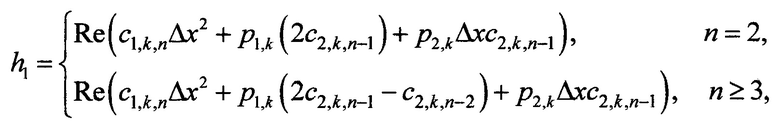
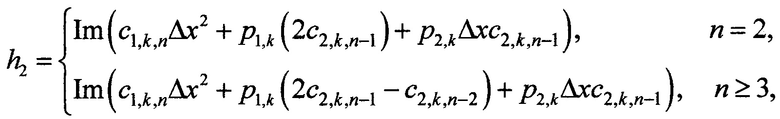
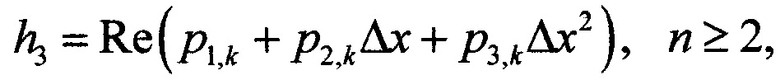
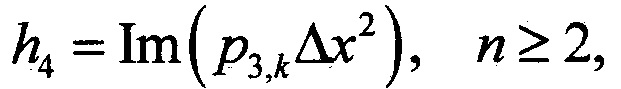
c1,k,n - значения k-го коэффициента c1,k(x) в n-м координатном узле;
Δх - величина приращения (постоянный дискретный шаг) по оси х;
Re - обозначение действительных частей выражений в скобках;
Im - обозначение мнимых частей выражений в скобках;
после вычисления всех коэффициентов c2,k(x) возвращаются к разложению искомой функции и получают ее в комплексной форме путем постолбцового одномерного обратного комплексного дискретного преобразования Фурье, применяемого к u2(t,x) в каждой координатной отметке поочередно, эквивалент напряжения распространения извлекают из действительной части u2(t,x), далее накладывают внешние помехи согласно формуле
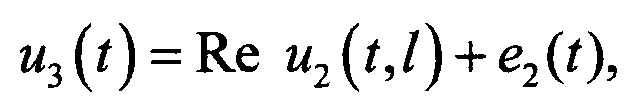
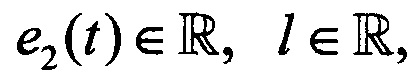
u3(t) - общее напряжение принятого радиосигнала вместе с помехами;
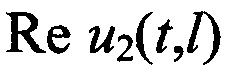 - действительная часть u2(t,x) на расчетном расстоянии;
- действительная часть u2(t,x) на расчетном расстоянии;
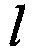 - расчетное расстояние;
- расчетное расстояние;
e2(t) - внешние помехи на расчетном расстоянии;
при этом расчетное расстояние 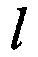 между антеннами в модели задают предварительно и равным действительному, оцененному ранее, расстоянию между антеннами, массив для e2(t) формируют генератором случайных чисел вычислительного устройства, максимальный уровень e2(t) принимают равным, оцененному ранее, максимальному уровню напряжения внешних помех, после наложения помех получают выходной сигнал модели u3(t), уравнение в частных производных решают дважды, уровень сигнала S рассчитывают по выборке u3(t) на выходе модели как среднее арифметическое для квадратов напряжений сигнала при отсутствии шумов и помех, то есть при нулевых e1(t), e2(t) уровень шума Е рассчитывают по выборке u3(t) на выходе модели как среднее арифметическое для квадратов напряжений шума при отсутствии полезного сигнала, то есть при нулевом s(t), после этого вычисляют отношение сигнал-шум по формуле
между антеннами в модели задают предварительно и равным действительному, оцененному ранее, расстоянию между антеннами, массив для e2(t) формируют генератором случайных чисел вычислительного устройства, максимальный уровень e2(t) принимают равным, оцененному ранее, максимальному уровню напряжения внешних помех, после наложения помех получают выходной сигнал модели u3(t), уравнение в частных производных решают дважды, уровень сигнала S рассчитывают по выборке u3(t) на выходе модели как среднее арифметическое для квадратов напряжений сигнала при отсутствии шумов и помех, то есть при нулевых e1(t), e2(t) уровень шума Е рассчитывают по выборке u3(t) на выходе модели как среднее арифметическое для квадратов напряжений шума при отсутствии полезного сигнала, то есть при нулевом s(t), после этого вычисляют отношение сигнал-шум по формуле
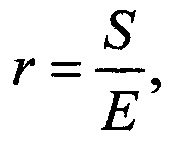
r - отношение сигнал-шум на антенне приемного устройства;
S - уровень сигнала на выходе модели;
Е - уровень шума на выходе модели;
при этом оценку минимального значения отношения сигнал-шум на выходе модели проводят на временном отрезке эталонного сигнала с минимальным уровнем амплитуды, оценку максимального значения отношения сигнал-шум на выходе модели проводят на временном отрезке эталонного сигнала с максимальным уровнем амплитуды, а в качестве итогового отношения сигнал-шум выбирают его минимальное значение.
2. Способ оценки отношения сигнал-шум на входе приемного устройства радиосигнала с цифровой модуляцией по п. 1, отличающийся тем, что если в частном случае действительная часть коэффициента q3 равна нулю, то в ходе моделирования каждый из коэффициентов c2,k(x) в координатных узлах дискретной решетки рассчитывают по упрощенной формуле

с последовательным вычислением действительной и мнимой частей c2,k,n, при этом условие равенства действительной части q3 нулю проверяют до применения основной расчетной формулы с параметрами h1,h2,h3,h4.
| Способ определения отношения сигнал/шум радиосигнала | 1990 |
|
SU1748095A1 |
| Способ измерения отношения сигнал/шум и устройство для его осуществления | 1989 |
|
SU1646064A1 |
| Устройство для измерения отношения сигнал/шум | 1980 |
|
SU883803A1 |
| Устройство для измерения отношения"СигНАл-шуМ | 1979 |
|
SU808996A1 |
Авторы
Даты
2019-07-29—Публикация
2018-10-29—Подача