Изобретение относится к вычислительной технике и может быть использовано в блоках сравнения модулярных чисел вычислительных систем, функционирующих в системе остаточных классов.
Известны устройства для сравнения n разрядных чисел. (А.С. №675420, Б.И. №27, 1979) состоящее из триггеров, логических элементов, узлов хранения, регистров, дешифраторов, запоминающих матриц и счетчика. Однако данное устройство обладает большой сложностью и функционально не может быть использовано для сравнения модулярных чисел.
Наиболее близким по технической сущности к заявленному устройству является устройство для сравнения чисел (А.С. №541164, БИ №48, 1977.), содержащее решающие матрицы, блоки анализа полиадических коэффициентов алгебраического сравнения, блоки анализа полиадических коэффициентов сравнений по модулю, блок формирования знака и логические элементы «или».
Недостатками данного устройства является низкое быстродействие и его сложность.
Целью настоящего изобретения является повышения скорости сравнения чисел и сокращение аппаратных затрат.
Поставленная цель достигается тем, что в устройство вводятся просмотровые таблицы (память), схема сдвига полярности и сумматор. Рассмотрим новый метод сравнения модулярных чисел, обладающий высоким быстродействием и низкими аппаратными затратами оборудования
С целью упрощения процесса сравнения модулярных чисел рассмотрим приближенный метод, который позволяет абсолютно правильно реализовать основные классы процедур принятия решений: анализ наличия определенного значения в конкретном разряде; проверка равенства (неравенства) двух значений; сравнение двух значений (больше, меньше), которые обеспечивают решение основного круга задач, возникающих при аппаратной или программной реализации реальных процессов.
Суть приближенного метода сравнения модулярных чисел основана на использовании относительной величины исходного числа к полному диапазону Китайской теоремы об остатках, которая связывает позиционное число A с его представлением в остатках (α1, α2, …, αn), где αi - наименьшие неотрицательные вычеты числа, относительно модулей системы остаточных классов p1, p2, …, pn следующим выражением

где 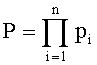
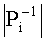
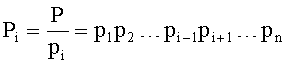
Если (1) разделить на константу P, то получим приближенное значение
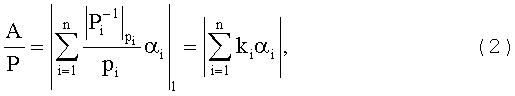
где 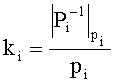
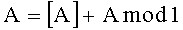
Пример 1. Пусть дана система оснований p1=2, p2=3, p3=5, p4=7, объем диапазона P=2·3·5·7=210. Допустим, что в заданной СОК будут представлены только положительные числа. Величины 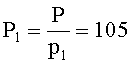
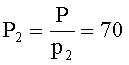
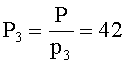
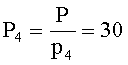
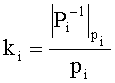
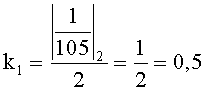
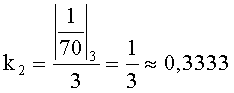
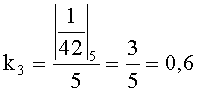
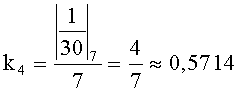
По (2) получим
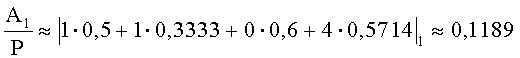
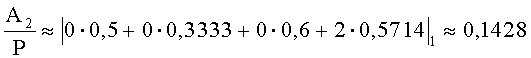
Так как 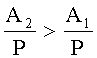
Рассмотрим случай, когда рабочий диапазон разбит на два интервала 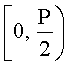
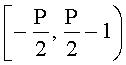
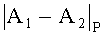
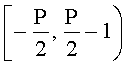
Пример 2. Вариант неправильного определения сравнения чисел на основе определения знака.
Пусть 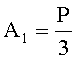
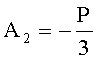
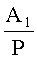
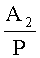
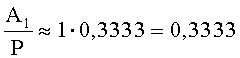
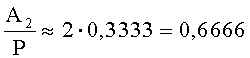
Число A2 входит в отрицательный интервал, то есть 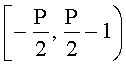
Следовательно сравнение приведет к неверному результату A1<A2.
Для правильного определения сравнения чисел необходимо проверить знаки A1 и A2 и тогда алгоритм сравнения будет иметь вид:
1. Определить знаки A1 и A2.
2. Если A1 и A2 без знаков, то положительный знак разности относительных величин означает большее число.
3. Если A1 и A2 имеют один и тот же знак, то проверяется 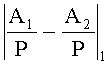
4. Если A1 и A2 имеют разные знаки, то 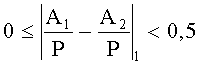
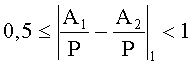
Таким образом, сравнение чисел со знаком требует предварительного анализа знаков сравниваемых чисел.
Известно, что при кодировании дополнительным кодом, отрицательная часть динамического диапазона находится у верхнего предела полного диапазона. Положительные числа из дополнительного диапазона отображаются на область 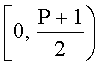
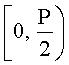
Это обстоятельство может привести к ошибке сравнения, так как отрицательные числа попадают в верхнюю часть полного диапазона, и все отрицательные числа будут давать ошибки, что не соответствует действительности в силу разнесения динамического диапазона.
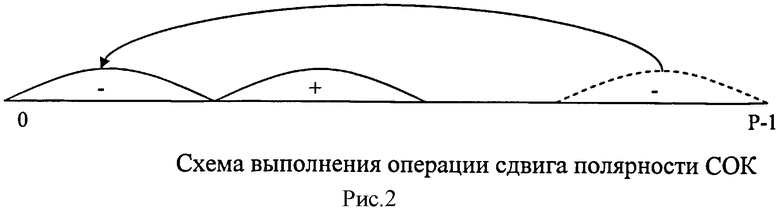
Для преодоления этой трудности необходимо произвести сдвиг отрицательной области путем вращения остаточного кольца в положение, указанное на рисунке 2. Пунктиром показана область, которая перенесена в начало диапазона.
В результате отрицательные числа будут отображены в начальной части динамического диапазона.
Показанное на рисунке 2 вращение, называется сдвигом полярности и его можно осуществить путем прибавления перед сравнением модулярных чисел константы 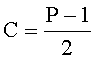
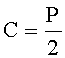
Если 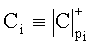
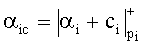
Пример 3. Сравнить модулярные числа разных знаков A1 и -A2. Система оснований СОК такая же, как и в примере 1: p1=2, p2=3, p3=5, p4=7.
Пусть число A1=17=(1,2,2,3), A2=-19=(1,1,4,5). Тогда дополнительный код A2=(p1-1,p2-1,p3-4.p4-5)=(1,2,1,2). Требуется сравнить числа A1 и A2.
Проверка знака числа A1. Для определения знака числа A1 сравним его с константой 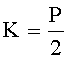
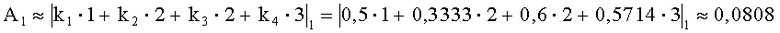
Представление константы 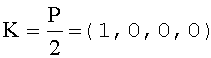
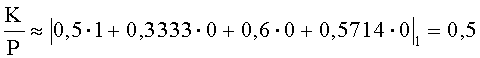
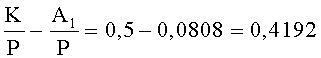
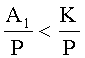
Проверка знака числа A2 проходит аналогично: 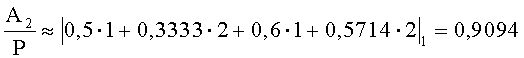
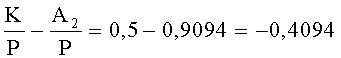
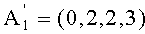
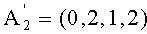
Определим относительные величины 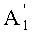
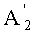
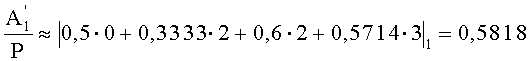
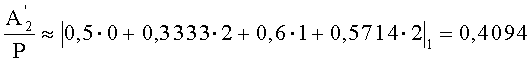
Найдем разность относительных величин, тогда 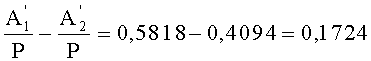
Рассмотренные методы определения таких позиционных характеристик модулярного кода, как: определение знака числа и сравнение чисел, показали, в отличие от известных, простоту их вычисления, так как для их реализации не используется вычисление коэффициентов ОПСС, которое требует больших аппаратных и временных затрат. По этой причине данный метод представляет собой особую важность и является одним из лучших решений на настоящее время. Перечисленные операции являются важнейшими для машинной модулярной арифметики и их применение может дать значительные преимущества не только в таких приложениях, в которых основная доля вычислений приходится на точное умножение, возведение в степень больших чисел в сочетании со сложением и вычитанием, но и в которых довольно часто появляется необходимость сравнения и определения знака числа. Известно, что теорема кодирования Сабо гласит, что нет лучших методов определения позиционных характеристик, при которых не используется их однозначность, чем перевод чисел из СОК в ОПСС, поскольку величины числа в модулярном представлении существенным образом зависят от всех остатков числа. Однако проведенные исследования по определению приблизительных характеристик, которые решают задачу формирования конструкций сравнения, не отвечают утверждению указанной теоремы Сабо. Таким образом можно сделать вывод о том, что теорема Сабо работает только при точных методах.
Схема модулярного сравнения чисел, основанная на принципах использования относительных величин приведена на рисунке 3 и содержит: входные регистры 1, 9 для хранения чисел, соответствующие A и B которые поступают по шинам 15 и 16; схема определения знаков чисел A и B, соответственно, 2 и 8, схема сдвига полярности 3, 7, соответственно чисел A и B, просмотровые таблицы 5, 7, содержание таблиц для хранения произведения констант и разрядов СОК 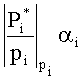
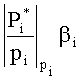
На входные регистры 1, 9 по шинам 15, 16, соответственно, поступают исходные числа A и B, представленные в СОК, которые необходимо сравнить. Выходы регистров соединены с 2, 3 и 7, 8, соответственно, для определения знака чисел A и B и сдвига полярности чисел A и B. Выходные сигналы схем определения знаков чисел 2 и 8, соответственно чисел A и B (0 - положительное число, 1 - отрицательное число), поступают на вход логического элемента «исключающего или» 4, который в случае разных знаков формирует сигнал сдвига полярности чисел, соответствующий константе Ci, и подает на вход схем 3 и 7, где происходит сдвиг полярности чисел. Выходы систем схем сдвига полярности 3 и 7, соответственно для чисел А и В, являются адресными входами просмотровых таблиц 5 и 6,
Элементы памяти, просмотровые таблицы (LUT - таблицы) 5-1, 5-2 5-n и 6-1, 6-2, 6-n, соответственно, хранят произведения 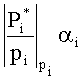
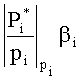
Пример 4. Пусть дана система оснований p1=2, p2=3, p3=5, p4=7. Сравнить модулярные числа A=(1,2,2,3) и B=(1,2,1,2). Исходные числа находятся в регистрах RGA и RGB, которые поступают на входы схем определения знака числа СОЗЧ-А и СОЗЧ-В. В этих схемах происходит сравнение исходных чисел с константой 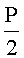
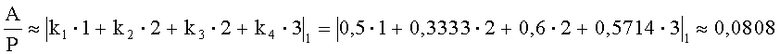
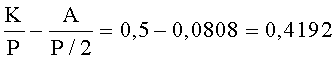
Разность положительная, то есть 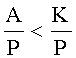
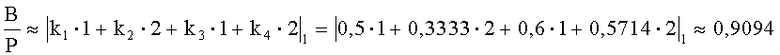
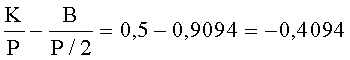
Разность отрицательная, поэтому число B входит во второй интервал и является отрицательным.
Результат анализа знаков чисел A и B образуется на выходе элемента исключающее «или» который поступает на вход схем сдвига полярности ССП-А и ССП-В. На выходах схем сдвига полярности образуются данные соответственно A=(1,2,2,3)+(1,0,0,0)=(0,2,2,3) и B=(1,2,1,2)+(1,0,0,0)=(0,2,1,2). Выходные данные схем сдвига полярности являются адресными входами просмотровых таблиц LUT-A и LUT-B, согласно которых осуществляется выборка значений констант 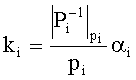
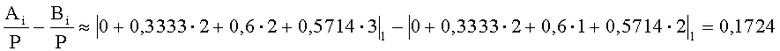
Разность положительная, так как дополнительный код положительного числа равен самому числу, следовательно A>B. Действительно, число A=17, B=-19.
Результаты сумматора анализируются в схеме сумматора, при этом:
если разность равна 0, то A=B,
если разность положительная, то A>B,
если разность отрицательная, то A<B.
В случае, если сравниваются положительные числа, то из схемы исключаются схемы определения знаков чисел. Тогда логическая глубина схемы (количество последовательно включенных элементов) будет n+3, где n - количество суммирований в сумматоре, при этом n определяется количеством модулей в системе.
Если же использовать рекурсивное сдваивание, тогда логическая глубина определяется выражением [log2n]+3. В известных схемах логическая глубина с учетом определения коэффициентов ОПСС определяется как 2n+5.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ЗНАКА МОДУЛЯРНОГО ЧИСЛА | 2011 |
|
RU2503995C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2006 |
|
RU2318238C1 |
| НЕЙРОННАЯ СЕТЬ ОСНОВНОГО ДЕЛЕНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2008 |
|
RU2400813C2 |
| УСТРОЙСТВО ДЛЯ ОСНОВНОГО ДЕЛЕНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2013 |
|
RU2559771C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ОБНАРУЖЕНИЯ ОШИБОК В СИММЕТРИЧНОЙ СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2007 |
|
RU2374678C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ПОЛИАДИЧЕСКОГО КОДА В КОД СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ | 2003 |
|
RU2258257C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ДЕЛЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2005 |
|
RU2305312C2 |
| УСТРОЙСТВО ДЛЯ ОСНОВНОГО ДЕЛЕНИЯ МОДУЛЯРНЫХ ЧИСЕЛ В ФОРМАТЕ СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ | 2013 |
|
RU2559772C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ВЫЧИСЛЕНИЯ ПОЗИЦИОННЫХ ХАРАКТЕРИСТИК НЕПОЗИЦИОННОГО КОДА | 2003 |
|
RU2257615C2 |
| НЕЙРОННАЯ СЕТЬ УСКОРЕННОГО МАСШТАБИРОВАНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2007 |
|
RU2359325C2 |

Изобретение относится к вычислительной технике и может быть использовано в вычислительных системах, функционирующих в системе остаточных классов. Техническим результатом является повышение быстродействия устройства и сокращение аппаратных затрат. Устройство содержит входные регистры, схемы определения знака, схемы сдвига полярности чисел, просмотровые таблицы (память) для хранения констант 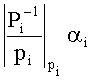 и
и 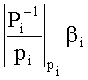 , сумматор и логический элемент «исключающее или», схему анализа знаков чисел. 3 ил.
, сумматор и логический элемент «исключающее или», схему анализа знаков чисел. 3 ил.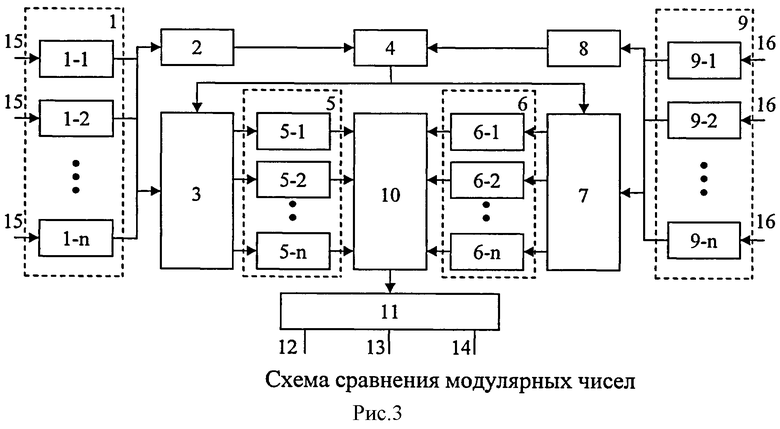
Устройство для сравнения чисел, представленных в системе остаточных классов, содержащее схему анализа знаков чисел, отличающееся тем, что в него введены схемы определения знаков чисел A и B, схемы сдвига полярности чисел, просмотровые таблицы (память) для хранения констант 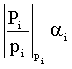
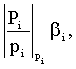
| Устройство для спавнения чисел | 1974 |
|
SU541164A1 |
| Устройство для сравнения чисел в системе остаточных классов | 1988 |
|
SU1619248A1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ОБНАРУЖЕНИЯ ОШИБОК В СИММЕТРИЧНОЙ СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2007 |
|
RU2374678C2 |
| US 7523151 B1, 21.04.2009 | |||
| US 2008155004 A1, 26.06.2008. | |||
Авторы
Даты
2014-01-10—Публикация
2011-09-27—Подача