Изобретение относится к вычислительным модулярным системам и предназначено для выполнения основного деления чисел, представленных в системе остаточных классов (СОК).
В СОК обычное целое число представляется в виде остатков от деления на набор модулей. Арифметические операции над числами заменяются операциями над остатками. Выполнение операций происходит параллельно и без межразрядных переносов, что позволяет очень быстро реализовать сложение, вычитание и умножение. Однако операция деления представляет определенные трудности, которые исследователи стараются упростить, предлагая новые архитектуры вычислений и аппаратные реализации.
Известно изобретение «Нейронная сеть для деления чисел, представленных в системе остаточных классов» (патент RU 2318239, G06F, опубл. 27.02.2008), содержащее нейронную сеть для расширения кортежа числовой системы вычетов, нейронные сети конечного кольца для суммирования и умножения.
Недостатком устройства является низкая скорость деления чисел и ограниченная функциональная возможность, так как в качестве делителя выбирается один их модулей системы остаточных классов (СОК).
Наиболее близкой к данному изобретению является «Нейронная сеть основного деления модулярных чисел» (патент RU 2400813, G06F 3/02, G06F 7/72, опубл. 27.04.2010). Недостатком устройства является большой объем оборудования. Известная нейронная сеть предназначена для деления модулярных чисел в случае, когда в качестве делителя используется целое положительное число, попарно простое с p1, p2, …, pn, либо целое положительное число, представляющее собой произведение чисел, попарно взаимно простых с pi. Для выполнения этого условия возникает необходимость нахождения приблизительного делителя путем использования обобщенной позиционной системы счисления (ОПСС). При вычислении приблизительного делителя нарушается регулярность структуры устройства деления, так как используются модульные и немодульные операции.
Техническим результатом данного изобретения является упрощение устройства за счет использования регулярной структуры, расширения функциональных возможностей и сокращения оборудования, что позволяет использовать предложенное изобретение в динамике вычислительного процесса. Указанный технический результат достигается тем, что устройство использует только модульные операции, то есть вычисления выполняются параллельно, в формате СОК. Предлагается устройство для основного деления модулярных чисел в формате системы остаточных классов, содержащее входные регистры делимого и делителя, выходы которых коммутируются мультиплексором для поочередного преобразования делимого и делителя, представленных в основной СОК, во вспомогательную СОК, выход мультиплексора соединен со входом блока расширения, расширяющего базу СОК, выход которого соединен со входом демультиплексора, выходы которого соединены с регистрами хранения остатков по расширенным основаниям, выход регистра делимого по расширенным основаниям соединен со входом умножителя, а выходы регистра делителя соединены с LUT-таблицей, преобразующей делитель по расширенным основаниям в мультипликативную инверсию, выходы которой соединены с умножителем, где реализуется вычислительная модель 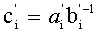
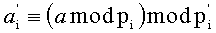
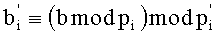
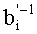
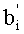
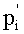
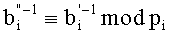
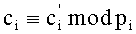
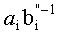
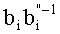
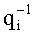
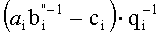
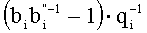
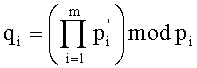
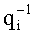
Устройство для основного деления модулярных чисел в формате системы остаточных классов содержит: входные шины для подачи делимого, шина 1, входные шины для подачи делителя, шина 2, и выходную шину частного, шина 53; регистр делимого 3 и регистр делителя 4; мультиплексор 5 для коммутации делимого и делителя на вход блока расширения 6, который коммутирует шины 28 и 29 на шину 30, являющуюся входом блока расширения 6, который преобразует делимое и делитель из основной системы оснований во вспомогательную систему оснований; демультиплексор 7 коммутирует выход блока расширения 6, шина 32, на вход 34 регистра делимого 8 и вход 35 регистра делителя 9, которые временно хранят делимое и делитель, представленные во вспомогательной СОК; умножитель 11, который выполняет операцию умножения делимого и мультипликативной инверсии делителя, представленных во вспомогательной СОК, поданных соответственно по шинам 36 и 37, 38 через LUT-таблицу 10, в которой происходит выборка мультипликативной инверсии делителя; шины 38 и 39 подаются на вход мультиплексора 12, который поочередно их коммутирует на выход 40, являющийся входом блока расширения 13, осуществляющего расширение поданных значений, представленных во вспомогательной СОК, в основную СОК; выход блока расширения 13, шина 42, поочередно коммутируется демультиплексором 16 на вход регистра 15, шина 44, и вход регистра 17, шина 45, для временного хранения, соответственно, мультипликативной инверсии и произведения делимого и мультипликативной инверсии, представленных в основной СОК; выход регистра 15, шина 46, подается на первые входы умножителей 18, 19, на вторые входы которых поступает делимое и делитель, представленные в основной СОК, шины 28 и 29; выходы умножителей 18 и 19, шины 48 и 49, произведений, соответственно, делимого и делителя на мультипликативную инверсию, представленных в основной СОК поступают через схемы ключей 24 и 25 на вход, соответственно, регистра делимого 3 и регистра делителя 4 по шинам 26 и 27, и одновременно данные по шинам 48 и 49, соответственно, поступают на первые входы схем вычитания и умножения 20 и 21, а на вторые входы поступает, соответственно, выход регистра 17, шина 47, хранящий произведения делимого и мультипликативной инверсии, преобразованные в основную СОК, и константа «1»; в схемах вычитания и умножения 20 и 21 полученные значения умножаются на константу 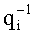
Управление процессом деления осуществляется блоком управления 14, который формирует адресные входы мультиплексоров 5, 12, шины, соответственно, 31 и 41, и адресные входы демультиплексоров 7, 16, шины, соответственно, 33 и 43.
Рассмотрим новый алгоритм основного деления модулярных чисел для случая, когда делимое и делитель представляют собой произвольные целые числа и делитель не приводится к случаю попарно простого с модулями СОК.
В последнее время проявляется значительный интерес к СОК, обладающей высоким уровнем естественного параллелизма при выполнении арифметических операций, высокой точностью, надежностью и стойкостью.
Специализированные процессоры на основе арифметики СОК могут сыграть важную роль в высокоскоростных системах обработки данных в режиме реального времени. Операции сложения, вычитания и умножения, называемые модульными операциями, могут быть реализованы очень быстро, без распространения межразрядных переносов. Немодульные операции деления, сравнения чисел, определения знака и переполнения диапазона остаются сравнительно медленными. Любое улучшение скорости этих медленных алгоритмов значительно улучшает производительность многомодульных арифметико-логических устройств (АЛУ) и расширяет приложения СОК. Обычно при рассмотрении деления в СОК выделяют три категории: деление с нулевым остатком, масштабирование и деление в общем случае. Проблема деления в СОК в общем виде привлекает внимание многих исследователей для разработки высокопроизводительных многомодульных АЛУ. Известные алгоритмы деления в СОК, основанные на масштабировании, округлении, расширении и других операциях, являются медленными и требуют выполнения большого количества арифметических действий. Большинство известных алгоритмов работает путем рекурсивного вычитания числа, кратного делителю, из делимого до тех пор, пока разность не станет меньше, чем делитель. В связи с этим возникает необходимость упростить структуру вычислений при делении. Одно из направлений упрощения структуры устройства деления состоит в том, что делимое, делитель и остаток представлены только в формате СОК.
Рассмотрим параллельный алгоритм деления в СОК, преимущество которого состоит в том, что делимое, делитель и все промежуточные вычисления выполняются в СОК.
Параллельный алгоритм.
1. Пусть p1, p2, …, pm есть набор модулей, (a1, a2, …, am) - делимое и (b1, b2, …, bm) - делитель.
2. Определим вспомогательную систему оснований 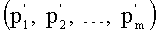
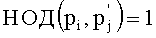
3. Вычислим (q1, q2, …, qm), где 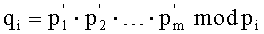
4. Переведем (a1, a2, …, am) по основаниям p1, p2, …, pm в 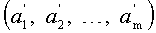
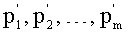
5. Переведем (b1, b2, …, bm) по основаниям p1, p2, …, pm в 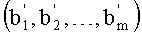
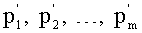
6. Вычисляем 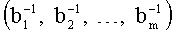
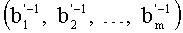
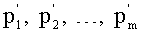
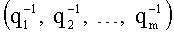
7. Вычисляем 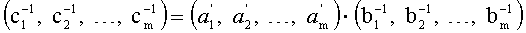
8. Переведем 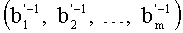
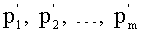
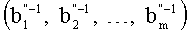
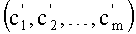
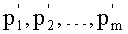
9. Вычисляем 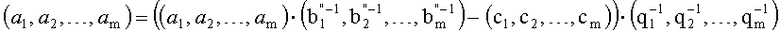
10. Вычисляем 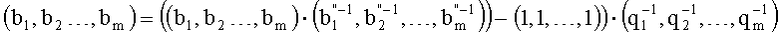
11. Если (b1, b2, …, bm)=(1, 1, …, 1), то (a 1, a 2, …, a m) есть частное; иначе - перейти к шагу 4.
Пример.
Возьмем исходную систему оснований (p1, p2, p3)=(7, 11, 13) и вспомогательную систему оснований 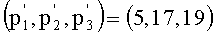
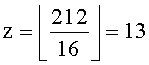
Операция деления выполняется следующим образом.
1. Вычисляем 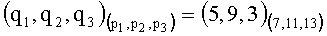
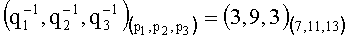
2. Переводим 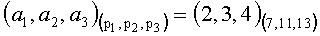
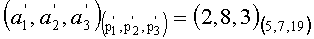
3. Переводим 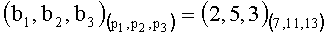
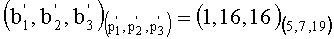
4. Переводим 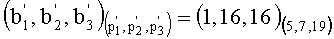
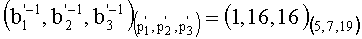
5. Вычисляем 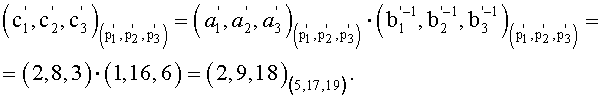
6. Переводим 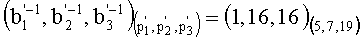
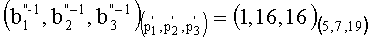
7. Переводим 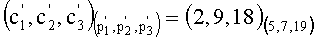
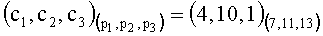
8. Вычисляем 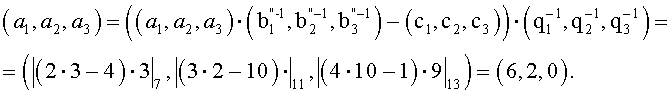
9. Вычисляем 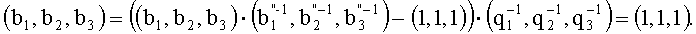
Так как (b1, b2, b3)=(1, 1, 1), то частное вычисляется как (6, 2, 0).
На чертеже (фиг. 1) представлена схема устройства для основного деления модулярных чисел в формате системы остаточных классов. Схема устройства пунктирной линией разделена на левую и правую части. В левой части вычисления ведутся в основной системе СОК, а в правой части во вспомогательной СОК. Принцип работы данного устройства излагается ниже.
Делимое a и делитель b, представленные в основной системе остаточных классов, по шинам 1 и 2 поступают на входные регистры делимого 3 и делителя 4. Выходные данные с регистров делимого 3 и делителя 4 по шинам соответственно 28 и 29 поступают на информационные входы мультиплексора 5. Под действием адресного входа, шина 31, формируемого блоком управления 14, мультиплексор 5 вначале подает делимое по шине 30 на вход блока расширения 6, который представляет собой нейронную сеть для расширения кортежа числовой системы вычетов (патент RU 2256226, Бюл. №19 от 10.07.2005). Блок расширения 6 преобразует делимое ai, представленное в основной СОК, в делимое 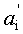
После преобразования делимого аналогичным образом осуществляется преобразование делителя b, представленного в основной СОК, в делитель b′, представленный во вспомогательной СОК. При этом демультиплексор 7 через шину 35 помещает данные делителя в регистр делителя 9. С выхода регистра делителя 9 по шине 37 делитель 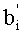
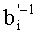
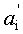
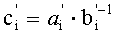
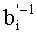
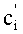
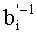
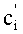
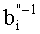
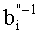
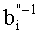
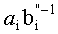
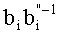
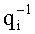
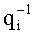
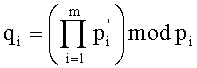
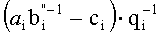
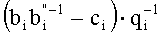
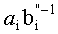
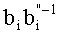
Итак, основное деление модулярных чисел осуществляется только с помощью модульных схем, что и обеспечивает регулярную структуру устройства.
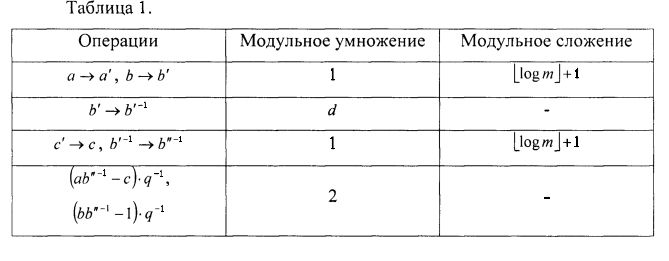
Анализ сложности устройства базируется на числе модулярных вычислений. Вычислительная сложность определяется вычислениями только по одному остатку, так как применяется параллельный алгоритм обработки. Модульное умножение выполняется по одному разу, а модульное сложение m+1 раз в преобразованиях a, b к a′, b′ и m+1 раз при преобразовании c′, b′-1 к c, b″-1. Вычисление b′-1 составляет O(d), где d - количество цифр в модуле. Сложность устройства представлена в таблице 1.
В устройстве все числа имеют остаточное представление, поэтому не возникает необходимость преобразования из остаточного представления в бинарное. Частное после вычисления также представляется в остатках. Таким образом, устройство обладает большой эффективностью при выполнении операции деления модулярных чисел.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ ОСНОВНОГО ДЕЛЕНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2013 |
|
RU2559771C2 |
| Устройство деления модулярных чисел | 2016 |
|
RU2628179C1 |
| Устройство вычисления модулярного произведения Монтгомери | 2017 |
|
RU2652450C1 |
| НЕЙРОННАЯ СЕТЬ ОСНОВНОГО ДЕЛЕНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2008 |
|
RU2400813C2 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ЗНАКА МОДУЛЯРНОГО ЧИСЛА | 2011 |
|
RU2503995C2 |
| СПОСОБ ИЗГОТОВЛЕНИЯ ВСЛЕПУЮ ЦИФРОВОЙ RSA-ПОДПИСИ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ (ВАРИАНТЫ) | 1998 |
|
RU2153191C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ДЕЛЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2006 |
|
RU2318239C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ДЕЛЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2005 |
|
RU2305312C2 |
| УСТРОЙСТВО ДЛЯ СРАВНЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2011 |
|
RU2503992C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ОБНАРУЖЕНИЯ, ЛОКАЛИЗАЦИИ И ИСПРАВЛЕНИЯ ОШИБОК В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2005 |
|
RU2301442C2 |
Изобретение относится к вычислительной технике и может быть использовано в арифметико-логических устройствах вычислительных систем, функционирующих в системе остаточных классов. Техническим результатом является повышение быстродействия и упрощение устройства. Устройство содержит регистры, мультиплексоры, блоки расширения, демультиплексоры, LUT-таблицу, умножители, схемы вычитания и умножения, ключи, схему сравнения, блок управления. 1 ил., 1 табл. 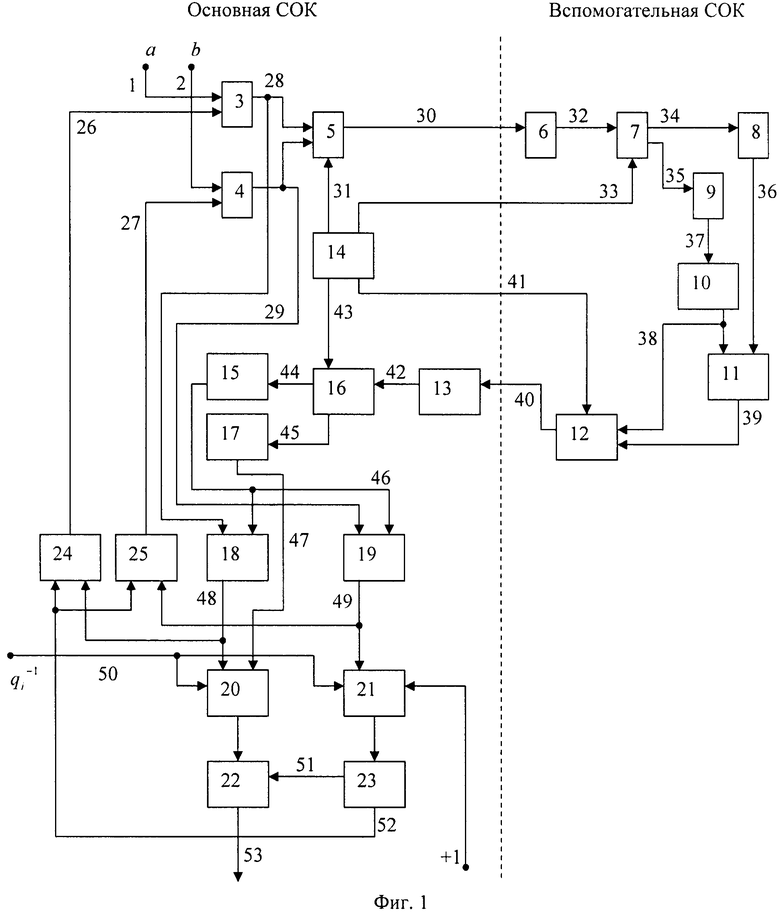
Устройство для основного деления модулярных чисел в формате системы остаточных классов, содержащее входные регистры делимого и делителя, выходы которых коммутируются мультиплексором для поочередного преобразования делимого и делителя, представленных в основной системе остаточных классов (СОК), во вспомогательную СОК, выход мультиплексора соединен со входом блока расширения, расширяющего базу СОК, выход которого соединен со входом демультиплексора, выходы которого соединены с регистрами хранения остатков по расширенным основаниям, выход регистра делимого по расширенным основаниям соединен со входом умножителя, а выходы регистра делителя соединены с LUT-таблицей, преобразующей делитель по расширенным основаниям в мультипликативную инверсию, выходы которой соединены с умножителем, где реализуется вычислительная модель 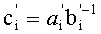
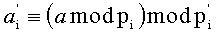
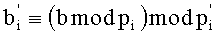
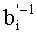
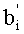
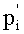
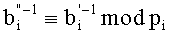
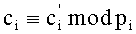
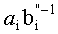
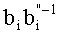
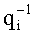
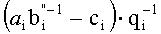
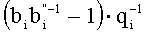
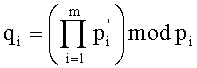
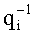
| НЕЙРОННАЯ СЕТЬ ОСНОВНОГО ДЕЛЕНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2008 |
|
RU2400813C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ДЕЛЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2006 |
|
RU2318239C1 |
| Устройство для деления чисел в модулярной системе счисления | 1990 |
|
SU1756887A1 |
| Арифметическое устройство по модулю | 1989 |
|
SU1633400A1 |
| US 2008114820 A1, 15.05.2008 | |||
| US 2005038845 A1, 17.02.2005 | |||
| US 6470372 B1, 22.10.2002 | |||
Авторы
Даты
2015-08-10—Публикация
2013-11-06—Подача