Изобретение относится к вычислительной технике и предназначено для выполнения операции сравнения двух чисел, представленных в системе остаточных классов.
Известно устройство для сравнения чисел, представленных в системе остаточных классов, основанное на приближенном методе (А.С. RU №2503992, БИ №1, 10.01.2014), содержащее входные регистры 1, 9 для хранения чисел, схемы определения знаков чисел 2 и 8, схемы сдвига полярности 3, 7, просмотровые таблицы 5, 6 для хранения произведения констант и разрядов СОК, сумматор 10, логический элемент «ИСКЛЮЧАЮЩЕЕ ИЛИ» 4, схемы анализа знака 11. Недостаток устройства - нет возможности проверить корректность получаемого результата сравнения чисел, поскольку не учитываются ошибки округления, образующиеся при вычислении приближенной относительной величины модулярного числа.
Наиболее близким к заявленному изобретению является устройство для сравнения чисел, представленных в системе остаточных классов на основе интервально-позиционных характеристик (А.С. RU №255744, БИ №7, 16.07.2015), содержащее группы входных регистров 1, 2 для хранения сравниваемых модулярных чисел, блоки вычисления интервально-позиционной характеристики 3, 5, блок поразрядного сравнения модулярных чисел 4, блоки проверки правильности интервально-позиционных характеристик 6, 8, блок сравнения интервально-позиционных характеристик 7, схему выдачи результата сравнения 9. Однако данное устройство использует трудоемкие операции в формате с плавающей точкой с направленным округлением.
Техническим результатом заявляемого устройства для сравнения чисел в системе остаточных классов является повышение быстродействия по отношению к другим устройствам на базе приближенных методов. Представленные положения обеспечиваются использованием целочисленной интервальной арифметики, которая реализуется с использованием стандартных двоичных устройств с фиксированной точкой без необходимости выполнения направленных округлений.
Описание устройства: в основе функционирования устройства для сравнения чисел в системе остаточных классов лежит метод целочисленной интервальной оценки относительной величины модулярного числа. Рассмотрим его.
Пусть базис системы остаточных классов (СОК) задан попарно взаимно простыми модулями p1,p2, …, pn и Р - произведение всех модулей. Тогда целое число X из интервала X∈[О, Р) будет представлено в виде независимых наименьших неотрицательных остатков (вычетов) (х1,х2, …, xn), причем xi ≡ X modpi ↔ |Х|pi. Согласно Китайской теореме об остатках (КТО), позиционное значение числа, представленного в СОК остатками 〈х1 х2, …, xn〉 по основаниям р1, р2, …, pn, вычисляется по формуле

где  - мультипликативная инверсия Pi по модулю pi, i∈[1,n],
- мультипликативная инверсия Pi по модулю pi, i∈[1,n],
n - количество модулей.
Согласно теоретико-числовой теореме Эйлера мультипликативную инверсию  , соответствующую сравнению
, соответствующую сравнению  , можно вычислить следующим образом
, можно вычислить следующим образом

где ϕ(pi) - функция Эйлера, равная количеству целых чисел в диапазоне [1, pi], взаимно простых с pi.
Пример. Вычислим значения мультипликативных инверсий Pi по модулям pi для системы с основаниями: p1 = 65535, p2 = 65534, p3 = 65533, р4 = 65531:

Относительная величина Е(Х/Р) модулярного числа Х - это отношение его позиционного значения к произведению модулей Р, то есть

Рассмотрим следующую величину

в которой целая часть определяет коэффициент R, а дробная - значение (X/P).
Поскольку точные рациональные значения величин 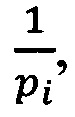 а следовательно и (Х/Р), в общем случае не представимы в ЭВМ с ограниченной разрядной сеткой, возникает задача их аппроксимации. Для решения этой задачи представим все величины
а следовательно и (Х/Р), в общем случае не представимы в ЭВМ с ограниченной разрядной сеткой, возникает задача их аппроксимации. Для решения этой задачи представим все величины  в виде интервалов с направленно округленными границами в формате с фиксированной точкой, как показано на фиг. 1. Следовательно, величина (3) также может быть представлена в виде интервала.
в виде интервалов с направленно округленными границами в формате с фиксированной точкой, как показано на фиг. 1. Следовательно, величина (3) также может быть представлена в виде интервала.
В случае, если значения всех модулей достаточно большие, величины pi могут быть представлены одним интервалом:
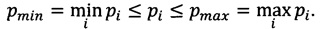
Обозначим pi∈[pmin; pmax] - интервальная величина всех модулей pi.
Тогда по правилам интервальных вычислений
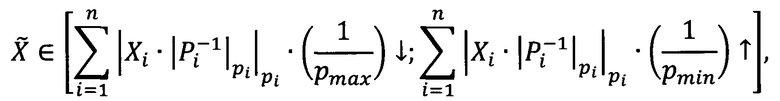
где ↑ говорит о том, что вычисление выполняется с округлением с избытком («вверх»),
↓ - с недостатком («вниз»).
Величины  и
и  могут быть вычислены заранее с определенной точностью. Как правило, величина модулей подбирается таким образом, чтобы их двоичным представлением было q-разрядное число, то есть
могут быть вычислены заранее с определенной точностью. Как правило, величина модулей подбирается таким образом, чтобы их двоичным представлением было q-разрядное число, то есть
2q-1<pi<2q.
Тогда обратная величина удовлетворяет условию

В случае, если величина q достаточно велика, то значение величины 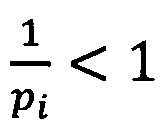 в формате с фиксированной точкой будет следующее:
в формате с фиксированной точкой будет следующее:
- значение целой части равно 0;
- первые (q - 1) разрядов дробной части равны 0;
- q-й разряд равен 1;
- следующие z разрядов равны нулю;
- следующие (q+z+1)-й, (q+z+2)-й и т.д. разряды определяются непосредственно значением величины 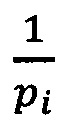 (фиг. 2.).
(фиг. 2.).
Таким образом, вместо чисел с плавающей точкой, определяющих значения  и
и  , можно использовать числа с фиксированной точкой - целые числа с масштабирующим коэффициентом.
, можно использовать числа с фиксированной точкой - целые числа с масштабирующим коэффициентом.
Величина  усеченная до q+t-1 разрядов после точки равна
усеченная до q+t-1 разрядов после точки равна
 ,
,
 ,
,
где 
 - наибольшее целое, не более, чем
- наибольшее целое, не более, чем 
 - наименьшее целое, не менее, чем
- наименьшее целое, не менее, чем 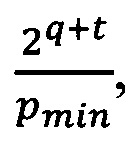 t - количество вычисляемых значащих цифр величины
t - количество вычисляемых значащих цифр величины 
Примем t=z. Тогда величины  и
и  соответственно будут равны
соответственно будут равны  ,
, 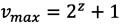 (фиг. 2).
(фиг. 2).
Обозначим

Интервальное число  назовем целочисленной интервальной характеристикой модулярного числа X.
назовем целочисленной интервальной характеристикой модулярного числа X.
Поскольку  - положительные целые числа разрядностью (q+z+log2n), где n - количество модулей в базисе, то
- положительные целые числа разрядностью (q+z+log2n), где n - количество модулей в базисе, то

где ⎣ ⎦ обозначает целую часть от деления на 2q+z.
Иными словами  - старшие log2 n разрядов чисел
- старшие log2 n разрядов чисел 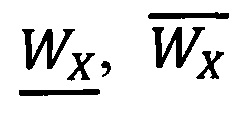 соответственно,
соответственно, 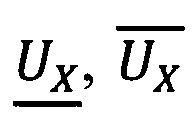 - младшие q+t разрядов чисел
- младшие q+t разрядов чисел  .Здесь Ux - целочисленный аналог относительной величины (Х/Р) модулярного числа X.
.Здесь Ux - целочисленный аналог относительной величины (Х/Р) модулярного числа X.
В случае, если  то
то  значения
значения 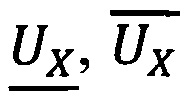 корректны и могут быть использованы для сравнения модулярных чисел. Если
корректны и могут быть использованы для сравнения модулярных чисел. Если
то необходима дополнительная информация об абсолютной величине числа: если 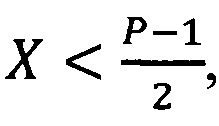 то
то  если
если  то
то 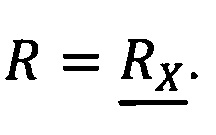 .
.
Абсолютную погрешность целочисленной интервальной характеристики характеризует ее диаметр

Пусть разность pmax - pmin=α, тогда 
Таким образом, верхняя оценка абсолютной погрешности ИПХ не зависит от конкретного модулярного числа и равна
diamWX<2t-q⋅α+1.
Объективной мерой точности целочисленной интервальной характеристики является ее относительная ошибка

Пусть в СОК с модулями р1,р2, …, pn даны беззнаковые числа А=〈alta2,...,ап〉 и В=〈bltb2, -,bn〉. Алгоритм их сравнения с использованием целочисленных интервальных характеристик формулируется следующим образом.
Шаг 0: предварительно с использованием расширенного алгоритма Евклида вычисляются и сохраняются значения мультипликативных инверсий |Pi-1|, i∈G [1,n], n - количество модулей.
Выбираются значения 
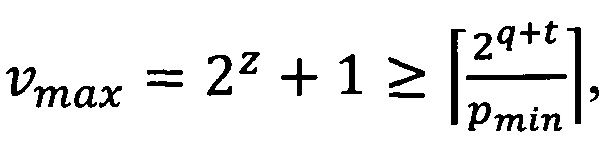 где
где 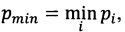
 i ∈ [1,n], n - количество модулей,
i ∈ [1,n], n - количество модулей,
 - наибольшее целое, не более, чем
- наибольшее целое, не более, чем  - наименьшее целое, не менее, чем
- наименьшее целое, не менее, чем 
Шаг 1. Выполняется попарное сравнение остатков для исключения тривиального случая: если ai=bi для всех i ∈ [1,n], то А=В и алгоритм завершается.
Шаг 2. Вычисляются вектора значений 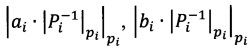 , i∈[1,n].
, i∈[1,n].
Шаг 3. Вычисляются значения 
 , i∈[1,n]
, i∈[1,n]
Шаг 4. Вычисляются верхние и нижние границы целочисленных интервальных характеристик чисел 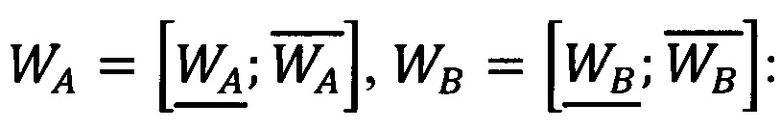
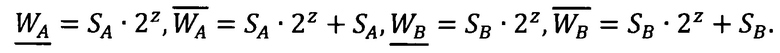
Выделяются из значений  значения
значения 
 - старшие log2 n разрядов чисел
- старшие log2 n разрядов чисел 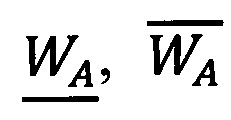 соответственно,
соответственно,  - младшие q+z разрядов чисел
- младшие q+z разрядов чисел  аналогично для второго числа, то есть
аналогично для второго числа, то есть

Шаг 5. Проверяется первое (необходимое) условие корректного сравнения: если  то переход к шагу 6, иначе - к шагу 7.
то переход к шагу 6, иначе - к шагу 7.
Шаг 6. Если  то алгоритм завершается с результатом А<В, если
то алгоритм завершается с результатом А<В, если  то алгоритм завершается с результатом А>В. Иначе осуществляется переход к шагу 7.
то алгоритм завершается с результатом А>В. Иначе осуществляется переход к шагу 7.
Шаг 7. Если не выполнены необходимые и достаточные условия для сравнения, то есть не выполнено хотя бы одно из условий 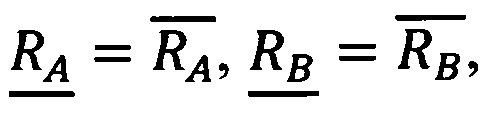
 то преобразовать числа А и В из СОК в систему со смешанными основаниями и сравнить цифры полиадических кодов, начиная со старшей, либо сформировать и выдать сигнал о невозможности сравнения чисел. Алгоритм при этом завершается.
то преобразовать числа А и В из СОК в систему со смешанными основаниями и сравнить цифры полиадических кодов, начиная со старшей, либо сформировать и выдать сигнал о невозможности сравнения чисел. Алгоритм при этом завершается.
Пример 2. Сравнить числа А=〈58765,15597,38429,19957〉 и В=〈18495,11904,64661,20480〉, представленные в СОК с модулями {65535,65534,65533,65531}. Для наглядности будем использовать десятичную, а не двоичную систему счисления, поэтому приведенный алгоритм будет иметь соответствующую десятичную интерпретацию.
0. Определим вначале все необходимые константы для заданной системы модулей:
- набор весов ортогональных базисов: {57343, 21845, 16383, 35496};
- разрядность модулей q=16, разрядность коэффициентов 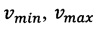 : t=z=13;
: t=z=13;
- интервальный коэффициент  .
.
1. Числа не равны, поэтому переходим к следующему шагу.
2. Вычислим вектора значений 
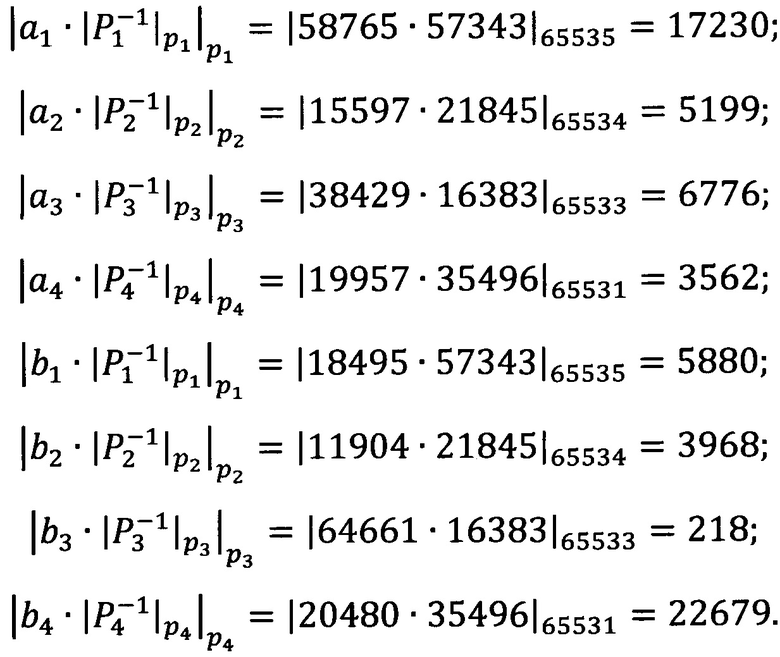
3. Вычислим значения 
SA=17230+5199+6776+3562=32767;
SB=113+51210+21945+25026=32763.
4. Вычислим верхние и нижние границы целочисленных интервальных характеристик чисел А и В 

Таким образом, SA и Sb соответствуют нижним границам целочисленных интервальных характеристик, сдвинутым на z разрядов.
Выделяем из значений  значения
значения 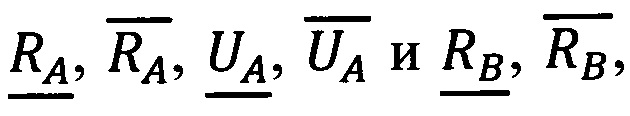

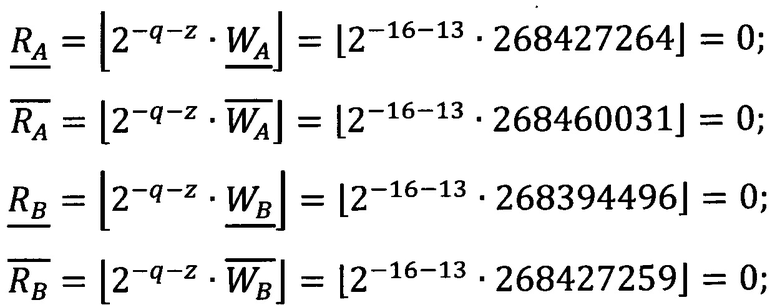

5. Выполним сравнение:
 следовательно, значения
следовательно, значения 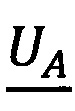 и
и 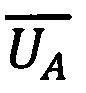 корректны.
корректны.
 следовательно, значения
следовательно, значения  и
и 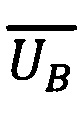 корректны.
корректны.
6. Сравним  и
и  268427264>268427259; сравним
268427264>268427259; сравним  и
и 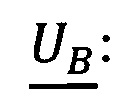 268460031>268394496.
268460031>268394496.  следовательно, В<А.
следовательно, В<А.
Для проверки преобразуем числа в позиционную систему: А=9221825012527697935, B=9220966382894533110, В<А. Таким образом, с использованием целочисленных интервальных характеристик получен правильный результат сравнения двух близлежащих модулярных чисел (числа различаются менее чем на 0,009%).
Выполним проверку корректности вычисления относительной величины модулярных чисел. Вычисления будем производить в десятичной системе счисления. Диапазон представления модулярных чисел Р=18443648025055395869. Вычислим значение Е(А/Р), Е(В/Р) с округлением до десяти цифр после запятой. А/Р ≈ 0,5000000542, В/Р ≈ 0,4999535.
Масштабируем значения  с округлением до десяти цифр после запятой:
с округлением до десяти цифр после запятой:

следовательно,
Относительная ошибка 0,009%,  Относительная ошибка 0,012%.
Относительная ошибка 0,012%.
Предложенный алгоритм позволил получить высокоточную информацию о величине числа в модулярном представлении без использования трудоемкого преобразования в позиционную систему.
Таким образом, при целочисленной интервальной аппроксимации относительной величины модулярного числа осуществляется естественный учет погрешностей округления, не требующий применения направленных округлений и арифметики с плавающей точкой. Это позволяет простым образом контролировать корректность результата немодульной операции, вне зависимости от числа модулей СОК и их разрядности.
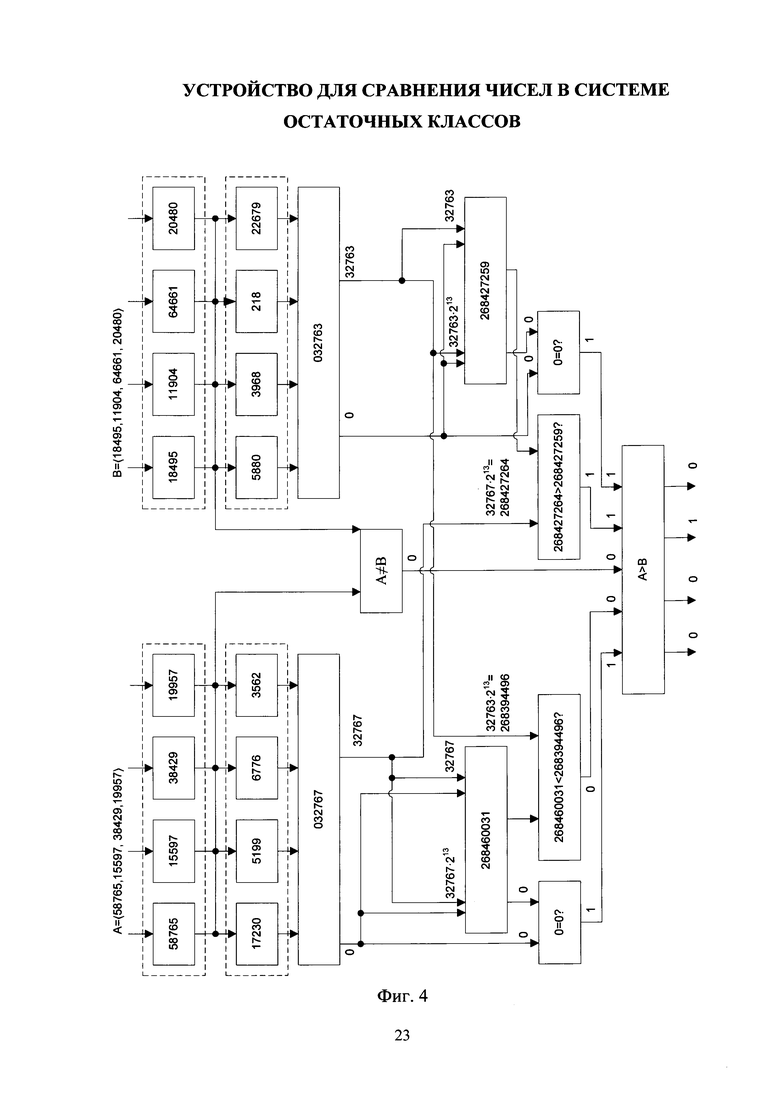
Схема заявляемого устройства для сравнения чисел в системе остаточных классов, функционирующего в соответствии с описанными принципами представлена на фиг.3. Устройство содержит группы входных регистров 1, 2 для хранения сравниваемых модулярных чисел, группы умножителей по модулям на константу 3, 4, параллельные многовходовые двоичные сумматоры 5, 6 для формирования нижних границ целочисленных интервальных характеристик первого и второго чисел соответственно, блок поразрядного сравнения модулярных чисел 7, двоичные сумматоры 8, 9 для формирования верхних границ целочисленных интервальных характеристик первого и второго чисел соответственно, блоки определения корректности вычисления целочисленных интервальных характеристик 10, 13 первого и второго чисел соответственно, блоки сравнения целочисленных интервальных характеристик 11, 12, схему выдачи результата сравнения 14.
Группа входных регистров 1 предназначена для хранения числа А, поступающего по шине данных 15, и содержит регистры 1.1, 1.2, …, 1.n, выходы которых соединены с информационными входами блоков 3.1, 3.2, …, 3.n и 7. В свою очередь, группа входных регистров 2 предназначена для хранения числа В, поступающего по шине данных 16, и содержит регистры 2.1, 2.2, …, 2.n, выходы которых соединены с информационнымип входами блоков 7 и 4.1, 4.2, …, 4.n. Выходы блоков 3.1,3.2, …3.n, 4.1, 4.2,…, 4.n соединены с входами блоков 5, 6 соответственно. Выход блока 7 соединен с одним из входов схемы 14. Выходы блока 5 соединены с входами блока 8, один из выходов блока 5 соединен с одним из входов блока 10, другой выход блока 5 соединен с одним из входов блока 12. Выходы блока 6 соединены с входами блока 9, один из выходов блока 6 соединен с одним из входов блока 11, другой выход блока 6 соединен с одним из входов блока 13. Один из выходов блока 8 соединен с одним из входов блока 10, другой выход блока 8 соединен с одним из входов блока 11. Один из выходов блока 9 соединен с одним из входов блока 13, другой выход блока 9 соединен с одним из входов блока 12. Выход блока 10 соединен с одним из входов схемы 14. Выходы блоков 11, 12 соединены со входами схемы 14. Выход блока 13 соединен с одним из входов схемы 14. Выходы схемы 14 соединены с шинами 17, 18, 19, 20.
Работа заявляемого устройства для сравнения чисел в системе остаточных классов осуществляется следующим образом. Сравниваемые модулярные числа А=〈а1, а2, …, an〉 и В=〈b1 b2, …, bn〉 поступают по шинам данных 15, 16 и записываются в группы регистров 1, 2 соответственно, откуда подаются на входы блока 7, который производит попарное сравнение остатков (ai, bi,), i=1, 2, ..., n, и формирует сигнал логической единицы, если все остатки попарно равны, и сигнал логического нуля в противном случае. Одновременно с этим, данные, записанные в группы регистров 1 и 2 соответственно, подаются на входы групп умножителей по модулю на константу 3 и 4 соответственно, далее вычисленные значения подаются на параллельные многовходовые сумматоры 5 и 6 соответственно, где вычисляются смещенные нижние границы целочисленных интервальных характеристик SA и SB соответственно. Вычисленные значения смещенных нижних границ целочисленных интервальных характеристик SA и SB подаются на входы двоичных сумматоров 8 и 9 соответственно, причем значение SA подается на старшие разряды первого входа двоичного сумматора 8 со сдвигом на z разрядов, на младшие z разрядов первого входа двоичного сумматора 8 подается логический ноль, значение SA подается на младшие разряды второго входа двоичного сумматора 8, на старшие разряды второго входа двоичного сумматора 8 подается логический ноль, значение SB подается на старшие разряды первого входа двоичного сумматора 9 со сдвигом на z разрядов, на младшие z разрядов первого входа двоичного сумматора 9 подается логический ноль, значение SB подается на младшие разряды второго входа двоичного сумматора 9, на старшие разряды второго входа двоичного сумматора 9 подается логический ноль. Таким образом вычисляются значения верхних границ целочисленных интервальных характеристик. Старшие log2 n разрядов параллельного многовходового сумматора 5 и старшие log2 n разрядов двоичного сумматора 8 подаются на входы блока определения корректности вычисления целочисленных интервальных характеристик 10, при этом, если значения на обоих входах блока 10 равны, то на выходе формируется сигнал логической единицы, иначе - логического ноля. Аналогичным образом работает блок определения корректности вычисления целочисленных интервальных характеристик 13. Старшие log2 n разрядов параллельного многовходового сумматора 6 и старшие log2 n разрядов двоичного сумматора 9 подаются на входы блока определения корректности вычисления целочисленных интервальных характеристик 13, при этом, если значения на обоих входах блока 13 равны, то на выходе формируется сигнал логической единицы, иначе - логического ноля. Младшие (z+q) разрядов параллельного многовходового сумматора 5 и младшие (z+q) разрядов двоичного сумматора 8 подаются на входы блока сравнения целочисленных интервальных характеристик 11, при этом, если значение на первом входе блока 11 меньше значения на втором входе блока 11, то на выходе формируется сигнал логической единицы, иначе - логического ноля. Младшие (z+q) разрядов параллельного многовходового сумматора 6 и младшие (z+q) разрядов двоичного сумматора 9 подаются на входы блока сравнения целочисленных интервальных характеристик 12, при этом, если значение на первом входе блока 12 больше значения на втором входе блока 12, то на выходе формируется сигнал логической единицы, иначе - логического ноля. Результаты работы блоков 10, 11, 12, 13 подаются на соответствующие входы схемы выдачи результата сравнения. Работа схемы 14 осуществляется следующим образом: если на входе, соответствующем выходу блока 7, установлена логическая единица, то подается сигнал на шину 17, свидетельствующий о том, что А=В. Иначе анализируются входы, соответствующие выходам блоков 10 и 13: если хотя бы на одном из них установлен логический ноль, то подается сигнал на шину 20, свидетельствующий о том, что результат сравнения чисел А и В не может быть определен в силу недостаточной точности вычисления их целочисленных интервальных характеристик. Иначе анализируются входы, соответствующие выходам блоков 11 и 12: если на входе, соответствующем выходу блока 11 установлена логическая единица, а на входе, соответствующем выходу блока 12, установлен логический ноль, то А<В и подается сигнал на шину 18; если на входе, соответствующем выходу блока 11 установлен логический ноль, а на входе, соответствующем выходу блока 12, установлена логическая единица, то А>В и подается сигнал на шину 19. Иначе подается сигнал на шину 20, свидетельствующий о том, что результат сравнения чисел А и В не может быть определен в силу недостаточной точности вычисления их целочисленных интервальных характеристик.
Пример работы заявляемого устройства для сравнения чисел в системе остаточных классов представлен на фиг. 4. Сравнивались числа А=〈58765,15597,38429,19957〉 и В=〈18495,11904,64661,20480〉, представленные в СОК с модулями {65535,65534,65533,65531}.
Трудоемкость заявляемого устройства оценивается следующим образом. Пусть СОК задана n модулями. Тогда для сравнения чисел А и В при условии, что они не равны, требуется выполнить следующие операции: по одной операции модулярного умножения на каждом из n параллельных умножителей по модулю на константу в блоках 3, 4 одновременно; log2 n операций для вычисления суммы в блоках 5 и 6; по одной операции позиционного сложения в блоках 8, 9 одновременно; по одной операции позиционного сравнения в блоках 10, 11, 12, 13 одновременно. Схема сравнения в блоке 7 позволяет одновременно сравнивать все разряды чисел, причем сравнение производится одновременно с выполнением остальных операций, поэтому время выполнения поразрядного сравнения не учитывается. Схема интерпретации результата 14 построена на базе логических элементов и не требует выполнения дополнительных арифметических операций.
Таким образом, сравнение двух неравных чисел, представленных в n-модульной СОК, будет выполнено за 2+log2n+1+1=log2n+3 операций. Для сравнения чисел с помощью устройствана основе вещественных интервальных позиционных характеристик требуется 6n+7 операций. Следовательно, эффект повышения быстродействия от использования заявляемого устройства может достигать в среднем 
 раз, где n - количество модулей СОК.
раз, где n - количество модулей СОК.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ организации выполнения операции умножения двух чисел в модулярно-логарифмическом формате представления с плавающей точкой на гибридных многоядерных процессорах | 2017 |
|
RU2666285C1 |
| Способ организации выполнения операции умножения двух чисел в модулярно-индексном формате представления с плавающей точкой на универсальных многоядерных процессорах | 2017 |
|
RU2652460C1 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ЗНАКОВ ЧИСЕЛ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2014 |
|
RU2557446C1 |
| УСТРОЙСТВО ДЛЯ СРАВНЕНИЯ ЧИСЕЛ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ НА ОСНОВЕ ИНТЕРВАЛЬНО-ПОЗИЦИОННЫХ ХАРАКТЕРИСТИК | 2014 |
|
RU2557444C1 |
| Устройство для масштабирования чисел | 1989 |
|
SU1667066A1 |
| Устройство для сложения чисел в модулярной системе счисления | 1989 |
|
SU1672448A1 |
| Устройство для преобразования непозиционного кода в позиционный код | 1987 |
|
SU1510097A1 |
| Устройство сравнения чисел, представленных в системе остаточных классов | 2020 |
|
RU2751992C1 |
| Устройство для умножения чисел в модулярной системе счисления | 1989 |
|
SU1667065A1 |
| Устройство для вычисления квадратного корня числа в модулярной системе счисления | 1985 |
|
SU1317434A1 |


Изобретение относится к вычислительной технике. Технический результат изобретения заключается в повышении быстродействия устройства для сравнения чисел в системе остаточных классов. Технический результат достигается за счет использования целочисленных интервалов, при этом не требуется выполнения медленных циклов вычислений в формате с плавающей точкой. Для этого в устройство включены следующие специфические блоки: блоки параллельного модулярного умножения на константу, многовходовые (параллельные) двоичные сумматоры, двухвходовые двоичные сумматоры, блок поразрядного сравнения модулярных чисел, блоки проверки правильности целочисленных интервальных характеристик и блоки сравнения целочисленных интервальных характеристик. 4 ил.
Устройство для сравнения чисел в системе остаточных классов, отличающееся тем, что содержит первую и вторую группы входных регистров, каждая из которых состоит из n регистров, хранящих сравниваемые модулярные числа А и В, первую и вторую группы умножителей по модулю на константу, каждый из которых состоит из n умножителей по модулю на константу, первый и второй параллельные многовходовые сумматоры, каждый из которых имеет n информационных входов и два выхода, первый и второй двоичные сумматоры, каждый из которых имеет два входа и два выхода, блок поразрядного сравнения модулярных чисел, имеющий 2n информационных входов и один выход, первый и второй двоичные сумматоры, каждый из которых имеет два информационных входа и два выхода, первый и второй блоки проверки корректности вычисления целочисленной интервальной характеристики, каждый из которых имеет два информационных входа и один выход, первый и второй блоки сравнения целочисленных интервальных характеристик, каждый из которых имеет два информационных входа и один выход, схему выдачи результата сравнения, имеющую пять входов и четыре выхода, причем выходы регистров первой группы соединены с первыми n информационными входами блока поразрядного сравнения модулярных чисел и с информационными входами первой группы умножителей по модулю на константу, выходы регистров второй группы соединены со вторыми n информационными входами блока поразрядного сравнения модулярных чисел и с информационными входами второй группы умножителей по модулю на константу, выход блока поразрядного сравнения модулярных чисел соединен с первым входом схемы выдачи результата сравнения, выходы первой группы умножителей по модулю на константу соединены с информационными входами первого параллельного многовходового сумматора, выходы второй группы умножителей по модулю на константу соединены с информационными входами второго параллельного многовходового сумматора, первый и второй выходы первого параллельного многовходового сумматора соединены с первым и вторым входами первого двоичного сумматора, причем первый и второй выходы первого параллельного многовходового сумматора соединены со старшими разрядами первого входа первого двоичного сумматора, на младшие z разрядов при этом подается логический ноль, первый и второй выходы первого параллельного многовходового сумматора соединены с младшими разрядами второго входа первого двоичного сумматора, на старшие разряды при этом подается логический ноль, первый и второй выходы второго параллельного многовходового сумматора соединены с первым и вторым входами второго двоичного сумматора, причем первый и второй выходы второго параллельного многовходового сумматора соединены со старшими разрядами первого входа второго двоичного сумматора, на младшие z разрядов при этом подается логический ноль, первый и второй выходы второго параллельного многовходового сумматоры соединены с младшими разрядами второго входа второго двоичного сумматора, на старшие разряды при этом подается логический ноль, первый выход первого параллельного многовходового сумматора соединен с первым входом первого блока проверки корректности вычисления целочисленной интервальной характеристики, второй выход первого параллельного многовходового сумматора соединен с первым входом второго блока сравнения целочисленных интервальных характеристик, первый выход второго параллельного многовходового сумматора соединен с первым входом второго блока проверки корректности вычисления целочисленной интервальной характеристики, второй выход второго параллельного многовходового сумматора соединен со вторым входом первого блока сравнения целочисленных интервальных характеристик, первый выход первого двоичного сумматора соединен со вторым входом первого блока проверки корректности вычисления целочисленной интервальной характеристики, второй выход первого двоичного сумматора соединен с первым входом первого блока сравнения целочисленных интервальных характеристик, первый выход второго двоичного сумматора соединен со вторым входом второго блока проверки корректности вычисления целочисленной интервальной характеристики, второй выход второго двоичного сумматора соединен со вторым входом второго блока сравнения целочисленных интервальных характеристик, выходы первого и второго блоков проверки корректности вычисления целочисленной интервальной характеристики соединены со вторым и третьим входами схемы выдачи результата сравнения, выходы первого и второго блоков сравнения целочисленных интервальных характеристик соединены с четвертым и пятым входами схемы выдачи результата сравнения, выходы схемы выдачи результата сравнения являются выходами устройства для сравнения чисел в системе остаточных классов: «А=В», «А>В», «А<В», «Результат сравнения не определен».
| УСТРОЙСТВО ДЛЯ СРАВНЕНИЯ ЧИСЕЛ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ НА ОСНОВЕ ИНТЕРВАЛЬНО-ПОЗИЦИОННЫХ ХАРАКТЕРИСТИК | 2014 |
|
RU2557444C1 |
| УСТРОЙСТВО ДЛЯ ОСНОВНОГО ДЕЛЕНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2013 |
|
RU2559771C2 |
| УСТРОЙСТВО ДЛЯ СРАВНЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2011 |
|
RU2503992C2 |
| Устройство для закрепления лыж на раме мотоциклов и велосипедов взамен переднего колеса | 1924 |
|
SU2015A1 |
| Многоступенчатая активно-реактивная турбина | 1924 |
|
SU2013A1 |
Авторы
Даты
2019-08-26—Публикация
2018-11-26—Подача