Изобретение относится к робототехнике и предназначено для определения пространственного положения по всем трем декартовым координатам и угловой ориентации по всем трем возможным направлениям вращения вокруг осей тележки мобильного робота при ее перемещении по поверхностям, близким к горизонтальным, например по напольным покрытиям производственных помещений. Данная информация необходима для идентификации положения и угловой ориентации робота.
Известен сигнализатор угла наклона (Патент РФ №2156957, кл. МКИ G01С 9/00, 2000), содержащий стакан с крышкой, в которой установлена шаровая опора с жестко закрепленными на ней двумя стержнями, нижний из которых соединен с маятником, расположенным внутри стакана, заполненного демпфирующей жидкостью, а верхний замыкает на массу контактные кольца при определенных углах крена машины, два регулировочных болта, каждый из которых соединен с одним из контактных колец так, что при их вывинчивании обеспечивается независимое перемещение контактных колец (соответственно вверх или вниз) вдоль оси сигнализатора.
Данный сигнализатор позволяет определять предельно допустимые углы наклона в вертикальных плоскостях, но не позволяет находить точное значение данных углов и их проекции на заданные ортогональные оси. Также рассматривается задача определения местоположения объекта по осям.
Также известен мобильный робот (Патент РФ №2210492, кл. МКИ В25J 9/00, 2003), который оснащен устройством определения местоположения, соединенным с управляющей частью, и содержащим обзорную видеокамеру для создания обзорного изображения потолка помещения и распознавания базового знака на потолке.
Данная система распознавания хорошо работает в тех помещениях, где потолок расположен на небольшой высоте, и совершенно не применима в средах, где потолок отсутствует либо на него нельзя наносить технологические изображения.
Наиболее близкой по совокупности признаков является система (In Procedings of the SPIE, volume 4868 (SPIE2002) pp.269-276. Boston, MA. August 2002 Sensor Coverage using Mobile Robots and Stationary Nodes Maxim A. Batalina and Gaurav S. Sukhatmea University of Southern California, Robotics Research Lab, Los Angeles, CA 90089, USA), включающая сеть статических многоцелевых датчиков, используемых, в том числе, для идентификации местоположения мобильных роботов. Используемая при этом радиосвязь позволяет найти координаты мобильного робота очень приближенно.
Задачей изобретения является автоматизированное уточненное определение пространственного положения по всем трем декартовым координатам и угловой ориентации по всем трем возможным направлениям вращения вокруг осей тележки мобильного робота.
Поставленная задача достигается тем, что предложен способ определения пространственного положения и угловой ориентации тележки транспортного средства при ее движении по плоской поверхности, имеющей неровности, заключающийся в установке статических маяков на местности с заданной абсолютной декартовой системой координат, в которой две оси направлены параллельно плоскости перемещения тележки, а одна ось перпендикулярна ей, отличающийся тем, что согласно изобретению число статических маяков принимают равным трем, их центры с известными абсолютными координатами располагают в плоскости перемещения тележки, на тележке выбирают локальную декартову систему координат с центром, находящимся на заданной высоте по отношению к плоской поверхности, горизонтальной продольной, горизонтальной поперечной и вертикальной осью, образующими правую тройку, устанавливают на тележке три датчика и определяют углы склонения относительно локальной плоскости перемещения тележки и углы поворота относительно этой плоскости положения маяков, после чего при известных допущениях по измеренным углам поворота рассчитывают приближенные абсолютные координаты центра тележки и угла поворота тележки вокруг вертикальной оси, а затем при начальном приближении определяют уточненные абсолютные координаты центра тележки и углы поворота тележки вокруг трех осей путем итерационного численного решения системы уравнений
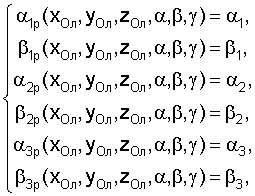
где (α1, α2, α3), (β1, β2, β3) - угловые положения маяков, измеренные при помощи датчиков.
αip(xОл, yОл, zол, α, β, γ), βip(xОл, yОл, zол, α, β, γ), где i=1, 2, 3 - расчетные значения соответствующих углов, определяемые по следующим зависимостям:
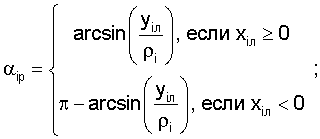
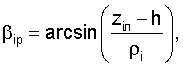
где 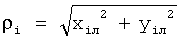 - радиус-вектор i-го маяка в локальной системе координат тележки;
- радиус-вектор i-го маяка в локальной системе координат тележки;
где хiл, yiл, ziл - видимые с тележки локальные координаты маяков, рассчитываемые по формулам
хiл=(cosβcosα+sinβsinγsinα)(xi-xОл)+(-cosβsinα+sinβsinγcosα)(yi-yОл)+(sinβcosγ)(zi-zОл)-xiл;
yiл=(cosγsinα)(xi-xОл)+(cosγcosα)(yi-yОл)-sinγ(zi-zОл)-yiл;
ziл=(-sinβcosα+cosβsinγsinα)(xi-xОл)+(sinβsinα+cosβsinγcosα)(yi-yОл)+(cosβcosγ)(zi-zОл)-ziл;
где xi, yi, zi - абсолютные координаты маяков;
хОл, yОл, zОл - абсолютные декартовые координаты центра тележки;
α, β, γ - углы поворота тележки вокруг осей x, y, z.
На фиг.1 схематически дан общий вид тележки 1 и помещения, в котором указана абсолютная система координат Oxyz. На тележке 1 указана локальная система координат Олxлyлzл, а также система координат Oлx'лy'лz'л, у которой оси ориентированы параллельно осям абсолютной системы координат Oxyz. Также на тележке 1 жестко закреплены датчики углового положения 2, 3, 4, имеющие локальные координаты (xл1, yл1, zл1), (xл2, yл2, zл2), (xл3, yл3, zл3). В помещении в точках с абсолютными координатами (x1, y1, z1), (х2, y2, z2), (х3, y3, z3) неподвижно установлены маяки 5, 6, 7.
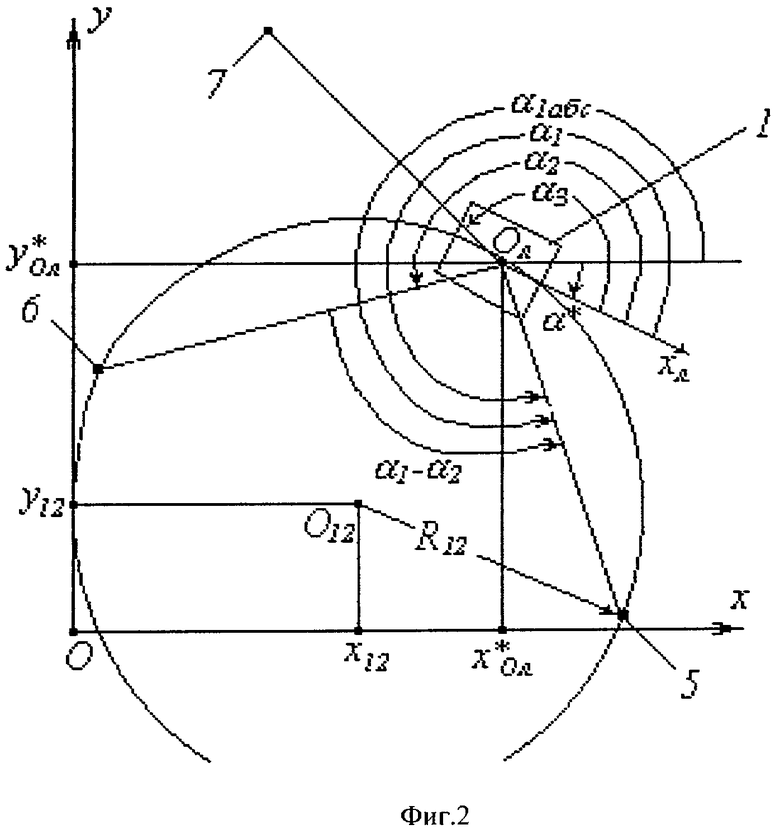
На фиг.2 показана проекция на абсолютную плоскость Oxy тележки и маяков при приближенном расчете - при допущениях zОл=h, β=0, γ=0, xiл≈0, yiл≈0, ziл≈0, (i=1, 2, 3).
Практически способ реализуется следующим образом. Следящие датчики 2, 3, 4 определяют углы склонения (β1, β2, β3) относительно плоскости Олxлyл и поворота (α1, α2, α3) относительно плоскости Oлxлzл, положения маяков 5, 6, 7 и передают данные величины вычислительному устройству. Поскольку величины данных углов связаны с величинами необходимых декартовых координат (хОл, yОл, zОл) центра локальной декартовой системы координат тележки Ол и углов поворота (α, β, γ) тележки вокруг осей z, y, x сложной зависимостью, то для ее раскрытия предлагается двухступенчатый алгоритм.
Первый шаг вычислений
Поскольку тележка перемещается по поверхностям, близким к горизонтальным, то положение точки Oл имеет координату по оси z, близкую к h, а углы перекоса тележки вокруг абсолютных осей x,y близки к нулю: zОл=h, β=0, γ=0. Также величины локальных координат (xл1, yл1, zл1), (хл2, yл2, zл2), (хл3, yл3, zл3) значительно меньше абсолютных декартовых координат (хОл, yОл) центра тележки, поэтому при приближенном расчете можно принять допущение о том, что датчики 2, 3, 4 находятся в центре тележки Ол: хлi≈0, yлi≈0, zлi≈0 (i=1, 2, 3).
При данных допущениях приближенные значения абсолютных декартовых координат (х*Ол, y*Ол) центра Ол и угла поворота α* тележки вокруг оси z могут быть найдены только по величинам углов поворота (α1, α2, α3) относительно плоскости Олxлzл положения маяков 5, 6, 7 (фиг.2).
Геометрическое место искомой точки Oл относительно маяков 5, 6 является дуга окружности, у которой угол равен (α1-α2).
Введя расстояние между маяками 5 и 6: ρ12=((x1-х2)2+(y1-y2)2)0,5, координаты (x12, y12) центра окружности O12 и ее радиус R12 предложено рассчитать по формулам
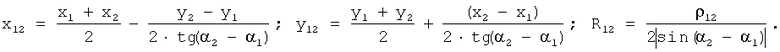
Аналогично можно рассчитать:
- координаты (x31, y31) центра O31 и радиус R31 окружности, проходящей через Ол и маяки 5, 7;
- координаты (x23, y23) центра О23 и радиус R23 окружности, проходящей через Ол и маяки 6, 7.
Для определения приближенных значений абсолютных декартовых координат (x*Ол, y*Ол) центра тележки Ол предложено использовать систему уравнений
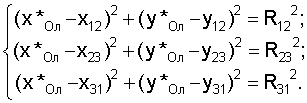
Она сводится к системе, линейной относительно неизвестных (x*Ол, y*Ол):
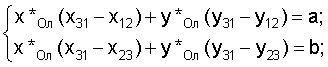
где
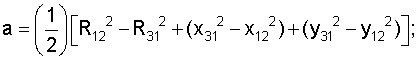
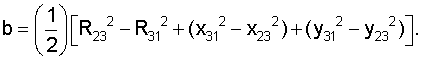
Решение системы имеет вид
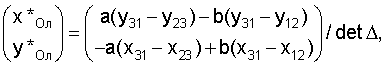
где
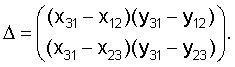
Для определения приближенного значения угла поворота α* тележки вокруг оси z по найденным приближенным значениям абсолютных декартовых координат (х*Ол, y*Ол) центра тележки Ол вычисляем угол α1абс, образованный направлением на маяк 5 с абсолютной осью x из соотношений:
ρ=((x*Ол-xМ1)2+(y*Ол-yМ1)2)0,5,
cosα1абс=(xМ1-x*Ол)/ρ;
sinα1абс=(yМ1-y*Ол)/ρ.
Приближенное значение угла поворота α* равно: α*=α1абс-α1.
Второй шаг вычислений
Принимая в качестве начального приближения величины координат (х*Ол, y*Ол, h, α*, 0, 0) точные их значения (хОл, yОл, zОл, α, β, γ) определяем путем численного решения системы уравнений
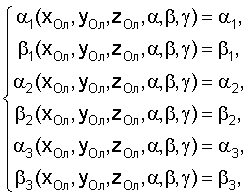
где (α1, α2, α3), (β1, β2, β3) - угловые положения маяков 5, 6, 7, измеренные при помощи датчиков 2, 3, 4.
αip(xОл, yОл, zОл, α, β, γ), βip(xОл, yОл, zОл, α, β, γ), (i=1, 2, 3) - расчетные значения соответствующих углов, определяемые по следующим зависимостям.
Для определения последних величин сначала находим видимые локальные координаты маяков их соответствующих датчиков:
хiл=(cosβcosα+sinβsinγsinα)(xi-xОл)+(-cosβsinα+sinβsinγcosα)(yi-yОл)+(sinβcosγ)(zi-zОл)-xiл;
yiл=(cosγsinα)(xi-xОл)+(cosγcosα)(yi-yОл)-sinγ(zi-zОл)-yiл;
ziл=(-sinβcosα+cosβsinγsinα)(xi-xОл)+(sinβsinα+cosβsinγcosα)(yi-yОл)+(cosβcosγ)(zi-zОл)-ziл;
Потом по найденным координатам рассчитываем видимые значения углов:
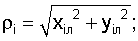 ;
;
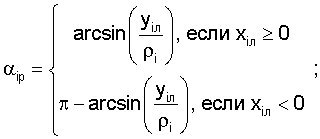
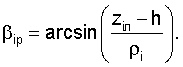
Пример
1. Общая характеристика окружающей среды и конструкции тележки
В окружающей среде помещены три маяка 5, 6, 7, координаты (х1, y1, z1), (x2, y2, z2), (х3, y3, z3) которых в абсолютной декартовой системе Oxyz будут следующими:
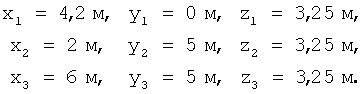
Расстояния между маяками в плоскости Oxy:
ρ12=((x1-x2)2+(y1-y2)2)0,5=((2,2)2+(5,0)2)0,5=5,463 м,
ρ31=((x1-x3)2+(y1-y3)2)0,5=((1,8)2+(5,0)2)0,5=5,314 м,
ρ23=((x2-x3)2+(y2-y3)2)0,5=((4,0)2+(0)2)0,5=4,000 м.
На тележке на высоте h=0,25 м жестко закреплены датчики 2, 3, 4 углового положения, имеющие локальные координаты:
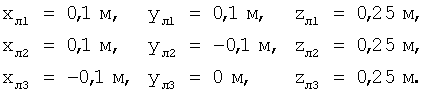
2. Выполненные измерения
По показаниям датчиков 2, 3, 4 определены наблюдаемые с них углы склонения (β1, β2, β3) относительно плоскости Олxлyл и поворота (α1, α2, α3) относительно плоскости Олxлzл положения маяков 5, 6, 7:
β1=37°2'; β2=42°18'; β3=34°48'; α1=343°49'; α2=152°39'; α3=87°18'.
3. Вычисления
Первый шаг
Вначале рассчитываем координаты центров и радиусы окружностей, проходящих через проекции маяков в плоскости Оху и центр тележки:
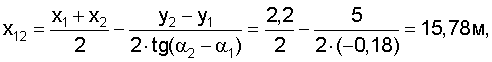
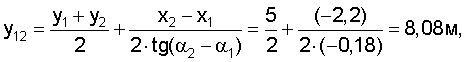
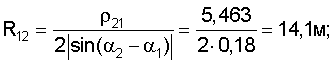
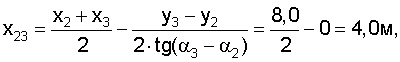
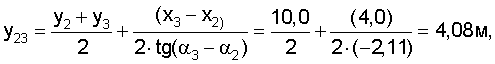
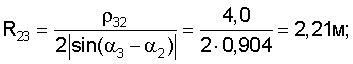
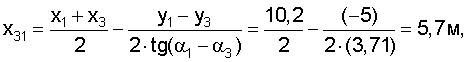
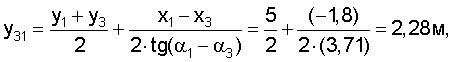
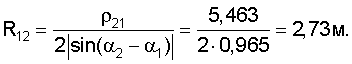
Затем рассчитываем вспомогательные величины
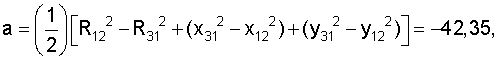
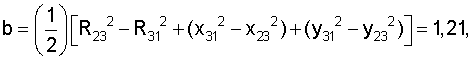
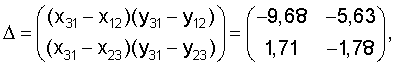
detΔ=(-9,68)(-1,78)-(1,71)(-5,63)=21,19.
Решение системы имеет вид:
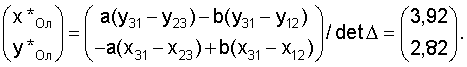
Для определения приближенного значения угла поворота α* тележки вокруг оси z вначале находим характеристики угла α1абс, образованного направлением на маяк 5 с абсолютной осью x:
ρ=((x*Ол-ХМ1)2+(y*Ол-yМ1)2)0,5=((3,92-4,2)2+(2,82-0)2)0,5=2,84;
cosα1абс=(xМ1-x*Ол)/ρ=1,13/2,78=-0,621;
sinα1абс=(yМ1-y*Ол)/ρ=-1,43/2,78=0,786.
По данным характеристикам вычисляем величину α1абс:
α1абс=-84°25'.
Завершаем первый шаг вычислением приближенного значения угла поворота α*:
α*=α1абс-α1=-84°25'-343°49'=-68°10'.
Таким образом, на первом шаге определены приближенные значения абсолютных декартовых координат (х*Ол y*Ол) центра Ол и угла поворота α* тележки вокруг оси z.
Второй шаг
Принимаем в качестве начального приближения для численного решения системы уравнений методом Розенброка величины координат:
xОл=х*=3,92 м, yОл=y*Ол=2,82 м, zОл=h=0,25 м,
α=α*=-68°10', β=0, γ=0.
Первая итерация численного расчета
Вычисляем видимые с тележки локальные координаты маяков:
x1л=(cosβcosα+sinβsinγsinα)(x1-xОл)+(-cosβsinα+sinβsinγcosα)(y1-yОл)+(sinβcosγ)(z1-zОл)-xл1=2,251;
x2л=(cosβcosα+sinβsinγsinα)(x2-xОл)+(-cosβsinα+sinβsinγcosα)(y2-yОл)+(sinβcosγ)(z2-zОл)-xл2=-3,01;
х3л=(cosβcosα+sinβsinγsinα)(x3-xОл)+(-cosβsinα+sinβsinγcosα)(y3-yОл)+(sinβcosγ)(z3-zОл)-хл3=-0,26;
y1л=(cosγsinα)(x1-xОл)+(cosγcosα)(y1-yОл)-sinγ(z1-zОл)-yл1=-1,68;
y2л=(cosγsinα)(x2-xОл)+(cosγcosα)(y2-yОл)-sinγ(z2-zОл)-yл2=-0,001;
y3л=(cosγsinα)(x3-xОл)+(cosγcosα)(y3-yОл)-sinγ(z3-zОл)-yл3=2,98;
z1л=(-sinβcosα+cosβsinγsinα)(x1-xОл)+(sinβsinα+cosβsinγcosα)(y1-yОл)+(cosβcosγ)(z1-zОл)-zл1=2,75;
z2л=(-sinβcosα+cosβsinγsinα)(x2-xОл)+(sinβsinα+cosβsinγcosα)(y2-yОл)+(cosβcosγ)(z2-zОл)-zл2=2,75;
z3л=(-sinβcosα+cosβsinγsinα)(x3-xОл)+(sinβsinα+cosβsinγcosα)(y3-yОл)+(cosβcosγ)(z3-zОл)-zл3=2,75
Потом по найденным координатам рассчитываем видимые значения углов:
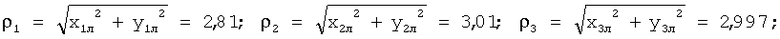
α1p=-36,79°; β1p=62,75°;
α2р=179,99°; β2p=56,3°;
α3p=94,96°; β3p=56,5°.
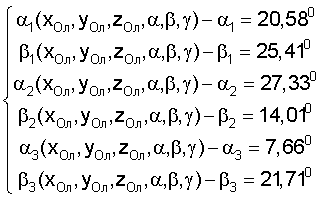
Зададим целевую функцию и критерий оптимальности в виде
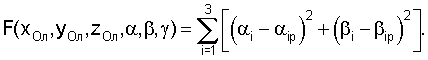
При найденных значениях
F(xОл, yОл, zОл, α, β, γ)=0,775.
Для решения системы уравнений использован метод Розенброка. Получены последовательные приближения декартовых координат и углов поворота тележки, которым соответствуют следующие значения целевой функции:
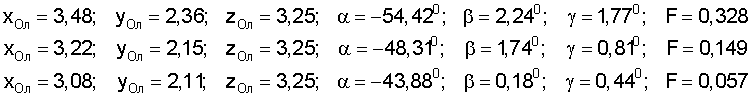
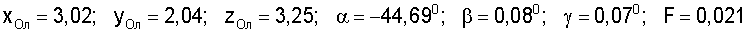
Таким образом, в результате получены уточненные величины декартовых координат хОл=3,02 м, yОл=2,04 м; zОл=3,25 м и углов поворота тележки α=-44,69°; β=0,08°; γ=0,07°, определяющие пространственное положение и угловую ориентацию тележки мобильного робота, что подтверждает предполагаемый результат.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ И УГЛОВ ОРИЕНТАЦИИ ЛЕТАТЕЛЬНОГО АППАРАТА ОТНОСИТЕЛЬНО ВЗЛЕТНО-ПОСАДОЧНОЙ ПОЛОСЫ | 2014 |
|
RU2548366C1 |
| Система бесконтактного определения координат мобильного робота и способ для ее реализации | 2021 |
|
RU2769636C1 |
| СПОСОБ ИЗМЕРЕНИЯ ТРЕХМЕРНЫХ КООРДИНАТ | 1991 |
|
RU2015564C1 |
| Способ обеспечения посадки вертолета | 2016 |
|
RU2621215C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ХАРАКТЕРИСТИКИ ПРЕОБРАЗОВАНИЯ ТРЕХКОМПОНЕНТНОГО МАГНИТОМЕТРА | 2011 |
|
RU2481593C9 |
| СПОСОБ ИЗМЕРЕНИЯ ТРЕХМЕРНЫХ КООРДИНАТ | 1991 |
|
RU2015565C1 |
| СПОСОБ АВТОМАТИЧЕСКОЙ АДАПТИВНОЙ ТРЕХМЕРНОЙ КАЛИБРОВКИ БИНОКУЛЯРНОЙ СИСТЕМЫ ТЕХНИЧЕСКОГО ЗРЕНИЯ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2003 |
|
RU2250498C2 |
| ОПТИКО-ЭЛЕКТРОННЫЙ ПРЕОБРАЗОВАТЕЛЬ ДЛЯ БЕСКОНТАКТНОГО ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ ОБЪЕКТОВ ОТНОСИТЕЛЬНО ДРУГ ДРУГА | 2002 |
|
RU2244904C2 |
| СПОСОБ СЕЙСМИЧЕСКОЙ РАЗВЕДКИ | 1991 |
|
RU2029318C1 |
| Способ коррекции углов визирования на точку | 2020 |
|
RU2758860C1 |
Изобретение относится к робототехнике и предназначено для определения пространственного положения по всем трем декартовым координатам и угловой ориентации по всем трем возможным направлениям вращения вокруг осей тележки мобильного робота при ее перемещении по поверхностям, близким к горизонтальным, например по напольным покрытиям производственных помещений. Данная информация необходима для идентификации положения и угловой ориентации робота. Способ заключается в установке трех статических маяков на местности с заданной абсолютной декартовой системой координат, в которой две оси направлены параллельно плоскости перемещения тележки, а одна ось перпендикулярна ей. Их центры с известными абсолютными координатами располагают в плоскости перемещения тележки, на тележке выбирают локальную декартову систему координат с центром, находящимся на заданной высоте по отношению к плоской поверхности, и устанавливают на тележке три датчика. Определяют углы склонения относительно локальной плоскости перемещения тележки и углы поворота относительно этой плоскости положения маяков, после чего рассчитывают приближенные абсолютные координаты центра тележки и угла поворота тележки вокруг вертикальной оси при допущении, что датчики находятся в центре тележки, а затем при начальном приближении определяют уточненные абсолютные координаты центра тележки и углы поворота тележки вокруг трех осей путем итерационного численного решения системы уравнений. Техническим результатом является возможность автоматизированного уточнения пространственного положения по всем трем декартовым координатам и угловой ориентации по всем трем возможным направлениям вращения вокруг осей тележки мобильного робота. 2 ил.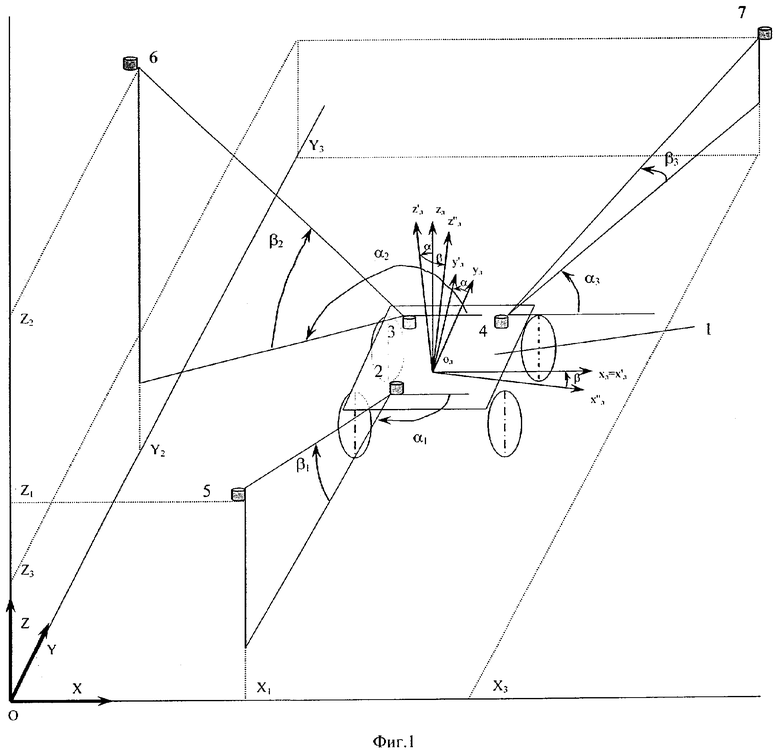
Способ определения пространственного положения и угловой ориентации тележки транспортного средства при ее движении по плоской поверхности, имеющей неровности, заключающийся в установке статических маяков на местности с заданной абсолютной декартовой системой координат, в которой две оси направлены параллельно плоскости перемещения тележки, а одна ось перпендикулярна ей, отличающийся тем, что число статических маяков принимают равным трем, их центры с известными абсолютными координатами располагают в плоскости перемещения тележки, на тележке выбирают локальную декартову систему координат с центром, находящимся на заданной высоте по отношению к плоской поверхности, горизонтальной продольной, горизонтальной поперечной и вертикальной осями, образующими правую тройку, устанавливают на тележке три датчика и определяют углы склонения относительно локальной плоскости перемещения тележки и углы поворота относительно этой плоскости положения маяков, после чего по измеренным углам поворота рассчитывают приближенные абсолютные координаты центра тележки и угла поворота тележки вокруг вертикальной оси при допущении, что датчики находятся в центре тележки, а затем, принимая найденные величины в качестве начального приближения, определяют уточненные абсолютные координаты центра тележки и углы поворота тележки вокруг трех осей путем итерационного численного решения системы уравнений
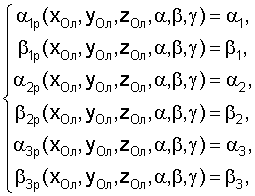
где (α1, α2, α3), (β1, β2, β3) - угловые положения маяков, измеренные при помощи датчиков,
αip(xОл, yОл, zОл, α, β, γ), βip(xОл, yОл, zОл, α, β, γ), где i=1, 2, 3, расчетные значения соответствующих углов, определяемые по следующим зависимостям:
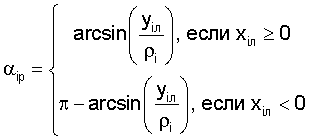
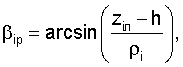
где 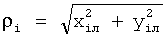 - радиус-вектор i-го маяка в локальной системе координат тележки,
- радиус-вектор i-го маяка в локальной системе координат тележки,
где xiл, yiл, ziл - видимые с тележки локальные координаты маяков, рассчитываемые по формулам:
xiл=(cosβcosα+sinβsinγsinα)(xi-xОл)+(-cosβsinα+sinβsinγcosα)(γi-yОл)+(sinβcosγ)(zi-zОл)-xлi;
yiл=(cosγsinα)(xi-xОл)+(cosγcosα)(yi-yОл)-sinγ(zi-zОл)-γлi;
ziл=(-sinβcosα+cosβsinγsinα)(xi-xОл)+(sinβsinα+cosβsinγcosα)(yi-yОл)+(cosβcosγ)(zi-zОл)-zлi,
где xi, γi, zi - абсолютные координаты маяков;
хОл, yОл, zОл - абсолютные декартовые координаты центра тележки;
α, β, γ - углы поворота тележки вокруг осей x, y, z.
| M.A.BATALIN et al | |||
| Sensor Coverage using Mobile Robots and Stationary Nodes | |||
| In Proceedings of the SPIE, v.48 (SPIE2002) p.269-276, Boston, MA, August 2002 | |||
| МОБИЛЬНЫЙ РОБОТ И СПОСОБ КОРРЕКТИРОВКИ ЕГО КУРСА | 2001 |
|
RU2210492C2 |
| СИГНАЛИЗАТОР УГЛА НАКЛОНА | 1998 |
|
RU2156957C2 |
| Способ определения пространственного положения подвижного объекта | 1990 |
|
SU1788435A1 |
| Устройство для определения угловой ориентации объекта И.Н.Кочергина | 1992 |
|
SU1831653A3 |
| DE 19830359 A1, 20.01.2000 | |||
| US 5751917 A, 12.05.1998. | |||
Авторы
Даты
2007-07-20—Публикация
2006-03-02—Подача