СПОСОБ ОЦЕНКИ УГЛОВЫХ ПАРАМЕТРОВ ИОНОСФЕРНЫХ СИГНАЛОВ Российский патент 2014 года по МПК G01S3/00 

Изобретение относится к радиотехнике, а именно к области пеленгации, и может быть использовано для измерения азимутов и углов места ионосферных сигналов в условиях приема нескольких интерферирующих лучей, в том числе при малых углах места. При приеме ионосферных сигналов в точку приема, как правило, приходят несколько лучей (1÷4), отраженных от разных слоев ионосферы, с азимутами, находящимися в области главного лепестка диаграммы направленности (Δα~5÷10 градусов). Вследствие интерференции суммарный главный лепесток диаграммы направленности антенной системы, состоящий из суммы диаграмм направленности отдельных лучей, существенно меняется, часто создавая ложные азимуты (пеленги), отличающиеся от истинных азимутов (пеленгов) на десятки градусов. В результате достоверность оценок азимутов, а также углов места ионосферных сигналов оказывается низкой. Кроме того, при пеленгации ионосферных сигналов существует проблема малых углов места. При приеме ионосферных сигналов на расстояниях более 2000 км угол места β оказывается в области значений от 0° до 15÷20°. В этих условиях пространственная база для определения угла места L=Rsin(β) становится малой и значительно возрастает дисперсия измеряемых углов места. Задачей пеленгации ионосферных сигналов является определение координат источника излучения. В связи с этим в способе пеленгации необходимо решение задачи выделения лучевой структуры сигнала и определение, по измеренной лучевой структуре, координат излучателя. При этом важна информация как об азимутах, так и об углах места многолучевого ионосферного сигнала.

Известны фазовые способы измерения азимута и угла места (пеленгации), осуществляемые путем измерений разности фаз между вибраторами антенной системы и оценки по этим измерениям азимутов и углов места (Патент RU №2263327, опубликован 27.10.2005 г.; Патент RU №2365931, опубликован 27.08.2009 г.; Патент RU №2429500, опубликован 20.09.2011; Патент RU №2450283, опубликован 10.05.2012 г.; Заявка на изобретение RU №2010143935, опубликована 10.05.2012 г.; Заявка RU №2003108306 от 25.03.2003 г., G01S 3/14, опубликована 10.10.2004 г.). Недостатком вышеуказанных способов является то, что используется только фазовая информации. Однозначное определение фазы волны на вибраторах возможно на интервале 0÷360°. Это требует малого, по сравнению с длиной волны, пространственного разнесения вибраторов $$\left|{\overline{R}}_{n+1}-{\overline{R}}_n\right|<\frac{\lambda }{2}$$ . В условиях приема двух или нескольких близких по азимуту лучей фазовые способы оценки азимута и угла места являются неустойчивыми. При разности фаз между лучами ~180° они дают отклонения азимута на десятки градусов (ложные пеленги), что значительно снижает достоверность оценок азимутов и углов места ионосферных сигналов. Разработанные к настоящему времени фазовые методы оценки азимутов и углов места (пеленгации) предназначены для оценок этих параметров для одного луча на заданной частоте. Антенная система, расположенная в плоскости земной поверхности, не может решить проблему малых углов в оценке азимутов и углов места ионосферных сигналов.

Известны способы пеленгации по максимуму диаграммы направленности антенной системы (Патент RU №2144200, опубликован 10.01.2000 г.; Патент RU №2258241, опубликован 10.08.2005 г.; Патент RU №2419805, опубликован 27.05.2011 г.; Патент RU №2201599, опубликован 27.03.2003 г.; Патент RU №2004100714, опубликован 20.06.2005 г.). В этом случае используется временное преобразование Фурье для частотного выделения сигнала от отдельных вибраторов антенной системы и различные формы пространственной обработки данных (формирование диаграммы направленности). Наилучшим образом диаграмма направленности формируется при использовании пространственного преобразования Фурье. В результате создается двумерный комплексный угловой спектр (диаграмма направленности антенной системы). При использовании пространственного преобразования Фурье диаграмма направленности формируется по выражению (комплексный вид):

$$\stackrel{\wedge }{U}({\alpha }_{}^{\text{'}},{\beta }_{}^{\text{'}})=\frac{1}{N}{\displaystyle \sum _{n=1}^N{\stackrel{\wedge }{E}}_n{e}^{-i\overline{K}(\alpha \text{'},\beta \text{'}){\overline{R}}_n}}(1)$$

где:

$${\stackrel{\wedge }{E}}_n$$ - комплексная амплитуда в n-точке пространства с радиус-вектором $${\overline{R}}_n$$ ,

$$\overline{K}(\alpha \text{'},\beta \text{'})$$ - оценочный волновой вектор ионосферного сигнала,

, $$\beta \text{'}$$ ' - оценочные значения азимута и угла места ионосферного сигнала.

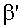
Квадрат модуля нормированной диаграммы направленности (расчетная форма) определяется выражением

$$U^2(a\text{'},\beta \text{'})=\frac{{\overline{E_n\cos ({\psi }_n-\overline{K}(\alpha \text{'},\beta \text{'}){\overline{R}}_n)}}^2+{\overline{E_n\sin ({\psi }_n-\overline{K}(\alpha \text{'},\beta \text{'}){\overline{R}}_n)}}^2}{{\overline{E}}_n^2},\text{ (2)}$$

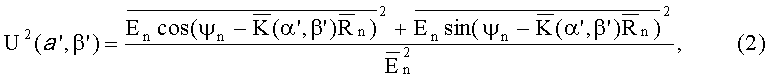
где черта сверху означает суммирование по индексу «n».

Недостатком вышеуказанных способов, связанных с оценкой углов места по максимуму диаграммы направленности антенной системы, является неустойчивость решения при наличии многолучевой интерференции при разности фаз между лучами ~180°. При приеме двух или нескольких интерферирующих лучей ионосферного сигнала (различие в азимутах меньше ширины диаграммы направленности) суммарная диаграмма направленности за счет изменения разности фаз между лучами (в области ~180 градусов) в значительной степени подавляется. Боковые или задние лепестки суммарной диаграммы направленности в этих условиях становятся больше по величине, чем основной лепесток диаграммы направленности. В результате азимут (пеленг) в амплитудном способе пеленгации определяется по максимальному боковому или заднему лепестку диаграммы направленности антенной системы. Отклонения азимута (ложные пеленги) достигают десятков градусов. В результате достоверность оценок азимутов и углов места ионосферных сигналов оказывается низкой. Кроме того, невозможно обеспечить работоспособность пеленгатора в широком частотном диапазоне 2÷30 МГц. Требования точности измерения пеленга в низкочастотной части диапазона (3÷4 МГц) определяют базу антенной системы 2R≥150 м. Однако при количестве вибраторов ~16 в высокочастотной части диапазона (20÷30 МГц) диаграмма направленности не формируется в связи с большим пространственным разнесением вибраторов по сравнению с длиной волны, что ограничивает частотный диапазон сверху. Расположение вибраторов антенной системы на поверхности земли (на плоскости) не может решить проблему малых углов при пеленгации ионосферных сигналов.

Известны способы определения азимута и угла места (пеленгации), антенная система в которых состоит из двух взаимно перпендикулярных линейных эквидистантных антенных решеток (Патент RU №2192651, опубликован 05.10.2000 г.). Способ включает в себя прием сигнала с помощью антенной системы, многоканального приемника, преобразование аналоговых сигналов в каждом канале в цифровую форму, использование двумерного углового преобразования Фурье, которое создает диаграмму направленности антенной системы. Максимум диаграммы направленности позволяет оценить азимут (пеленг) и угол места. Недостатком этого способа пеленгации является зависимость точности измерения пеленга от взаимной ориентации антенной системы и пеленга. При пеленгации ионосферных сигналов в условиях приема двух или нескольких интерферирующих лучей могут возникать ложные пеленги, что значительно снижает достоверность оценок азимутов и углов места ионосферных сигналов. Расположение вибраторов антенной системы на поверхности земли (в плоскости) не может решить проблему малых углов при пеленгации ионосферных сигналов данным способом пеленгации.

Известны способы оценки азимутов и углов места (пеленгации), антенная система в которых состоит из ограниченного количества вибраторов (3÷5 вибратора) (Патент RU №2262119, опубликован 10.10.2005 г.; Патент RU №2253877, опубликован 10.06.2005 г.). Недостатками этого способа пеленгации является малая помехоустойчивость, вследствие отсутствия статистической обработки данных, наличие ложных пеленгов при приеме двух или нескольких близких по азимуту лучей ионосферного сигнала, невозможность решения проблемы малых углов места.

Наиболее близким (прототип) к предлагаемому способу оценки угловых параметров при приеме многолучевых ионосферных сигналов является «Способ пеленгации с учетом корреляционной взаимосвязи между лучами», патент RU №2305294, МПК G01S 3/16, опубликован 27.08.2007 г.

Согласно данному способу пеленгации (прототип) последовательность действий следующая. С помощью антенной системы, состоящей из N-вибраторов, расположенных равномерно по окружности радиуса R (пространственная база сигнала) 1) принимают ионосферные сигналы, 2) преобразуют их по частоте, 3) усиливают посредством многоканального приемника. Аналоговые сигналы на выходах многоканального приемника в каждом канале (от каждого вибратора) 4) преобразуют в цифровую форму посредством многоканального аналого-цифрового преобразователя (АЦП). 5) Определяют амплитуды E_n и фазы ψ_n принятого ионосферного сигнала в каждом канале (от каждого вибратора) с помощью временного преобразования Фурье. 6) Формируют суммарную четырехмерную (для двух лучей) диаграмму направленности с учетом коэффициента корреляции $$\stackrel{\wedge }{A}1$$ между лучами по выражениям

$$\stackrel{\wedge }{U}({\alpha }_1^{\text{'}},{\beta }_1^{\text{'}},{\alpha }_2^{\text{'}},{\beta }_2^{\text{'}})=\frac{{\stackrel{\wedge }{U}}_1\overline{E_n^{*}\exp (-i\overline{k_1}({\alpha }_1^{\text{'}},{\beta }_1^{\text{'}}){\overline{R}}_n)}+{\stackrel{\wedge }{U}}_2\overline{E_n^{*}\exp (-i\overline{k_2}({\alpha }_2^{\text{'}},{\beta }_2^{\text{'}}){\overline{R}}_n)}}{\overline{{\stackrel{\wedge }{E}}_n{\stackrel{\wedge }{E}}_n^{*}}}\text{ (3)}$$

где

$${\stackrel{\wedge }{U}}_1=\frac{\overline{E_n^{}\exp (i\overline{k_1}({\alpha }_1^{\text{'}},{\beta }_1^{\text{'}}){\overline{R}}_n)}+\overline{E_n^{}\exp (i\overline{k_2}({\alpha }_2^{\text{'}},{\beta }_2^{\text{'}}){\overline{R}}_n)}\stackrel{\wedge }{A}1}{\overline{1-\stackrel{\wedge }{A}1\stackrel{\wedge }{A}{1}_{}^{*}}}$$

$${\stackrel{\wedge }{U}}_2=\frac{\overline{E_n^{}\exp (i\overline{k_2}({\alpha }_2^{\text{'}},{\beta }_2^{\text{'}}){\overline{R}}_n)}+\overline{E_n^{}\exp (i\overline{k_1}({\alpha }_1^{\text{'}},{\beta }_1^{\text{'}}){\overline{R}}_n)}\stackrel{\wedge }{A}{1}^{*}}{\overline{1-\stackrel{\wedge }{A}1\stackrel{\wedge }{A}{1}_{}^{*}}}$$

$$\stackrel{\wedge }{A}1=\overline{\exp (i({\overline{k}}_2({\alpha }_2^{\text{'}},{\beta }_2^{\text{'}})-{\overline{k}}_1({\alpha }_1^{\text{'}},{\beta }_1^{\text{'}})){\overline{R}}_n}$$

$${\stackrel{\wedge }{E}}_n$$ - комплексная амплитуда сигнала, измеренная на n вибраторе,

$${\overline{R}}_n$$ - радиус-вектор, определяющий местоположение n вибратора,

$${\overline{k}}_1({\alpha }_1^{\text{'}},{\beta }_1^{\text{'}})$$ , $${\overline{k}}_2({\alpha }_2^{\text{'}},{\beta }_2^{\text{'}})$$ - волновые векторы первого и второго лучей ионосферного сигнала, зависящие от оценочных азимутов $${\alpha }_1^{\text{'}}$$ , $${\alpha }_2^{\text{'}}$$ и углов места $${\beta }_1^{\text{'}}$$ , $${\beta }_2^{\text{'}}$$ ,

$$\stackrel{\wedge }{A}1$$ - коэффициент корреляции между лучами.

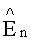
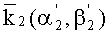
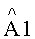
Черта сверху означает суммирование по индексу n.

Знак * означает комплексное сопряжение,

Знак ∧ означает комплексную величину.

7) Производят сканирование диаграммой направленности в четырехмерном пространстве за счет изменения оценочных азимутов и углов места $${\alpha }_1^{\text{'}}$$ , $${\alpha }_2^{\text{'}}$$ и $${\beta }_1^{\text{'}}$$ , $${\beta }_2^{\text{'}}$$ в указанных угловых диапазонах с определенным шагом и запоминая значения параметров $${\alpha }_1^{\text{'}}$$ , $${\alpha }_2^{\text{'}}$$ , $${\beta }_1^{\text{'}}$$ , $${\beta }_2^{\text{'}}$$ , $${\stackrel{\wedge }{U}}_1$$ , $${\stackrel{\wedge }{U}}_2$$ , $$\stackrel{\wedge }{U}({\alpha }_1^{\text{'}},{\beta }_1^{\text{'}},{\alpha }_2^{\text{'}},{\beta }_2^{\text{'}})$$ . Азимут и угол места каждого луча определяются по максимуму четырехмерной диаграммы направленности.

Недостатком способа пеленгации с учетом корреляционной взаимосвязи между лучами (прототипа) является его ограниченность, связанная с приемом только одного или двух лучей ионосферного сигнала, в то время как в ионосферном сигнале количество лучей может достигать четырех и более. Вторым недостатком этого способа является большая трудоемкость, связанная с необходимостью перебора (сканирования диаграммой направленности) двух азимутов и двух углов места ( $${\alpha }_1^{\text{'}}$$ , $${\beta }_1^{\text{'}}$$ и $${\alpha }_2^{\text{'}}$$ , $${\beta }_2^{\text{'}}$$ ) с шагом по азимуту Δα≤0.5° в диапазоне 0÷360 градусов и с шагом по углу места Δβ≤0.5° в диапазоне 0÷90 градусов в четырехмерном пространстве азимутов и углов места. При увеличении количества лучей в этом способе пеленгации время, требуемое для расчета параметров, увеличивается экспоненциально с увеличением количества лучей. Если Т - необходимое время расчета параметров одного луча в одной точке области определения и М - количество точек, то для N лучей требуется время Т_Т=Т*M^2N. Третьим недостатком является наличие проблемы малых углов места при данном способе пеленгации ионосферных сигналов, обусловленное плоской (двумерной) антенной системой.

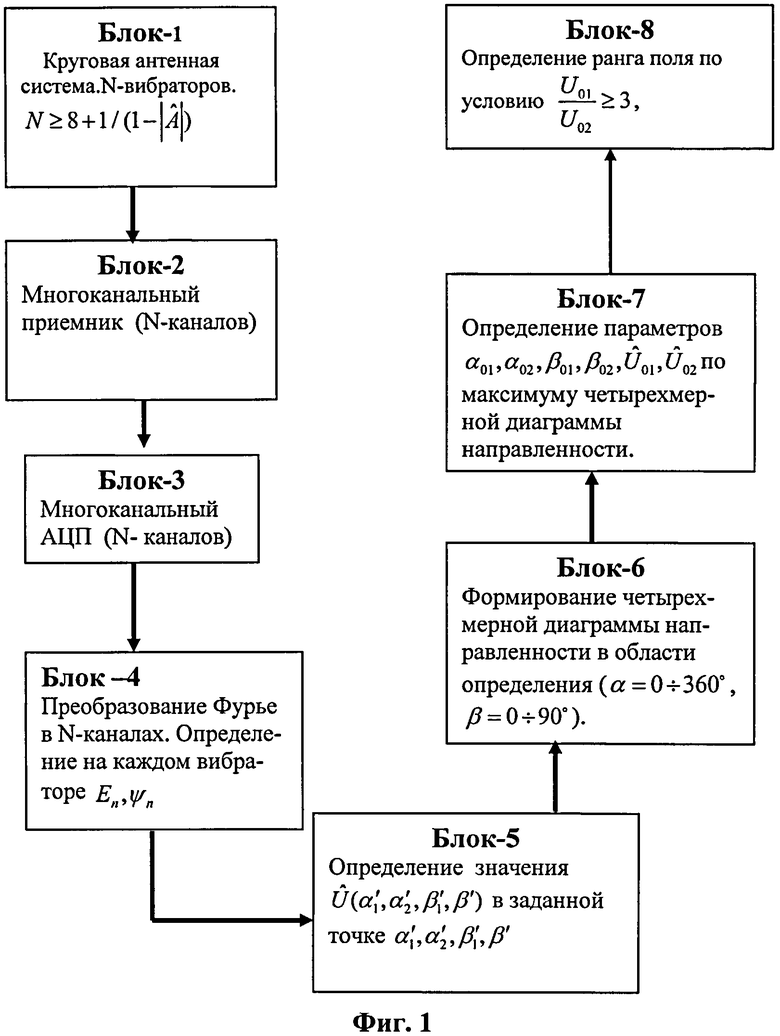
Блок-схема технической реализации данного способа пеленгации (прототипа) представлена на фиг.1. Согласно способу пеленгации с учетом корреляционной взаимосвязи между лучами последовательность действий следующая.

1. Принимают сигналы с помощью круговой антенной системы,

состоящей из N вибраторов $$(N\ge N1+\frac{1}{(1-{\left|\stackrel{\wedge }{A}1\right|}^2)},N1=8)$$ , расположенных на поверхности земли равномерно по окружности радиуса R $$(R\ge \frac{2\pi }{3\left|\overline{k}({\alpha }_{01},{\beta }_{01})-{\overline{k}}_2({\alpha }_{02},{\beta }_{02})\right|})$$ (блок 1). Количество вибраторов определяется количеством параметров ионосферного сигнала и заданным значением отношения сигнал/шум. Радиус антенной системы определяется размером пространственных интерференционных максимумов на поверхности земли.

2. С помощью многоканального приемника преобразуют сигналы от каждой антенны (в каждом канале) по частоте, усиливают и фильтруют (блок 2).

3. Преобразуют аналоговые сигналы на выходах многоканального приемника от каждого вибратора в цифровую форму с помощью многоканального аналого-цифрового преобразователя (АЦП) (блок 3).

4. Определяют амплитуды E_n и фазы ψ_n сигналов от каждого

вибратора (в каждом канале), например, с помощью временного преобразования Фурье (блок 4).

5.Задают точку в пространстве оценочных азимутов $${\alpha }_1^{\text{'}}$$ , $${\alpha }_2^{\text{'}}$$ и углов места $${\beta }_1^{\text{'}}$$ , $${\beta }_2^{\text{'}}$$ и определяют согласно (3) четырехмерную диаграмму направленности $$\stackrel{\wedge }{U}({\alpha }_1^{\text{'}},{\beta }_1^{\text{'}},{\alpha }_2^{\text{'}},{\beta }_2^{\text{'}})$$ в заданной точке по выборке данных $${\stackrel{\wedge }{E}}_n$$ и запоминают ее значения и значения переменных $${\stackrel{\wedge }{U}}_1,{\stackrel{\wedge }{U}}_2$$ (Блок 5).

6. Повторяют действия (5) с другими значениями параметров $${\alpha }_1^{\text{'}}$$ , $${\alpha }_2^{\text{'}}$$ и $${\beta }_1^{\text{'}}$$ , $${\beta }_2^{\text{'}}$$ (из области их определения) с шагом по азимуту Δα≤0.5° в диапазоне 0÷360 градусов и с шагом по углу места Δβ≤0.5° в диапазоне 0÷90 градусов и создают поверхность в четырехмерном пространстве азимутов и углов места (четырехмерную диаграмму направленности) (блок 6).

7. Определяют максимальное значение четырехмерной диаграммы направленности и фиксируют параметры $${\alpha }_1^{\text{'}}={\alpha }_{01}$$ , $${\beta }_1^{\text{'}}={\beta }_{01}$$ , $${\alpha }_2^{\text{'}}={\alpha }_{02}$$ , $${\beta }_2^{\text{'}}={\beta }_{02}$$ , а также $${\stackrel{\wedge }{U}}_1={\stackrel{\wedge }{U}}_{01}$$ , $${\stackrel{\wedge }{U}}_2={\stackrel{\wedge }{U}}_{02}$$ (блок 7).

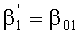
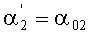
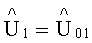
8. Определяют ранг поля (однолучевое или двулучевое) по условию U₀₁/U₀₂≥3 и оставляют решения, удовлетворяющие этому условию (блок 8).

Целью предлагаемого изобретения «Способ оценки угловых параметров ионосферных сигналов» (технический результат) является:

- расширение возможностей «Способа пеленгации с учетом корреляционной взаимосвязи» на случай приема М лучей (М=1÷4 и более),

- решение проблемы малых углов места при пеленгации ионосферных сигналов,

- сокращение времени расчета угловых параметров многолучевого ионосферного сигнала.

Технический результат достигается тем, что круговую антенную систему, расположенную на поверхности земли, дополняют линейной системой вибраторов, расположенных вдоль вертикали к поверхности земли (например, 5 вибраторов с интервалом между вибраторами 10 м). С помощью сформированной таким образом антенной системы (трехмерная антенная система), многоканального приемника, многоканального аналого-цифрового преобразователя (АЦП) и временного преобразования Фурье формируют пространственно-временной массив комплексных данных $${\stackrel{\wedge }{E}}_{n,m}$$ , отображающий значения напряженности поля в n точках трехмерного пространства (n - номер вибратора на поверхности земли и вдоль вертикальной линейки вибраторов) и в m моменты времени, с интервалами 1-2 секунды (индекс m определяет номер временного среза данных на n вибраторах, m=1÷М+1). Количество временных срезов данных берется на единицу больше, чем количество лучей М. Формируют корреляционную матрицу $$\stackrel{\wedge }{A}$$ , размерностью, равной количеству лучей ((М)*(М)), и правый вектор-столбец данных $$\overline{b}={(b_1÷b_{м})}^T$$ , элементы которых усредняются по индексу n (по вибраторам, по пространству), решая векторное уравнение (4), определяют неопределенные коэффициенты $${\stackrel{\wedge }{\alpha }}_1÷{\stackrel{\wedge }{\alpha }}_{м}$$ ,

$$\stackrel{\wedge }{A}\overline{\alpha }=\overline{b},\text{ (4)}$$

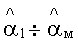
где

А - корреляционная матрица с элементами $$\overline{{\stackrel{\wedge }{E}}_{n,k}{\stackrel{\wedge }{E}}_{n,p}^{*}}$$ ,

m=1÷M, p=1÷M, n=1÷N, черта сверху означает суммирование по индексу n. $$\overline{b}={(b_1÷b_M)}^T$$ - вектор-столбец с координатами $$b_m=\overline{{\stackrel{\wedge }{E}}_{n,M+1}{\stackrel{\wedge }{E}}_{n,m}^{*}}$$ (черта сверху определяет суммирование по индексу n, по вибраторам, m=1÷M).

$$\overline{\alpha }={({\alpha }_1÷{\alpha }_M)}^T$$ - вектор-столбец неопределенных коэффициентов.

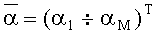
Формируют полином $$\stackrel{\wedge }{Y}(\omega )$$ (5), частотная зависимость которого позволяет оценить значения доплеровских сдвигов частот ω_m лучей ионосферного сигнала по М минимумам полинома.

$$\stackrel{\wedge }{Y}(\omega )={\stackrel{\wedge }{x}}^M+{\stackrel{\wedge }{\alpha }}_{{}_M}{\stackrel{\wedge }{x}}^{M-1}+{\stackrel{\wedge }{\alpha }}_{{}_{M-1}}{\stackrel{\wedge }{x}}^{M-2}+\dots \dots {\stackrel{\wedge }{\alpha }}_{{}_2}\stackrel{\wedge }{x}+{\stackrel{\wedge }{\alpha }}_{{}_1}=0(5)$$

Где $$\stackrel{\wedge }{x}=\exp (i\omega \Delta t)$$ .

Определяют элементы импульсных последовательностей М фильтров для выделения отдельных однолучевых полей $${\stackrel{\wedge }{E}}_n^{(m)}$$ .

$${\stackrel{\wedge }{C}}_m^{(m)}={\stackrel{\wedge }{\alpha }}_1^{(m)}{\stackrel{\wedge }{x}}_{}^{*}$$ , $${\stackrel{\wedge }{C}}_2^{(m)}={\stackrel{\wedge }{\alpha }}_2^{(m)}+{\stackrel{\wedge }{C}}_1^{(m)}){\stackrel{\wedge }{x}}^{*}$$ , $$\dots \dots$$ , $${\stackrel{\wedge }{C}}_m^{(m)}={\stackrel{\wedge }{\alpha }}_m^{(m)}+{\stackrel{\wedge }{C}}_{m-1}^{(m)}){\stackrel{\wedge }{x}}^{*}$$ , $$\dots \dots$$ , $${\stackrel{\wedge }{C}}_M^{(m)}=1$$

Выделяют (фильтруют) однолучевые m поля $${\stackrel{\wedge }{E}}_n^{(m)}$$ из совокупности М полей ионосферного сигнала по выражениям (6). Верхний индекс в скобках в выражении (6) определяет номер однолучевого поля.

$$\frac{{\stackrel{\wedge }{E}}_{{}_n}^{(1)}={\stackrel{\wedge }{E}}_{{}_{n\mathrm{,1}}}{\stackrel{\wedge }{C}}_1^{(1)}+{\stackrel{\wedge }{E}}_{{}_{n\mathrm{,2}}}{\stackrel{\wedge }{C}}_2^{(1)}+\dots \dots +{\stackrel{\wedge }{E}}_{{}_{n,M}}{\stackrel{\wedge }{C}}_M^{(1)}=\stackrel{}{{\stackrel{\wedge }{U}}_1\exp (-i{\overline{K}}_1{\overline{R}}_n)}}{{\stackrel{\wedge }{E}}_{{}_n}^{(M)}={\stackrel{\wedge }{E}}_{{}_{n\mathrm{,1}}}{\stackrel{\wedge }{C}}_1^{(M)}+{\stackrel{\wedge }{E}}_{{}_{n\mathrm{,2}}}{\stackrel{\wedge }{C}}_2^{(M)}+\dots \dots +{\stackrel{\wedge }{E}}_{{}_{n,M}}{\stackrel{\wedge }{C}}_M^{(M)}=\stackrel{\wedge }{{\stackrel{\wedge }{U}}_M\exp (-i{\overline{K}}_M{\overline{R}}_n)}}(6)$$

Формируют диаграммы направленности для выделенных М лучей ионосферного сигнала с помощью пространственного преобразования Фурье, сканируют ими по азимуту и углу места и по максимумам углового спектра оценивают азимуты, углы места и амплитуды лучей ионосферного сигнала $${\alpha }_m^{\text{'}}$$ , $${\beta }_m^{\text{'}}$$ , $${\stackrel{\wedge }{U}}_m^{\text{'}}$$ .

Существенные отличия предлагаемого способа пеленгации от прототипа следующие.

- Вместо плоской (двумерной) антенной системы (прототип) создается трехмерная антенная система, с помощью которой решается проблема малых углов места при пеленгации ионосферных сигналов.

- Исключается операция создания четырехмерной диаграммы направленности и сканирование этой диаграммой в четырехмерном пространстве, которая значительно увеличивает время расчета параметров ионосферного сигнала и не позволяет реализовать способ (прототип) с большим количеством лучей.

- Пространственная информация, получаемая с помощью антенной системы, дополняется необходимой информацией во времени (срезы 10 данных) и проводится наиболее оптимальная совместная пространственно-временная обработка данных.

- Определяются элементы М импульсных последовательностей фильтров для выделения М однолучевых полей из суммы полей ионосферного сигнала и выделяются (фильтруются) однолучевые поля ионосферного сигнала.

- Вместо оценок параметров лучей по максимуму четырехмерной диаграммы направленности в прототипе, в предлагаемом способе пеленгации производятся оценки параметров лучей ионосферного сигнала по максимумам двумерных диаграмм направленностей выделенных М полей ионосферного сигнала.

Обоснованием предлагаемого способа оценки угловых параметров ионосферных сигналов является следующее.

Запишем сигнал на n вибраторе и в m точке по времени $${\stackrel{\wedge }{E}}_{n,m}$$ в комплексной форме в виде

$${\stackrel{\wedge }{E}}_{n,m}={\displaystyle \sum _{p=1}^M{\stackrel{\wedge }{U}}_p{e}^{i({\omega }_p{t}_m-{\overline{K}}_p({\alpha }_{\mathrm{0,}p},{\beta }_{\mathrm{0,}p}){\overline{R}}_n)}}(6)$$

где $${\stackrel{\wedge }{U}}_p$$ - комплексная амплитуда р луча ионосферного сигнала,

$${}_{{\overline{K}}_p({\alpha }_{\mathrm{0,}p},{\beta }_{\mathrm{0,}p})}$$ - волновой вектор р луча ионосферного сигнала,

$${\alpha }_{\mathrm{0,}p}$$ , $${\beta }_{\mathrm{0,}p}$$ - значения азимута и угла места р луча ионосферного сигнала,

$${\overline{R}}_n$$ - местоположение n вибратора,

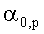
t_m - время отсчетов напряженности поля (m меняется в пределах от 1 до М+1, Р=М - количество лучей в ионосферном сигнале,

ω_p - доплеровский сдвиг частоты р луча ионосферного сигнала.

Элементарные вибраторы антенной системы располагаются по окружности радиуса R и вдоль вертикали к поверхности земли Z.

Используя временную последовательность данных, исключим переменные, описывающие поля Р-1 лучей ( $${\stackrel{\wedge }{U}}_p$$ , $${\overline{K}}_p({\alpha }_{\mathrm{0,}p},{\beta }_{\mathrm{0,}p}),{\omega }_p)$$ . В результате получим выражение (7) с неопределенными коэффициентами $${\stackrel{\wedge }{C}}_1÷{\stackrel{\wedge }{C}}_M$$ (М=Р), выражение в правой части которого описывает поле лишь одной волны (индекс р у переменных убран).

$${\displaystyle \sum _{m=1}^M{\stackrel{\wedge }{C}}_m{\stackrel{\wedge }{E}}_{n,m}={\stackrel{\wedge }{U}}_p{e}^{i(\omega t_m-\overline{K}({\alpha }_0,{\beta }_0){\overline{R}}_n)}}(7)$$

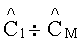
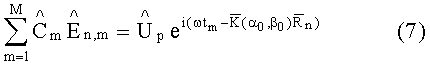
Неопределенные коэффициенты 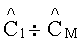$${\stackrel{\wedge }{C}}_1÷{\stackrel{\wedge }{C}}_M$$ не зависят от номера вибратора n и номера среза данных m. Они зависят лишь от временного интервала Δt. Следовательно, они одинаковы для выражения (7) при разных значениях индекса m. На основании этого запишем

$${\displaystyle \sum _{m=1}^M{\stackrel{\wedge }{C}}_m{\stackrel{\wedge }{E}}_{n,m+1}=\stackrel{\wedge }{U}{e}^{i(\omega t_m-\overline{K}({\alpha }_0,{\beta }_0){\overline{R}}_n)}}{e}^{i\omega \Delta t}(8)$$

Объединяя (7) и (8) и переобозначив коэффициенты, получим

$${\displaystyle \sum _{m=1}^M{\stackrel{\wedge }{a}}_m{\stackrel{\wedge }{E}}_{n,m}=\stackrel{\wedge }{E}}n,m={\stackrel{\wedge }{E}}_{n,M+1}(9)$$

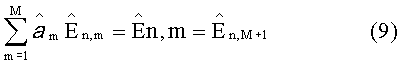
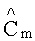
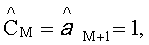
Взаимосвязь коэффициентов $${\stackrel{\wedge }{C}}_m$$ и $${\stackrel{\wedge }{a}}_m$$ определяется выражениями

$${\stackrel{\wedge }{C}}_{{}_1}={\stackrel{\wedge }{a}}_{{}_1}{\stackrel{\wedge }{x}}^{*},$$ $${\stackrel{\wedge }{C}}_2=({\stackrel{\wedge }{a}}_2+{\stackrel{\wedge }{C}}_1){\stackrel{\wedge }{x}}^{*},\dots \dots ,$$ $${\stackrel{\wedge }{C}}_m=({\stackrel{\wedge }{a}}_m+{\stackrel{\wedge }{Cm-}}_1){\stackrel{\wedge }{x}}^{*},\dots \dots ,$$

$${\stackrel{\wedge }{C}}_M=\stackrel{\wedge }{a}{}_{M+1}=\mathrm{1,}$$ $${\stackrel{\wedge }{x}}^{*}=\exp (-i\omega \Delta t)(10)$$

Используя выражение (9) запишем функционал правдоподобия в виде

$$\Delta ({\stackrel{\wedge }{a}}_1\dots {\stackrel{\wedge }{a}}_M)={\displaystyle \sum _n^N{\left|{\displaystyle \sum _m^M{\stackrel{\wedge }{a}}_{{}_m}{\stackrel{\wedge }{E}}_{{}_{n,m}}-{\stackrel{\wedge }{E}}_{{}_{n,M+1}}}\right|}^2(11)}$$

Дифференцируя выражение (11) по коэффициентам 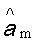$${\stackrel{\wedge }{a}}_m$$ и приравнивая дифференциалы к нулю, можно получить матричное уравнение. В векторной форме оно имеет вид (4)

$$\stackrel{\wedge }{A}\overline{a}=\overline{b},\text{ (4)}$$

где

$$\stackrel{\wedge }{A}$$ - корреляционная матрица с элементами $$\overline{{\stackrel{\wedge }{E}}_{n,k}{\stackrel{\wedge }{E}}_{n,p}^{*}}$$ ,

m=1÷M, p=1÷M, n=1÷N, черта сверху означает суммирование по индексу n, $$\overline{b}={(b_1÷b_M)}^T$$ - вектор-столбец с координатами $$b_m=\overline{{\stackrel{\wedge }{E}}_{n,M+1}{\stackrel{\wedge }{E}}_{n,m}^{*}}$$ (черта сверху определяет суммирование по индексу n, по вибраторам, m=1÷М).

$$\overline{\alpha }={({\alpha }_1÷{\alpha }_M)}^T$$ - вектор-столбец неопределенных коэффициентов.

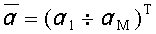
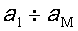
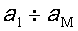
Решая векторное уравнение (4), можно получить значения коэффициентов $$a_1÷a_M$$ вектора $$\overline{a}$$ . Используя коэффициенты $$a_1÷a_M$$ , составим полином, зависящий от частоты ω (5).

$$\stackrel{\wedge }{Y}(\omega )={\stackrel{\wedge }{x}}^M+{\stackrel{\wedge }{a}}_{{}_M}{\stackrel{\wedge }{x}}^{M-1}+{\stackrel{\wedge }{a}}_{{}_{M-1}}{\stackrel{\wedge }{x}}^{M-2}+\dots \dots {\stackrel{\wedge }{a}}_{{}_2}\stackrel{\wedge }{x}+{\stackrel{\wedge }{a}}_{{}_1}=0(5)$$

Корни полинома М степени дают М решений $${\stackrel{\wedge }{x}}^{(m)}=\exp (i{\omega }_m\Delta t)$$ . Следовательно, по выражениям (10) можно определить коэффициенты $${\stackrel{\wedge }{C}}_p^{(m)}$$ , которые представляют собой элементы импульсной последовательности фильтра для выделения однолучевого поля из суммы полей ионосферного сигнала. Используя коэффициенты $${\stackrel{\wedge }{C}}_p^{(m)}$$ , можно выделить (отфильтровать) однолучевые поля $${\stackrel{\wedge }{E}}_n^m$$ (выражения (6)).

$$\frac{{\stackrel{\wedge }{E}}_{{}_n}^{(1)}={\stackrel{\wedge }{E}}_{{}_{n\mathrm{,1}}}{\stackrel{\wedge }{C}}_1^{(1)}+{\stackrel{\wedge }{E}}_{{}_{n\mathrm{,2}}}{\stackrel{\wedge }{C}}_2^{(1)}+\dots \dots +{\stackrel{\wedge }{E}}_{{}_{n,M}}{\stackrel{\wedge }{C}}_M^{(1)}=\stackrel{}{{\stackrel{\wedge }{U}}_1\exp (-i{\overline{K}}_1{\overline{R}}_n)}}{{\stackrel{\wedge }{E}}_{{}_n}^{(M)}={\stackrel{\wedge }{E}}_{{}_{n\mathrm{,1}}}{\stackrel{\wedge }{C}}_1^{(M)}+{\stackrel{\wedge }{E}}_{{}_{n\mathrm{,2}}}{\stackrel{\wedge }{C}}_2^{(M)}+\dots \dots +{\stackrel{\wedge }{E}}_{{}_{n,M}}{\stackrel{\wedge }{C}}_M^{(M)}=\stackrel{\wedge }{{\stackrel{\wedge }{U}}_M\exp (-i{\overline{K}}_M{\overline{R}}_n)}}(6)$$

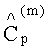
Для каждого однолучевого поля, выполняя пространственное преобразование Фурье, можно получить диаграмму направленности.

$${\stackrel{\wedge }{U}}_m({\alpha }_m^{\text{'}},{\beta }_m^{\text{'}})={\displaystyle \sum _n^N{\stackrel{\wedge }{E}}_n^{(m)}\exp (i{\overline{K}}_m({\alpha }_m^{\text{'}},{\beta }_m^{\text{'}}){\overline{R}}_n)},m=1÷M(12)$$

По максимумам диаграмм направленности определяют значения азимутов α_m, углов места β_m и амплитуд $${\stackrel{\wedge }{U}}_m$$ , для М лучей ионосферного сигнала.

Дисперсия азимута D_α и дисперсия углов места D_β для однолучевого поля (дисперсия Рао-Крамера) при трехмерной антенной системе определяются выражениями.

$$D_{\alpha }=\frac{2{\sigma }^2}{\left|\stackrel{\wedge }{E}\right|{(k_{0}R\cos (\beta ))}^{2}N}$$

$$D_{\beta }=\frac{6{\sigma }^2}{{\left|\stackrel{\wedge }{E}\right|}^2{k}_0^2({(3R\sin (\beta ))}^{2}N+2{(Z\cos (\beta \text{'}))}^{2}M1)}(13)$$

где σ^{2 -} дисперсия шума,

$$\left|\stackrel{\wedge }{E}\right|$$ - модуль напряженности однолучевого поля,

K₀=2π/λ - волновое число, λ - длина волны,

R -радиус антенной системы,

Z - координата, перпендикулярная поверхности земли,

N, M1 - количество вибраторов на окружности радиуса R и вдоль координаты Z.

Дисперсия азимута определяется только вибраторами, расположенными по окружности на земле (N). Дисперсия угла места зависит как от горизонтальной пространственной базы, так и от вертикальной базы антенной системы. При β=0 дисперсия угла места определяется выражением

$$D_{\beta |}{}_{b=0}=\frac{3{\sigma }^2}{{\left|\stackrel{\wedge }{E}\right|}^2{(k_{0}Z)}^{2}M1}(14)$$

Таким образом, дисперсия угла места зависит от новой пространственной базы:

$$L=\sqrt{{(R\sin (\beta ))}^{2}N+2{\left(\frac{Z}{3}\cos (\beta \text{'})\right)}^{2}M1}(14)$$

Эта база не обращается в нулевое значение при значении β, стремящемся к нулю. Следовательно, дисперсия трехмерной антенной системы не будет увеличиваться при приближении β к нулю. Задача малых углов места при пеленгации ионосферных сигналов оказывается решенной.

Сущность предлагаемого способа оценки угловых параметров ионосферных сигналов поясняется следующими рисунками и диаграммами.

На фиг.1 представлена структурная схема устройства, с помощью которого реализуется прототип «Способ пеленгации с учетом корреляционной взаимосвязи между лучами».

На фиг.2 представлена структурная схема устройства, с помощью которого реализуется предлагаемый способ «Способ оценки угловых параметров ионосферного сигнала». По сравнению с прототипом второй, третий, четвертый блоки идентичны блокам прототипа, вместо 1,5÷8 блоков прототипа предлагаются действия новых блоков 1,5÷12. С помощью этих блоков формируется пространственно-временной массив, создаются корреляционная матрица и правый вектор-столбец векторного уравнения. При решении векторного уравнения находятся значения коэффициентов, формируется полином и находятся его корни. Это дает возможность определить элементы импульсной последовательности фильтров и выделить (отфильтровать) однолучевые поля. Определяются диаграммы направленности для отдельных лучей, и по максимумам диаграмм направленностей оцениваются амплитуды и угловые характеристики.

На фиг.3 показано расположение антенн на поверхности земли, составляющих круговую антенную систему (16 вибраторов), дополненную вертикальной линейкой вибраторов (5 вибраторов, установленных через интервал 10 м) «Круг-Z». Радиус антенной системы равен 65 м.

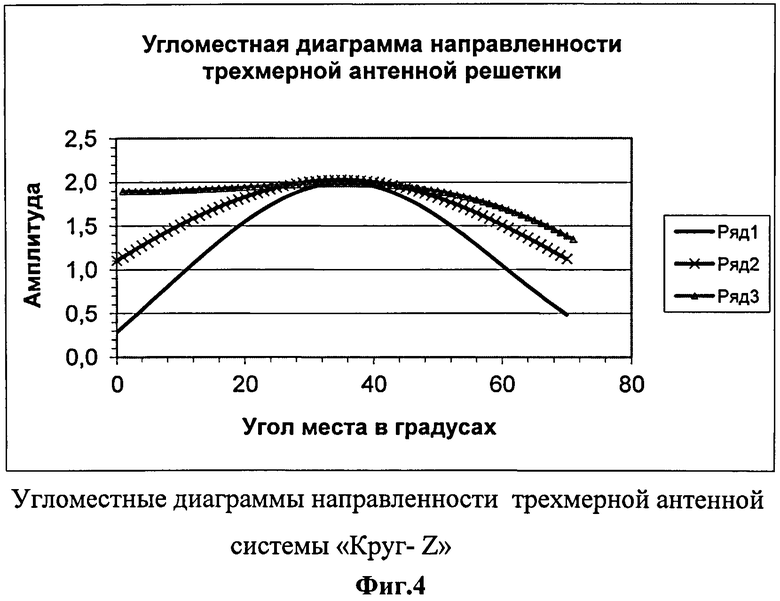
На фиг.4 показаны угломестные диаграммы направленности антенной системы «Круг-Z» на частоте 10 МГц (линия 2), на частоте 15 МГц (линия 1) и угломестная диаграмма направленности плоской круговой антенной системы на частоте 10 МГц (линия 3). В области малых значений углов места плоская антенная система не имеет четко выраженного максимума, а следовательно, углы места определяются с большими погрешностями. Так, например, если плоская волна приходит под углом места 10°, тогда антенная система "Круг-Z" имеет максимум диаграммы направленности при β=10°. В то же время диаграмма направленности плоской антенной системы "Круг" имеет плоскую вершину от 0° до 20°. Это и приводит к проблеме малых углов при приеме ионосферных сигналов.

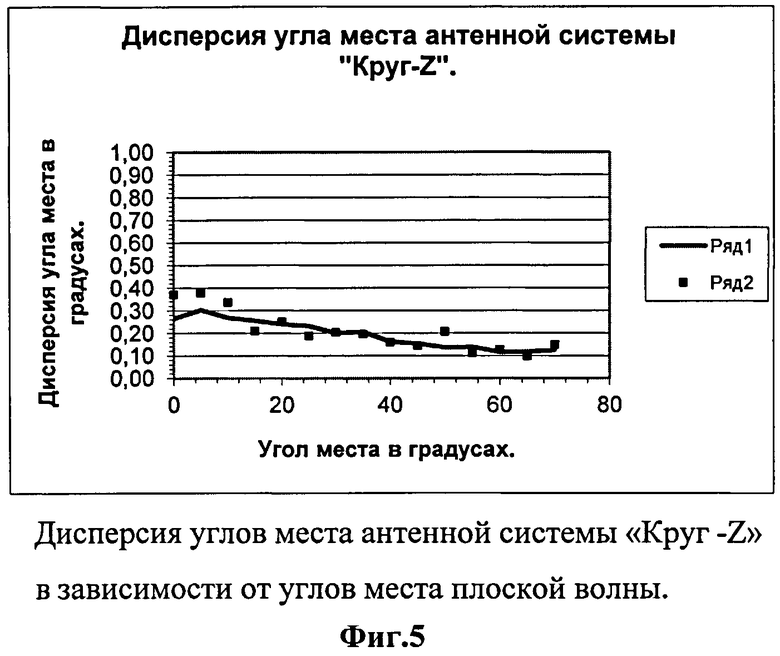
На фиг.5 показана дисперсия углов места антенной системы «Круг -Z» в зависимости от углов места плоской волны. Сплошная линия представляет расчет дисперсии углов места по выражению (13). Точками отмечены дисперсии углов места, полученных при ее оценке по 50-ти расчетам. Таким образом, добавление к плоской антенной системе типа "Круг" линейки вибраторов на высотах от 0 до 40 м вполне решает проблему малых углов при приеме ионосферных сигналов.

На фиг.6 показаны углы места многолучевого ионосферного сигнала, полученные с помощью восьмиканального пеленгатора, работающего по алгоритму предлагаемого способа пеленгации. С помощью пеленгатора ведется прием сигналов радиостанцией «Би-Би-Си» (Англия). f=6,02 МГц. Отмечается наличие как двухлучевой структуры ионосферного сигнала, так и трехлучевой структуры. Получить такие оценки углов места с помощью классических методов пеленгации не представляется возможным.

Структурная схема устройства, в котором реализуется способ оценки угловых параметров ионосферных сигналов, представлена на фиг.2.

Согласно предлагаемому способу последовательность действий следующая (фиг.2).

1. Принимают ионосферный сигнал с помощью круговой антенной системы, дополненной вертикальной по отношению к поверхности земли линейкой вибраторов. Создают трехмерную антенную систему (блок 1).

2. Преобразуют сигналы в каждом канале (от каждого вибратора) по частоте, усиливают и фильтруют с помощью многоканального приемника (блок 2).

3. Преобразуют аналоговые сигналы на выходах многоканального приемника в цифровую форму с помощью многоканального аналого-цифрового преобразователя (АЦП) (блок 3).

4. Получают частотный спектр сигнала в N каналах с помощью преобразования Фурье. Формируют пространственный массив комплексных данных $${\stackrel{\wedge }{E}}_n$$ , выделяя максимумы частотных спектров (блок 4).

5. Формируют пространственно-временной массив данных $${\stackrel{\wedge }{E}}_{n,m}$$ , повторяя действия 1÷4 через интервалы 1÷2 с. Количество временных срезов данных на единицу больше (m=1÷M+1), чем количество лучей М (блок 5).

6. Формируют корреляционную матрицу $$\stackrel{\wedge }{A}$$ , размерностью, равной количеству лучей ((М)*(М)), и правый вектор-столбец данных $$\overline{b}={(b_1÷b_M)}^T$$ , элементы которых усредняются по индексу n (по вибраторам, по пространству) (блок 6).

7. Определяют коэффициенты $$\overline{\alpha }={({\alpha }_1÷{\alpha }_M)}^T$$ при решении векторного уравнения (4) (блок 7). $$\stackrel{\wedge }{A}\overline{a}=\overline{b}.\text{ (4)}$$

8. Формируют полином 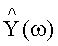$$\stackrel{\wedge }{Y}(\omega )$$ , степени М для оценки значений доплеровских сдвигов частот ионосферного сигнала по выражению (5) и оценки по минимумам полинома $$\stackrel{\wedge }{Y}(\omega )$$ М доплеровских сдвигов частот ионосферного сигнала ω_m (блок 8).

$$\stackrel{\wedge }{Y}(\omega )={\stackrel{\wedge }{x}}^M+{\stackrel{\wedge }{a}}_{{}_M}{\stackrel{\wedge }{x}}^{M-1}+{\stackrel{\wedge }{a}}_{{}_{M-1}}{\stackrel{\wedge }{x}}^{M-2}+\dots \dots {\stackrel{\wedge }{a}}_{{}_2}\stackrel{\wedge }{x}+{\stackrel{\wedge }{a}}_{{}_1}=\mathrm{0,}$$ $${\stackrel{\wedge }{x}}_m=\exp (i{\omega }_m\Delta t)(5)$$

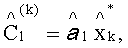
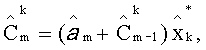
9. Определяют элементы импульсных последовательностей фильтров $${\stackrel{\wedge }{C}}_1^{(k)}={\stackrel{\wedge }{a}}_1^{}{\stackrel{\wedge }{x}}_k^{*},$$ $${\stackrel{\wedge }{C}}_m^k=({\stackrel{\wedge }{a}}_m^{}+{\stackrel{\wedge }{C}}_{m-1}^k){\stackrel{\wedge }{x}}_k^{*},$$ $${\stackrel{\wedge }{C}}_m^{(k)}=\mathrm{1,}$$

k=1÷M (блок 9).

10. Выделяют (фильтруют) однолучевые поля 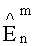$${\stackrel{\wedge }{E}}_n^m$$ из совокупности полей ионосферного сигнала по выражениям (6) (блок 10).

$$\frac{{\stackrel{\wedge }{E}}_{{}_n}^{(1)}={\stackrel{\wedge }{E}}_{{}_{n\mathrm{,1}}}{\stackrel{\wedge }{C}}_1^{(1)}+{\stackrel{\wedge }{E}}_{{}_{n\mathrm{,2}}}{\stackrel{\wedge }{C}}_2^{(1)}+\dots \dots +{\stackrel{\wedge }{E}}_{{}_{n,M}}{\stackrel{\wedge }{C}}_M^{(1)}=\stackrel{}{{\stackrel{\wedge }{U}}_1\exp (-i{\overline{K}}_1{\overline{R}}_n)}}{{\stackrel{\wedge }{E}}_{{}_n}^{(M)}={\stackrel{\wedge }{E}}_{{}_{n\mathrm{,1}}}{\stackrel{\wedge }{C}}_1^{(M)}+{\stackrel{\wedge }{E}}_{{}_{n\mathrm{,2}}}{\stackrel{\wedge }{C}}_2^{(M)}+\dots \dots +{\stackrel{\wedge }{E}}_{{}_{n,M}}{\stackrel{\wedge }{C}}_M^{(M)}=\stackrel{\wedge }{{\stackrel{\wedge }{U}}_M\exp (-i{\overline{K}}_M{\overline{R}}_n)}}(6)$$

11. Формируют для каждого выделенного поля $${\stackrel{\wedge }{E}}_n^m$$ диаграммы направленности с помощью пространственного преобразования Фурье по выражению (12) и сканируют этой диаграммой направленности в диапазоне оценочных азимутов α'=0÷360° и углов места β'=0÷90°.

$${\stackrel{\wedge }{U}}_m({\alpha }_m^{\text{'}},{\beta }_m^{\text{'}})={\displaystyle \sum _n^N{\stackrel{\wedge }{E}}_n^{(m)}\exp (i{\overline{K}}_m({\alpha }_m^{\text{'}},{\beta }_m^{\text{'}}){\overline{R}}_n)},m=1÷M(блок\text{ 11})(12)$$

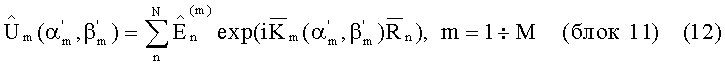
12. Оценивают азимуты $${\alpha }_m^{\text{'}}={\alpha }_{\mathrm{0,}m}$$ , углы места $${\beta }_m^{\text{'}}={\beta }_{\mathrm{0,}m}$$ и амплитуды $${\stackrel{\wedge }{U}}_m$$ по максимуму диаграммы направленности для М лучей ионосферного сигнала (блок 12).

Изобретение относится к радиотехнике, а именно к области пеленгации. Достигаемый технический результат - расширение возможностей пеленгации, сокращение времени расчета угловых параметров многолучевого ионосферного сигнала. Технический результат достигается тем, что круговую антенную систему, расположенную на поверхности земли, дополняют линейной системой вибраторов, расположенных вдоль вертикали к поверхности земли. С помощью сформированной таким образом антенной системы (трехмерная антенная система), многоканального приемника, многоканального аналого-цифрового преобразователя (АЦП) и временного преобразования Фурье формируют пространственно-временной массив комплексных данных $${\stackrel{\wedge }{E}}_{n,m}$$ , отображающий значения напряженности поля в n точках трехмерного пространства (n - номер вибратора) и в m-е моменты времени, с интервалами 1-2 секунды (индекс m определяет номер временного среза данных на n вибраторах, m=1÷M+1). Количество временных срезов данных берется на единицу больше, чем количество лучей М. Затем осуществляют соответствующую математическую обработку, фильтруют однолучевые поля из совокупности полей ионосферного сигнала, формируют для каждого выделенного поля диаграммы направленности, сканируют диаграммой направленности в диапазоне оценочных максимумов и углов места и оценивают азимуты, углы места и амплитуды по максимуму диаграммы направленности для М лучей ионосферного сигнала. 6 ил.

Способ оценки угловых параметров ионосферных сигналов, включающий прием ионосферного сигнала с помощью круговой антенной системы, состоящей из N вибраторов, расположенных равномерно по окружности радиуса R, преобразование по частоте и усиление сигналов от каждого n вибратора с помощью многоканального приемника, преобразование аналоговых сигналов на выходах многоканального приемника в каждом n канале в цифровую форму с помощью многоканального аналого-цифрового преобразователя, определение амплитуды E_n и фазы ψ_n принятого ионосферного сигнала в каждом канале с помощью временного преобразования Фурье, отличающийся тем, что круговую антенную систему дополняют вертикальной линейкой вибраторов с номерами n=N+1÷N1, создавая трехмерную антенную систему, дополнительно с помощью антенной системы, многоканального приемника, многоканального АЦП, блока преобразования Фурье формируют пространственно-временной массив данных E_n,k, ψ_n,k, повторяя измерения через временной интервал Δt=1÷2 с, где индекс n=1÷N1 определяет номер вибратора, а индекс k=1÷K определяет номер временного среза данных, причем K=M+1, формируют с помощью пространственно-временного массива данных корреляционную матрицу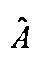, размерностью, равной количеству лучей М, с элементами 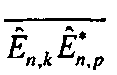, где индекс p=1÷K, и правый вектор-столбец , где T означает транспонирование вектора-столбца, элементы которых усредняют по индексу n (по вибраторам), решая векторное уравнение $$\widehat{A}\overline{a}=\overline{b},$$ находят значения М коэффициентов вектора , 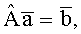равное количеству лучей, формируют полином степени, равной количеству лучей м, 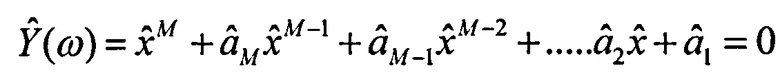, где $${\widehat{x}}_m=\exp (i{\omega }_m\Delta t),$$ и находят М решений (, m=1÷M) этого полинома, равное количеству лучей, определяют с помощью полученных решений элементы M импульсных последовательностей фильтров , равное количеству лучей, с помощью которых выделяют (фильтруют) М однолучевых полей ионосферного сигнала, равное количеству лучей, по которым формируют двумерные диаграммы направленности, оценивают по максимумам диаграмм направленностей азимуты α_m и углы места β_m М лучей ионосферного сигнала.