СПОСОБ ОРГАНИЗАЦИИ АРИФМЕТИЧЕСКОГО УСКОРИТЕЛЯ ДЛЯ РЕШЕНИЯ БОЛЬШИХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ Российский патент 2015 года по МПК G06F17/12 G06F17/14 G06F17/16 

Изобретение относится к вычислительной технике, в частности к способу организации арифметического ускорителя для решения больших систем линейных уравнений, и может быть использовано для создания новой технологии инженерных расчетов, в том числе объемных интегральных уравнений, электродинамики, гидроакустики, медицинских исследований.

Известен способ организации многопроцессорной ЭВМ, заключающийся в параллельном исполнении нити вычислений по средствам хранимого в виртуальной памяти распределенного представления дескриптора нити, выполнение первичной выборки архитектурных команд по средствам мониторов нитей, формирование графоинформационных зависимостей транзакций, которые выдают через сеть в исполнительные кластеры, переводит активную нить в резидентную очередь ждущих завершения транзакций и выбирают следующую активную нить, принимают транзакции, переписывают их команды, осуществляют выборку и передачу готовых команд кластеру, корректируют граф, передают результат завершения транзакции монитору и переводят нить с коррекцией корня представления дескриптора нити (см., например, патент РФ 2312388, G06F 15/16, 2005 г.).

Известный способ труден в отношении разработки.

Наиболее близким к заявляемому способу является способ организации арифметического ускорителя для решения больших систем линейных уравнений, включающий способ организации арифметического ускорителя для решения больших систем линейных уравнений, включающий общую память, доступную для первичных и одного или более вторичных процессоров, прием множества коэффициентов, связанных с набором линейных уравнений в общую память и разделением их на блоки коэффициентов с использованием одного или более первичных процессоров, выявление доступного вторичного процессора для обработки выбранного блока коэффициентов, передачу его из общей памяти в блок локальной памяти вторичного процессора с последующей обработкой для получения промежуточного результата и передачей его в общую память (см., например, патент РФ №7236998, G06F 7/00).

Основным недостатком известного способа является квадратичный рост числа арифметических операций от числа неизвестных.

Технической задачей, на решение которой направлен заявляемый способ с указанием технического результата, является создание такого способа, который позволил бы уменьшить рост числа арифметических операций и сделать его пропорциональным числу неизвестных.

Технический результат связан с использованием метода быстрого умножения циркулянтных матриц на вектор, основанный на быстром дискретном преобразовании Фурье.

Технический результат достигается путем построения вычислительной среды, позволяющей производить наименьшее количество операций и реализовать рост числа арифметических операций пропорционально числу неизвестных.

Решение технической задачи достигается тем, что способ организации арифметического ускорителя для решения больших систем линейных уравнений, включающий общую память, доступную для первичных и одного или более вторичных процессоров, прием множества коэффициентов, связанных с набором линейных уравнений в общую память и разделением их на блоки коэффициентов с использованием одного или более первичных процессоров, выявление доступного вторичного процессора для обработки выбранного блока коэффициентов, передачу его из общей памяти в блок локальной памяти вторичного процессора с последующей обработкой для получения промежуточного результата и передачей его в общую память, согласно изобретению производят доступ к блоку общей памяти одного или более третичных или четвертичных процессоров, выбранных из произвольного множества разнородных процессоров, выявляют свободный первичный процессор и разделяют промежуточный результат на группы, производят индексирование и записывают значения промежуточного результата в каждой группе в блок общей памяти, выявляют свободный третичный процессор и производят ранжирование индексов и по одному из трех последовательных индексов, выбранных из множества индексов, производят быстрое дискретное преобразование Фурье, записывают результаты преобразования в блок общей памяти, выявляют свободный четвертичный процессор, рассматривают значения элементов матрицы для первого индекса последовательно и производят быстрые дискретные преобразования Фурье по двум другим индексам, затем умножают почленно получившиеся значения по этим двум индексам на Фурье преобразования теплицевой матрицы для этих индексов, затем производят обратное быстрое дискретное преобразование Фурье по этим двум индексам, результаты преобразований записывают в локальную память четвертичного процессора, по окончании процесса производят обратное быстрое дискретное преобразование Фурье по первому индексу, записывают результат в общую память.

На чертеже изображена общая блок-схема по изобретению, показывающая процессоры 1, 2, 3, 4, модуль 5 индексирования, модули 6, 7 Фурье преобразования, модуль 8 обратного Фурье преобразования, блок 9 общей памяти, блоки 10, 11, 12, 13 локальной памяти.

На схеме представлена последовательность действий, отраженная в формуле изобретения, а именно:

Матрица системы линейных уравнений, получающаяся после дискретизации интегральных уравнений, описывающих задачи инженерных расчетов, в том числе объемных интегральных уравнений, электродинамики, гидроакустики, медицинских исследований, например, рассеяние электромагнитных волн на диэлектрических трехмерных структурах имеет форму блочно-теплицевой матрицы. При этом основные вычислительные затраты при умножении матрицы системы линейных уравнений (СЛАУ) на вектор, а это самая затратная вычислительная операция при использовании итерационных алгоритмов, связаны с вычислением сумм вида:

,

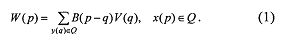где Q - область рассеивающего тела, находящегося внутри параллелепипеда П.

Для вычисления W(p) в узловых точках х(р)∈Q требуется выполнить ~N² арифметических операций.

Для уменьшения числа арифметических операций будем применять технику быстрого умножения циркулянтных матриц на вектор, основанную на быстром дискретном преобразовании Фурье.

Доопределим величины V(q) нулем в точках x(q) параллелепипеда П, не принадлежащих области Q. Тогда (1) можно записать в виде:

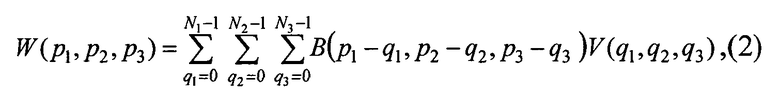
где матричная функция дискретного аргумента В{р) определена для значений:

-(N₁-1)≤p₁≤(N₁-1); -(N₂-1)≤p₂≤(N₂-1); -(N₃-1)≤p₃≤(N₃-1).

Для электромагнитных задач имеем:

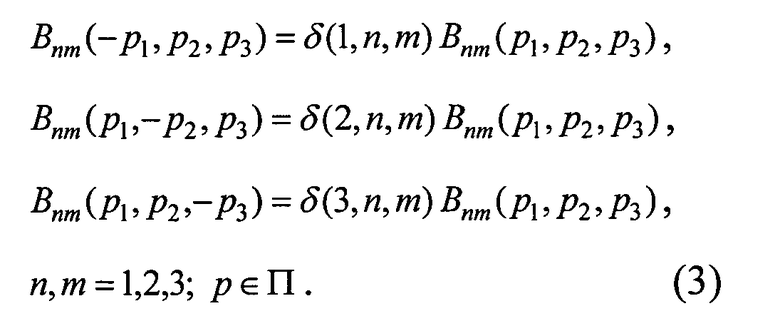
Здесь функция дискретного аргумента δ(k, n, m) определяется формулой

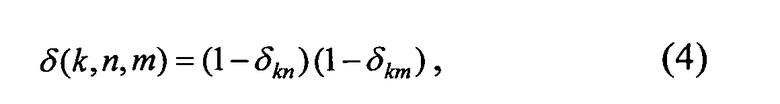
где δ_kn - символ Кронекера.

Обозначим через П₂ параллелепипед со сторонами 2N₁h₁, 2N₂h₂ и 2N₃h₃. Продолжим матричную функцию дискретного аргумента В(р₁, р₂, р₃) на все целочисленные значения р₁, р₂, p₃, полагая ее периодической по каждой переменной с периодами соответственно 2N₁, 2N₂, 2N₃. При этом доопределим В(р₁, р₂, р₃) нулем в точках (N₁, p₂, p₃), (p₁, N₂, p₃), (p₁, p₂, N₃), где p₁, p₂, p₃ - любые целые числа. Далее доопределим вектор функции дискретного аргумента V(p₁, p₂, p₃) нулем во всех узловых точках П₂, не принадлежащих П, и продолжим ее на все целочисленные значения р₁, р₂, р₃, полагая ее периодической по каждой переменной с периодами соответственно 2N₁, 2N₂, 2N₃, тогда:

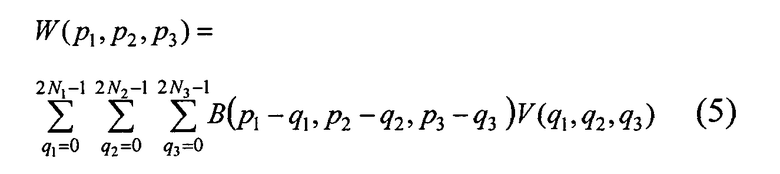
Учитывая изложенное при х(р)∈П функция W(p₁, p₂, p₃) из (5) совпадает со значениями W(p₁, p₂, p₃) из (2). Ниже через П и П₂ будем обозначать целочисленные параллелепипеды с числом дискретных аргументов по каждой оси N₁, N₂, N₃ и 2N₁, 2N₂, 2N₃ соответственно. Теперь проводя дискретное преобразование Фурье по каждой переменной от обеих частей (5), получим следующее равенство:

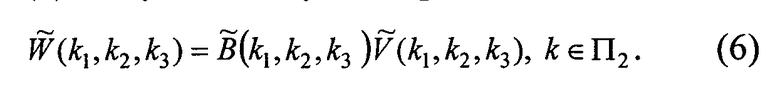
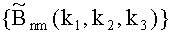
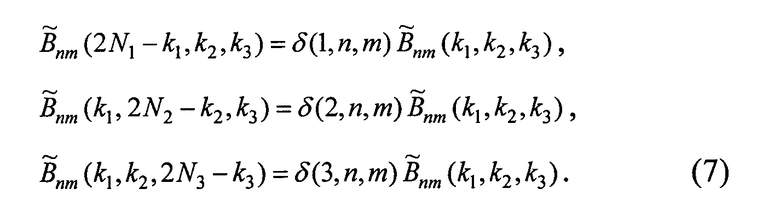
Из (3) и периодичности функций следует, что элементы массива $$\{{\tilde{B}}_{nm}(k_1,k_2,k_3)\}$$ , k∈П₂, удовлетворяют соотношениям:

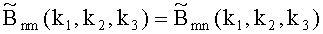
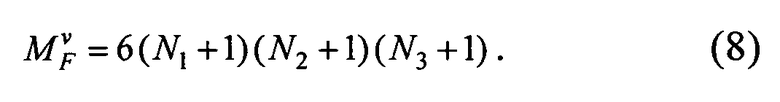
Таким образом, учитывая, что $${\tilde{B}}_{nm}(k_1,k_2,k_3)={\tilde{B}}_{mn}(k_1,k_2,k_3)$$ , ясно, что количество элементов массива, которые надлежит вычислить и хранить в памяти компьютера, определяется формулой

При вычислении W(p), p∈П, основные вычислительные затраты, без учета нахождения 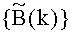$$\{\tilde{B}(k)\}$$ , k∈П₂ (этот массив вычисляется один раз и затем без изменения используется при вычислении итераций), связаны с прямым и обратным быстрым преобразованием Фурье функций дискретного аргумента. При прямом преобразовании Фурье функция V(p) отличается от нуля только при значениях р∈П. С другой стороны, при обратном преобразовании Фурье значение функции W(p) требуется определить только при значениях р∈П. Кроме того, алгоритмы прямого и обратного быстрого дискретного преобразования Фурье можно применять в любой последовательности переменных. Принимая вышесказанное во внимание, сначала изложим по шагам схему эффективного вычисления вектора функции W(p), р∈П.

Шаг 1. Проведем ранжирование и расположим N₁, N₂, N₃ в порядке убывания, т.е. N₁≥N₂≥N₃.

Шаг 2. Произведем быстрое дискретное преобразование Фурье по целочисленной переменной р₁. Получаем массив чисел V_n(k₁, p₂, p₃), 0≤k₁≤2N₁-1, 0≤p₂≤N₂-1, 0≤p₃≤N₃-1; n=1, 2, 3. Общее количество комплексных чисел в этом массиве равно 6 N₁N₂N₃.

Шаг 3. Для каждого фиксированного k₁, 0≤k₁≤2N₁-1 последовательно производим быстрое дискретное преобразование Фурье по переменным р₂, р₃. Затем при том же k₁, используя формулу (6), получаем значения 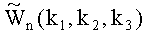$${\tilde{W}}_n(k_1,k_2,k_3)$$ . Далее по переменным k₂, k₃ производим обратное быстрое дискретное преобразование Фурье. В результате для каждого k₁, 0≤k₁≤2N₁-1, получаем значения W_n(k₁, p₂, p₃), 0≤p₂≤N₂-1, 0≤р₃≤N₃-1. Для реализации этого шага требуется дополнительный массив для хранения 12 N₂N₃ комплексных чисел для проведения преобразований Фурье. Ясно, что, как правило, эта величина существенно меньше чем 6 N₁N₂N₃.

Шаг 4. Произведем быстрое обратное дискретное преобразование Фурье по переменной k₁. Получаем требуемые значения W_n(p₁, p₂, p₃), 0≤p₁≤N₁-1, 0≤p₂≤N₂-1, 0≤p₃≤N₃-1.

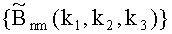
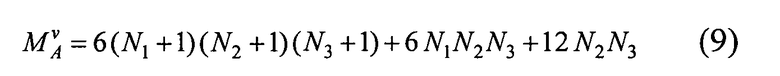
Для реализации изложенной схемы необходим объем памяти для хранения массива, равного $$\{{\tilde{B}}_{nm}(k_1,k_2,k_3)\}$$ , k∈П₂, число элементов которого определяется формулой (8), и двух вышеупомянутых массивов. Таким образом, для реализации вышеизложенной эффективной схемы умножения матрицы СЛАУ на вектор, общее количество комплексных чисел, которое надлежит одновременно хранить в памяти компьютера, определяется формулой

Число арифметических операций, требуемое для вычисления W_n(p), p∈П, оценивается формулой

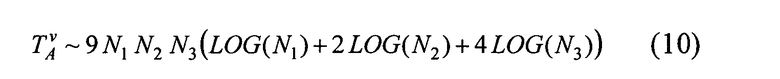
где LOG(N)=N определяется как сумма всех делителей целого числа N с учетом их кратности.

Действительно, при проведении преобразования Фурье вычисления можно проводить в любой последовательности переменных. Поэтому очевидно, что наименьшее количество операций потребуется для приведенной выше последовательности.

Если числа N₁, N₂, N₃ являются степенями числа 2, то можно воспользоваться известным быстрым преобразованием Фурье. Тогда число арифметических операций для вычисления функций дискретного аргумента W(p), p∈П, оценивается формулой

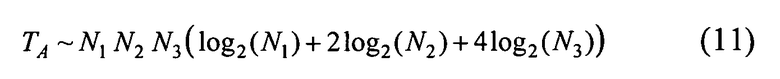
Если для умножения матрицы СЛАУ на вектор использовать (6) без применения рассмотренной схемы, то количество арифметических операций и требуемый объем памяти будут в несколько раз больше.

Обычно при использовании быстрого дискретного преобразования Фурье выбираются значения N, кратные степени 2. Однако при дискретизации интегральных уравнений, это, во многих случаях, может привести к значительным дополнительным вычислительным затратам, поскольку скважность чисел степени 2 весьма велика. Поясним на примере. Пусть N₁=N₂=N₃=N₀, т.е. П-куб. Предположим, что для аппроксимации решения с требуемой точностью, достаточно взять значение N₀=150. Ближайшие степени двойки - числа 128 и 256. Значение 128 не удовлетворяет требованию аппроксимации решения, поэтому, если мы хотим воспользоваться стандартным БПФ, то необходимо брать значение N₀=256. Пусть Т(N₀) - число арифметических операций, которое требуется для умножения матрицы СЛАУ на вектор, в зависимости от значений N₀. Тогда имеем,

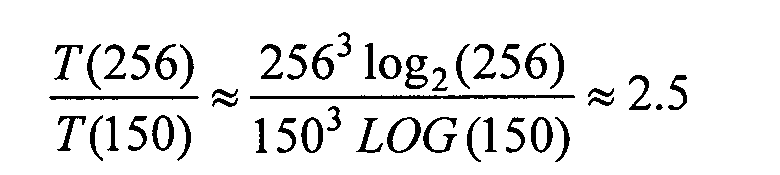
Объем памяти для хранения матрицы СЛАУ при N₀=256 в несколько раз больше, чем при N₀=150. Значит, использование БПФ для значения N₀=150 значительно более эффективно, чем использование БПФ со степенью 2.

Отметим, что использование БПФ дает для числа арифметических операций практически линейную зависимость от размерности СЛАУ по сравнению с квадратичной зависимостью, которая появляется при умножении матрицы на вектор без применения специальных быстрых алгоритмов. Это чрезвычайно важно при численном решении объемных интегральных уравнений, которые после дискретизации сводятся к СЛАУ огромной размерности (больше 10⁶). При этом нужно отметить, что объем памяти также имеет практически линейную зависимость от размерности матрицы. Это обстоятельство очень важно, поскольку без использования эффективных методов дискретизации объем требуемой памяти имеет квадратичную зависимость от размерности.

На этой основе предлагается реализовать способ организации арифметического ускорителя для решения больших систем линейных уравнений.

Проведем ранжирование и расположим N₁, N₂, N₃ в порядке убывания, т.е. N₁≥N₂≥N₃.

Произведем быстрое дискретное преобразование Фурье по целочисленной переменной р₁. Получаем массив чисел V_n(k₁, p₂, p₃), 0≤k₁≤2N₁-1, 0≤p₂≤N₂-1, 0≤p₃≤N₃-1; n=1, 2, 3. Общее количество комплексных чисел в этом массиве равно 6 N₁N₂N₃.

Для каждого фиксированного k₁, 0≤k₁≤2N₁-1, последовательно производим быстрое дискретное преобразование Фурье по переменным р₂, р₃. Затем при том же k₁, используя формулу (6), получаем значения 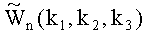$${\tilde{W}}_n(k_1,k_2,k_3)$$ . Далее по переменным k₂, k₃ производим обратное быстрое дискретное преобразование Фурье. В результате для каждого k₁, 0≤k₁≤2N₁-1, получаем значения W_n(k₁, p₂, p₃), 0≤p₂≤N₂-1, 0≤p₃≤N₃-1. Для реализации этого шага требуется дополнительный массив для хранения 12 N₂N₃ комплексных чисел для проведения преобразований Фурье. Ясно, что, как правило, эта величина существенно меньше чем 6 N₁N₂N₃.

Произведем быстрое обратное дискретное преобразование Фурье по переменной k₁. Получаем требуемые значения W_n(p₁, p₂, p₃), 0≤p₁≤N₁-1, 0≤p₂≤N₂-1, 0≤p₃≤N₃-1.

Предложенный способ реализуется следующим образом.

Производят доступ к блоку общей памяти одного или более третичных или четвертичных процессоров, выбранных из произвольного множества разнородных процессоров, затем выявляют свободный первичный процессор и разделяют промежуточный результат на группы, производят индексирование и записывают значения промежуточного результата в каждой группе в блок общей памяти. Далее выявляют свободный третичный процессор и производят ранжирование индексов и по одному из трех последовательных индексов, выбранных из множества индексов, производят быстрое дискретное преобразование Фурье, записывают результаты преобразования в блок общей памяти, затем выявляют свободный четвертичный процессор, рассматривают значения элементов матрицы для первого индекса последовательно и производят быстрые дискретные преобразования Фурье по двум другим индексам, затем умножают почленно получившиеся значения по этим двум индексам на Фурье преобразования теплицевой матрицы для этих индексов, затем производят обратное быстрое дискретное преобразование Фурье по этим двум индексам, результаты преобразований записывают в локальную память четвертичного процессора, по окончании процесса производят обратное быстрое дискретное преобразование Фурье по первому индексу, записывают результат в общую память.

Технический результат заключается в уменьшении роста числа арифметических операций и реализации роста арифметических операций пропорционально числу неизвестных и связан с использованием метода быстрого умножения циркулянтных матриц на вектор, основанный на быстром дискретном преобразовании Фурье.

Изобретение относится к вычислительной технике и может быть использовано для создания арифметического ускорителя для решения больших систем линейных уравнений. Техническим результатом является уменьшение числа арифметических операций. Способ содержит этапы, на которых: производят доступ к блоку общей памяти одного или более третичных или четвертичных процессоров, выбранных из произвольного множества разнородных процессоров, выявляют свободный первичный процессор, разделяют промежуточный результат на группы, производят индексирование и записывают значения промежуточного результата в каждой группе в блок общей памяти, выявляют свободный третичный процессор и производят ранжирование индексов и по одному из трех последовательных индексов, выбранных из множества индексов, производят быстрое дискретное преобразование Фурье, записывают результаты преобразования в блок общей памяти, выявляют свободный четвертичный процессор, рассматривают значения элементов матрицы для первого индекса последовательно, производят быстрые дискретные преобразования Фурье по двум другим индексам, умножают почленно получившиеся значения по этим двум индексам на Фурье преобразования теплицевой матрицы для этих индексов, производят обратное быстрое дискретное преобразование Фурье по этим двум индексам, результаты преобразований записывают в локальную память четвертичного процессора, производят обратное быстрое дискретное преобразование Фурье по первому индексу, записывают результат в общую память. 1 ил.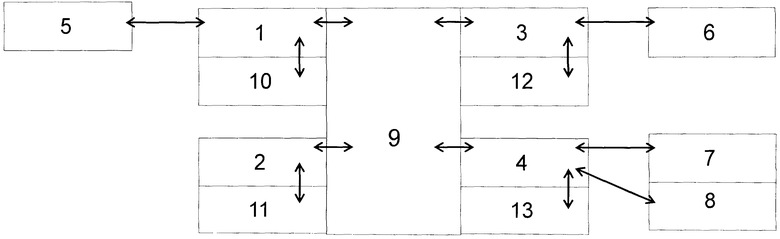

Способ организации арифметического ускорителя для решения больших систем линейных уравнений, включающий общую память, доступную для первичных и одного или более вторичных процессоров, прием множества коэффициентов, связанных с набором линейных уравнений в общую память и разделением их на блоки коэффициентов с использованием одного или более первичных процессоров, выявление доступного вторичного процессора для обработки выбранного блока коэффициентов, передачу его из общей памяти в блок локальной памяти вторичного процессора с последующей обработкой для получения промежуточного результата и передачей его в общую память, отличающийся тем, что производят доступ к блоку общей памяти одного или более третичных или четвертичных процессоров, выбранных из произвольного множества разнородных процессоров, выявляют свободный первичный процессор и разделяют промежуточный результат на группы, производят индексирование и записывают значения промежуточного результата в каждой группе в блок общей памяти, выявляют свободный третичный процессор и производят ранжирование индексов и по одному из трех последовательных индексов, выбранных из множества индексов, производят быстрое дискретное преобразование Фурье, записывают результаты преобразования в блок общей памяти, выявляют свободный четвертичный процессор, рассматривают значения элементов матрицы для первого индекса последовательно и производят быстрые дискретные преобразования Фурье по двум другим индексам, затем умножают почленно получившиеся значения по этим двум индексам на Фурье преобразования теплицевой матрицы для этих индексов, затем производят обратное быстрое дискретное преобразование Фурье по этим двум индексам, результаты преобразований записывают в локальную память четвертичного процессора, по окончании процесса производят обратное быстрое дискретное преобразование Фурье по первому индексу, записывают результат в общую память.