Изобретение относится к вычислительной технике и предназначено для выполнения операции умножения чисел, представленных в модулярно-логарифмическом формате с плавающей точкой на гибридных многоядерных процессорах.
Известен способ организации выполнения операции умножения двух чисел в модулярно-позиционном формате представления с плавающей точкой на универсальных многоядерных процессорах (A.C. RU №2509345, БИ №7, 10.03.2014), в котором операция умножения t-разрядных позиционных мантисс сомножителей заменяется n параллельно выполняемыми операциями умножения q-разрядных знакопозиций чисел в системе счисления в остаточных классах. Недостаток данного способа состоит в том, что не определено, каким образом выявляются ситуации переполнения диапазона представления модулярных мантисс при выполнении операции умножения и выполняется процедура масштабирования мантисс, таким образом, способ (A.C. RU №2509345, БИ №7, 10.03.2014) может быть использован для выполнения операции умножения не для всех операндов из заявленного диапазона представления.
Наиболее близким к заявленному способу является способ организации выполнения операции умножения двух чисел в модулярно-позиционном формате (Исупов К.С., Мальцев А.Н. Способ представления чисел с плавающей точкой большой разрядности, ориентированный на параллельную обработку //Вычислительные методы и программирование: новые вычислительные технологии. 2014. Т. 15, №4. С. 631-643), в котором масштабирование мантиссы осуществляется методом, использующим таблицы поправочных коэффициентов с применением интервально-позиционных характеристик. Недостаток данного способа состоит в том, что необходимо хранить таблицы поправочных коэффициентов большого размера, а также использовать вычислительные устройства с плавающей точкой для вычисления интервальной позиционной характеристики.
Техническим результатом применения способа организации выполнения операции умножения двух чисел в модулярно-логарифмическом формате представления с плавающей точкой на гибридных многоядерных процессорах является оптимизация выполнения операции умножения в 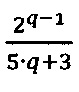 раз, где q - разрядность знакопозиций чисел в системе счисления в остаточных классах, за счет использования только целочисленных операций при умножении, проверке выхода за границы диапазона, масштабировании модулярных мантисс степенью двойки, при этом не требуется использования операций с плавающей точкой и подстановочных таблиц. Минимальное время выполнения операции умножения предложенным способом равно минимальному времени выполнения операции умножения способом (A.C. RU №2509345, БИ №7, 10.03.2014), при этом способ может быть применен для умножения любых операндов из заявленного диапазона представления, в чем заключается универсальность предлагаемого способа.
раз, где q - разрядность знакопозиций чисел в системе счисления в остаточных классах, за счет использования только целочисленных операций при умножении, проверке выхода за границы диапазона, масштабировании модулярных мантисс степенью двойки, при этом не требуется использования операций с плавающей точкой и подстановочных таблиц. Минимальное время выполнения операции умножения предложенным способом равно минимальному времени выполнения операции умножения способом (A.C. RU №2509345, БИ №7, 10.03.2014), при этом способ может быть применен для умножения любых операндов из заявленного диапазона представления, в чем заключается универсальность предлагаемого способа.
Описание способа организации выполнения операции умножения двух чисел в модулярно-логарифмическом формате представления с плавающей точкой на гибридных многоядерных процессорах: реализация способа осуществляется посредством подачи набора электрических, нейронных либо других сигналов на устройства управления каждого вычислительного ядра многоядерного гибридного процессора, которые, в соответствии с данными сигналами, формируют управляющие команды для операционных устройств соответствующих вычислительных ядер.
В позиционных двоичных форматах с плавающей точкой стандарта IEEE-754 любое вещественное число представляется трехэлементным набором:
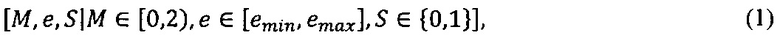
где М - рациональная мантисса, е - порядок числа, emin=2-2ν-1 и emax=2ν-1-1, S-знак числа.
Величина чисел, записанных в таком формате, выражается формулой -1S⋅М⋅2е. Машинными представлениями чисел вида (1) являются (ν+t+1)-разрядные двоичные векторы (Srν-1…r2r1dt…d2d1), где разряды с d1 по dt отводятся под представление рациональных двоичных мантисс М=dtdt-1…d2d1, разряды с r1 по rν отводятся под представление целочисленных двоичных порядков е, записанных в форме с избытком Е=rνrν-1…r2r1=е+emax, разряд S выражает знак числа.
Определим целочисленную мантиссу М'=dtdt-1…d2d1 как t-разрядное неотрицательное целое двоичное число, такое, что М=М'⋅21-t. Определим перемещенный порядок λ как целое двоичное число со знаком, такое, что λ=е-t+1, где е - ν-разрядный порядок числа, представленного в двоичном формате (1).
Зададим n целочисленных положительных q-разрядных оснований системы остаточных классов p1,р2, …, pn, таких, что ∀i1, i2∈{1, 2, …, n), i1≠i2:  , q≤k, где
, q≤k, где 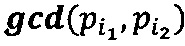 - наибольший общий делитель для
- наибольший общий делитель для 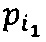 и
и  , k - размер разрядной сетки процессора.
, k - размер разрядной сетки процессора.
Целочисленную мантиссу М'=dtdt-1…d2d1 преобразуем в систему остаточных классов с заданными основаниями р1, p2, …, pn, получая тем самым модулярную мантиссу  :
:
 ,
,
где mi∈[0, рi-1], i=1, 2, …, n - q-разрядные цифры (модулярные разряды) модулярной мантиссы 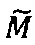 , q - разрядность оснований p1, p2, …, pn,
, q - разрядность оснований p1, p2, …, pn,  - операция получения остатка от деления М' на i-ое основание pi.
- операция получения остатка от деления М' на i-ое основание pi.
Определим ранг модулярной мантиссы как значение R, такое, что выполняется условие:
 ,
,
где 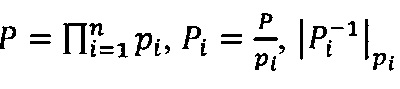 - мультипликативная инверсия Рi по модулю рi∈[1, n], n - количество модулей.
- мультипликативная инверсия Рi по модулю рi∈[1, n], n - количество модулей.
R∈[0,n-1] и вычисляется по формуле:
 ,
,
где  - наибольшее целое, не превышающее
- наибольшее целое, не превышающее 
При условии, что 2q-1<pi<2q, где q - разрядность оснований р1, р2, …, рn, величина 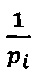 может быть вычислена по формуле
может быть вычислена по формуле  , где wi - s-разрядные весовые коэффициенты. Тогда величина ранга может быть вычислена по формуле:
, где wi - s-разрядные весовые коэффициенты. Тогда величина ранга может быть вычислена по формуле:
 .
.
Определим верхнюю и нижнюю границы величины ранга модулярного числа как
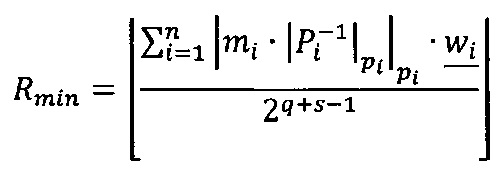 ,
,  ,
,
где  ,
,  , при условии, что 2q-1<рi<2q,
, при условии, что 2q-1<рi<2q,  - наибольшее целое, не превышающее
- наибольшее целое, не превышающее 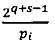 , s - разрядность коэффициентов wi.
, s - разрядность коэффициентов wi.
Согласно теоретико-числовой теореме Эйлера мультипликативную инверсию  , соответствующую сравнению
, соответствующую сравнению  , можно вычислить следующим образом
, можно вычислить следующим образом
 ,
,
где ϕ(pi) - функция Эйлера, равная количеству целых чисел в диапазоне [1, рi], взаимно простых с рi.
Пример. Вычислим значения мультипликативных инверсий Pi по модулям рi для системы с основаниями: р1=11, р2=13, р3=15:
 ; ϕ(11)=10;
; ϕ(11)=10;  ;
;
 ; ϕ(13)=12;
; ϕ(13)=12; 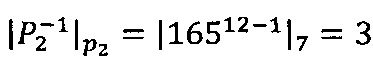 ;
;
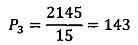 ; ϕ(15)=12;
; ϕ(15)=12; 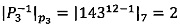
Определим логарифмическую характеристику числа как значение двоичного логарифма от этого числа. Тогда логарифмическая характеристика модуля числа, представленного в формате [М, е, S], вычисляется следующим образом:
log2(М'⋅21-t⋅2е)=log2(М')+е-t+1=log2(М')+λ.
Определим интервальную логарифмическую характеристику мантиссы числа как целочисленный интервал [Lmin, Lmах], нижняя и верхняя границы Lmin, Lmах которого представлены r-разрядными двоичными числами без знака и вычисляются следующим образом:
Lmin=[log2(М')⋅2r-h-1],
Lmах=Lmin+1
где  ,
, 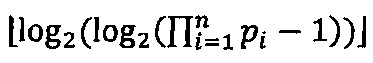 - наибольшее целое, не превышающее
- наибольшее целое, не превышающее  , [log2(М')⋅2r-h-1] - наибольшее целое, не превышающее log2(М')⋅2r-h-1.
, [log2(М')⋅2r-h-1] - наибольшее целое, не превышающее log2(М')⋅2r-h-1.
Диапазон представления нижней и верхней границ Lmin, Lmах интервальной логарифмической характеристики:
 ;
;  ,
,
где  - значение нижней границы интервальной логарифмической характеристики диапазона представления модулярных мантисс
- значение нижней границы интервальной логарифмической характеристики диапазона представления модулярных мантисс  ,
,  - наибольшее целое, не превышающее
- наибольшее целое, не превышающее 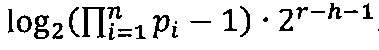 .
.
Таким образом, число с плавающей точкой вида (1) можно преобразовать к следующему модулярно-логарифмическому формату:

где 〈m1, m2, …, mn〉 - набор знакопозиций (модулярных разрядов) модулярной мантиссы 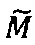 , λ- позиционный перемещенный порядок, представляющий собой целое двоичное число со знаком, Lmin, Lmax - границы интервальной логарифмической характеристики мантиссы числа, представляющие собой целые двоичные числа без знака, σ - знак числа, причем если σ=-1, то число отрицательное, σ=1 - положительное, σ=0 - машинный ноль.
, λ- позиционный перемещенный порядок, представляющий собой целое двоичное число со знаком, Lmin, Lmax - границы интервальной логарифмической характеристики мантиссы числа, представляющие собой целые двоичные числа без знака, σ - знак числа, причем если σ=-1, то число отрицательное, σ=1 - положительное, σ=0 - машинный ноль.
Диапазон допустимых значений модулярных мантисс 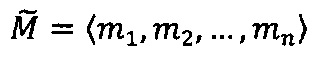 в системе остаточных классов с основаниями p1, p2, … , рn определяется интервалом
в системе остаточных классов с основаниями p1, p2, … , рn определяется интервалом 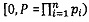 ; таким образом, t-разрядная позиционная мантисса М=dtdt-1…d2d1 может быть представлена в системе остаточных классов набором из n взаимно независимых q-разрядных знакопозиций 〈m1, m2, …, mn〉, причем q≈t/n (при условии, что все основания р1, p2, …, pn q-разрядные).
; таким образом, t-разрядная позиционная мантисса М=dtdt-1…d2d1 может быть представлена в системе остаточных классов набором из n взаимно независимых q-разрядных знакопозиций 〈m1, m2, …, mn〉, причем q≈t/n (при условии, что все основания р1, p2, …, pn q-разрядные).
Примеры преобразования позиционных чисел с плавающей точкой в модулярно-логарифмический формат: пусть числа представлены в 10-разрядном двоичном формате вида (1), в котором под смещенный порядок Е, отводится четыре бита (максимальный порядок еmax=24-1-1=7, соответственно е=Е-7), под дробную часть мантиссы - пять бит (т.е. t=6, причем целая часть d6 рациональной мантиссы М в явном виде не записана) и под знак числа - один бит.Пусть для представления модулярных мантисс в модулярно-логарифмическом формате [〈m1, m2, …, mn〉, λ, Lmin, Lmax, σ] используется три основания: р1=11, р2=13, р3=15. Диапазон представления чисел Р=11⋅13⋅15=2145. Разрядность оснований q=4, разрядность интервальной логарифмической характеристики r=5.
Пример 1: необходимо перевести число X=3.312510=[1.65625, 1, 0]=-10⋅1.65625⋅21, представленное в двоичном формате [М, е, S], в модулярно-логарифмический формат [〈m1, m2, …, mn〉, Lmin, Lmax, λ, σ].
С учетом принятых характеристик двоичного формата [М, е, S], число X будет записано в памяти ЭВМ в виде двоичного вектора 〈0100010101〉. Для его преобразования в модулярно-логарифмический формат (2) необходимо выполнить следующие действия:
1. Выделить составные части числа X: знак числа S=0, дробная часть рациональной мантиссы d5…d2d1=101012, смещенный (избыточный) порядок Е=10002=8.
2. Восстановить целую часть d6 мантиссы М=d6d5…d2d1:d6=1, т.к. Е>0, следовательно, М=1.101012.
3. Определить порядок е: е=Е-еmax=8-7=1, т.к. Е>0.
4. Определить знак σ, перемещенный позиционный порядок λ и целочисленную мантиссу М': σ=1, λ=е-t+1=1-6+1=-4, М'=d6d5…d2d1=1101012=53.
5. Найти модулярную мантиссу  :
:  .
.
6. Вычислить интервально-логарифмическую характеристику мантиссы Lmin, Lmах: Lmin=[log2(53)⋅25-3-1]=11, Lmax=11+1=12.
В результате получается число X, представленное в модулярно-логарифмическом формате с плавающей точкой: X=[〈9, 1, 8〉, 11, 12, -4, 1].
Пример 2: необходимо перевести число X=0.0278320312510=[1.78125, -5, 1]=-11⋅1.78125⋅2-5 из двоичного формата [М, е, S] в модулярно-логарифмический формат [〈m1, m2, …, mn〉, Lmin, Lmax, λ, σ].
С учетом принятых характеристик двоичного формата [М, е, S], число X будет записано в памяти ЭВМ в виде двоичного вектора 〈1000111001〉. Для его преобразования в модулярно-логарифмический формат (2) необходимо выполнить следующие действия:
1. Выделить составные части числа X: знак числа S=1, дробная часть d5…d2d1=110002, смещенный порядок Е=00012=1.
2. Восстановить целую часть d6 мантиссы М=d6d5…d2d1:d6=1, т.к. Е>0, следовательно, М=1.110012.
3. Определить порядок е. е=еmin=1-7=-6, т.к. Е=0.
4. Определить знак σ, перемещенный порядок λ и целочисленную мантиссу М': σ=-1, λ=e-t+l=-6-6+1=-11, М'=d6d5…d2d1=1110012=57.
5. Найти модулярную мантиссу  :
: 
6. Вычислить интервально-логарифмическую характеристику мантиссы Lmin, Lmax: Lmin=log2(57)⋅25-3-1]=11, Lmax=11+1=12.
В результате получается число X, представленное в модулярно-логарифмическом формате с плавающей точкой: X=[〈2, 5, 12〉, 11, 12, -11, -1].
Алгоритм 1. Вычисление ранга числа, представленного в модулярно-логарифмическом формате.
Пусть  - число, представленное в модулярно-логарифмическом формате с плавающей точкой, где
- число, представленное в модулярно-логарифмическом формате с плавающей точкой, где 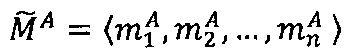 - модулярная мантисса числа А. Для того чтобы найти ранг R модулярной мантиссы
- модулярная мантисса числа А. Для того чтобы найти ранг R модулярной мантиссы  , необходимо:
, необходимо:
1. Вычислить значение минимальной величины ранга Rmin модулярной мантиссы  :
: 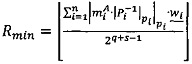 , где
, где  ,
, 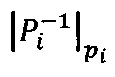 , мультипликативная инверсия Рi по модулю рi,
, мультипликативная инверсия Рi по модулю рi, 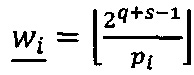 ,
,  - наибольшее целое, не превышающее
- наибольшее целое, не превышающее 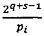 ,
,  - наибольшее целое, не превышающее
- наибольшее целое, не превышающее  , s - разрядность
, s - разрядность  , при условии, что 2q-1<рi<2q, s>1+log2n.
, при условии, что 2q-1<рi<2q, s>1+log2n.
2. Вычислить значение максимальной величины ранга Rmax модулярной мантиссы 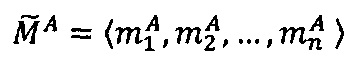 :
: 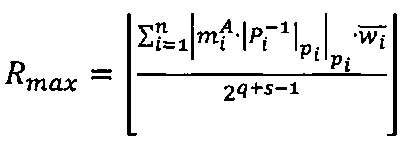 где
где  ,
,  - мультипликативная инверсия Рi по модулю рi,
- мультипликативная инверсия Рi по модулю рi,  ,
, 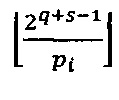 - наибольшее целое, не превышающее
- наибольшее целое, не превышающее  ,
, 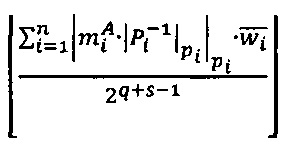 - наибольшее целое, не превышающее
- наибольшее целое, не превышающее 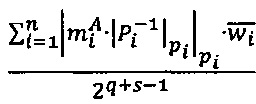 , s - разрядность
, s - разрядность  , при условии, что 2q-1<рi<2q, s>1+log2n.
, при условии, что 2q-1<рi<2q, s>1+log2n.
3. Если Rmin=Rmax, то R=Rmin, иначе выполнить сравнение: если  , то есть значение мантиссы меньше половины максимально возможного значения, то R=Rmax, если
, то есть значение мантиссы меньше половины максимально возможного значения, то R=Rmax, если  , то есть значение мантиссы больше или равно половине максимально возможного значения, то R=Rmin, где LР/2=LР-2r-h-1,
, то есть значение мантиссы больше или равно половине максимально возможного значения, то R=Rmin, где LР/2=LР-2r-h-1, 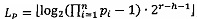 ,
, 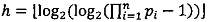 , r - разрядность интервальной логарифмической характеристики числа
, r - разрядность интервальной логарифмической характеристики числа  .
.
Пример: необходимо вычислить ранги чисел A=53 и B=57. Используется три основания: р1=11, р2=13, р3=15. Р=р1⋅р2⋅р3=2145 - произведение оснований (верхний предел допустимого диапазона представления модулярных мантисс). 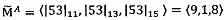 ,
,  ,
,  ,
,  ,
,  ,
,  . Разрядность оснований q=4. Разрядность коэффициентов wi:s=5.
. Разрядность оснований q=4. Разрядность коэффициентов wi:s=5.
Значения верхних и нижних границ  ,
, 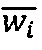 коэффициентов для значений модулей р1=11, р2=13, р3=15 равны соответственно
коэффициентов для значений модулей р1=11, р2=13, р3=15 равны соответственно 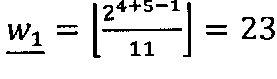 ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Значения мультипликативных инверсий  для модулей р1=11, р2=13, р3=15 равны соответственно
для модулей р1=11, р2=13, р3=15 равны соответственно 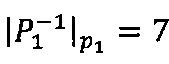 ,
,  ,
, 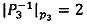 .
.
Вычислим значение ранга первого числа.
1. Вычислим значение минимальной величины ранга Rmin модулярной мантиссы:

2. Вычислим значение максимальной величины ранга Rmax модулярной мантиссы:

3. Так как Rmin=Rmax, то RA=Rmin=1. Вычислим значение ранга второго числа.
Вычислим значение ранга второго числа.
1. Вычислим значение минимальной величины ранга Rmin модулярной мантиссы:
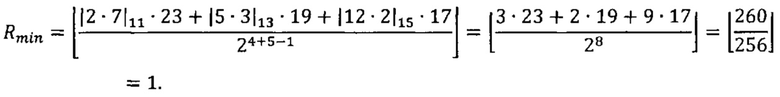
2. Вычислим значение максимальной величины ранга Rmax модулярной мантиссы:

3. Так как Rmin=Rmax, то RB=Rmin=1.
Алгоритм 2. Деление модулярной мантиссы числа, представленного в модулярно-логарифмическом формате, на число 2x (масштабирование степенью двойки).
Пусть 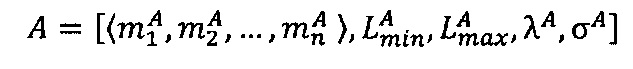 - число, представленное в модулярно-логарифмическом формате с плавающей точкой, где
- число, представленное в модулярно-логарифмическом формате с плавающей точкой, где 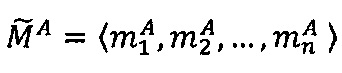 - модулярная мантисса числа А. Для того чтобы найти результат деления модулярного числа
- модулярная мантисса числа А. Для того чтобы найти результат деления модулярного числа  на позиционное число 2x, необходимо:
на позиционное число 2x, необходимо:
1. Вычислить α. Если x>q-1, то вычислить значение 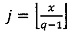 , где
, где 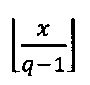 - наименьшее целое, не превышающее
- наименьшее целое, не превышающее  , α=|х|q-1; если x≤q-1, то α=х.
, α=|х|q-1; если x≤q-1, то α=х.
2. Вычислить значение ранга R для модулярного числа в соответствии с алгоритмом 1.
3. Вычислить остаток от деления модулярного числа на рn+1=2q-1:

где  ,
, 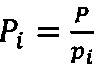 ,
, 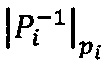 - мультипликативная инверсия Рi по модулю рi.
- мультипликативная инверсия Рi по модулю рi.
Если 0<α<q-1, то 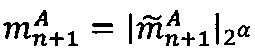 , если α=0, то уменьшить j на 1.
, если α=0, то уменьшить j на 1.
4. Вычислить значение 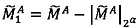 , для чего вычесть из каждого значения знакопозиций модулярного числа
, для чего вычесть из каждого значения знакопозиций модулярного числа  значение остатка от деления
значение остатка от деления  на 2α
на 2α 
 .
.
5. Вычислить значение  , для чего умножить каждое значение знакопозиций модулярного числа
, для чего умножить каждое значение знакопозиций модулярного числа  на мультипликативные инверсии 2α по соответствующим модулям.
на мультипликативные инверсии 2α по соответствующим модулям.
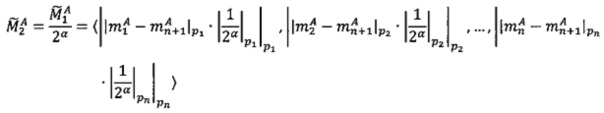 ,
,
где  - мультипликативная инверсия числа 2α по модулю рi - результат сравнения
- мультипликативная инверсия числа 2α по модулю рi - результат сравнения 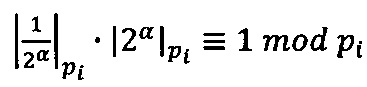 .
.
6. Если  , то прибавить к
, то прибавить к  величину
величину  .
.
7. Шаги 2-6 выполнить j раз для α=q-1.
Пример. Необходимо разделить числа А=53 и В=57 на число 21. Используется три основания: р1=11, р2=13, р3=15. Р=р1⋅р2⋅р3=2145 - произведение оснований (верхний предел допустимого диапазона представления модулярных мантисс),  ,
, 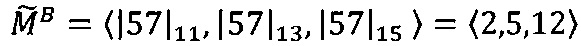 . Разрядность оснований q=4.
. Разрядность оснований q=4.
Значения мультипликативных инверсий  для модулей р1=11, р2=13, р3=15 равны соответственно
для модулей р1=11, р2=13, р3=15 равны соответственно 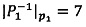 ,
,  ,
,  .
.
Значения мультипликативных инверсий  по модулям р1=11, р2=13, р3=15 и для значений α=1, 2, 3 равны соответственно
по модулям р1=11, р2=13, р3=15 и для значений α=1, 2, 3 равны соответственно 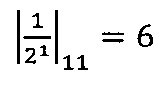 ;
; 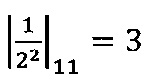 ;
; 

 ;
;  ;
;  ;
; 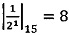 ;
; 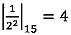 ;
;  .
.
Значения остатков от деления  и
и  на 2α для значений модулей р1=11, р2=13, р3=15 и для значений α=1, 2, 3 равны соответственно
на 2α для значений модулей р1=11, р2=13, р3=15 и для значений α=1, 2, 3 равны соответственно
 ;
;  ;
;  ;
;
 ;
;  ;
;  ;
;
 ;
;  ;
; 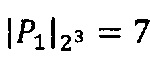 ;
;
 ;
;  ;
;  ;
;
Вычисляем значение  .
.
1. α=x=1, так как x=1<q=4-1.
2. Вычисляем ранг числа A=53 соответствии с алгоритмом 1. RA=1.
3. Вычисляем остаток от деления модулярного числа на 24-1=8:
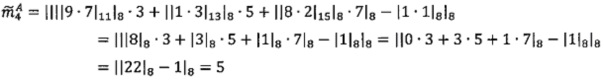 .
.
Вычисляем остаток от деления модулярного числа на р4=21 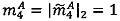 .
.
4. Вычитаем из модулярного числа  модулярное значение остатка от деления на 2
модулярное значение остатка от деления на 2 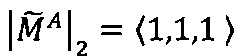 :
:

5. Умножаем на мультипликативные инверсии двойки по соответствующим модулям:

6. Прибавляем к величину 1=(1, 1, 1), так как
величину 1=(1, 1, 1), так как  :
:

Вычисляем значение 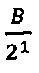
1. α=х=1, так как х=1<q=4-1.
2. Вычисляем ранг числа В=57 соответствии с алгоритмом 1. RB=1.
3. Вычисляем остаток от деления модулярного числа на 24-1=8:

Вычисляем остаток от деления модулярного числа на р4=21 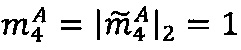
4. Вычитаем из модулярного числа  модулярное значение остатка от деления на 2
модулярное значение остатка от деления на 2  :
:
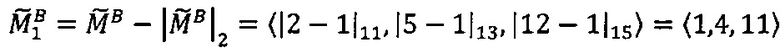
5. Умножаем на мультипликативные инверсии двойки по соответствующим модулям:
 .
.
6. Прибавляем к  величину 1=(1, 1, 1), так как
величину 1=(1, 1, 1), так как  :
:

Алгоритм 3. Выполнение операции умножения с плавающей точкой в модулярно-логарифмическом формате. Для того чтобы найти произведение  чисел
чисел 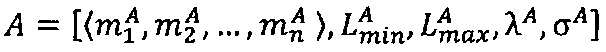 и
и  , представленных в модулярно-логарифмическом формате с плавающей точкой, необходимо:
, представленных в модулярно-логарифмическом формате с плавающей точкой, необходимо:
1. Проверить результат на равенство 0. Если σС=σА⋅σВ=0, что означает равенство нулю одного из операндов или обоих операндов сразу, то
 .
.
Если оба операнда ненулевые, то перейти к следующему шагу.
2. Присвоить знак произведению σС=σА⋅σВ. Определить верхнюю и нижнюю границы интервальной логарифмической характеристики результата  ,
,  . Определить порядок результата λС=λА+λВ.
. Определить порядок результата λС=λА+λВ.
3. Проверить выход результата за границы диапазона представления чисел. Если  , то
, то
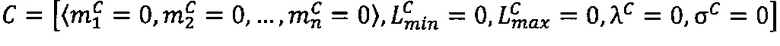 . Если
. Если  ,то
,то . Если
. Если  и
и  , то перейти к следующему шагу.
, то перейти к следующему шагу.
4. Проверить выход мантиссы результата за границы диапазона представления модулярных мантисс и выполнить умножение модулярных мантисс.
4.1. Если 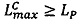 , то выполнить коррекцию операндов следующим образом:
, то выполнить коррекцию операндов следующим образом:
4.1.1. Вычислить значения поправочных коэффициентов L1 и L2:  ,
, 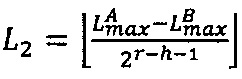 , где
, где 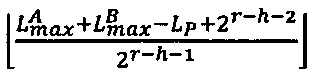 - наибольшее целое, не превышающее
- наибольшее целое, не превышающее  ,
, 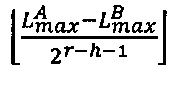 - наибольшее целое, не превышающее
- наибольшее целое, не превышающее 
Если |L1|≤|L2| и L2≥0, то zА=L1, zВ=0.
Если |L1|≤|L2| и L2<0, то zА=0, zВ=L1.
Если |L1|>|L2|и |L1+L2|2=1, то  ,
,  .
.
Если |L1|>|L2|и |L1+L2|2=0, то. ,
,  .
.
4.1.2. Вычислить значения скорректированных мантисс и
и 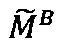 операндов и скорректировать значение верхней и нижней границы интервальной логарифмической характеристики результата.
операндов и скорректировать значение верхней и нижней границы интервальной логарифмической характеристики результата.
Если  и
и  I, то
I, то  ,
,  .
.
Если 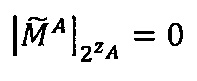 и
и  , то
, то 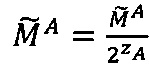 ,
,  , если
, если  , то
, то  .
.
Если  и
и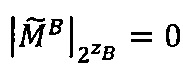 , то
, то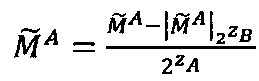 ,
, 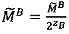 , если
, если 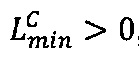 , то
, то  .
.
Если 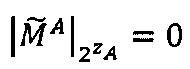 и
и  , то
, то 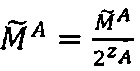 ,
,  если
если  , то
, то  .
.
Если  и
и  , то
, то  ,
, 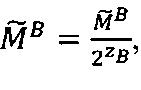 если
если  , то
, то  .
.
Если  и
и  , то
, то  ,
,  , если
, если  , то
, то  , иначе
, иначе  .
.
Если 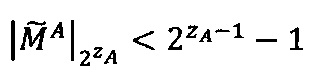 и
и  , то
, то 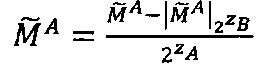 ,
,  , если
, если 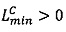 то
то  если
если  , то
, то  .
.
Если  и
и  , то
, то  ,
,  , если
, если 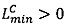 , то
, то  , если
, если  , то
, то 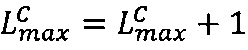 .
.
Если  и
и  , то
, то  ,
, 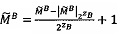 , если
, если 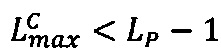 , то
, то  , иначе
, иначе  .
.
4.1.3. Скорректировать значение порядка результата λC=λC+L1.
4.1.4. Скорректировать значение верхней и нижней границы интервальной логарифмической характеристики результата если  , то
, то 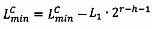 , иначе
, иначе  ;
; 
4.2. Выполнить умножение модулярных мантисс 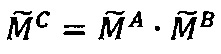 путем нахождения значений
путем нахождения значений  , где
, где  - наибольшее целое, не превышающее
- наибольшее целое, не превышающее 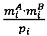
4.3. Если 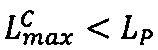 и
и  , то выполнить коррекцию результата следующим образом.
, то выполнить коррекцию результата следующим образом.
4.3.1. Вычислить значение поправочного коэффициента  .
.
4.3.2. Вычислить значение скорректированной мантиссы 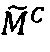 результата:
результата: 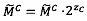 .
.
4.3.3. Вычислить значение порядка результата λC=λC-zC.
4.3.4. Выполнить коррекцию значений верхней и нижней границы интервальной логарифмической характеристики результата  ,
, 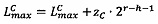 .
.
4.4. Если 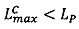 и
и  , то выполнить коррекцию результата следующим образом:
, то выполнить коррекцию результата следующим образом:
4.4.1. Вычислить значение поправочного коэффициента  .
.
4.4.2. Вычислить значение скорректированной мантиссы  результата и скорректировать значение верхней и нижней границы интервальной логарифмической характеристики результата.
результата и скорректировать значение верхней и нижней границы интервальной логарифмической характеристики результата.
Если 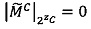 , то
, то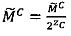 .
.
Если 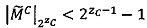 , то
, то  , если
, если  , то
, то  .
.
Если  то
то  если
если  , то
, то 
 .
.
4.4.3. Вычислить значение порядка результата λС=λС+zС.
4.4.4. Выполнить коррекцию значений верхней и нижней границы интервальной логарифмической характеристики результата  ;
;  .
.
В результате выполнения данных операций получается произведение 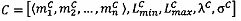 чисел
чисел 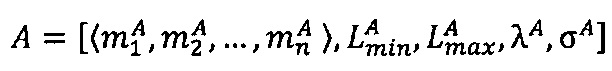 и
и 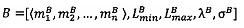 , представленное в модулярно-логарифмическом формате с плавающей точкой.
, представленное в модулярно-логарифмическом формате с плавающей точкой.
Пусть 
 - числа, представленные в модулярно-логарифмическом формате с плавающей точкой, где
- числа, представленные в модулярно-логарифмическом формате с плавающей точкой, где 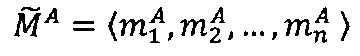 и
и 
 - модулярные мантиссы чисел А и В соответственно. Тогда способ умножения С=А⋅В чисел А и В, представленных в модулярно-логарифмическом формате с плавающей точкой (2), на гибридном многоядерном процессоре, содержащем n q-разрядных модулярных вычислительных ядер, одно k-разрядное и два r-разрядных универсальных целочисленных ядра, два специализированных s-разрядных векторных ядра, одно специализированное q-разрядное векторное ядро, одно специализированное управляющее ядро, определяется следующим образом.
- модулярные мантиссы чисел А и В соответственно. Тогда способ умножения С=А⋅В чисел А и В, представленных в модулярно-логарифмическом формате с плавающей точкой (2), на гибридном многоядерном процессоре, содержащем n q-разрядных модулярных вычислительных ядер, одно k-разрядное и два r-разрядных универсальных целочисленных ядра, два специализированных s-разрядных векторных ядра, одно специализированное q-разрядное векторное ядро, одно специализированное управляющее ядро, определяется следующим образом.
1. Множитель 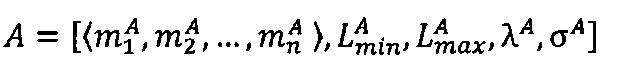 и множимое
и множимое 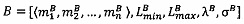 , представленные в модулярно-логарифмическом формате с плавающей точкой, загружают в гибридный многоядерный процессор, содержащий n q-разрядных модулярных вычислительных ядер, одно k-разрядное и два r-разрядных универсальных целочисленных ядра, два специализированных s-разрядных векторных ядра, одно специализированное q-разрядное векторное ядро, одно специализированное управляющее ядро, следующим образом:
, представленные в модулярно-логарифмическом формате с плавающей точкой, загружают в гибридный многоядерный процессор, содержащий n q-разрядных модулярных вычислительных ядер, одно k-разрядное и два r-разрядных универсальных целочисленных ядра, два специализированных s-разрядных векторных ядра, одно специализированное q-разрядное векторное ядро, одно специализированное управляющее ядро, следующим образом:
- в первое модулярное ядро гибридного многоядерного процессора загружают разрядные двоичные представления первых знакопозиций  и
и  модулярных мантисс
модулярных мантисс  и
и  чисел А и В соответственно, а также основание системы остаточных классов р1 и значение мультипликативной инверсии Р1 по модулю р1
чисел А и В соответственно, а также основание системы остаточных классов р1 и значение мультипликативной инверсии Р1 по модулю р1  ;
;
- параллельно с этим во второе модулярное ядро гибридного многоядерного процессора загружают q-разрядные двоичные представления вторых знакопозиций  и
и  модулярных мантисс
модулярных мантисс  и
и  чисел А и В соответственно, а также основание системы остаточных классов р2 и значение мультипликативной инверсии Р2 по модулю р2
чисел А и В соответственно, а также основание системы остаточных классов р2 и значение мультипликативной инверсии Р2 по модулю р2 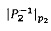 ;
;
- и т.д.;
- параллельно с этим в n-ое модулярное ядро гибридного многоядерного процессора загружают q-разрядные двоичные представления n-ых знакопозиций 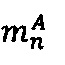 и
и  модулярных мантисс
модулярных мантисс  и
и  чисел А и В соответственно, а также основание системы остаточных классов рn и значение мультипликативной инверсии Рn по модулю рn
чисел А и В соответственно, а также основание системы остаточных классов рn и значение мультипликативной инверсии Рn по модулю рn  ;
;
- параллельно с этим в первое универсальное вычислительное ядро загружают k-разрядные двоичные порядки λА и λВ, а также знаки σА и σВ чисел А и В соответственно;
- параллельно с этим во второе универсальное вычислительное ядро загружают r-разрядные значения нижних границ интервальных логарифмических характеристик 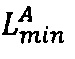 и
и  чисел А и В соответственно;
чисел А и В соответственно;
- параллельно с этим в третье универсальное вычислительное ядро загружают r-разрядные значения верхних границ интервальных логарифмических характеристик  и
и 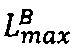 чисел А я В соответственно, а также r-разрядное значение нижней границы интервальной логарифмической характеристики диапазона представления модулярных мантисс Lр;
чисел А я В соответственно, а также r-разрядное значение нижней границы интервальной логарифмической характеристики диапазона представления модулярных мантисс Lр;
- параллельно с этим в первое векторное вычислительное ядро загружают вектор s-разрядных констант коэффициентов  ;
;
- параллельно с этим во второе векторное вычислительное ядро загружают вектор s-разрядных констант коэффициентов  ;
;
- параллельно с этим в третье векторное вычислительное ядро загружают вектор разрядных констант остатков от деления  ;
;
- параллельно с этим в управляющее ядро загружают k-разрядные двоичные порядки λА и λВ, r-разрядные значения нижних границ интервальных логарифмических характеристик 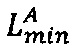 и
и  и r-разрядные значения верхних границ интервальных логарифмических характеристик
и r-разрядные значения верхних границ интервальных логарифмических характеристик  и
и 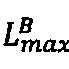 чисел А и В соответственно, а также r-разрядное значение нижней границы интервальной логарифмической характеристики диапазона представления модулярных мантисс Lр.
чисел А и В соответственно, а также r-разрядное значение нижней границы интервальной логарифмической характеристики диапазона представления модулярных мантисс Lр.
2. После того, как множитель  и множимое
и множимое  представленные в модулярно-логарифмическом формате с плавающей точкой, загружены в гибридный процессор, содержащий n q-разрядных модулярных вычислительных ядер, одно k-разрядное и два r-разрядных универсальных целочисленных ядра, два специализированных s-разрядных векторных ядра, одно специализированное q-разрядное векторное ядро, одно специализированное управляющее ядро, операция их умножения выполняется следующим образом:
представленные в модулярно-логарифмическом формате с плавающей точкой, загружены в гибридный процессор, содержащий n q-разрядных модулярных вычислительных ядер, одно k-разрядное и два r-разрядных универсальных целочисленных ядра, два специализированных s-разрядных векторных ядра, одно специализированное q-разрядное векторное ядро, одно специализированное управляющее ядро, операция их умножения выполняется следующим образом:
- в первом модулярном вычислительном ядре процессора выполняется операция целочисленного умножения  по модулю р1 q-разрядных двоичных представлений знакопозиций
по модулю р1 q-разрядных двоичных представлений знакопозиций  и
и  модулярных мантисс
модулярных мантисс  и
и 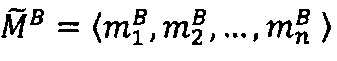 чисел А и В соответственно, путем нахождения значения
чисел А и В соответственно, путем нахождения значения  , где
, где  - наибольшее целое, не превышающее
- наибольшее целое, не превышающее  ; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
-параллельно с этим во втором модулярном вычислительном ядре процессора выполняется операция целочисленного умножения  по модулю р2 q-разрядных двоичных представлений знакопозиций
по модулю р2 q-разрядных двоичных представлений знакопозиций  и
и  модулярных мантисс
модулярных мантисс 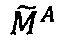 и
и  чисел А и В соответственно; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
чисел А и В соответственно; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
- и т.д.
- параллельно с этим в -ом модулярном вычислительном ядре процессора выполняется операция целочисленного умножения  по модулю рn q-разрядных двоичных представлений знакопозиций
по модулю рn q-разрядных двоичных представлений знакопозиций  и
и 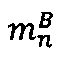 модулярных мантисс
модулярных мантисс 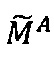 и
и  чисел А и В соответственно; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
чисел А и В соответственно; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
- параллельно с этим в первом универсальном вычислительном ядре процессора выполняется сложение λC=λА+λВ двоичных порядков λА и λВ, а также умножение σС=σА⋅σВ знаков σА и σВ чисел А и В соответственно;
- параллельно с этим во втором универсальном вычислительном ядре процессора выполняется сложение 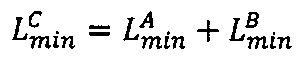 двоичных значений нижних границ интервальных логарифмических характеристик
двоичных значений нижних границ интервальных логарифмических характеристик 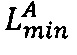 и
и 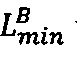 чисел А и В соответственно;
чисел А и В соответственно;
- параллельно с этим в третьем универсальном вычислительном ядре процессора выполняется сложение  двоичных значений верхних границ интервальных логарифмических характеристик
двоичных значений верхних границ интервальных логарифмических характеристик 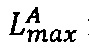 и
и  чисел А и В соответственно;
чисел А и В соответственно;
- параллельно с этим в управляющем ядре вычисляются следующие значения поправочных коэффициентов:  ,
,  ,
,  ,
, 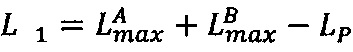 ,
,  , zА=L1+1, zВ=0, если |L1|≤|L2| и L2≥0, zА=0, zВ=L1+1, если |L1|≤|L2| и L2<0,
, zА=L1+1, zВ=0, если |L1|≤|L2| и L2≥0, zА=0, zВ=L1+1, если |L1|≤|L2| и L2<0,  ,
,  , если |L1|>|L2| и |L1+L2|2=1,
, если |L1|>|L2| и |L1+L2|2=1, 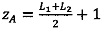 ,
, 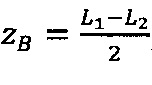 , если |L1|>|L2| и |L1+L2|2=0.
, если |L1|>|L2| и |L1+L2|2=0.
3. После того, как получено промежуточное значение произведения  чисел
чисел  и
и  , выполняется коррекция результата следующим образом:
, выполняется коррекция результата следующим образом:
3.1. Если знак  промежуточного результата
промежуточного результата произведения чисел А и Вне равен 0, и порядок
произведения чисел А и Вне равен 0, и порядок  промежуточного результата
промежуточного результата  произведения чисел А и В принадлежит интервалу [2-2k-1; 2k-1-2], и значение
произведения чисел А и В принадлежит интервалу [2-2k-1; 2k-1-2], и значение 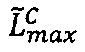 верхней границы интервальной логарифмической характеристики промежуточного результата
верхней границы интервальной логарифмической характеристики промежуточного результата 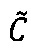 произведения чисел А и В меньше значения нижней границы интервальной логарифмической характеристики максимально возможного значения мантиссы, то есть
произведения чисел А и В меньше значения нижней границы интервальной логарифмической характеристики максимально возможного значения мантиссы, то есть  ,
, 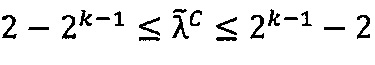 ,
,  , то коррекции результата не требуется.
, то коррекции результата не требуется.
3.2. Если знак  промежуточного результата
промежуточного результата  произведения чисел А и В равен 0, то есть
произведения чисел А и В равен 0, то есть , то:
, то:
- в первом универсальном вычислительном ядре процессора выполняется обнуление 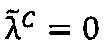 двоичного порядка
двоичного порядка  промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
- параллельно с этим во втором универсальном вычислительном ядре процессора выполняется обнуление 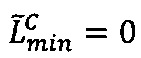 двоичного значения нижней границы интервальной логарифмической характеристики
двоичного значения нижней границы интервальной логарифмической характеристики  промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
- параллельно с этим в третьем универсальном вычислительном ядре процессора выполняется обнуление  двоичного значения верхней границы интервальной логарифмической характеристики
двоичного значения верхней границы интервальной логарифмической характеристики 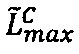 промежуточного результата
промежуточного результата  произведения чисел А и В.
произведения чисел А и В.
3.3. Если знак  промежуточного результата
промежуточного результата  произведения чисел А и В не равен 0 и значение
произведения чисел А и В не равен 0 и значение  , то есть модуль промежуточного результата
, то есть модуль промежуточного результата  произведения чисел А и В выходит за границы минимально возможного представления, то:
произведения чисел А и В выходит за границы минимально возможного представления, то:
- в первом универсальном вычислительном ядре процессора выполняется обнуление  двоичного порядка
двоичного порядка  и
и  знака
знака  промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
- параллельно с этим во втором универсальном вычислительном ядре процессора выполняется обнуление  двоичного значения нижней границы интервальной логарифмической характеристики
двоичного значения нижней границы интервальной логарифмической характеристики  промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
- параллельно с этим в третьем универсальном вычислительном ядре процессора выполняется обнуление  двоичного значения верхней границы интервальной логарифмической характеристики
двоичного значения верхней границы интервальной логарифмической характеристики  промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
- параллельно с этим в первом модулярном вычислительном ядре процессора выполняется обнуление 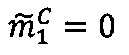 значения первой знакопозиций
значения первой знакопозиций 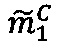 промежуточного
промежуточного  результата произведения чисел А и В;
результата произведения чисел А и В;
-параллельно с этим во втором модулярном вычислительном ядре процессора выполняется обнуление  значения второй знакопозиций
значения второй знакопозиций 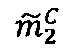 промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
- и т.д.
- параллельно с этим в n-ом модулярном вычислительном ядре процессора выполняется обнуление  значения n-ой знакопозиций
значения n-ой знакопозиций  промежуточного результата
промежуточного результата  произведения чисел А и В.
произведения чисел А и В.
3.4. Если знак  промежуточного результата
промежуточного результата  произведения чисел А и В не равен 0 и значение
произведения чисел А и В не равен 0 и значение  , то есть модуль промежуточного результата
, то есть модуль промежуточного результата 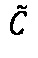 произведения чисел А и В выходит за границы максимального возможного представления, то:
произведения чисел А и В выходит за границы максимального возможного представления, то:
- в первом универсальном вычислительном ядре процессора выполняется присвоение 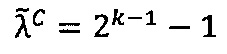 двоичному порядку
двоичному порядку  промежуточного результата
промежуточного результата 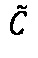 произведения числе А и В;
произведения числе А и В;
- параллельно с этим во втором универсальном вычислительном ядре процессора выполняется обнуление 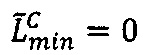 двоичного значения нижней границы интервальной логарифмической характеристики
двоичного значения нижней границы интервальной логарифмической характеристики  промежуточного результата
промежуточного результата 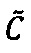 произведения чисел А и В;
произведения чисел А и В;
- параллельно с этим в третьем универсальном вычислительном ядре процессора выполняется обнуление  двоичного значения верхней границы интервальной логарифмической характеристики
двоичного значения верхней границы интервальной логарифмической характеристики  промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
- параллельно с этим в первом модулярном вычислительном ядре процессора выполняется обнуление 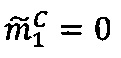 значения первой знакопозиции
значения первой знакопозиции  промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
- параллельно с этим во втором модулярном вычислительном ядре процессора выполняется обнуление  значения второй знакопозиции
значения второй знакопозиции  промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
- и т.д.
- параллеьно с этим в n-ом модулярном вычислительном ядре процессора выполняется обнуление 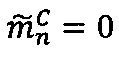 значения n-ой знакопозиции
значения n-ой знакопозиции  промежуточного результта
промежуточного результта  произведения чисел А и В.
произведения чисел А и В.
3.5. Знак 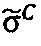 промежутоного результата
промежутоного результата  произведения чисел А и В не равен 0, и порядок
произведения чисел А и В не равен 0, и порядок 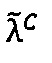 промежуточного результата
промежуточного результата 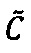 умножения чисел А и В принадлежит интервалу
умножения чисел А и В принадлежит интервалу  , где
, где  - наибольшее целое, не превышающее
- наибольшее целое, не превышающее  , и значение
, и значение  верхней границы интервальной логарифмической характеристики промежуточного результата
верхней границы интервальной логарифмической характеристики промежуточного результата  произведения чисел А и В меньше значения нижней границы интервальной логарифмической характеристики максимально возможного значения мантиссы
произведения чисел А и В меньше значения нижней границы интервальной логарифмической характеристики максимально возможного значения мантиссы  , то управляющее ядро передает во все модулярные и все универсальные целочисленные ядра значения поправочных коэффициентов:
, то управляющее ядро передает во все модулярные и все универсальные целочисленные ядра значения поправочных коэффициентов:  ,
, 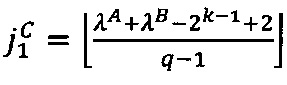 , где
, где  - наибольшее целое, не превышающее
- наибольшее целое, не превышающее  , после чего:
, после чего:
- в первом модулярном вычислительном ядре процессора выполняется операция целочисленного умножения  по модулю р1 q-разрядного двоичного представления знакопозиций
по модулю р1 q-разрядного двоичного представления знакопозиций  модулярной мантиссы
модулярной мантиссы 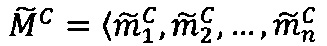 ) промежуточного результата
) промежуточного результата  произведения чисел А и В и значения
произведения чисел А и В и значения  следующим образом: выполняется операция целочисленного умножения
следующим образом: выполняется операция целочисленного умножения  по модулю р1 q-разрядного двоичного представления знакопозиций
по модулю р1 q-разрядного двоичного представления знакопозиций  модулярной мантиссы
модулярной мантиссы 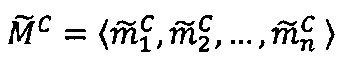 промежуточного результата
промежуточного результата  произведения чисел А и В и значения
произведения чисел А и В и значения  , полученного сдвигом числа 1 на
, полученного сдвигом числа 1 на 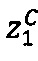 двоичных разрядов влево, путем нахождения значения
двоичных разрядов влево, путем нахождения значения 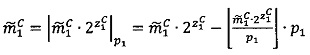 , где
, где  - наибольшее целое, не превышающее
- наибольшее целое, не превышающее  ; затем, если
; затем, если  , то
, то  раз выполняется операция целочисленного умножения
раз выполняется операция целочисленного умножения  по модулю р1 q-разрядного двоичного представления знакопозиций
по модулю р1 q-разрядного двоичного представления знакопозиций 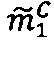 модулярной мантиссы
модулярной мантиссы  промежуточного результата
промежуточного результата  произведения чисел А и В и значения 2q-1, полученного сдвигом числа 1 на (q-1) двоичных разрядов влево, путем нахождения значения
произведения чисел А и В и значения 2q-1, полученного сдвигом числа 1 на (q-1) двоичных разрядов влево, путем нахождения значения  , где
, где  - наибольшее целое, не превышающее
- наибольшее целое, не превышающее  ; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
- параллельно с этим во втором модулярном вычислительном ядре процессора
выполняется операция целочисленного умножения  по модулю р2 q-разрядного двоичного представления знакопозиций
по модулю р2 q-разрядного двоичного представления знакопозиций  модулярной мантиссы
модулярной мантиссы промежуточного результата
промежуточного результата  произведения чисел А и В и значения
произведения чисел А и В и значения следующим образом: выполняется операция целочисленного умножения
следующим образом: выполняется операция целочисленного умножения  по модулю р2; затем, если
по модулю р2; затем, если  , то
, то  раз выполняется операция целочисленного умножения
раз выполняется операция целочисленного умножения 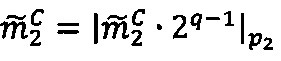 по модулю р2;
по модулю р2;
- и т.д.
- параллельно с этим в -ом модулярном вычислительном ядре процессора выполняется операция целочисленного умножения  по модулю рn q-разрядного двоичного представления знакопозиций
по модулю рn q-разрядного двоичного представления знакопозиций  модулярной мантиссы
модулярной мантиссы  промежуточного результата
промежуточного результата  произведения чисел А и В и значения
произведения чисел А и В и значения  следующим образом: выполняется операция целочисленного умножения
следующим образом: выполняется операция целочисленного умножения  по модулю рn; затем, если
по модулю рn; затем, если  , то
, то  раз выполняется операция целочисленного умножения
раз выполняется операция целочисленного умножения  по модулю рn;
по модулю рn;
- параллельно с этим в первом универсальном вычислительном ядре процессора выполняется коррекция 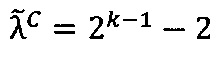 двоичного порядка
двоичного порядка  промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
- параллельно с этим во втором универсальном вычислительном ядре процессора выполняется коррекция 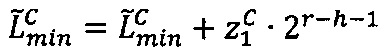 двоичного значения нижней границы интервальной логарифмической характеристики
двоичного значения нижней границы интервальной логарифмической характеристики  промежуточного результата
промежуточного результата 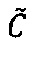 произведения чисел А и В;
произведения чисел А и В;
- параллельно с этим в третьем универсальном вычислительном ядре процессора выполняется коррекция двоичного значения верхней границы интервальной логарифмической характеристики
двоичного значения верхней границы интервальной логарифмической характеристики  промежуточного результата
промежуточного результата произведения чисел А и В.
произведения чисел А и В.
3.6. Если знак промежуточного результата
промежуточного результата произведения чисел А и В не равен 0, и порядок
произведения чисел А и В не равен 0, и порядок  промежуточного результата
промежуточного результата  произведения чисел А и В принадлежит интервалу
произведения чисел А и В принадлежит интервалу  , где
, где 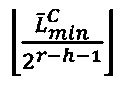 - наибольшее целое, не превышающее
- наибольшее целое, не превышающее 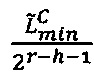 , и значение
, и значение  верхней границы интервальной логарифмической характеристики промежуточного результата
верхней границы интервальной логарифмической характеристики промежуточного результата 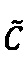 произведения чисел А и В меньше значения нижней границы интервальной логарифмической характеристики максимально возможного значения мантиссы
произведения чисел А и В меньше значения нижней границы интервальной логарифмической характеристики максимально возможного значения мантиссы 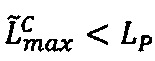 , то управляющее ядро передает во все модулярные и все универсальные целочисленные ядра значение поправочного коэффициента
, то управляющее ядро передает во все модулярные и все универсальные целочисленные ядра значение поправочного коэффициента 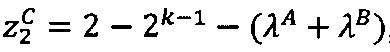 , после чего:
, после чего:
3.6.1. Выполняется загрузка мультипликативных инверсий 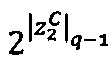 и 2q-1:
и 2q-1:
- в первое модулярное ядро загружают ^-разрядные двоичные значения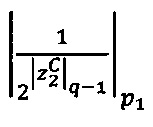 и
и 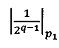 , мультипликативных инверсий
, мультипликативных инверсий 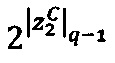 и 2q-1 по модулю р1;
и 2q-1 по модулю р1;
- параллельно с этим во второе модулярное ядро загружают q-разрядные двоичные значения  и
и  мультипликативных инверсий
мультипликативных инверсий  и 2q-1 по модулю р2;
и 2q-1 по модулю р2;
- и т.д.;
- параллельно с этим в n-ое модулярное ядро загружают q-разрядные двоичные значения 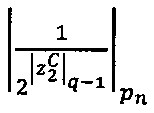 и
и  мультипликативных инверсий
мультипликативных инверсий  и 2q-1 по модулю рn;
и 2q-1 по модулю рn;
- параллельно с этим в первом универсальном вычислительном ядре процессора выполняется коррекция  двоичного порядка
двоичного порядка  промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
- параллельно с этим в управляющем ядре вычисляется количество итераций j: j=0, если  ,
,  , если
, если  , где
, где  - наибольшее целое, не превышающее
- наибольшее целое, не превышающее  .
.
3.6.2. Если  , то действия 3.6.3-3.6.7 выполняются один раз для
, то действия 3.6.3-3.6.7 выполняются один раз для  , затем если количество итераций j≥1, то действия 3.6.3-3.6.7 выполняются j раз для α=q-1.
, затем если количество итераций j≥1, то действия 3.6.3-3.6.7 выполняются j раз для α=q-1.
3.6.3. Вычисляются значения элементов вектора  :
:
- в первом модулярном вычислительном ядре процессора выполняется операция целочисленного умножения  по модулю р1 q-разрядного двоичного представления знакопозиций
по модулю р1 q-разрядного двоичного представления знакопозиций  модулярной мантиссы
модулярной мантиссы промежуточного результата
промежуточного результата произведения чисел А и В и значения мультипликативной инверсии Р1 по модулю р1
произведения чисел А и В и значения мультипликативной инверсии Р1 по модулю р1  , путем нахождения значения
, путем нахождения значения 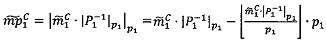 где
где 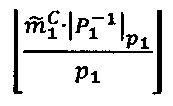 - наибольшее целое, не превышающее
- наибольшее целое, не превышающее  ; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
- параллельно с этим во втором модулярном вычислительном ядре процессора выполняется операция целочисленного умножения  по модулю р2 q-разрядного двоичного представления знакопозиций
по модулю р2 q-разрядного двоичного представления знакопозиций  модулярной мантиссы
модулярной мантиссы  промежуточного результата
промежуточного результата  произведения чисел А и В и значения мультипликативной инверсии Р2 по модулю р2
произведения чисел А и В и значения мультипликативной инверсии Р2 по модулю р2 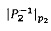 ;
;
- и т.д.
- параллельно с этим в -ом модулярном вычислительном ядре процессора выполняется операция целочисленного умножения по модулю рn q-разрядного двоичного представления знакопозиций
по модулю рn q-разрядного двоичного представления знакопозиций  модулярной мантиссы
модулярной мантиссы 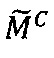 промежуточного результата
промежуточного результата  произведения чисел А и В и значения мультипликативной инверсии Рn по модулю рn
произведения чисел А и В и значения мультипликативной инверсии Рn по модулю рn  .
.
3.6.4. После того, как получены значения элементов вектора 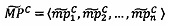 , данный вектор загружается в векторные ядра следующим образом:
, данный вектор загружается в векторные ядра следующим образом:
- в первое векторное вычислительное ядро загружают вектор q-разрядных элементов  , q≤s;
, q≤s;
- параллельно с этим во второе векторное вычислительное ядро загружают вектор q-разрядных элементов  , q≤s;
, q≤s;
- параллельно с этим в третье векторное вычислительное ядро загружают вектор q-разрядных элементов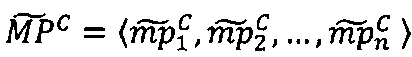 ;
;
3.6.5. После того, как элементы вектора  загружены в векторные ядра, производится вычисление ранга и частичного остатка от деления на 2q-1 модулярной мантиссы
загружены в векторные ядра, производится вычисление ранга и частичного остатка от деления на 2q-1 модулярной мантиссы  промежуточного результата
промежуточного результата  произведения чисел А я В:
произведения чисел А я В:
-в первом векторном вычислительном ядре вычисляют скалярное произведение векторов 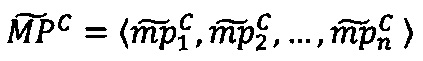 и
и  , вычисляют значение
, вычисляют значение  , где
, где  - наибольшее целое, не превышающее
- наибольшее целое, не превышающее 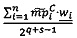 значение
значение 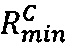 передается в управляющее ядро;
передается в управляющее ядро;
- параллельно с этим во втором векторном вычислительном ядре вычисляют скалярное произведение векторов  и
и 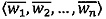 вычисляют значение
вычисляют значение  , где
, где  - наибольшее целое, не превышающее
- наибольшее целое, не превышающее 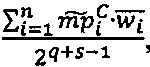 , значение
, значение  передается в управляющее ядро;
передается в управляющее ядро;
- параллельно с этим в третьем векторном вычислительном ядре вычисляют скалярное произведение векторов  и
и 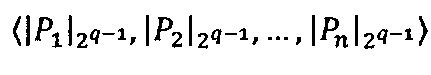 , значение
, значение  передается в управляющее ядро.
передается в управляющее ядро.
3.6.6. После того, как результаты скалярного произведения векторов переданы в управляющее ядро, в управляющем ядре вычисляется значение ранга 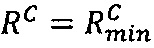 , если
, если  или
или 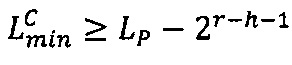 , R=Rmax, если
, R=Rmax, если  , и значение остатка от деления модулярной мантиссы
, и значение остатка от деления модулярной мантиссы  промежуточного результата
промежуточного результата  произведения чисел А и В
произведения чисел А и В 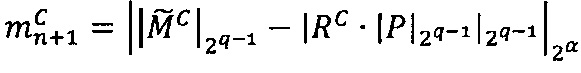 .
.
3.6.7. После того, как управляющее ядро передаст во все модулярные и все универсальные целочисленные ядра значения  и α, выполняется деление модулярной мантиссы
и α, выполняется деление модулярной мантиссы  промежуточного результата
промежуточного результата произведения чисел А и В на число 2α:
произведения чисел А и В на число 2α:
- в первом модулярном вычислительном ядре процессора выполняется операция вычитания  по модулю р1 q-разрядного двоичного представления знакопозиций
по модулю р1 q-разрядного двоичного представления знакопозиций 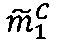 модулярной мантиссы
модулярной мантиссы  промежуточного результата
промежуточного результата  произведения чисел А и В и значения
произведения чисел А и В и значения  следующим образом: если
следующим образом: если  , то
, то  , если
, если , то
, то ; после чего выполняется операция умножения
; после чего выполняется операция умножения  по модулю р1 q-разрядного двоичного представления знакопозиций
по модулю р1 q-разрядного двоичного представления знакопозиций  модулярной мантиссы
модулярной мантиссы промежуточного результата
промежуточного результата произведения чисел А и В и значения мультипликативной инверсии 2α по модулю р1
произведения чисел А и В и значения мультипликативной инверсии 2α по модулю р1 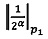 путем нахождения значения
путем нахождения значения  , где
, где  - наибольшее целое, не превышающее
- наибольшее целое, не превышающее  ; после чего если
; после чего если  выполняется операция сложения
выполняется операция сложения  по модулю р1 q-разрядного двоичного представления знакопозиций
по модулю р1 q-разрядного двоичного представления знакопозиций  модулярной мантиссы
модулярной мантиссы 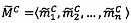 промежуточного результата
промежуточного результата 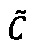 произведения чисел А и В следующим образом: если
произведения чисел А и В следующим образом: если  , то
, то  если
если 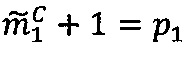 , то
, то ; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
- параллельно с этим во втором модулярном вычислительном ядре процессора выполняется операция вычитания 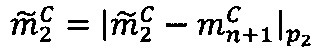 по модулю р2 q-разрядного двоичного представления знакопозиций
по модулю р2 q-разрядного двоичного представления знакопозиций  модулярной мантиссы
модулярной мантиссы 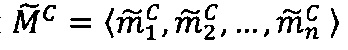 промежуточного результата
промежуточного результата произведения чисел А и В и значения
произведения чисел А и В и значения 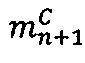 , после чего выполняется операция умножения
, после чего выполняется операция умножения 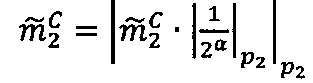 по модулю р2 q-разрядного двоичного представления знакопозиций
по модулю р2 q-разрядного двоичного представления знакопозиций  и значения мультипликативной инверсии 2α по модулю р2
и значения мультипликативной инверсии 2α по модулю р2  ; после чего если
; после чего если  выполняется операция сложения
выполняется операция сложения  по модулю р2;
по модулю р2;
- и т.д.
- параллельно с этим в -ом модулярном вычислительном ядре процессора выполняется операция вычитания 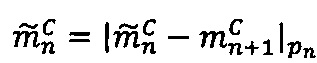 по модулю рn q-разрядного двоичного представления знакопозиций
по модулю рn q-разрядного двоичного представления знакопозиций  модулярной мантиссы
модулярной мантиссы 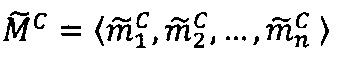 промежуточного результата
промежуточного результата  произведения чисел А и В и значения
произведения чисел А и В и значения  ; после чего выполняется операция умножения
; после чего выполняется операция умножения  по модулю рn q-разрядного двоичного представления знакопозиций
по модулю рn q-разрядного двоичного представления знакопозиций  и значения мультипликативной инверсии 2α по модулю рn
и значения мультипликативной инверсии 2α по модулю рn 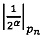 ; после чего если
; после чего если 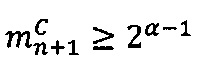 выполняется операция сложения
выполняется операция сложения 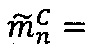
 по модулю р1n;
по модулю р1n;
- параллельно с этим во втором универсальном вычислительном ядре процессора выполняется коррекция 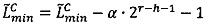 если
если  , иначе
, иначе  двоичного значения нижней границы интервальной логарифмической характеристики
двоичного значения нижней границы интервальной логарифмической характеристики  промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
- параллельно с этим в третьем универсальном вычислительном ядре процессора выполняется коррекция  , если
, если 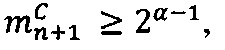 иначе
иначе  двоичного значения верхней границы интервальной логарифмической характеристики
двоичного значения верхней границы интервальной логарифмической характеристики  промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
3.7. Если знак  промежуточного результата
промежуточного результата  произведения чисел А и В не равен 0, и значение
произведения чисел А и В не равен 0, и значение  верхней границы интервальной логарифмической характеристики промежуточного результата
верхней границы интервальной логарифмической характеристики промежуточного результата  произведения чисел А и В больше или равно значению нижней границы интервальной логарифмической характеристики максимально возможного значения мантиссы
произведения чисел А и В больше или равно значению нижней границы интервальной логарифмической характеристики максимально возможного значения мантиссы 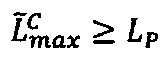 , то управляющее ядро передает во все модулярные и все универсальные целочисленные ядра значение поправочных коэффициентов zА, zВ, после чего:
, то управляющее ядро передает во все модулярные и все универсальные целочисленные ядра значение поправочных коэффициентов zА, zВ, после чего:
3.7.1. Выполняется загрузка мультипликативных инверсий  ,
, 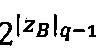 и 2q-1:
и 2q-1:
- в первое модулярное ядро загружают q-разрядные двоичные значения 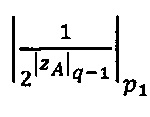 ,
,  и
и 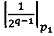 мультипликативных инверсий
мультипликативных инверсий  ,
, 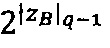 и 2q-1 по модулю р1;
и 2q-1 по модулю р1;
- параллельно с этим во второе модулярное ядро загружают q-разрядные двоичные значения  ,
,  и
и  мультипликативных инверсий
мультипликативных инверсий  ,
,  и 2q-1 по модулю р2;
и 2q-1 по модулю р2;
- и т.д.;
- параллельно с этим в и-ое модулярное ядро загружают q-разрядные двоичные значения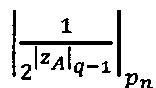 ,
,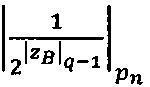 и
и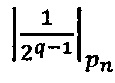 мультипликативных инверсий
мультипликативных инверсий 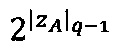 ,
,  и 2q-1 по модулю рn;
и 2q-1 по модулю рn;
- параллельно с этим в первом универсальном вычислительном ядре процессора выполняется коррекция  двоичного порядка
двоичного порядка 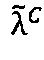 промежуточного результата
промежуточного результата 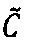 произведения чисел А и В;
произведения чисел А и В;
- параллельно с этим в управляющем ядре вычисляется количество итераций jА=0, если zА<q-1,  , если zА>q-1 и jВ=0, если zВ<q-1,
, если zА>q-1 и jВ=0, если zВ<q-1,  , если zВ>q-1.
, если zВ>q-1.
3.7.2. Если |ZA|q-1>0, то действия 3.7.3-3.7.7 выполняются один раз для  затем если количество итераций jА≥1, то действия 3.7.3-3.7.7 выполняются jА раз для α=q-1.
затем если количество итераций jА≥1, то действия 3.7.3-3.7.7 выполняются jА раз для α=q-1.
3.7.3. Вычисляются значения элементов вектора  :
:
- в первом модулярном вычислительном ядре процессора выполняется операция целочисленного умножения  по модулю р1 q-разрядного двоичного представления знакопозиций
по модулю р1 q-разрядного двоичного представления знакопозиций 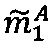 модулярной мантиссы
модулярной мантиссы  числа А и значения мультипликативной инверсии Р1 по модулю р1
числа А и значения мультипликативной инверсии Р1 по модулю р1  , путем нахождения значения
, путем нахождения значения  , где
, где  - наибольшее целое, не превышающее
- наибольшее целое, не превышающее ; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
- параллельно с этим во втором модулярном вычислительном ядре процессора выполняется операция целочисленного умножения 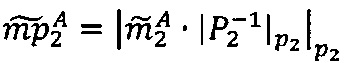 по модулю р2 q-разрядного двоичного представления знакопозиций
по модулю р2 q-разрядного двоичного представления знакопозиций  модулярной мантиссы
модулярной мантиссы  и значения мультипликативной инверсии Р2 по модулю р2
и значения мультипликативной инверсии Р2 по модулю р2  ;
;
- и т.д.
- параллельно с этим в -ом модулярном вычислительном ядре процессора выполняется операция целочисленного умножения  по модулю рn q-разрядного двоичного представления знакопозиций
по модулю рn q-разрядного двоичного представления знакопозиций  модулярной мантиссы
модулярной мантиссы 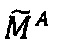 и значения мультипликативной инверсии Рn по модулю рn
и значения мультипликативной инверсии Рn по модулю рn  ;
;
3.7.4. После того, как получены значения элементов вектора  , данный вектор загружается в векторные ядра следующим образом:
, данный вектор загружается в векторные ядра следующим образом:
- в первое векторное вычислительное ядро загружают вектор q-разрядных элементов  , q≤s;
, q≤s;
- параллельно с этим во второе векторное вычислительное ядро загружают вектор q-разрядных элементов  , q≤s;
, q≤s;
- параллельно с этим в третье векторное вычислительное ядро загружают вектор q-разрядных элементов 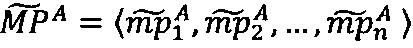 .
.
3.7.5. После того, как элементы вектора  загружены в векторные ядра, производится вычисление ранга и частичного остатка от деления на 2q-1 модулярной мантиссы
загружены в векторные ядра, производится вычисление ранга и частичного остатка от деления на 2q-1 модулярной мантиссы 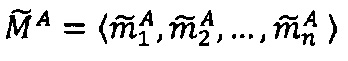 числа А следующим образом:
числа А следующим образом:
- в первом векторном вычислительном ядре вычисляют скалярное произведение векторов  и
и 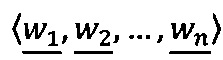 , вычисляют значение
, вычисляют значение  , где
, где  - наибольшее целое, на превышающее
- наибольшее целое, на превышающее 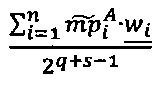 , значение
, значение 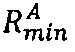 передается в управляющее ядро;
передается в управляющее ядро;
- параллельно с этим во втором векторном вычислительном ядре вычисляют скалярное произведение векторов  и
и  , вычисляют значение
, вычисляют значение  , где
, где 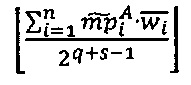 - наибольшее целое, не превышающее
- наибольшее целое, не превышающее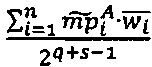 , значение
, значение  передается в управляющее ядро;
передается в управляющее ядро;
- параллельно с этим в третьем векторном вычислительном ядре вычисляют скалярное произведение векторов  и
и  , значение
, значение 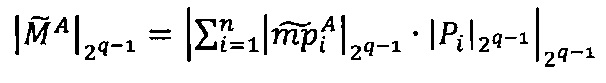 передается в управляющее ядро.
передается в управляющее ядро.
3.7.6. После того, как результаты скалярного произведения векторов переданы в управляющее ядро, в управляющем ядре вычисляется значение ранга 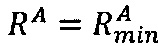 , если
, если 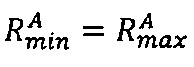 или
или , R=Rmах, если
, R=Rmах, если  и значение остатка от деления модулярной мантиссы
и значение остатка от деления модулярной мантиссы  числа А на 2α:
числа А на 2α:  .
.
3.7.7. После того, как управляющее ядро передаст во все модулярные и все универсальные целочисленные ядра значения 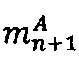 и α, выполняется деление модулярной мантиссы
и α, выполняется деление модулярной мантиссы  числа А на число 2α:
числа А на число 2α:
- в первом модулярном вычислительном ядре процессора выполняется операция вычитания  по модулю р1 q-разрядного двоичного представления знакопозиций
по модулю р1 q-разрядного двоичного представления знакопозиций 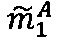 модулярной мантиссы
модулярной мантиссы 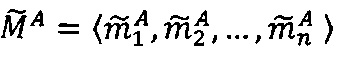 числа А и значения
числа А и значения 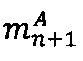 следующим образом: если
следующим образом: если  , то
, то  , если
, если , то
, то 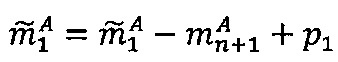 ; после чего выполняется операция умножения
; после чего выполняется операция умножения  по модулю р1 q-разрядного двоичного представления знакопозиций
по модулю р1 q-разрядного двоичного представления знакопозиций 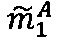 модулярной мантиссы
модулярной мантиссы  числа А и значения мультипликативной инверсии 2α по модулю р1
числа А и значения мультипликативной инверсии 2α по модулю р1 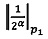 путем нахождения значения
путем нахождения значения  , где
, где  - наибольшее целое, не превышающее
- наибольшее целое, не превышающее  ; после чего если
; после чего если 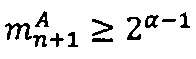 выполняется операция сложения
выполняется операция сложения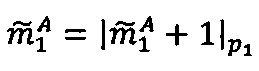 по модулю р1 q-разрядного двоичного представления знакопозиций
по модулю р1 q-разрядного двоичного представления знакопозиций  модулярной мантиссы
модулярной мантиссы 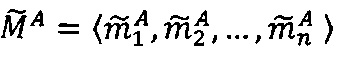 числа А следующим образом: если
числа А следующим образом: если  , то
, то  если
если 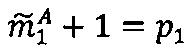 , то
, то  ; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
- параллельно с этим во втором модулярном вычислительном ядре процессора выполняется операция вычитания  по модулю р2 q-разрядного двоичного представления знакопозиций
по модулю р2 q-разрядного двоичного представления знакопозиций  модулярной мантиссы
модулярной мантиссы  числа А и значения
числа А и значения  , после чего выполняется операция умножения
, после чего выполняется операция умножения  по модулю р2 q-разрядного двоичного представления знакопозиций
по модулю р2 q-разрядного двоичного представления знакопозиций 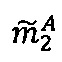 и значения мультипликативной инверсии 2α по модулю р2
и значения мультипликативной инверсии 2α по модулю р2  ; после чего если
; после чего если  выполняется операция сложения
выполняется операция сложения  по модулю р2;
по модулю р2;
- и т.д.
- параллельно с этим в -ом модулярном вычислительном ядре процессора выполняется операция вычитания 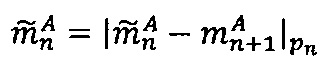 по модулю рn q-разрядного двоичного представления знакопозиций
по модулю рn q-разрядного двоичного представления знакопозиций 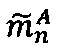 модулярной мантиссы
модулярной мантиссы  числа А и значения
числа А и значения  ; после чего выполняется операция умножения
; после чего выполняется операция умножения  по модулю рn q-разрядного двоичного представления знакопозиций
по модулю рn q-разрядного двоичного представления знакопозиций 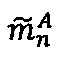 и значения мультипликативной инверсии 2α по модулю рn
и значения мультипликативной инверсии 2α по модулю рn 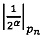 ; после чего если
; после чего если  выполняется операция сложения
выполняется операция сложения  по модулю рn;
по модулю рn;
- параллельно с этим во втором универсальном вычислительном ядре процессора выполняется коррекция 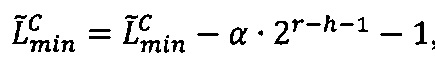 , если
, если  , иначе
, иначе 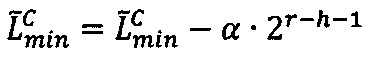 двоичного значения нижней границы интервальной логарифмической характеристики
двоичного значения нижней границы интервальной логарифмической характеристики промежуточного результата
промежуточного результата произведения чисел А и В;
произведения чисел А и В;
- параллельно с этим в третьем универсальном вычислительном ядре процессора выполняется коррекция  , если
, если 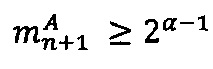 , иначе
, иначе 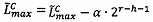 двоичного значения верхней границы интервальной логарифмической характеристики
двоичного значения верхней границы интервальной логарифмической характеристики 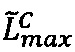 промежуточного результата
промежуточного результата 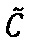 произведения чисел А и В;
произведения чисел А и В;
3.7.8. Если |zB|q-1>0, то действия 3.7.9-3.7.13 выполняются один раз для α=|zB|q-1; затем если количество итераций jВ≥1, то действия 3.7.9-3.7.13 выполняются затем jВ раз для α=q-1.
3.7.9. Вычисляются значения элементов вектора  :
:
- в первом модулярном вычислительном ядре процессора выполняется операция целочисленного умножения  по модулю р1 q-разрядного двоичного представления знакопозиций
по модулю р1 q-разрядного двоичного представления знакопозиций  модулярной мантиссы
модулярной мантиссы  числа В и значения мультипликативной инверсии Р1 по модулю р1
числа В и значения мультипликативной инверсии Р1 по модулю р1  , путем нахождения значения
, путем нахождения значения  , где
, где 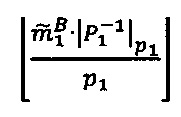 - наибольшее целое, не превышающее
- наибольшее целое, не превышающее  ; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
- параллельно с этим во втором модулярном вычислительном ядре процессора выполняется операция целочисленного умножения  по модулю р2 q-разрядного двоичного представления знакопозиций
по модулю р2 q-разрядного двоичного представления знакопозиций 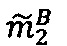 модулярной мантиссы
модулярной мантиссы  и значения мультипликативной инверсии Р2 по модулю р2
и значения мультипликативной инверсии Р2 по модулю р2 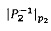 ;
;
- и т.д.
- параллельно с этим в -ом модулярном вычислительном ядре процессора выполняется операция целочисленного умножения  по модулю рn q-разрядного двоичного представления знакопозиций
по модулю рn q-разрядного двоичного представления знакопозиций 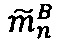 модулярной мантиссы
модулярной мантиссы  и значения мультипликативной инверсии Рn по модулю рn
и значения мультипликативной инверсии Рn по модулю рn  ;
;
3.7.10. После того, как получены значения элементов вектора 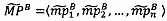 , данный вектор загружается в векторные ядра следующим образом:
, данный вектор загружается в векторные ядра следующим образом:
- в первое векторное вычислительное ядро загружают вектор q-разрядных элементов  ;
;
- параллельно с этим во второе векторное вычислительное ядро загружают вектор q-разрядных элементов 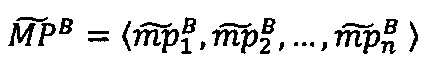 ;
;
- параллельно с этим в третье векторное вычислительное ядро загружают вектор q-разрядных элементов 
3.7.11. После того, как элементы вектора 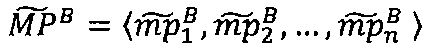 загружены в векторные ядра, производится вычисление ранга и остатка от деления на 2q-1 следующим образом:
загружены в векторные ядра, производится вычисление ранга и остатка от деления на 2q-1 следующим образом:
- в первом векторном вычислительном ядре вычисляют скалярное произведение векторов  и
и  значение
значение  передается в управляющее ядро;
передается в управляющее ядро;
- параллельно с этим во втором векторном вычислительном ядре вычисляют скалярное произведение векторов 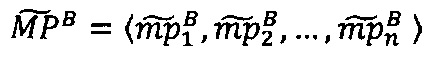 и
и  , значение
, значение 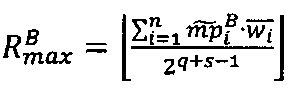 передается в управляющее ядро;
передается в управляющее ядро;
- параллельно с этим в третьем векторном вычислительном ядре вычисляют скалярное произведение векторов  и
и  , значение
, значение  передается в управляющее ядро;
передается в управляющее ядро;
3.7.12. После того, как результаты скалярного произведения векторов переданы в управляющее ядро, в управляющем ядре вычисляется значение ранга  , если
, если  или
или 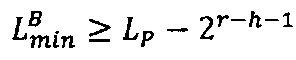 ,
,  , если
, если 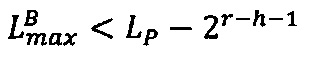 и значение остатка от деления модулярной мантиссы
и значение остатка от деления модулярной мантиссы  числа В на 2α:
числа В на 2α:  .
.
3.7.13. После того, как управляющее ядро передаст во все модулярные и все универсальные целочисленные ядра значения  и α, выполняется деление модулярной мантиссы
и α, выполняется деление модулярной мантиссы 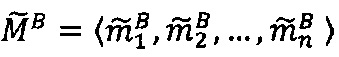 числа В на число 2α:
числа В на число 2α:
- в первом модулярном вычислительном ядре процессора выполняется операция вычитания  по модулю р1 q-разрядного двоичного представления знакопозиций
по модулю р1 q-разрядного двоичного представления знакопозиций 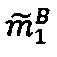 модулярной мантиссы
модулярной мантиссы 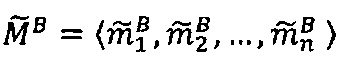 числа В и значения
числа В и значения  следующим образом: если
следующим образом: если  , то
, то  , если
, если 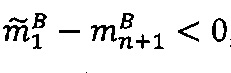 , то
, то  , после чего выполняется операция умножения
, после чего выполняется операция умножения  по модулю р1 q-разрядного двоичного представления знакопозиций
по модулю р1 q-разрядного двоичного представления знакопозиций  модулярной мантиссы
модулярной мантиссы  числа В и значения мультипликативной инверсии 2α по модулю р1
числа В и значения мультипликативной инверсии 2α по модулю р1 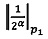 путем нахождения значения
путем нахождения значения  , где
, где  - наибольшее целое, не превышающее
- наибольшее целое, не превышающее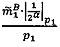 ; после чего если
; после чего если  , выполняется операция сложения
, выполняется операция сложения  по модулю р1 q-разрядного двоичного представления знакопозиций
по модулю р1 q-разрядного двоичного представления знакопозиций  модулярной мантиссы
модулярной мантиссы  числа В следующим образом: если
числа В следующим образом: если , то
, то , если
, если  то
то 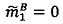 ; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
- параллельно с этим во втором модулярном вычислительном ядре процессора выполняется операция вычитания 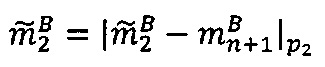 по модулю р2 q-разрядного двоичного представления знакопозиций
по модулю р2 q-разрядного двоичного представления знакопозиций 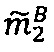 модулярной мантиссы
модулярной мантиссы  числа В и значения
числа В и значения  , после чего выполняется операция умножения
, после чего выполняется операция умножения 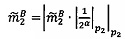 по модулю р2 q-разрядного двоичного представления знакопозиций
по модулю р2 q-разрядного двоичного представления знакопозиций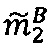 и значения мультипликативной инверсии 2α по модулю p2
и значения мультипликативной инверсии 2α по модулю p2 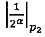 ; после чего, если
; после чего, если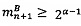 , выполняется операция сложения
, выполняется операция сложения 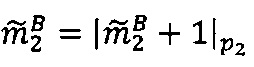 по модулю р2;
по модулю р2;
- и т.д.
-параллельно с этим в -ом модулярном вычислительном ядре процессора выполняется операция вычитания  по модулю рn q-разрядного двоичного представления знакопозиций
по модулю рn q-разрядного двоичного представления знакопозиций 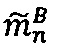 модулярной мантиссы
модулярной мантиссы  числа В и значения
числа В и значения  ; после чего выполняется операция умножения
; после чего выполняется операция умножения  по модулю рn q-разрядного двоичного представления знакопозиций
по модулю рn q-разрядного двоичного представления знакопозиций  и значения мультипликативной инверсии 2α по модулю рn
и значения мультипликативной инверсии 2α по модулю рn  после чего, если
после чего, если выполняется операция сложения
выполняется операция сложения  по модулю рn;
по модулю рn;
- параллельно с этим во втором универсальном вычислительном ядре процессора выполняется коррекция  , если
, если 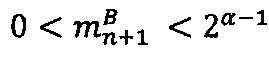 , иначе
, иначе  двоичного значения нижней границы интервальной логарифмической характеристики
двоичного значения нижней границы интервальной логарифмической характеристики  промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
- параллельно с этим в третьем универсальном вычислительном ядре процессора выполняется коррекция  , если
, если , иначе
, иначе 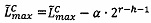 двоичного значения верхней границы интервальной логарифмической характеристики
двоичного значения верхней границы интервальной логарифмической характеристики  промежуточного результата
промежуточного результата 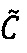 произведения чисел А и В;
произведения чисел А и В;
3.7.14. После того, как выполнена коррекция мантисс  и
и  чисел А и В соответственно, выполняется их умножение следующим образом:
чисел А и В соответственно, выполняется их умножение следующим образом:
- в первом модулярном вычислительном ядре процессора выполняется операция целочисленного умножения по модулю р1 q-разрядных двоичных представлений знакопозиций
по модулю р1 q-разрядных двоичных представлений знакопозиций  и
и  модулярных мантисс
модулярных мантисс  и
и 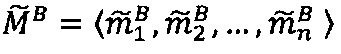 чисел А и В соответственно, путем нахождения значения
чисел А и В соответственно, путем нахождения значения 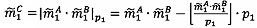 , где
, где  - наибольшее целое, не превышающее
- наибольшее целое, не превышающее  ; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
- параллельно с этим во втором модулярном вычислительном ядре процессора выполняется операция целочисленного умножения по модулю р2 q-разрядных двоичных представлений знакопозиций
по модулю р2 q-разрядных двоичных представлений знакопозиций  и
и 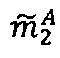 модулярных мантисс
модулярных мантисс  и
и  чисел А и В соответственно; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
чисел А и В соответственно; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
- и т.д.
- параллельно с этим в -ом модулярном вычислительном ядре процессора выполняется операция целочисленного умножения 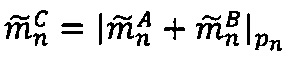 по модулю рn q-разрядных двоичных представлений знакопозиций
по модулю рn q-разрядных двоичных представлений знакопозиций  и
и  модулярных мантисс
модулярных мантисс  и
и  чисел А и В соответственно; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления.
чисел А и В соответственно; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления.
В результате выполнения данных операций получается произведение  чисел
чисел  и
и  , представленное в модулярно-логарифмическом формате с плавающей точкой.
, представленное в модулярно-логарифмическом формате с плавающей точкой.
Для выполнения операции сложения двух целых q-разрядных двоичных чисел требуется устройство, состоящее из q элементарных двоичных устройств, для выполнения операции умножения двух целых q-разрядных двоичных чисел требуется устройство, состоящее из q×q элементарных двоичных устройств, для выполнения операции модулярного умножения двух целых q-разрядных двоичных чисел требуется устройство, состоящее из 2×q×q элементарных двоичных устройств, для хранения одного бита информации требуется устройство, состоящее из одного элементарного двоичного устройства, для сложения двух q-разрядных двоичных чисел в формате с плавающей точкой с направленным округлением требуется устройство, состоящее из 2×q элементарных двоичных устройств. Для выполнения операции умножения способом (A.C. RU №2509345, БИ №7, 10.03.2014) требуется устройство, состоящее из (2×k×k×n+k) элементарных двоичных устройств, где k - разрядность одного ядра универсального многоядерного процессора, n - количество модулей. Для выполнения операции умножения способом (К.С. Исупов, А.Н. Мальцев. «Способ представления чисел с плавающей точкой большой разрядности, ориентированный на параллельную обработку», Вычислительные методы и программирование, 15:4 (2014), с. 631-643.), требуется устройство, состоящее из (2β-l)×n×q+2×q×q×n+k+2×2×γ, где β - шаг масштабирования, n - количество моделей, q - разрядность модулей, k - разрядность порядка, γ - разрядность интервальной позиционной характеристики). Для выполнения операции умножения предложенным способом, требуется устройство, состоящее из 2×q×q×n+k+2×r+2×(n×s×s+(n-1)×(s+log2n))+(n×q×q+(n-1)×q), где n - количество моделей, q - разрядность модулей, k -разрядность порядка, r - разрядность интервальной логарифмической характеристики, s -разрядность весовых коэффициентов. При условии, что k=r=s=q, β=q-1, γ=2⋅q, для выполнения операции умножения способом (A.C. RU №2509345, БИ №7, 10.03.2014) требуется устройство, состоящее из (q⋅(2⋅n⋅q+1)) элементарных двоичных устройств, для выполнения операции умножения способом (К.С. Исупов, А.Н. Мальцев. «Способ представления чисел с плавающей точкой большой разрядности, ориентированный на параллельную обработку», Вычислительные методы и программирование, 15:4 (2014), с. 631-643.), требуется устройство, состоящее из (q⋅((2q-1-1)⋅n+2⋅q+9)), для выполнения операции умножения предложенным способом, требуется устройство, состоящее из (5⋅n⋅q2+3⋅n⋅q+(n-1)⋅log2n).
Предложенный способ полностью описывает процедуру умножения двух чисел в модулярном формате с плавающей точкой, включая контроль переполнения, потери порядка, масштабирования, при этом требует для своего выполнения устройство всего в  раза сложнее, чем требуется для выполнения способа (A.C. RU №2509345, БИ №7, 10.03.2014) и в
раза сложнее, чем требуется для выполнения способа (A.C. RU №2509345, БИ №7, 10.03.2014) и в  раз проще, чем требуется для способа (Исупов К.С., Мальцев А.Н. Способ представления чисел с плавающей точкой большой разрядности, ориентированный на параллельную обработку // Вычислительные методы и программирование: новые вычислительные технологии. 2014. Т. 15, №4. С. 631-643).
раз проще, чем требуется для способа (Исупов К.С., Мальцев А.Н. Способ представления чисел с плавающей точкой большой разрядности, ориентированный на параллельную обработку // Вычислительные методы и программирование: новые вычислительные технологии. 2014. Т. 15, №4. С. 631-643).
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ организации выполнения операции умножения двух чисел в модулярно-индексном формате представления с плавающей точкой на универсальных многоядерных процессорах | 2017 |
|
RU2652460C1 |
| СПОСОБ ОРГАНИЗАЦИИ ВЫПОЛНЕНИЯ ОПЕРАЦИИ УМНОЖЕНИЯ ДВУХ ЧИСЕЛ В МОДУЛЯРНО-ПОЗИЦИОННОМ ФОРМАТЕ ПРЕДСТАВЛЕНИЯ С ПЛАВАЮЩЕЙ ТОЧКОЙ НА УНИВЕРСАЛЬНЫХ МНОГОЯДЕРНЫХ ПРОЦЕССОРАХ | 2012 |
|
RU2509345C1 |
| Устройство для сравнения чисел в системе остаточных классов | 2018 |
|
RU2698413C1 |
| УСТРОЙСТВО ДЛЯ СРАВНЕНИЯ ЧИСЕЛ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ НА ОСНОВЕ ИНТЕРВАЛЬНО-ПОЗИЦИОННЫХ ХАРАКТЕРИСТИК | 2014 |
|
RU2557444C1 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ЗНАКОВ ЧИСЕЛ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2014 |
|
RU2557446C1 |
| Устройство вычисления модулярного произведения Монтгомери | 2017 |
|
RU2652450C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ДЕЛЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2005 |
|
RU2305312C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ВЫЧИСЛЕНИЯ ПОЗИЦИОННЫХ ХАРАКТЕРИСТИК НЕПОЗИЦИОННОГО КОДА | 2003 |
|
RU2257615C2 |
| Арифметическое устройство в модулярной системе счисления | 1987 |
|
SU1432517A1 |
| Устройство для умножения чисел в модулярной системе счисления | 1986 |
|
SU1368878A1 |
Изобретение относится к вычислительной технике и предназначено для выполнения операции умножения двух чисел в модулярно-логарифмическом формате с плавающей точкой. Техническим результатом является упрощение выполнения операции умножения. Способ осуществляется на гибридных многоядерных процессорах и содержит процедуру умножения двух чисел в модулярном формате с плавающей точкой, включая контроль переполнения, потери порядка, масштабирования.
Способ организации выполнения операции умножения двух чисел в модулярно-логарифмическом формате представления с плавающей точкой на гибридных многоядерных процессорах, заключающийся в том, что:
в гибридном многоядерном вычислителе, содержащем n q-разрядных модулярных вычислительных ядер, одно k-разрядное и два r-разрядных универсальных целочисленных ядра, два специализированных s-разрядных векторных ядра, одно специализированное q-разрядное векторное ядро и одно специализированное управляющее ядро, выполняется система из  операций, в состав которой входят операции арифметического умножения и арифметического сложения над числами, представленными в позиционных целочисленных форматах данных, операции скалярного произведения векторов n чисел, представленными в позиционных целочисленных форматах данных, операции передачи управления и информации между ядрами;
операций, в состав которой входят операции арифметического умножения и арифметического сложения над числами, представленными в позиционных целочисленных форматах данных, операции скалярного произведения векторов n чисел, представленными в позиционных целочисленных форматах данных, операции передачи управления и информации между ядрами;
при организации выполнения операций умножения каждое число, множитель и множимое, представляется в модулярно-логарифмическом формате с плавающей точкой в виде (2+k+2⋅r+q⋅n) -элементного вектора, где:
первые два разряда слева σ являются старшими разрядами в формате числа и отводятся под значение знака числа, причем если σ=+1, то число считается положительным, если σ=-1, то число считается отрицательным, если σ=0, то число равно 0;
следующие за первыми двумя разрядами σ числа k разрядов отводятся под хранение порядка числа, представляющего собой целое двоичное число λ со знаком sλ, изменяющееся для конечных чисел с плавающей точкой в диапазоне λmin≤λ≤λmах и получаемое в результате преобразования числа из позиционного формата с плавающей точкой посредством вычисления выражения λ=е-t+1, где е определяет величину числа в двоичном позиционном формате с плавающей точкой в выражении -1S⋅М⋅2е при 0≤М≤2, являющейся рациональной t-разрядной мантиссой числа в двоичном позиционном формате с плавающей точкой, λmin=2-2k-1, λmax=2k-1-2, при sλ=0, порядок λ считается положительным, а при sλ=1 порядок λ считается отрицательным;
следующие за (k+2) разрядами 2⋅r разрядов отводятся под хранение интервальной логарифмической характеристики числа, представляющей собой пару целых двоичных чисел Lmin, Lmax без знака, изменяющихся в диапазоне 0≤Lmin≤LP, 0≤Lmax≤LP и получаемых в результате преобразования числа из позиционного формата с плавающей точкой -1S⋅М⋅2е посредством вычисления выражений Lmin= Lmax=Lmin+1, где М' - целое неотрицательное двоичное число, определяемое выражением М'=М⋅2t-1, М - рациональная t-разрядная мантисса числа в двоичном позиционном формате с плавающей точкой,
Lmax=Lmin+1, где М' - целое неотрицательное двоичное число, определяемое выражением М'=М⋅2t-1, М - рациональная t-разрядная мантисса числа в двоичном позиционном формате с плавающей точкой, 

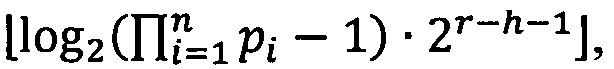
 - наибольшее целое, не превышающее log2(M')⋅2r-h-1,
- наибольшее целое, не превышающее log2(M')⋅2r-h-1, 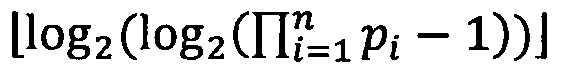 - наибольшее целое, не превышающее
- наибольшее целое, не превышающее  ,
, - наибольшее целое, не превышающее
- наибольшее целое, не превышающее 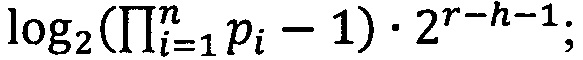
следующие за (2⋅r+k+2) разрядами q⋅n разрядов отводятся для представления мантиссы числа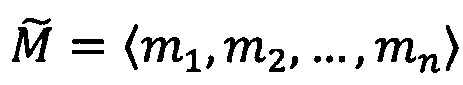 в модулярно-логарифмическом формате, причем данная мантисса представляется в системе остаточных классов с n основаниями P1, P2, …, Рn, n - количество знакопозиций мантиссы, q - разрядность каждой знакопозиции; причем каждая i-ая знакопозиция, где 1≤i≤n, представляется целым неотрицательным числом mi в двоичной позиционной системе счисления; значение mi каждой i-ой знакопозиции определяется по выражению mi=
в модулярно-логарифмическом формате, причем данная мантисса представляется в системе остаточных классов с n основаниями P1, P2, …, Рn, n - количество знакопозиций мантиссы, q - разрядность каждой знакопозиции; причем каждая i-ая знакопозиция, где 1≤i≤n, представляется целым неотрицательным числом mi в двоичной позиционной системе счисления; значение mi каждой i-ой знакопозиции определяется по выражению mi= 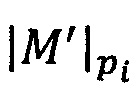 , где М' - целое неотрицательное двоичное число, определяемое выражением М'=М⋅2t-1, М - рациональная t-разрядная мантисса числа в двоичном позиционном формате с плавающей точкой,
, где М' - целое неотрицательное двоичное число, определяемое выражением М'=М⋅2t-1, М - рациональная t-разрядная мантисса числа в двоичном позиционном формате с плавающей точкой, 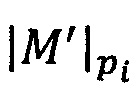 - операция получения остатка от деления М' на i-ое основание рi;
- операция получения остатка от деления М' на i-ое основание рi;
диапазон изменения модулярной мантиссы  в позиционной системе счисления определяется интервалом
в позиционной системе счисления определяется интервалом
значения порядка λ, мантиссы 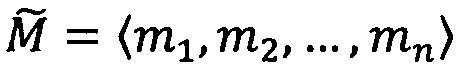 и верхней и нижней границ интервальной логарифмической характеристики Lmin, Lmax положительных конечных чисел при σ=+1 в модулярно-логарифмическом формате [〈m1, m2, …, mn〉, Lmin, Lmax, λ, σ] находятся соответственно в следующих диапазонах: 2-2k-1≤λ≤2k-1-2,
и верхней и нижней границ интервальной логарифмической характеристики Lmin, Lmax положительных конечных чисел при σ=+1 в модулярно-логарифмическом формате [〈m1, m2, …, mn〉, Lmin, Lmax, λ, σ] находятся соответственно в следующих диапазонах: 2-2k-1≤λ≤2k-1-2,  0≤Lmin≤LP, 0≤Lmax≤Lp,
0≤Lmin≤LP, 0≤Lmax≤Lp,
значения порядка λ, мантиссы  и интервальной логарифмической характеристики Lmin, Lmax отрицательных конечных чисел при σ=-1 в модулярно-логарифмическом формате находятся соответственно в следующих диапазонах: 2-2k-1≤λ≤2k-1-2,
и интервальной логарифмической характеристики Lmin, Lmax отрицательных конечных чисел при σ=-1 в модулярно-логарифмическом формате находятся соответственно в следующих диапазонах: 2-2k-1≤λ≤2k-1-2,  0≤Lmin≤LP, 0≤Lmax≤LP;
0≤Lmin≤LP, 0≤Lmax≤LP;
значение машинного нуля представляется в модулярно логарифмическом формате следующим образом: σ=0, λ=0,  Lmin=0, Lmax=0;
Lmin=0, Lmax=0;
значение положительной бесконечности представляется в модулярно-логарифмическом формате следующим образом: σ=+1, λ=λmах+1=2k-1-1, 
 Lmin=0, Lmax=0;
Lmin=0, Lmax=0;
значение отрицательной бесконечности представляется в модулярно-логарифмическом формате следующим образом: σ=-1, λ=λmаx+1=2k-1-1, 
 Lmin=0, Lmax=0;
Lmin=0, Lmax=0;
для положительных нечисловых величин (NaN) в модулярно-логарифмическом формате при σ=+1 значение позиционного порядка λ определяется выражением λ=λmах+1=2k-1-1, значение мантиссы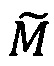 находится в диапазоне 〈11, 12, …, 1n〉≤
находится в диапазоне 〈11, 12, …, 1n〉≤ ≤〈р1-1), (р2-1), …, (р2-1)〉, значение верхней и нижней границ интервальной логарифмической характеристики Lmin, Lmax находятся в диапазонах 0≤Lmin≤LP, 0≤Lmax≤LP,
≤〈р1-1), (р2-1), …, (р2-1)〉, значение верхней и нижней границ интервальной логарифмической характеристики Lmin, Lmax находятся в диапазонах 0≤Lmin≤LP, 0≤Lmax≤LP,
для отрицательных нечисловых величин (NaN) в модулярно-логарифмическом формате при σ=-1 значение позиционного порядка λ определяется выражением λ=λmах+1=2k-1-1, значение мантиссы находится в диапазоне 〈11, 12, …, 1n〉≤
находится в диапазоне 〈11, 12, …, 1n〉≤ ≤ 〈р1-1), (р2-1), ..., (р2-1)〉, значение верхней и нижней границ интервальной логарифмической характеристики Lmin, Lmax находятся в диапазонах 0≤Lmin≤LP, 0≤Lmax≤LP;
≤ 〈р1-1), (р2-1), ..., (р2-1)〉, значение верхней и нижней границ интервальной логарифмической характеристики Lmin, Lmax находятся в диапазонах 0≤Lmin≤LP, 0≤Lmax≤LP;
по сигналу процессора множитель и множимое
и множимое  представленные в модулярно-логарифмическом формате с плавающей точкой, загружают в гибридный многоядерный процессор следующим образом:
представленные в модулярно-логарифмическом формате с плавающей точкой, загружают в гибридный многоядерный процессор следующим образом:
в первое модулярное ядро гибридного многоядерного процессора загружают q-разрядные двоичные представления первых знакопозиций  и
и  модулярных мантисс
модулярных мантисс  и
и  чисел А и В соответственно, а также основание системы остаточных классов р1 и значение мультипликативной инверсии Р1 по модулю
чисел А и В соответственно, а также основание системы остаточных классов р1 и значение мультипликативной инверсии Р1 по модулю 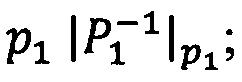
параллельно с этим во второе модулярное ядро загружают q-разрядные двоичные представления вторых знакопозиций  и
и  модулярных мантисс
модулярных мантисс  и
и  чисел А и В соответственно, а также основание системы остаточных классов р2 и значение мультипликативной инверсии Р2 по модулю
чисел А и В соответственно, а также основание системы остаточных классов р2 и значение мультипликативной инверсии Р2 по модулю 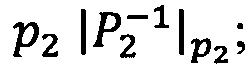
параллельно с этим в третье ÷ n-ое модулярные ядра загружают q-разрядные двоичные представления третьих ÷ n-ых знакопозиций 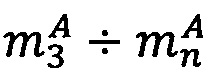 и
и  модулярных мантисс
модулярных мантисс 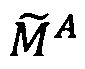 и
и  чисел А и В соответственно, а также основания системы остаточных классов р3÷рn и значения мультипликативных инверсий Р3÷Рn по модулям р3÷рn
чисел А и В соответственно, а также основания системы остаточных классов р3÷рn и значения мультипликативных инверсий Р3÷Рn по модулям р3÷рn

параллельно с этим в первое универсальное вычислительное ядро загружают k-разрядные двоичные порядки λА и λB, а также знаки σА и σB чисел А и В соответственно;
параллельно с этим во второе универсальное вычислительное ядро загружают r-разрядные значения нижних границ интервальных логарифмических характеристик 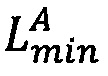 и
и 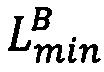 чисел А и В соответственно;
чисел А и В соответственно;
параллельно с этим в третье универсальное вычислительное ядро загружают r-разрядные значения верхних границ интервальных логарифмических характеристик 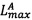 и
и 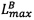 чисел А и В соответственно, а также r-разрядное значение нижней границы интервальной логарифмической характеристики диапазона представления модулярных мантисс LP;
чисел А и В соответственно, а также r-разрядное значение нижней границы интервальной логарифмической характеристики диапазона представления модулярных мантисс LP;
параллельно с этим в первое векторное вычислительное ядро загружают вектор s-разрядных коэффициентов 
параллельно с этим во второе векторное вычислительное ядро загружают вектор s-разрядных коэффициентов 
параллельно с этим в третье векторное вычислительное ядро загружают вектор q-разрядных остатков от деления 
после того, как множитель  и множимое
и множимое  загружены в гибридный многоядерный процессор, операция их умножения выполняется следующим образом:
загружены в гибридный многоядерный процессор, операция их умножения выполняется следующим образом:
в первом модулярном вычислительном ядре процессора выполняется операция целочисленного умножения 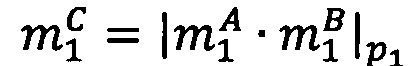 по модулю р1 q-разрядных двоичных представлений знакопозиций
по модулю р1 q-разрядных двоичных представлений знакопозиций 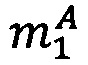 и
и  модулярных мантисс
модулярных мантисс 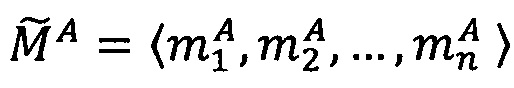 и
и 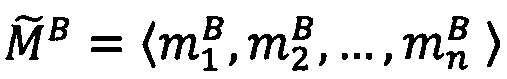 чисел А и В соответственно, путем нахождения значения
чисел А и В соответственно, путем нахождения значения 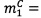
 - наибольшее целое, не превышающее
- наибольшее целое, не превышающее
 все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
параллельно с этим во втором модулярном вычислительном ядре процессора выполняется операция целочисленного умножения 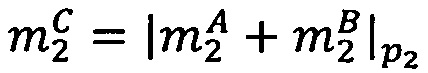 по модулю р2 q-разрядных двоичных представлений знакопозиций
по модулю р2 q-разрядных двоичных представлений знакопозиций  и
и  модулярных мантисс
модулярных мантисс 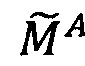 и
и 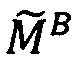 чисел А и В соответственно;
чисел А и В соответственно;
параллельно с этим в третьем ÷ n-ом модулярном вычислительном ядре процессора выполняется операция целочисленного умножения 
 по модулю р3 ÷ рn q-разрядных двоичных представлений знакопозиций
по модулю р3 ÷ рn q-разрядных двоичных представлений знакопозиций 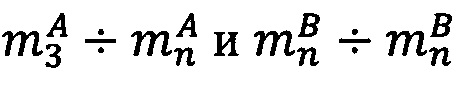 модулярных мантисс
модулярных мантисс  и
и  чисел А и В соответственно;
чисел А и В соответственно;
параллельно с этим в первом универсальном вычислительном ядре процессора выполняется сложение λC=λA+λB двоичных порядков λА и λB, а также умножение σC=σА⋅σB знаков σА и σB чисел А и В соответственно;
параллельно с этим во втором универсальном вычислительном ядре процессора выполняется сложение  двоичных значений нижних границ интервальных логарифмических характеристик
двоичных значений нижних границ интервальных логарифмических характеристик 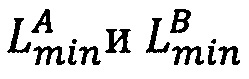 чисел А и В соответственно;
чисел А и В соответственно;
параллельно с этим в третьем универсальном вычислительном ядре процессора выполняется сложение  двоичных значений верхних границ интервальных логарифмических характеристик
двоичных значений верхних границ интервальных логарифмических характеристик чисел А и В соответственно;
чисел А и В соответственно;
параллельно с этим в управляющем ядре вычисляются следующие значения поправочных коэффициентов: 
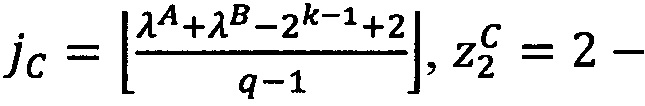


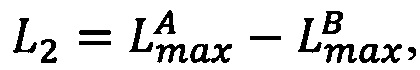
 если
если 
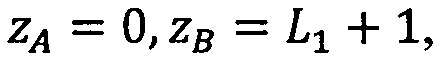 если
если 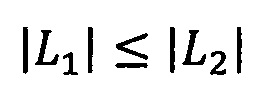 и L2<0,
и L2<0, zB=
zB=  если
если  и
и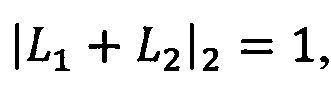
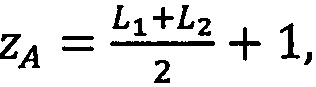
 если
если  и
и

после того, как получено промежуточное значение произведения 
 чисел
чисел  и
и 
 выполняется коррекция результата следующим образом:
выполняется коррекция результата следующим образом:
в случае если знак  промежуточного результата
промежуточного результата  произведения чисел А и В не равен 0, и порядок
произведения чисел А и В не равен 0, и порядок  промежуточного результата
промежуточного результата 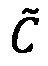 произведения чисел А и В принадлежит интервалу [2-2k-1; 2k-1-2], и значение
произведения чисел А и В принадлежит интервалу [2-2k-1; 2k-1-2], и значение 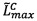 верхней границы интервальной логарифмической характеристики промежуточного результата
верхней границы интервальной логарифмической характеристики промежуточного результата  произведения чисел А и В меньше значения нижней границы интервальной логарифмической характеристики максимально возможного значения мантиссы, то есть
произведения чисел А и В меньше значения нижней границы интервальной логарифмической характеристики максимально возможного значения мантиссы, то есть
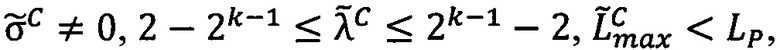 то коррекции результата не требуется;
то коррекции результата не требуется;
в случае если знак  промежуточного результата
промежуточного результата  произведения чисел А и В равен 0, то есть
произведения чисел А и В равен 0, то есть 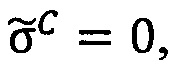 то:
то:
в первом универсальном вычислительном ядре процессора выполняется обнуление 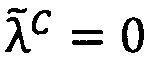 двоичного порядка
двоичного порядка 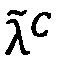 промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
параллельно с этим во втором универсальном вычислительном ядре процессора выполняется обнуление 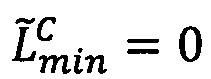 двоичного значения нижней границы интервальной логарифмической характеристики
двоичного значения нижней границы интервальной логарифмической характеристики  промежуточного результата
промежуточного результата 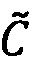 произведения чисел А и В;
произведения чисел А и В;
параллельно с этим в третьем универсальном вычислительном ядре процессора выполняется обнуление  двоичного значения верхней границы интервальной логарифмической характеристики
двоичного значения верхней границы интервальной логарифмической характеристики  промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
в случае если знак  промежуточного результата
промежуточного результата 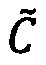 произведения чисел А и В не равен 0 и значение
произведения чисел А и В не равен 0 и значение  то есть модуль промежуточного результата
то есть модуль промежуточного результата  произведения чисел А и В выходит за границы минимально возможного представления, то:
произведения чисел А и В выходит за границы минимально возможного представления, то:
в первом универсальном вычислительном ядре процессора выполняется обнуление  двоичного порядка
двоичного порядка  и
и  знака
знака  промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
параллельно с этим во втором универсальном вычислительном ядре процессора выполняется обнуление  двоичного значения нижней границы интервальной логарифмической характеристики
двоичного значения нижней границы интервальной логарифмической характеристики 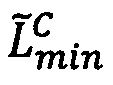 промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
параллельно с этим в третьем универсальном вычислительном ядре процессора выполняется обнуление 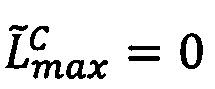 двоичного значения верхней границы интервальной логарифмической характеристики
двоичного значения верхней границы интервальной логарифмической характеристики  промежуточного результата
промежуточного результата 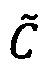 произведения чисел А и В;
произведения чисел А и В;
параллельно с этим в первом модулярном вычислительном ядре процессора выполняется обнуление 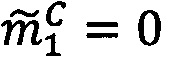 значения первой знакопозиции
значения первой знакопозиции 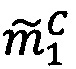 промежуточного результата
промежуточного результата 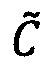 произведения чисел А и В;
произведения чисел А и В;
параллельно с этим во втором модулярном вычислительном ядре процессора выполняется обнуление  значения второй знакопозиции
значения второй знакопозиции  промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
параллельно с этим в третьем ÷ n-ом модулярном вычислительном ядре процессора выполняется обнуление  значения третьей ÷ n-ой знакопозиции
значения третьей ÷ n-ой знакопозиции 
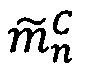 промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
в случае если знак  промежуточного результата С произведения чисел А и В не равен 0 и значение
промежуточного результата С произведения чисел А и В не равен 0 и значение  то есть модуль промежуточного результата
то есть модуль промежуточного результата  произведения чисел А и В выходит за границы максимально возможного представления, то:
произведения чисел А и В выходит за границы максимально возможного представления, то:
в первом универсальном вычислительном ядре процессора выполняется присвоение  двоичному порядку
двоичному порядку  промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
параллельно с этим во втором универсальном вычислительном ядре процессора выполняется обнуление 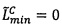 двоичного значения нижней границы интервальной логарифмической характеристики
двоичного значения нижней границы интервальной логарифмической характеристики  промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
параллельно с этим в третьем универсальном вычислительном ядре процессора выполняется обнуление 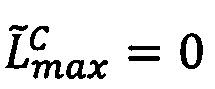 двоичного значения верхней границы интервальной логарифмической характеристики
двоичного значения верхней границы интервальной логарифмической характеристики 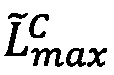 промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
параллельно с этим в первом модулярном вычислительном ядре процессора выполняется обнуление  значения первой знакопозиции
значения первой знакопозиции  промежуточного результата
промежуточного результата 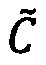 произведения чисел А и В;
произведения чисел А и В;
параллельно с этим во втором модулярном вычислительном ядре процессора выполняется обнуление 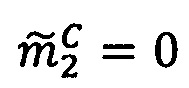 значения второй знакопозиции
значения второй знакопозиции 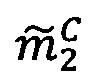 промежуточного результата
промежуточного результата 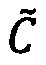 произведения чисел А и В;
произведения чисел А и В;
параллельно с этим в третьем ÷ n-ом модулярном вычислительном ядре процессора выполняется обнуление 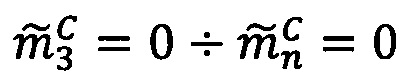 значения третьей ÷ n-ой знакопозиции
значения третьей ÷ n-ой знакопозиции 
 промежуточного результата
промежуточного результата 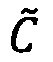 произведения чисел А и В;
произведения чисел А и В;
в случае если знак 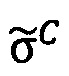 промежуточного результата
промежуточного результата  произведения чисел А и В не равен 0, и порядок
произведения чисел А и В не равен 0, и порядок  промежуточного результата
промежуточного результата 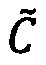 произведения чисел А и В принадлежит интервалу
произведения чисел А и В принадлежит интервалу  и значение
и значение  верхней границы интервальной логарифмической характеристики промежуточного результата
верхней границы интервальной логарифмической характеристики промежуточного результата 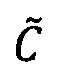 произведения чисел А и В меньше значения нижней границы интервальной логарифмической характеристики максимально возможного значения мантиссы
произведения чисел А и В меньше значения нижней границы интервальной логарифмической характеристики максимально возможного значения мантиссы 
 то управляющее ядро передает во все модулярные и все универсальные целочисленные ядра значения поправочных коэффициентов
то управляющее ядро передает во все модулярные и все универсальные целочисленные ядра значения поправочных коэффициентов 
 после чего:
после чего:
в первом модулярном вычислительном ядре процессора выполняется операция целочисленного умножения  по модулю р1 знакопозиции
по модулю р1 знакопозиции  модулярной мантиссы
модулярной мантиссы 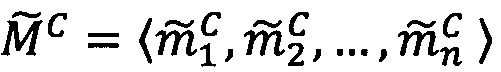 промежуточного результата
промежуточного результата  произведения чисел А и В и значения
произведения чисел А и В и значения  следующим образом: выполняется операция целочисленного умножения
следующим образом: выполняется операция целочисленного умножения  по модулю р1 знакопозиции
по модулю р1 знакопозиции 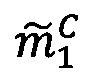 модулярной мантиссы
модулярной мантиссы 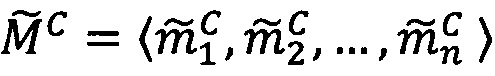 промежуточного результата
промежуточного результата  произведения чисел А и В и значения
произведения чисел А и В и значения 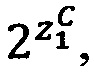 полученного сдвигом числа 1 на
полученного сдвигом числа 1 на  двоичных разрядов влево, путем нахождения значения
двоичных разрядов влево, путем нахождения значения  где
где  - наибольшее целое, не превышающее
- наибольшее целое, не превышающее 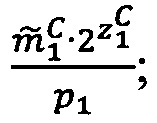 затем, если jC>0, то jC раз выполняется операция целочисленного умножения
затем, если jC>0, то jC раз выполняется операция целочисленного умножения  по модулю р1 знакопозиции
по модулю р1 знакопозиции 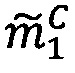 модулярной мантиссы
модулярной мантиссы  промежуточного результата
промежуточного результата  произведения чисел А и В и значения 2q-1, полученного сдвигом числа 1 на (q-1) двоичных разрядов влево, путем нахождения значения
произведения чисел А и В и значения 2q-1, полученного сдвигом числа 1 на (q-1) двоичных разрядов влево, путем нахождения значения  где
где  - наибольшее целое, не превышающее
- наибольшее целое, не превышающее 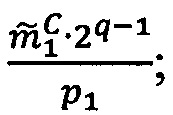 все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
параллельно с этим во втором модулярном вычислительном ядре процессора выполняется операция целочисленного умножения  по модулю р2 знакопозиции
по модулю р2 знакопозиции  модулярной мантиссы
модулярной мантиссы  промежуточного результата
промежуточного результата  произведения чисел А и В и значения
произведения чисел А и В и значения  следующим образом: выполняется операция целочисленного умножения
следующим образом: выполняется операция целочисленного умножения  по модулю р2; затем, если jC>0, то jC раз выполняется операция целочисленного умножения
по модулю р2; затем, если jC>0, то jC раз выполняется операция целочисленного умножения  по модулю р2;
по модулю р2;
параллельно с этим в третьем ÷ n-ом модулярном вычислительном ядре процессора выполняется операция целочисленного умножения 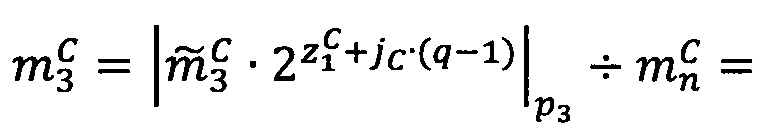
 по модулю р3÷рn q-разрядного двоичного представления знакопозиции
по модулю р3÷рn q-разрядного двоичного представления знакопозиции 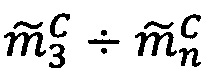 модулярной мантиссы
модулярной мантиссы  промежуточного результата
промежуточного результата 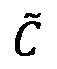 произведения чисел А и В и значения
произведения чисел А и В и значения 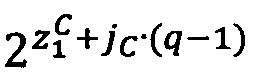 следующим образом: выполняется операция целочисленного умножения
следующим образом: выполняется операция целочисленного умножения  по модулю р3÷рn; затем, если jC>0, то jC раз выполняется операция целочисленного умножения
по модулю р3÷рn; затем, если jC>0, то jC раз выполняется операция целочисленного умножения  по модулю р3÷рn;
по модулю р3÷рn;
параллельно с этим в первом универсальном вычислительном ядре процессора выполняется коррекция 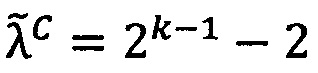 двоичного порядка
двоичного порядка 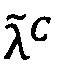 промежуточного результата
промежуточного результата 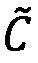 произведения чисел А и В;
произведения чисел А и В;
параллельно с этим во втором универсальном вычислительном ядре процессора выполняется коррекция  двоичного значения нижней границы интервальной логарифмической характеристики
двоичного значения нижней границы интервальной логарифмической характеристики 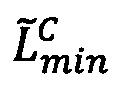 промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
параллельно с этим в третьем универсальном вычислительном ядре процессора выполняется коррекция  двоичного значения верхней границы интервальной логарифмической характеристики
двоичного значения верхней границы интервальной логарифмической характеристики  промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
в случае если знак  промежуточного результата
промежуточного результата 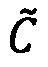 произведения чисел А и В не равен 0, и порядок
произведения чисел А и В не равен 0, и порядок  промежуточного результата С произведения чисел А и В принадлежит интервалу
промежуточного результата С произведения чисел А и В принадлежит интервалу  и значение
и значение  верхней границы интервальной логарифмической характеристики промежуточного результата
верхней границы интервальной логарифмической характеристики промежуточного результата 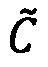 произведения чисел А и В меньше значения нижней границы интервальной логарифмической характеристики максимально возможного значения мантиссы
произведения чисел А и В меньше значения нижней границы интервальной логарифмической характеристики максимально возможного значения мантиссы 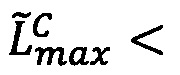
 то управляющее ядро передает во все модулярные и все универсальные целочисленные ядра значение поправочного коэффициента
то управляющее ядро передает во все модулярные и все универсальные целочисленные ядра значение поправочного коэффициента  после чего:
после чего:
в первое модулярное ядро загружают q-разрядные двоичные значения  и
и  мультипликативных инверсий
мультипликативных инверсий  по модулю р1;
по модулю р1;
параллельно с этим во второе модулярное ядро загружают q-разрядные двоичные значения 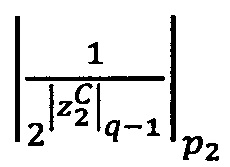 и
и  мультипликативных инверсий
мультипликативных инверсий  и 2q-1 по модулю р2;
и 2q-1 по модулю р2;
параллельно с этим в третье ÷ n-ое модулярное ядро загружают q-разрядные двоичные значения 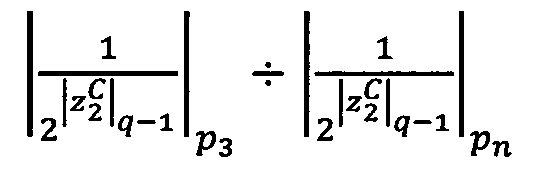 и
и  мультипликативных инверсий
мультипликативных инверсий 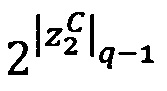 и 2q-1 по модулю p3÷рn;
и 2q-1 по модулю p3÷рn;
параллельно с этим в первом универсальном вычислительном ядре процессора выполняется коррекция  двоичного порядка
двоичного порядка  промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
параллельно с этим в управляющем ядре вычисляется количество итераций j=0, если  если
если 
в случае если  выполняется один цикл деления на 2α, где
выполняется один цикл деления на 2α, где  затем, если количество итераций j≥1, выполняется j циклов деления на 2α, где α=q-1;
затем, если количество итераций j≥1, выполняется j циклов деления на 2α, где α=q-1;
цикл деления на 2α состоит в следующем:
в первом модулярном вычислительном ядре процессора выполняется операция целочисленного умножения  по модулю р1 q-разрядного двоичного представления знакопозиции
по модулю р1 q-разрядного двоичного представления знакопозиции  модулярной мантиссы
модулярной мантиссы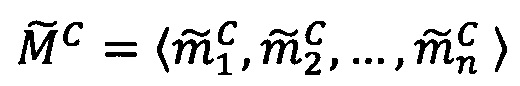 промежуточного результата
промежуточного результата  произведения чисел А и В и значения мультипликативной инверсии P1 по модулю
произведения чисел А и В и значения мультипликативной инверсии P1 по модулю  путем нахождения значения
путем нахождения значения 
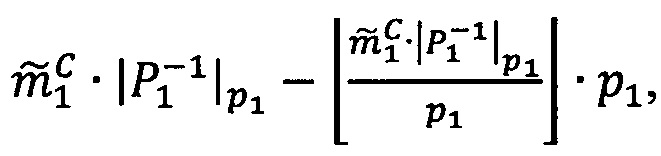 где
где 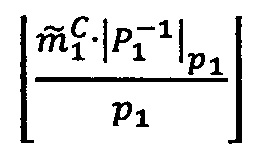 - наибольшее целое, не превышающее
- наибольшее целое, не превышающее 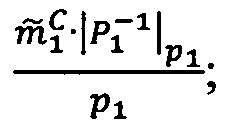 все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
параллельно с этим во втором модулярном вычислительном ядре процессора выполняется операция целочисленного умножения  по модулю р2 q-разрядного двоичного представления знакопозиции
по модулю р2 q-разрядного двоичного представления знакопозиции  модулярной мантиссы
модулярной мантиссы  промежуточного результата
промежуточного результата  произведения чисел А и В и значения мультипликативной инверсии Р2 по модулю
произведения чисел А и В и значения мультипликативной инверсии Р2 по модулю 
параллельно с этим в третьем ÷ n-ом модулярном вычислительном ядре процессора выполняется операция целочисленного умножения  по модулю рn q-разрядного двоичного представления знакопозиции
по модулю рn q-разрядного двоичного представления знакопозиции  модулярной мантиссы
модулярной мантиссы  промежуточного результата
промежуточного результата  произведения чисел А и В и значения мультипликативной инверсии Рn по модулю
произведения чисел А и В и значения мультипликативной инверсии Рn по модулю 
после того, как получены значения элементов вектора  данный вектор загружается в векторные ядра следующим образом:
данный вектор загружается в векторные ядра следующим образом:
в первое векторное вычислительное ядро загружают вектор q-разрядных элементов 
параллельно с этим во второе векторное вычислительное ядро загружают вектор q-разрядных элементов 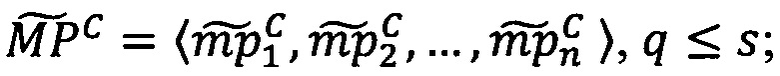
параллельно с этим в третье векторное вычислительное ядро загружают вектор q-разрядных элементов 
после того, как элементы вектора 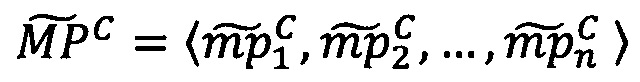 загружены в векторные ядра, производится вычисление ранга и частичного остатка от деления на 2q-1 модулярной мантиссы
загружены в векторные ядра, производится вычисление ранга и частичного остатка от деления на 2q-1 модулярной мантиссы 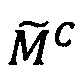 промежуточного результата
промежуточного результата  произведения чисел А и В:
произведения чисел А и В:
- в первом векторном вычислительном ядре вычисляют скалярное произведение векторов 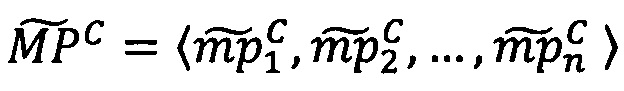 и
и вычисляют значение
вычисляют значение 
 где
где  - наибольшее целое, не превышающее
- наибольшее целое, не превышающее  значение
значение  передается в управляющее ядро;
передается в управляющее ядро;
- параллельно с этим во втором векторном вычислительном ядре вычисляют скалярное произведение векторов  и
и 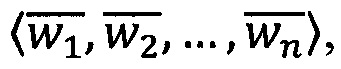 вычисляют значение
вычисляют значение  где
где  - наибольшее целое, не превышающее
- наибольшее целое, не превышающее  значение
значение  передается в управляющее ядро;
передается в управляющее ядро;
- параллельно с этим в третьем векторном вычислительном ядре вычисляют скалярное произведение векторов 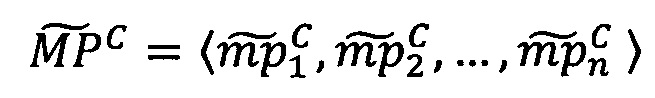 и
и  значение
значение  передается в управляющее ядро;
передается в управляющее ядро;
после того, как результаты скалярного произведения векторов переданы в управляющее ядро, в управляющем ядре вычисляется значение ранга  если
если  или
или  R=Rmax, если
R=Rmax, если  и значение остатка от деления модулярной мантиссы
и значение остатка от деления модулярной мантиссы  промежуточного результата
промежуточного результата  произведения чисел
произведения чисел 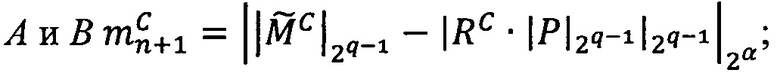
после того, как управляющее ядро передаст во все модулярные и все универсальные целочисленные ядра значения  и α, выполняется деление модулярной мантиссы
и α, выполняется деление модулярной мантиссы  промежуточного результата
промежуточного результата  произведения чисел А и В на число 2α:
произведения чисел А и В на число 2α:
в первом модулярном вычислительном ядре процессора выполняется операция вычитания  по модулю р1 q-разрядного двоичного представления знакопозиции
по модулю р1 q-разрядного двоичного представления знакопозиции  модулярной мантиссы
модулярной мантиссы  промежуточного результата
промежуточного результата  произведения чисел А и В и значения
произведения чисел А и В и значения  следующим образом: если
следующим образом: если 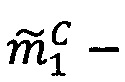
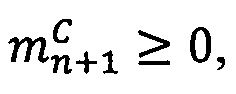 то
то 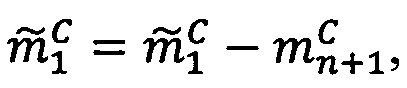 если
если 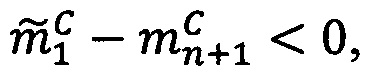 то
то  после чего выполняется операция умножения
после чего выполняется операция умножения  по модулю р1 q-разрядного двоичного представления знакопозиции
по модулю р1 q-разрядного двоичного представления знакопозиции  модулярной мантиссы
модулярной мантиссы 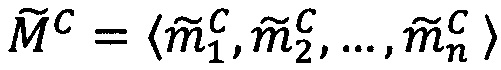 промежуточного результата
промежуточного результата  произведения чисел А и В и значения мультипликативной инверсии 2α по модулю
произведения чисел А и В и значения мультипликативной инверсии 2α по модулю  путем нахождения значения
путем нахождения значения 
 - наибольшее целое, не превышающее
- наибольшее целое, не превышающее  после чего, если
после чего, если  , выполняется операция сложения
, выполняется операция сложения 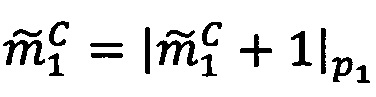 по модулю р1 q-разрядного двоичного представления знакопозиции
по модулю р1 q-разрядного двоичного представления знакопозиции  модулярной мантиссы
модулярной мантиссы 
 промежуточного результата
промежуточного результата  произведения чисел А и В следующим образом: если
произведения чисел А и В следующим образом: если 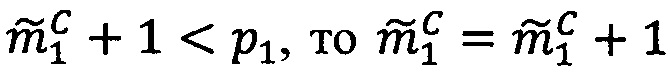 , если
, если  то
то  все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
параллельно с этим во втором модулярном вычислительном ядре процессора выполняется операция вычитания 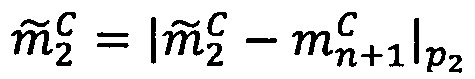 по модулю р2 q-разрядного двоичного представления знакопозиции
по модулю р2 q-разрядного двоичного представления знакопозиции  модулярной мантиссы
модулярной мантиссы  промежуточного результата
промежуточного результата 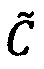 произведения чисел А и В и значения
произведения чисел А и В и значения  после чего выполняется операция умножения
после чего выполняется операция умножения  по модулю р2 q-разрядного двоичного представления знакопозиции
по модулю р2 q-разрядного двоичного представления знакопозиции 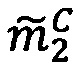 и значения мультипликативной инверсии 2α по модулю
и значения мультипликативной инверсии 2α по модулю 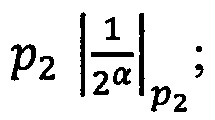 после чего, если
после чего, если  , выполняется операция сложения
, выполняется операция сложения  по модулю р2;
по модулю р2;
параллельно с этим в третьем ÷ n-ом модулярном вычислительном ядре процессора выполняется операция вычитания  по модулю р1n q-разрядного двоичного представления знакопозиции
по модулю р1n q-разрядного двоичного представления знакопозиции  модулярной мантиссы
модулярной мантиссы 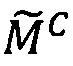 промежуточного результата
промежуточного результата  произведения чисел А и В и значения
произведения чисел А и В и значения  после чего выполняется операция умножения
после чего выполняется операция умножения  по модулю рn q-разрядного двоичного представления знакопозиции
по модулю рn q-разрядного двоичного представления знакопозиции 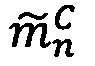 и значения мультипликативной инверсии 2α по модулю
и значения мультипликативной инверсии 2α по модулю 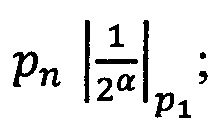 после чего, если
после чего, если 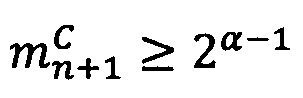 , выполняется операция сложения
, выполняется операция сложения  по модулю рn;
по модулю рn;
параллельно с этим во втором универсальном вычислительном ядре процессора выполняется коррекция  если
если  иначе
иначе  двоичного значения нижней границы интервальной логарифмической характеристики
двоичного значения нижней границы интервальной логарифмической характеристики 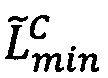 промежуточного результата
промежуточного результата 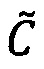 произведения чисел А и В;
произведения чисел А и В;
параллельно с этим в третьем универсальном вычислительном ядре процессора выполняется коррекция  если
если  иначе
иначе 
 двоичного значения верхней границы интервальной логарифмической характеристики
двоичного значения верхней границы интервальной логарифмической характеристики  промежуточного результата
промежуточного результата  произведения чисел А и В; цикл деления на 2α заканчивается;
произведения чисел А и В; цикл деления на 2α заканчивается;
если знак  промежуточного результата
промежуточного результата 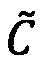 произведения чисел А и В не равен 0 и значение
произведения чисел А и В не равен 0 и значение  верхней границы интервальной логарифмической характеристики промежуточного результата
верхней границы интервальной логарифмической характеристики промежуточного результата  произведения чисел А и В больше или равно значению нижней границы интервальной логарифмической характеристики максимально возможного значения мантиссы
произведения чисел А и В больше или равно значению нижней границы интервальной логарифмической характеристики максимально возможного значения мантиссы  то управляющее ядро передает во все модулярные и все универсальные целочисленные ядра значение поправочных коэффициентов zA, zB, после чего:
то управляющее ядро передает во все модулярные и все универсальные целочисленные ядра значение поправочных коэффициентов zA, zB, после чего:
в первое модулярное ядро загружают q-разрядные двоичные значения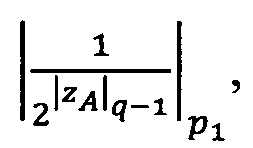
 мультипликативных инверсий
мультипликативных инверсий 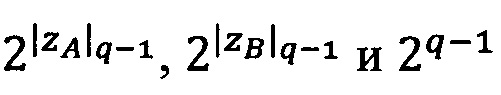 по модулю р1;
по модулю р1;
параллельно с этим во второе модулярное ядро загружают q-разрядные двоичные значения 
 и
и  мультипликативных инверсий
мультипликативных инверсий 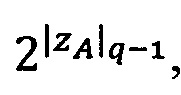
 и 2q-1 по модулю р2;
и 2q-1 по модулю р2;
параллельно с этим в третье ÷ n-ое модулярное ядро загружают q-разрядные двоичные значения 
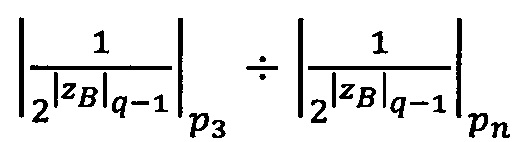 и
и 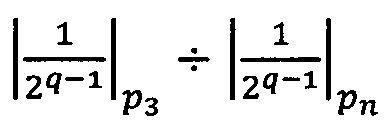 мультипликативных инверсий
мультипликативных инверсий 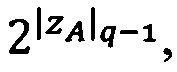
 и 2q-1 по модулю р3÷рn;
и 2q-1 по модулю р3÷рn;
параллельно с этим в первом универсальном вычислительном ядре процессора выполняется коррекция  двоичного порядка
двоичного порядка  промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
параллельно с этим в управляющем ядре вычисляется количество итераций jA=0, если zA≤q-1,  если zA>q-1 и jB=0, если zB≤q-1,
если zA>q-1 и jB=0, если zB≤q-1, 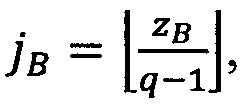 если zB>q-1.
если zB>q-1.
в случае если 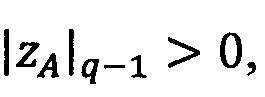 выполняется один цикл деления
выполняется один цикл деления  на 2α, где
на 2α, где 
 затем, если количество итераций jA≥1, выполняется jA циклов деления
затем, если количество итераций jA≥1, выполняется jA циклов деления на 2α, где α=q-1;
на 2α, где α=q-1;
цикл деления  на 2α состоит в следующем:
на 2α состоит в следующем:
в первом модулярном вычислительном ядре процессора выполняется операция целочисленного умножения  по модулю р1 q-разрядного двоичного представления знакопозиции
по модулю р1 q-разрядного двоичного представления знакопозиции  модулярной мантиссы
модулярной мантиссы 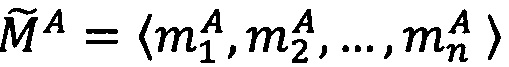 числа А и значения мультипликативной инверсии Р1 по модулю р1
числа А и значения мультипликативной инверсии Р1 по модулю р1  , путем нахождения значения
, путем нахождения значения 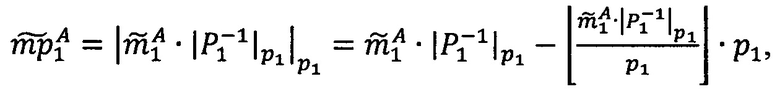 где
где  - наибольшее целое, не превышающее
- наибольшее целое, не превышающее 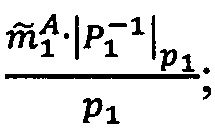 все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
параллельно с этим во втором модулярном вычислительном ядре процессора выполняется операция целочисленного умножения 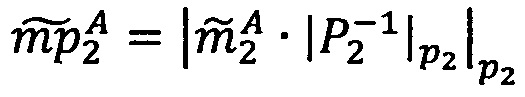 по модулю р2 q- разрядного двоичного представления знакопозиции
по модулю р2 q- разрядного двоичного представления знакопозиции  модулярной мантиссы
модулярной мантиссы 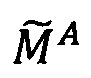 и значения мультипликативной инверсии Р2 по модулю
и значения мультипликативной инверсии Р2 по модулю 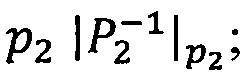
параллельно с этим в третьем ÷ n-ом модулярном вычислительном ядре процессора выполняется операция целочисленного умножения 
 по модулю р3÷рn q-разрядного двоичного представления знакопозиции
по модулю р3÷рn q-разрядного двоичного представления знакопозиции  модулярной мантиссы
модулярной мантиссы  и значения мультипликативной инверсии Р3÷Рn по модулю
и значения мультипликативной инверсии Р3÷Рn по модулю 
после того, как получены значения элементов вектора  данный вектор загружается в векторные ядра следующим образом:
данный вектор загружается в векторные ядра следующим образом:
в первое векторное вычислительное ядро загружают вектор q-разрядных элементов 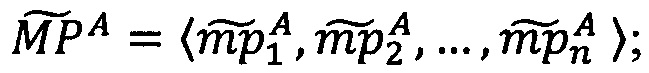
параллельно с этим во второе векторное вычислительное ядро загружают вектор q-разрядных элементов 
параллельно с этим в третье векторное вычислительное ядро загружают вектор q-разрядных элементов 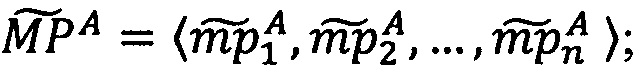
после того, как элементы вектора  загружены в векторные ядра производится вычисление ранга и частичного остатка от деления на 2q-1 модулярной мантиссы
загружены в векторные ядра производится вычисление ранга и частичного остатка от деления на 2q-1 модулярной мантиссы 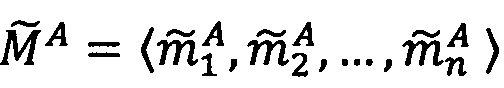 числа А следующим образом:
числа А следующим образом:
- в первом векторном вычислительном ядре вычисляют скалярное произведение векторов 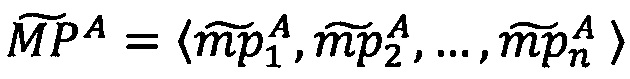 и
и 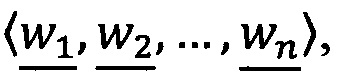 вычисляют значение
вычисляют значение 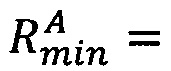
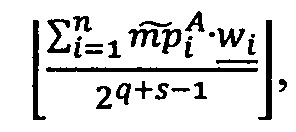 где
где  - наибольшее целое, на превышающее
- наибольшее целое, на превышающее  значение
значение  передается в управляющее ядро;
передается в управляющее ядро;
- параллельно с этим во втором векторном вычислительном ядре вычисляют скалярное произведение векторов  и
и  вычисляют значение
вычисляют значение  где
где 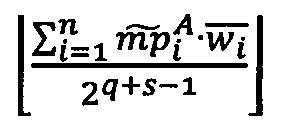 - наибольшее целое, не превышающее
- наибольшее целое, не превышающее 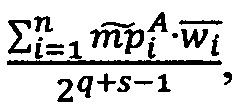 значение
значение 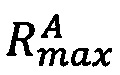 передается в управляющее ядро;
передается в управляющее ядро;
- параллельно с этим в третьем векторном вычислительном ядре вычисляют скалярное произведение векторов 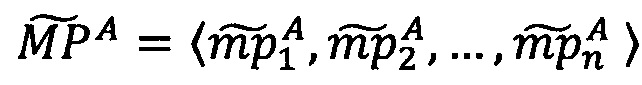 и
и 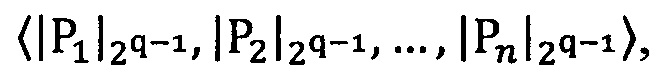 значение
значение  передается в управляющее ядро;
передается в управляющее ядро;
после того, как результаты скалярного произведения векторов переданы в управляющее ядро, в управляющем ядре вычисляется значение ранга  , если
, если  или
или  если
если  и значение остатка от деления модулярной мантиссы
и значение остатка от деления модулярной мантиссы  числа А
числа А 
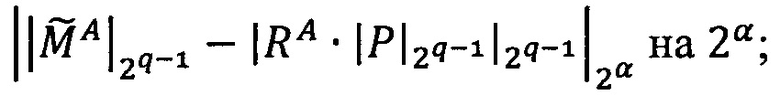
после того, как управляющее ядро передаст во все модулярные и все универсальные целочисленные ядра значения  и α, выполняется деление модулярной мантиссы
и α, выполняется деление модулярной мантиссы  числа А на число 2α:
числа А на число 2α:
в первом модулярном вычислительном ядре процессора выполняется операция вычитания 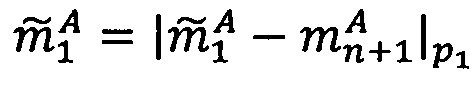 по модулю р1 q-разрядного двоичного представления знакопозиции
по модулю р1 q-разрядного двоичного представления знакопозиции  модулярной мантиссы
модулярной мантиссы 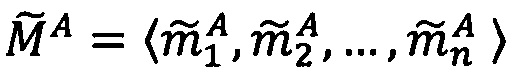 числа А и значения
числа А и значения  следующим образом: если
следующим образом: если  то
то  если
если 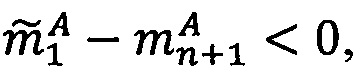 то
то  после чего выполняется операция умножения
после чего выполняется операция умножения 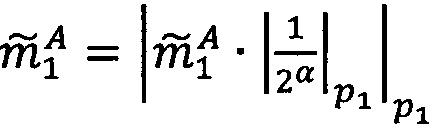 по модулю р1 q-разрядного двоичного представления знакопозиции
по модулю р1 q-разрядного двоичного представления знакопозиции  модулярной мантиссы
модулярной мантиссы  числа А и значения мультипликативной инверсии 2α по
числа А и значения мультипликативной инверсии 2α по
модулю P1 путем нахождения значения
путем нахождения значения  -
-  где
где 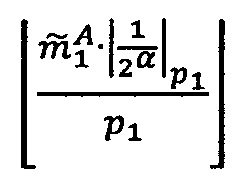 - наибольшее целое, не превышающее
- наибольшее целое, не превышающее  после чего, если
после чего, если  , выполняется операция сложения
, выполняется операция сложения 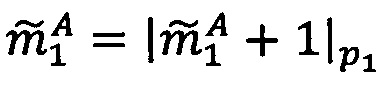 по модулю р1 q-разрядного двоичного представления знакопозиции
по модулю р1 q-разрядного двоичного представления знакопозиции  модулярной мантиссы
модулярной мантиссы 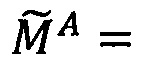
 числа А следующим образом: если
числа А следующим образом: если  то
то  , если
, если  то
то 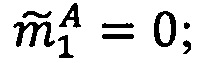 все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
параллельно с этим во втором модулярном вычислительном ядре процессора выполняется операция вычитания 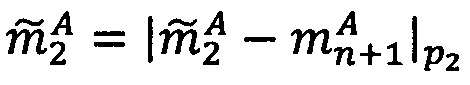 по модулю р2 q-разрядного двоичного представления знакопозиции
по модулю р2 q-разрядного двоичного представления знакопозиции  модулярной мантиссы
модулярной мантиссы 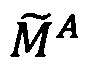 числа А и значения
числа А и значения 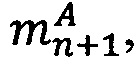 после чего выполняется операция умножения
после чего выполняется операция умножения 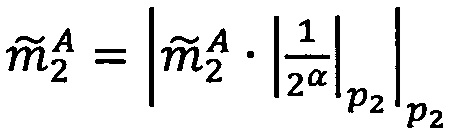 по модулю р2 q-разрядного двоичного представления знакопозиции
по модулю р2 q-разрядного двоичного представления знакопозиции  и значения мультипликативной инверсии 2α по модулю
и значения мультипликативной инверсии 2α по модулю  после чего, если
после чего, если  , выполняется операция сложения
, выполняется операция сложения 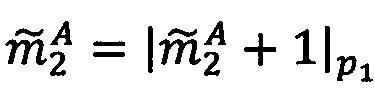 по модулю р2;
по модулю р2;
параллельно с этим в третьем ÷ n-ом модулярном вычислительном ядре процессора выполняется операция вычитания 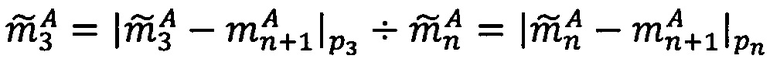 по модулю р3÷рn q-разрядного двоичного представления знакопозиции
по модулю р3÷рn q-разрядного двоичного представления знакопозиции 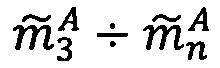 модулярной мантиссы
модулярной мантиссы 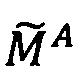 числа А и значения
числа А и значения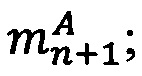 после чего выполняется операция умножения
после чего выполняется операция умножения  по модулю р3÷рn q-разрядного двоичного представления знакопозиции
по модулю р3÷рn q-разрядного двоичного представления знакопозиции  и значения мультипликативной инверсии 2α по модулю
и значения мультипликативной инверсии 2α по модулю 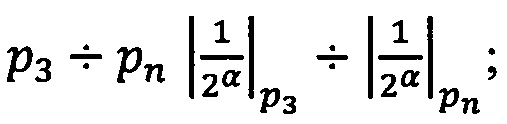 после чего, если
после чего, если  , выполняется операция сложения
, выполняется операция сложения  по модулю р3÷рn;
по модулю р3÷рn;
параллельно с этим во втором универсальном вычислительном ядре процессора выполняется коррекция  если
если 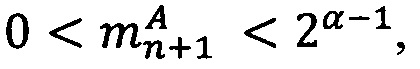 иначе
иначе 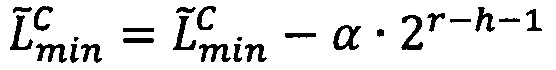 двоичного значения нижней границы интервальной логарифмической характеристики
двоичного значения нижней границы интервальной логарифмической характеристики  промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
параллельно с этим в третьем универсальном вычислительном ядре процессора выполняется коррекция  если
если  иначе
иначе 
 двоичного значения верхней границы интервальной логарифмической характеристики
двоичного значения верхней границы интервальной логарифмической характеристики  промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
цикл деления  завершается;
завершается;
в случае если 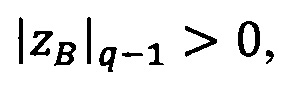 выполняется один цикл деления
выполняется один цикл деления  на 2α, где α=
на 2α, где α= затем если количество итераций jB≥1, выполняется jB циклов деления
затем если количество итераций jB≥1, выполняется jB циклов деления  на 2α, где α=q-1;
на 2α, где α=q-1;
цикл деления  на 2α состоит в следующем:
на 2α состоит в следующем:
в первом модулярном вычислительном ядре процессора выполняется операция целочисленного умножения  по модулю р1 q-разрядного двоичного представления знакопозиции
по модулю р1 q-разрядного двоичного представления знакопозиции  модулярной мантиссы
модулярной мантиссы  числа В и значения мультипликативной инверсии Р1 по модулю р1
числа В и значения мультипликативной инверсии Р1 по модулю р1  путем нахождения значения
путем нахождения значения  - наибольшее целое, не превышающее
- наибольшее целое, не превышающее  все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
параллельно с этим во втором модулярном вычислительном ядре процессора выполняется операция целочисленного умножения  по модулю р2 q-разрядного двоичного представления знакопозиции
по модулю р2 q-разрядного двоичного представления знакопозиции  модулярной мантиссы
модулярной мантиссы  и значения мультипликативной инверсии Р2 по модулю
и значения мультипликативной инверсии Р2 по модулю 
параллельно с этим в третьем ÷ n-ом модулярном вычислительном ядре процессора выполняется операция целочисленного умножения 
 по модулю р3÷рn q-разрядного двоичного представления знакопозиции
по модулю р3÷рn q-разрядного двоичного представления знакопозиции  модулярной мантиссы
модулярной мантиссы  и значения мультипликативной инверсии Р3÷Рn по модулю
и значения мультипликативной инверсии Р3÷Рn по модулю 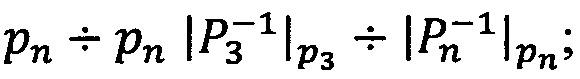
после того, как получены значения элементов вектора  данный вектор загружается в векторные ядра следующим образом:
данный вектор загружается в векторные ядра следующим образом:
в первое векторное вычислительное ядро загружают вектор q-разрядных элементов 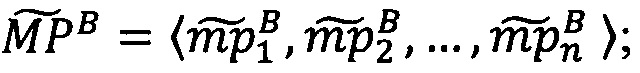
параллельно с этим во второе векторное вычислительное ядро загружают вектор q-разрядных элементов 
параллельно с этим в третье векторное вычислительное ядро загружают вектор q-разрядных элементов 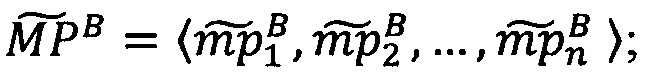
после того, как элементы вектора  загружены в векторные ядра, производится вычисление ранга и остатка от деления на 2q-1 следующим образом:
загружены в векторные ядра, производится вычисление ранга и остатка от деления на 2q-1 следующим образом:
в первом векторном вычислительном ядре вычисляют скалярное произведение векторов  и
и  значение
значение  передается в управляющее ядро;
передается в управляющее ядро;
параллельно с этим во втором векторном вычислительном ядре вычисляют скалярное произведение векторов  и
и  значение
значение  передается в управляющее ядро;
передается в управляющее ядро;
параллельно с этим в третьем векторном вычислительном ядре вычисляют скалярное произведение векторов  и
и  значение
значение 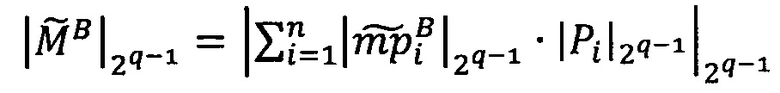 передается в управляющее ядро;
передается в управляющее ядро;
после того, как результаты скалярного произведения векторов переданы в управляющее ядро, в управляющем ядре вычисляется значение ранга RB=RBmin, если 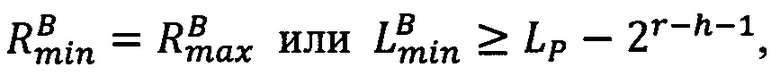
 если
если 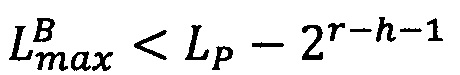 и значение остатка от деления модулярной мантиссы
и значение остатка от деления модулярной мантиссы  числа В
числа В 

после того, как управляющее ядро передаст во все модулярные и все универсальные целочисленные ядра значения 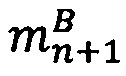 и α, выполняется деление модулярной мантиссы
и α, выполняется деление модулярной мантиссы  числа В на число 2α:
числа В на число 2α:
в первом модулярном вычислительном ядре процессора выполняется операция вычитания  по модулю р1 q-разрядного двоичного представления знакопозиции
по модулю р1 q-разрядного двоичного представления знакопозиции  модулярной мантиссы,
модулярной мантиссы,  числа В и значения
числа В и значения  следующим образом: если
следующим образом: если 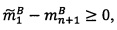 то
то 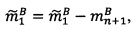 если
если 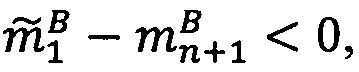 то
то  после чего выполняется операция умножения
после чего выполняется операция умножения  по модулю р1 q-разрядного двоичного представления знакопозиции
по модулю р1 q-разрядного двоичного представления знакопозиции  модулярной мантиссы
модулярной мантиссы  числа В и значения мультипликативной инверсии 2α по модулю p1
числа В и значения мультипликативной инверсии 2α по модулю p1 путем нахождения значения
путем нахождения значения  -
- 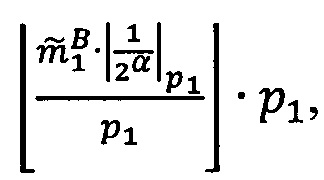 где
где 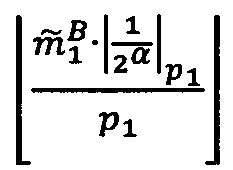 - наибольшее целое, не превышающее
- наибольшее целое, не превышающее  после чего, если
после чего, если  , выполняется операция сложения
, выполняется операция сложения  по модулю р1 q-разрядного двоичного представления знакопозиции
по модулю р1 q-разрядного двоичного представления знакопозиции 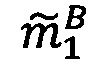 модулярной мантиссы
модулярной мантиссы 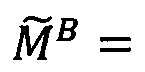
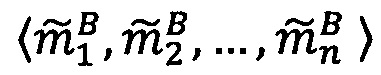 числа В следующим образом: если
числа В следующим образом: если  то
то 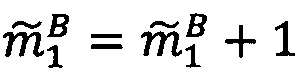 , если
, если 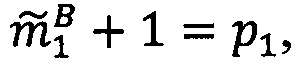 то
то 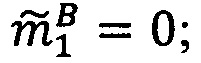 все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
параллельно с этим во втором модулярном вычислительном ядре процессора выполняется операция вычитания 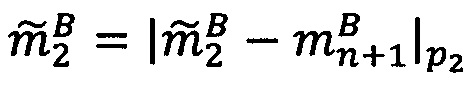 по модулю р2 q-разрядного двоичного представления знакопозиции
по модулю р2 q-разрядного двоичного представления знакопозиции  модулярной мантиссы
модулярной мантиссы 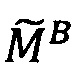 числа В и значения
числа В и значения 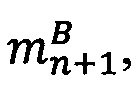 после чего выполняется операция умножения
после чего выполняется операция умножения  по модулю р2 q-разрядного двоичного представления знакопозиции
по модулю р2 q-разрядного двоичного представления знакопозиции  и значения мультипликативной инверсии 2α по модулю
и значения мультипликативной инверсии 2α по модулю 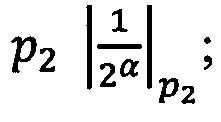 после чего, если
после чего, если 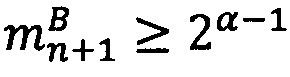 , выполняется операция сложения
, выполняется операция сложения  по модулю р2;
по модулю р2;
параллельно с этим в третьем ÷ n-ом модулярном вычислительном ядре процессора выполняется операция вычитания  по модулю р3÷рn q-разрядного двоичного представления знакопозиции
по модулю р3÷рn q-разрядного двоичного представления знакопозиции  модулярной мантиссы
модулярной мантиссы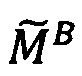 числа В и значения
числа В и значения  после чего выполняется операция умножения
после чего выполняется операция умножения  по модулю р3÷рn q-разрядного двоичного представления знакопозиции
по модулю р3÷рn q-разрядного двоичного представления знакопозиции  и значения мультипликативной инверсии 2α по модулю
и значения мультипликативной инверсии 2α по модулю  после чего, если
после чего, если  , выполняется операция сложения
, выполняется операция сложения 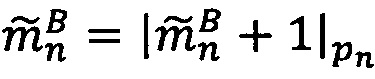 по модулю р3÷рn;
по модулю р3÷рn;
параллельно с этим во втором универсальном вычислительном ядре процессора выполняется коррекция  если
если  иначе
иначе  двоичного значения нижней границы интервальной логарифмической характеристики
двоичного значения нижней границы интервальной логарифмической характеристики  промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
параллельно с этим в третьем универсальном вычислительном ядре процессора выполняется коррекция  если
если  иначе
иначе 
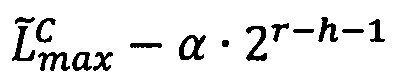 двоичного значения верхней границы интервальной логарифмической характеристики
двоичного значения верхней границы интервальной логарифмической характеристики  промежуточного результата
промежуточного результата  произведения чисел А и В;
произведения чисел А и В;
цикл деления  на 2α завершается;
на 2α завершается;
после того, как выполнена коррекция мантисс 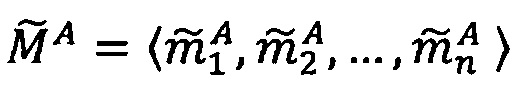 и
и 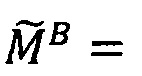
 чисел А и В соответственно, выполняется их умножение следующим образом:
чисел А и В соответственно, выполняется их умножение следующим образом:
в первом модулярном вычислительном ядре процессора выполняется операция целочисленного умножения  по модулю р1 q-разрядных двоичных представлений знакопозиций
по модулю р1 q-разрядных двоичных представлений знакопозиций 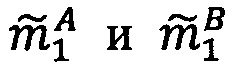 модулярных мантисс
модулярных мантисс 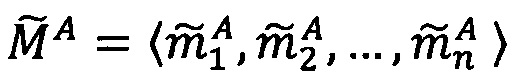 и
и  чисел А и В соответственно, путем нахождения значения
чисел А и В соответственно, путем нахождения значения 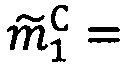
 где
где  - наибольшее целое, не превышающее
- наибольшее целое, не превышающее 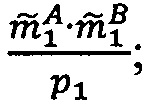
параллельно с этим во втором модулярном вычислительном ядре процессора выполняется операция целочисленного умножения  по модулю р2 q-разрядных двоичных представлений знакопозиций
по модулю р2 q-разрядных двоичных представлений знакопозиций  модулярных мантисс
модулярных мантисс 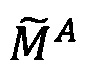 и
и  чисел А и В соответственно; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
чисел А и В соответственно; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
параллельно с этим в третьем ÷ n-ом модулярном вычислительном ядре процессора выполняется операция целочисленного умножения 
 по модулю р3÷рn q-разрядных двоичных представлений знакопозиций
по модулю р3÷рn q-разрядных двоичных представлений знакопозиций  модулярных мантисс
модулярных мантисс  и
и  чисел А и В соответственно; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
чисел А и В соответственно; все операции являются целочисленными и выполняются в позиционной двоичной системе счисления;
в результате выполнения данных операций получается произведение 
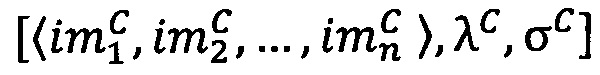 чисел
чисел  и
и 
 представленное в модулярно-логарифмическом формате с плавающей точкой.
представленное в модулярно-логарифмическом формате с плавающей точкой.
| СПОСОБ ОРГАНИЗАЦИИ ВЫПОЛНЕНИЯ ОПЕРАЦИИ УМНОЖЕНИЯ ДВУХ ЧИСЕЛ В МОДУЛЯРНО-ПОЗИЦИОННОМ ФОРМАТЕ ПРЕДСТАВЛЕНИЯ С ПЛАВАЮЩЕЙ ТОЧКОЙ НА УНИВЕРСАЛЬНЫХ МНОГОЯДЕРНЫХ ПРОЦЕССОРАХ | 2012 |
|
RU2509345C1 |
| СПОСОБ, УСТРОЙСТВО И КОМАНДА ДЛЯ ВЫПОЛНЕНИЯ ЗНАКОВОЙ ОПЕРАЦИИ УМНОЖЕНИЯ | 2003 |
|
RU2275677C2 |
| Способ приготовления мыла | 1923 |
|
SU2004A1 |
| US 5144574 A, 01.09.1992 | |||
| US 4366549 A, 28.12.1982. | |||
Авторы
Даты
2018-09-06—Публикация
2017-10-06—Подача