Изобретение относится к вычислительной технике и предназначено для выполнения операции сравнения двух чисел, представленных в системе остаточных классов.
Известно устройство для сравнения чисел, выраженных в системе остаточных классов (А.С. SU №608155, БИ №19, 19.01.1976), которое содержит блоки преобразования 1, 2, каждый из которых состоит из регистра 3, сумматора 4, узла деления 5, группы элементов ИЛИ 6, группы элементов И 7, элементы И 8, 9, элемент ИЛИ 10, распределитель импульсов 11, регистр 12 хранения модулей, блок 13 выбора модулей, блок сравнения 14, блок сравнения на равенство 15, коммутаторы 16, 17, элемент ИЛИ 18. Данное устройство основано на точном методе преобразования модулярных чисел к системе счисления со смешанными основаниями. Недостаток данного устройства - большая сложность и низкое быстродействие.
Наиболее близким к заявленному изобретению является устройство для сравнения чисел, представленных в системе остаточных классов, основанное на приближенном методе (А.С. RU №2503992, БИ №1, 10.01.2014), содержащее входные регистры 1, 9 для хранения чисел, схемы определения знаков чисел 2 и 8, схемы сдвига полярности 3, 7, просмотровые таблицы 5, 6 для хранения произведения констант и разрядов СОК, сумматор 10, логический элемент «ИСКЛЮЧАЮЩЕЕ ИЛИ» 4, схемы анализа знака 11. Однако данное устройство не позволяет проверить корректность получаемого результата сравнения двух близлежащих модулярных чисел, поскольку не учитываются ошибки округления, образующиеся при вычислении приближенной относительной величины модулярного числа.
Техническим результатом заявляемого устройства для сравнения чисел в системе остаточных классов является повышение быстродействия по отношению к устройствам, основанным на преобразовании сравниваемых чисел в позиционную систему счисления со смешанными основаниями, и обеспечение контроля корректности результата операции сравнения. Представленные положения обеспечиваются за счет использования новой интервально-позиционной характеристики модулярной арифметики, которая аппроксимирует с двух сторон относительную величину числа в модулярном представлении.
Описание устройства: в основе функционирования заявляемого устройства для сравнения чисел в системе остаточных классов лежит новый метод интервальной оценки относительной величины модулярного числа. Рассмотрим его.
Пусть базис системы остаточных классов (СОК) задан попарно взаимно простыми модулями р1, p2, …, pn и Р - произведение всех модулей. Тогда целое число Х из интервала [0, Р-1] будет представлено в виде независимых наименьших неотрицательных остатков (вычетов) 〈х1, х2, …, xn〉, причем xi≡Х mod pi↔|X|pi. Позиционная величина числа X в соответствии с Китайской теоремой об остатках определяется соотношением
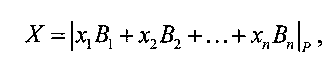
где В1, В2, …, Bn - ортогональные базисы СОК, каждый i-й из которых суть произведение чисел Pi=Р/pi и 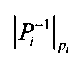 . Здесь
. Здесь 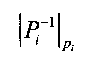 - это вес ортогонального базиса (мультипликативная инверсия от Pi по модулю pi). Относительная величина Е(Х/Р) модулярного числа X - это отношение его позиционного значения к произведению модулей Р, то есть
- это вес ортогонального базиса (мультипликативная инверсия от Pi по модулю pi). Относительная величина Е(Х/Р) модулярного числа X - это отношение его позиционного значения к произведению модулей Р, то есть
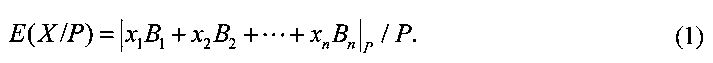
Поскольку точное рациональное значение Е(Х/Р), изменяющееся в полуинтервале [0, 1), в общем случае не представимо в ЭВМ с ограниченной разрядной сеткой, возникает задача его аппроксимации. Для решения этой задачи служит интервально-позиционная характеристика (ИПХ) 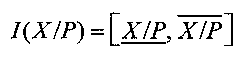 , которая определяется как отрезок (замкнутый вещественный интервал) с направленно округленными границами
, которая определяется как отрезок (замкнутый вещественный интервал) с направленно округленными границами  и
и 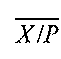 , удовлетворяющими условию
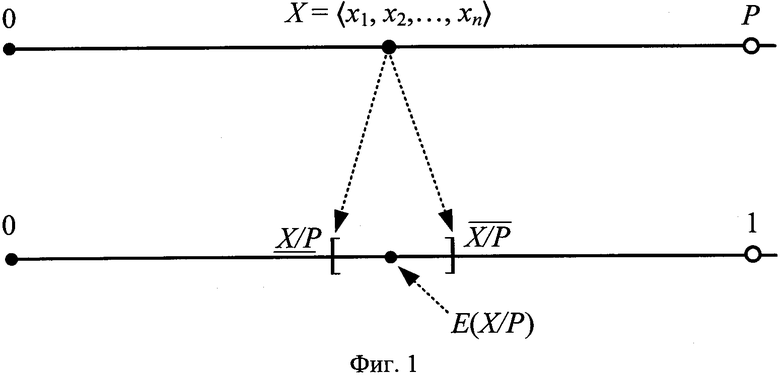
, удовлетворяющими условию 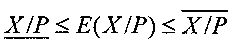 . Таким образом, ИПХ проецирует диапазон СОК на полуинтервал [0, 1), ассоциируя всякое модулярное число X с парой округленных позиционных чисел - границ, которые локализуют его относительную величину, как показано на фиг. 1.
. Таким образом, ИПХ проецирует диапазон СОК на полуинтервал [0, 1), ассоциируя всякое модулярное число X с парой округленных позиционных чисел - границ, которые локализуют его относительную величину, как показано на фиг. 1.
Границы ИПХ представляются в виде двоичных чисел с плавающей точкой
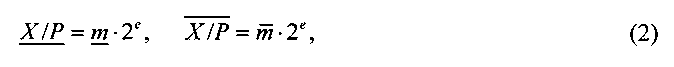
где  и
и  - мантиссы, е - порядок, который одинаков для обеих границ. При этом нижняя граница всегда вычисляется с округлением «вниз», а верхняя - с округлением «вверх». За счет этого обеспечивается включение I(Х/Р)∈Е(Х/Р), то есть точная относительная величина (1) модулярного числа X локализуется его ИПХ.
- мантиссы, е - порядок, который одинаков для обеих границ. При этом нижняя граница всегда вычисляется с округлением «вниз», а верхняя - с округлением «вверх». За счет этого обеспечивается включение I(Х/Р)∈Е(Х/Р), то есть точная относительная величина (1) модулярного числа X локализуется его ИПХ.
Абсолютную погрешность ИПХ характеризует ее диаметр

Объективной мерой точности ИПХ является ее относительная ошибка
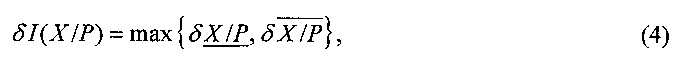
где 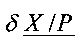 и
и 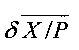 определяются отношениями абсолютных погрешностей границ (2) к величине (3) при Х≠0. В предельном случае имеем
определяются отношениями абсолютных погрешностей границ (2) к величине (3) при Х≠0. В предельном случае имеем

Пусть n - количество модулей СОК, Р - произведение модулей СОК, k - разрядность мантисс в представлении границ (2), ε - предел допустимой относительной ошибки ИПХ. Введем обозначения
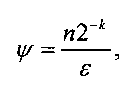
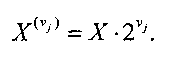
Алгоритм вычисления ИПХ с погрешностью (4), не превышающей допустимого предела ε, формулируется следующим образом.
АЛГОРИТМ 1.
Шаг 0: предварительно с использованием расширенного алгоритма Евклида вычисляются и сохраняются веса ортогональных базисов

Кроме этого, вычисляется и сохраняется в памяти вектор натуральных степеней двойки

где νj=log2(1/2jψj) для всех j=1, 2, …, g, причем g=log2(1/Р)/(1+log2ψ)-1.
Также вычисляется и сохраняется в памяти матрица смещенных весов ортогональных базисов, строки которой ассоциированы с элементами вектора v, а столбцы - с модулями

Шаг 1. Вычисляется значение верхней границы ИПХ (формула прямо следует из Китайской теоремы об остатках)

где ↑ говорит о том, что вычисление и суммирование слагаемых выполняется с округлением с избытком («вверх»).
Шаг 2. Если 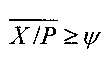 , то осуществляется переход к шагу 3, иначе - к шагу 4.
, то осуществляется переход к шагу 3, иначе - к шагу 4.
Шаг 3. Вычисляется значение нижней границы ИПХ
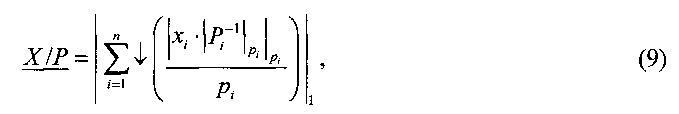
где ↓ говорит о том, что вычисление и суммирование слагаемых осуществляется с округлением с недостатком («вниз»). Далее осуществляется переход к шагу 10.
Шаг 4. Устанавливается начальный индекс смещения j=1. Далее - переход к шагу 5.
Шаг 5. Вычисляется смещенная верхняя граница ИПХ

где Mj,i - i-й элемент j-й строки матрицы М.
Шаг 6. Если  , то заданная точность вычислений достигнута. В этом случае перейти к шагу 8, иначе - к шагу 7.
, то заданная точность вычислений достигнута. В этом случае перейти к шагу 8, иначе - к шагу 7.
Шаг 7. Индекс j увеличивается на единицу и выполняется возврат к шагу 5.
Шаг 8. В соответствии с найденным в итерационном блоке индексом смещения j выбирается j-я строка матрицы М и вычисляется смещенная нижняя граница

Шаг 9. По индексу смещения j выбирается из вектора v элемент 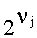
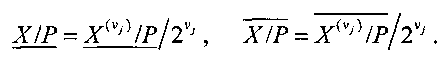
Шаг 10. Алгоритм завершается, возвращая значения границ  и
и 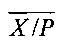 .
.
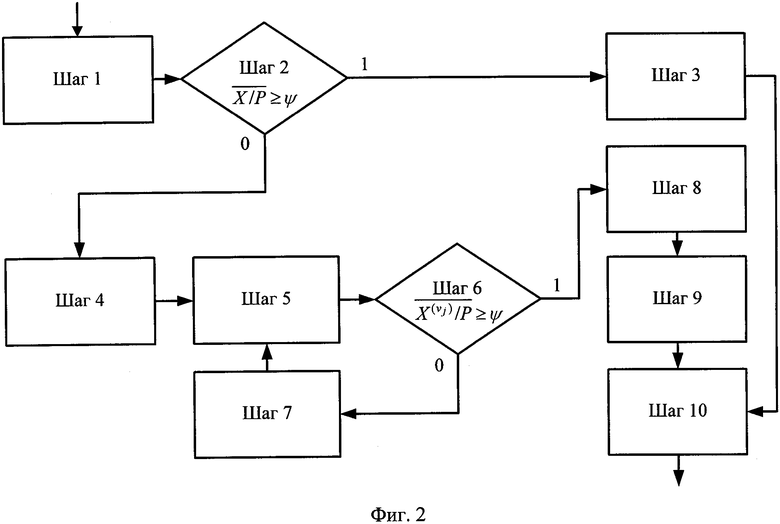
Схема алгоритма 1 представлена на фиг. 2. Конечность алгоритма (отсутствие зацикливания) обеспечивается принятым способом задания вектора v, который гарантирует, что  , где
, где  .
.
Максимальное количество итераций составляет

При этом гарантируется, что за g итераций ИПХ для самого малого ненулевого числа Х=1 будет вычислена с относительной ошибкой, которая не превышает ε, то есть diam I(Х/Р)/(1/Р)≤ε.
Ограничения представленного алгоритма: во-первых, должно выполняться условие ψ<0,5; во-вторых, минимальный показатель степени (порядок) emin в формате с плавающей точкой, который используется для представления границ ИПХ, должен быть не больше разности е-νj, где е - порядок в экспоненциальном представлении границы ИПХ, а νj - показатель смещающей степени двойки, подбираемый на шагах 5-6-7. Рассмотрим пример.
ПРИМЕР 1.
Пусть модулярная система определена набором модулей {7, 9, 11, 13}. Требуется вычислить ИПХ для чисел Х=〈1,6,10,0〉 и Y=〈4,7,3,2〉 с погрешностью, не превышающей 1%, в четырехзначной десятичной арифметике, то есть с округлением до четырех значащих цифр (значащие цифры числа - это все цифры в его записи, начиная с первой ненулевой слева). Для наглядности будем использовать десятичную, а не двоичную систему счисления, поэтому приведенный выше алгоритм 1 будет иметь соответствующую десятичную интерпретацию.
1. Определим все необходимые константы для заданной системы модулей:
- набор весов ортогональных базисов (5): {6, 5, 9, 10};
- проверочное число ψ=4·10-4/0,01=0,04;
- вектор смещающих степеней (6): v=(101, 102, 103);
- матрица смещенных весов ортогональных базисов (7)
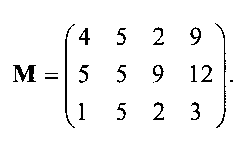
2. Вначале вычислим ИПХ числа X.
2.1. Вычисляем верхнюю границу по формуле (8):

2.2. Так как 0,3722>0,04, то уточнение ИПХ не требуется. Вычисляем нижнюю границу по формуле (9)
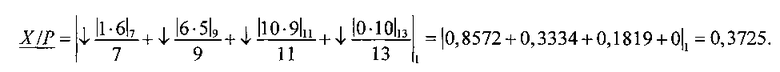
Таким образом, относительная величина числа Х=〈1,6,10,0〉 локализуется интервалом [0,3722, 0,3725]. Для проверки преобразуем X в позиционную систему: Х=3354, следовательно, 0,3722<Е(Х/Р)=3354/9009<0,3725. Относительная ошибка 0,08%.
3. Теперь вычислим ИПХ числа Y.
3.1. Вычисляем верхнюю границу по формуле (8)

3.2. Поскольку 0,0029<0,04, то требуемая точность ИПХ не обеспечена. Значит надо применять уточняющие итерации. Примем j=1 и вычислим смещенную верхнюю границу по формуле (10), выбирая в качестве мультипликативных инверсий первую строку матрицы М
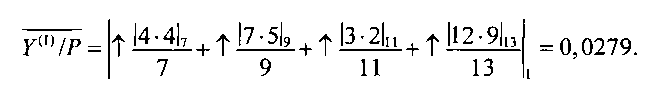
3.3. Требуемая точность не достигнута, так как 0,0279<0,04. Поэтому принимаем j=2 и вновь вычисляем смещенную верхнюю границу по формуле (10), но с использованием второй строки матрицы М

3.4. Так как 0,2777>0,04, то точность достигнута. Вычисляем нижнюю границу в соответствии с выражением (11)
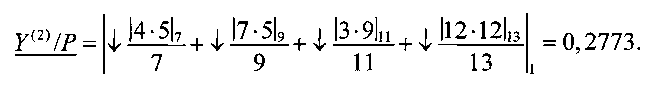
3.5. Делением смещенных границ на второй элемент вектора V получается результатная ИПХ I(Y/Р)=[0,002773, 0,002777] (ведущие нули не хранятся в регистрах ЭВМ, а отражают отрицательное значение порядка). Для проверки преобразуем Y в позиционную систему: Y=25, следовательно, 0,002773<Е(Х/Р)=25/9009<0,2777. Относительная ошибка 0,072%. Следовательно, алгоритм 1 позволил получить высокоточную информацию о величине числа в модулярном представлении без использования трудоемкого преобразования в позиционную систему.
Таким образом, при интервальной аппроксимации относительной величины модулярного числа осуществляется естественный учет погрешностей округления, не требующий рассмотрения специфики используемой модели машинных вычислений. Это позволяет простым образом контролировать корректность результата немодульной операции, вне зависимости от числа модулей СОК и их разрядности.
Пусть в СОК с модулями р1, р2, …, pn даны беззнаковые числа X=〈х1, х2, …, xn〉 и Y=〈y1, y2, …, yn〉. Алгоритм их сравнения с использованием интервально-позиционных характеристик формулируется следующим образом.
АЛГОРИТМ 2.
Шаг 1. Выполняется попарное сравнение остатков для исключения тривиального случая: если xi=yi для всех i=1, 2, …, n, то X=Y и алгоритм завершается.
Шаг 2. По приведенному выше высокоточному алгоритму 1 вычисляются ИПХ операндов, I(Х/Р) и I(Y/Р) соответственно.
Шаг 3. Проверяется первое формальное условие корректного сравнения: если 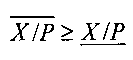 и
и 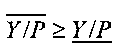 , то условие выполняется. В этом случае выполняется переход к шагу 4, иначе - к шагу 6.
, то условие выполняется. В этом случае выполняется переход к шагу 4, иначе - к шагу 6.
Шаг 4. Если  , то алгоритм завершается с результатом Х>Y. Иначе осуществляется переход к шагу 5.
, то алгоритм завершается с результатом Х>Y. Иначе осуществляется переход к шагу 5.
Шаг 5. Если 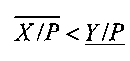 , то алгоритм завершается с результатом Х<Y. Невыполнение этого неравенства на данном шаге говорит о нарушении второго формального условия корректного сравнения из-за недостаточной точности вычисления ИПХ. При этом следует перейти к шагу 6.
, то алгоритм завершается с результатом Х<Y. Невыполнение этого неравенства на данном шаге говорит о нарушении второго формального условия корректного сравнения из-за недостаточной точности вычисления ИПХ. При этом следует перейти к шагу 6.
Шаг 6. Если повышение точности вычисления ИПХ неосуществимо в рамках разрядности используемых форматов данных, то преобразовать числа X и Y из СОК в систему со смешанными основаниями и сравнить цифры полиадических кодов, начиная со старшей, либо сформировать и выдать сигнал о невозможности сравнения чисел из-за недостаточной точности вычисления ИПХ. Алгоритм при этом завершается.
Конъюнкция первого и второго формальных условий составляет признак (достаточное условие) корректности результата немодульной операции сравнения чисел, инвариантный как к числу модулей СОК, так и к их разрядности.
ПРИМЕР 2.
Требуется сравнить числа Х=〈1,6,0,5〉 и Y=〈2,3,4,7〉, представленные в СОК с модулями {1,9,11,13}.
1. Числа, очевидно, не равны, поэтому вычисляем их ИПХ в соответствии с алгоритмом 1 с округлением до четырех значащих десятичных цифр:


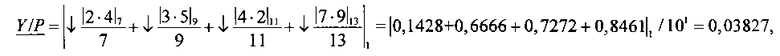

2. Интервалы I(Х/Р)=[0,03662, 0,03665] и I(Y/Р)=[0,03827, 0,03831] обеспечивают выполнение первого формального условия корректного сравнения, так как 0,03665>0,03662 и 0,03831>0,03827.
3. Условие 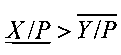 , не выполняется, так как 0,03662<0,03831. Сравниваем противоположные границы: 0,03665<0,03827, следовательно, Х<Y.
, не выполняется, так как 0,03662<0,03831. Сравниваем противоположные границы: 0,03665<0,03827, следовательно, Х<Y.
4. Проверка преобразованием в десятичную систему: Х=330, Y=345. Таким образом, с использованием ИПХ получен правильный результат сравнения двух близлежащих модулярных чисел.
Схема заявляемого устройства для сравнения чисел в системе остаточных классов на основе интервально-позиционных характеристик, функционирующего в соответствии с описанными принципами, представлена на фиг. 3. Устройство содержит группы входных регистров 1, 2 для хранения сравниваемых модулярных чисел, блоки вычисления интервально-позиционной характеристики 3, 5, блок поразрядного сравнения модулярных чисел 4, блоки проверки правильности интервально-позиционных характеристик 6, 8, блок сравнения интервально-позиционных характеристик 7, двухвходовой двоичный дешифратор 9.
Группа входных регистров 1 предназначена для хранения числа X, представленного в виде n-кортежа (где n - количество модулей СОК) и поступающего по шине данных 10, и содержит регистры 1.1, 1.2, …, 1.n, выходы которых соединены с информационными входами блоков 3 и 4. В свою очередь, группа входных регистров 2 предназначена для хранения числа Y, также представленного в виде n-кортежа и поступающего по шине данных 11, и содержит регистры 2.1, 2.2, …, 2.n, выходы которых соединены с информационными входами блоков 5 и 4. Выход блока 4 соединен с управляющими входами блоков 3, 5. Выходы блоков 3, 5 соединены с входами блоков 6, 8, соответственно, а также с информационными входами блока 7. Выходы блоков 6, 8 соединены с управляющими входами блока 7. Выходы блока 7 соединены со входами дешифратора 9. Выходы дешифратора 9 соединены с выходными шинами 12, 13, 14, 15.
Работа заявляемого устройства для сравнения чисел в системе остаточных классов на основе интервально-позиционных характеристик осуществляется следующим образом. Сравниваемые модулярные числа X=〈х1, х2, …, xn〉, Y=〈у1, у2, …, yn〉 поступают по шинам данных 10, 11 и записываются в группы регистров 1, 2 соответственно. Из группы регистров 1 данные подаются на входы блока 3, а также на первые n входов блока 4. Из группы регистров 2 данные подаются на входы блока 5, а также на вторые n входов блока 4. Блок 4 производит попарное сравнение остатков (xi,yi), i=1, 2, …, n, и формирует сигнал логического нуля, если все остатки попарно равны, и сигнал логической единицы в противном случае. Этот сигнал подается на управляющие входы блоков 3, 5, в которых, в случае, если числа не равны (на выходе блока 4 сформирована логическая единица), осуществляется вычисление ИПХ I(Х/Р) и I(Y/Р) соответственно. Если на выходе блока 4 сформирован логический ноль, то на каждом из выходов блоков 3, 5 также устанавливается нулевое значение. Вычисленные ИПХ, каждая из которых представляется в виде двух двоичных чисел с плавающей точкой, соответственно  ,
,  и
и  ,
,  , подаются на блоки 6, 8 соответственно, а также на блок 7. Блок 6 производит сравнение границ
, подаются на блоки 6, 8 соответственно, а также на блок 7. Блок 6 производит сравнение границ 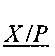 и
и 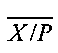 : если
: если  , то на соответствующий управляющий вход блока 7 подается сигнал логической единицы. Если
, то на соответствующий управляющий вход блока 7 подается сигнал логической единицы. Если  , то на соответствующий управляющий вход блока 7 подается сигнал логического нуля. Аналогичным образом работает блок 8. В блоке 7 осуществляется сравнение противоположных границ ИПХ и результат подается на входы дешифратора 9: если
, то на соответствующий управляющий вход блока 7 подается сигнал логического нуля. Аналогичным образом работает блок 8. В блоке 7 осуществляется сравнение противоположных границ ИПХ и результат подается на входы дешифратора 9: если 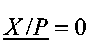 ,
, 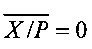 ,
,  ,
, 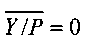 , то на первом и втором выходах блока 7 формируются сигналы логического нуля; в противном случае, если
, то на первом и втором выходах блока 7 формируются сигналы логического нуля; в противном случае, если 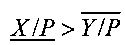 , то на первом выходе блока 7 формируется сигнал логического нуля, а на втором выходе блока 7 формируется сигнал логической единицы; в противном случае, если
, то на первом выходе блока 7 формируется сигнал логического нуля, а на втором выходе блока 7 формируется сигнал логической единицы; в противном случае, если 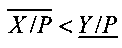 , то на первом выходе блока 7 формируется сигнал логической единицы, а на втором выходе блока 7 формируется сигнал логического нуля; в противном случае, а также если хотя бы на одном из управляющих входов блока 7 установлен логический ноль, на обоих выходах блока 7 формируются сигналы логической единицы. Дешифратор 9 работает следующим образом: если на обоих его входах установлены сигналы логического нуля (код «00»), то подается сигнал на шину 12, свидетельствующий о том, что Х=Y; если на первом входе установлен логический ноль, а на втором - логическая единица (код «01»), то подается сигнал на шину 13, свидетельствующий о том, что Х>Y; если на первом входе установлена логическая единица, а на втором - логический ноль (код «10»), то подается сигнал на шину 14, свидетельствующий о том, что Х<Y; если на обоих его входах установлены сигналы логической единицы (код «11»), то подается сигнал на шину 15, свидетельствующий о том, что результат сравнения чисел X и Y не может быть определен в силу недостаточной точности вычисления их интервально-позиционных характеристик.
, то на первом выходе блока 7 формируется сигнал логической единицы, а на втором выходе блока 7 формируется сигнал логического нуля; в противном случае, а также если хотя бы на одном из управляющих входов блока 7 установлен логический ноль, на обоих выходах блока 7 формируются сигналы логической единицы. Дешифратор 9 работает следующим образом: если на обоих его входах установлены сигналы логического нуля (код «00»), то подается сигнал на шину 12, свидетельствующий о том, что Х=Y; если на первом входе установлен логический ноль, а на втором - логическая единица (код «01»), то подается сигнал на шину 13, свидетельствующий о том, что Х>Y; если на первом входе установлена логическая единица, а на втором - логический ноль (код «10»), то подается сигнал на шину 14, свидетельствующий о том, что Х<Y; если на обоих его входах установлены сигналы логической единицы (код «11»), то подается сигнал на шину 15, свидетельствующий о том, что результат сравнения чисел X и Y не может быть определен в силу недостаточной точности вычисления их интервально-позиционных характеристик.
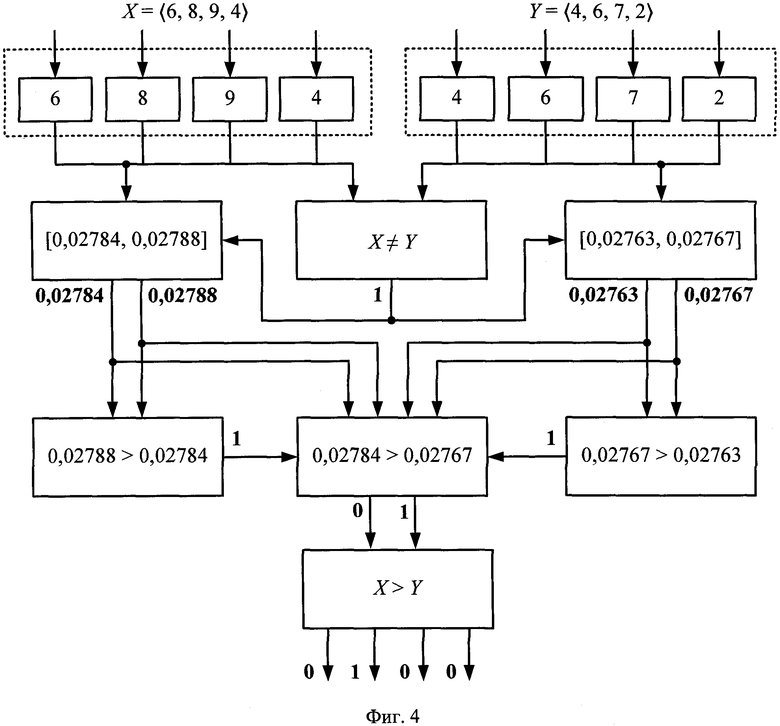
Пример работы заявляемого устройства для сравнения чисел в системе остаточных классов на основе интервально-позиционных характеристик представлен на фиг. 4. Выполнялось сравнение чисел Х=〈6,8,9,4〉 и Y=〈4,6,7,2〉, представленных в СОК с модулями {7,9,11,13}. Интервально-позиционные характеристики вычислялись в блоках 3 и 4 с округлением до четырех значащих десятичных цифр.
Трудоемкость заявляемого устройства зависит от значений сравниваемых модулярных чисел: чем меньше значения, тем большее количество итераций необходимо выполнить для вычисления ИПХ в соответствии с алгоритмом 1 (и тем дольше работают блоки 3 и 5). Приведем оценки трудоемкости для случая, когда числа достаточно большие и выполнение шагов 4-9 алгоритма 1 не требуется. В этом случае для вычисления верхней границы ИПХ 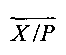 на шаге 1 необходимо выполнить n умножений модулярных разрядов xi на мультипликативные инверсии
на шаге 1 необходимо выполнить n умножений модулярных разрядов xi на мультипликативные инверсии 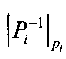 , n делений полученных произведений на модули pi с округлением «вниз» (переключение режима округления арифметико-логического устройства (АЛУ) требует выполнения одной операции - загрузки предустановленной маски в регистр управления), n-1 сложений с накоплением и одну операцию получения дробной части результатной суммы. В общей сложности вычисление нижней границы ИПХ требует выполнения 3n+1 операций арифметических операций с плавающей точкой. Одну операцию позиционного сравнения требуется выполнить на шаге 2 при условии, что константа ψ вычислена заранее. Если нижняя граница уже вычислена, то для вычисления верхней нижней границы
, n делений полученных произведений на модули pi с округлением «вниз» (переключение режима округления арифметико-логического устройства (АЛУ) требует выполнения одной операции - загрузки предустановленной маски в регистр управления), n-1 сложений с накоплением и одну операцию получения дробной части результатной суммы. В общей сложности вычисление нижней границы ИПХ требует выполнения 3n+1 операций арифметических операций с плавающей точкой. Одну операцию позиционного сравнения требуется выполнить на шаге 2 при условии, что константа ψ вычислена заранее. Если нижняя граница уже вычислена, то для вычисления верхней нижней границы  на шаге 3 алгоритма 1 не нужно повторно умножать мультипликативные инверсии на остатки числа xi, остается выполнить одно переключение АЛУ в режим округления «вниз», n делений, n-1 сложений и одно отбрасывание целой части суммы, итого 2n+1 операций. Кроме этого, необходимо установить АЛУ в режим округления «до ближайшего». Таким образом, при последовательном вычислении ИПХ по алгоритму 1 для случая, когда выполнение уточняющих шагов не требуется, необходимо выполнить в общей сложности 5n+4 операций с плавающей точкой. Отсюда трудоемкость заявляемого устройства оценивается следующим образом. Пусть СОК задана n модулями. Тогда для сравнения чисел X и Υ, при условии, что они не равны, требуется выполнить следующие операции: n операций позиционного сравнения пар остатков необходимо выполнить в блоке 4; 5n+4 операций необходимо выполнить для одновременного вычисления ИПХ в блоках 3 и 5; по одной операции позиционного сравнения необходимо выполнить одновременно в блоках 6 и 7; две операции позиционного сравнения (в худшем случае) необходимо выполнить в блоке 7. Таким образом, в лучшем случае сравнение двух неравных чисел, представленных в n-модульной СОК, будет выполнено за n+5n+4+1+2=6n+7 операций. Для сравнения чисел с помощью устройства на базе метода преобразования модулярных представлений в систему счисления со смешанными основаниями требуется около 2n2 операций. Следовательно, эффект повышения быстродействия от использования заявляемого устройства может достигать в среднем 0,33n раз, где n - количество модулей СОК.
на шаге 3 алгоритма 1 не нужно повторно умножать мультипликативные инверсии на остатки числа xi, остается выполнить одно переключение АЛУ в режим округления «вниз», n делений, n-1 сложений и одно отбрасывание целой части суммы, итого 2n+1 операций. Кроме этого, необходимо установить АЛУ в режим округления «до ближайшего». Таким образом, при последовательном вычислении ИПХ по алгоритму 1 для случая, когда выполнение уточняющих шагов не требуется, необходимо выполнить в общей сложности 5n+4 операций с плавающей точкой. Отсюда трудоемкость заявляемого устройства оценивается следующим образом. Пусть СОК задана n модулями. Тогда для сравнения чисел X и Υ, при условии, что они не равны, требуется выполнить следующие операции: n операций позиционного сравнения пар остатков необходимо выполнить в блоке 4; 5n+4 операций необходимо выполнить для одновременного вычисления ИПХ в блоках 3 и 5; по одной операции позиционного сравнения необходимо выполнить одновременно в блоках 6 и 7; две операции позиционного сравнения (в худшем случае) необходимо выполнить в блоке 7. Таким образом, в лучшем случае сравнение двух неравных чисел, представленных в n-модульной СОК, будет выполнено за n+5n+4+1+2=6n+7 операций. Для сравнения чисел с помощью устройства на базе метода преобразования модулярных представлений в систему счисления со смешанными основаниями требуется около 2n2 операций. Следовательно, эффект повышения быстродействия от использования заявляемого устройства может достигать в среднем 0,33n раз, где n - количество модулей СОК.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ЗНАКОВ ЧИСЕЛ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2014 |
|
RU2557446C1 |
| Устройство для сравнения чисел в системе остаточных классов | 2018 |
|
RU2698413C1 |
| Способ организации выполнения операции умножения двух чисел в модулярно-логарифмическом формате представления с плавающей точкой на гибридных многоядерных процессорах | 2017 |
|
RU2666285C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ДЕЛЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2005 |
|
RU2305312C2 |
| Устройство вычисления модулярного произведения Монтгомери | 2017 |
|
RU2652450C1 |
| Устройство для перевода чисел из системы остаточных классов и расширения оснований | 2020 |
|
RU2744815C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ РАСШИРЕНИЯ КОРТЕЖА ЧИСЛОВОЙ СИСТЕМЫ ВЫЧЕТОВ | 2003 |
|
RU2256226C2 |
| НЕЙРОННАЯ СЕТЬ УСКОРЕННОГО МАСШТАБИРОВАНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2007 |
|
RU2359325C2 |
| АДАПТИВНАЯ ПАРАЛЛЕЛЬНО-КОНВЕЙЕРНАЯ НЕЙРОННАЯ СЕТЬ ДЛЯ КОРРЕКЦИИ ОШИБОК | 2003 |
|
RU2279131C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ВЫЧИСЛЕНИЯ ПОЗИЦИОННОЙ ХАРАКТЕРИСТИКИ РАНГА ЧИСЛА, ПРЕДСТАВЛЕННОГО В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2003 |
|
RU2271569C2 |
Изобретение относится к вычислительной технике и предназначено для выполнения операции сравнения двух чисел, представленных в системе остаточных классов. Техническим результатом является повышение быстродействия и обеспечение контроля корректности результата операции сравнения. Представленные положения обеспечиваются за счет использования новой интервально-позиционной характеристики модулярной арифметики, которая аппроксимирует с двух сторон относительную величину числа в модулярном представлении. Устройство содержит группы входных регистров для хранения сравниваемых модулярных чисел, блоки вычисления интервально-позиционной характеристики, блок поразрядного сравнения модулярных чисел, блоки проверки правильности интервально-позиционных характеристик, блок сравнения интервально-позиционных характеристик, двухвходовой двоичный дешифратор. 4 ил.
Устройство для сравнения чисел в системе остаточных классов на основе интервально-позиционных характеристик, содержащее первую и вторую группы входных регистров, каждая из которых состоит из n регистров, хранящих сравниваемые модулярные числа X и Υ, отличающееся тем, что содержит первый и второй блоки вычисления интервально-позиционной характеристики, каждый из которых имеет n информационных входов, один управляющий вход и два выхода, блок поразрядного сравнения модулярных чисел, имеющий 2n информационных входов и один выход, первый и второй блоки проверки правильности интервально-позиционной характеристики, каждый из которых имеет два информационных входа и один выход, блок сравнения интервально-позиционных характеристик, имеющий четыре информационных входа, два управляющих входа и два выхода, двоичный дешифратор, имеющий два входа и четыре выхода, причем выходы входных регистров первой группы соединены с первыми n информационными входами блока поразрядного сравнения модулярных чисел и с информационными входами первого блока вычисления интервально-позиционной характеристики, выходы входных регистров второй группы соединены со вторыми n информационными входами блока поразрядного сравнения модулярных чисел и с информационными входами второго блока вычисления интервально-позиционной характеристики, выход блока поразрядного сравнения модулярных чисел соединен с управляющими входами первого и второго блоков вычисления интервально-позиционной характеристики, первый и второй выходы первого блока вычисления интервально-позиционной характеристики соединены со входами первого блока проверки правильности интервально-позиционной характеристики, а также с первым и вторым входами блока сравнения интервально-позиционных характеристик, первый и второй выходы второго блока вычисления интервально-позиционной характеристики соединены со входами второго блока проверки правильности интервально-позиционной характеристики, а также с третьим и четвертым входами блока сравнения интервально-позиционных характеристик, выход первого блока проверки правильности интервально-позиционной характеристики соединен с первым управляющим входом блока сравнения интервально-позиционных характеристик, выход второго блока проверки правильности интервально-позиционной характеристики соединен со вторым управляющим входом блока сравнения интервально-позиционных характеристик, первый и второй выходы блока сравнения интервально-позиционных характеристик соединены с первым и вторым входами двоичного дешифратора, выходы двоичного дешифратора являются выходами устройства для сравнения чисел в системе остаточных классов на основе интервально-позиционных характеристик: «X=Y», «X>Y», «X<Y», «Результат сравнения не определен».
| УСТРОЙСТВО ДЛЯ СРАВНЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2011 |
|
RU2503992C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ВЫЧИСЛЕНИЯ ПОЗИЦИОННЫХ ХАРАКТЕРИСТИК НЕПОЗИЦИОННОГО КОДА | 2003 |
|
RU2257615C2 |
| Устройство для сравнения чисел в системе остаточных классов | 1988 |
|
SU1552171A1 |
| Устройство для сравнения чисел в системе остаточных классов | 1986 |
|
SU1325460A1 |
| US 2008155004 A1, 26.06.2008 | |||
| US 7523151 B1, 21.04.2009 | |||
| CN 102930097 A, 13.02.2013 | |||
Авторы
Даты
2015-07-20—Публикация
2014-07-16—Подача