Изобретение относится к вычислительной технике и предназначено для определения знака числа, представленного в системе остаточных классов.
Известно устройство для определения знаков чисел в системе остаточных классов (патент РФ 2557446, опубл. 20.07.2015), содержащее группу входных регистров для хранения числа, представленного в коде симметричной системы остаточных классов, энергонезависимые регистры для хранения интервально-позиционной характеристики константы - наибольшего положительного числа в симметричной системе остаточных классов, блок вычисления интервально-позиционной характеристики, блок проверки правильности интервально-позиционной характеристики, блок сравнения интервально-позиционных характеристик, двухвходовой двоичный дешифратор.
Недостатком данного устройства является использование ресурсоемких операций деления с числами с плавающей точкой, что снижает скорость работы и требует округлений.
Наиболее близким к заявленному изобретению является устройство для определения знака модулярного числа (патент РФ 2503995, опубл. 10.01.2014), содержащее входные регистры для хранения разрядов исходного числа, блоки умножения, выполненные в виде памяти для хранения произведений 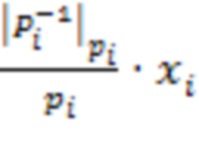 и параллельный сумматор.
и параллельный сумматор.
Недостатком данного устройства является низкая точность, связанная с представлением чисел в формате с плавающей точкой, а именно с ошибками округления.
Техническим результатом заявляемого изобретения является увеличение скорости и точности вычислений определения знака чисел, представленных в системе остаточных классов.
Данный технический результат достигается тем, что в устройство определения знака числа, представленного в системе остаточных классов, содержащее 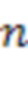 входов остатка, где
входов остатка, где 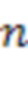 - количество модулей
- количество модулей 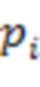 системы остаточных классов,
системы остаточных классов, 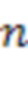 регистров для хранения разрядов исходного числа,
регистров для хранения разрядов исходного числа, 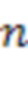 блоков умножения, где входы остатка подключены к входам соответствующих регистров для хранения разрядов исходного числа, введены
блоков умножения, где входы остатка подключены к входам соответствующих регистров для хранения разрядов исходного числа, введены 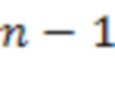 вычислительная ступень, при этом
вычислительная ступень, при этом 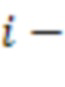 я вычислительная ступень, где
я вычислительная ступень, где 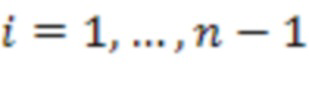 , содержит
, содержит 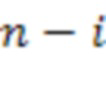 сумматоров по модулю
сумматоров по модулю 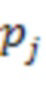 и
и 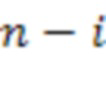 блоков умножения на веса
блоков умножения на веса 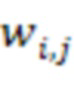 по модулю
по модулю 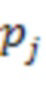 , где
, где 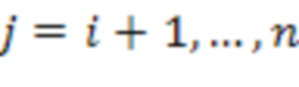 и
и 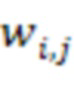 - мультипликативная инверсия модуля
- мультипликативная инверсия модуля 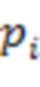 по модулю
по модулю 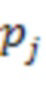 и модули упорядочены по возрастанию и
и модули упорядочены по возрастанию и 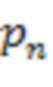 является степенью 2, в первой вычислительной ступени первые информационные входы
является степенью 2, в первой вычислительной ступени первые информационные входы 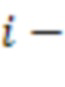 х сумматоров по модулю
х сумматоров по модулю 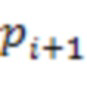 через инверторы подключены к выходу первого регистра для хранения разрядов исходного числа, вторые информационные входы
через инверторы подключены к выходу первого регистра для хранения разрядов исходного числа, вторые информационные входы 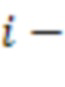 х сумматоров по модулю
х сумматоров по модулю 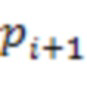 подключены к выходам
подключены к выходам 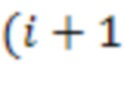 )-х регистров для хранения разрядов исходного числа, на входы переносов
)-х регистров для хранения разрядов исходного числа, на входы переносов 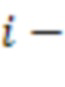 х сумматоров по модулю
х сумматоров по модулю 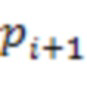 подается сигнал логической единицы, выходы
подается сигнал логической единицы, выходы 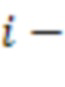 х сумматоров по модулю
х сумматоров по модулю 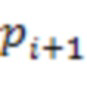 подключены ко входам соответствующих блоков умножения на веса
подключены ко входам соответствующих блоков умножения на веса 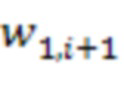 по модулю
по модулю 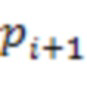 ,
, 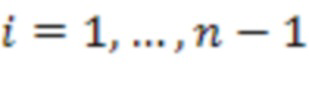 , в
, в 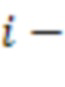 x вычислительных ступенях,
x вычислительных ступенях, 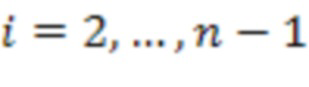 , первые информационные входы
, первые информационные входы 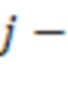 х сумматоров по модулю
х сумматоров по модулю 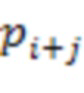 через инверторы подключены к выходу первого блока умножения на веса
через инверторы подключены к выходу первого блока умножения на веса 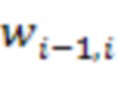 по модулю
по модулю 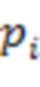
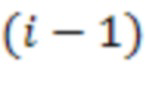 -ой вычислительной ступени, вторые информационные входы
-ой вычислительной ступени, вторые информационные входы 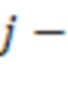 х сумматоров по модулю
х сумматоров по модулю 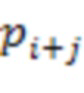 подключены к выходам
подключены к выходам 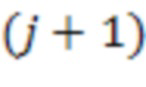 -ых блоков умножения на веса
-ых блоков умножения на веса 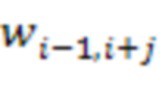 по модулю
по модулю 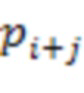
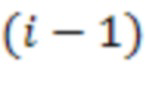 -ой вычислительной ступени, на входы переносов
-ой вычислительной ступени, на входы переносов 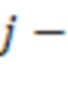 х сумматоров по модулю
х сумматоров по модулю 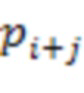 подается сигнал логической единицы, выходы
подается сигнал логической единицы, выходы 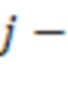 х сумматоров по модулю
х сумматоров по модулю 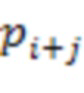 подключены к входам
подключены к входам 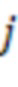 -ых блоков умножения на веса
-ых блоков умножения на веса 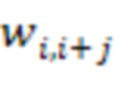 по модулю
по модулю 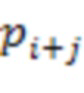 ,
, 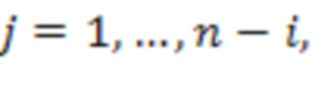 старший бит выхода блока умножения на веса
старший бит выхода блока умножения на веса 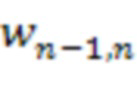
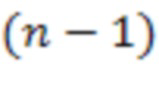 -й вычислительной ступени является выходом знака устройства.
-й вычислительной ступени является выходом знака устройства.
Сущность изобретения основана на следующем математическом аппарате. В системе остаточных классов (СОК) любое число 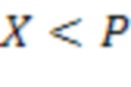 однозначно представляется набором остатков
однозначно представляется набором остатков 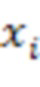 от деления числа
от деления числа 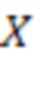 на взаимно простые модули СОК
на взаимно простые модули СОК 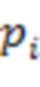 , где
, где 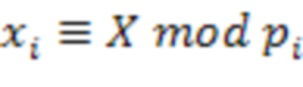 ,
, 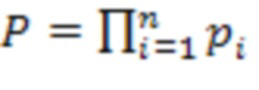 - рабочий диапазон СОК,
- рабочий диапазон СОК, 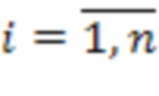 . Возьмем систему остаточных классов с модулями
. Возьмем систему остаточных классов с модулями 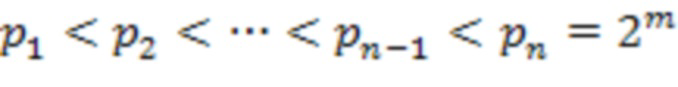 . Знак в системе остаточных классов чаще всего вводится разбиением диапазона на две части, тогда с учетом динамического диапазона
. Знак в системе остаточных классов чаще всего вводится разбиением диапазона на две части, тогда с учетом динамического диапазона 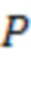 в СОК можно представить числа
в СОК можно представить числа 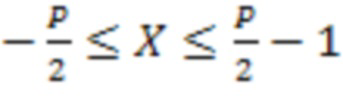 , если
, если 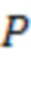 четное.
четное.
Функция определения знака числа, представленного в СОК, определяется следующим образом:

Таким образом 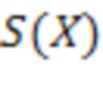 можно представить в виде:
можно представить в виде:
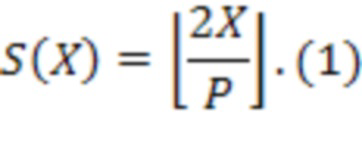
Используя свойство 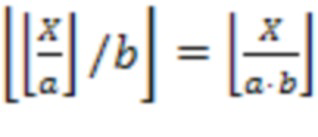 и формулу (1) определение знака сводится двухэтапному алгоритму: первый этап - деление на
и формулу (1) определение знака сводится двухэтапному алгоритму: первый этап - деление на 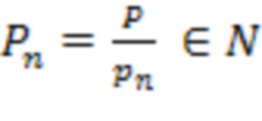 , второй этап - деление на
, второй этап - деление на 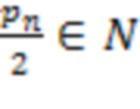 , формально математически определяется следующей формулой
, формально математически определяется следующей формулой
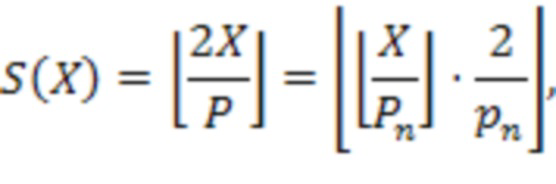
Запишем процесс определения в виде алгоритма:
Алгоритм 1. Определение знака числа
Вход:
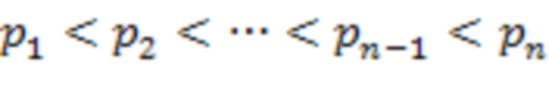 - модули СОК
- модули СОК
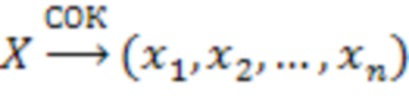 - представление числа
- представление числа 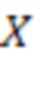 в СОК
в СОК
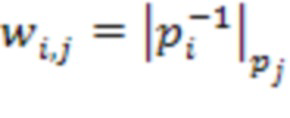 - синоптические веса
- синоптические веса
Выход: 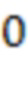 - положительное число,
- положительное число, 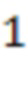 - отрицательное число
- отрицательное число
1. Для 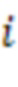 от
от 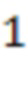 до
до 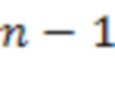 выполнять:
выполнять:
1.1. Для 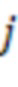 от
от 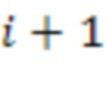 до
до 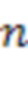 выполнять: \\ деление на
выполнять: \\ деление на 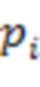
1.1.1. 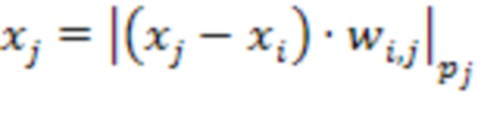
2. Возвратить 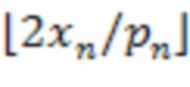
На первом этапе вычисляется 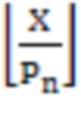 с помощью
с помощью 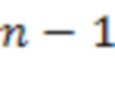 деления на модули СОК
деления на модули СОК 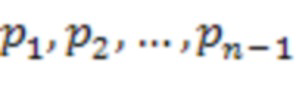 соответственно. На втором этапе вычисляется
соответственно. На втором этапе вычисляется 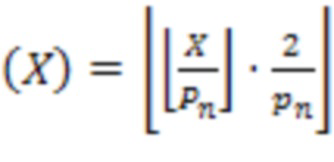 .
.
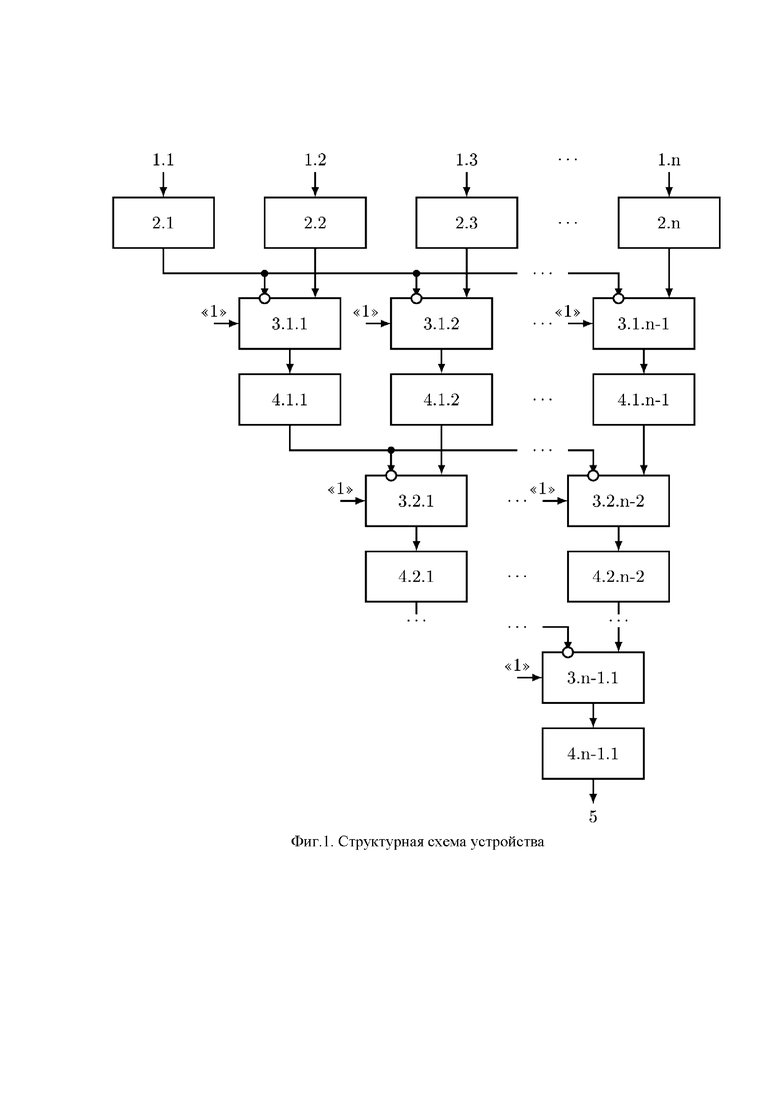
Устройство поясняется фигурой 1, которая содержит 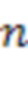 входов остатка 1.1-1.n, которые соединены с
входов остатка 1.1-1.n, которые соединены с 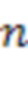 регистрами для хранения разрядов исходного числа 2.1-2.n. Устройство содержит n-1 вычислительных ступеней, при этом
регистрами для хранения разрядов исходного числа 2.1-2.n. Устройство содержит n-1 вычислительных ступеней, при этом 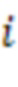 -я вычислительная ступень, где
-я вычислительная ступень, где 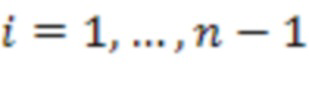 , содержит
, содержит 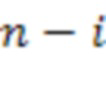 сумматоров по модулю
сумматоров по модулю 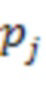 3.i.1 - 3.i.n-i и
3.i.1 - 3.i.n-i и 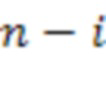 блоков умножения на веса
блоков умножения на веса 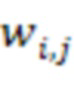 по модулю
по модулю 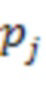 4.i.1 - 4.i.n-i, где
4.i.1 - 4.i.n-i, где 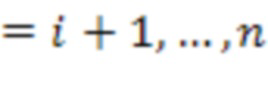 и
и 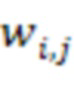 - мультипликативная инверсия модуля
- мультипликативная инверсия модуля 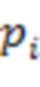 по модулю
по модулю 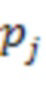 . В первой вычислительной ступени первые информационные входы
. В первой вычислительной ступени первые информационные входы 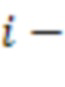 х сумматоров по модулю
х сумматоров по модулю 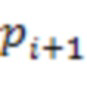 3.1.1 - 3.1.n-1 через инверторы подключены к выходу первого регистра для хранения разрядов исходного числа 2.1, вторые информационные входы
3.1.1 - 3.1.n-1 через инверторы подключены к выходу первого регистра для хранения разрядов исходного числа 2.1, вторые информационные входы 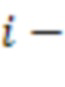 х сумматоров по модулю
х сумматоров по модулю 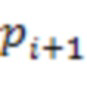 3.1.1 - 3.1.n-1 подключены к выходам соответствующих
3.1.1 - 3.1.n-1 подключены к выходам соответствующих 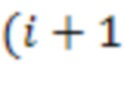 )-х регистров для хранения разрядов исходного числа 2.2-2.n, на входы переносов
)-х регистров для хранения разрядов исходного числа 2.2-2.n, на входы переносов 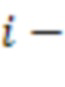 х сумматоров по модулю
х сумматоров по модулю 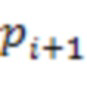 3.1.1 - 3.1.n-1 подается сигнал логической единицы, выходы
3.1.1 - 3.1.n-1 подается сигнал логической единицы, выходы 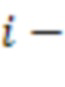 х сумматоров по модулю
х сумматоров по модулю 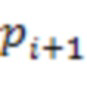 3.1.1 - 3.1.n-1 подключены ко входам соответствующих блоков умножения на веса
3.1.1 - 3.1.n-1 подключены ко входам соответствующих блоков умножения на веса 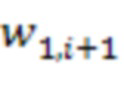 по модулю
по модулю 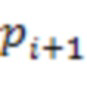 4.1.1 - 4.1.n-1,
4.1.1 - 4.1.n-1, 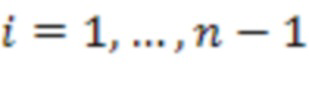 . Во второй вычислительной ступени первые информационные входы
. Во второй вычислительной ступени первые информационные входы 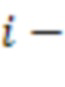 х сумматоров по модулю
х сумматоров по модулю 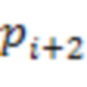 3.2.1 - 3.2.n-2 через инверторы подключены к выходу первого блока умножения на веса
3.2.1 - 3.2.n-2 через инверторы подключены к выходу первого блока умножения на веса 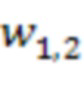 по модулю
по модулю 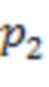 первой ступени, вторые информационные входы
первой ступени, вторые информационные входы 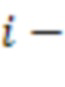 х сумматоров по модулю
х сумматоров по модулю 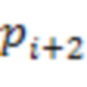 3.2.1 - 3.2.n-2 подключены к выходам соответствующих
3.2.1 - 3.2.n-2 подключены к выходам соответствующих 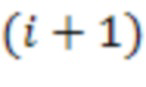 -ых блоков умножения на веса
-ых блоков умножения на веса 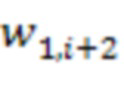 по модулю
по модулю 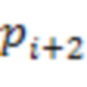 первой ступени, на входы переносов
первой ступени, на входы переносов 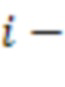 х сумматоров по модулю
х сумматоров по модулю 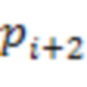 3.2.1 - 3.2.n-2 второй ступени подается сигнал логической единицы, выходы
3.2.1 - 3.2.n-2 второй ступени подается сигнал логической единицы, выходы 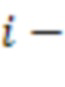 х сумматоров по модулю
х сумматоров по модулю 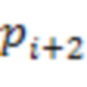 3.2.1 - 3.2.n-2 второй ступени подключены ко входам соответствующих
3.2.1 - 3.2.n-2 второй ступени подключены ко входам соответствующих 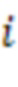 -ых блоков умножения на веса
-ых блоков умножения на веса 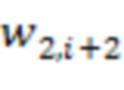 по модулю
по модулю 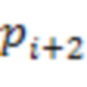 4.2.1 - 4.2.n-2,
4.2.1 - 4.2.n-2, 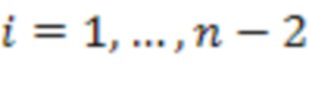 . И так далее, на
. И так далее, на 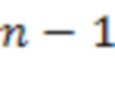 вычислительной ступени первый информационный вход сумматора по модулю
вычислительной ступени первый информационный вход сумматора по модулю 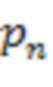 3.n-1.1 через инвертор подключен к выходу первого блока умножения на веса
3.n-1.1 через инвертор подключен к выходу первого блока умножения на веса 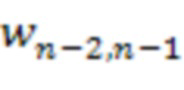 по модулю
по модулю 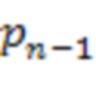 4.n-2.1
4.n-2.1 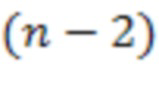 -й ступени, второй информационный вход сумматора по модулю
-й ступени, второй информационный вход сумматора по модулю 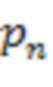 3.n-1.1 подключен к выходу второго блока умножения на веса
3.n-1.1 подключен к выходу второго блока умножения на веса 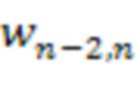 по модулю
по модулю 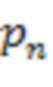 4.n-2.2
4.n-2.2 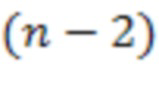 -й ступени , на вход переноса поступает сигнал логической единицы, а выход соединен со входом первого блока умножения на веса
-й ступени , на вход переноса поступает сигнал логической единицы, а выход соединен со входом первого блока умножения на веса 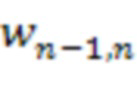 по модулю
по модулю 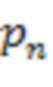 4.n-1.1
4.n-1.1 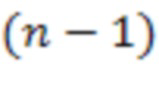 -й ступени, старший бит выхода которого является выходом знака 5.
-й ступени, старший бит выхода которого является выходом знака 5.
При этом блоки 4 умножения на веса 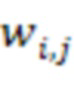 по модулю
по модулю 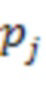 могут быть выполнены как в виде памяти, так и в виде вычислительных устройств. Сумматоры 3 по модулю
могут быть выполнены как в виде памяти, так и в виде вычислительных устройств. Сумматоры 3 по модулю 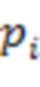 за счет инвертирования сигнала с одного из входов и сигнала логической единицы на входе переноса фактически выполняют операцию вычитания.
за счет инвертирования сигнала с одного из входов и сигнала логической единицы на входе переноса фактически выполняют операцию вычитания.
На основе примера рассмотрим работу устройства.
Пусть задана система остаточных классов с модулями 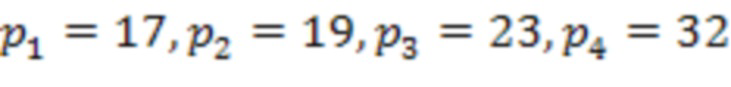 . Тогда количество входов остатка 1 и регистров для хранения разрядов исходного числа 2 равно 4, а количество вычислительных ступеней равно 3. Для них веса, на которые происходит умножение в блоках 4 умножения на веса
. Тогда количество входов остатка 1 и регистров для хранения разрядов исходного числа 2 равно 4, а количество вычислительных ступеней равно 3. Для них веса, на которые происходит умножение в блоках 4 умножения на веса 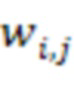 по модулю
по модулю 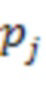 равны
равны
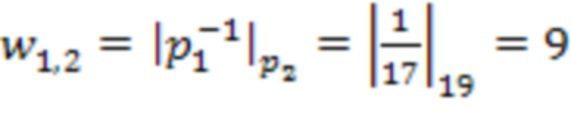 ,
,
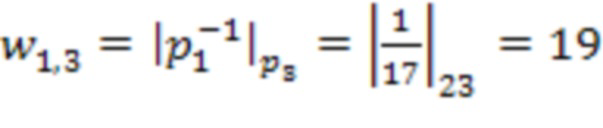 ,
,
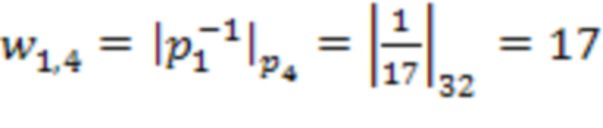
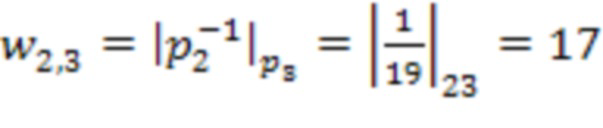 ,
,
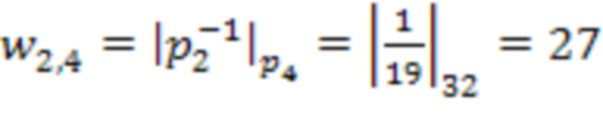
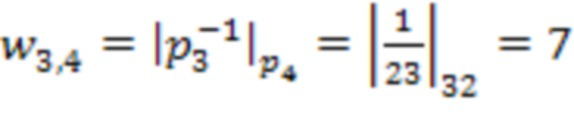 .
.
Пусть на входы 1.1-1.4 поступает число 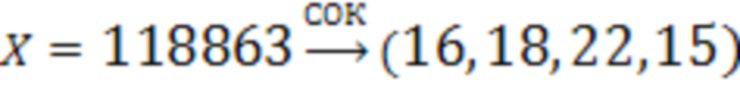 , тогда в регистрах для хранения разрядов исходного числа 2.1-2.4 будут храниться соответственно числа 16, 18, 22, 15.
, тогда в регистрах для хранения разрядов исходного числа 2.1-2.4 будут храниться соответственно числа 16, 18, 22, 15.
В первом сумматоре 3.1.1 по модулю 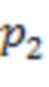 первой вычислительной ступени выполняется операция вычитания из значения 18 второго регистра для хранения разрядов исходного числа 2.2 значения 16 первого регистра для хранения разрядов исходного числа 2.1, на выход сумматора 3.1.1 по модулю
первой вычислительной ступени выполняется операция вычитания из значения 18 второго регистра для хранения разрядов исходного числа 2.2 значения 16 первого регистра для хранения разрядов исходного числа 2.1, на выход сумматора 3.1.1 по модулю 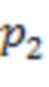 поступает значение 2. Во втором сумматоре 3.1.2 по модулю
поступает значение 2. Во втором сумматоре 3.1.2 по модулю 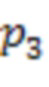 первой вычислительной ступени выполняется операция вычитания из значения 22 третьего регистра для хранения разрядов исходного числа 2.3 значения 16 первого регистра для хранения разрядов исходного числа 2.1, на выход сумматора 3.1.2 по модулю
первой вычислительной ступени выполняется операция вычитания из значения 22 третьего регистра для хранения разрядов исходного числа 2.3 значения 16 первого регистра для хранения разрядов исходного числа 2.1, на выход сумматора 3.1.2 по модулю 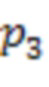 поступает значение 6. В третьем сумматоре 3.1.3 по модулю
поступает значение 6. В третьем сумматоре 3.1.3 по модулю  первой вычислительной ступени выполняется операция вычитания из значения 15 четвертого регистра для хранения разрядов исходного числа 2.4 значения 16 первого регистра для хранения разрядов исходного числа 2.1, на выход сумматора 3.1.3 по модулю
первой вычислительной ступени выполняется операция вычитания из значения 15 четвертого регистра для хранения разрядов исходного числа 2.4 значения 16 первого регистра для хранения разрядов исходного числа 2.1, на выход сумматора 3.1.3 по модулю  поступает значение 31.
поступает значение 31.
В первом блоке умножения на веса 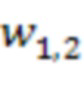 по модулю
по модулю 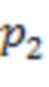 4.1.1 первой ступени происходит умножение по модулю значения 2 с выхода сумматора 3.1.1 по модулю
4.1.1 первой ступени происходит умножение по модулю значения 2 с выхода сумматора 3.1.1 по модулю 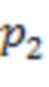 на сохраненное значение веса
на сохраненное значение веса 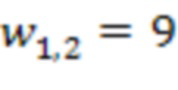 , т.е.
, т.е. 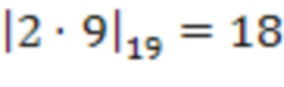 . Во втором блоке умножения на веса
. Во втором блоке умножения на веса 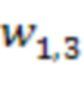 по модулю
по модулю 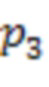 4.1.2 первой ступени происходит умножение по модулю значения 6 с выхода сумматора 3.1.2 по модулю
4.1.2 первой ступени происходит умножение по модулю значения 6 с выхода сумматора 3.1.2 по модулю 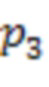 на сохраненное значение веса
на сохраненное значение веса 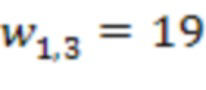 , т.е.
, т.е.  . Во третьем блоке умножения на веса
. Во третьем блоке умножения на веса 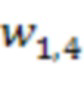 по модулю
по модулю  4.1.3 первой ступени происходит умножение по модулю значения 31 с выхода сумматора 3.1.3 по модулю
4.1.3 первой ступени происходит умножение по модулю значения 31 с выхода сумматора 3.1.3 по модулю  на сохраненное значение веса
на сохраненное значение веса 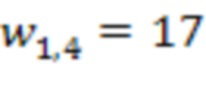 , т.е.
, т.е. 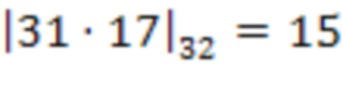 .
.
В первом сумматоре 3.2.1 по модулю 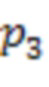 второй вычислительной ступени выполняется операция вычитания из значения 22 второго блока умножения на веса
второй вычислительной ступени выполняется операция вычитания из значения 22 второго блока умножения на веса 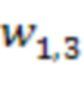 по модулю
по модулю 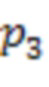 4.1.2 первой ступени значения 18 первого блока умножения на веса
4.1.2 первой ступени значения 18 первого блока умножения на веса 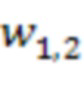 по модулю
по модулю 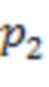 первой ступени, на выход первого сумматора 3.2.1 по модулю
первой ступени, на выход первого сумматора 3.2.1 по модулю 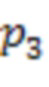 поступает значение 4. Во втором сумматоре 3.2.2 по модулю
поступает значение 4. Во втором сумматоре 3.2.2 по модулю  второй вычислительной ступени выполняется операция вычитания из значения 15 третьего блока умножения на веса
второй вычислительной ступени выполняется операция вычитания из значения 15 третьего блока умножения на веса 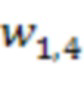 по модулю
по модулю  4.1.3 первой ступени значения 18 первого блока умножения на веса
4.1.3 первой ступени значения 18 первого блока умножения на веса 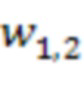 по модулю
по модулю 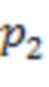 первой ступени, на выход второго сумматора 3.2.2 по модулю
первой ступени, на выход второго сумматора 3.2.2 по модулю  поступает значение 29.
поступает значение 29.
В первом блоке умножения на веса 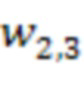 по модулю
по модулю 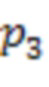 4.2.1 второй ступени происходит умножение по модулю значения 4 с выхода первого сумматора 3.2.1 по модулю
4.2.1 второй ступени происходит умножение по модулю значения 4 с выхода первого сумматора 3.2.1 по модулю 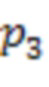 на сохраненное значение веса
на сохраненное значение веса 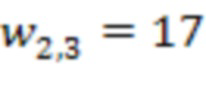 , т.е.
, т.е. 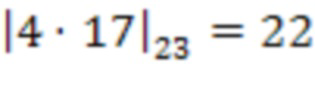 . Во втором блоке умножения на веса
. Во втором блоке умножения на веса 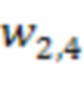 по модулю
по модулю  4.2.2 второй ступени происходит умножение по модулю значения 29 с выхода второго сумматора 3.2.2 по модулю
4.2.2 второй ступени происходит умножение по модулю значения 29 с выхода второго сумматора 3.2.2 по модулю  второй ступени на сохраненное значение веса
второй ступени на сохраненное значение веса 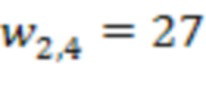 , т.е.
, т.е. 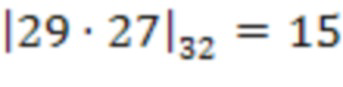 .
.
В первом сумматоре 3.3.1 по модулю  третьей вычислительной ступени выполняется операция вычитания из значения 15 второго блока умножения на веса
третьей вычислительной ступени выполняется операция вычитания из значения 15 второго блока умножения на веса 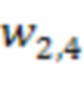 по модулю
по модулю  4.2.2 первой ступени значения 22 первого блока умножения на веса
4.2.2 первой ступени значения 22 первого блока умножения на веса 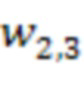 по модулю
по модулю 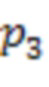 второй ступени, на выход первого сумматора 3.3.1 по модулю
второй ступени, на выход первого сумматора 3.3.1 по модулю  поступает значение 25.
поступает значение 25.
В первом блоке умножения на веса 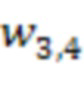 по модулю
по модулю  4.4.1 третьей ступени происходит умножение по модулю значения 25 с выхода первого сумматора 3.3.1 по модулю
4.4.1 третьей ступени происходит умножение по модулю значения 25 с выхода первого сумматора 3.3.1 по модулю  на сохраненное значение веса
на сохраненное значение веса 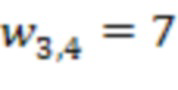 , т.е.
, т.е. 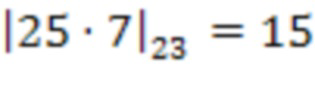 . В двоичной системе счисления данное число равно 01111 и на выход знака 5 подается старший бит 0.
. В двоичной системе счисления данное число равно 01111 и на выход знака 5 подается старший бит 0.
Таким образом, в СОК с модулями 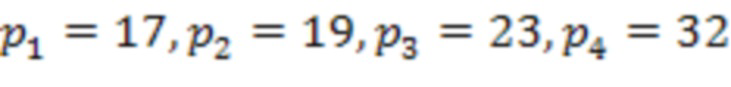 число
число 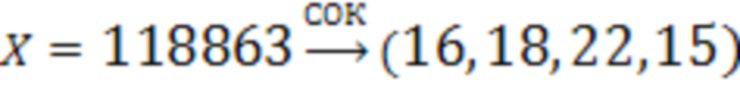 положительное.
положительное.
Рассмотрим другой пример: 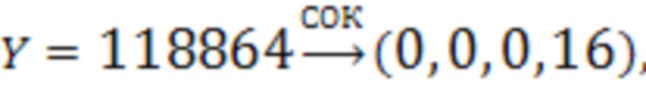 тогда в регистрах для хранения разрядов исходного числа 2.1-2.4 будут храниться соответственно числа 0, 0, 0, 16.
тогда в регистрах для хранения разрядов исходного числа 2.1-2.4 будут храниться соответственно числа 0, 0, 0, 16.
В первом сумматоре 3.1.1 по модулю 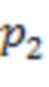 первой вычислительной ступени выполняется операция вычитания из значения 0 второго регистра для хранения разрядов исходного числа 2.2 значения 0 первого регистра для хранения разрядов исходного числа 2.1, на выход сумматора 3.1.1 по модулю
первой вычислительной ступени выполняется операция вычитания из значения 0 второго регистра для хранения разрядов исходного числа 2.2 значения 0 первого регистра для хранения разрядов исходного числа 2.1, на выход сумматора 3.1.1 по модулю 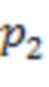 поступает значение 0. Во втором сумматоре 3.1.2 по модулю
поступает значение 0. Во втором сумматоре 3.1.2 по модулю 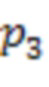 первой вычислительной ступени выполняется операция вычитания из значения 0 третьего регистра для хранения разрядов исходного числа 2.3 значения 0 первого регистра для хранения разрядов исходного числа 2.1, на выход сумматора 3.1.2 по модулю
первой вычислительной ступени выполняется операция вычитания из значения 0 третьего регистра для хранения разрядов исходного числа 2.3 значения 0 первого регистра для хранения разрядов исходного числа 2.1, на выход сумматора 3.1.2 по модулю 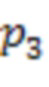 поступает значение 0. В третьем сумматоре 3.1.3 по модулю
поступает значение 0. В третьем сумматоре 3.1.3 по модулю  первой вычислительной ступени выполняется операция вычитания из значения 16 четвертого регистра для хранения разрядов исходного числа 2.4 значения 0 первого регистра для хранения разрядов исходного числа 2.1, на выход сумматора 3.1.3 по модулю
первой вычислительной ступени выполняется операция вычитания из значения 16 четвертого регистра для хранения разрядов исходного числа 2.4 значения 0 первого регистра для хранения разрядов исходного числа 2.1, на выход сумматора 3.1.3 по модулю  поступает значение 16.
поступает значение 16.
В первом блоке умножения на веса 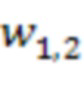 по модулю
по модулю 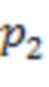 4.1.1 первой ступени происходит умножение по модулю значения 0 с выхода сумматора 3.1.1 по модулю
4.1.1 первой ступени происходит умножение по модулю значения 0 с выхода сумматора 3.1.1 по модулю 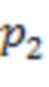 на сохраненное значение веса
на сохраненное значение веса 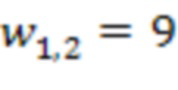 , т.е.
, т.е.  . Во втором блоке умножения на веса
. Во втором блоке умножения на веса 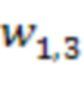 по модулю
по модулю 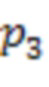 4.1.2 первой ступени происходит умножение по модулю значения 0 с выхода сумматора 3.1.2 по модулю
4.1.2 первой ступени происходит умножение по модулю значения 0 с выхода сумматора 3.1.2 по модулю 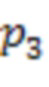 на сохраненное значение веса
на сохраненное значение веса 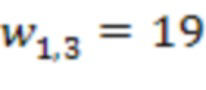 , т.е.
, т.е. 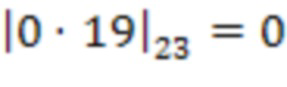 . Во третьем блоке умножения на веса
. Во третьем блоке умножения на веса 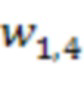 по модулю
по модулю  4.1.3 первой ступени происходит умножение по модулю значения 16 с выхода сумматора 3.1.3 по модулю
4.1.3 первой ступени происходит умножение по модулю значения 16 с выхода сумматора 3.1.3 по модулю  на сохраненное значение веса
на сохраненное значение веса 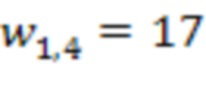 , т.е.
, т.е. 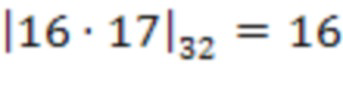 .
.
В первом сумматоре 3.2.1 по модулю 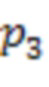 второй вычислительной ступени выполняется операция вычитания из значения 0 второго блока умножения на веса
второй вычислительной ступени выполняется операция вычитания из значения 0 второго блока умножения на веса 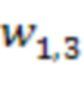 по модулю
по модулю 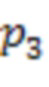 4.1.2 первой ступени значения 0 первого блока умножения на веса
4.1.2 первой ступени значения 0 первого блока умножения на веса 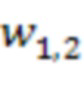 по модулю
по модулю 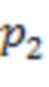 первой ступени, на выход первого сумматора 3.2.1 по модулю
первой ступени, на выход первого сумматора 3.2.1 по модулю 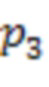 поступает значение 0. Во втором сумматоре 3.2.2 по модулю
поступает значение 0. Во втором сумматоре 3.2.2 по модулю  второй вычислительной ступени выполняется операция вычитания из значения 16 третьего блока умножения на веса
второй вычислительной ступени выполняется операция вычитания из значения 16 третьего блока умножения на веса 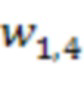 по модулю
по модулю  4.1.3 первой ступени значения 0 первого блока умножения на веса
4.1.3 первой ступени значения 0 первого блока умножения на веса 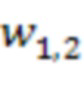 по модулю
по модулю 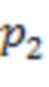 первой ступени, на выход второго сумматора 3.2.2 по модулю
первой ступени, на выход второго сумматора 3.2.2 по модулю  поступает значение 16.
поступает значение 16.
В первом блоке умножения на веса 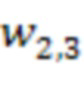 по модулю
по модулю 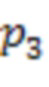 4.2.1 второй ступени происходит умножение по модулю значения 0 с выхода первого сумматора 3.2.1 по модулю
4.2.1 второй ступени происходит умножение по модулю значения 0 с выхода первого сумматора 3.2.1 по модулю 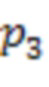 на сохраненное значение веса
на сохраненное значение веса 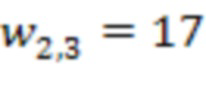 , т.е.
, т.е. 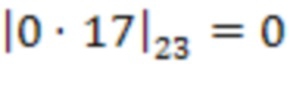 . Во втором блоке умножения на веса
. Во втором блоке умножения на веса 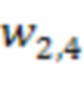 по модулю
по модулю  4.2.2 второй ступени происходит умножение по модулю значения 16 с выхода второго сумматора 3.2.2 по модулю
4.2.2 второй ступени происходит умножение по модулю значения 16 с выхода второго сумматора 3.2.2 по модулю  второй ступени на сохраненное значение веса
второй ступени на сохраненное значение веса 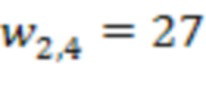 , т.е.
, т.е. 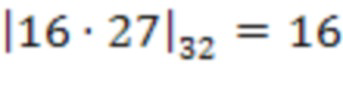 .
.
В первом сумматоре 3.3.1 по модулю  третьей вычислительной ступени выполняется операция вычитания из значения 16 второго блока умножения на веса
третьей вычислительной ступени выполняется операция вычитания из значения 16 второго блока умножения на веса 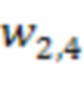 по модулю
по модулю  4.2.2 первой ступени значения 0 первого блока умножения на веса
4.2.2 первой ступени значения 0 первого блока умножения на веса 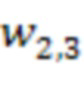 по модулю
по модулю 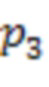 второй ступени, на выход первого сумматора 3.3.1 по модулю
второй ступени, на выход первого сумматора 3.3.1 по модулю  поступает значение 16.
поступает значение 16.
В первом блоке умножения на веса 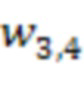 по модулю
по модулю  4.4.1 третьей ступени происходит умножение по модулю значения 16 с выхода первого сумматора 3.3.1 по модулю
4.4.1 третьей ступени происходит умножение по модулю значения 16 с выхода первого сумматора 3.3.1 по модулю  на сохраненное значение веса
на сохраненное значение веса 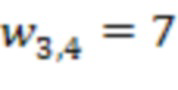 , т.е.
, т.е. 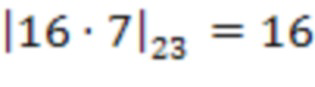 . В двоичной системе счисления данное число равно 10000 и на выход знака 5 подается старший бит 1.
. В двоичной системе счисления данное число равно 10000 и на выход знака 5 подается старший бит 1.
Таким образом, в СОК с модулями 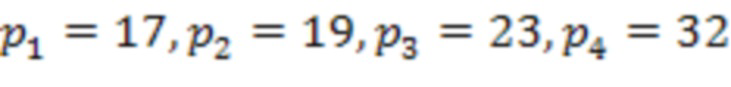 число
число 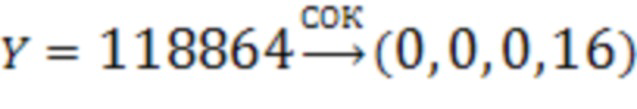 отрицательное.
отрицательное.
Поскольку все вычисления выполняются над целочисленными значениями малой размерности, увеличивается скорость вычисления и отсутствуют ошибки округления.
Реализация всего устройства возможна с использованием программируемых логических интегральных схем (ПЛИС) и может использоваться как отдельное устройство, так и как сопроцессор для выполнения немодульных операций.
| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для вычисления ранга модулярного числа | 2021 |
|
RU2780400C1 |
| Устройство сравнения чисел, представленных в системе остаточных классов | 2020 |
|
RU2751992C1 |
| Устройство для перевода чисел из системы остаточных классов и расширения оснований | 2020 |
|
RU2744815C1 |
| Способ определения знака числа в системе остаточных классов | 2021 |
|
RU2767450C1 |
| Устройство для операций над матрицами | 1989 |
|
SU1777153A1 |
| Генератор функций Попенко-Турко | 1990 |
|
SU1753464A1 |
| УСТРОЙСТВО ДЛЯ МАСШТАБИРОВАНИЯ ЧИСЛА В МОДУЛЯРНОЙ СИСТЕМЕ СЧИСЛЕНИЯ | 2002 |
|
RU2246753C2 |
| Устройство для контроля @ групп регистров | 1986 |
|
SU1322378A1 |
| Устройство для сравнения чисел в системе остаточных классов | 2018 |
|
RU2698413C1 |
| ПРОЦЕССОР БЫСТРОГО ПРЕОБРАЗОВАНИЯ СИГНАЛОВ ПО УОЛШУ С УПОРЯДОЧЕНИЕМ ПО АДАМАРУ | 1991 |
|
RU2025772C1 |
Изобретение относится к области вычислительной техники. Техническим результатом является увеличение скорости и точности вычислений определения знака чисел, представленных в системе остаточных классов. Раскрыто устройство определения знака числа, представленного в системе остаточных классов, содержащее  входов остатка, где
входов остатка, где  – количество модулей
– количество модулей 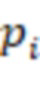 системы остаточных классов,
системы остаточных классов,  регистров для хранения разрядов исходного числа,
регистров для хранения разрядов исходного числа,  блоков умножения, где входы остатка подключены к входам соответствующих регистров для хранения разрядов исходного числа, при этом в него введены
блоков умножения, где входы остатка подключены к входам соответствующих регистров для хранения разрядов исходного числа, при этом в него введены 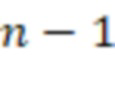 вычислительных ступеней, при этом
вычислительных ступеней, при этом 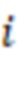 -я вычислительная ступень, где
-я вычислительная ступень, где 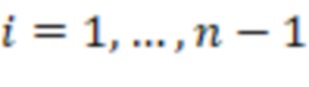 , содержит
, содержит 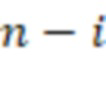 сумматоров по модулю
сумматоров по модулю 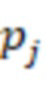 и
и 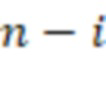 блоков умножения на веса
блоков умножения на веса 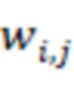 по модулю
по модулю 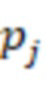 , где
, где 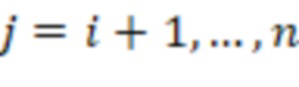 и
и 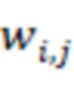 – мультипликативная инверсия модуля
– мультипликативная инверсия модуля 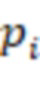 по модулю
по модулю 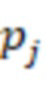 и модули упорядочены по возрастанию и
и модули упорядочены по возрастанию и 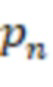 является степенью 2, в первой вычислительной ступени первые информационные входы
является степенью 2, в первой вычислительной ступени первые информационные входы 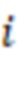 -х сумматоров по модулю
-х сумматоров по модулю 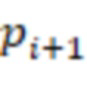 через инверторы подключены к выходу первого регистра для хранения разрядов исходного числа, вторые информационные входы
через инверторы подключены к выходу первого регистра для хранения разрядов исходного числа, вторые информационные входы 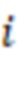 -х сумматоров по модулю
-х сумматоров по модулю 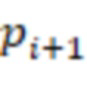 подключены к выходам
подключены к выходам 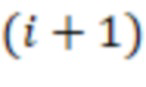 -х регистров для хранения разрядов исходного числа, на входы переносов
-х регистров для хранения разрядов исходного числа, на входы переносов 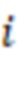 -х сумматоров по модулю
-х сумматоров по модулю 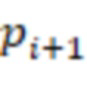 подается сигнал логической единицы, выходы
подается сигнал логической единицы, выходы 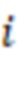 -х сумматоров по модулю
-х сумматоров по модулю 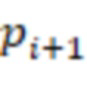 подключены ко входам соответствующих блоков умножения на веса
подключены ко входам соответствующих блоков умножения на веса 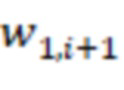 по модулю
по модулю 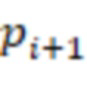 ,
, 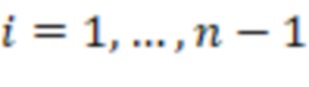 , в
, в 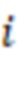 -x вычислительных ступенях,
-x вычислительных ступенях, 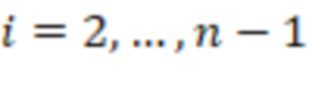 , первые информационные входы
, первые информационные входы 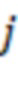 -х сумматоров по модулю
-х сумматоров по модулю 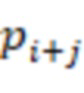 через инверторы подключены к выходу первого блока умножения на веса
через инверторы подключены к выходу первого блока умножения на веса 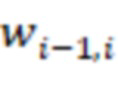 по модулю
по модулю 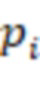
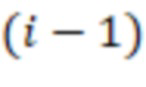 -й вычислительной ступени, вторые информационные входы
-й вычислительной ступени, вторые информационные входы 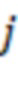 -х сумматоров по модулю
-х сумматоров по модулю 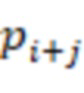 подключены к выходам
подключены к выходам 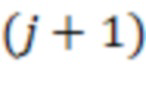 -х блоков умножения на веса
-х блоков умножения на веса 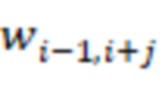 по модулю
по модулю 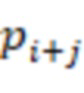
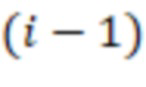 -й вычислительной ступени, на входы переносов
-й вычислительной ступени, на входы переносов 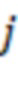 -х сумматоров по модулю
-х сумматоров по модулю 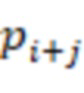 подается сигнал логической единицы, выходы
подается сигнал логической единицы, выходы 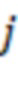 -х сумматоров по модулю
-х сумматоров по модулю 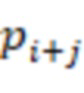 подключены к входам
подключены к входам 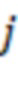 -х блоков умножения на веса
-х блоков умножения на веса 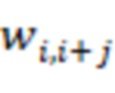 по модулю
по модулю 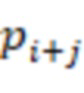 ,
, 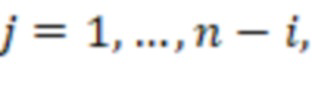 старший бит выхода блока умножения на веса
старший бит выхода блока умножения на веса 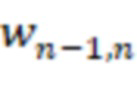
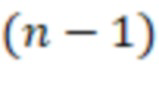 -й вычислительной ступени является выходом знака устройства. 1 ил.
-й вычислительной ступени является выходом знака устройства. 1 ил.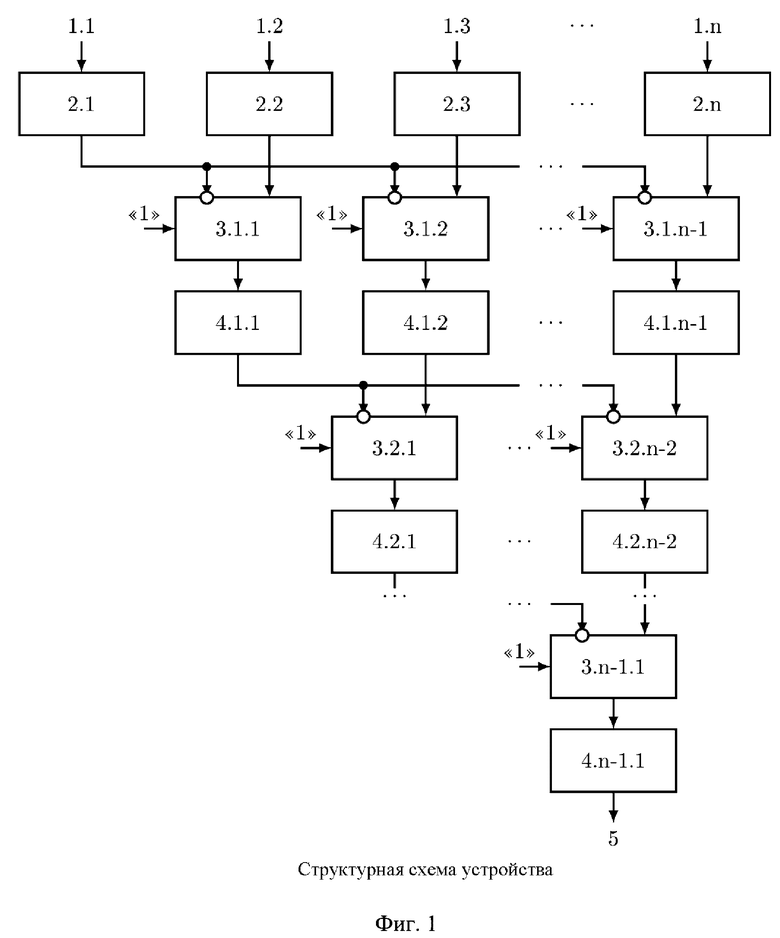
Устройство определения знака числа, представленного в системе остаточных классов, содержащее  входов остатка, где
входов остатка, где  – количество модулей
– количество модулей 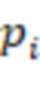 системы остаточных классов,
системы остаточных классов,  регистров для хранения разрядов исходного числа,
регистров для хранения разрядов исходного числа,  блоков умножения, где входы остатка подключены к входам соответствующих регистров для хранения разрядов исходного числа, отличающееся тем, что в него введены
блоков умножения, где входы остатка подключены к входам соответствующих регистров для хранения разрядов исходного числа, отличающееся тем, что в него введены 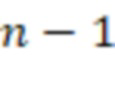 вычислительных ступеней, при этом
вычислительных ступеней, при этом 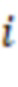 -я вычислительная ступень, где
-я вычислительная ступень, где 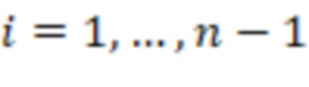 , содержит
, содержит 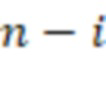 сумматоров по модулю
сумматоров по модулю 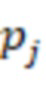 и
и 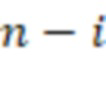 блоков умножения на веса
блоков умножения на веса 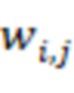 по модулю
по модулю 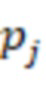 , где
, где 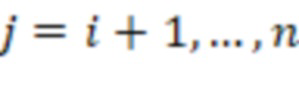 и
и 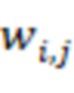 – мультипликативная инверсия модуля
– мультипликативная инверсия модуля 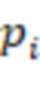 по модулю
по модулю 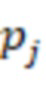 и модули упорядочены по возрастанию и
и модули упорядочены по возрастанию и 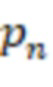 является степенью 2, в первой вычислительной ступени первые информационные входы
является степенью 2, в первой вычислительной ступени первые информационные входы 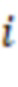 -х сумматоров по модулю
-х сумматоров по модулю 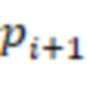 через инверторы подключены к выходу первого регистра для хранения разрядов исходного числа, вторые информационные входы
через инверторы подключены к выходу первого регистра для хранения разрядов исходного числа, вторые информационные входы 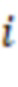 -х сумматоров по модулю
-х сумматоров по модулю 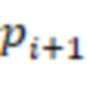 подключены к выходам
подключены к выходам 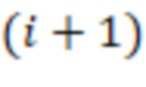 -х регистров для хранения разрядов исходного числа, на входы переносов
-х регистров для хранения разрядов исходного числа, на входы переносов 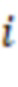 -х сумматоров по модулю
-х сумматоров по модулю 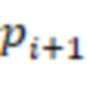 подается сигнал логической единицы, выходы
подается сигнал логической единицы, выходы 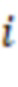 -х сумматоров по модулю
-х сумматоров по модулю 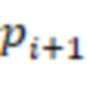 подключены ко входам соответствующих блоков умножения на веса
подключены ко входам соответствующих блоков умножения на веса 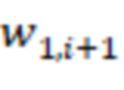 по модулю
по модулю 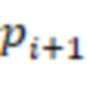 ,
, 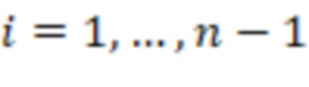 , в
, в 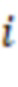 -x вычислительных ступенях,
-x вычислительных ступенях, 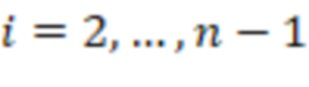 , первые информационные входы
, первые информационные входы 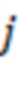 -х сумматоров по модулю
-х сумматоров по модулю 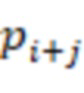 через инверторы подключены к выходу первого блока умножения на веса
через инверторы подключены к выходу первого блока умножения на веса 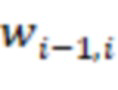 по модулю
по модулю 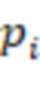
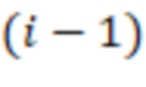 -й вычислительной ступени, вторые информационные входы
-й вычислительной ступени, вторые информационные входы 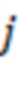 -х сумматоров по модулю
-х сумматоров по модулю 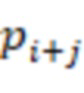 подключены к выходам
подключены к выходам 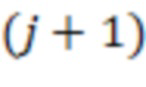 -х блоков умножения на веса
-х блоков умножения на веса 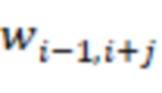 по модулю
по модулю 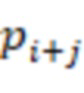
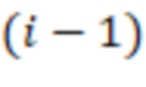 -й вычислительной ступени, на входы переносов
-й вычислительной ступени, на входы переносов 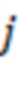 -х сумматоров по модулю
-х сумматоров по модулю 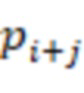 подается сигнал логической единицы, выходы
подается сигнал логической единицы, выходы 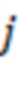 -х сумматоров по модулю
-х сумматоров по модулю 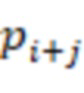 подключены к входам
подключены к входам 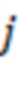 -х блоков умножения на веса
-х блоков умножения на веса 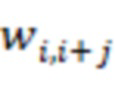 по модулю
по модулю 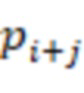 ,
, 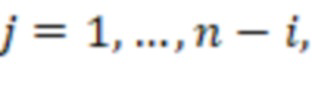 старший бит выхода блока умножения на веса
старший бит выхода блока умножения на веса 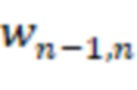
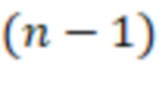 -й вычислительной ступени является выходом знака устройства.
-й вычислительной ступени является выходом знака устройства.
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ЗНАКА МОДУЛЯРНОГО ЧИСЛА | 2011 |
|
RU2503995C2 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ЗНАКОВ ЧИСЕЛ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2014 |
|
RU2557446C1 |
| УСТРОЙСТВО ДЛЯ СРАВНЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2011 |
|
RU2503992C2 |
| US 7523151 B1, 21.04.2009. | |||
Авторы
Даты
2021-05-04—Публикация
2020-10-22—Подача