СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ ПОДВИЖНОГО ОБЪЕКТА ПРИ НАВИГАЦИОННЫХ ИЗМЕРЕНИЯХ Российский патент 2014 года по МПК G01S19/45 

Изобретение относится к способам определения и прогнозирования местоположения объекта в пространстве и может быть использовано для повышения точности местоположения движущихся объектов при навигационных измерениях. Способ может найти применение в системах навигации, в системах ближней навигации и посадки, в системах управления и автоматического управления движущимися объектами, в системах управления воздушным движением и системах предупреждения столкновений, в системах автоматической стыковки движущихся объектов, в системах радиолокации, например, в ситуациях, когда цель идентифицирована и известны ее потенциальные возможности по перемещению в пространстве, а частота обновления радиолокационной информации низкая.

В настоящее время известны различные способы определения местоположения объекта.

Так, из описания к патенту РФ №2202102 (опубликован 10.04.2003) известен способ определения координат подвижных наземных объектов, легких летательных аппаратов, катеров, яхт. Способ включает измерение в калибровочном цикле контрольных значений горизонтальных проекций суммарного вектора напряженности магнитного поля Земли и магнитного поля объекта, измерение за время рабочего цикла усредненных значений проекций ускорения силы тяжести и проекций суммарного вектора напряженности поля Земли и магнитного поля объекта. С учетом коэффициентов коррекции определяют значения горизонтальных проекций вектора напряженности поля Земли. Определяют угол направления движения. Определяют приращения координат за время рабочего цикла. Определяют относительные координаты суммированием приращений координат. Определяют координаты объекта суммированием относительных координат и координат начальной точки. Измеряют с помощью приемника спутниковой навигационной системы координаты объекта, с учетом которых проводят коррекцию относительных координат и координат начальной точки. Определяют корректирующие коэффициенты, с учетом которых в каждом рабочем цикле проводят коррекцию угла направления движения и приращения пути. Обеспечивается повышение точности измерения направления движения и координат объекта и упрощение калибровки устройства.

Также из патента РФ №2399065 (опубликован 10.09.2010) известен способ определения местоположения подвижного объекта посредством гибридной навигационной системы, объединяющей приемник спутниковой навигационной системы для приема навигационного сигнала, который позволяет определять позицию спутников, скорость спутников, псевдорасстояния до объекта наблюдения и оценку допплеровского смещения несущей частоты навигационного сигнала, измерительное устройство инерционной навигационной системы и вычислительное устройство, расположенные на подвижном объекте, с которого поступают угловые скорости по каждой ортогональной оси X, Y и Z, линейные ускорения по ортогональным осям, заключающийся в том, что считают, что начальное местоположение подвижного объекта и начальное значение вектора его скорости известно, принятые данные со спутников, которые находятся в зоне радиовидимости, используют для формирования посредством вычислительного устройства двух матриц поворота, одна из которых - матрица поворота для координат спутников, другая - матрица поворота для скоростей спутников, используя сформированные матрицы поворота посредством вычислительного устройства осуществляют преобразование координат спутников и их скоростей из геоцентрической фиксированной системы координат в локальную систему координат, принимают данные с измерительного устройства инерционной навигационной системы подвижного объекта - угловые скорости и линейные ускорения подвижного объекта, используя принятые данные об угловых скоростях подвижного объекта, формируют матрицу поворота R из системы координат, связанной с подвижным объектом, в локальную систему координат, используя сформированную матрицу поворота R, преобразуют полученные данные о линейных ускорениях подвижного объекта; формируют матрицу перехода для вектора состояния, корреляционную матрицу ошибок инерционных измерений Q, характеризующую измерения, осуществляемые измерительным устройством инерционной навигационной системы, корреляционную матрицу ошибок измерения W, характеризующую данные, поступающие с приемника спутниковой навигационной системы, используя полученные преобразованные данные о линейных ускорениях подвижного объекта, а также значения местоположения, скорости, сформированные матрицы поворота, посредством вычислительного устройства вычисляют местоположение подвижного объекта и его скорость движения; преобразованные данные со спутников, матрицу перехода для вектора состояния, корреляционную матрицу ошибок инерционных измерений Q, корреляционную матрицу ошибок измерения W, вычисленные местоположение подвижного объекта и его скорость движения, используют для формирования матрицы Н, описывающей линейную связь всех измерений с компонентами вектора состояния, для вычисления прогнозируемых значений вектора состояния dx и для вычисления корреляционной матрицы ошибок оценки компонентов вектора состояния Р, используя вычисленные значения, вычисляют вектор состояния и его корреляционную матрицу ошибок, по результатам вычисленного вектора состояния определяют текущее местоположение объекта, отличающийся тем, что сформированные корреляционную матрицу ошибок инерционных измерений Q и корреляционную матрицу ошибок измерений W умножают на соответствующие им весовые коэффициенты, используя вычислительное устройство, при вычислении прогнозируемых значений вектора состояния dx и корреляционной матрицы его ошибок выполняют посредством вычислительного устройства обращение матрицы по приближенной формуле:

(W+H·P·HT )-1≈ 1/W(1-H·P·HT/W),

где T - операция транспонирования матрицы, при этом весовые коэффициенты выбирают таким образом, чтобы выполнялось условие H·P·H ^T/W<1, элементы корреляционной матрицы ошибок вектора состояния сравнивают с заданной величиной порога, если хотя бы один из элементов превышает заданную величину порога, то для вычисления вектора состояния текущего этапа используют вычисленные значения матрицы ошибок вектора состояния предыдущего этапа, в случае превышения порога хотя бы одним из элементов возвращается матрица дисперсии, вычисленная на предыдущем шаге.

Наиболее близким аналогом к изобретению является способ определения координат подвижных объектов, основанный на приеме сигналов космических аппаратов глобальных навигационных спутниковых систем, измерении псевдодальностей, введении поправок и вычислении координат подвижных объектов, отличающийся тем, что проводят n измерений псевдодальностей и координат движущегося объекта по известному маршруту, определяют точки x_io, y_io, z_io на известном маршруте, соответствующие кратчайшему расстоянию до точек с измеренными координатами x_i*, y_i*, z_i*, и определяют поправки путем решения системы из 3 n уравнений

x = a_xxi x_i+a_xyi y_i+a_xzi z_i,
y = a_yxi x_i+a_yyi y_i+a_yzi z_i,
z = a_zxi x_i+a_zyi y_i+a_zzi z_i,
где i = 1, n;

а_xxi, а_xyi, а_xzi, а_yxi, a_yyi, a_yzi, a_zxi, a_zyi, a_zzi - коэффициенты пересчета координат из специальной топоцентрической системы координат с центром в точке X_io, Y_io, Z_io, осями X_тi и Y_тi, лежащими в горизонтальной плоскости, и осью Z_тi, направленной вертикально вверх, причем точка x_i*, y_i*, z_i* лежит в плоскости X_тi, Z_тi, а касательная к известному маршруту лежит в плоскости Y_тi, Z_тi, в геоцентрическую систему координат;
x_i = b_xxi(x_i - x_io) + b_xyi(y_i - y_io) + b_xzi(z_i - z_io),

z_i = b_zxi(x_i - x_io) + b_zyi(y_i - y_io) + b_zzi(z_i - z_io),

b_xxi, b_xyi, b_xzi, b_zxi, b_zyi, b_zzi - коэффициенты пересчета координат из геометрической системы координат в специальную топоцентрическую систему координат с указанными характеристиками;
y_i - n сопутствующих неизвестных;
x, y, z - определяемые поправки (патент РФ №2145423, опубликован 10.02.2000).

Однако предлагаемые технические решения требуют или дополнительных навигационных измерений, или опорных точек с заранее известными геодезическими координатами и наличием канала связи между движущимся объектом и опорным пунктом, или полностью известных и с заданной точностью прогнозируемых траекторий движения объекта.

Техническим результатом изобретения является повышение точности определения местоположения движущегося объекта в пространстве на основе использования его динамических характеристик.

Предлагаемый способ определения местоположения (координат) движущихся объектов при навигационных измерениях отличается от известных тем, что на основе динамических свойств объекта прогнозируется область пространства возможного местоположения объекта в момент последующих навигационных измерений. Скорректированным местоположением объекта в пространстве при последующих навигационных измерениях считается пересечение областей пространства последующих навигационных измерений с прогнозируемыми областями.

Заявленный технический результат достигается за счет осуществления способа определения местоположения движущегося объекта в пространстве, характеризующегося тем, что осуществляют, по меньшей мере, три навигационных измерения, в результате которых определяют координаты 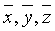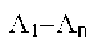$$\overline{x},\overline{y},\overline{z}$$ центра масс подвижного объекта в момент времени t₁-t_n, по данным результатов навигационных измерений определяют область пространства, в котором находится объект в момент времени t₁-t_n:

$${\Lambda }_1=\left\{\begin{array}{l}({\overline{x}}_1-h_X)+m\Delta x;\\ ({\overline{y}}_1-h_Y)+n\Delta y;\\ ({\overline{z}}_1-h_Z)+k\Delta z\end{array}\right\}$$

…

$${\Lambda }_n=\left\{\begin{array}{l}({\overline{x}}_n-h_X)+m\Delta x;\\ ({\overline{y}}_n-h_Y)+n\Delta y;\\ ({\overline{z}}_n-h_Z)+k\Delta z\end{array}\right\}$$

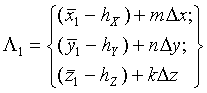
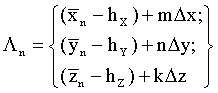
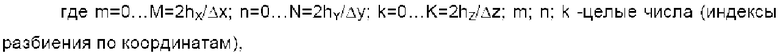
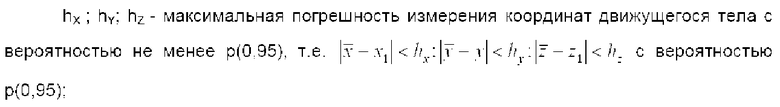
при этом при навигационных измерениях определяют следующие условия:

- погрешность каждого последующего измерения и сами значения измерений не зависят от результатов предыдущих измерений и их погрешностей, они статистически независимы;

- погрешность каждого измерения не зависит от местоположения объекта в пространстве, либо такой зависимостью в рамках нескольких последовательных измерений координат можно пренебречь и полагать, что hx; hy; hz = const при нескольких последовательных навигационных измерениях,

- далее определяют прогнозируемую область пространства, которую занимает объект через интервал времени Δt с учетом параметров ограничения движения, которые определяют посредством бортовых измерителей, расположенных на подвижном объекте, при этом в качестве параметров ограничения принимают:

- курсовую скорость V_{K MAX} - максимально возможную скорость по курсу при движении объекта (на каждом из этапов движения);

- максимальное курсовое ускорение а_{K MAX} - максимально возможное ускорение объекта по курсу (на каждом из этапов движения);

- максимальную вертикальную скорость - V_{В MAX};

- а _{В MAX} - максимально возможное вертикальное ускорение (на каждом из этапов движения);

- максимально возможное изменение угла рыскания Ψ _MAX за время Δt между очередными навигационными измерениями;

- максимально возможное изменение угла тангажа Θ_MAX за время Δt между очередными навигационными измерениями и обобщенные условия ограничения местоположения объекта по данным навигационных измерений и динамических свойств объекта выражают в виде системы неравенств:

Значения V_{K MAX}; a_{K MAX}; V_{B MAX}; a_{B MAX}; Θ_MAX; Ψ_MAX в системе неравенств обобщенных условий ограничения местоположения объекта по данным навигационных измерений с учетом влияния ветра можно записать как показания бортовых измерителей следующим образом:

где

Λ_ПР1 - прогнозируемая в момент t₁ область пространства, которую может занимать движущееся тело в момент времени t₂ через Δt, лежит в пределах конуса, образованного касательными к поверхностям сфер Λ₁ и Λ₂;

далее истинное, крайнее, положение курса увеличивают на угол максимально возможного за время Δt отклонения объекта по углам тангажа и углу курса, в результате чего получают прогнозируемое пространство Λ_ПР2 возможного местоположения объекта в момент времени t₂ в виде выпуклого эллиптического конуса с углами раскрыва θ_MAX и Ψ_MAX, причем высоту указанного конуса определяют максимально возможной курсовой скоростью передвижения объекта за время Δt, а истинное местоположение объекта после второго навигационного измерения через интервал Δt (пространство выигрыша) определяют пересечением областей пространства

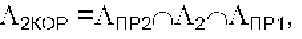
при этом совместная вероятность равна р(0,95)×р(0,95)=0,9025, а пространство выигрыша Λ_ПР2∩Λ₂∩Λ_ПР1 следует увеличить по всем трем координатам x; y; z, входящим в пространство Λ₂ в процентном отношении, равном процентному отношению случайной величины р(0,95)/з(0,9025), далее осуществляют коррекцию местоположения движущихся объектов по результатам трех навигационных измерений следующим образом:

по результатам первого и второго навигационного измерения по вышеизложенному алгоритму определяют Λ_2КОР - выигрыш в определении местоположения после второго навигационного измерения, при этом коррекцию проводят по скорости и максимальным углам отклонения;

на основании закона распределения случайной величины - погрешности навигационных измерений - определяют область пространства Λ'_2КОР (р(0,95)) с вероятностью не менее 0,95, при этом истинное положение объекта Λ'_2КОР (р(0,95)) находится внутри объема пространства Λ₂;

при получении данных третьего навигационного измерения - область Λ₃ - определяют область Λ_3КОР - выигрыш в определении местоположения после третьего навигационного измерения, используя в качестве исходных данных показания второго и третьего измерения, при этом коррекцию проводят по скорости и максимальным углам отклонения, а в качестве исходной для прогнозирования принимают область скорректированного пространства местоположения объекта в момент второго навигационного измерения Λ'_2КОР (р(0,95));

после чего на основании закона распределения случайной величины - погрешности навигационных измерений - определяют область пространства Λ'_3КОР (р(0,95)) с вероятностью не менее 0,95, при этом Λ'_3КОР (р(0,95)) находится внутри объема пространства Λ₃,

на основании всех трех навигационных измерений вновь определяют область Λ_{3КОР УСК} - выигрыш в определении местоположения после третьего навигационного измерения, при этом коррекция происходит по значениям ускорений, а в качестве исходной для прогнозирования принимается область Λ'_2КОР (р(0,95)) - уже скорректированного объема пространства возможного местоположения объекта в момент второго навигационного измерения;

на основании закона распределения случайной величины - погрешности навигационных измерений - определяют область пространства Λ'_{3 УСК} (р(0,95)) с вероятностью не менее 0,95, при этом Λ'_{3 УСК} (р(0,95)) находится внутри объема пространства Λ₃;

определяют пересечение объемов пространства найденных скорректированных объемов пространства местоположения объекта Λ'_3КОР (р(0,95)) с Λ'_{3КОР УСК} (р(0,95)), пространство пересечения указанных объемов Λ_{3КОР ОКОНЧ.} будет являться окончательным скорректированным положением объекта в момент времени t₃;

далее, на основании закона распределения случайной величины - погрешности навигационных измерений - определяют область пространства Λ'_{3КОР ОКОН} (р(0,95)) с вероятностью не менее 0,95, при этом Λ'_{3КОР ОКОН} (р(0,95)) находится внутри объема пространства Λ₃ и для области пространства третьего измерения получают значения диапазона индексов координат x; y; z (i…j; r…p; q…f), входящих в пространство окончательно скорректированного положения объекта в момент времени t₃ Λ'_{3КОР ОКОН} (р(0,95)):

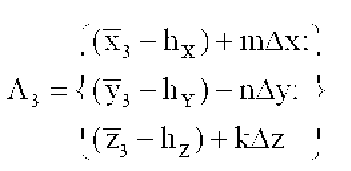
m=i…j - диапазон индексов координаты х, входящих в пространство Λ'_{3КОР ОКОН};

n=r…p - диапазон индексов координаты y, входящих в пространство Λ'_{3КОР ОКОН};

k=q…f - диапазон индексов координаты z, входящих в пространство Λ'_{3КОР ОКОН};

в качестве конечного результата местоположения объекта в пространстве с вероятностью не менее р(0,95) считают геометрическую середину скорректированной области пространства Λ'_{3КОР ОКОН} со скорректированными координатами x_(j-i)/2; y_(p-r)/2; z_(f-q)/2.

Суть вышеизложенного метода заключается в следующем.

Пусть x,y,z,- истинные координаты объекта в базовой системе координат, связанной с центром масс объекта, а 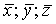$$\overline{x};\overline{y};\overline{z}$$ - результаты навигационного измерения его местоположения в какой-то момент t. Пусть для навигационной системы погрешность измеряемой величины определена с вероятностью р(0,95), т.е. с вероятностью 95% можно говорить о том, что погрешность измерения навигационного параметра не превысит своих максимальных значений h_X; h_Y; h_Z, известных из тактико-технических характеристик навигационной системы.

Например, для глобальных спутниковых систем навигации GPS или ГЛОНАСС с вероятностью не менее р(0,95) можно утверждать, что истинное значение будет отличаться от измеренного не более чем на 8-10 метров в горизонтальной плоскости и в 1,5÷2 раза выше погрешность в вертикальной плоскости.

Результаты любых навигационных измерений можно представить как пространственную область, где с вероятностью р(0,95) ошибка измерений не превысит значений h_X; h_Y; h_Z. Для глобальных спутниковых систем навигации такую область пространства можно интерпретировать как вертикальный эллипсоид. Предположим, что при навигационных измерениях выполняются следующие условия:

погрешность каждого последующего и сами значения измерений не зависят от результатов предыдущих измерений и их погрешностей, они статистически независимы;

погрешность каждого измерения не зависит от местоположения объекта в пространстве, либо такой зависимостью в рамках нескольких последовательных измерений координат можно пренебречь и полагать, что h_X;h_Y;h_Z=const при нескольких последовательных навигационных измерениях.

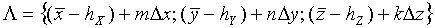
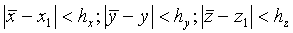
Пусть по данным результатов навигационных измерений в момент времени t задана область пространства Λ. Ее можно представить в дискретном виде как $$\Lambda =\left\{(\overline{x}-h_X)+m\Delta x;(\overline{y}-h_Y)+n\Delta y;(\overline{z}-h_Z)+k\Delta z\right\}$$ , где m=0…M=2h_X/Δx; n=0…N=2h_Y/Δy; k=0…K=2h_Z/Δz; m; n; k -целые числа (индексы разбиения по координатам). Значения h_X ; h_Y; h_Z - максимальная погрешность измерения координат движущегося тела с вероятностью не менее p(0,95), т.е. $$\left|\overline{x}-x_1\right|<h_x;\left|\overline{y}-y\right|<h_y;\left|\overline{z}-z_1\right|<h_z$$ с вероятностью p(0,95); Δx;Δy;Δz-интервалы разбиения (можно трактовать как интервалы разбиения для обеспечения необходимой точности дискретизации пространства).

Рассмотрим последовательные навигационные измерения в моменты времени t₁-t_n, определяющие области пространства Λ₁-Λ_n местоположения объекта в моменты времени t₁-t_n:

$${\Lambda }_1=\left\{\begin{array}{l}({\overline{x}}_1-h_X)+m\Delta x;\\ ({\overline{y}}_1-h_Y)+n\Delta y;\\ ({\overline{z}}_1-h_Z)+k\Delta z\end{array}\right\}$$

…

$${\Lambda }_n=\left\{\begin{array}{l}({\overline{x}}_n-h_X)+m\Delta x;\\ ({\overline{y}}_n-h_Y)+n\Delta y;\\ ({\overline{z}}_n-h_Z)+k\Delta z\end{array}\right\}$$

$${\overline{x}}_1\mathrm{...}{\overline{x}}_n,{\overline{y}}_1\mathrm{...}{\overline{y}}_n,{\overline{z}}_1\mathrm{...}{\overline{z}}_n$$ - данные навигационных измерений в момент времени t₁-t_n.

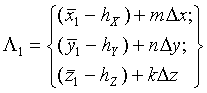
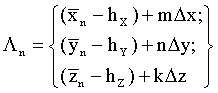
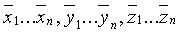
Для прогнозирования области каждого последующего навигационного измерения Λ_ПР выбираются параметры ограничения местоположения объекта из-за его динамических свойств, в качестве которых могут выступать: максимальная скорость и ускорение (в зависимости от задач могут быть вертикальная и горизонтальная, курсовая и снижения, прочие линейные и угловые скорости и ускорения); максимальное изменение угла азимута (или рыскания); угла места (или крена) или прочие параметры.

Например, в качестве параметров ограничения движения могут выступать: курсовая скорость V_{K MAX}- максимально возможная скорость по курсу при движении объекта (на каждом из этапов движения); максимальное курсовое ускорение а_{K MAX}- максимально возможное ускорение объекта по курсу (на каждом из этапов движения); максимальная вертикальная скорость - V_{В MAX}; а_{В MAX} -максимально возможное вертикальное ускорение (на каждом из этапов движения); максимально возможное изменение угла рыскания ψ_MAX за время Δt между очередными навигационными измерениями; максимально возможное изменение угла тангажа θ_MAX за время Δt между очередными навигационными измерениями; при необходимости возможно использование максимального изменения угла крена γ_MAX за время Δt между очередными навигационными измерениями.

Обобщенные условия ограничения местоположения объекта по данным навигационных измерений и динамических свойств объекта можно записать так:

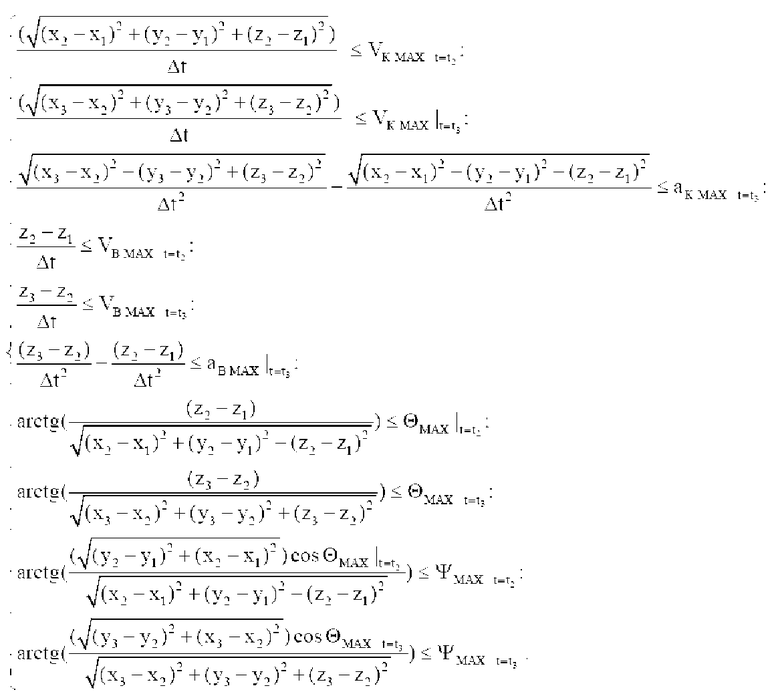(1)

при этом :

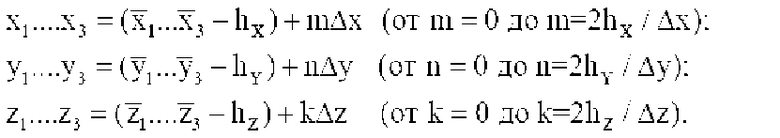(2)\tab\tab\tab\tab

t₁-t₃ - моменты времени трех последовательных навигационных измерений.

Данные неравенства следует трактовать следующим образом.

Первое неравенство - скорость прохождения объектом пути за время Δt между первым и вторым измерением не может превышать максимально возможную курсовую скорость.

Второе неравенство - аналогично, но между вторым и третьим измерением.

Третье неравенство - курсовое ускорение объекта не должно превышать максимально возможное.

Четвертое-шестое неравенство аналогично 1-3 неравенству для вертикальной скорости и ускорения.

Седьмое-восьмое неравенство определяет максимально возможный угол наклона объекта от вертикали (что фактически определяет угол тангажа) для второго и третьего измерения.

Девятое-десятое неравенство определяет максимально возможный угол отклонения от курса для второго и третьего измерения.

Максимальные значения возможных скоростей, ускорений и углов отклонений в выражениях (1)-(2) должны учитывать силу ветра и его влияние на движущийся объект. Для конкретных технических задач и объектов условия ограничения местоположения объекта из-за его динамических свойств могут иметь несколько иной вид.

В качестве максимально возможных скоростей, ускорений и углов отклонений можно принимать как физически невозможные для подвижного объекта (например, для автомобиля), так и не рекомендуемые на данном этапе движения (например, этапе полета) по соображениям безопасности движения (например, критические углы атаки, глиссады, критическая скорость снижения и т.д.). Как правило, например, на борту воздушного судна имеются системы предупреждения о критических режимах движения (превышении максимальных значений скоростей, ускорений и углов отклонений). В силу этого, с вероятностью не менее p(0,95) можно утверждать, что объект не превышает указанных критических значений.

Для повышения точности местоположения объекта в пространстве возможно использование не предельных значений скоростей, ускорений и изменения угловых положений объекта, а текущих реальных данных бортовых измерителей (БИ) параметров движения объекта (скоростей, углов, ускорений). Максимальные параметры V_{K MAX}; a_{K MAX}; V_{B MAX}; a_{B MAX}; Θ_MAX; Ψ_MAX определяются текущими показаниями бортовых измерителей, их погрешностями, показаниями датчиков ветра и направлением ветра, а также приращением измеряемых параметров за время между навигационным измерением и ближайшим после него поступлением информации от бортового измерителя.

В этом случае (и с учетом влияния ветра) значения V_{K MAX}; a_{K MAX}; V_{B MAX}; a_{B MAX}; Θ_MAX; Ψ_MAX в системе неравенств (1) обобщенных условий ограничения местоположения объекта по данным навигационных измерений можно записать как показания бортовых измерителей следующим образом:

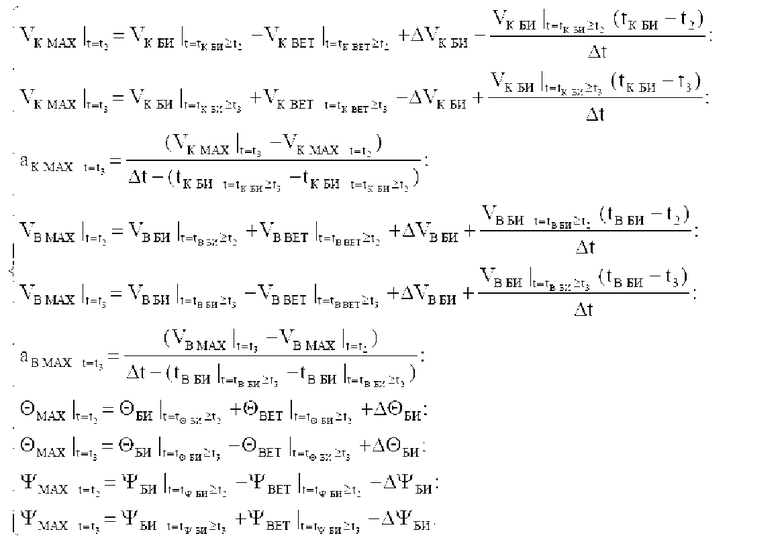(3)

где

В данных выражениях значения погрешностей показаний бортовых измерителей и частота обновления информации бортовых измерителей определяется тактико-техническими характеристиками (ТТД) конкретных приборов. Зачастую, значение погрешностей измерений по ТТД выражается в процентном отношении от значений измеряемых параметров.

Таким образом, используя ограничения на возможность передвижения объекта (1)-(3) можно прогнозировать область пространства возможного местоположения каждого последующего после начального навигационного измерения.

Пусть известны два навигационных измерения в моменты времени t₁: $${\overline{x}}_1;{\overline{y}}_1;{\overline{z}}_1$$ и t₂: $${\overline{x}}_2;{\overline{y}}_2;{\overline{z}}_2$$ в базовой системе координат и соответственно области пространства возможных точных измерений координат Δ₁ и Δ₂ (см. фиг.1). Λ_ПР1 - прогнозируемая в момент t₁ область пространства, которую может занимать движущееся тело в момент времени t₂ через Δt (интервал обновления навигационной информации) ввиду своих динамических свойств по возможности перемещения. Λ₁ ∈Λ_ПР1, т.е. Λ_ПР1 вбирает в себя Λ₁. Так как после первого измерения курс объекта не очевиден, то пространство Λ_ПР1 определяется максимально возможной скоростью передвижения объекта за время Δt.

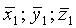
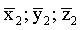
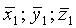
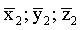
Направление, определяемое прямой, соединяющей точки навигационных измерений $${\overline{x}}_1;{\overline{y}}_1;{\overline{z}}_1$$ и $${\overline{x}}_2;{\overline{y}}_2;{\overline{z}}_2$$ , является псевдокурсом. Истинное максимально возможное (с точностью р(0,95)) положение курса лежит в пределах конуса, образованного касательными к поверхностям сфер Λ₁ и Λ₂, как это представлено на фиг.1. Для простоты графического представления, будем считать, что h_X=h_Y=h_Z. и Λ₁; Λ₂; Λ₃ являются сферами (хотя для глобальных спутниковых навигационных систем правильно было бы считать, что h_X=h_Y, а h_Z≈1,5÷2 h_X).

Истинное, крайнее положение курса необходимо увеличить на угол максимально возможного (за время Δt) отклонения объекта по углам тангажа и углу курса. Рассмотрим сечение сфер Λ₁ и Λ₂ относительно оси псевдокурса в горизонтальной и вертикальной плоскости. В результате, получим прогнозируемое пространство Λ_ПР2 возможного местоположения объекта в момент времени t₂ в виде выпуклого эллиптического конуса (углы раскрыва определяются θ_MAX и ψ_MAX)_. Высота указанного конуса определяется максимально возможной курсовой скоростью передвижения объекта за время Δt. Истинное местоположение объекта после второго навигационного измерения через интервал Δt будет определяться не областью Λ₂, а пересечением областей пространств Λ_ПР2∩Λ₂∩Λ_ПР1.

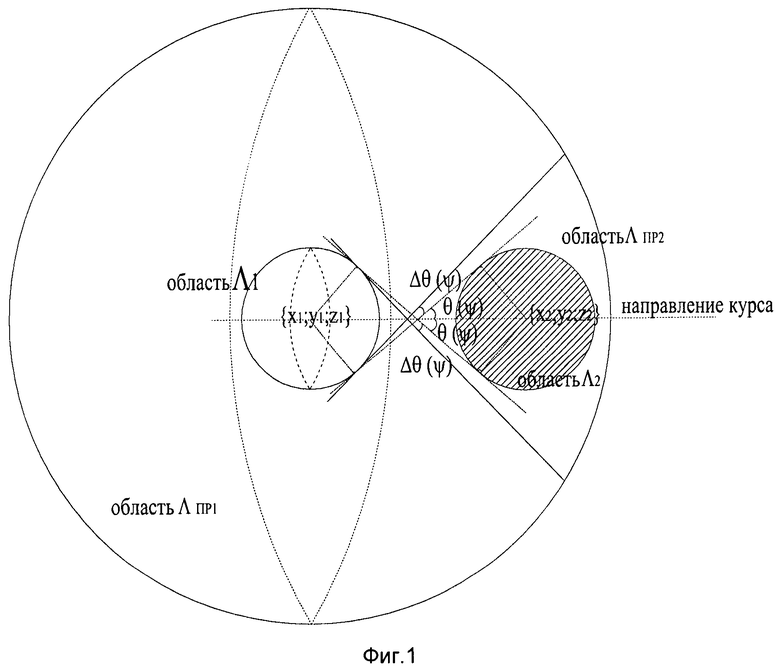
Возможны следующие случаи прогнозирования положения объекта, они схематично показаны на фигурах 1-3.

В первом случае (фигура 1) область Λ₂ полностью принадлежит области Λ_ПР2, и выигрыша в определении местоположения движущегося объекта нет.

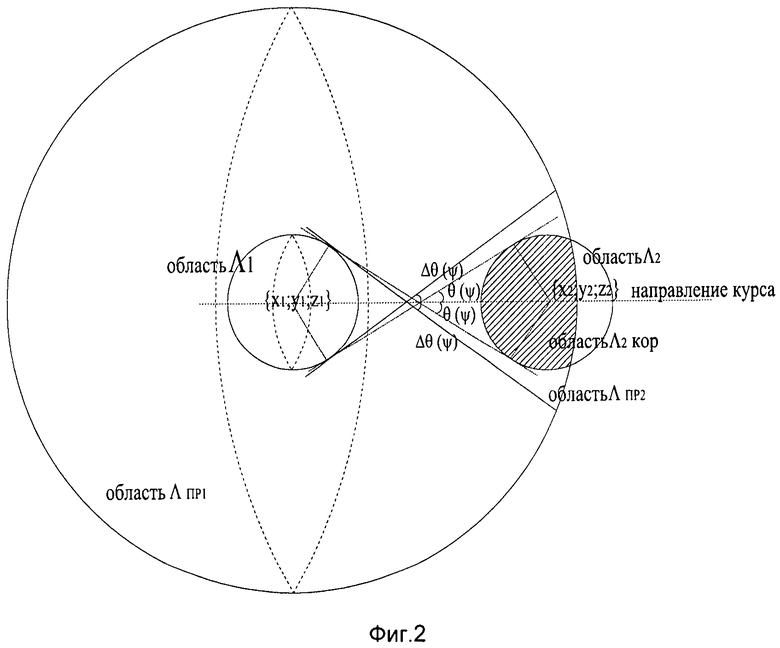
Во втором случае (фигура 2) Λ_ПР2∩Λ₂∩Λ_ПР1<Λ₂, и имеется выигрыш в определении местоположения движущегося объекта.

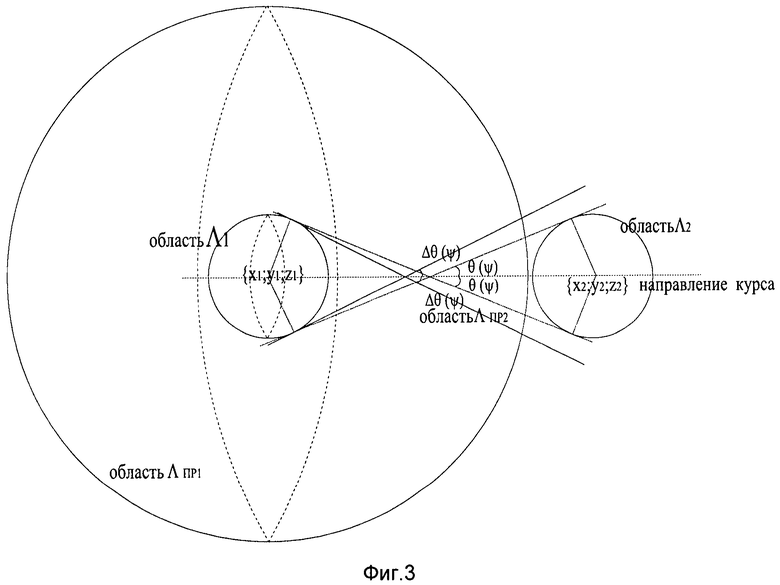
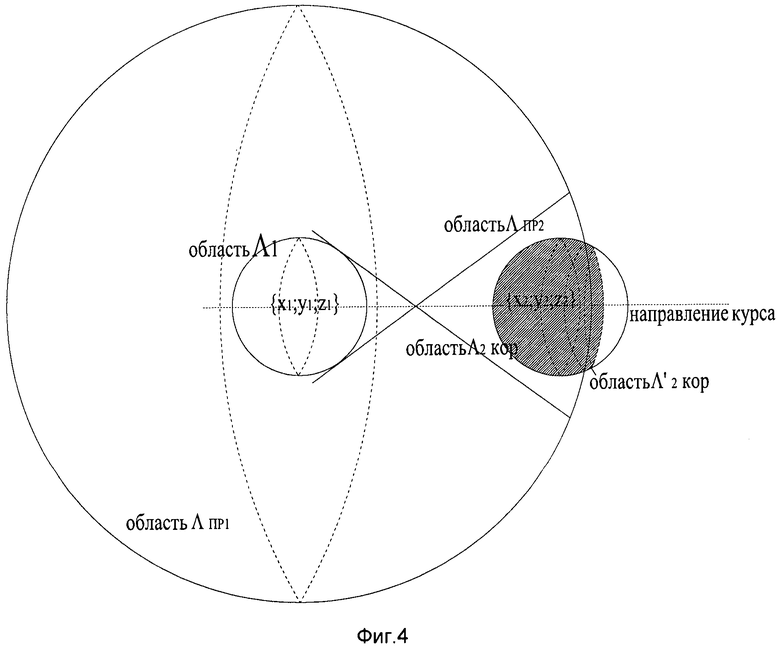
В третьем случае (фигура 3) пересечение Λ_ПР2 и Λ₂ является пустым множеством. В данном случае результат второго навигационного измерения не согласуются с данными, прогнозируемым по динамическим характеристикам местоположением объекта. Это означает, что либо велика погрешность данного навигационного измерения (выпадает из доверительного интервала в p(0,95)), либо неверно (или с большой погрешностью) оценены динамические свойства движущегося объекта. Вероятность того, что оба навигационных измерения в моменты t₁ и t₂ лежат в интервале p(0,95) несколько ниже. Поскольку в начальных условиях принимается, что навигационные измерения в разные моменты времени статистически независимы, совместная вероятность равна p(0,95)х p(0,95)=0,9025. Если знать закон распределения случайной величины погрешности навигационных измерений, то пространство выигрыша Λ_ПР2∩Λ₂∩Λ_ПР1 следует увеличить (по всем трем координатам x;y;z, но так, чтобы они входили в пространство Λ₂) в процентном отношении, равном процентному отношению случайной величины p(0,95)/p(0,9025). Это несколько снижает выигрыш в определении местоположения объекта, но при этом скорректированный объем пространства возможного местоположения движущегося объекта будет определяться с вероятностью не менее p(0,95). Пример получившегося объема пространства показан на фигуре 4.

Обозначим выигрыш в определении местоположения как Λ_2КОР = Λ_ПР2∩Λ₂∩Λ_ПР1 и Λ'_2КОР (р(0,95)) - выигрыш в определении местоположения с вероятностью не менее 0,95.

Для практической реализации предлагается использовать следующий алгоритм коррекции местоположения движущихся объектов по результатам трех навигационных измерений:

1. По результатам первого и второго навигационного измерения по вышеизложенному алгоритму определим Λ_2КОР - выигрыш в определении местоположения после второго навигационного измерения. При этом для прогнозирования местоположения используем показания бортовых измерителей на основании неравенств (1)-(3). Коррекция происходит по скорости и максимальным углам отклонения.

2. На основании закона распределения случайной величины- погрешности навигационных измерений определим область пространства Λ'_2КОР (р(0,95)) с вероятностью не менее 0,95. При этом Λ'_2КОР (р(0,95)) находится внутри объема пространства Λ₂.

3. При получении данных третьего навигационного измерения (область Λ₃), аналогично пункту 1 определим область Λ_3КОР - выигрыш в определении местоположения после третьего навигационного измерения, используя в качестве исходных данных показания второго и третьего измерения. Коррекция происходит по скорости и максимальным углам отклонения. Отличие от пункта 1 состоит в том, что в качестве исходной для прогнозирования принимается область не Λ₂ , а Λ'_2КОР (р(0,95)) - уже скорректированный объем пространства возможного местоположения объекта в момент второго навигационного измерения.

4. На основании закона распределения случайной величины - погрешности навигационных измерений определим область пространства Λ'_3КОР (р(0,95)) с вероятностью не менее 0,95. При этом Λ'_3КОР (р(0,95)) находится внутри объема пространства Λ₃.

5. На основании всех трех навигационных измерений вновь определим область Λ_{3КОР УСК} - выигрыш в определении местоположения после третьего навигационного измерения. При этом коррекция происходит по значениям ускорений. В качестве исходной для прогнозирования принимается область не Λ₂, а Λ'_2КОР (р(0,95)) - уже скорректированный объем пространства возможного местоположения объекта в момент второго навигационного измерения.

6. На основании закона распределения случайной величины - погрешности навигационных измерений определим область пространства Λ'_{3КОР УСК} (р(0,95)) с вероятностью не менее 0,95. При этом Λ'_{3КОР УСК} (р(0,95)) находится внутри объема пространства Λ₃.

7. Определим пересечение объемов пространства, найденных в пунктах 4 и 6, т.е. Λ'_3КОР (р(0,95)) ∩ Λ'_{3КОР УСК} (р(0,95)) = Λ_{3КОР ОКОНЧ.} -окончательное (по предложенному алгоритму) скорректированное положение объекта в момент времени t₃.

8. На основании закона распределения случайной величины - погрешности навигационных измерений определим область пространства Λ'_{3КОР ОКОН} (р(0,95)) с вероятностью не менее 0,95. При этом Λ'_{3КОР ОКОН} (р(0,95)) находится внутри объема пространства Λ₃.

Предложенный алгоритм является одним из вариантов коррекции местоположения объекта на основании данных навигационных измерений и наложения ограничений, связанных с динамическими свойствами движущегося объекта. Данный метод определения местоположения объекта в пространстве, уточняя навигационные данные за счет наложения ограничений, связанных с динамическими свойствами движущегося объекта, можно назвать методом динамической рекуррентной коррекции.

Повысить точность определения местоположения движущегося объекта, можно используя не только три первых измерения, но и результаты последующих четвертого и пятого измерений. В этом случае первая коррекция будет с задержкой в 5 шагов (5Δt), а каждый последующий результат измерений будет идти с задержкой в 2 шага (2Δt), где Δt-частота обновления навигационной информации.

Использование метода определения местоположения объекта в пространстве, уточняя навигационные данные за счет наложения ограничений, связанных с динамическими свойствами движущегося объекта, зависит от точностных характеристик навигационной системы, точности показаний бортовых измерителей параметров движения и скорости и силы ветра.

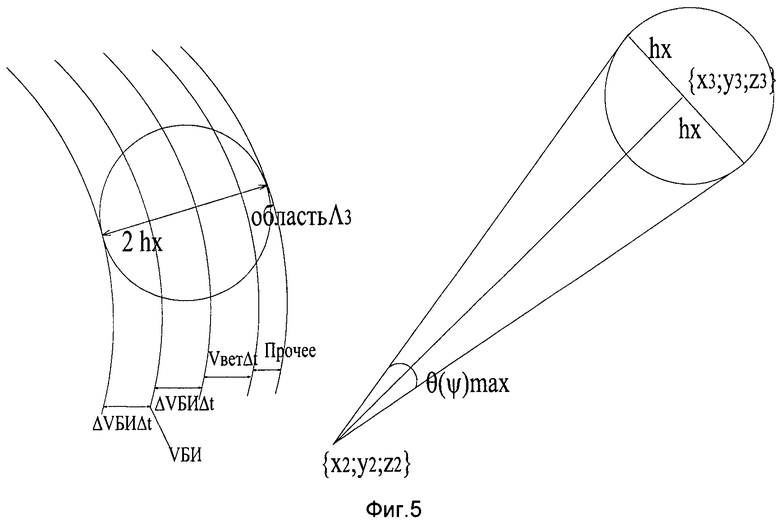
Условиями возможности использовать динамическую рекуррентную коррекцию можно считать превышение точности определения параметров движения по сравнению с точностью определения местоположения навигационной системой (фигура 5):

Таким образом, получение выигрыша от применения динамической рекуррентной коррекции возможно для разных значений скоростей и боковых смещений объекта, если возможно обеспечить точное прогнозирование (точные измерения его параметров движения).

Возможны ситуации, изображенные на фигуре 3, когда данные последующих навигационных измерений не согласуются с данными, прогнозируемым по динамическим характеристикам местоположением объекта. В данном случае с вероятностью P(95%) можно утверждать, что такого значения измерения быть не должно. Однако такие случаи возможны вследствие отказов навигационных средств, а также при прохождении летательных аппаратов через «пораженные зоны», где из-за переотражений или других дестабилизирующих факторов погрешность измерений резко возрастает. Отдельные подобные случаи можно полагать промахами, но при их повторении в выборке накопленных значений навигационных измерений более критического значения, навигационная система считается отказавшей. Для этих целей можно воспользоваться любым статистическим критерием оценки, при известном статистическом законе распределения вероятности погрешности навигационных измерений.

Сопоставляя и статистически анализируя области пространства последовательных навигационных измерений местоположения объекта и прогнозируемую область пространства возможного местоположения объекта (исходя из его динамических свойств по перемещению в пространстве) в момент следующего измерения, можно делать выводы о достоверности показаний навигационных средств.

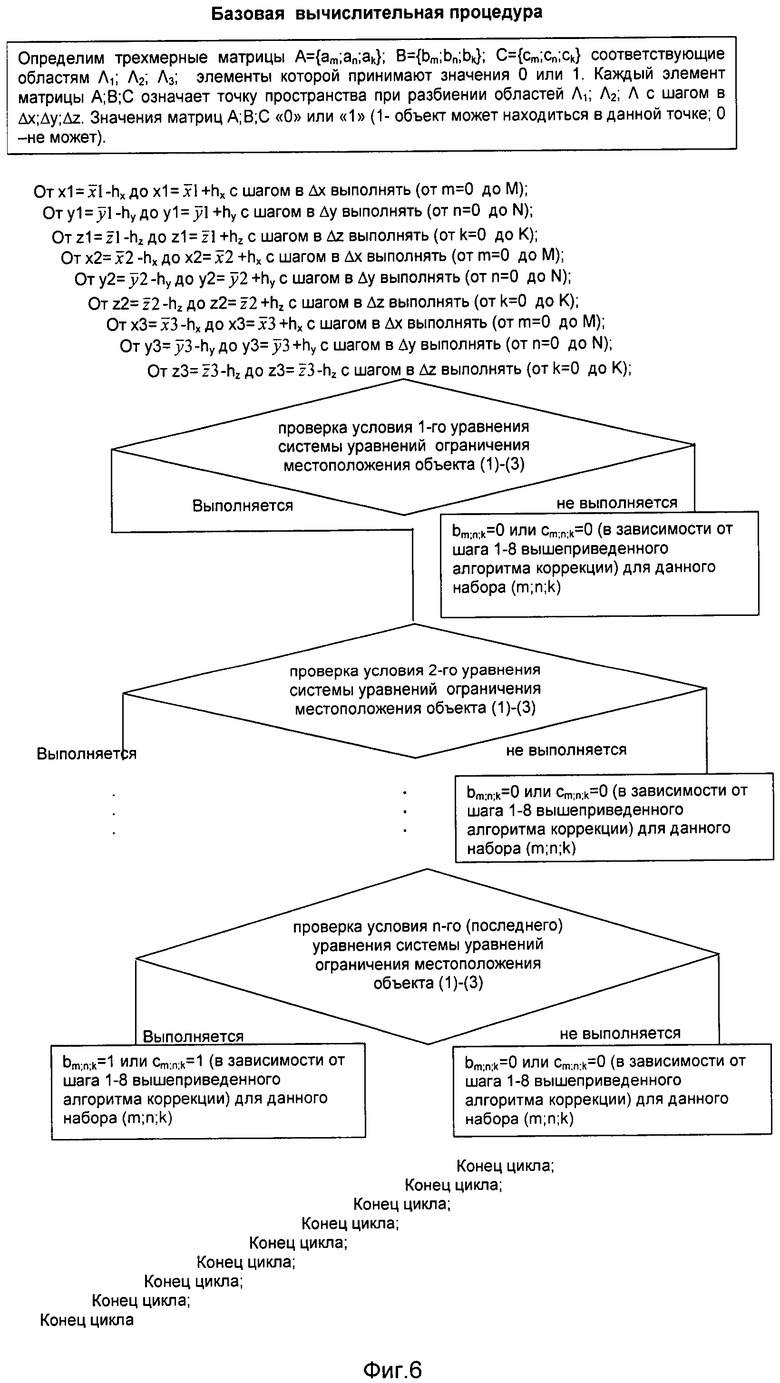
Аналогично, можно выявлять и ошибки показаний бортовых измерителей параметров движения объекта (например, ДИСС, баровысотомер, радиовысотомер и др.). Для практической реализации можно предложить следующую процедуру нахождения области пространства возможного местоположения движущегося объекта с использованием условий динамических ограничений (см.фиг.6).

Определим трехмерные матрицы A={a_m;а_n;а_k}; B={b_m;b_n;b_k}; C={c_m;c_n;c_k}, соответствующие областям Λ₁; Λ₂; Λ₃; элементы которой принимают значения 0 или 1. Каждый элемент матрицы А;В;С означает точку пространства при разбиении областей Λ₁; Λ₂; Λ с шагом в Δх;Δy;Δz. Значения матриц А; В; С «0» или «1» (1- объект может находиться в данной точке; 0 -не может). При начальном шаге вычислений (получении исходных данных) все элементы матриц считаются равными 1 (нескорректированные значения навигационного измерения).

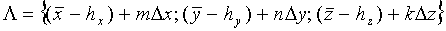
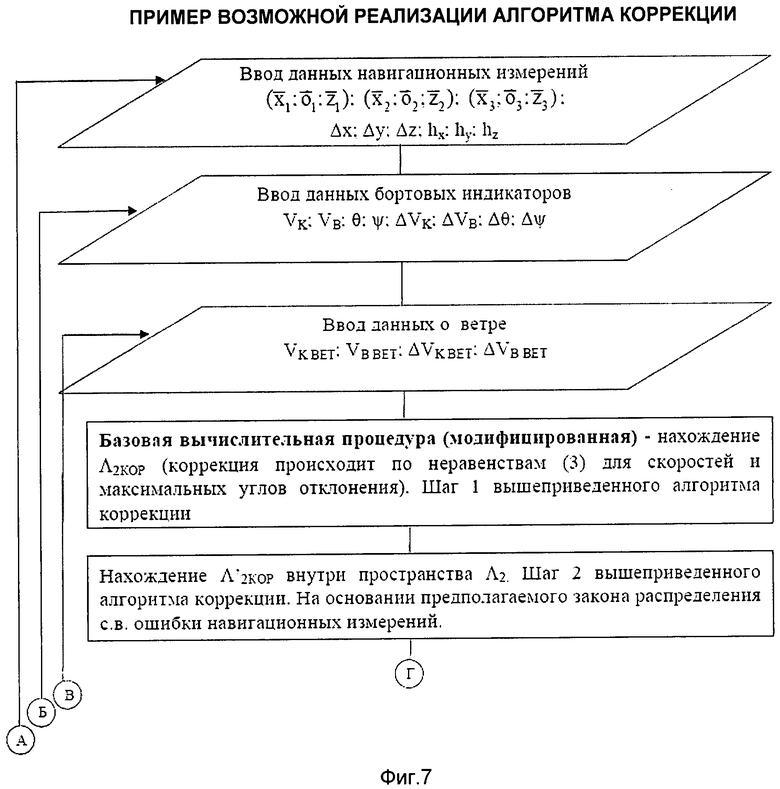
В базовой процедуре происходит просто перебор всех возможных значений матриц А,В,С (точек пространств Λ₁; Λ₂; Λ₃), удовлетворяющих условиям динамических ограничений (1)-(3). Итогом вычисления являются матрицы В или С (в зависимости от шага 1-8 вышеприведенного алгоритма коррекции), такие, что ее элементы B={b_m;b_n;b_k} или C={c_m;c_n;c_k} определяют возможность находиться в пространстве $$\Lambda =\left\{(\overline{x}-h_x)+m\Delta x;(\overline{y}-h_y)+n\Delta y;(\overline{z}-h_z)+k\Delta z\right\}$$ .

В примере реализации алгоритма (см.фиг.7) коррекции базовая вычислительная процедура при втором и последующих циклах вычисления должна быть модифицирована. Смысл модификации заключается в том, что выполняется проверка не всех условий уравнений динамической коррекции или не для всей области пространства предыдущего навигационного измерения, а для области пространства предыдущего измерения, уже ограниченного предыдущим циклом вычислений. При этом сокращается и количество вычислений.

Выигрыш в определении местоположения объекта можно оценить как отношение количества элементов матрицы, не равных нулю, к общему количеству элементов матрицы.

Предлагаемый алгоритм и базовая вычислительная процедура являются лишь одним из возможных вариантов реализации динамической рекуррентной коррекции. Реальный алгоритм для конкретного объекта может учитывать лишь часть предлагаемых условий коррекции (1)-(3) либо учитывать свои условия.

Предложенный алгоритм предполагает модификации базовой вычислительной процедуры (перебора точек области пространства) при первичном и последующих циклах измерений. При последующих циклах расчетов в качестве исходной области для прогнозирования принимается область пространства возможного местоположения, уже скорректированная предыдущими измерениями. Алгоритм реализации динамической рекуррентной коррекции позволяет обрабатывать данные с БИ, датчиков ветра и навигационной системы в режиме реального времени по мере их поступления.

При практической реализации необходимо предусмотреть возможность прекращения подачи данных с навигационной системы. При прекращении поступления навигационных данных на период более времени обновления навигационной информации, вычисления необходимо начинать заново, с первичного цикла расчетов.

При реализации базового алгоритма в реальном времени, необходимо выполнить весь объем вычислений за время, меньшее, чем минимальное время обновления информации исходных данных расчетов. Для уменьшения вычислительной сложности базового алгоритма, сокращения количества вычислений и реализации его в реальном времени, можно оптимизировать его следующим образом:

последовательно уменьшать интервал разбиения пространства возможного местоположения объекта Δx; Δy;Δz. Первоначально можно сделать расчет при большом разбиении, потом на границе области пространства уточненного местоположения объекта сделать расчет при меньшем разбиении;

использовать (либо не использовать) условия ограничения местоположения объекта, связанные с ускорением. Если априорно известно, что движущийся объект имеет положительные ускорения (линейные или угловые), то уравнения, связанные с ускорением, можно не использовать. Тогда в основной вычислительной процедуре базового алгоритма будет не девять, а шесть циклов расчета.

Поступающие данные с бортовых измерителей, датчиков ветра и навигационной системы могут быть дискретными с определенной частотой обновления, тогда осуществлять расчеты необходимо через интервалы минимальной частоты обновления информации бортовых измерителей. Если потоки данных от бортовых измерителей являются аналоговыми, то изменения таких данных и перерасчеты можно проводить при заданном пороге изменения таких данных (при преобразовании формата данных устанавливать либо пороговые, либо дифференциальные ограничения). Если потоки данных являются дискретными и случайными (переменное время поступления информации), то изменения таких данных и перерасчеты необходимо проводить сразу при их поступлении (в реальном времени).

В качестве примера, предлагается один из вариантов блок-схемы устройства, с помощью которого возможно осуществить способ динамической рекуррентной коррекции (фиг.8).

Данные бортовых измерителей, датчиков ветра и навигационной системы поступают по отдельным каналам в соответствующие им блоки преобразования формата данных 1, 2 и 3 соответственно. Блоки 1-3 осуществляет преобразование данных с бортовых измерителей, датчиков ветра и навигационной системы для возможности обработки численных данных в блоке бортового вычислителя 6. Далее по отдельным каналам преобразованные данные поступают в блок измерителя временного интервала поступления данных 5, в котором происходит формирование информации о временных промежутках поступления данных, а также все данные синхронизируются по времени с помощью блока синхронизации вычислений времени 4. Из блока измерителя 5 данные поступают в блок бортового вычислителя 6 (решающее устройство по алгоритму динамической коррекции), который реализует алгоритм динамической коррекции местоположения движущегося объекта. Из блока 6 обработанные данные поступают на выход, а также заносятся в буфер памяти, в котором уже хранятся данные предыдущих измерений.

Для преобразования формата данных (по уровню и формату представления) в зависимости от типа бортового измерителя могут использоваться АЦП (при аналоговых выходных сигналах с измерителей) или, при необходимости, преобразователи интерфейсов (например, RS485/RS232 или аналогичные). В качестве измерителей временных интервалов возможно использование счетчиков с тактовыми генераторами и фиксаторов временного положения импульса. В качестве бортового вычислителя используется бортовая ЭВМ или отдельный мини-компьютер.

В процессе проведения вычислений (по вышеприведенному алгоритму коррекции местоположения движущихся объектов по результатам трех навигационных измерений) получаем область пространства Λ'_{3КОР ОКОН} (р(0,95)), которая находится внутри объема пространства Λ₃, при этом для области пространства третьего измерения получены значения:

m=i…j - диапазон индексов координаты x, входящих в пространство Λ'_{3КОР ОКОН};

n=r…p - диапазон индексов координаты y, входящих в пространство Λ'_{3КОР ОКОН};

k=q…f - диапазон индексов координаты z, входящих в пространство Λ'_{3КОР ОКОН}.

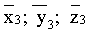
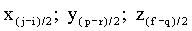
В таком случае, в качестве конечного результата повышения точности обработки навигационных измерений с вероятностью не менее р(0,95) можно считать геометрическую середину скорректированной области пространства Λ'_{3КОР ОКОН}, т.е. вместо значений третьего измерения $${\overline{x}}_3;{\overline{y}}_3;{\overline{z}}_3$$ окончательными выходными скорректированными данными третьего измерения (на выходе бортового вычислителя 6 по схеме на фиг.8) будут координаты $$x_{(j-i)/2};y_{(p-r)/2};z_{(f-q)/2}$$ .

Структурную схему (фиг.8) можно рассматривать как схему комплексирования бортовых измерителей параметров движения объекта с навигационной системой объекта.

Таким образом, использование способа определения местоположения объекта в пространстве по изобретению, уточняя навигационные данные за счет наложения ограничений, связанных с динамическими свойствами движущегося объекта, позволяет:

- повысить точность местоположения объекта в пространстве;

- не требует проведения дополнительных навигационных измерений, или опорных точек с заранее известными геодезическими координатами, или априорно известной траектории движения объекта;

- может применяться для различных значений скоростей и угловых смещений объекта;

- является алгоритмичным и не требует сложных вычислительных процедур;

- позволяет комплексировать оборудование бортовых измерителей параметров движения и навигационное оборудование. Позволяет повысить надежность выявления отказов бортовых измерителей параметров движения и навигационного оборудования.

Изобретение относится к способам определения и прогнозирования местоположения объекта в пространстве. Технический результат состоит в повышении точности определения местоположения движущихся объектов в пространстве при навигационных измерениях на основе использования его динамических характеристик. Для этого на основе динамических свойств объекта прогнозируется область пространства возможного местоположения объекта в момент последующих навигационных измерений. Скорректированным местоположением объекта в пространстве при последующих навигационных измерениях считается пересечение областей пространства последующих навигационных измерений с прогнозируемыми областями. 8 ил.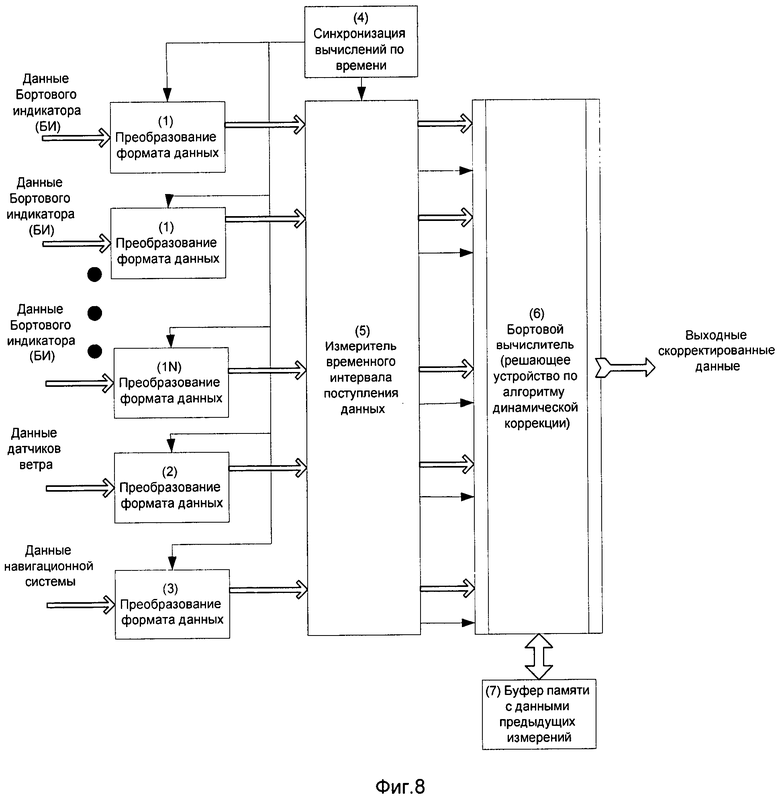

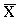
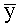
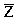
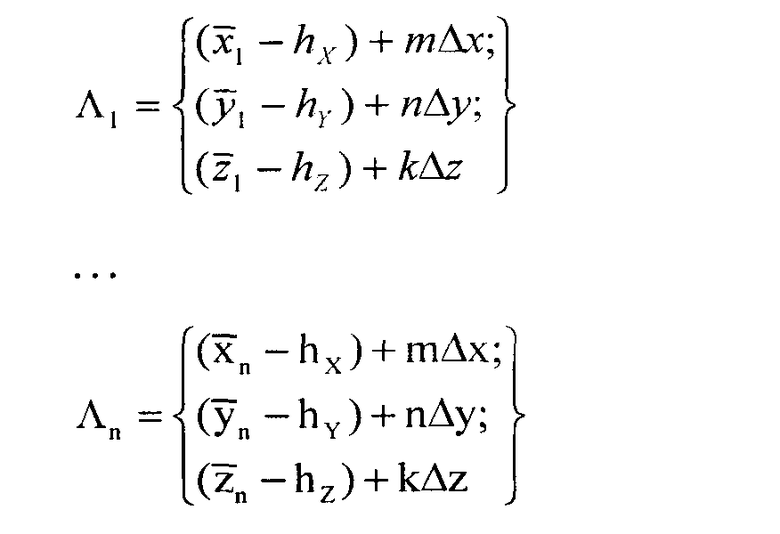
Способ определения местоположения движущегося объекта в пространстве, характеризующийся тем, что осуществляют, по меньшей мере, три навигационных измерения, в результате которых определяют координаты $$\overline{x}$$ , $$\overline{y}$$ , $$\overline{z}$$ центра масс подвижного объекта в момент времени t₁-t_n, по данным результатов навигационных измерений определяют область Λ₁-Λ_n пространства, в котором находится объект в момент времени t₁-t_n:

где m=0…M=2h_X/Δx; n=0…N=2h_Y/Δ_y; k=0…K=2h_Z/Δz; m; n; k - целые числа (индексы разбиения по координатам),
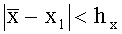
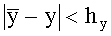
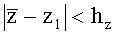
h_X; h_Y; h_Z - максимальная погрешность измерения координат движущегося тела с вероятностью не менее p(0,95), т.е. $$\left|\overline{x}-x_1\right|<h_x$$ ; $$\left|\overline{y}-y\right|<h_y$$ ; $$\left|\overline{z}-z_1\right|<h_z$$ с вероятностью p(0,95);
Δx; Δy; Δz - интервалы разбиения для обеспечения необходимой точности дискретизации пространства,
$${\overline{x}}_1\dots {\overline{x}}_n$$ , $${\overline{y}}_1\dots {\overline{y}}_n$$ , $${\overline{z}}_1\dots {\overline{z}}_n$$ - данные навигационных измерений в момент времени t₁-t_n,
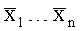
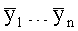
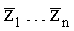
x₁…x_n, y₁…y_n, z₁…z_n - данные истинного положения объекта в момент времени t₁-t_n,
при этом при навигационных измерениях определяют следующие условия:
- погрешность каждого последующего измерения и сами значения измерений не зависят от результатов предыдущих измерений и их погрешностей, они статистически независимы;
- погрешность каждого измерения не зависит от местоположения объекта в пространстве, либо такой зависимостью в рамках нескольких последовательных измерений координат можно пренебречь и полагать, что h_X; h_Y; h_Z=const при нескольких последовательных навигационных измерениях,
- далее определяют прогнозируемую область пространства, которую занимает объект через интервал времени Δt с учетом параметров ограничения движения, которые определяют посредством бортовых измерителей, расположенных на подвижном объекте, при этом в качестве параметров ограничения принимают:
- курсовую скорость V_{К MAX} - максимально возможную скорость по курсу при движении объекта (на каждом из этапов движения);
- максимальное курсовое ускорение а _{К MAX} - максимально возможное ускорение объекта по курсу (на каждом из этапов движения);
- максимальную вертикальную скорость - V_{B MAX};
- a _{B MAX} - максимально возможное вертикальное ускорение (на каждом из этапов движения);
- максимально возможное изменение угла рыскания ψ_MAX за время Δt между очередными навигационными измерениями;
- максимально возможное изменение угла тангажа θ_MAX за время Δt между очередными навигационными измерениями,
и обобщенные условия ограничения местоположения объекта по данным навигационных измерений и динамических свойств объекта выражают в виде системы неравенств:

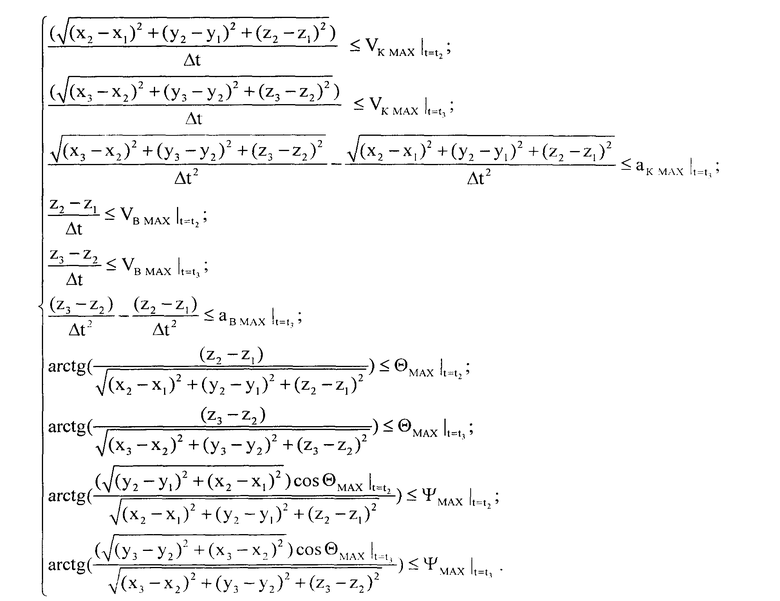
при этом:

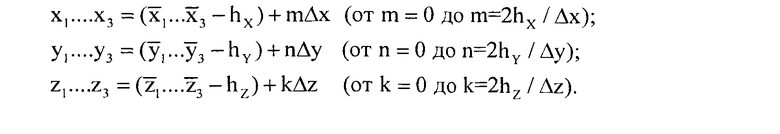
значения V_{К MAX}; a _{К MAX}; V_{B MAX}; a _{B MAX}; Θ_MAX; ψ_MAX в системе неравенств обобщенных условий ограничения местоположения объекта по данным навигационных измерений с учетом влияния ветра можно записать как показания бортовых измерителей следующим образом:

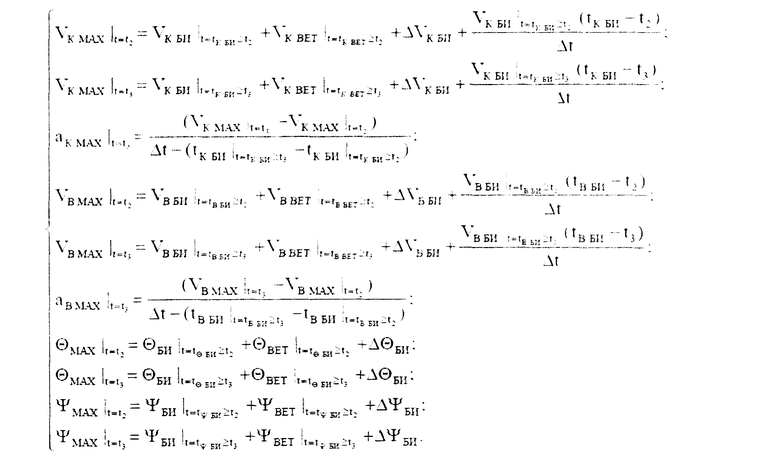
где
$$V_{К}{}_{БИ}|{{}_{t=t}}_{{}_K{}_{БИ}\ge t_2}$$ ; $$V_{К}{}_{БИ}|{{}_{t=t}}_{{}_K{}_{БИ}\ge t_3}$$ - значение курсовой скорости по показаниям бортового измерителя в моменты времени поступления информации от бортового измерителя сразу же после навигационных измерений в моменты t₂ и t₃;
$$V_{К}{}_{ВЕТ}|{{}_{t=t}}_{{}_K{}_{ВЕТ}\ge t_2}$$ $$V_{К}{}_{ВЕТ}|{{}_{t=t}}_{{}_K{}_{ВЕТ}\ge t_3}$$ - составляющая курсовой скорости вследствие влияния ветра (по данным датчиков ветра) сразу же после навигационных измерений в моменты t₂ и t₃;
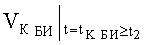
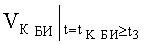
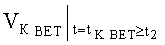
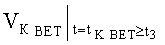
ΔV_{К БИ} - погрешность показаний бортового измерителя курсовой скорости;
$$V_{В}{}_{БИ}|{{}_{t=t}}_{{}_{К}{}_{БИ}\ge t_2}$$ ; $$V_{В}{}_{БИ}|{{}_{t=t}}_{{}_{К}{}_{БИ}\ge t_3}$$ ; $$V_{В}{}_{ВЕТ}|{{}_{t=t}}_{{}_{К}{}_{ВЕТ}\ge t_2}$$ ; $$V_{В}{}_{ВЕТ}|{{}_{t=t}}_{{}_{К}{}_{ВЕТ}\ge t_3}$$ ; ΔV_{В БИ} - значения вертикальной скорости по показаниям бортового измерителя, данным датчиков ветра и погрешность показаний бортового измерителя вертикальной скорости, при этом все значения аналогичны значениям приведенных выше величин;
$$\Delta t_{КБИ}=\left(t_{КБИ}|{{}_{t=t}}_{{}_{К}{}_{БИ}\ge t_3}-t_{КБИ}|{{}_{t=t}}_{{}_{К}{}_{БИ}}{}_{\ge t_2}\right)$$ - частота обновления показаний бортового измерителя курсовой скорости;
$$\Delta t_{ВБИ}=\left(t_{ВБИ}|{{}_{t=t}}_{{}_{В}{}_{БИ}\ge t_3}-t_{ВБИ}|{{}_{t=t}}_{{}_{В}{}_{БИ}}{}_{\ge t_2}\right)$$ - частота обновления показаний бортового измерителя вертикальной скорости;
$${\Theta }_{БИ}{}_{|t=t_{\Theta }{}_{БИ}\ge t_2}$$ ; $${\Theta }_{БИ}|{{}_{t=t}}_{{}_{\Theta }{}_{БИ}}{{}_{\ge t}}_{{}_3}$$ - значение угла наклона объекта от вертикали (что фактически определяет угол тангажа) по показаниям бортового измерителя сразу же после навигационных измерений в моменты t₂ и t₃;
$${\Theta }_{{}_{ВЕТ}}{}_{|t=t_{\Theta }{}_{БИ}\ge t_2}$$ ; $${\Theta }_{ВЕТ}|{{}_{t=t}}_{{}_{\Theta }{}_{БИ}}{}_{\ge t_3}$$ - составляющая угла наклона объекта от вертикали вследствие влияния ветра (по данным датчиков ветра) сразу же после навигационных измерений в моменты t₂ и t₃;
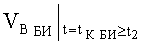
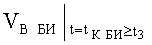
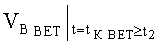
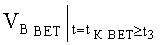
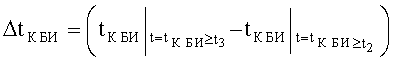
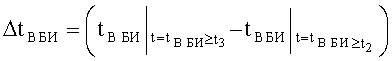
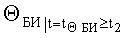
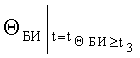
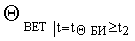
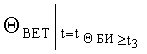
ΔΘ_БИ - погрешность показаний бортового измерителя угла наклона объекта от вертикали;
$${\Theta }_{БИ}{}_{|t=t_{\Theta }{}_{БИ}\ge t_2}$$ ; $${\Theta }_{БИ}|{{}_{t=t}}_{{}_{\Theta }{}_{БИ}}{}_{\ge t_3}$$ ; $${\Psi }_{{}_{ВЕТ}}{}_{|t=t_{\psi }{}_{БИ}\ge t_2}$$ ; $${\Psi }_{ВЕТ}|{{}_{t=t}}_{{}_{\psi }{}_{БИ}}{}_{\ge t_3}$$ ; Δψ_БИ - значения угла отклонения курса по показаниям бортового измерителя, данным датчиков ветра и погрешность показаний бортового измерителя угла отклонения курса;
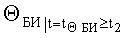
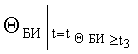
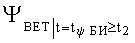
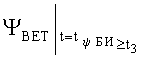
Λ_ПР1 - прогнозируемая в момент t₁ область пространства, которую может занимать движущееся тело в момент времени t₂ через Δt, лежит в пределах конуса, образованного касательными к поверхностям сфер Λ₁ и Λ₂;
далее истинное, крайнее, положение курса увеличивают на угол максимально возможного за время Δt отклонения объекта по углам тангажа и углу курса, в результате чего получают прогнозируемое пространство Λ_ПР2 возможного местоположения объекта в момент времени t₂ в виде выпуклого эллиптического конуса с углами раскрыва θ_MAX и ψ_MAX, причем высоту указанного конуса определяют максимально возможной курсовой скоростью передвижения объекта за время Δt, а истинное местоположение объекта после второго навигационного измерения через интервал Δt (пространство выигрыша) определяют пересечением областей пространства
Λ_2КОР=Λ_ПР2∩Λ₂∩Λ_ПР1,
при этом совместная вероятность равна p(0,95)×p(0,95)=0,9025, а пространство выигрыша Λ_ПР2∩Λ₂∩Λ_ПР1 следует увеличить по всем трем координатам x; y; z, входящим в пространство Λ₂ в процентном отношении, равном процентному отношению случайной величины p(0,95)/p(0,9025), далее осуществляют коррекцию местоположения движущихся объектов по результатам трех навигационных измерений следующим образом:
по результатам первого и второго навигационного измерения по вышеизложенному алгоритму определяют Λ_2КОР - выигрыш в определении местоположения после второго навигационного измерения, при этом коррекцию проводят по скорости и максимальным углам отклонения;
на основании закона распределения случайной величины - погрешности навигационных измерений - определяют область пространства Λ′_2КОР (p(0,95)) с вероятностью не менее 0,95, при этом истинное положение объекта Λ′_2КОР (p(0,95)) находится внутри объема пространства Λ₂; при получении данных третьего навигационного измерения - область Λ₃ - определяют область Λ_3КОР - выигрыш в определении местоположения после третьего навигационного измерения, используя в качестве исходных данных показания второго и третьего измерений, при этом коррекцию проводят по скорости и максимальным углам отклонения, а в качестве исходной для прогнозирования принимают область скорректированного пространства местоположения объекта в момент второго навигационного измерения Λ′_2КОР (p(0,95));
после чего на основании закона распределения случайной величины - погрешности навигационных измерений - определяют область пространства Λ′_3КОР (p(0,95)) с вероятностью не менее 0,95, при этом Λ′_3КОР (p(0,95)) находится внутри объема пространства Λ₃,
на основании всех трех навигационных измерений вновь определяют область Λ_{3КОР УСК} - выигрыш в определении местоположения после третьего навигационного измерения, при этом коррекция происходит по значениям ускорений, а в качестве исходной для прогнозирования принимается область Λ′_2КОР (p(0,95)) - уже скорректированного объема пространства возможного местоположения объекта в момент второго навигационного измерения;
на основании закона распределения случайной величины - погрешности навигационных измерений - определяют область пространства Λ′_{3КОР УСК} (p(0,95)) с вероятностью не менее 0,95, при этом Λ′_{3КОР УСК} (p(0,95)) находится внутри объема пространства Λ₃;
определяют пересечение объемов пространства найденных скорректированных объемов пространства местоположения объекта Λ′_3КОР (p(0,95)) с Λ′_{3КОР УСК} (p(0,95)), пространство пересечения указанных объемов Λ_{3КОР ОКОН} будет являться окончательным скорректированным положением объекта в момент времени t₃;
далее, на основании закона распределения случайной величины - погрешности навигационных измерений - определяют область пространства Λ′_{3КОР ОКОН} (p(0,95)) с вероятностью не менее 0,95, при этом Λ′_{3КОР ОКОН} (p(0,95)) находится внутри объема пространства Λ₃, и для области пространства третьего измерения получают значения диапазона индексов координат x; y; z (i…j; r…p; q…f), входящих в пространство окончательно скорректированного положения объекта в момент времени t₃ Λ′_{3КОР ОКОН} (p(0,95)):

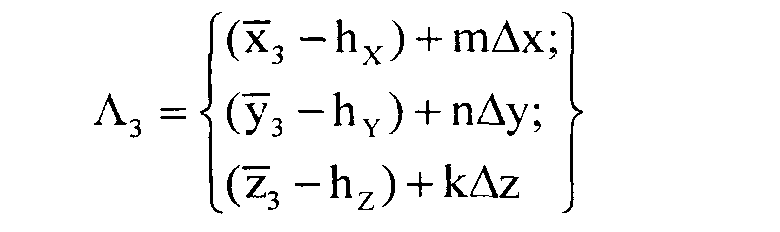
m=i…j - диапазон индексов координаты x, входящих в пространство Λ′_{3КОР ОКОН};
n=r…p - диапазон индексов координаты y, входящих в пространство Λ′_{3КОР ОКОН};
k=q…f - диапазон индексов координаты z, входящих в пространство Λ′_{3КОР ОКОН},
в качестве конечного результата местоположения объекта в пространстве с вероятностью не менее p(0,95) считают геометрическую середину скорректированной области пространства Λ′_{3КОР ОКОН} со скорректированными координатами x_(j-i)/2; y_(p-r)/2; z_(f-q)/2.